Open Access Article
Open Access ArticleA unique trimeric triphenylene radical cation: stacking aggregation, bonding, and stability†
Rameswar
Bhattacharjee
 a,
Megan E.
McCormack
b,
Zheng
Zhou
a,
Megan E.
McCormack
b,
Zheng
Zhou
 bc,
Zheng
Wei
bc,
Zheng
Wei
 b,
Marina A.
Petrukhina
b,
Marina A.
Petrukhina
 *b and
Miklos
Kertesz
*b and
Miklos
Kertesz
 *a
*a
aDepartment of Chemistry and Institute of Soft Matter, Georgetown University, 37th and O Streets, NW, Washington, DC 20057-1227, USA. E-mail: kertesz@georgetown.edu
bDepartment of Chemistry, University at Albany, State University of New York, 1400 Washington Avenue, Albany, NY 12222, USA. E-mail: mpetrukhina@albany.edu
cSchool of Materials Science and Engineering, Tongji University, 4800 Cao'an Road, Shanghai 201804, China
First published on 27th August 2024
Abstract
A new and unique π-stacking triphenylene trimer cation radical unit appears in the crystal structure of a newly synthesized salt with an oligomeric gallium(III) chloride, [(C18H12)3]˙+(Ga3Cl10)−, which is the first triphenylene aggregate observed. The structure is attributed to a shared electron distributed over the trimer displaying π-stacking pancake bonding. Computational modeling rationalizes the appearance of a “chain-shaped” rather than a “star-shaped” gallium chloride anion as well as the reasons why the trimer, rather than a radical cation aggregate of different size, is preferred in this system. Moreover, the calculations allowed evaluation of larger cationic triphenylene radical π-stacked aggregates. Additional stabilization due to the shared single unpaired electron is calculated to remain significant at 5–7 kcal mol−1 for aggregates as large as 5–6 units.
1. Introduction
The aggregation of π-conjugated molecules in a parallel face-to-face π-stacking configuration is at the basis of many of their important functions including transport of electrons and spins,1–4 excitons,5 and their chemical reactivity in supramolecular chemistry.6 A particularly interesting subclass contains units that can be formally identified as radicals,7 with the radical electrons delocalized over more than one π-conjugated molecule.3,8–11 A variety of aggregate sizes occur in these systems, from dimers (n = 2) to trimers (n = 3), to infinite π-stacked chains.1–3,12 However, the preference for certain aggregate sizes, as well as their electronic structures and bonding, still remains poorly understood. Aggregation into a stacking configuration is most commonly attributed to van der Waals interactions (here we use the term to include dispersion, electrostatics, and steric repulsion interactions), resulting in familiar atom-over-bond or atom-over-ring configurations, as often illustrated by the stacking of base pairs in DNA.13 A less common type displays atom-over-atom maximally overlapping π-stacking with short direct intermolecular contacts.14 This configuration provides an effective overlap that dominates certain physical properties, such as electron and spin transport. Such intermolecular interactions have been recognized as an electron-sharing multicenter covalent-like bond, a “pancake bond” for short, connecting these π-conjugated molecules, where the intermolecular distances are shorter than the respective vdW contact distances.15 This intermolecular electron sharing is a consequence of the unpaired electrons contained in the delocalized π-system in contrast to closed shells, which interact via weak vdW interactions only. The multicenter electron sharing is often described by an intermolecular formal bond order (FBO). For the discussions in this work, this is defined as:| FBO = no. of intermol. bonding electron pairs − no. of intermol. antibonding electron pairs | (1) |
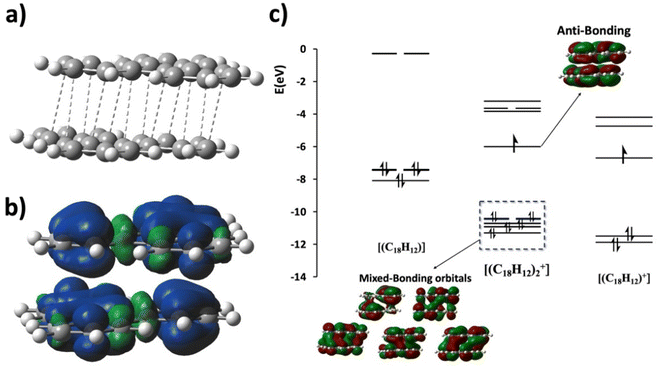
For example, using the classic example of the phenalenyl radical dimer, FBO = 1 (Fig. 1a; see the ESI† for BO calculations). There are more complex situations of pancake bonding, where the atom-over-atom overlap is not perfect because the maximum overlap is not possible due to lower symmetry and other factors such as side groups and crystal packing. Many highly conducting organic crystals are charge transfer salts that contain pancake bonding between well overlapping π-conjugated molecules with an FBO that is less than 1.0. Another class of highly conducting organics, Haddon's spiro-PLY materials,3 have an FBO = 0.5. It adds to the interest in pancake bonding, that cases with double (FBO = 2)18 and even triple (FBO = 3)19 pancake bonds are mentioned in the literature. The majority of pancake bonded dimers and other pancake-bonded aggregates occur in charged and not in neutral radicals.2,3,12
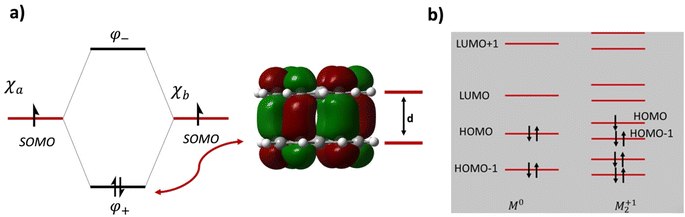 | ||
| Fig. 1 (a) Molecular orbital diagram and the intermolecular bonding orbital of the prototypical phenalenyl (PLY) dimer with an intermolecular formal bond order of FBO = 1. d is the equilibrium π-stacking bond distance. The intermolecular bonding electron pair originates from the electrons in the singly occupied molecular orbitals (SOMOs) of the PLY radicals. (b) Molecular orbital diagram of a generic M21+ dimer with an intermolecular formal bond order of FBO = 0.5. Note that the HOMO of the dimer is antibonding in the intermolecular sense and it is the HOMO−1 that provides the driving force for pancake bonding. This figure is partially adapted from ref. 15–17. | ||
Using a combination of crystallographic and theoretical tools, we recently revealed the importance of pancake bonding and cation–anion interactions in stabilizing pyrene and perylene radical dimers.8,17,20 Although a wealth of research has been done on TCNQ and other conjugated π-stacking materials,1–4 investigations of polycyclic aromatic hydrocarbons (PAHs) with different symmetries and sizes still remain limited. Even considering such a typical small PAH as triphenylene (TP, C18H12), where the formation of the TP cation has been previously documented, we found a lack of crystallographic structural evidence in the literature. The first detection of a cationic radical of triphenylene was made in 1965, using in situ electron paramagnetic resonance (EPR) during chemical oxidation.21 Later, in 1988, another EPR study in solution further confirmed the formation of the radical cations, also achieved by chemical oxidation.22 Moreover, in 1980, electrochemical oxidation led to the formation of two conducting solids, [(C18H12)x]˙+(PF6−) and [(C18H12)x]˙+(AsF6−), with ESR signals supporting the existence of radical species with unknown stoichiometry.23 Besides direct oxidation, the triphenylene radical cation has also been identified through hydrogen-atom abstraction and ionization,24,25 but, to the best of our knowledge, no crystal structures have been reported for the oxidized TP products.
After demonstrating the effect of alkali metal counterions on magnetic interactions between the triphenylene anion radicals in crystalline solids,26 we set out to explore triphenylene oxidation in this work. Using a chemical reaction of triphenylene with GaCl3, we isolated a unique product and confirmed its composition as [(C18H12)3]˙+(Ga3Cl10)− through X-ray diffraction analysis. This first triphenylene trimer radical cation was then used for advancing our understanding of bonding, the stability of π-stacking and the preference for certain aggregate sizes with the help of theoretical tools. Using well-established and validated versions of density functional theory (see the ESI† for more details), we considered periodic boundary computations on the crystal and molecular orbital computations on isolated molecules and π-stacked aggregates. In order to get deeper insights, we considered a number of factors, namely charge and spin distributions within the stacks and in the crystal, binding energies, structural features and their relationships with the relevant frontier orbitals, reduction and oxidation potentials, and preferred configurations of both cations and anions.
2. Results and discussion
2.1. Preparation and characterization of [(C18H12)3]˙+(Ga3Cl10)−
In this work, we investigated the chemical oxidation of triphenylene (TP) with GaCl3 in anhydrous fluorobenzene. Mixing these reagents in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 ratio at room temperature afforded a bright pink solution within two minutes. Subsequent slow evaporation of this solution over two weeks at 40 °C produced dark purple blocks suitable for X-ray diffraction analysis (see the ESI† for more details). X-ray diffraction analysis confirmed that crystals conform to a monoclinic P21 (Z = 2) space group with a volume of 2507.1(4) Å3 and revealed the product composition as [(C18H12)3]˙+(Ga3Cl10)− with no solvent incorporation. In the crystal structure, there are three crystallographically independent TP molecules with an overall positive charge for each Ga3Cl10− anion (Fig. 2a and b).
1.5 ratio at room temperature afforded a bright pink solution within two minutes. Subsequent slow evaporation of this solution over two weeks at 40 °C produced dark purple blocks suitable for X-ray diffraction analysis (see the ESI† for more details). X-ray diffraction analysis confirmed that crystals conform to a monoclinic P21 (Z = 2) space group with a volume of 2507.1(4) Å3 and revealed the product composition as [(C18H12)3]˙+(Ga3Cl10)− with no solvent incorporation. In the crystal structure, there are three crystallographically independent TP molecules with an overall positive charge for each Ga3Cl10− anion (Fig. 2a and b).
In the solid state, three TPs (designated as A, B, and C) are π-stacked with short interplanar distances ranging over 3.293(5)–3.371(5) Å in a face-to-face arrangement with high surface overlap. Within the TP stacks, the middle molecule is related to the top and bottom neighbors via inversion symmetry operations through two local inversion centers (Fig. S4†). The neighboring TP stacks are nearly perpendicular to each other (89.88°) and exhibit weak C–H⋯π interactions (2.871(5)–2.899(5) Å) to form a 2D network (Fig. 2d).
Each triphenylene in the trimer exhibits different H⋯Cl bonding interactions with the anionic moiety (Fig. S6†). Specifically, triphenylene C shows more H⋯Cl contacts with the Ga3Cl10− anion in comparison with A and B. Despite this, the central triphenylene B experienced the most significant core deformation, as evidenced by C–C bond length distances (Table S2†). Some bonds, such as c, e, and k, exhibit more notable contraction (0.041 Å, 0.034 Å, and 0.035 Å, respectively), while bonds i, j, and l show significant elongation (0.071 Å, 0.072 Å, and 0.033 Å, respectively). However, triphenylene A demonstrates the most significant deviation in dihedral angles, suggesting a slight loss of planarity compared to neutral triphenylene (Table S3†).
Interestingly, the gallium(III) chloride anion, Ga3Cl10−, in this charge transfer salt exhibits a “chain-shaped”27 rather than a “star-shaped” configuration.28 The preference of the former over the latter is discussed and rationalized below in the theory section.
In addition to single crystal X-ray diffraction, further product characterization was performed through electron paramagnetic resonance (EPR) spectroscopy (Fig. 3), UV-vis spectroscopy (Fig. S7†), powder X-ray diffraction (Fig. S8†), and ATR-IR spectroscopy (Fig. S9†). The EPR spectra were collected on the crystalline samples of [(C18H12)3]˙+(Ga3Cl10)− (Fig. 3), showing a g-factor of 2.0031 and confirming the presence of organic-based radicals in the product (see the ESI† for the details). The presence of unpaired electrons is essential for understanding the special aggregation mechanism via pancake bonding, as discussed in the next section.
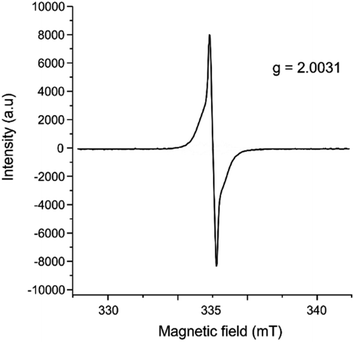 | ||
| Fig. 3 EPR spectrum of crystalline [(C18H12)3]˙+(Ga3Cl10)−, collected at 31.9 °C on a LINEV ADANI Spinscan X Electron Paramagnetic Resonance Spectrometer. | ||
2.2. Computational investigation
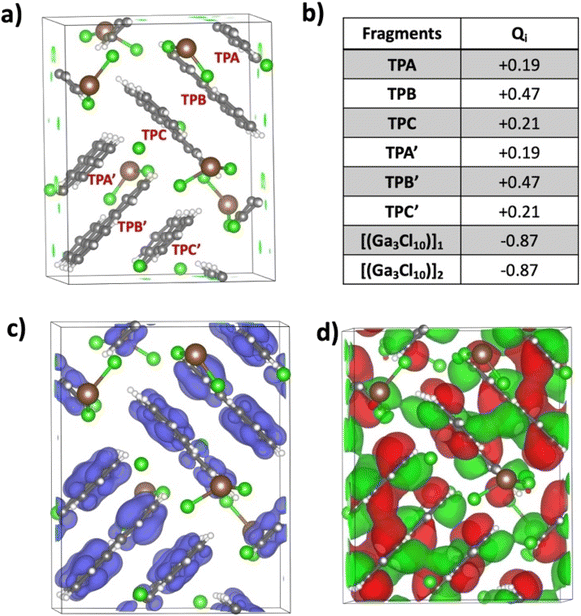
Pancake bonding plays a central role in unraveling the structural features and preferences to be discussed next. The consequence of pancake bonding is an atom-over-atom geometry and a shorter than vdW packing with a partial covalent character. Two measures of interaction energies, the total interaction energy (ΔEint,nq, eqn (S1) in the ESI†) and the average interaction energy per pair (ΔEpairq, eqn (S2) in the ESI†), are discussed. In addition, the charge distribution among the different TP units provides further insights, which is the starting point of the computational analysis. Fig. 4a illustrates the unit cell of the crystal structure of [(C18H12)3]˙+(Ga3Cl10)−, containing two formula units and consisting of six TP units organized into two isolated trimers, each carrying a +1 charge. The crystal's charge neutrality is achieved through the inclusion of two “chain-shaped” Ga3Cl10− counterions within the unit cell. The charge analysis indicates that the q = +2 charge is distributed among the two TP trimers, each carrying a Q = +1 charge. This charge is unevenly distributed within one trimer across three TP units. Specifically, the central triphenylene (TP-B/TP-B′) holds the most significant positive charge of +0.47, while the charges on the terminal units (TP-A/TP-A′ and TP-C/TP-C′) are +0.21 and +0.19, respectively. Note that the small difference between the two terminal charges is due to the lack of symmetry in the crystal structure, in contrast to the charge distribution in the isolated trimer, as discussed below. Fig. 4b presents the computed charges for each TP within the unit cell. Correspondingly, the spin density plot shown in Fig. 4c corroborates the Bader charge analysis, indicating that the middle TP unit possesses the highest spin density, and thus the greatest positive charge, compared to the two terminal units. Additionally, analysis of the HOMO−1 of the unit cell reveals significant intermolecular orbital overlap, indicating the presence of pancake bonding within the trimer. We focused on the HOMO−1 because it plays a crucial role in the properties of a +1-charged perylene dimer in our earlier studies.17,20The crystal structure underscored the distinct formation of a trimeric TP aggregate, prompting a thorough exploration of its bonding and underlying formation mechanism. To this end, we evaluated the free energy (ΔG) required for a one-electron reduction of the chain-shaped Ga3Cl10−, which was found to be −166.2 kcal mol−1. This energy threshold sets the limit for oxidizing species with an oxidation free energy that is lower than this value. Fig. 5a presents the calculated free energies of oxidation for triphenylene in its monomeric, dimeric, and trimeric forms. Specifically, the oxidation of the monomer [(C18H12)] and the dimer [(C18H12)2] would require 179.1 kcal mol−1 and 169.8 kcal mol−1 respectively, making oxidation by the chain-shaped Ga3Cl10− anion not viable due to the resulting positive, non-spontaneous reaction free energies. However, the situation differs for the trimer [(C18H12)3], where the oxidation energy is 162.7 kcal mol−1, 3.5 kcal mol−1 less than the reduction free energy of the Ga3Cl10− chain. This permits the oxidation of the trimer by the chain-shaped Ga3Cl10−, rendering the overall reaction and the formation of [(C18H12)3]˙+(Ga3Cl10)− energetically favorable and exergonic by 3.5 kcal mol−1.
A star-shaped isomer of Ga3Cl10− has been described in the literature.27,28 Why is the chain structure favored in the title crystal structure over the “star-shaped” one? According to the computational modeling presented in Fig. 5a, the reduction is strongly preferred by the chain-shaped Ga3Cl10−, which is indeed the observed configuration in the crystal. Further details on both types of Ga3Cl10− are provided in the ESI (see Scheme S2†). It is crucial to recognize that while Madelung (electrostatic, Coulomb) energy significantly contributes to the stability of an ionic crystal, it predominates only after the crystal forms and the ions are appropriately arranged in the crystal phase. This analysis not only justifies our use of the chain variant of Ga3Cl10− but also elucidates why the trimeric TP cluster preferentially forms under the experimental conditions.
In the following, we address the nature of intermolecular electron sharing by discussing the computational modeling of different-size TP aggregates all with q = +1 charge (see eqn S(3)†). We begin with the n = 3, [(C18H12)3]+, trimer, followed by other π-stacked aggregates. This investigation primarily focused on delineating the strength of the interactions among TPs within the trimer and other aggregates. The total interaction energy among the triphenylene units in the trimer is computed to be −44.1 kcal mol−1. This is a relatively high interaction energy compared to the typical van der Waals interaction energy and we show that it is due to pancake bonding (PCB).29 PCB is distinguished by its robust, directionally specific nature, arising from atom-over-atom overlaps, which play a pivotal role in stabilizing radical-containing PAH systems.11,15,17,30 In the optimized trimer, 24 short C⋯C contacts were identified with an average interplanar distance (dav, see eqn (3) in the ESI†) of 3.29 Å, noticeably below the van der Waals contact distance of 3.40 Å, another feature of pancake bonding. Both the top and side views of the optimized structures of [(C18H12)3]+ are depicted in Fig. 6a and b, respectively. Charge distribution within the trimer revealed an uneven yet symmetric charge distribution: the central TP possesses a charge of +0.62e, with each terminal TP unit carrying +0.19e. This pattern aligns with the Bader charge distribution previously computed for the unit cell. To further validate this uneven charge distribution in the trimer, additional popular charge analyses—NPA,31 Mulliken, and Hirshfeld32—were conducted, with the results summarized in Table S5.† Additionally, the spin density plot, shown in Fig. 6c, also supports the observation of the uneven charge distribution across the trimer.
Orbital analysis further reveals that the SOMO of the trimer exhibits antibonding characteristics, and three occupied orbitals demonstrate significant intermolecular bonding interactions, as illustrated in Fig. 6e, indicating the characteristic pancake bonding within the trimer.
Although the trimeric aggregate was the focus of our experimental observations, altering experimental conditions in the [(C18H12)n]+ series may potentially enable the isolation of other types as well. Understanding the nature of interactions among TP molecules within these aggregates is crucial for exploring their properties and potential applications. The simplest aggregate, the dimer, is next, followed by larger aggregates. In all cases q = +1 overall charge is assumed. We follow how the unpaired electron generates a variety of pancake-bonded structures, and how this effect diminishes as n is increased up to n = 6.
The average interplanar distance (dav) in the [(C18H12)2]+ dimer is computed to be 3.26 Å, suggesting the involvement of interactions beyond van der Waals forces. As depicted in Fig. 7a, twelve C⋯C short contacts ranging from 3.23 Å to 3.30 Å were identified. Orbital analysis revealed the antibonding nature of the SOMO and a series of occupied orbitals demonstrating bonding (in-phase) intermolecular orbital overlap, confirming the presence of pancake bonding (PCB), as depicted in the MO diagram in Fig. 7c. An FBO value of 1/2 can be deduced from this MO diagram. The interaction energy between TP molecules in the dimer is calculated to be −24.6 kcal mol−1, significantly larger than typical van der Waals values. In comparison, we note that the experimentally determined binding energy in the benzene cation dimer is ΔH = 17.6 kcal mol−1,33 significantly larger than the vdW binding energy. Moreover, the equal charge distribution of the q = +1 charge (+0.5 e on each TP) and consistent symmetrical spin density distribution (Fig. 7b) across the dimer underscore the delocalization of the unpaired electron and validate the interpretation of this bonding as a PCB interaction. We note parenthetically that employing the same DFT and basis set of (U)M05-2X/6-311G(d), we obtained ΔHbinding = 18.9 kcal mol−1 for [(C6H6)2]+, which is in very good agreement with the experimental value33 of 17.6 kcal mol−1, in line with our earlier validation study providing strong support to use this level of theory for pancake bonding of PAHs.34
We analyze the pancake bonding in the [(C18H12)n]+ aggregate series in terms of the intermolecular packing and charge distribution first, and then turn to the interaction energies. Fig. 8 summarizes how the additional q = +1 charge is delocalized over the constituent TPs and shows the average interplanar distances (dav). The respective FBO value remains 1/2 as per eqn (1), although this bond order is distributed among n − 1 intermolecular contacts. As noted earlier, in the dimer, each triphenylene uniformly carries the total +1 charge, while in the trimer, an uneven but symmetrical charge distribution is evident. In the tetramer, the charge distribution remains symmetrical but unequal: the two central TP units bear +0.40e charge each, and the terminal molecules each have +0.10e. Our observations indicate that the charges on the terminal TPs diminish as the column length increases, disappearing almost entirely beyond n = 4. As shown in the last two images for n = 5 and 6, the charge distribution among the central TP units remains symmetrical, and the two terminal TP units are neutral. Thus, the influence of the +1 charge does not extend significantly beyond n = 4.
The average interplanar distances (dav) also show an interesting pattern. For the dimer and trimer, the values are significantly below the vdW distance of 3.4 Å in concordance with PCBs. The picture changes for n > 3. Already at n = 4 only the central dav remains significantly below 3.4 Å, while the two terminal dav values approach 3.4 Å. This trend continues as n increases, and for n = 6 the terminal dav values are nearly 3.4 Å. At the same time, the central dav values also decrease. These trends suggest that for larger n the two terminal TPs are attached to the rest of the aggregate by an interaction not very different from ordinary vdW, without the assistance of PCB. At the same time, the single unpaired electron that is available for PCB is being diluted, and all dav values gradually approach the vdW value. Is the analysis of the energetics showing the same trends?
The computational method section describes the approach for calculating the total interaction energy (ΔEint,nq) between triphenylene molecules in stacked columns, as shown in eqn (S1) in the ESI.† Those interaction energies for both mono-cationic and neutral aggregates are detailed in Table 1. The interaction energy differences between the charged and neutral aggregates are denoted as ΔEint,nq=+1 and ΔEint,nq=0, respectively. This key difference highlights that the presence of a +1 charge favors the aggregation with stronger cohesion within the TP π-stacks due to pancake bonding. While the attachment of the second TP is smaller than the first (−22.1 vs. −24.6 kcal mol−1), it is still a remarkably strong bonding interaction. A similar effect has been observed on the heteromolecular attachment of the second benzene molecule to a naphthalene +1 cation vs. the attachment of the first, both with essentially the same ∼8 kcal mol−1.35
| TP column | ΔEint,nq=+1 | ΔEint,nq=0 | ΔEpairq=+1 | ΔEpairq=0 |
|---|---|---|---|---|
| [(C18H12)2]q | −24.6 | −12.7 | −24.6 | −12.7 |
| [(C18H12)3]q | −44.1 | −24.6 | −22.1 | −12.3 |
| [(C18H12)4]q | −60.5 | −36.2 | −20.2 | −12.1 |
| [(C18H12)5]q | −75.0 | −47.8 | −18.7 | −11.9 |
| [(C18H12)6]q | −88.2 | −59.5 | −17.6 | −11.9 |
The dependency of these interaction energies on the number of triphenylenes (n) in the π-stacking aggregate is illustrated in Fig. 9a. For neutral stacks, the plot of ΔEint,nqversus n is perfectly linear, with an R2 value of 1.0. In contrast, the energy relationship for stacks carrying a +1 charge displays a slightly nonlinear trend and a steeper slope for small n values. The absolute difference becomes more pronounced as n increases, likely due to a larger number of close carbon–carbon (C⋯C) contacts as more triphenylenes are added to the column.
 | ||
| Fig. 9 (a) The variation of total interaction energy (ΔEint,nq) as a function of the number of triphenylenes (n) in the stacked column in the [(C18H12)n]q series. (b) Variation in interaction energy (ΔEnq), eqn (1). Red marks represent the mono-cationic cluster (q = +1), and black marks denote the corresponding neutral cluster (q = 0). | ||
To compute the average interaction energy per pair (ΔEpairq) of triphenylene molecules in a π-stacked column, we introduced an extension of eqn (S1),† defined as eqn (S2) in the ESI section.† The values for ΔEpairq are also listed in Table 1, showing that the average interaction energy remains relatively constant for neutral stacks. In contrast, for mono-cationic stacks, this value decreases gradually from −24.6 kcal mol−1 for the dimer to −17.6 kcal mol−1 for the hexamer. This analysis confirms that the additional positive charge significantly influences the structural stability within the stacks.
We further explored the interaction energy, denoted as ΔEnq, involved in sequentially adding one neutral TP ring to the complex [(C18H12)n−1]q to form [(C18H12)n]q. This measure provides an estimate of the affinity of [(C18H12)n−1]q to incorporate another TP unit into the column. This interaction energy is calculated using the following equation:
| ΔEnq = E[(C18H12)nq] − E[(C18H12)n−1q] − E[(C18H12)]1 | (2) |
The higher negative value of ΔEnq=+1 at any given 1/n suggests a stronger tendency for [(C18H12)n−1]+1 to attract another TP. The steeper slope of −34.11 in the plot (depicted by a black line through red data points in Fig. 9b) indicates that the affinity for adsorbing an additional neutral TP onto the mono-cationic [(C18H12)n−1]+1 aggregate decreases sharply as 1/n decreases (cf. Fig. S10†). This phenomenon is largely due to the presence of PCB, which is more effective when there is a higher concentration of unpaired electron density among the TPs. As the number of TPs increases, this effect diminishes since the electron density becomes more distributed. However, and this is one of the key results here, for aggregates as large as n = 3 or 4, there is still substantial pancake bonding present, driving the formation of the aggregates.
Several studies demonstrated the impact of fractional charges on bond length alternation (BLA),36 a key indicator of conjugation patterns in π-electron systems.8,17,37 This effect is also observed in triphenylene, as illustrated in Fig. S11.† In its neutral state, triphenylene exhibits a high degree of symmetry of the D3h point group. However, when the charge is increased to +1, the symmetry decreases to Cs. Another structure of TP+, belonging to the C2v point group, is nearly energetically equivalent to the Cs form and exhibits a minimal imaginary mode frequency of 15 cm−1. This symmetry reduction is primarily due to Jahn–Teller (JT) distortion, a phenomenon previously discussed in depth by Keszthelyi et al.38 As a result of JT distortion, the C–C bond lengths in the +1 charged triphenylene become uneven: some bonds elongate while others shorten, as shown in Fig. S11d,† when compared to the symmetric neutral state in Fig. S11a.† The triphenylene molecule with a fractional charge (Q) of +0.5 also exhibits Cs symmetry, akin to the fully +1 charged state, but with variations in the degree of bond elongation and compression, as depicted in Fig. S11c.† The structures of the other triphenylenes with different fractional charges are also provided in Fig. S12.† It is important to note that when discussing fractional charges (Qi), the resulting structure does not represent a true minimum of a single TP but rather is part of an aggregate.
To better understand the structural changes in triphenylene as its charge (Q) varies, we employed the harmonic oscillator model of aromaticity (HOMA),39 a geometry-based aromaticity index, for triphenylene with various fractional charges (Fig. S12†). Triphenylene features two types of six-membered rings: one central and three peripheral rings. The central ring in triphenylene is less aromatic compared to the peripheral ones and as noted by Krygowski and Szatylowicz,40 the lower aromaticity of the central TP ring correlates with higher bond length alternation (BLA) values. This ring is referred to as the ‘empty’ ring in Clar's classification system, which signifies a deficit of π-electrons.41 However, our analysis reveals that increasing the fractional charge on triphenylene slightly enhances the aromaticity of the central ring. Conversely, the peripheral rings exhibit a decrease in aromaticity with increasing positive charge, although this effect is less pronounced.
3. Conclusions
In this work, we report a unique triphenylene salt, wherein chemical oxidation of triphenylene with GaCl3 and subsequent crystallization confirmed the formation of [(C18H12)3]˙+(Ga3Cl10)− through X-ray diffraction analysis. Structural analysis revealed unusual trimers of TP units showing a face-to-face arrangement, sufficient surface overlap, and interplanar distances ranging from 3.293(5) to 3.371(5) Å. In the solid state, an extended 2D-network is formed through weak C–H⋯π interactions between neighboring TP trimers and H⋯Cl contacts with a unique “chain-shaped” Ga3Cl10− anion. The presence of unpaired electrons is confirmed by EPR (g = 2.0031) and these are key to the special aggregation mechanism provided by the sharing of this unpaired electron among the trimeric TP units in pancake bonding.According to the computational analysis, the “chain-shaped” Ga3Cl10− isomer as the counter anion is preferred over the “star-shaped” isomer. Notably, the findings suggest that the smallest energetically favorable configuration for a singly positively charged TP stack, when paired with a Ga3Cl10− chain as the counter anion, is a trimer, identified as [(C18H12)3]+, and this aggregate is indeed the form found experimentally.
We identified pancake bonding interactions within the trimeric TP aggregate, as well as in other aggregates with varying numbers of π-stacked TP units. For comparison, the binding energy between TPs in the dimer, [(C18H12)2]+, is calculated to be 11.9 kcal mol−1 higher than that of its neutral counterpart, indicating a robust pancake bonding interaction. In the trimer, this pancake bonding interaction is slightly weaker, attributed to the distribution of a single electron among three TP units, as opposed to two. As a general pattern, the strength of the pancake bonding interaction diminishes as the number of TP units in the stack increases. However, additional interaction energy due to pancake bonding remains significant even in the pentamer and the hexamer of TP. This additional interaction energy is available to stabilize larger aggregates than would be otherwise available for closed-shell neutral PAHs. This type of aggregation promoted by unpaired electrons in radicals has been proposed as a possible mechanism in the formation of naturally occurring PAH asphaltene aggregates.42
The preferred size of the aggregate is affected by a number of factors, and any discussion is, by necessity, only qualitative. Nevertheless, important insights and trends can be obtained. The synergy of π-stacking aggregation in the vicinity of a cation or anion has been shown to be a rather general phenomenon.6,43 We point out in the presented work that in the context of a specific anion, the aggregation attains an optimum size due to a diminishing synergistic energy gain limiting the growth of the aggregate on the one hand, and a minimum size that ensures favorable ΔG for oxidation–reduction necessary to achieve charge transfer that allows multicenter pancake bonding to occur.
By considering π-stacked aggregates with increasing sizes, several interesting trends have been revealed. The charge distribution is uniform in the dimer but it becomes uneven yet symmetrical in larger clusters. As the size is increased, the terminal units share less and less of the additional single charge, while the rest of the charge is distributed more and more evenly over the π-stacked TP aggregate. The per unit charge therefore overall decreases with increasing size, and this dilution of the pancake bonding effect reduces the relative energy stabilization gained by each additional TP molecule. Still, the additional stabilization energy remains substantial, as large as 5–7 kcal mol−1 for aggregates as large as 5–6 units. It is likely that with an appropriate choice of counterion and PAH combination, a number of such aggregates will be discovered. Therefore, the new findings of this work should pave the way for future experimental discoveries in this field.
Data availability
Synthetic procedures, UV-vis and IR spectra, powder X-ray diffraction data, X-ray crystallographic data, and computational details are included in the ESI.†Author contributions
R. B. and M. E. M. contributed equally. Z. Z. first synthesized the product, and M. E. M. optimized the synthesis, improved the crystal structure, and completed product characterization and data analysis. X-ray diffraction experiments and refinements were performed by Z. W. R. B. carried out all calculations and wrote the first draft. M. A. P. and M. K. supervised this project and secured the funding.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support from the U.S. National Science Foundation for this research to M. A. P. (CHE-2404031) and to M. K. (CHE-2107820) is gratefully acknowledged.References
- J. Ferraris, D. Cowan, V. t. Walatka and J. Perlstein, Electron transfer in a new highly conducting donor-acceptor complex, J. Am. Chem. Soc., 1973, 95(3), 948–949 CrossRef CAS.
- A. Heeger, Charge-Density Wave Phenomena in One-Dimensional Metals: TTF-TCNQ and Related Organic Conductors, in Highly conducting one-dimensional solids, Springer, 1979; pp. pp. 69–145 Search PubMed.
- S. Pal, M. Itkis, F. Tham, R. Reed, R. Oakley and R. Haddon, Resonating valence-bond ground state in a phenalenyl-based neutral radical conductor, Science, 2005, 309(5732), 281–284 CrossRef CAS.
- A. Shimizu, T. Kubo, M. Uruichi, K. Yakushi, M. Nakano, D. Shiomi, K. Sato, T. Takui, Y. Hirao and K. Matsumoto, Alternating covalent bonding interactions in a one-dimensional chain of a phenalenyl-based singlet biradical molecule having Kekulé structures, J. Am. Chem. Soc., 2010, 132(41), 14421–14428 CrossRef CAS.
- X.-H. Jin, M. B. Price, J. R. Finnegan, C. E. Boott, J. M. Richter, A. Rao, S. M. Menke, R. H. Friend, G. R. Whittell and I. Manners, Long-range exciton transport in conjugated polymer nanofibers prepared by seeded growth, Science, 2018, 360(6391), 897–900 CrossRef CAS PubMed.
- A.-B. Bornhof, A. Bauzá, A. Aster, M. Pupier, A. Frontera, E. Vauthey, N. Sakai and S. Matile, Synergistic Anion–(π)n–π Catalysis on π-Stacked Foldamers, J. Am. Chem. Soc., 2018, 140(14), 4884–4892 CrossRef CAS.
- V. Enkelmann, K. Göckelmann, G. Wieners and M. Monkenbusch, Radical Cation Salts of Arenes. Structure, Properties and Model Character for Conducting Polymers, Mol. Cryst. Liq. Cryst., 1985, 120(1), 195–204 CrossRef CAS.
- C. Flynn, Z. Zhou, M. E. McCormack, Z. Wei, M. A. Petrukhina and M. Kertesz, Bonding and uneven charge distribution in infinite pyrene pi-stacks, CrystEngComm, 2022, 24(32), 5757–5766, 10.1039/d2ce00933a.
- Z. Mou and M. Kertesz, Pancake Bond Orders of a Series of π-Stacked Triangulene Radicals, Angew. Chem., Int. Ed., 2017, 56(34), 10188–10191 CrossRef CAS.
- K. Molčanov, C. Jelsch, B. Landeros, J. Hernández-Trujillo, E. Wenger, V. Stilinović, B. Kojić-Prodić and E. C. Escudero-Adán, Partially Covalent Two-Electron/Multicentric Bonding between Semiquinone Radicals, Cryst. Growth Des., 2019, 19(1), 391–402, DOI:10.1021/acs.cgd.8b01484.
- K. E. Preuss, Pancake bonds: π-stacked dimers of organic and light-atom radicals, Polyhedron, 2014, 79, 1–15 CrossRef CAS.
- F. H. Herbstein and M. Kapon, Classification of closed shell TCNQ salts into structural families and comparison of diffraction and spectroscopic methods of assigning charge states to TCNQ moieties, Crystallogr. Rev., 2008, 14(1), 3–74 CrossRef CAS.
- C. R. Martinez and B. L. Iverson, Rethinking the term “pi-stacking”, Chem. Sci., 2012, 3(7), 2191–2201 RSC.
- T. Devic, M. Yuan, J. Adams, D. C. Fredrickson, S. Lee and D. Venkataraman, The maximin principle of π-radical packings, J. Am. Chem. Soc., 2005, 127(42), 14616–14627 CrossRef CAS.
- M. Kertesz, Pancake bonding: An unusual Pi-stacking interaction, Chem.–Eur. J., 2019, 25(2), 400–416 CrossRef CAS.
- Z.-h. Cui, A. Gupta, H. Lischka and M. Kertesz, Concave or convex π-dimers: the role of the pancake bond in substituted phenalenyl radical dimers, Phys. Chem. Chem. Phys., 2015, 17(37), 23963–23969 RSC.
- R. Bhattacharjee, H. Jervis, M. E. McCormack, M. A. Petrukhina and M. Kertesz, Structure and Bonding in π-Stacked Perylenes: The Impact of Charge on Pancake Bonding, J. Am. Chem. Soc., 2024, 146(15), 10465–10477, DOI:10.1021/jacs.3c14065.
- Z.-h. Cui, H. Lischka, H. Z. Beneberu and M. Kertesz, Double pancake bonds: Pushing the limits of strong π–π stacking interactions, J. Am. Chem. Soc., 2014, 136(37), 12958–12965 CrossRef CAS.
- L. Barluzzi, S. P. Ogilvie, A. B. Dalton, P. Kaden, R. Gericke, A. Mansikkamaki, S. R. Giblin and R. A. Layfield, Triply bonded pancake π-dimers stabilized by tetravalent actinides, J. Am. Chem. Soc., 2024, 146(6), 4234–4241 CrossRef CAS PubMed.
- M. E. McCormack, R. Bhattacharjee, H. Jervis, Z. Wei, M. Kertesz and M. A. Petrukhina, Stabilizing Cationic Perylene Dimers through Pancake Bonding and Equal Charge Share, Cryst. Growth Des., 2023, 23(10), 7496–7503, DOI:10.1021/acs.cgd.3c00912.
- I. C. Lewis and L. Singer, Electron spin resonance of radical cations produced by the oxidation of aromatic hydrocarbons with SbCl5, J. Chem. Phys., 1965, 43(8), 2712–2727 CrossRef CAS.
- J. L. Courtneidge, A. G. Davies and D. C. Mcguchan, The electron spin resonance spectra of the radical cations of p-terphenyl, triphenylene and triptycene, Recl. Trav. Chim. Pays-Bas, 1988, 107(3), 190–196 CrossRef CAS.
- C. Kröhnke, V. Enkelmann and G. Wegner, Radical Cation Salts of Simple Arenes—A New Family of “Organic Metals”, Angew. Chem., Int. Ed. Engl., 1980, 19(11), 912–919 CrossRef.
- A. Kira and M. Imamura, Absorption spectra of dimer cations and other cationic species produced by warming of. gamma.-irradiated glassy solutions of aromatic hydrocarbons, J. Phys. Chem., 1979, 83(17), 2267–2273 CrossRef CAS.
- V. Kofman, P. Sarre, R. Hibbins, I. Ten Kate and H. Linnartz, Laboratory spectroscopy and astronomical significance of the fully-benzenoid PAH triphenylene and its cation, Mol. Astrophys., 2017, 7, 19–26 CrossRef.
- Z. Zhou, O. Ungor, Z. Wei, M. Shatruk, A. Tsybizova, R. Gershoni-Poranne and M. A. Petrukhina, Tuning magnetic interactions between triphenylene radicals by variation of crystal packing in structures with alkali metal counterions, Inorg. Chem., 2021, 60(19), 14844–14853 CrossRef CAS PubMed.
- M. Gorlov, A. Fischer and L. Kloo, One-step synthesis of a platinum (0)-gallium(III) chrysene complex, Angew. Chem., Int. Ed., 2005, 44(25), 3906–3908 CrossRef CAS PubMed.
- D. Freudenmann and C. Feldmann, [Bi3GaS5]2[Ga3Cl10]2[GaCl4]2·S8 containing heterocubane-type [Bi3GaS5]2+, star-shaped [Ga3Cl10]−, monomeric [GaCl4]− and crown-like S8, Dalton Trans., 2011, 40(2), 452–456 RSC.
- R. S. Mulliken and W. B. Person, Molecular complexes: a lecture and reprint volume, 1969 Search PubMed.
- Z. Mou, K. Uchida, T. Kubo and M. Kertesz, Evidence of σ- and π-Dimerization in a Series of Phenalenyls, J. Am. Chem. Soc., 2014, 136(52), 18009–18022 CrossRef CAS.
- J. P. Foster and F. Weinhold, Natural hybrid orbitals, J. Am. Chem. Soc., 1980, 102(24), 7211–7218 CrossRef CAS.
- F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- M. Rusyniak, Y. Ibrahim, E. Alsharaeh, M. Meot-Ner and M. S. El-Shall, Mass-selected ion mobility studies of the isomerization of the benzene radical cation and binding energy of the benzene dimer cation. Separation of isomeric ions by dimer formation, J. Phys. Chem. A, 2003, 107(38), 7656–7666 CrossRef CAS.
- Z. Mou, Y.-H. Tian and M. Kertesz, Validation of density functionals for pancake-bonded π-dimers; dispersion is not enough, Phys. Chem. Chem. Phys., 2017, 19(36), 24761–24768 RSC.
- I. K. Attah, S. P. Platt, M. Meot-Ner, M. S. El-Shall, R. Peverati and M. Head-Gordon, What is the structure of the naphthalene–benzene heterodimer radical cation? Binding energy, charge delocalization, and unexpected charge-transfer interaction in stacked dimer and trimer radical cations, J. Phys. Chem. Lett., 2015, 6(7), 1111–1118 CrossRef CAS PubMed.
- T. J. Kistenmacher, T. E. Phillips and D. O. Cowan, The crystal structure of the 1:1 radical cation–radical anion salt of 2,2′-bis-l,3-dithiole (TTF) and 7,7,8,8-tetracyanoquinodimethane (TCNQ), Acta Crystallogr., 1974, 30(3), 763–768 CrossRef CAS.
- J. Poater, M. Duran and M. Solà, Aromaticity determines the relative stability of kinked vs. straight topologies in polycyclic aromatic hydrocarbons, Front. Chem., 2018, 6, 425890 Search PubMed.
- T. Keszthelyi, G. Balakrishnan, R. Wilbrandt, W. A. Yee and F. Negri, Evidence of Dynamical Jahn–Teller Effect on Triphenylene Radical Cation: Resonance Raman Spectrum and ab Initio Quantum-Chemical Calculations, J. Phys. Chem. A, 2000, 104(40), 9121–9129 CrossRef CAS.
- T. M. Krygowski, Crystallographic studies of inter-and intramolecular interactions reflected in aromatic character of. pi.-electron systems, J. Chem. Inf. Comput. Sci., 1993, 33(1), 70–78 CrossRef CAS.
- T. M. Krygowski and H. Szatylowicz, Aromaticity: what does it mean?, ChemTexts, 2015, 1, 1–10 CrossRef CAS.
- E. Clar and R. Schoental, Polycyclic hydrocarbons, Springer, 1964 Search PubMed.
- Y. L. Zhang, M. Siskin, M. R. Gray, C. C. Walters and R. P. Rodgers, Mechanisms of Asphaltene Aggregation: Puzzles and a New Hypothesis, Energy Fuels, 2020, 34(8), 9094–9107, DOI:10.1021/acs.energyfuels.0c01564.
- A. Frontera, D. Quiñonero, C. Garau, A. Costa, P. Ballester and P. M. Deyà, MP2 Study of Cation–(π)n–π Interactions (n = 1–4), J. Phys. Chem. A, 2006, 110(30), 9307–9309 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedure, UV-vis spectra, powder X-ray diffraction and X-ray crystallographic data, and computational details. CCDC 2361118. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc03774j |
| This journal is © The Royal Society of Chemistry 2024 |