Open Access Article
Open Access ArticlePILOT: equivariant diffusion for pocket-conditioned de novo ligand generation with multi-objective guidance via importance sampling†
Julian
Cremer
 *ac,
Tuan
Le
*ac,
Tuan
Le
 *ab,
Frank
Noé
bd,
Djork-Arné
Clevert
*ab,
Frank
Noé
bd,
Djork-Arné
Clevert
 a and
Kristof T.
Schütt
a and
Kristof T.
Schütt
 a
a
aMachine Learning & Computational Sciences, Pfizer Worldwide R&D, Berlin, Germany. E-mail: julian.cremer@pfizer.com; tuan.le@pfizer.com
bDepartment of Mathematics and Computer Science, Freie Universität Berlin, Germany
cComputational Science Laboratory, Universitat Pompeu Fabra, PRBB, Spain
dMicrosoft Research AI4Science, Microsoft, Berlin, Germany
First published on 20th August 2024
Abstract
The generation of ligands that both are tailored to a given protein pocket and exhibit a range of desired chemical properties is a major challenge in structure-based drug design. Here, we propose an in silico approach for the de novo generation of 3D ligand structures using the equivariant diffusion model PILOT, combining pocket conditioning with a large-scale pre-training and property guidance. Its multi-objective trajectory-based importance sampling strategy is designed to direct the model towards molecules that not only exhibit desired characteristics such as increased binding affinity for a given protein pocket but also maintains high synthetic accessibility. This ensures the practicality of sampled molecules, thus maximizing their potential for the drug discovery pipeline. PILOT significantly outperforms existing methods across various metrics on the common benchmark dataset CrossDocked2020. Moreover, we employ PILOT to generate novel ligands for unseen protein pockets from the Kinodata-3D dataset, which encompasses a substantial portion of the human kinome. The generated structures exhibit predicted IC50 values indicative of potent biological activity, which highlights the potential of PILOT as a powerful tool for structure-based drug design.
1 Introduction
Structure-based drug discovery (SBDD) has fundamentally transformed the landscape of drug development by facilitating the design of molecules that precisely target biological macromolecules, such as proteins, which play a critical role in disease processes. These designed molecules interact with a specific pocket of a target protein, either activating or inhibiting its function, thus influencing the disease pathway. This strategy is underpinned by a detailed understanding of the 3D structure of the target, usually acquired through X-ray crystallography or nuclear magnetic resonance (NMR) spectroscopy.1,2 By grasping the structural intricacies of the target protein, researchers are equipped to create ligands that specifically modulate its activity, offering potential therapeutic benefits.A major challenge in SBDD is the vast chemical space that must be navigated to discover molecules with desired properties. Recently, machine learning (ML) has been applied to SBDD, promising to enable researchers to rapidly pinpoint drug candidates, significantly reducing the reliance on labor-intensive and costly experimental methods. ML algorithms are capable of analyzing vast datasets of molecular structures and properties to discern patterns, predict outcomes and generate de novo molecules. This might not only accelerate the drug discovery process but also enhance the efficiency and efficacy of identifying viable therapeutic agents. Early work by Ragoza et al.3 used 3D convolutional neural networks (3D-CNNs) in voxel space and encoded the atomic density grids of protein–ligand complexes and the protein pockets in two separate latent spaces, both of which are used to decode 3D ligands with variational autoencoders (VAEs). A similar approach was applied in the DeepFrag architecture by Green et al.,4 which focused on fragment-based ligand optimization. Wang et al.5 also used 3D CNNs in voxel space on density grids, but instead of using VAEs that optimize a lower bound on the data probability, they train generative adversarial networks (GANs) end-to-end. Since voxelized grid representations are large and have sparse values (most voxels are empty), high memory consumption is a disadvantage. Treating protein–ligand complexes as atomic point clouds can circumvent this problem and, in combination with graph neural networks, enable the generative modeling of ligands bound to protein pockets. SBDD with autoregressive models that factorize the data probability were used in combination with SE(3)-invariant GNNs.6–8 Autoregressive models for SBDD were further improved by using SE(3) equivariant networks such as in Pocket2Mol,9 which places individual atoms one after the other during generation, or in FRAME,10 which places fragments from a predefined library in successive steps.
Another innovative machine learning technique increasingly employed in structure-based drug discovery is the application of generative diffusion models which generate the entire structure in one-shot, but allow its refinement through successive steps. Originally utilized in fields like computer vision and natural language processing, these models also excel in capturing the complex patterns of 3D molecular structures, particularly when enhanced with features that reflect the symmetry and specific target-related characteristics of proteins.6,9,11–13 Another line of research leverages diffusion models as methodology to build ML based docking models.14,15
The effectiveness of these models hinges on training with detailed protein structures, which allows for the generation of ligands that are not only structurally compatible but also specifically designed for the interaction with target proteins. However, while generated ligands fit well in a protein binding pocket, these methods lack a mechanism to guide the generative process towards ligands with desired chemical properties such as binding affinity, stability, or bioavailability. Additionally, 3D generative models often yield ligands with a high prevalence of fused rings and low synthetic accessibility.12,13,16–18
In this study, we introduce PILOT (Pocket-Informed Ligand OpTimization) – an equivariant diffusion model designed for de novo ligand generation. As shown in Fig. 1, PILOT operates in three distinct stages: unconditional diffusion pre-training, pocket-conditional fine-tuning, and property-guided inference. During the inference stage, we employ an importance sampling scheme to replace less desirable intermediate samples with more favorable ones, thereby re-weighting trajectories during generation. This strategy enables the use of any pre-trained, unconditioned diffusion score model for sampling, which is subsequently enhanced by integrating the capabilities of an external model, similar to classifier guidance.19 However, while classifier guidance may drive the sampling trajectory to adversarial, out-of-distribution structures,19 trajectory re-weighting ensures that samples remain within distribution. As trajectory re-weighting can be conducted in parallel for multiple properties, we focus on three critical properties for drug discovery: synthetic accessibility (SA), docking score, and potency (IC50). Our findings demonstrate that PILOT generates ligands that not only exhibit a significant improvement in synthesizability and drug-likeness but also achieve favorable docking scores and predicted inhibition.
 | ||
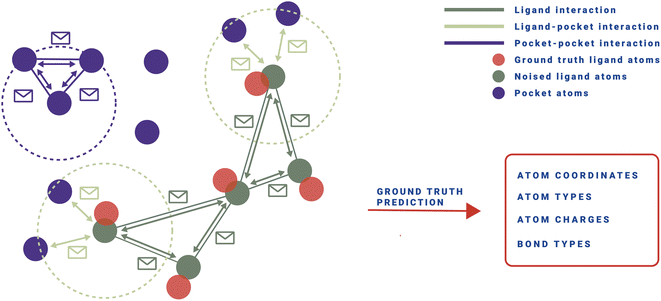
| Fig. 1 Top: PILOT is first pre-trained unconditionally on an Enamine Real subset from the ZINC database.20 We employ OpenEye's Omega to create at most five conformers per molecule.21 Afterwards, we fine-tune the model on CrossDocked2020 conditioned on the atoms of the pocket.22 Middle: Given the binding pocket of a protein, a noisy state of a ligand is sampled from the diffusion forward trajectory (here, t = 300) as input to the diffusion model during training. The model has to retrieve the ground truth ligand (M0). For training, a composite loss (ld) is used for continuous (mean squared error) and categorical features (cross-entropy loss), respectively, together with a timestep-dependent loss weighting (w(t)). Bottom: at inference, a point cloud is sampled from a Gaussian prior (t = 500). Given a binding pocket, the model retrieves a fitting ligand by following the reverse diffusion trajectory. At pre-specified steps, a property surrogate model (green crosses) guides the diffusion process towards desired regions in chemical space using importance sampling. | ||
2 Results and discussion
2.1 Pre-training of pocket-conditioned 3D diffusion models
Pre-training enables deep neural networks to build efficient representations by learning the underlying structure of the data. It proves to be a successful strategy across various fields of machine learning, particularly in the development of large language models (LLMs).23,24 The success of these methods provides a compelling case for applying similar methodologies in the domain of scientific research, specifically in computational chemistry and drug discovery.25–27 In the context of de novo molecular diffusion models, pre-training allows the models to learn fundamental chemical properties and interactions from large datasets of molecular structures. This foundational knowledge includes understanding bond types, molecular geometries, and basic physicochemical properties, which are critical for predicting how novel molecules might interact with biological targets.Pre-training molecular diffusion models on extensive datasets of low-fidelity 3D molecule data is a beneficial strategy for enhancing de novo molecule generation capabilities. It significantly enhances the ability of the model to generate structurally diverse and chemically plausible molecules, when subsequently fine-tuned on smaller, high-fidelity datasets.28 In this work, we train PILOT as illustrated in Fig. 2. For pre-training, we utilize the Enamine Real Diversity subset present in the ZINC database20 which we downloaded from the Enamine website. To prepare the dataset, we employ OpenEye's Omega software,21 which we use for the creation of up to five conformers per molecule with classic default parameters, resulting in a substantial corpus of approximately 109 million 3D structures. Additionally, we simplify the molecular representations by removing all hydrogens.
We study the impact of pre-training on molecules and fine-tuning on ligand–pocket complexes on model performance using the CrossDocked2020 dataset6 following the methodologies described in the EQGAT-diff model by Le et al.28 and detailed in Section 4. Table 1 shows the results with evaluation of metrics related to the generated molecular structures, such as molecular validity, the number of connected components, and the distribution of bond angles and lengths. This includes a comparison between models trained from scratch and those that have been pre-trained. The chosen distance cutoff of the pocket–ligand complex is a critical factor for model performance in terms of computational cost and accuracy (see Section 4.4). We find that pre-training improves our models across all measured metrics, and the pre-trained model with 7 Å cutoff achieves state-of-the-art performance for 8 out of the 9 evaluated metrics. In particular, over 98% of molecules sampled by the model are PoseBusters-valid (compared to 81% by TargetDiff). We measure PoseBusters-validity by summing over all non-overlapping evaluations of the “dock” and “mol” configuration in the PoseBusters tool and divide by the number of evaluations. The PoseBusters test suite validates chemical and geometric consistency of a ligand including its stereochemistry, and the physical plausibility of intra- and intermolecular measurements such as the planarity of aromatic rings, standard bond lengths, and protein–ligand clashes.29
| Model | PILOTscratchpocket,5A | PILOTpre-trainpocket,5A | PILOTscratchpocket,6A | PILOTpre-trainpocket,6A | PILOTscratchpocket,7A | PILOTpre-trainpocket,7A | TargetDiff10A |
|---|---|---|---|---|---|---|---|
| Validity ↑ | 93.40 ± 5.11 | 96.08 ± 3.53 | 93.48 ± 5.13 | 95.47 ± 3.91 | 92.06 ± 6.26 | 96.05 ± 3.83 | 78.91 ± 2.45 |
| Pose busters-valid ↑ | 96.93 ± 1.91 | 97.39 ± 1.58 | 97.88 ± 1.41 | 97.49 ± 1.72 | 96.92 ± 1.91 | 98.21 ± 1.51 | 80.53 ± 1.21 |
| Connect. comp. ↑ | 95.61 ± 4.15 | 97.44 ± 2.66 | 95.04 ± 5.02 | 97.19 ± 3.38 | 93.96 ± 5.99 | 97.81 ± 3.18 | 88.02 ± 2.54 |
| Diversity ↑ | 72.12 ± 9.05 | 72.99 ± 9.01 | 72.03 ± 9.48 | 71.66 ± 9.79 | 70.36 ± 9.59 | 71.52 ± 9.84 | 75.12 ± 6.41 |
| QED ↑ | 0.50 ± 0.12 | 0.51 ± 0.12 | 0.51 ± 0.14 | 0.53 ± 0.13 | 0.49 ± 0.14 | 0.53 ± 0.12 | 0.42 ± 0.09 |
| SA ↑ | 0.67 ± 0.08 | 0.69 ± 0.07 | 0.66 ± 0.09 | 0.69 ± 0.07 | 0.66 ± 0.07 | 0.69 ± 0.06 | 0.61 ± 0.06 |
| Lipinski ↑ | 4.53 ± 0.53 | 4.54 ± 0.49 | 4.54 ± 0.61 | 4.57 ± 0.56 | 4.46 ± 0.65 | 4.60 ± 0.51 | 4.64 ± 0.31 |
| Bond angles W1 ↓ | 4.03 ± 1.29 | 3.04 ± 1.19 | 3.47 ± 1.02 | 3.09 ± 1.06 | 4.00 ± 1.10 | 2.39 ± 0.98 | 9.71 ± 4.67 |
| Bond lenghts W1 [10−2] ↓ | 0.27 ± 0.01 | 0.24 ± 0.007 | 0.27 ± 0.09 | 0.23 ± 0.08 | 0.29 ± 0.09 | 0.21 ± 0.08 | 5.12 ± 2.05 |
| Ligand size | 23.70 ± 8.80 | 24.08 ± 8.83 | 24.56 ± 8.81 | 24.70 ± 8.74 | 24.39 ± 8.74 | 24.85 ± 8.94 | 22.21 ± 9.20 |
The model achieves a Wasserstein distance error of 2.39 ± 0.98 for bond angles. This constitutes 4x improvement over TargetDiff, a recent SOTA baseline, which indicates a markedly improved ability to learn the underlying data distribution. Beyond that, all PILOT models outperform TargetDiff in quantitative estimates of drug-likeness (QED) and synthetic accessibility (SA) scores, indicating that PILOT not only generates more structurally accurate molecules but also produces compounds that are more drug-like and better synthesizable.
We extend our evaluation using a range of metrics from PoseCheck30 to assess their ability to generate ligands that form appropriate poses within the vicinity of the protein pocket. However, it is important to clarify that TargetDiff, and PILOT are not specifically designed or trained to produce exact poses, unlike tools like DiffDock,14 which are explicitly developed and trained for docking applications. Still, de novo models should generate ligand poses without spatial conflicts, such as clashing with the pocket – a common issue highlighted in recent studies.29,30 Furthermore, strain energy is a crucial metric used to evaluate ligands; it measures the energy required to alter a ligand's conformation to fit its binding pose. Those with lower strain energy are generally favorable as they are likely to exhibit stronger binding with the protein. The strain energy is calculated as the difference between the internal energy of a relaxed pose and the created pose. Both the relaxation and energy ratings are calculated using the Universal Force Field (UFF)31 using RDKit as suggested by Harris et al.30. Fig. 3 shows that our pre-trained model significantly excels in terms of reducing strain energy. Note that the pre-training on molecules without pocket does not lead to an increase of clashes between ligand and pocket atoms in the complex. The metrics concerning the number of hydrogen acceptors, donors, van der Waals contacts, and hydrophilicity remain consistent across models.
The reduction in strain energy observed in the pre-trained model might be attributed to two main factors. First, the diffusion model is exposed to a vast array of conformers during its pre-training phase, likely featuring low strain energy due to the conformer generation techniques employed. This results in the generation of 3D conformers with optimal torsional profiles and minimized torsional strains, contributing to overall lower energy values in the ligands produced. Second, the enamine real diversity subset used for pre-training typically includes a wide variety of stable ring systems. Thus, the model likely encounters fewer unfavorable ring systems (e.g. 3- or 9-membered rings), which could contribute to higher strain energies. These insights further underscore the importance of the initial pre-training phase to generate relevant and biologically active ligands, further validating the efficacy of our approach in advancing the field of structure-based drug discovery. Notice that the PILOT architecture closely resembles EQGAT-diff (see Section 4.5), and thus its superior performance over TargetDiff, e.g. in terms of molecular validity, arises from the application of timestep-dependent loss weighting as well as bond diffusion.28 Higher validity comes from the correct construction of the bond graph whose atoms maintain the correct valencies, where EQGAT-diff and PILOT both have the advantage, unlike TargetDiff, of being able to directly predict the bond features. The TargetDiff architecture creates the bond graph in a post-processing step using OpenBabel with the predicted atom coordinates as input. While EQGAT-diff is pre-trained on the PubChem3D dataset, we pre-train PILOT on a subset of Enamine REAL to incorporate a larger and more diverse set of synthesizable molecules.
2.2 Multi-objective de novo generation using importance sampling
In previous studies utilizing 3D target-aware molecule generation, a significant challenge has been the poor synthetic accessibility (SA) of the generated molecules. These models often produce molecules with complex, fused, and uncommon ring systems, which are difficult to synthesize.12,13,16 This issue underscores the need for approaches that not only produce molecules with strong binding affinities but also ensure that these molecules can be feasibly synthesized. To address this, we propose a trajectory-based importance sampling method that utilizes property-specific expert models explained in Section 4.The evaluation of the importance sampling approach is performed for both single- and multi-objective optimization scenarios, focusing on SA and docking score guidance. We refer to guidance with an SA score model as SA-conditional and using a docking score model as docking-conditional. When both objectives are considered, we refer to the model as SA-docking-conditional. In each case, the unconditional base model is augmented with the respective property model during the sampling process.
Fig. 5 shows the correlation matrix of the CrossDocked2020 dataset. The SA scores exhibit a negative correlation with ligand size, i.e., larger molecules tend to be less synthetically accessible on average. Conversely, the positive correlation between SA scores and QED suggests that molecules with higher QED are generally more synthetically accessible. Docking scores show a strong negative correlation with both the number of rings and the number of atoms. This implies that models driven by docking scores tend to generate larger molecules with more (fused) rings. However, such molecular characteristics typically result in decreased SA scores and QED, presenting a trade-off between optimizing for docking score and maintaining synthetic feasibility. By incorporating these insights into our modeling approach, we aim to balance the dual objectives of binding efficacy and synthetic accessibility, thereby enhancing the practical utility of the generated molecules in drug discovery.
| Model | QVina2 (all) ↓ | QVina2 (Top-10%) ↓ | QED ↑ | SA ↑ | Lipinski ↑ | Diversity ↑ |
|---|---|---|---|---|---|---|
| Training set | −7.57 ± 2.09 | — | 0.53 ± 0.20 | 0.75 ± 0.10 | 4.57 ± 0.91 | — |
| Test set | −6.88 ± 2.33 | — | 0.47 ± 0.20 | 0.72 ± 0.13 | 4.34 ± 1.14 | — |
| TargetDiff | −7.32 ± 2.47 | −9.67 ± 2.55 | 0.48 ± 0.20 | 0.58 ± 0.13 | 4.59 ± 0.83 | 0.75 ± 0.09 |
| Unconditional | −7.33 ± 2.19 | −9.28 ± 2.26 | 0.49 ± 0.22 | 0.64 ± 0.13 | 4.40 ± 1.05 | 0.69 ± 0.07 |
| SA-conditional | −7.32 ± 2.25 | −8.91 ± 2.29 | 0.58 ± 0.19 | 0.77 ± 0.10 | 4.82 ± 0.54 | 0.73 ± 0.08 |
| Docking-conditional | −9.17 ± 2.48 | −10.94 ± 2.51 | 0.54 ± 0.13 | 0.62 ± 0.08 | 4.70 ± 0.41 | 0.57 ± 0.10 |
| SA-docking-conditional | −8.35 ± 2.75 | −10.36 ± 2.62 | 0.58 ± 0.17 | 0.72 ± 0.12 | 4.88 ± 0.44 | 0.68 ± 0.09 |
| SA-docking-conditional (norm) | −7.92 ± 2.44 | −9.85 ± 2.33 | 0.56 ± 0.19 | 0.78 ± 0.11 | 4.84 ± 0.47 | 0.75 ± 0.13 |
Table 2 shows that our model reproduces the observed correlations of the dataset. When guiding the unconditional model with the SA score, we notice a significant enhancement not only in the SA score, which increases to 0.77, but also improvements in QED and Lipinski's rule of five compliance. The mean docking scores remain consistent with those of the unconditional model. However, there is a notable reduction of docking performance in the top-10 ligands, consistent with the correlations observed in the dataset. Conversely, applying docking score guidance exclusively results in diminished SA scores and QED, while the docking scores themselves increase considerably. This reflects the trade-offs involved in optimizing for docking efficacy at the expense of synthetic accessibility and drug-likeness. When applying both SA and docking score guidance, the model achieves comparably high values for SA, QED, and Lipinski, while significantly improving docking scores and outperforming TargetDiff by a large margin.
To mitigate the adverse impact on SA scores and drug-likeness typically associated with high docking scores of larger molecules, we introduce a normalization strategy where docking scores are adjusted by the square root of the number of atoms per ligand. The results of this adjusted model, denoted as SA-docking-conditional (norm), are presented in the last row of Table 2. Here, we observe a significant increase in docking scores compared to the unconditional model, while the SA scores improve to 0.78, compared to 0.77 in the SA-conditional model. This illustrates how our multi-objective optimization strategy balances different property demands. Such balanced outcomes are critical for advancing the practical utility of generated molecules in drug discovery, ensuring that they not only bind effectively but are also feasible for synthesis.
We investigate how various molecular properties are affected by the application of guidance to further study the impact of importance sampling guidance on molecular design. Fig. 6 shows molecular characteristics such as ligand sizes, number of rings, number of rotatable bonds, and logP values across different models. Based on previous observations (Fig. 5), we expect SA guidance to result in smaller ligands with fewer rings, contrasting with the effect of docking guidance. First, we determine the most likely ligand size given a target from the training distribution and allow for the addition of up to ten atoms during inference. Fig. 6 (top) shows that ligands indeed tend to be smaller and possess fewer rings under SA guidance. The SA-docking-conditional model, which integrates both SA and docking objectives, represents a balanced compromise between these extremes.
Lipinski's rule of five is an important measure for assessing drug-likeness, including criteria such as the number of rotatable bonds and logP values. The number of rotatable bonds exhibits a strong positive correlation with the number of atoms mitigating the slight negative correlation with both SA and docking scores, while logP shows a positive correlation with SA- and docking scores. Fig. 6 (bottom) illustrates effective conditioning as both the SA- and docking-conditional models generally result in a lower average number of rotatable bonds compared to the unconditional model. In contrast, the partition coefficient logP tends to increase under both conditions.
Fig. 7 illustrates the evolution of the sample space across the unconditional, SA-conditional, docking-conditional, and SA-docking-conditional models. Each plot in this figure includes a red rectangle that identifies the regions where samples exceed the respective means of the test set, indicating improved property scores. The first row of Fig. 7 compares the drug-likeness (QED) of sampled ligands with their synthetic accessibility (SA) scores. The SA-conditional model shows a notable shift with most of the sample mass residing within the red rectangle. Thus, it successfully generates samples with notably higher SA scores compared to both the unconditional model and the test set ligands, while largely preserving docking scores. In contrast, the docking-conditional model exhibits lower docking scores on average at the expense of the SA scores. The SA-docking-conditional model demonstrates a good balance, transitioning towards both high SA scores and low docking scores. Remarkably, most of the sampled ligands from this model not only fall within the red rectangle but also significantly surpass the test set ligands in terms of docking scores with equal SA scores as listed in Table 2, while the model with normalization improves in both metrics.
We compare our importance sampling approach against the classifier guidance method19 using the fine-tuned model trained on the CrossDocked dataset with 5 Å cutoff. For classifier guidance, we calculate the gradients with respect to atomic coordinates by using the autograd engine for the outputs of the surrogate models during the reverse sampling trajectory. Guided by maximizing SA and minimizing docking scores, we find that the mean run time per protein pocket in the test set using classifier guidance is approximately 4.3 times slower than importance sampling, largely due to the gradient calculations (see Section C.1 in the ESI†). Notice that for classifier guidance the batch size has to be reduced in order to avoid out of memory issues which are caused by the autograd engine. The importance sampling approach does not require gradients and enables practitioners to maintain a significantly larger batch-size. The molecular validity for our proposed importance sampling method is also significantly higher at 93.40% compared to classifier guidance, which achieves a validity of 77.17% for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated ligands. This shows that sampling a given set of valid molecules takes even longer, as classifier guidance results in a significant increase in adversarial structures. Nevertheless, we find that the mean SA and docking scores of 0.82 and −8.43, respectively, are better than those for importance sampling (0.75 and −7.7). However, if we perform classifier guidance with the same number of update steps as the importance sampling, the validity increases to 93.18% similarly to importance sampling, but the SA and docking scores are significantly less optimized, reaching 0.72 and −7.15, respectively. Additionally, we measure the effect of importance sampling and classifier guidance on the uniqueness rate (number of unique molecules per 100 sampled ligands). The unconditional model achieves a uniqueness rate of 0.83, which diminishes slightly to 0.75 when using importance sampling and more significantly to 0.65 using classifier guidance.
000 generated ligands. This shows that sampling a given set of valid molecules takes even longer, as classifier guidance results in a significant increase in adversarial structures. Nevertheless, we find that the mean SA and docking scores of 0.82 and −8.43, respectively, are better than those for importance sampling (0.75 and −7.7). However, if we perform classifier guidance with the same number of update steps as the importance sampling, the validity increases to 93.18% similarly to importance sampling, but the SA and docking scores are significantly less optimized, reaching 0.72 and −7.15, respectively. Additionally, we measure the effect of importance sampling and classifier guidance on the uniqueness rate (number of unique molecules per 100 sampled ligands). The unconditional model achieves a uniqueness rate of 0.83, which diminishes slightly to 0.75 when using importance sampling and more significantly to 0.65 using classifier guidance.
Overall, our findings demonstrate that using importance sampling as a guidance mechanism in the diffusion model is a potent strategy for steering the generation of molecules towards desired regions of chemical space while being computationally several times cheaper compared to classifier guidance. The method effectively modifies molecular properties in line with desired multi-objective property profiles, albeit within the constraints set by the data distribution used for training. Unlike classifier-guidance, our approach does not require (prohibitively) expensive backpropagation. Instead, we achieve the aforementioned results using only a few importance sampling steps (forward calls to the surrogate models).
We evaluate the models on a hold-out test set comprising ten kinase targets that were not included in either the training or validation datasets. The performance of our pIC50-conditional model is summarized in Table 3. The pIC50-conditional model shows a significant improvement in predicted mean pIC50 values of 7.65 ± 0.78 compared to the test set ligands (6.41 ± 1.56). At the same time, it maintains robust performance metrics in terms of docking scores and other critical properties such as QED and compliance with Lipinski's rule of five.
| Model | Vina (all) ↓ | Vina (top-10%) ↓ | pIC50 ↑ | QED ↑ | SA ↑ | Lipinski ↑ | Diversity ↑ |
|---|---|---|---|---|---|---|---|
| Training set | −9.20 ± 1.13 | — | 7.05 ± 1.28 | 0.49 ± 0.16 | 0.75 ± 0.07 | 4.73 ± 0.52 | — |
| Test set | −8.78 ± 1.13 | — | 6.41 ± 1.56 | 0.61 ± 0.14 | 0.79 ± 0.05 | 4.96 ± 0.22 | — |
| Unconditional | −8.49 ± 1.05 | −9.79 ± 0.87 | 6.28 ± 0.68 | 0.63 ± 0.14 | 0.75 ± 0.13 | 4.95 ± 0.25 | 0.65 ± 0.06 |
| pIC50-conditional | −8.60 ± 0.98 | −9.75 ± 0.86 | 7.65 ± 0.78 | 0.62 ± 0.16 | 0.67 ± 0.09 | 4.94 ± 0.28 | 0.57 ± 0.06 |
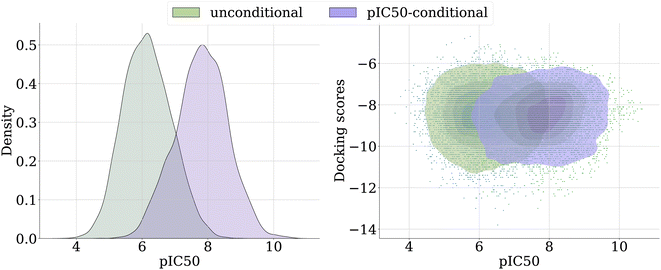
Fig. 8 provides a visual comparison of the sample spaces generated by the unconditional and the pIC50-conditional model. We observe a significant shift in the overall density of samples towards higher predicted pIC50 when using the importance sampling guidance (left panel). Fig. 8 (right) illustrates the relationship between docking scores and pIC50. While the pIC50-conditional model yields samples with higher pIC50 on average, the ligands maintain competitive docking scores. This suggests that the model does not compromise docking efficacy for higher expected pIC50.
Note, that the current approach is limited as pIC50 values are inherently noisy, in particular when collected across various data sources.32 Thus, the predicted binding affinities should be interpreted cautiously. To alleviate this problem, we propose to adopt ensemble modeling techniques to enhance the meaningfulness of predictions in the importance sampling pipeline. Similar approaches are, for example, commonly used for stabilizing machine learning force fields.33
Fig. 9 (top) demonstrates how ensemble techniques significantly improve the robustness of pIC50 predictions. We employ an ensemble of property models for importance sampling guidance. Each property model, denoted as seed1, seed2, etc., is trained with a different global seed. The base model is used to sample 100 ligands per test target, both with and without ensemble guidance. The term single model guidance refers to the base model guiding itself. We observe that single model guidance results in a notable offset between the predictions of the base model and those of all other property models, indicating poor generalization performance. That is, self-guidance exploits the predicted pIC50 value too much, as it was trained on. However, with ensemble guidance, even just two additional seed models (seed500 and seed1000) lead to greater improvement in generality. This enhancement is evident in the pIC50 predictions of all seed models not included in the ensemble guidance (i.e., seed1, seed2, seed15, and seed800). As shown in Fig. 9 (bottom), further increasing the ensemble size, such as by adding another model, here seed800, leads to additional refinement in predictions and consequently, increased generality of pIC50 predictions.
We observe improved generalization performance for the ensemble compared to the single models. We evaluate the five models on the Kinodata-3D test set, which achieve an average mean squared error of 1.34. In contrast, the ensemble built from these five models achieves a lower error of 1.23.
3 Conclusions
We have introduced PILOT, a novel equivariant diffusion-based model tailored for de novo ligand generation conditioned on protein pockets in three-dimensional space. Our research demonstrates the superior performance of PILOT compared to existing state-of-the-art models in this domain, as evidenced by a comprehensive evaluation across a spectrum of metrics critical in medicinal chemistry and drug design.A significant finding of our study is the substantial enhancement in downstream performance achieved by pre-training our model on a vast dataset of molecular conformers. This underscores the pivotal role of pre-training in the structure-based drug discovery pipeline, demonstrating its efficacy in improving the quality of generated ligands. Beyond that, we have proposed a trajectory-based importance sampling strategy, which enables targeted steering of ligand generation towards desired chemical properties. This technique guides the generation process towards ligands with desired properties such as synthetic accessibility, drug-likeness, docking scores, and predicted binding affinities by using surrogate models trained on experimental data. This strategy represents an important advancement in structure-based drug discovery, offering researchers a powerful tool to design molecules with tailored properties using 3D equivariant diffusion models.
The dependency on the availability and quality of training data remains a critical challenge for deploying AI models like PILOT in drug discovery pipelines. In the domain of structure-based drug design, data can often be sparse, noisy, and of varying quality, which significantly impacts the learning and predictive capabilities of ML models. While our method heavily relies on surrogate models and proxies such as the RDKit synthetic accessibility (SA) scores to estimate the synthesizability of generated ligands, these scores may not fully capture the complexities and practical challenges of medicinal chemistry. Addressing these challenges will require a concerted effort to enhance data collection practices, improve data quality, and expand the variety of data sources.
Moving forward, we see potential applications of PILOT in the drug discovery pipeline by integrating this model with other AI-driven tools and technologies, such as automated synthesis platforms and high-throughput screening to accelerate drug design. Furthermore, the scope of our model may be extended from small molecule drugs to biologic therapeutics involving for example peptides or antibodies.
4 Methods
4.1 Pocket conditioned 3D diffusion models
We aim to generate novel molecules M de novo, conditioned on a protein pocket P while optimizing multiple objectives c, such as synthetic accessibility, docking score, and predicted half-maximal inhibitory concentration (IC50). Recent developments have utilized 3D diffusion models to implement pθ(M|P), where the task of the model is to denoise an initially random ligand structure, while maintaining the protein pocket as a fixed condition.12,13,28 This is achieved by following a stochastic path that targets the distribution of training data, iteratively moving towards more defined structures pθ(Mt−1|Mt, P) as illustrated in Fig. 1.During training, the reverse distribution pθ(Mt−1|Mt, P) is parameterized using the approach as proposed by Le et al.28. That is, a noisy ligand Mt = (Xt, Ht, Et) at time step t is represented by perturbed atomic coordinates Xt, element types Ht, and bond features Et, while the diffusion model pθ is tasked in predicting the noise-free structure ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) 0=(
0=(![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) 0,Ĥ0,Ê0), acting as denoiser with the inherent goal to iteratively attain a cleaner structure. We optimize the variational lower bound of the log-likelihood log
0,Ĥ0,Ê0), acting as denoiser with the inherent goal to iteratively attain a cleaner structure. We optimize the variational lower bound of the log-likelihood log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(M0|P) and minimize the timestep-dependent diffusion loss
p(M0|P) and minimize the timestep-dependent diffusion loss
 | (1) |
 reveals as mean-squared-error loss for 3D coordinates, and cross-entropy loss for discrete-valued data types like atom, bond, and charge-types.28 To obtain the noisy ligand Mt, we apply the forward noising process with Gaussian diffusion for continuous valued coordinates, while discrete valued data like atom, bond- and charge-types are perturbed using categorical diffusion which both reads
reveals as mean-squared-error loss for 3D coordinates, and cross-entropy loss for discrete-valued data types like atom, bond, and charge-types.28 To obtain the noisy ligand Mt, we apply the forward noising process with Gaussian diffusion for continuous valued coordinates, while discrete valued data like atom, bond- and charge-types are perturbed using categorical diffusion which both reads | (2) |
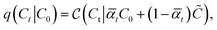 | (3) |
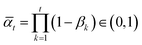 determines a variance-preserving (VP) adaptive noise scheduler with empirical distribution
determines a variance-preserving (VP) adaptive noise scheduler with empirical distribution ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) estimated from the training set for categorical data (H, E).34
estimated from the training set for categorical data (H, E).34
4.2 Multi-objective importance sampling
To sample ligands from the distribution pθ(M|P, c), we utilize Bayes' theorem to decompose the probability density into pθ(M|P, c) ∝ pδ(c|M, P)pθ(M|P). We further assume that multiple properties c = (c1, c2, …, ck) are conditionally independent, leading to the factorization , where each pδl(cl|M, P) can be interpreted as an expert surrogate model for a specific property. These surrogate models must be able to predict the properties of interest at any step of the diffusion trajectory, similar to classifier-guidance.19 While classifier-guidance requires backpropagation at every step, making it quickly unfeasible for ligand–pocket complexes with several hundred atoms, our proposed importance sampling approach eliminates the need for backpropagation. Moreover, far fewer steps are needed to update the diffusion model compared to classifier-guidance, which also often tends to steer the model towards adversarial structures.19
, where each pδl(cl|M, P) can be interpreted as an expert surrogate model for a specific property. These surrogate models must be able to predict the properties of interest at any step of the diffusion trajectory, similar to classifier-guidance.19 While classifier-guidance requires backpropagation at every step, making it quickly unfeasible for ligand–pocket complexes with several hundred atoms, our proposed importance sampling approach eliminates the need for backpropagation. Moreover, far fewer steps are needed to update the diffusion model compared to classifier-guidance, which also often tends to steer the model towards adversarial structures.19As properties such as synthetic accessibility are determined solely based on the ligand, whereas others, like docking scores, depend on the interaction between the ligand and the protein pocket, suitable property predictors pδi may be defined as required. During the sampling process of a set of K noisy ligands {M1, M2, …, MK}, we use importance weights derived from pδ(c|M, P) to rank each intermediate noisy sample at its current position in the state space, as described in Algorithm 1. Our goal is to generate samples from pθ(M|c, P) ∝ pδ(c|M, P)pθ(M|P) under the condition c, which specifies the property that the ligand M must achieve. For continuous properties, we choose a Gaussian distribution with a standard deviation of 1 to model p(c|M, P). Specifically, this takes the form  . This formulation also establishes a natural connection to maximum-likelihood training for the property predictor fδ. Since the reverse diffusion trajectory is inherently stochastic, our goal is to preferentially select samples that are most likely to follow a path resulting in ligands meeting the specified conditions c. This process is schematically depicted in Fig. 4. To accurately predict these conditions, we train pδ(c|M, P) as pδ(c|Mt, P, t) along the forward noising diffusion trajectory, where Mt represents the state of the ligand at time step t. The property model pδ is trained using the mean squared error and cross-entropy loss for continuous and discrete properties, respectively. The rationale behind this training approach is that denoising steps closer to the original data distribution retain a clearer signal of the input ligand, making them highly informative. In contrast, steps closer to the prior noise distribution, although less informative, can still provide valuable discriminative insights for pδ. This strategy leverages the nuanced progression of information degradation during the diffusion process to efficiently guide the generation of desired ligands without mode collapse.
. This formulation also establishes a natural connection to maximum-likelihood training for the property predictor fδ. Since the reverse diffusion trajectory is inherently stochastic, our goal is to preferentially select samples that are most likely to follow a path resulting in ligands meeting the specified conditions c. This process is schematically depicted in Fig. 4. To accurately predict these conditions, we train pδ(c|M, P) as pδ(c|Mt, P, t) along the forward noising diffusion trajectory, where Mt represents the state of the ligand at time step t. The property model pδ is trained using the mean squared error and cross-entropy loss for continuous and discrete properties, respectively. The rationale behind this training approach is that denoising steps closer to the original data distribution retain a clearer signal of the input ligand, making them highly informative. In contrast, steps closer to the prior noise distribution, although less informative, can still provide valuable discriminative insights for pδ. This strategy leverages the nuanced progression of information degradation during the diffusion process to efficiently guide the generation of desired ligands without mode collapse.
The algorithm is inspired by the Sequential Monte Carlo (SMC) method.35,36 A similar replacement strategy has previously been applied by Trippe et al.37 and Wu et al.38 in the context of diffusion models for protein backbone modeling and motif scaffolding. In Algorithm 1, we focus on maximizing property values by scoring each predicted property value among the samples in the population. To achieve this, we employ softmax normalization on the predicted property values fδ(Mk, P) for maximization. If the goal is to minimize a certain property, the predicted property values must be multiplied by −1 to compute the importance weights before applying the softmax operation. These importance weights represent the probability of selecting samples from the finite population set for the next iteration. When specific property values c are desired, instead of relying solely on the predicted property values ck = fδ(Mk, P), we compute the probability using a Gaussian kernel as described earlier. Notice that we additionally need to employ another normalization scheme to rank each unique probability value. For simplicity, we choose to use softmax normalization again. On CrossDocked, we employ the importance sampling every N = 10 steps and first filter for trajectories with highly synthetic accessible samples in timesteps 100–250, while ligands with better docking scores are weighted in steps 300–400 during the reverse trajectory which involves 500 steps. Both importance filtering steps are applied with temperature τ = 0.1. We refer to the ESI section C† for more details.
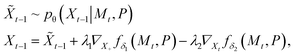 | (4) |
 and the first equation samples the atomic coordinates with respect to the current noisy molecule and protein pocket disregarding the SA and docking scores property. The second equation applies the gradient guidance with scales λ1, λ2 > 0 to maximize SA and minimize docking scores. In our experiments we set λ1 = λ2 = 0.1.
and the first equation samples the atomic coordinates with respect to the current noisy molecule and protein pocket disregarding the SA and docking scores property. The second equation applies the gradient guidance with scales λ1, λ2 > 0 to maximize SA and minimize docking scores. In our experiments we set λ1 = λ2 = 0.1.
4.3 Datasets
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 protein–ligand complexes for the training set and 100 for the test set.
000 protein–ligand complexes for the training set and 100 for the test set.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pocket-ligand complexes for training, and save 310 and 136 complexes for validation and testing, respectively.
000 pocket-ligand complexes for training, and save 310 and 136 complexes for validation and testing, respectively.
4.4 Choosing the cutoff for protein–ligand complex creation
The CrossDocked2020 dataset implements a pre-defined cutoff surrounding the bound ligands to cut out the protein pockets. Based on this, TargetDiff12 uses a cutoff region of 10 Å with the centers of mass (CoM) of the residues acting as reference points for measuring distances to ligand atoms. Residues whose CoM are within or equal to the cutoff distance are included in the Protein–Ligand (PL) complex. Conversely, DiffSBDD includes the entire residue in the PL complex if any atom within that residue falls inside the cutoff region.13 Our work adopts the latter approach as it offers a more physically plausible representation of the interaction space. We ablate different cutoff values {5,6,7}Å on the CrossDocked2020 dataset and observe that the model trained on the 7 Å cutoff performs best as illustrated in Table 1 for the pre-trained model. We hypothesize that the trade-off between smaller cutoff and model performance is caused by the complexity and tendency to overfit on smaller complexes. Note that a smaller cutoff leads to PL complexes with fewer atoms as shown in Figure and Table B1 in the ESI.†4.5 Model architecture
The PILOT architecture is an extension of EQGAT-diff28 with minor changes to handle protein–ligand (PL) complexes. To perform message-passing, we calculate the interactions in the protein–ligand and protein–protein graphs using a radius graph with a cutoff of 5 Å. We perform fully-connected message-passing for all ligand–ligand interactions. Unlike the EQGAT-diff architecture, we also incorporate a residual connection of the transformed initial ligand–ligand edge encodings into the PILOT architecture. Assuming that the small molecule consists of n atoms, the initial one-hot encoded edge features categorize the presence of none, single, double, triple and aromatic bonds. We further calculate the distance matrix of
categorize the presence of none, single, double, triple and aromatic bonds. We further calculate the distance matrix of  and compute an initial edge-feature between atom i and j as
and compute an initial edge-feature between atom i and j as  , which computes an outer product between the one-hot encoding of the bond feature with an exponential radial basis function with 20 channels. The embedding
, which computes an outer product between the one-hot encoding of the bond feature with an exponential radial basis function with 20 channels. The embedding  is vectorized into shape
is vectorized into shape 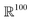 and linearly transformed to obtain the hidden edge embedding
and linearly transformed to obtain the hidden edge embedding 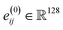 prior to the message passing. After L = 12 rounds of message-passing, we use separate prediction heads for predicting coordinates, atoms, charges, and bond types, as suggested in the initial EQGAT-diff architecture. We use 256 scalar and vector channels and 128 edge channels across the network. We observe improved model performance when including the initial embedding of edge features through a residual connection after each message-passing layer. We hypothesize that this information enables better 3D coordinates as well as bond predictions by the diffusion model because the dependency between bonds and atomic coordinates is included in each message-passing layer.
prior to the message passing. After L = 12 rounds of message-passing, we use separate prediction heads for predicting coordinates, atoms, charges, and bond types, as suggested in the initial EQGAT-diff architecture. We use 256 scalar and vector channels and 128 edge channels across the network. We observe improved model performance when including the initial embedding of edge features through a residual connection after each message-passing layer. We hypothesize that this information enables better 3D coordinates as well as bond predictions by the diffusion model because the dependency between bonds and atomic coordinates is included in each message-passing layer.
4.6 Training details
We train PILOT with T = 500 diffusion timesteps (in contrast to TargetDiff, which uses T = 1000). For training, we draw a random batch of protein–ligand complexes and uniformly sample timesteps t ∈ U(1, 500). The diffusion loss Lt is optimized for each sample, which under the data prediction parameterization means a mean-squared-error (MSE) loss for atomic coordinates and cross-entropy (CE) loss for discrete-valued modalities including atom- and bond types of the ligand molecule. For more details we refer to Le et al.28. The Enamine model was pre-trained for 10 epochs with the goal of learning a broad chemical space of molecules not limited to pocket–ligand complex data. We trained the models for 300 epochs from scratch on the CrossDocked2020 and Kinodata 3D dataset. When leveraging the pre-trained Enamine model as a starting point, we only fine-tuned for 100 epochs on the CrossDocked2020 dataset. In all (pre-)trainings we use the AdamW optimizer with AMSGrad and a learning rate of 2 × 10−4, weight-decay of 1 × 10−12, and gradient clipping for values higher than 10 throughout all experiments.![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) 0 and ĉ, respectively). This is achieved by including additional prediction heads, e.g. MLPs, operating on the node/edge embeddings of the final message-passing layer. As the synthetic accessibility (SA) score only depends on the ligand we also pre-train the Enamine model to jointly predict the SA score in addition to the denoising task. When fine-tuning on CrossDocked, we load the model weights from Enamine and add an extra head for docking score prediction. However, importance sampling can be performed using any external model trained on a diffusion trajectory, as long as it uses the same transition kernels as the diffusion model. In preliminary studies, we experimented with separately trained models and found that they also worked. However, for simplicity, we used joint training in this work. We adapt the timestep dependent loss weighting as in Le et al.,28 such that the gradient signal for larger timesteps is damped, following the property loss
0 and ĉ, respectively). This is achieved by including additional prediction heads, e.g. MLPs, operating on the node/edge embeddings of the final message-passing layer. As the synthetic accessibility (SA) score only depends on the ligand we also pre-train the Enamine model to jointly predict the SA score in addition to the denoising task. When fine-tuning on CrossDocked, we load the model weights from Enamine and add an extra head for docking score prediction. However, importance sampling can be performed using any external model trained on a diffusion trajectory, as long as it uses the same transition kernels as the diffusion model. In preliminary studies, we experimented with separately trained models and found that they also worked. However, for simplicity, we used joint training in this work. We adapt the timestep dependent loss weighting as in Le et al.,28 such that the gradient signal for larger timesteps is damped, following the property loss| Lp,t = w(t)‖c0 − pθ,δ(Mt, t, P)‖2. | (5) |
Data availability
The processed CrossDocked2020 dataset can be downloaded from https://github.com/pengxingang/Pocket2Mol/tree/main/data. The Kinodata-3D dataset can be downloaded from https://volkamerlab.org/projects/kinodata-3d. The Enamine REAL data used in this study for pre-training the model is licensed and thus cannot be made available. However, we provide all information needed to reproduce the dataset.Author contributions
Conceptualization: J. C., T. L.; data curation: J. C., T. L.; formal analysis: J. C., T. L.; investigation: J. C., T. L.; methodology: J. C., T. L.; resources: D. A. C.; supervision: D. A. C., K. T. S.; visualization: J. C., T. L.; writing — original draft: J. C., T. L., K. T. S.; proofreading: J. C., T. L., F. N., D. A. C., K. T. S.; writing — review and editing: J. C., T. L., K. T. S.Conflicts of interest
There are no conflicts to declare.Acknowledgements
JC and DAC acknowledge the support from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Actions grant agreement “Advanced Machine Learning for Innovative Drug Discovery (AIDD)” No. 956832. DAC additionally acknowledges the funding from the European Commission's Horizon 2020 Framework Programme (AiChemist; grant no. 101120466).References
- A. C. Anderson, Chem. Biol., 2003, 10, 787–797 CrossRef PubMed.
- M. Batool, B. Ahmad and S. Choi, Int. J. Mol. Sci., 2019, 20, 2783 CrossRef PubMed.
- M. Ragoza, T. Masuda and D. R. Koes, Chem. Sci., 2022, 13, 2701–2713 RSC.
- H. Green, D. R. Koes and J. D. Durrant, Chem. Sci., 2021, 12, 8036–8047 RSC.
- L. Wang, R. Bai, X. Shi, W. Zhang, Y. Cui, X. Wang, C. Wang, H. Chang, Y. Zhang, J. Zhou, W. Peng, W. Zhou and B. Huang, Sci. Rep., 2022, 12, 15100 CrossRef PubMed.
- S. Luo, J. Guan, J. Ma and J. Peng, Adv. Neural Inf. Process. Syst., 2021, 6229–6239 Search PubMed.
- M. Liu, Y. Luo, K. Uchino, K. Maruhashi and S. Ji, Proceedings of the 39th International Conference on Machine Learning, 2022, pp. 13912–13924 Search PubMed.
- C. Tan, Z. Gao, S. Z. Li, Target-aware Molecular Graph Generation, arXiv, 2022, preprint, arXiv:2202.04829, DOI:10.48550/arXiv.2202.04829.
- X. Peng, S. Luo, J. Guan, Q. Xie, J. Peng and J. Ma, Proceedings of the 39th International Conference on Machine Learning, 2022, pp. 17644–17655 Search PubMed.
- A. S. Powers, H. H. Yu, P. Suriana, R. V. Koodli, T. Lu, J. M. Paggi and R. O. Dror, ACS Cent. Sci., 2023, 9, 2257–2267 CrossRef PubMed.
- E. Hoogeboom, V. G. Satorras, C. Vignac and M. Welling, Proceedings of the 39th International Conference on Machine Learning, 2022, pp. 8867–8887 Search PubMed.
- J. Guan, W. W. Qian, X. Peng, Y. Su, J. Peng and J. Ma, The Eleventh International Conference on Learning Representations, 2023 Search PubMed.
- A. Schneuing, Y. Du, C. Harris, A. Jamasb, I. Igashov, W. Du, T. Blundell, P. Lió, C. Gomes, M. Welling, M. Bronstein and B. Correia, Structure-based Drug Design with Equivariant Diffusion Models, arXiv, 2023, preprint, arXiv:2210.13695, DOI:10.48550/arXiv.2210.13695.
- G. Corso, H. Stärk, B. Jing, R. Barzilay and T. S. Jaakkola, The Eleventh International Conference on Learning Representations, 2023 Search PubMed.
- J. Zhu, Z. Gu, J. Pei and L. Lai, Chem. Sci., 2024, 15, 7926–7942 RSC.
- Y. Xia, K. Wu, P. Deng, R. Liu, Y. Zhang, H. Guo, Y. Cui, Q. Pei, L. Wu, S. Xie, S. Chen, X. Lu, S. Hu, J. Wu, C.-K. Chan, S. Chen, L. Zhou, N. Yu, H. Liu, J. Guo, T. Qin and T.-Y. Liu, Target-aware Molecule Generation for Drug Design Using a Chemical Language Model, 2024, https://www.biorxiv.org/content/early/2024/01/08/2024.01.08.574635 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- R. Winter, F. Montanari, A. Steffen, H. Briem, F. Noé and D.-A. Clevert, Chem. Sci., 2019, 10, 8016–8024 RSC.
- P. Dhariwal and A. Q. Nichol, Diffusion models beat GANs on image synthesis, Adv. Neural Inf. Process. Syst., 2021, 34, 8780–8794 Search PubMed , https://papers.nips.cc/paper_files/paper/2021/hash/49ad23d1ec9fa4bd8d77d02681df5cfa-Abstract.html.
- T. Sterling and J. J. Irwin, J. Chem. Inf. Model., 2015, 55, 2324–2337 CrossRef CAS.
- P. C. D. Hawkins and A. Nicholls, J. Chem. Inf. Model., 2012, 52, 2919–2936 CrossRef CAS PubMed.
- P. G. Francoeur, T. Masuda, J. Sunseri, A. Jia, R. B. Iovanisci, I. Snyder and D. R. Koes, J. Chem. Inf. Model., 2020, 60, 4200–4215 CrossRef CAS.
- T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever and D. Amodei, Adv. Neural Inf. Process. Syst., 2020, 1877–1901 Search PubMed.
- J. Devlin, M. W. Chang, K. Lee and K. Toutanova, BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding, NAACL-HLT, 2019, 1(2019), pp. 4171–4186, DOI:10.18653/V1/N19-1423.
- R. Winter, F. Montanari, F. Noé and D.-A. Clevert, Chem. Sci., 2019, 10, 1692–1701 RSC.
- S. Liu, H. Guo and J. Tang, The Eleventh International Conference on Learning Representations, 2023 Search PubMed.
- S. Zaidi, M. Schaarschmidt, J. Martens, H. Kim, Y. W. Teh, A. Sanchez-Gonzalez, P. Battaglia, R. Pascanu and J. Godwin, The Eleventh International Conference on Learning Representations, 2023 Search PubMed.
- T. Le, J. Cremer, F. Noé, D.-A. Clevert and K. Schütt, The Twelfth International Conference on Learning Representations, 2024 Search PubMed.
- M. Buttenschoen, G. M. Morris and C. M. Deane, PoseBusters: AI-based docking methods fail to generate physically valid poses or generalise to novel sequences, 2024, 10.1039/D3SC04185A.
- C. Harris, K. Didi, A. R. Jamasb, C. K. Joshi, S. V. Mathis, P. Lio and T. Blundell, Benchmarking Generated Poses: How Rational is Structure-based Drug Design with Generative Models?, 2023 Search PubMed.
- A. K. Rappé, C. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- G. A. Landrum and S. Riniker, J. Chem. Inf. Model., 2024, 64, 1560–1567 CrossRef PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- C. Vignac, N. Osman, L. Toni and P. Frossard, Machine Learning and Knowledge Discovery in Databases: Research Track, European Conference, ECML PKDD 2023, Turin, Italy, September 18-22, 2023, Proceedings, Part II, 2023, pp. 560–576 Search PubMed.
- A. Doucet, N. de Freitas and N. Gordon, in An Introduction to Sequential Monte Carlo Methods, Springer New York, New York, NY, 2001, pp. 3–14 Search PubMed.
- P. Del Moral, A. Doucet and A. Jasra, J. R. Stat. Soc. Ser. B Stat. Method, 2006, 68, 411–436 CrossRef.
- B. L. Trippe, J. Yim, D. Tischer, D. Baker, T. Broderick, R. Barzilay and T. S. Jaakkola, The Eleventh International Conference on Learning Representations, 2023 Search PubMed.
- L. Wu, B. L. Trippe, C. A. Naesseth, J. P. Cunningham and D. Blei, Thirty-seventh Conference on Neural Information Processing Systems, 2023 Search PubMed.
- P. G. Francoeur, T. Masuda, J. Sunseri, A. Jia, R. B. Iovanisci, I. Snyder and D. R. Koes, J. Chem. Inf. Model., 2020, 60, 4200–4215 CrossRef CAS PubMed.
- M. Backenköhler, J. Groß, V. Wolf and A. Volkamer, J. Chem. Inf. Model., 2024, 64, 4009–4020 CrossRef.
- D. Schaller, C. D. Christ, J. D. Chodera and A. Volkamer, Benchmarking Cross-Docking Strategies for Structure-Informed Machine Learning in Kinase Drug Discovery, 2023, https://www.biorxiv.org/content/early/2023/09/14/2023.09.11.557138 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03523b |
| This journal is © The Royal Society of Chemistry 2024 |