Formation of uranium disulfide from a uranium thioamidate single-source precursor

Abstract

A single-source-precursor approach was developed to synthesize uranium-based materials outside of the typically-studied oxides. This approach allows for shorter reaction times, milder reaction conditions, and control over the chemicals present in synthesis. To this end, the first homoleptic uranium thioamidate complex was synthesized as a precursor for US₂ materials. Pyrolysis of the thioamidate results in decomposition via an alkene elimination pathway and formation of γ-US₂, which has historically been hard to access without the need for a secondary sulfur source. Despite the oxophilicity of uranium, the method successfully forms US₂ without the inclusion of oxygen in the bulk final product. These findings are supported by simultaneous thermal analysis, elemental analysis, powder X-ray diffraction, and uranium L₃-edge X-ray absorption fine-structure spectroscopy. This work represents the first example of a single-source precursor approach to target and synthesize actinide materials other than the oxides.

---

Introduction

Actinide materials and coordination complexes have been studied because of the unusual properties associated with 5f-electrons. In particular, 5f-electrons may be localized or itinerant,^1,2 which affects interactions with the electronic states of the anions in their compounds. These interactions lead to properties such as magnetic order,^3,4 the Kondo effect,⁵ and superconductivity.⁶ Although the study of actinide materials is a growing field, the structural complexity of experimental samples is a major challenge that hinders further understanding. It is therefore of interest to develop actinide materials with minimal imperfections (such as crystallographic defects and grain boundaries) and improved chemical homogeneity.⁴

Single-source precursors have been used to synthesize oxidation-state pure, phase-pure, and morphology-controlled compounds of the transition-metals and lanthanides;^7–14 however, development of actinide single-source precursor chemistry has been limited to oxides.^15–18 Single-source precursors are distinct from conventional precursors because of the existence of pre-formed metal-sulfur bonds (in the case of precursors for sulfides).¹⁹ While traditional precursor methods have previously led to successful synthesis of non-oxide actinide thin films,^20–23 the use of single-source precursors provides additional advantages such as control over reagents as well as control of properties (such as solubility and volatility) desirable for a range of synthetic methods. For example, modulation of the substituent groups on the coordinated ligands enables tunable solubility and volatility, meaning these precursors can potentially be adaptable to colloidal nanoparticle syntheses as well as gas-phase materials syntheses like chemical vapor deposition (CVD) and atomic layer deposition (ALD).^4,7–10 Additionally, ligand modifications can tune thermal stability, which allows for material formation at lower temperatures than those used in more conventional synthetic routes.^7–10,14

Within the actinides, single-source precursors have been used to synthesize ThO₂ ¹⁵ and UO₂,¹⁶ with the actinide oxides being the most well-studied of the binary materials for their technological interest as nuclear fuels.^24,25 However, to gain a better understanding of the interactions of 5f-electrons with the electronic states of other anions, it is appealing to develop precursors to target materials beyond the commonly-studied oxides. We targeted US₂ because, as the heavier chalcogen analogue to UO₂, it enables development of sulfide precursor chemistry analogous to that of the oxides while still studying a fundamentally different system. Though UO₂ and US₂ have the same oxidation state and number of valence electrons, this does not translate to the same fundamental properties. For example, US₂ and UO₂ are structurally different, both in the gas phase²⁶ and the solid state.^27–33 Beyond structural comparison, UO₂ exhibits antiferromagnetism,³⁴ whereas US₂ exhibits weak ferromagnetism.^28,30,35 Therefore, the data on uranium oxides does not describe uranium sulfides, and there is room to study the differences in electronic structure of these materials, as indicated by the differences in magnetism.

Historically, work on US₂ has focused on the synthesis of different crystal phases and study of their thermodynamic and magnetic properties.^{26,28–31,35–48} More recently, there has been interest in the electronic structure of US₂,^49,50 and its utility in actinide–actinide separations.^51,52 However, US₂ has been difficult to study due to the oxophilicity of uranium, which leads to challenges in isolating pure uranium sulfide materials outside of inert atmospheres. Once synthesized, maintaining purity is challenging, as US₂ readily oxidizes or hydrolyzes in the presence of air or water.^29,53,54 Additionally, typical synthetic methods towards US₂ feature high temperatures, long reaction times, toxic reagents, and/or hard-to-remove byproducts.⁵⁵ For example, the synthesis of α- and β-US₂via chemical vapor transport requires the heating of uranium metal and elemental sulfur at ≥950 °C for up to three weeks.^{30,36,37,46,47,50} The γ-US₂ phase is less straightforward to obtain, proceeding through U₃S₅, followed by reduction under a stream of H₂S or by elemental sulfur at 330 °C.^28,29 Other studies have synthesized US₂ by treating the oxides with CS₂ under pressure, with difficult-to-separate uranium oxysulfides as byproducts.⁵²

To develop new methods of synthesizing and analyzing the properties of binary actinide materials without the concern of oxophilicity, temperature, reaction time, and structural defects, we have used a single-source precursor approach to synthesize US₂. Based on previous success in the use of amidate complexes towards morphology and size-controlled actinide dioxide materials^15,16,56 and the use of thioamidate complexes to prepare tin sulfide materials,^11,57 we hypothesized that homoleptic uranium thioamidate complexes would be promising precursors for the synthesis of US₂via pyrolysis. Here we report the first single-source precursor for non-oxide actinide materials by pyrolyzing a uranium thioamidate to form US₂ materials. This work demonstrates an extension of our synthetic actinide materials toolkit beyond the more commonly studied uranium oxide materials.

Results & discussion

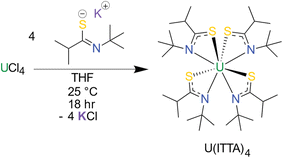
The thioamidate proligand, 2-methyl-N-(2-methyl-2-propanyl)propanthioamide, (H(ITTA), for “Isopropyl, Tert-butyl ThioAmide”), was synthesized according to literature methods.¹¹ Following deprotonation, the potassium salt K(ITTA) was treated with UCl₄ to prepare the uranium thioamidate complex U(ITTA)₄ (Scheme 1). The room temperature ¹H NMR spectrum (Fig. S6†) reveals approximately six peaks, rather than the three attributable to the tert-butyl, isopropyl methine, and isopropyl methyl protons, suggesting low symmetry for the molecule in the solution state. Thioamidate ligands have been shown to be hemilabile, which allows for ready conversion between isomers.^58,59 To assess this possibility, EXSY, HSQC, COSY, and variable temperature ¹H NMR (Fig. S1–S5†) were conducted and suggest that there are three species in solution, likely corresponding to three isomers of U(ITTA)₄ (Fig. S8†). Further assignment was hindered by paramagnetic broadening of ligand resonances coupling to the uranium center.⁶⁰

Scheme 1 Synthesis of the homoleptic thioamidate complex, U(ITTA)₄.

Green crystals suitable for single crystal X-ray diffraction (SCXRD) were grown from hexane; the data revealed a bidentate κ²-S,N coordination mode for the ITTA ligand to the U(IV) center, typical of other homoleptic metal thioamidate^11,57 and actinide amidate complexes^15,16,56 (Fig. 1). The thioamidate complexes show average U–S and U–N bond lengths of 2.7735(6) Å and 2.594(2) Å, respectively. The U–S bond length is comparable to other U(IV) complexes with similar ligands: 2.7735(6) Å in this work, compared to 2.829(2) Å reported by Gaunt et al.,⁶¹ 2.803(2) reported by Behrle et al.,⁶² and 2.768(4) reported by Wang et al.⁶³ The U–N bond length is also in agreement with similar ligand systems.^16,61

Fig. 1 X-ray crystal structure of U(ITTA)₄ with all atoms represented with 50% probability thermal ellipsoids and hydrogens omitted for clarity.

The thermal decomposition of U(ITTA)₄ was studied to understand its utility as a precursor to US₂ by using simultaneous thermal analysis (STA), which combines thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) (Fig. 2 and S15†). Under an Ar atmosphere and with a heating rate of 5 °C min⁻¹, U(ITTA)₄ shows a single step decomposition at 213 °C (onset at 202 °C). The measured mass loss at 238 °C, after the decomposition step, is 58.6%, increasing to 59.9% at the maximum temperature of 850 °C. This is lower than the predicted mass loss of 65.32% based on the stoichiometric decomposition of U(ITTA)₄ to US₂. This could suggest the incorporation of impurities in the final product that artificially raise the apparent mass. These decompositions were conducted in lidded alumina crucibles, which could prohibit the removal of volatile byproducts that would eventually carbonize as more U(ITTA)₄ decomposes. This thermogram is consistent with the thermogram of previously-studied amidate complexes, which led us to hypothesize that the thioamidate decomposes in a similar manner, following an alkene elimination pathway described in Scheme 2.¹⁶

Fig. 2 Thermogram of U(ITTA)₄ collected under argon at a heating rate of 5 °C min⁻¹.

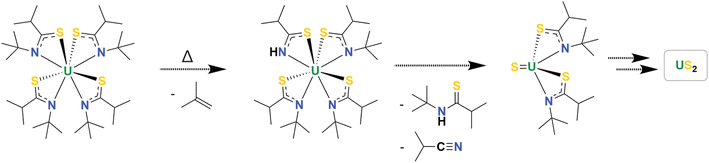Scheme 2 Proposed thermal decomposition mechanism for U(ITTA)₄ into US₂. The organic byproducts were observed by ¹H NMR, however the two putative uranium intermediates were not isolated.

To further elucidate the decomposition mechanism, a small amount of U(ITTA)₄ was heated to 300 °C in a sealed NMR tube under an atmosphere of nitrogen for 16 h. The tube was then cooled in liquid nitrogen to condense any volatile reaction products. Addition of C₆D₆ resulted in a colorless solution and a small amount of undissolved black solid. Resonances attributable to isobutylene, isobutyronitrile, and H(ITTA) were present in the ¹H NMR spectrum (Fig. S9†), which supports the mechanism shown in Scheme 2. We note that these byproducts were not observed in the expected 1 : 1 : 1 ratio; however, no other resonances were observed that would indicate a secondary decomposition pathway. Since these products are all volatile and/or soluble in organic solvents, they can be removed easily after pyrolysis.

To characterize the black solid observed during the NMR-scale pyrolysis reaction, larger quantities of U(ITTA)₄ were pyrolyzed in a tube furnace under a flowing atmosphere of argon gas. One sample was pyrolyzed at 250 °C for 2 h, which resulted in a black powder. A separate sample was heated first to 250 °C for 1 h to complete the pyrolysis, and then at 850 °C for an additional 5 h to anneal the sample and improve crystallinity; this reaction yielded a shiny, black solid. The non-annealed (250 °C pyrolysis) and annealed (250 °C, followed by 850 °C) samples are henceforth abbreviated as 1-US₂ and 2-US₂, respectively.

1-US₂ and 2-US₂ were probed using scanning electron microscopy (SEM) to assess how temperature affected the grain size and morphology of the products and to confirm that annealing was successful, thus affording crystallinity that would be useful in diffraction studies. SEM images (Fig. 3 and S14†) show a difference in the morphology among the precursor and the products, as well as between 1-US₂ and 2-US₂. Good uniformity in particle size is observed for 1-US₂, and the material has a stacked, sheet-like morphology (Fig. 3a). This sample also has smaller grains on some surfaces (Fig. 3b). On the other hand, 2-US₂ predominantly resembles that of a hollowed sphere and includes nanometer-sized particles (Fig. 3c and d). The effect of temperature on the morphology of the final products is evident from the electron microscopy images: the sample pyrolyzed at 250 °C has distinct morphology from that pyrolyzed at 850 °C, implying that annealing was successful and 2-US₂ might render useful diffraction data.

Fig. 3 Scanning electron microscopy (SEM) images of 1-US₂ (a and b) and 2-US₂ (c and d).

To understand the chemical composition of the black solid, elemental analysis (EA) and PXRD were conducted. EA for 1-US₂ found 21.4% sulfur content, consistent with the formation of US₂ (S calcd: 22%) and decomposition of the U(ITTA)₄ precursor (S exptl: 14.39%, calcd: 14.70%). Reduction in the amount of hydrogen (H exptl: 7.25%, calcd: 7.40%) and nitrogen (N exptl: 6.21%, calcd: 6.40%) observed for U(ITTA)₄ were also found for 1-US₂, which had H and N in trace amounts that were within error for the detection method. The sample had 2.33% carbon content, which was reduced from that seen in U(ITTA)₄ (C exptl: 43.67%, calcd: 44.00%). The carbon content found in 1-US₂ is comparable to carbon contamination found in materials prepared with similar precursors and is in line with the STA data.^15,16 Overall, the shift in the sulfur and carbon contents from precursor to 1-US₂ is supportive of the decomposition of U(ITTA)₄ to US₂. In considering the chemical composition of 2-US₂, the 1% mass change in the STA data suggests that the two samples are chemically similar, and that the addition of the annealing step likely improves only the crystallinity, not the sample purity.

The PXRD pattern on a powdered sample of 2-US₂ shows broadened peaks, and Scherrer analysis yields particle sizes of 35(18) μm, which is consistent with sizes observed with SEM. The pattern is qualitatively consistent with the formation of γ-US₂ ^28,29 for the bulk of the sample, thus we have assigned the 2-US₂ sample to the γ-phase (Fig. 4). There are differences in peak intensities between the observed pattern and the calculated pattern for γ-US₂, indicating that the 110 orientation (the most intense peak in the sample) is the preferred orientation when the sample is annealed in a quartz tube. Comparison to calculated γ-US₂ with a March–Dollase parameter for the 110 orientation of 0.46 compares well to the observed pattern (Fig. S16†); meanwhile, comparison to other polymorphs of US₂ (Fig. S17†) do not match. An additional peak at ca. 27° and others broadened into the baseline are consistent with the presence of a small amount of UOS,⁶⁴ attributable to surface oxidation due to adventitious oxygen while storing the sample in a glovebox, especially given that the sulfur content found in elemental analysis is consistent with US₂, not a combination of US₂/UOS. The peak broadening in combination with other semi-crystalline impurities challenges indexing of the pattern for quantitative assignment. 1-US₂ was amorphous and showed no discernible diffraction.

Fig. 4 Powder X-ray diffraction pattern of 2-US₂ (bottom, black) and calculated pattern for γ-US₂ (pink, top) shown for reference. The star at ca. 27° aligns with UOS, which likely arises from surface oxidation of US₂ due to adventitious oxygen during sample storage.

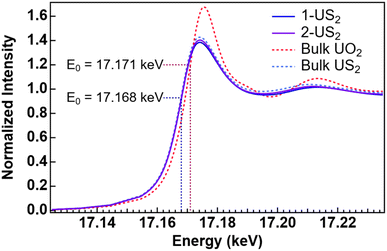
X-ray absorption fine-structure spectroscopy (XAFS) was used to better understand the chemical structure of the complex, as it can provide information on the local atomic structure of the pyrolysis samples and does not rely on crystallinity. To our knowledge, there are no U(IV) disulfide XANES spectra reported for comparison, so the XANES region of a measured bulk β-US₂ sample was compared with bulk UO₂ (Fig. 5). The energy of the inflection point for US₂ (17.168 keV) is 3 eV below that of UO₂ (17.171 keV). This demonstrates that the two tetravalent uranium samples have unique fingerprints and can be distinguished by XANES measurements. The XANES for both pyrolysis samples match the edge energy for bulk US₂, with inflection points around 17.168 keV, thus supporting the formation of US₂.

Fig. 5 XANES comparing 1-US₂ (blue, solid), 2-US₂ (purple, solid), bulk US₂ (blue, dotted), and bulk UO₂ (pink, dotted), with E₀ labeled to demonstrate the energy shift. The E₀ for UO₂ is 17.171 keV, and 17.168 keV for US₂.

Fitting of the extended X-ray absorption fine structure (EXAFS) region further supports the formation of US₂ (Fig. 6). 1-US₂ has only one scattering shell, which is indicative of small crystal size or low crystallinity; given the substantial grain sizes observed in the SEM images, we attribute this case to low crystallinity. The R space data (Fig. 6a) fits well (R% = 16.50, Table 1) with a single U–S′ scattering path (Fig. 7, top). In γ-US₂, the first coordination sphere consists of two crystallographically distinct sulfur types: six sulfur atoms with U–S distance of 2.749 Å and three sulfur atoms with U–S distance of 2.894 Å.^28–33 Within a 95% confidence interval, the coordination number (N) of 5.0(4) as well as the average bond distance (R) of 2.766(6) Å fits well to the expected U–S′ bonds for the six sulfurs found at 2.749 Å in the first coordination shell. Additional single scattering and multiscattering paths at higher R (including the sulfur atoms at 2.894 Å from the central uranium) do not statistically improve the fit model (determined using an F-test). Additionally, the EXAFS data further supports the absence of UO₂ in the pyrolyzed material, as a typical U–O bond length is 2.372 Å, well outside of the error for the model in this material.⁶⁵

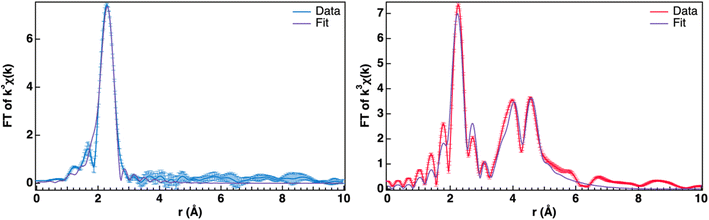Fig. 6 EXAFS U L₃-edge spectra of 1-US₂ (blue, left) and 2-US₂ (pink, right) samples, including fits (purple) and error bars.

Table 1 EXAFS-derived fitting parameters for 1-US₂ and 2-US₂

Sample	Path	ΔE (eV)	N	R (Å)	σ ^2 (Å^2)
1-US2	U–S′	−6.0(1)	5.0(4)	2.766(6)	0.0088(6)
2-US2	U–S′	−5.1(3)	4(1)	2.74(1)	0.004(1)
	U–S′	−5.1(3)	1(1)	2.94(2)	0.002(3)
	U–U	−5.1(3)	2	4.109(8)	0.0004(5)
	U–U	−5.1(3)	12	4.6(2)	0.0004

---

Fig. 7 Crystal structure of γ-US₂.^28–33 Top, the first coordination sphere is shown with the average bond distance for U–S′ scattering labeled in blue. Bottom, the second coordination sphere is shown, with the average distance for U–U scattering labeled in pink.

2-US₂ has additional shells, demonstrating that these samples have greater long-range order, indicative of the higher crystallinity of the sample, therefore enabling more precise fitting (Fig. 6b). To fit the data, additional scattering paths were used in the model, including an additional first shell U–S′ scattering path and a second shell U–U scattering path. The two sulfur types in the first coordination sphere were fit well with an R of 2.74(1) Å and N of 4(1) for the first sulfur type, and R of 2.94(2) Å and N of 1(1) for the second sulfur type (R% = 15.57%, Table 1). In γ-US₂, the second coordination sphere (Fig. 7, bottom) includes two crystallographically distinct U–U scattering paths: two uranium atoms with U–U interatomic distance 4.0740(2) Å and twelve uranium atoms with U–U interatomic distance 4.6530(2) Å.^28–33 The coordination numbers for the second shell were constrained to their crystallographic values in γ-US₂. The modeled second shell U–U interatomic distances of 4.109(8) and 4.6(2) Å match well for the two U–U scattering paths in γ-US₂ (R% = 15.57, Table 1). This EXAFS spectrum is overall in good agreement with tetravalent, hexagonal uranium disulfide.

Additionally, comparison of reported EXAFS for bulk UO₂ ⁶⁶ (which is cubic Fm3̄m) to our measured US₂ samples demonstrates the difference between these two tetravalent materials, both in the first and second scattering shells. The first shell for UO₂ has one scatter, whereas US₂ has two scatters. The R distances are also significantly different between the samples (2.34(3) for UO₂ compared to 2.766(6) for 1-US₂ and 2.74(1) for 2-US₂ in the first shell). Additionally, the second shell U–U scatter for both samples have significantly different U–U interatomic distances (3.87(1) for UO₂ compared to 4.109(8) and 4.6(2) for 2-US₂). This together with the XANES and PXRD data supports the absence of UO₂ in the bulk of the sample.

Comparing the EXAFS of the pyrolysis samples further demonstrates the difference in the crystallinity of the samples. Beyond the lack of a second shell scatter in 1-US₂, the Debye–Waller factor is indicative of crystallinity difference; for the first shell U–S′ scatter, the Debye–Waller factor is higher for 1-US₂ (0.0088(6) Ų) compared to 2-US₂ (0.004(1) and 0.002(3) Ų). This supports the successful annealing of the sample pyrolyzed at 850 °C, as annealing of a material will lead to less disorder in the structure. Despite differences in crystallinity, the agreement between the coordination number and bond distances in the first U–S′ scattering shell of both samples demonstrates that this method is suitable for confirming the formation of tetravalent uranium sulfide materials whether the sample has low crystallinity or high.

Conclusions

This work reports the first homoleptic, tetravalent uranium thioamidate complex, U(ITTA)₄, and demonstrates its viability as a single-source precursor for US₂ materials via solid-state pyrolysis. The U(ITTA)₄ precursor fully decomposed upon heating to 250 °C, and analysis by STA and NMR showed that the decomposition proceeded via alkene elimination, comparable to the analogous amidate complex. Formulation of the solid product as US₂ was confirmed by EA, PXRD, and uranium L₃-edge XANES. Addition of an annealing step in the thermal decomposition increases crystallinity, and the γ-phase of US₂ was clearly identified using PXRD and uranium L₃-edge EXAFS. Imaging by SEM showed that annealing also induces a different morphology, which provides an initial demonstration that there is versatility in controlling material characteristics by controlling the decomposition conditions. Hence, this method provides valuable access to γ-US₂, which has previously been harder to obtain than α- and β-US₂, as it requires multiple steps and a secondary sulfur source to synthesize.^28,29 The presence of the preexisting bond between uranium and sulfur in U(ITTA)₄ and the well-defined decomposition mechanism suggests that U(ITTA)₄ is functioning as a single-source precursor to US₂. The uranium thioamidate complex described here and related analogs have promising potential as precursors to nanomaterials with broad applications, the investigation of which is ongoing in our lab. Additional future work will focus on characterizing the decomposition of U(ITTA)₄ under different physical conditions.

Data availability

Crystallographic data for U(ITTA)₄ has been deposited at the Cambridge Crystallographic Data Centre under deposition number 2353086.† Other data supporting this article have been included as part of the ESI.†

Author contributions

S. N. Kelly performed the synthetic experimental work; recorded and interpreted the NMR and PXRD data; and wrote the original draft of the manuscript. D. R. Russo recorded and interpreted the XAS data. E. T. Ouellette and M. A. Boreen recorded and interpreted the SCXRD data. D. Roy and L. M. Moreau recorded and interpreted the SEM data. A. J. Swift collected the STA data. P. W. Smith recorded the XAS data and provided guidance on 2D-NMR experiments. L. M. Moreau, J. Arnold, and S. G. Minasian conceptualized the research, acquired funding, administrated the project, and supervised the work. All authors revised and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work described here was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, Heavy Element Chemistry Program at the Lawrence Berkeley National Laboratory (LBNL) under contract DE-AC02-05CH11231. S. N. K. acknowledges the U.S. DOE Integrated University Program for a graduate research fellowship. The Advanced Light Source (ALS) is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. DOE under Contract No. DE-AC02-05CH11231. STA work was performed under the auspices of the U.S. Department of Energy (DOE) by Lawrence Livermore National Laboratory (LLNL) under Contract No. DE-AC52-07NA27344. XAFS work was performed at the Stanford Synchrotron Radiation Lightsource, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under contract No. DE-AC02-76SF00515. The authors acknowledge the Franceschi Microscopy & Imaging Center (FMIC) at Washington State University for use of SEM instrumentation. Dr Hasan Celik and the UC Berkeley NMR facility in the College of Chemistry (CoC-NMR) are thanked for spectroscopic assistance. Dr Simon J. Teat is thanked for his assistance during crystallography experiments at the ALS. Dr Mark Straub, Dr Jade Fostvedt, Dr Amy Kynman, Dr Jennifer Wacker, and Dr Christopher Ye are thanked for helpful discussions.

References

1. G. H. Lander, Science, 2003, 301, 1057–1059.
2. H. L. Skriver, O. K. Andersen and B. Johansson, Phys. Rev. Lett., 1978, 41, 42–45.
3. T. Durakiewicz, J. J. Joyce, G. H. Lander, C. G. Olson, M. T. Butterfield, E. Guziewicz, C. D. Batista, A. J. Arko, L. Morales, K. Mattenberger and O. Vogt, Phys. B, 2006, 378–380, 1033–1034.
4. K. D. Vallejo, F. Kabir, N. Poudel, C. A. Marianetti, D. H. Hurley, P. J. Simmonds, C. A. Dennett and K. Gofryk, Rep. Prog. Phys., 2022, 85, 123101.
5. W. Feng, P. Yang, B. Yuan, Z. Hu, X. Zhu, Q. Hao, Y. Zhang, Q. Zhang, B. Wang, S. Tan, X. Lai, Q. Liu and Q. Chen, Phys. Rev. B, 2023, 107, 075136.
6. H. H. Hill, Physica, 1971, 55, 186–206.
7. J. C. Sarker and G. Hogarth, Chem. Rev., 2021, 121, 6057–6123.
8. W. E. Buhro, Adv. Mater. Opt. Electron., 1996, 6, 175–184.
9. L. McElwee-White, Dalton Trans., 2006,(45), 5327.
10. M. D. Khan, M. Opallo and N. Revaprasadu, Dalton Trans., 2021, 50, 11347–11359.
11. A. L. Catherall, S. Harris, M. S. Hill, A. L. Johnson and M. F. Mahon, Cryst. Growth Des., 2017, 17, 5544–5551.
12. A. L. Catherall, M. S. Hill, A. L. Johnson, G. Kociok-Köhn and M. F. Mahon, J. Mater. Chem. C, 2016, 4, 10731–10739.
13. M. Vehkamäki, T. Hatanpää, M. Ritala and M. Leskelä, J. Mater. Chem., 2004, 14, 3191–3197.
14. S. T. Barry, Coord. Chem. Rev., 2013, 257, 3192–3201.
15. M. D. Straub, E. T. Ouellette, M. A. Boreen, J. A. Branson, A. Ditter, A. L. D. Kilcoyne, T. D. Lohrey, M. A. Marcus, M. Paley, J. Ramirez, D. K. Shuh, S. G. Minasian and J. Arnold, Chem. Commun., 2021, 57, 4954–4957.
16. M. D. Straub, J. Leduc, M. Frank, A. Raauf, T. D. Lohrey, S. G. Minasian, S. Mathur and J. Arnold, Angew. Chem., Int. Ed., 2019, 58, 5749–5753.
17. L. Appel, J. Leduc, C. L. Webster, J. W. Ziller, W. J. Evans and S. Mathur, Angew. Chem., 2015, 127, 2237–2241.
18. A. Raauf, J. Leduc, M. Frank, D. Stadler, D. Graf, M. Wilhelm, M. Grosch and S. Mathur, Inorg. Chem., 2021, 60, 1915–1921.
19. A. H. Cowley and R. A. Jones, Polyhedron, 1994, 13, 1149–1157.
20. A. C. Dunbar, J. E. Gozum, W. Lin, V. J. Flores and G. S. Girolami, Inorg. Chem., 2023, 62, 4106–4115.
21. B. L. Scott, J. J. Joyce, T. D. Durakiewicz, R. L. Martin, T. M. McCleskey, E. Bauer, H. Luo and Q. Jia, Coord. Chem. Rev., 2014, 266–267, 137–154.
22. L. M. Harding, E. Lawrence Bright, J. Laverock, D. T. Goddard and R. Springell, Thin Solid Films, 2023, 768, 139690.
23. R. Nicholls, C. Bell, R. Springell, G. H. Lander and J. Bouchet, Phys. Rev. Mater., 2022, 6, 103407.
24. W. V. Goeddel and J. N. Siltanen, Annu. Rev. Nucl. Sci., 1967, 17, 189–250.
25. International Atomic Energy Agency, Thorium Fuel Cycle – Potential Benefits and Challenges, Vienna, 2005.
26. L. Andrews, X. Wang, B. Liang, F. Ruipérez, I. Infante, A. D. Raw and J. A. Ibers, Eur. J. Inorg. Chem., 2011, 2011, 4457–4463.
27. B. T. M. Willis, J. Phys., 1964, 25, 431–439.
28. A. Daoudi, J. C. Levet, M. Potel and H. Noel, Mater. Res. Bull., 1996, 31, 1213–1218.
29. H. Kohlmann and H. P. Beck, Z. Anorg. Allg. Chem., 1997, 623, 785–790.
30. W. Suski, T. Gibiński, A. Wojakowski and A. Czopnik, Phys. Status Solidi A, 1972, 9, 653–658.
31. R. C. L. Mooney Slater, Z. Kristallogr., 1964, 120, 278–285.
32. G. V. Ehllert, G. M. Kuz’micheva, A. A. Eliseev, V. K. Slovyanskikh and S. P. Morozov, Zh. Neorg. Khim., 1974, 19, 2834–2838.
33. F. Grønvold, H. Haraldsen, T. Thurmann-Moe and T. Tufte, J. Inorg. Nucl. Chem., 1968, 30, 2117–2125.
34. H. Sakai, H. Kato, Y. Tokunaga, S. Kambe, R. E. Walstedt, A. Nakamura, N. Tateiwa and T. C. Kobayashi, J. Magn. Magn. Mater., 2004, 272–276, E413–E414.
35. S. Ikeda, H. Sakai, T. D. Matsuda, N. Tateiwa, A. Nakamura, E. Yamamoto, D. Aoki, Y. Homma, Y. Shiokawa, M. Hedo, Y. Uwatoko, Y. Haga and Y. Ōunki, Phys. B, 2008, 403, 893–894.
36. H. Sakai, Y. Tokunaga, Y. Haga, S. Kambe, S. K. Ramakrishna, A. P. Reyes, P. F. S. Rosa, F. Ronning, J. D. Thompson, Z. Fisk and E. D. Bauer, Proceedings of the International Conference on Strongly Correlated Electron Systems (SCES2019), JPS. Conf. Proc., 2020, 30, 011169.
37. H. Noel and J. Y. Le Marouille, J. Solid State Chem., 1984, 52, 197–202.
38. E. D. Cater, E. G. Rauh and R. J. Thorn, J. Chem. Phys., 1968, 48, 538.
39. E. D. Cater, E. G. Rauh and R. J. Thorn, J. Chem. Phys., 1966, 44, 3106–3111.
40. L. Gerward, J. S. Olsen, U. Benedict, J.-P. Dancausse and S. Heathman, in AIP Conference Proceedings, AIP, Colorado Springs, Colorado, USA, 1994, vol. 309, pp. 453–456.
41. F. Grønvold and E. F. Westrum, J. Inorg. Nucl. Chem., 1968, 30, 2127–2133.
42. H. Kohlmann and H. P. Beck, J. Solid State Chem., 2000, 150, 336–341.
43. B. Liang, L. Andrews, N. Ismail and C. J. Marsden, Inorg. Chem., 2002, 41, 2811–2813.
44. J. L. Settle and P. A. G. O’Hare, J. Chem. Thermodyn., 1984,(16), 1175–1180.
45. L. Shlyk and R. Troc, Phys. B, 1999, 262(1–2), 90–97.
46. P. K. Smith and L. Cathey, J. Electrochem. Soc., 1967, 114, 973.
47. S. Ikeda, H. Sakai, N. Tateiwa, T. D. Matsuda, D. Aoki, Y. Homma, E. Yamamoto, A. Nakamura, Y. Shiokawa, Y. Ota, K. Sugiyama, M. Hagiwara, K. Kindo, K. Matsubayashi, M. Hedo, Y. Uwatoko, Y. Haga and Y. Ōnuki, J. Phys. Soc. Jpn., 2009, 78, 114704.
48. E. D. Eastman, L. Brewer, L. A. Bromley, P. W. Gilles and N. L. Lofgren, J. Am. Chem. Soc., 1950, 72, 4019–4023.
49. S.-C. Li, Y.-L. Zheng, S.-G. Ma, T. Gao and B.-Y. Ao, Chin. Phys. B, 2015, 24, 127101.
50. N. Metoki, H. Sakai, E. Yamamoto, Y. Haga, T. D. Matsuda and S. Ikeda, J. Korean Phys. Soc., 2013, 62, 1782–1786.
51. A. Kirishima, Y. Amano, T. Nihei, T. Mitsugashira and N. Sato, IOP Conf. Ser.: Mater. Sci. Eng., 2010, 9, 012062.
52. N. Sato and A. Kirishima, Energy Procedia, 2011, 7, 444–448.
53. F. R. Livens, M. J. Jones, A. J. Hynes, J. M. Charnock, J. F. W. Mosselmans, C. Hennig, H. Steele, D. Collison, D. J. Vaughan, R. A. D. Pattrick, W. A. Reed and L. N. Moyes, J. Environ. Radioact., 2004, 74, 211–219.
54. V. V. Klepov and H.-C. Zur Loye, Inorg. Chem., 2018, 57, 11175–11183.
55. L. S. Breton, V. V. Klepov and H.-C. Zur Loye, J. Am. Chem. Soc., 2020, 142, 14365–14373.
56. M. D. Straub, S. Hohloch, S. G. Minasian and J. Arnold, Dalton Trans., 2018, 47, 1772–1776.
57. A. Catherall, Doctoral Thesis, University of Bath, 2017.
58. D. K. Gioftsidou, M. G. Kallitsakis, K. Kavaratzi, A. G. Hatzidimitriou, M. A. Terzidis, I. N. Lykakis and P. A. Angaridis, Dalton Trans., 2024, 53, 1469–1481.
59. E. Raper, Coord. Chem. Rev., 1996, 153, 199–255.
60. F. Gendron and J. Autschbach, J. Chem. Theory Comput., 2016, 12, 5309–5321.
61. A. J. Gaunt, B. L. Scott and M. P. Neu, Inorg. Chem., 2006, 45, 7401–7407.
62. A. C. Behrle, A. J. Myers, A. Kerridge and J. R. Walensky, Inorg. Chem., 2018, 57, 10518–10524.
63. D. Wang, G. Hou, G. Zi and M. D. Walter, Organometallics, 2021, 40, 383–396.
64. N. Sato, H. Masuda, M. Wakeshima, K. Yamada and T. Fujino, J. Alloys Compd., 1998, 265, 115–120.
65. F. Gronvold and H. Haraldsen, Nature, 1948, 162, 69–70.
66. L. M. Moreau, A. Herve, M. D. Straub, D. R. Russo, R. J. Abergel, S. Alayoglu, J. Arnold, A. Braun, G. J. P. Deblonde, Y. Liu, T. D. Lohrey, D. T. Olive, Y. Qiao, J. A. Rees, D. K. Shuh, S. J. Teat, C. H. Booth and S. G. Minasian, Chem. Sci., 2020, 11, 4648–4668.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2353086. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc03422h

---