Open Access Article
Open Access ArticleEnhanced condensation kinetics in aqueous microdroplets driven by coupled surface reactions and gas-phase partitioning†
Meng
Li‡
 a,
Shu
Yang‡
a,
Shu
Yang‡
 b,
Meenal
Rathi
b,
Meenal
Rathi
 c,
Satish
Kumar
c,
Satish
Kumar
 c,
Cari S.
Dutcher
c,
Cari S.
Dutcher
 *bc and
Vicki H.
Grassian
*bc and
Vicki H.
Grassian
 *a
*a
aDepartment of Chemistry and Biochemistry, University of California San Diego, La Jolla, CA 92093, USA. E-mail: vhgrassian@ucsd.edu
bDepartment of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA. E-mail: cdutcher@umn.edu
cDepartment of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA
First published on 18th July 2024
Abstract
Although aqueous microdroplets have been shown to exhibit enhanced chemical reactivity compared to bulk solutions, mechanisms for these enhancements are not completely understood. Here we combine experimental measurements and kinetic modeling to show the strong coupling of interfacial reactions and gas/droplet partitioning in the condensation reaction of pyruvic acid (PA) to yield zymonic acid (ZA) in acidic aqueous microdroplets. Experimental analysis of single microdroplets reveals the substantial influence of evaporation of PA and partitioning of water on the size-, relative humidity (RH)- and temperature-dependent sigmoidal reaction kinetics for the condensation reaction. A newly developed diffusion–reaction–partitioning model is used to simulate the complex kinetics observed in the microdroplets. The model can quantitatively predict the size and compositional changes as the reaction proceeds under different environmental conditions, and provides insights into how microdroplet reactivity is controlled by coupled interfacial reactions and the gas-phase partitioning of PA and water. Importantly, the kinetic model best fits the data when an autocatalytic step is included in the mechanism, i.e. a reaction step where the product, ZA, catalyzes the interfacial condensation reaction. Overall, the dynamic nature of aqueous microdroplet chemistry and the coupling of interfacial chemistry with gas-phase partitioning are demonstrated. Furthermore, autocatalysis of small organic molecules at the air–water interface for aqueous microdroplets, shown here for the first time, has implications for several fields including prebiotic chemistry, atmospheric chemistry and chemical synthesis.
Introduction
Microdroplet chemistry has major implications in a wide range of fields including atmospheric chemistry, organic synthesis and the origin of life.1–5 An increasingly large number of studies have shown that aqueous microdroplets can enhance reaction rates6–13 and initiate reactions that are otherwise limited in bulk solutions.14–19 The unique properties of the air–water interface have been suggested to be the driving factors for this enhanced reactivity.20–25 As microdroplets have surface-to-volume ratios orders of magnitude higher than bulk solutions, interfacial kinetics and thermodynamics can dominate the reactivity.1,26,27 Additionally, besides the high surface-to-volume ratio, microdroplets are more highly dynamic systems relative to bulk systems. They undergo fast gas/droplet partitioning during the reaction. For example, aqueous microdroplets will change composition to achieve thermodynamic equilibrium with the surrounding gas phase, including with water vapor and acidic gases.28–30 At a specific relative humidity (RH), differences in hygroscopicity of reactants and products will alter water content within microdroplets as the reaction proceeds, leading to shifts not only in the concentration of reactants and products in the microdroplet but also in droplet size. Both concentration and droplet size variations can impact the reaction kinetics in microdroplets; however, there currently lacks a complete understanding of the dynamic nature of partitioning and its impact on microdroplet reactivity.We recently showed that pyruvic acid (PA), a key molecule in biochemistry31–34 and prebiotic chemistry,35 undergoes condensation at the air–water interface in microdroplets but not in the bulk phase. This reaction leads to the formation of zymonic acid (ZA).36 It is known that partial solvation of reactants22 and higher acidity37,38 at the air–water interface can facilitate acid-catalyzed condensation reactions and are highly likely the major contributors to interfacial reactivity. The size-dependent reaction kinetics also exhibit sigmoidal behavior, i.e., three different time-dependent regimes. These include induction followed by reaction and then completion, for both reactant loss and product growth.36 Sigmoidal reaction kinetics have often been suggested as evidence of autocatalysis. Autocatalysis occurs when the product catalyzes its own formation.39,40 Autocatalysis of small organic molecules, including acid/base autocatalytic reactions41,42 and asymmetric autocatalytic reactions,43–46 holds interesting applications including in the nonlinear amplification of organic synthesis. Importantly, autocatalysis of small organic molecules of biological relevance may play a key role in the construction of more complex biomolecules in the origin of life.3,39,47–49 Sigmoidal kinetic profiles may also arise from other distinct processes such as autoinduction and catalyst activation in bulk solutions.44,47,50 Additionally, unlike bulk reactions, the evaporation of PA and the partitioning of water caused by both the evaporation of PA and reaction of PA to less hygroscopic ZA under RH-controlled condition, can affect the concentration profile of both PA and ZA in microdroplets. Therefore, the dynamic nature of the microdroplet composition, size, and surface reactivity driven in part by the gas/droplet partitioning gives rise to complex reaction kinetics, and the reaction mechanism and driving factors behind the sigmoidal kinetics in microdroplets are difficult to deduce and currently unknown.
Here, we show that size-dependent sigmoidal reaction kinetics of PA condensation in acidic aqueous microdroplets exhibit RH and temperature dependences as well as microdroplet size evolution across the sigmoidal reaction kinetic profile. In addition, the product ZA dependence in the kinetics is examined by comparing the kinetics of the reaction of PA when there is only PA within an aqueous microdroplet to when ZA and PA are both initially present. In the latter case, no induction period was observed. Furthermore, experiments were conducted under equilibrium condition to prevent PA evaporation and the corresponding water loss. It is found that the reaction is largely reduced, demonstrating the key role of gas/droplet partitioning in microdroplet chemistry. To disentangle the driving factors behind the complex kinetics, we have developed a diffusion–reaction–partitioning model that combines interfacial reactions, diffusion of PA and ZA, evaporation of PA and partitioning of water under RH-controlled conditions to quantitatively explain the kinetics observed for this condensation reaction. Importantly, although sigmoidal kinetics are observed both in the presence and absence of an additional autocatalytic step in microdroplets, the model only fits key features of the data well when the autocatalytic step is included. Overall, both the model simulation and experiments demonstrate that evaporation of PA and partitioning of water driven by PA loss and ZA formation accelerate the reaction, and the sigmoidal reaction kinetics of PA condensation in microdroplet are driven by coupled interfacial reactions, including an autocatalytic step in the mechanism, and rapid gas/droplet partitioning.
Results and discussion
Acid catalyzed PA condensation in aqueous microdroplets: size-, RH- and temperature-dependent sigmoidal reaction kinetics and droplet size changes
The reaction of PA in single microdroplets and the size change of the microdroplets were monitored by confocal Raman spectroscopy and optical microscopy, respectively. Aqueous microdroplets were prepared from bulk solutions by depositing microdroplets onto a hydrophobic substrate inside a temperature- and RH-controlled environmental cell. The RH was controlled by high-purity N2 gas mixtures of wet and dry flows so that the microdroplet was in equilibrium with water vapor only. Raman spectra of individual acidic aqueous microdroplets containing PA were monitored as a function of time as reaction occurred. In all of these experiments, the initial microdroplet pH was less than 1. Utilizing the ratiometric method, as discussed in the Methods Section and in detail in Li et al.,36 the concentration of PA in the microdroplet was determined for each spectrum and new peaks for ZA were observed that mirrored the loss of PA (vide infra).Fig. 1 combines several different experimental results that show the size dependence of the reaction kinetics at a fixed RH and temperature, the change in the size of the microdroplet over time, and the RH and temperature dependencies for a fixed microdroplet size. As shown in Fig. 1a, the PA concentration profile (mPA) exhibits a sigmoidal shape and, as discussed previously, a droplet size-dependent induction time and slope during the reaction period. Along with the lack of reactivity in bulk solutions and the absence of gas-phase reaction, this demonstrates that the reaction occurs at the air–water interface.36 The droplet decreases in size during the induction and reaction periods, with the size decreasing fastest during the reaction period (Fig. 1b). The decrease in size is associated with both the evaporation of PA, equilibration with RH, and reaction of PA to form ZA, which is less hygroscopic. Moreover, it is found that a decrease in RH, corresponding to an increase in mPA and a reduction in water content, accelerates the reaction, as shown in Fig. 1c. Finally, the influence of temperature on the sigmoidal reaction kinetics was investigated by comparing the mPA profile under different temperature conditions. As shown in Fig. 1d, we observed a shorter induction period and a higher mPA loss rate with increasing temperature. The accelerated reaction kinetics at higher temperature can be attributed to factors including faster diffusion and evaporation, and higher reaction rate constants. Taken together, the experimental data for PA condensation in acidic aqueous microdroplets show size-, RH- and temperature-dependent sigmoidal reaction kinetics and the droplet size is dynamic due to the evaporation and reaction of PA and equilibration with RH. To further understand the reaction kinetics, the presence of ZA, the product of the reaction, on the sigmoidal reaction kinetics is investigated.
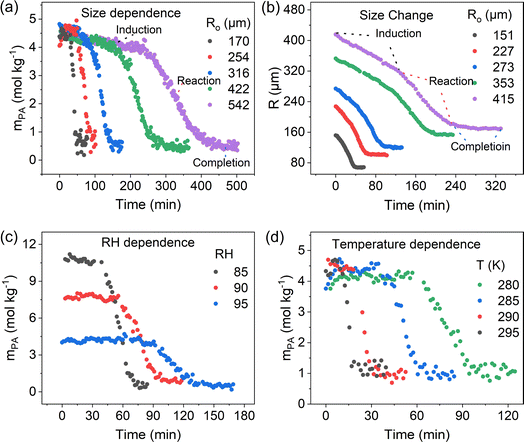 | ||
| Fig. 1 Pyruvic acid (PA) condensation in acidic aqueous microdroplets show size-, RH- and temperature-dependent sigmoidal reaction kinetics as well as microdroplet size evolution. (a) PA concentration (mPA) changes as a function of time in droplets with different initial radii (Ro) at 95% RH, 295 K. (b) Time evolution of microdroplet radius (R) at 95% RH and 295 K. (c) Time evolution of mPA at different RHs and 295 K in droplets with Ro = 320 ± 5 μm. (d) Time evolution of mPA at different temperatures and 95% RH in droplets with Ro = 117 ± 5 μm. The black trace (Ro = 170 μm) in (a), the black (Ro = 151 μm), green (Ro = 353 μm) and purple (Ro = 353 μm) trace in (b), and the black (RH = 85%) and blue (RH = 95%) trace in (c) are reproduced from Li et al.36 | ||
The induction period eliminated by the presence of ZA
In bulk solution, when the reaction is autocatalytic, the induction period of the sigmoidal kinetic profile can be eliminated by adding products to the reaction.39,40,47,50 For reaction in microdroplet, this is done by comparing the kinetics of the reaction of PA when there is only PA within an aqueous microdroplet to when both ZA and PA are present. The droplets initially containing both PA and ZA were produced by adding PA to a reacted ZA droplet. The experimental scheme is shown in Fig. 2 and the Raman and optical data are shown.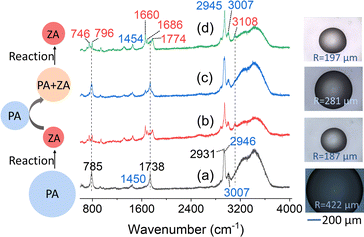 | ||
Fig. 2 Experimental scheme along with examples of Raman spectra and optical images. Left: schematic illustrating the general experimental procedure. An acidic aqueous microdroplet initially containing only PA undergoes condensation, producing mostly ZA, as discussed in detail previously.36 Subsequently, another PA droplet is combined through coalescence with the ZA droplet to produce a new droplet containing both PA and ZA. This droplet is then monitored for the reaction of PA to form ZA. All of the reaction and coalescence experiments were performed at 295 K and 95% RH. Center and right: representative Raman spectra of droplet reactions and coalescence (center) and the corresponding droplet images (right) obtained from the bright-field image of the micro-Raman spectroscopy. (a) The black trace shows the initial Raman spectrum of a 422 μm PA droplet. The peaks from low wavenumber to high wavenumber are ν(C–C) at 785 cm−1, δ(CH3) at 1450 cm−1, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) at 1738 cm−1, ν(CH3)sym of the PA keto form at 2931 cm−1, ν(CH3)sym of the PA diol form at 2946 cm−1, and ν(CH3)asym at 3007 cm−1.51,52 (b) The red trace shows the Raman spectrum after reaction. The droplet now contains mainly ZA.52,53 (c) The blue trace shows the Raman spectrum after more PA is added to the droplet (coalescence). (d) The green trace shows the Raman spectrum after reaction. The droplet now contains mainly ZA. The peak at 796 cm−1 can be assigned to ν(C–C) adjacent to the carboxylic acid group. The peaks at 1660 and 1686 cm−1 are from different ν(C O) at 1738 cm−1, ν(CH3)sym of the PA keto form at 2931 cm−1, ν(CH3)sym of the PA diol form at 2946 cm−1, and ν(CH3)asym at 3007 cm−1.51,52 (b) The red trace shows the Raman spectrum after reaction. The droplet now contains mainly ZA.52,53 (c) The blue trace shows the Raman spectrum after more PA is added to the droplet (coalescence). (d) The green trace shows the Raman spectrum after reaction. The droplet now contains mainly ZA. The peak at 796 cm−1 can be assigned to ν(C–C) adjacent to the carboxylic acid group. The peaks at 1660 and 1686 cm−1 are from different ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) of different forms of ZA, and peaks at 1774 and 3108 cm−1 originate from ν(C C) of different forms of ZA, and peaks at 1774 and 3108 cm−1 originate from ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and vinylic ν( O) and vinylic ν(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H) of ZA, respectively.52,53 The peaks from ZA are labeled in red, the peaks from PA are labeled in black, and the overlapping peaks from both PA and ZA are labeled in blue. C–H) of ZA, respectively.52,53 The peaks from ZA are labeled in red, the peaks from PA are labeled in black, and the overlapping peaks from both PA and ZA are labeled in blue. | ||
The analysis of kinetic data for these different experimental schemes is presented in Fig. 3. A comparison of the data in Fig. 3a and b shows that there is no induction period for microdroplets initially containing both PA and ZA, in contrast to microdroplets with PA only. For ZA formation, a symmetric kinetic profile is observed with the loss of PA (Fig. 3c and d – plotted in terms of the peak areas). These results suggest that ZA accelerates the reaction by eliminating the induction period. Moreover, in Fig. 3 we also compared the reaction kinetics of microdroplets initially containing both PA and ZA of different sizes (Fig. 3b). In addition to comparing droplets with similar initial mPA (red and blue), we also examined a droplet with a lower initial mPA (green), corresponding to a higher initial ZA concentration under RH-controlled condition. Given the varied initial droplet chemical composition and the identical final composition, we used the final droplet size at the end of reaction (Rfinal) rather than the initial size (Ro) when investigating the size dependence, aiming to eliminate the influence from composition. As shown in Fig. 3a and b, the reaction kinetics exhibits a clear dependence on droplet size, as indicated by the faster loss of mPA for smaller microdroplets. Additionally, the size dependence of maximum apparent reaction rate obtained from droplets initially containing both PA and ZA shows good agreement with that obtained from droplets initially containing only PA (Fig. S1 in the ESI†). Indeed, when comparing the time evolution curve of mPA in two microdroplets with identical Rfinal, one initially containing only PA and the other initially containing both PA and ZA, we observe an excellent overlay of the reaction profiles between the two curves after shifting one curve in time (Fig. 3e). This means that the added ZA and ZA formed during the reaction influence the concentration profile of PA in a similar way. The purposeful addition of ZA advances the reaction to the reactive portion of the corresponding sigmoidal kinetic curve.
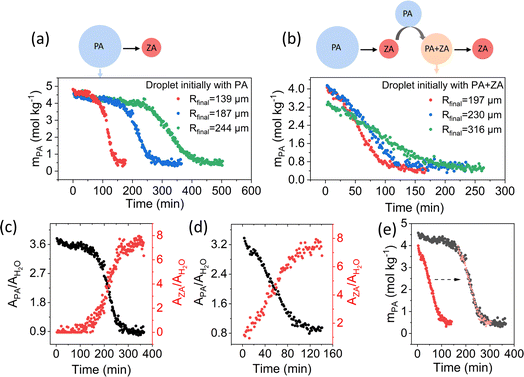 | ||
| Fig. 3 The presence of ZA eliminates the induction period of the reaction kinetic profile of PA condensation in aqueous microdroplets. (a and b) Time evolution of mPA in droplets initially containing only PA (a) compared to droplets initially containing both PA and ZA (b). The droplet initially containing both PA and ZA was produced by the coalescence of a ZA droplet formed from PA reaction and an unreacted PA droplet. (c and d) Time evolution of the peak area ratio of PA and H2O (APA/AH2O) (black) and the peak area ratio of ZA and H2O (AZA/AH2O) (red) in droplet initially containing PA (c) and droplet initially containing both PA and ZA (d). Due to the lack of a standard for ZA, AZA/AH2O was used to reflect ZA concentration. Similarly, APA/AH2O was used to reflect PA concentration. The similar shape between the time evolution of APA/AH2O and mPA in (e), suggests that the peak area ratio is a good choice to reflect the concentration as discussed previously.36 (e) Comparison of changes in mPA in microdroplets with identical final size (Rfinal = 182 ± 2 μm) but different initial composition. Black circles represent the droplet initially containing only PA. Red circles represent the droplet initially containing both PA and ZA. Pink circles correspond to the red data points shifted in time by 165 minutes as indicated by the dashed arrow. | ||
If this occurred for a bulk solution, the sigmoidal reaction kinetics for PA alone and the elimination of the induction period by the addition of ZA would suggest that the condensation of PA is autocatalytic. This is because the reaction rate is proportional to the concentration of product in an autocatalytic reaction when the initial reactant concentration is constant.39,40 However, in microdroplets, the presence of ZA decreases the concentration of PA under RH-controlled condition and moves the reaction to the reactive stage. The reaction of PA in droplets initially with both PA and ZA is intrinsically the same as that in microdroplets initially containing only PA as indicated by the good overlay in Fig. 3e. Therefore, the elimination of induction period by the addition of ZA does not necessarily mean the reaction is autocatalytic in microdroplets. The increasing presence of the lower volatility product, ZA, changes the partitioning of water by absorbing water molecules from the gas phase to the droplet phase. The water absorbed by ZA dilutes PA in the droplet, leading to a decrease in PA concentration and thereby eliminating the induction period. This will be discussed more in the kinetic modelling section (vide infra). Although the elimination of the induction period does not imply autocatalysis in microdroplets, it demonstrates the key role of droplet composition and water partitioning on the reaction kinetics of PA condensation in microdroplets. This is examined more in the next section by controlling PA concentration in the gas-phase.
Key role of gas-phase partitioning of PA and water in reaction kinetics
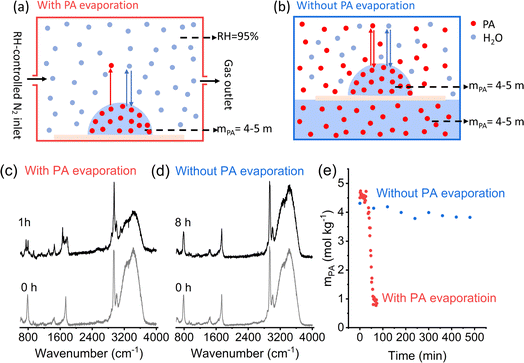
As already noted, all microdroplet experiments discussed above were conducted in an RH-controlled environmental cell, with a continuous flow of humidified N2 to maintain the desired RH since the reaction is RH dependent. In this experimental setup, gas-phase PA is negligible, and the microdroplet remains equilibrium with water vapor, i.e., the water activity in the microdroplet equals RH in the gas phase (Fig. 4a). Since PA is semi-volatile, PA continuously evaporates from the droplet, leading to a decrease in PA concentration and thus an increase in water activity. To reach equilibrium with the gas phase RH, water partitions from the microdroplet to the gas phase along with PA evaporation. To further investigate the role of PA evaporation in the reaction kinetics, the reaction was conducted under an equilibrium pressure of PA by placing a hydrophobic substrate with a deposited PA aqueous microdroplet on top of a PA solution in a sealed container (Fig. 4b). In this case, the microdroplet and bulk solution have identical PA concentrations and they are in equilibrium with the water vapor as well as gas-phase PA; therefore, PA does not evaporate. Importantly, when comparing PA reactivity under these two conditions, we ensure that the microdroplets have an identical initial chemical composition in the droplet phase, as indicated by their identical initial Raman spectra (Fig. 4c and d, gray curves), to avoid any influence from concentration difference.Most strikingly, the experimental data show that the reaction is largely hindered, i.e. without PA evaporation, no significant reactions take place even after 8 hours in a droplet with an Ro of 207 μm. This compares to when PA evaporation occurs, the reaction completes within 1 hour for a droplet of similar size of 211 μm (Fig. 4c–e, and S2 ESI†), suggesting that the time evolution of mZA is caused by the evaporation of PA, partitioning of water and the reaction of PA. These results demonstrate that the evaporation of PA and the corresponding partitioning of water play a crucial role in the reaction kinetics in microdroplets as discussed in more detail below.
Overall, these experimental data clearly show the role of microdroplet/gas partitioning, i.e., PA evaporation and partitioning of water caused by the evaporation and reaction of PA as well as the formation/addition of ZA, on the sigmoidal reaction kinetics of PA condensation at the air–water interface in microdroplets. These data also highlight the need for a mechanism coupling the interfacial reaction and droplet/gas partitioning to fully understand the sigmoidal kinetics and its size, RH and temperature dependence.
Kinetic modeling of aqueous microdroplet reactivity and autocatalysis at the air–water interface
The experimental data provide important insights into the condensation of PA in acidic aqueous microdroplets including important dependencies on size, RH, temperature and gas-phase partitioning, that if quantitatively modeled can provide rich insights into reactions in aqueous microdroplets. Here we present a detailed kinetic model of surface reactions, coupled with evaporation, partitioning and diffusion in a hemispherical microdroplet. The diffusion–reaction–partitioning model enables the estimation of reaction rate coefficients through experimental data fitting and provides insights into the underlying physical mechanisms governing the induction–reaction–completion process. Fig. 5a shows the relevant processes involved in the kinetic model including evaporation, diffusion, and reaction (with and without an autocatalytic step). The detailed equations for the model are provided in the Methods section and the ESI.† | ||
| Fig. 5 Kinetic modeling of autocatalytic condensation reaction of PA at the air–water interface in aqueous microdroplets. (a) Relevant microdroplet processes in the kinetic model include: evaporation of PA and partitioning of water (W); diffusion of PA and ZA; interfacial reactions of PA to form ZA. (b) Proposed mechanism for the autocatalytic PA condensation reaction revealing the role of ZA (red) in catalyzing its own formation at the air–water interface. The reaction is proposed to undergo multiple acid-catalyzed aldol addition, step (1) and (2), in analogy to the formose reaction, where glycolaldehyde formed from the condensation of formaldehyde catalyzes its own formation.54 This is followed by a cyclization (step 3) and an inverse aldol reaction (step 4). (Note: a more detailed mechanism is presented in the ESI Fig. S5.†) (c–f) The model (solid lines) fits the experimental data points (c) (e) in the absence autocatalysis, using reaction rate coefficients kf1 = 0.9 kg mol−1 s−1, kf2 = 0 kg2 mol−2 s−1, kb1 = 0.5 s−1, kb2 = 0 kg mol−1 s−1, and (d) (f) with autocatalysis using reaction rate coefficients kf1 = 0.25 kg mol−1 s−1, kf2 = 0.65 kg2 mol−2 s−1, kb1 = 0.1 s−1, kb2 = 0.08 kg mol−1 s−1. The time evolution of (c) (d) mPA at r = R/2 and (e) (f) R were examined at different Ro. | ||
The interfacial reactions at the water surface involve the reactant PA and the product ZA in the following ways:
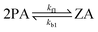 | (1) |
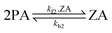 | (2) |
To understand the interplay among diffusion, evaporation, and reactions, we first examine the influence of diffusion. Experimental findings (ESI Fig. S6†) and modeling computations (ESI Fig. S7†) demonstrate negligible PA concentration gradients along the radius. This indicates that rapid diffusion significantly diminishes the formation of concentration gradients resulting from surface reactions and evaporation. Furthermore, the Damköhler number (Da), measuring the ratio of reaction rate to diffusion rate, can be approximated by (DPA/R2)/(kf1m2PA) for the first reaction and (DPA/R2)/(kf2m2PAmZA) for the second reaction, with values ranging from 100 to 1000. The minimal concentration gradient and high Da both indicate that diffusion is not the dominant process in the system compared to reaction and evaporation.
Evaporation is driven by the differences in PA concentration at the droplet surface and in the surrounding gas phase. The reaction and evaporation (or droplet size change) are coupled through the concentrations of PA and ZA. Alongside PA evaporation, changes in droplet sizes also arise from PA and ZA volume change due to reactions, and water exchange due to PA and ZA concentration variation. Under controlled RH conditions, water content depends on the amount of PA and ZA. Loss of one mole of PA through reactions or evaporation result in kPA moles of water evaporation, while production of one mole of ZA from reactions leads to corresponding kZA moles of water condensation. Since the concentration gradient along the radius is negligible due to rapid diffusion, mPA at r = R/2 can be approximated by the mean PA concentration ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) PA
PA
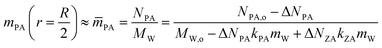 | (3) |
The loss of PA due to both reaction consumption and evaporation results in corresponding water loss but does not change mPA. Thus, when neglecting water absorption by ZA, mPA remains constant at its initial value: mPA = (NPA,o −ΔNPA)/(MW,o − ΔNPAkPAmW) = 4.5 mol kg−1, with this (3) can be reformulated as
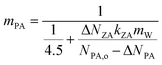 | (4) |
Eqn (4) indicates that mPA depends on the ratio of ZA production rate to PA depletion rate, meaning that mPA is influenced by the extent to which water absorbed by ZA dilutes the current NPA. The interplay between reaction and evaporation at each stage of induction–reaction–completion can be elucidated by (4). During the induction stage at early times, minimal ZA is formed, ΔNZA is low. Water absorption by a limited quantity of ZA does not significantly influence PA and mPA remains approximately 4.5 mol kg−1. The primary process is PA and water evaporation. Over time, as more PA transforms to ZA and PA evaporates, the increase in ΔNZA and ΔNPA reduces mPA, signifying the transition into the reaction phase. The heightened presence of ZA absorbs more water, which dilutes PA and consequently lowers mPA, even in the absence of autocatalytic reaction (consistent with the numerical results shown in Fig. 5). A detailed discussion on the role of evaporation of PA and partitioning of water is presented in the ESI.† Moreover, during the induction and reaction stage, the PA consumed by reaction is 40% less than that lost by evaporation (ESI Fig. S8†). Until mPA approaches zero, the PA evaporation slows down, while ZA maintains a concentration that equalizes the water fraction between the surface and gas phase. Both reactions and evaporation reach completion with minimal temporal variation.
Additionally, both the experimental data and modeling shows that all of the droplets exhibit a similar ratio of ∼0.8 between the size at the end of the induction period and Ro and a ratio of ∼0.45 between the size at the end of reaction period and Ro (Fig. 5f). This uniformity in ratios across droplets of varying sizes arises because the relative time scale of PA evaporation to reaction remains constant at identical mPA. This temporal relationship dictates the extent of droplet evaporation or size reduction until sufficient ZA is generated, marking the conclusion of either the induction or reaction stage.
A key advantage of modeling is the ability to disentangle the effects of reaction and evaporation, providing a clearer understanding of their individual contributions to mPA. Fig. 6a and b present a comparison of mPA and R evolution across various scenarios: initially addition of ZA, no reaction (kfi = kbi = 0), and no PA evaporation. In the presence of ZA within the initial droplet composition, the induction stage is absent, as a greater quantity of ZA begins to absorb water and dilute PA immediately, consistent with experimental results shown in Fig. 3b. Completion occurs more rapidly and results in significantly larger final droplet radii.
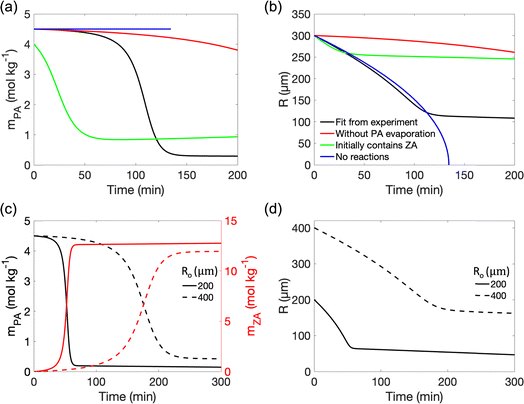 | ||
| Fig. 6 Kinetic modeling revealing the driving factors for the autocatalytic condensation reaction of PA in aqueous microdroplets. (a and b) Time evolution of (a) mPA and (b) R is examined under different conditions: using parameters fitted from experiments, in the absence of PA evaporation, with initial inclusion of 4 mol kg−1 ZA in droplets, and when no reactions occur (kfi = kbi = 0). (c and d) Time evolution of (c) mPA (indicated by black lines with left axis) and ZA concentration (mZA, indicated by red lines with right axis) and (d) R is examined for droplets with Ro of 200 μm (solid lines) and 400 μm (dashed lines). The reaction rate constants used here are the same as those in Fig. 5d and f. | ||
In the absence of reaction, the departure of PA and water from the droplet occurs at a consistent ratio, thereby maintaining a constant mPA until complete liquid evaporation occurs (Fig. 6a and b). Initially, the reaction accelerates evaporation by promoting water departure through the consumption of PA but later slows down the reduction in R as water is absorbed by ZA. Autocatalysis can amplify ZA generation and corresponding water absorption, resulting in a noticeable acceleration of the slope for both R and mPA during the reaction phase. Conversely, such augmentation is less pronounced in the absence of autocatalysis, as illustrated in Fig. 5. Note that, Fig. 6b also shows that during the induction period when reactions are minimal, the rate of change in R is insignificant.
In the absence of PA evaporation, the decline in mPA exhibits a notably slower rate as shown in Fig. 6a, aligning with experimental results shown in Fig. 4e. PA evaporation accelerates the reduction in mPA through two mechanisms: Firstly, PA evaporation reduces the total number of moles of PA (NPA), leading to stronger dilution of PA with the same absorbed water by ZA. This is evident in (4), where mPA decreases with decreasing NPA = NPA,o − ΔNPA. Secondly, PA evaporation concentrates ZA, accelerating autocatalytic reaction.
The preceding analysis demonstrates a mutual reinforcement between PA evaporation and reaction, particularly evident in the presence of autocatalytic reactions. Note that Fig. 5 indicates the autocatalysis reaction plays a more significant role in achieving precise predictions for droplets with larger Ro, thus prompting further investigation into the influence of Ro on microdroplet kinetics. Fig. 6c and d compare the kinetics of microdroplets with Ro = 200 μm and 400 μm. To elucidate the results, we estimate mZA by dividing the total number of moles of ZA generated by surface reaction by the total mass of water:
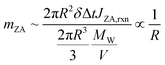 | (5) |
Conclusions
Here we show that PA condensation at the air–water interface in microdroplets exhibits size-, RH- and temperature-dependent sigmoidal reaction kinetics as well as microdroplet size evolution. Moreover, it is found that the presence of ZA, evaporation of PA and the corresponding partitioning of water under RH-controlled condition have strong effects on the reaction kinetics. We develop a kinetic model combining the interfacial reaction with diffusion, evaporation and partitioning to simulate the complex reaction kinetics in microdroplets. Combining experimental measurements and kinetic model analysis demonstrate that the strong coupling of interfacial reactions and gas/droplet partitioning drives PA condensation kinetics in aqueous microdroplets. Overall, we show interfacial processes drive the chemistry of microdroplets. These processes include interfacial reactions and partitioning which explain the size-dependent sigmoidal kinetics in a quantitative way as well as the dependence on RH, temperature, and dynamic changes in microdroplet size as the reaction proceeds. Furthermore, these findings may provide new insights into autocatalytic reactions, a class of reactions that have been discussed in great detail given their proposed role in prebiotic chemistry.Methods
Experimental methods
The generation of microdroplets, in situ micro-Raman spectroscopy analysis and kinetics analysis have been previously described in detail.36 Briefly, a single aqueous microdroplet is deposited on a hydrophobic coverslip using a micropipette, and the coverslip is placed inside an RH- and temperature-controlled environmental cell (Linkam, LTS 120). The microdroplet was generated using a micropipette and within less than 10 seconds it was deposited on the substrate. After this step, the focus of the laser was adjusted on the droplet and a spectrum was collected within another ∼1.5 minutes. All experiments, except for those investigating the influence of temperature and RH, were performed at 95% RH and 295 K under dark conditions. The RH was controlled by high-purity N2 gas mixtures of wet and dry flows with a total flow rate of 1 L min−1. A confocal Raman microscope (Horiba, LabRamn HR evolution) is used to collect optical images and Raman spectra utilizing a 532 nm laser during the microdroplet reaction. As already noted, the concentration of PA in microdroplets was determined using a ratiometric calibration method which correlates the Raman peak area ratio of PA and water to PA concentration. For the droplet coalescence experiments, a microdroplet containing PA was placed on the coverslip and allowed to react to completion to form ZA. Following the reaction, additional PA was added to the reacted droplet to produce a new droplet with PA and ZA. The kinetics of PA to form ZA was then monitored. The PA bulk solution used to generate droplets had a concentration of 4.5 mol kg−1, corresponding to the PA concentration in aqueous microdroplets in equilibrium with 95% RH within the environmental cell. A discussion on the influence of non-equilibrium water loss following the sample preparation on size and concentration changes is present in the ESI.† Although the bulk solution was 4.5 mol kg−1, it is worth noting that the droplet concentration did not remain precisely at 4.5 mol kg−1, instead, the concentration when equilibrated at 95% RH was in the range of range of 4 to 5 mol kg−1, due to small fluctuations of the RH (±1%) inside the environmental cell. For reactions under conditions without PA evaporation, a single microdroplet deposited on a hydrophobic coverslip was placed on the top of a PA solution with a concentration of 4.5 mol kg−1 in a Petri dish with an inner diameter of 22 mm and a height of 7 mm. The Petri dish was covered by a coverslip to allow for the equilibrium between the bulk solution, microdroplet and gas-phase water and PA.Kinetic model
The model characterizes a hemispherical droplet with a radius R containing solutes PA and ZA, both of which undergo surface reactions (1) and (2). The choice of hemispherical geometry is based on experimental observations indicating that the droplet shape closely resembles a hemisphere with a contact angle of 94 ± 4°.36 Here we neglect specific adsorption/desorption processes within the microdroplets, so PA and ZA will not exhibit surfactant properties in the model. PA, along with water, experiences evaporation, whereas ZA exhibits non-volatile behavior. Given the symmetry in both polar and azimuthal directions, the problem is confined to the radial coordinate r and time t. PA and ZA have bulk concentrations CX(r,t), where the subscript X can be PA or ZA. Note that here we employ molar concentration CX (moles per cubic meter of solution) in the following derivations, the result will later be converted to mX (moles per kilogram of water) for comparison with experimental data. The primary nomenclature used in the derivation is listed in Table 1. In the droplet (0 < r < R(t)), the bulk concentration is governed by diffusion equations: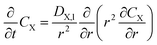 | (6) |
| Parameter | Nomenclature | Units |
|---|---|---|
| C X | Ratio of mole of solute to the volume of solvent | mol m−3 |
| m X | Ratio of mole of solute to per kilogram water | mol kg−1 |
| V X | Volume | m3 |
| v X | Molar volume | m3 mol−1 |
The diffusion coefficient DX,l of substance X in the liquid phase is provided in Table 2, along with other parameters used in the governing equations. At r = 0, there is no-flux boundary condition:
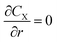 | (7) |
| Parameter | Value | Units |
|---|---|---|
| D PA,l | 2.5 × 10−10 | m2 s−1 |
| D ZA,l | 1.8 × 10−10 | m2 s−1 |
| D PA,g | 9.8 × 10−6 | m2 s−1 |
| P sat,PA | 107 | Pa |
| ν PA | 7.0 × 10−5 | m3 mol−1 |
| ν ZA | 1.3 × 10−4 | m3 mol−1 |
| ν w | 1.8 × 10−5 | m3 mol−1 |
At r = R, the boundary conditions come from the conservation of mass, for PA:
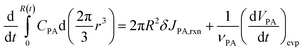 | (8) |
The left-hand side of (8) is the rate of change of the total moles of PA in the droplet. On the right-hand side, the first term is the moles of PA consumed at the interface per unit time through reaction. δ is the thickness of reaction surface, and we set δ = 1 nm, similar to the studies of Wilson and coworkers.2,26,27 The rate change of CPA (r = R) due to reaction is denoted by JPA,rxn. The second term is the moles of PA leaving droplet per unit time via evaporation (this term will be given in (14)), where νPA is the molar volume of PA, denoting the volume of PA per mole. Similarly, for nonvolatile ZA, the mass conservation equation is:
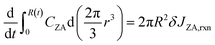 | (9) |
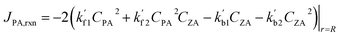 | (10) |
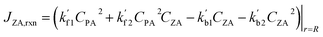 | (11) |
Note that 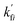 and
and 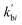 are reaction rate coefficients associated with molar concentration.
are reaction rate coefficients associated with molar concentration.
Using Leibniz's rule and substituting (6) into (8) and (9) yields boundary conditions at r = R:
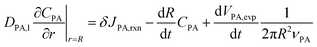 | (12) |
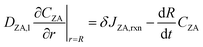 | (13) |
The diffusion eqn (6) is subject to mass-conservation conditions (12) and (13) at the moving boundary r = R(t). The following size-changing model is developed to derive the expression for R(t), which can be influenced by PA evaporation, PA and ZA reactions, and water partitioning. For diffusion-controlled evaporation in a hemispherical droplet, the volume change due to the evaporation of PA can be calculated by integrating evaporative flux −DPA,g ΔCPAνPA/r2 over the hemispherical surface:55,56
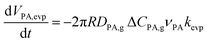 | (14) |
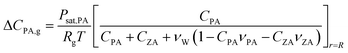 | (15) |
The dimensionless constant correction kevp in (14) quantifies the relative difference in evaporation rates between the model and experimental data, and in this work, it is a fitting parameter. This disparity may arise from the non-ideal mixing of the microdroplet, neglected adsorption and desorption processes within the droplet, and the perfect hemisphere assumption. In particular, since the activity coefficient of PA and the impact of other non-ideal factors on the evaporation rate are unknown, kevp needs to be determined through fitting from the induction period. The induction period can be used to parameterize this difference in how evaporation is captured, because during this period, the reaction is minimal, and the droplet size evolution is dominated by evaporation PA and water. In all the results presented above, kevp = 0.6.
The change in volume of X resulting from reactions are:
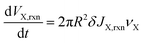 | (16) |
Under RH-controlled conditions, the water partitioning in microdroplets is determined by the content of PA and ZA according to the Zdanovskii–Stokes–Robinson mixing rule.57 As discussed in the Results and discussion section, at a given RH, the change of one mole of X corresponds to a change of kX moles of water, leading to the relation dVW/dVX = kXνw/νX. kX is RH dependent. Here at RH = 95%, we have kPA = 12.4 and kZA = 4.2 calculated from the molality of pure PA and pure ZA at 95% RH, respectively. PA molality is obtained from the mPA during the induction period and has a value of 4.5 mol kg−1 under 95% RH. ZA molality is estimated to 13.3 mol kg−1 under 95% RH using the Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients (AIOMFAC) model58 (aiomfac.lab.mcgill.ca). The molality of pure PA and pure ZA at different RHs is provided in ESI Table S2.† Consequently, the water content change resulting from X content change is:
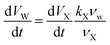 | (17) |
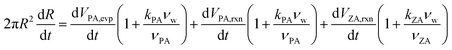 | (18) |
The diffusion-reaction-partitioning process in the droplet is described by coupled governing eqn (18), (6, 7), and (12, 13). To solve this moving boundary problem, a coordinate transformation (r, t) → (η,τ) is performed with the relations:
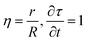 | (19) |
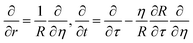 | (20) |
After applying transformation (19, 20) to (6, 7) and (12, 13), the centered second-order finite-difference method is used for the discretization of the spatial domain of the resulting governing equations on the constant domain η ∈ (0,1). Time stepping is performed using the ode15s solver in MATLAB. The convergence analysis indicates that employing 100 grid points in the spatial domain was more than sufficient. It should be noted that our model disregards the deviations from ideal hemispherical droplet shapes and potential variations in the molecular forms of PA and ZA. Our objective is to develop a simplified model to characterize the kinetics in the sessile microdroplets and predict experimental results quantitatively. The optimal values of reaction rate constants were obtained based on fitting the experimental data.
Data availability
The experimental data supporting this article have been included in the main text and the ESI.† The data that support the findings of each model related figure in this study are openly available in figshare at https://doi.org/10.6084/m9.figshare.26339230.Author contributions
M. L., V. H. G., S. Y. and C. S. D. designed the research. M. L. performed the experiments. S. Y., M. R., S. K. and C. S. D. developed the model. M. L., V. G. H., S. Y., C. S. D., M. R. and S. K. discussed the results. M. L., S. Y., C. S. D and V. H. G. wrote the manuscript with input from all co-authors.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is supported by the Air Force Office of Scientific Research FA9550-22-1-0199 (MURI-22). VHG would like to thank Professors Veronica Vaida and Barney Ellison for thoughtful discussions.Notes and references
- B. R. Bzdek, J. P. Reid and M. I. Cotterell, Open questions on the physical properties of aerosols, Commun. Chem., 2020, 3, 105 CrossRef CAS PubMed.
- M. D. Willis and K. R. Wilson, Coupled interfacial and bulk kinetics govern the timescales of multiphase ozonolysis reactions, J. Phys. Chem. A, 2022, 126, 4991–5010 CrossRef CAS PubMed.
- H. Lu, A. Blokhuis, R. Turk-MacLeod, J. Karuppusamy, A. Franconi, G. Woronoff, C. Jeancolas, A. Abrishamkar, E. Loire, F. Ferrage, P. Pelupessy, L. Jullien, E. Szathmary, P. Nghe and A. D. Griffiths, Small-molecule autocatalysis drives compartment growth, competition and reproduction, Nat. Chem., 2024, 16, 70–78 CrossRef CAS PubMed.
- C. M. Dobson, G. B. Ellison, A. F. Tuck and V. Vaida, Atmospheric aerosols as prebiotic chemical reactors, Proc. Natl. Acad. Sci. U.S.A., 2000, 97, 11864–11868 CrossRef CAS PubMed.
- D. T. Holden, N. M. Morato and R. G. Cooks, Aqueous microdroplets enable abiotic synthesis and chain extension of unique peptide isomers from free amino acids, Proc. Natl. Acad. Sci. U.S.A., 2022, 119, e2212642119 CrossRef CAS PubMed.
- Z. Wei, Y. Li, R. G. Cooks and X. Yan, Accelerated reaction kinetics in microdroplets: Overview and recent developments, Annu. Rev. Phys. Chem., 2020, 71, 31–51 CrossRef CAS PubMed.
- H. Song, D. L. Chen and R. F. Ismagilov, Reactions in droplets in microfluidic channels, Angew. Chem., Int. Ed., 2006, 45, 7336–7356 CrossRef CAS PubMed.
- X. Yan, R. M. Bain and R. G. Cooks, Organic reactions in microdroplets: Reaction acceleration revealed by mass spectrometry, Angew. Chem., Int. Ed., 2016, 55, 12960–12972 CrossRef CAS PubMed.
- T. Liu and J. P. D. Abbatt, Oxidation of sulfur dioxide by nitrogen dioxide accelerated at the interface of deliquesced aerosol particles, Nat. Chem., 2021, 13, 1173–1177 CrossRef CAS PubMed.
- W. Wang, M. Liu, T. Wang, Y. Song, L. Zhou, J. Cao, J. Hu, G. Tang, Z. Chen, Z. Li, Z. Xu, C. Peng, C. Lian, Y. Chen, Y. Pan, Y. Zhang, Y. Sun, W. Li, T. Zhu, H. Tian and M. Ge, Sulfate formation is dominated by manganese-catalyzed oxidation of SO2 on aerosol surfaces during haze events, Nat. Commun., 2021, 12, 1993 CrossRef CAS PubMed.
- K. J. Angle, E. E. Neal and V. H. Grassian, Enhanced rates of transition-metal-ion-catalyzed oxidation of S(IV) in aqueous aerosols: Insights into sulfate aerosol formation in the atmosphere, Environ. Sci. Technol., 2021, 55, 10291–10299 CrossRef CAS PubMed.
- G. Rovelli, M. I. Jacobs, M. D. Willis, R. J. Rapf, A. M. Prophet and K. R. Wilson, A critical analysis of electrospray techniques for the determination of accelerated rates and mechanisms of chemical reactions in droplets, Chem. Sci., 2020, 11, 13026–13043 RSC.
- A. Fallah-Araghi, K. Meguellati, J.-C. Baret, A. E. Harrak, T. Mangeat, M. Karplus, S. Ladame, C. M. Marques and A. D. Griffiths, Enhanced chemical synthesis at soft interfaces: A universal reaction-adsorption mechanism in microcompartments, Phys. Rev. Lett., 2014, 112, 028301 CrossRef PubMed.
- J. K. Lee, D. Samanta, H. G. Nam and R. N. Zare, Micrometer-sized water droplets induce spontaneous reduction, J. Am. Chem. Soc., 2019, 141, 10585–10589 CrossRef CAS PubMed.
- J. K. Lee, K. L. Walker, H. S. Han, J. Kang, F. B. Prinz, R. M. Waymouth, H. G. Nam and R. N. Zare, Spontaneous generation of hydrogen peroxide from aqueous microdroplets, Proc. Natl. Acad. Sci. U.S.A., 2019, 116, 19294–19298 CrossRef CAS PubMed.
- S. Jin, H. Chen, X. Yuan, D. Xing, R. Wang, L. Zhao, D. Zhang, C. Gong, C. Zhu, X. Gao, Y. Chen and X. Zhang, The Spontaneous electron-mediated redox processes on sprayed water microdroplets, JACS Au, 2023, 3, 1563–1571 CrossRef CAS PubMed.
- K. Li, Y. Guo, S. A. Nizkorodov, Y. Rudich, M. Angelaki, X. Wang, T. An, S. Perrier and C. George, Spontaneous dark formation of OH radicals at the interface of aqueous atmospheric droplets, Proc. Natl. Acad. Sci. U.S.A., 2023, 120, e2220228120 CrossRef CAS PubMed.
- Z. Rao, X. Li, Y.-G. Fang, J. S. Francisco, C. Zhu and C. Chu, Spontaneous oxidation of thiols and thioether at the air–water interface of a sea spray microdroplet, J. Am. Chem. Soc., 2023, 145, 10839–10846 CrossRef CAS PubMed.
- Y. Meng, E. Gnanamani and R. N. Zare, Catalyst-free decarboxylative amination of carboxylic acids in water microdroplets, J. Am. Chem. Soc., 2022, 145, 32–36 CrossRef PubMed.
- H. Hao, I. Leven and T. Head-Gordon, Can electric fields drive chemistry for an aqueous microdroplet?, Nat. Commun., 2022, 13, 280 CrossRef CAS PubMed.
- M. T. C. Martins-Costa and M. F. Ruiz-López, Electrostatics and chemical reactivity at the air–water interface, J. Am. Chem. Soc., 2023, 145, 1400–1406 CrossRef CAS PubMed.
- L. Qiu, Z. Wei, H. Nie and R. G. Cooks, Reaction acceleration promoted by partial solvation at the gas/solution interface, ChemPlusChem, 2021, 86, 1362–1365 CrossRef CAS PubMed.
- K.-H. Huang, Z. Wei and R. G. Cooks, Accelerated reactions of amines with carbon dioxide driven by superacid at the microdroplet interface, Chem. Sci., 2021, 12, 2242–2250 RSC.
- A. J. Colussi, Mechanism of hydrogen peroxide formation on sprayed water microdroplets, J. Am. Chem. Soc., 2023, 145, 16315–16317 CrossRef CAS PubMed.
- M. F. Ruiz-López and M. T. C. Martins-Costa, Disentangling reaction rate acceleration in microdroplets, Phys. Chem. Chem. Phys., 2022, 24, 29700–29704 RSC.
- K. R. Wilson and A. M. Prophet, Chemical kinetics in microdroplets, Annu. Rev. Phys. Chem., 2024, 75, 185–208 CrossRef PubMed.
- K. R. Wilson, A. M. Prophet, G. Rovelli, M. D. Willis, R. J. Rapf and M. I. Jacobs, A kinetic description of how interfaces accelerate reactions in micro-compartments, Chem. Sci., 2020, 11, 8533–8545 RSC.
- R. E. H. Miles, M. Guillon, L. Mitchem, D. McGloin and J. P. Reid, The influence of resonant absorption and heating on the equilibrium size of aqueous-solute aerosol droplets, Phys. Chem. Chem. Phys., 2009, 11, 7312–7317 RSC.
- K. J. Angle and V. H. Grassian, Direct quantification of changes in pH within single levitated microdroplets and the kinetics of nitrate and chloride depletion, Chem. Sci., 2023, 14, 6259–6268 RSC.
- K. J. Angle, C. M. Nowak and V. H. Grassian, Organic acid evaporation kinetics from aqueous aerosols: implications for aerosol buffering capacity in the atmosphere, Environ. Sci.: Atmos., 2023, 3, 316–327 CAS.
- M. I. Guzman and S. T. Martin, Prebiotic metabolism: Production by mineral photoelectrochemistry of α-ketocarboxylic acids in the reductive tricarboxylic acid cycle, Astrobiology, 2009, 9, 833–842 CrossRef CAS PubMed.
- G. D. Cody, N. Z. Boctor, T. R. Filley, R. M. Hazen, J. H. Scott, A. Sharma and H. S. Yoder, Primordial carbonylated iron-sulfur compounds and the synthesis of pyruvate, Science, 2000, 289, 1337–1340 CrossRef CAS PubMed.
- N. Maleki and M. A. Eiteman, Recent progress in the microbial production of pyruvic acid, Fermentation, 2017, 3, 8 CrossRef.
- G. Cooper, C. Reed, D. Nguyen, M. Carter and Y. Wang, Detection and formation scenario of citric acid, pyruvic acid, and other possible metabolism precursors in carbonaceous meteorites, Proc. Natl. Acad. Sci. U.S.A., 2011, 108, 14015–14020 CrossRef CAS PubMed.
- N. F. Kleimeier, A. K. Eckhardt, P. R. Schreiner and R. I. Kaiser, Interstellar formation of biorelevant pyruvic acid (CH3COCOOH), Chem, 2020, 6, 3385–3395 CAS.
- M. Li, C. Boothby, R. E. Continetti and V. H. Grassian, Size-dependent sigmoidal reaction kinetics for pyruvic acid condensation at the air–water interface in aqueous microdroplets, J. Am. Chem. Soc., 2023, 145, 22317–22321 CrossRef CAS PubMed.
- S. Das, M. Bonn and E. H. G. Backus, The surface activity of the hydrated proton Is substantially higher than that of the hydroxide ion, Angew. Chem., Int. Ed., 2019, 58, 15636–15639 CrossRef CAS PubMed.
- K.-Y. Chiang, L. Dalstein and Y.-C. Wen, Affinity of hydrated protons at intrinsic water/vapor interface revealed by ion-induced water alignment, J. Phys. Chem. Lett., 2020, 11, 696–701 CrossRef CAS PubMed.
- A. J. Bissette and S. P. Fletcher, Mechanisms of autocatalysis, Angew. Chem., Int. Ed., 2013, 52, 12800–12826 CrossRef CAS PubMed.
- A. I. Hanopolskyi, V. A. Smaliak, A. I. Novichkov and S. N. Semenov, Autocatalysis: Kinetics, mechanisms and design, ChemSystemsChem, 2021, 3, e2000026 CrossRef CAS.
- K. Ichimura, Nonlinear organic reactions to proliferate acidic and basic molecules and their applications, Chem. Rec., 2002, 2, 46–55 CrossRef CAS PubMed.
- Y. Xu, Q. Chen, Y.-j. Zhao, J. Lv, Z.-h. Li and X.-b. Ma, Autocatalytic kinetic study of dimethyl oxalate consecutive hydrolysis, Ind. Eng. Chem. Res., 2014, 53, 4207–4214 CrossRef CAS.
- T. Kawasaki, Y. Matsumura, T. Tsutsumi, K. Suzuki, M. Ito and K. Soai, Asymmetric autocatalysis triggered by carbon isotope (13C/12C) chirality, Science, 2009, 324, 492–495 CrossRef CAS PubMed.
- D. G. Blackmond, Autocatalytic models for the origin of biological homochirality, Chem. Rev., 2020, 120, 4831–4847 CrossRef CAS PubMed.
- K. Soai, T. Kawasaki and A. Matsumoto, Asymmetric autocatalysis of pyrimidyl alkanol and its application to the study on the origin of homochirality, Acc. Chem. Res., 2014, 47, 3643–3654 CrossRef CAS PubMed.
- D. G. Blackmond, Asymmetric autocatalysis and its implications for the origin of homochirality, Proc. Natl. Acad. Sci. U.S.A., 2004, 101, 5732–5736 CrossRef CAS PubMed.
- D. G. Blackmond, An examination of the role of autocatalytic cycles in the chemistry of proposed primordial reactions, Angew. Chem., Int. Ed., 2009, 48, 386–390 CrossRef CAS PubMed.
- B. J. Cafferty, A. S. Y. Wong, S. N. Semenov, L. Belding, S. Gmür, W. T. S. Huck and G. M. Whitesides, Robustness, entrainment, and hybridization in dissipative molecular networks, and the origin of life, J. Am. Chem. Soc., 2019, 141, 8289–8295 CrossRef CAS PubMed.
- S. N. Semenov, L. J. Kraft, A. Ainla, M. Zhao, M. Baghbanzadeh, V. E. Campbell, K. Kang, J. M. Fox and G. M. Whitesides, Autocatalytic, bistable, oscillatory networks of biologically relevant organic reactions, Nature, 2016, 537, 656–660 CrossRef CAS PubMed.
- M. P. Mower and D. G. Blackmond, Mechanistic rationalization of unusual sigmoidal kinetic profiles in the Machetti–De Sarlo cycloaddition reaction, J. Am. Chem. Soc., 2015, 137, 2386–2391 CrossRef CAS PubMed.
- I. D. Reva, S. G. Stepanian, L. Adamowicz and R. Fausto, Combined FTIR matrix isolation and ab initio studies of pyruvic acid: Proof for existence of the second conformer, J. Phys. Chem. A, 2001, 105, 4773–4780 CrossRef CAS.
- B. P. Gordon, F. G. Moore, L. F. Scatena and G. L. Richmond, On the rise: Experimental and computational vibrational sum frequency spectroscopy studies of pyruvic acid and its surface-active oligomer species at the air–water interface, J. Phys. Chem. A, 2019, 123, 10609–10619 CrossRef CAS PubMed.
- R. J. Perkins, R. K. Shoemaker, B. K. Carpenter and V. Vaida, Chemical equilibria and kinetics in aqueous solutions of zymonic acid, J. Phys. Chem. A, 2016, 120, 10096–10107 CrossRef CAS PubMed.
- R. Breslow, On the mechanism of the formose reaction, Tetrahedron Lett., 1959, 1, 22–26 CrossRef.
- A.-M. Cazabat and G. Guéna, Evaporation of macroscopic sessile droplets, Soft Matter, 2010, 6, 2591–2612 RSC.
- S. Armstrong, G. McHale, R. Ledesma-Aguilar and G. G. Wells, Pinning-free evaporation of sessile droplets of water from solid surfaces, Langmuir, 2019, 35, 2989–2996 CrossRef CAS PubMed.
- R. Stokes and R. Robinson, Interactions in aqueous nonelectrolyte solutions. I. Solute-solvent equilibria, J. Phys. Chem., 1966, 70, 2126–2131 CrossRef CAS.
- A. Zuend, C. Marcolli, A. M. Booth, D. M. Lienhard, V. Soonsin, U. K. Krieger, D. O. Topping, G. McFiggans, T. Peter and J. H. Seinfeld, New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic–inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 2011, 11, 9155–9206 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03014a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |