Multiconfigurational actinide nitrides assisted by double Möbius aromaticity

Abstract

Understanding the bonding nature between actinides and main-group elements remains a key challenge in actinide chemistry due to the involvement of f orbitals. Herein, we propose a unique “aromaticity-assisted multiconfiguration” (AAM) model to elucidate the bonding nature in actinide nitrides (An₂N₂, An = Ac, Th, Pa, U). Each planar four-membered An₂N₂ with equivalent An–N bonds possesses four delocalized π electrons and four delocalized σ electrons, forming a new family of double Möbius aromaticity that contributes to the molecular stability. The unprecedented aromaticity further supports actinide nitrides to exhibit multiconfigurational characters, where the unpaired electrons (2, 4 or 6 in naked Th₂N₂, Pa₂N₂ or U₂N₂, respectively) either are spin-free and localized on metal centres or form metal–ligand bonds. High-level multiconfigurational computations confirm an open-shell singlet ground state for actinide nitrides, with small energy gaps to high spin states. This is consistent with the antiferromagnetic nature observed experimentally in uranium nitrides. The novel AAM bonding model can be authenticated in both experimentally identified compounds containing a U₂N₂ motif and other theoretically modelled An₂N₂ clusters and is thus expected to be a general chemical bonding pattern between actinides and main-group elements.

---

Introduction

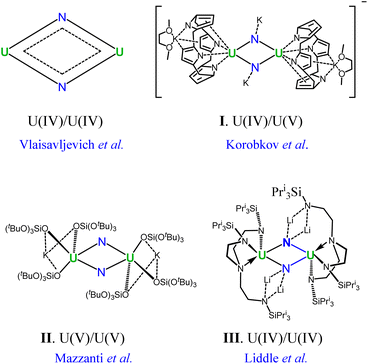
Actinide chemistry, despite its fundamental and practical significance, remains one of the most unexplored domains in the periodic table.^1–4 Notably, uranium–nitrogen chemistry is of vital importance as uranium nitrides have the potential to be next-generation nuclear fuels.⁵ Furthermore, most recently there has been growing interest in uranium nitrides due to their high reactivity towards N₂ fixation and small-molecule activation.^6–10 For instance, uranium nitride materials have been used as catalysts in the Haber–Bosch process for the synthesis of NH₃ from N₂ and H₂.^11–13 Beyond practical applications in nuclear energy and catalytic processes, interest in uranium nitrides also arises from their fundamental role in understanding the chemical bonding of molecular actinides where f orbitals are involved.^14–16 Although so far only three uranium nitride solids have been well-identified,¹⁷ a plethora of molecular species containing terminal and bridged uranium nitrides have been reported over the past few decades.^18–22 But the abundance of molecular uranium nitrides has not been translated into a comprehensive understanding of the uranium–nitrogen bonding nature, which lags far behind the well-established bonding regimes between uranium and other main-group elements.^23–25 Accordingly, the development of rational synthetic routes to molecular uranium nitrides and their applications is still at an early stage.²⁶

In this context, the U₂N₂ nitrides emerge as an attractive target for gaining an in-depth understanding of the uranium–nitrogen bonding. In 2002, Korobkov and coworkers prepared an anionic compound containing a U(IV)/U(V) motif (I in Fig. 1).²⁷ Furthermore, U₂N₂ nitrides featuring U(V) and U(IV) centers were subsequently identified by Mazzanti's and Liddle's groups,^28,29 respectively, and are found to exhibit antiferromagnetic coupling (II and III in Fig. 1). It is worth noting that the crystal structures of I–III are centrosymmetric with the C_i symmetry, having opposite pairs of U–N ring bonds. Remarkably, Vlaisavljevich et al. isolated and recognized the naked U₂N₂ cluster with argon matrix-isolated IR absorption spectra.³⁰ Despite variations in the oxidized states of uranium in complexes I–III and naked U₂N₂, all species exhibit very similar structural geometries of equivalent U–N bonds and electronic structures. This highlights an intrinsic bonding pattern in the four-membered U₂N₂ ring.

Fig. 1 Experimentally identified compounds featuring the U₂N₂ nitride motif.

The chemical bonding to actinide is usually predicted to be local,^31–33 but the diffusion of the 5f and 6d orbitals enables early actinides to engage in delocalized bonds.^34–37 Given that aromaticity can provide extra stability and diverse reactivity to conjugated molecules, clusters and materials,^38,39 enormous efforts have been devoted to identify stable and functional actinide compounds with aromaticity. Nevertheless, such compounds are rather limited so far due to the great challenges in their synthesis and characterization. Liddle et.al. prepared a crystalline tri-thorium cluster featuring the first delocalized 3c–2e thorium–thorium bond,⁴⁰ which has been interpreted to have a novel core–shell syngenetic σ-aromaticity.⁴¹ Most recently, we reported the unprecedented planar double Craig–Möbius aromaticity in diboron protactinium (Pa₂B₂),⁴² providing an opportunity for establishing aromatic systems between actinides and main-group elements. Since 5f elements exhibit a strong relativistic effect and multiconfigurational character, experimental tools have generally failed to yield quantitative measurements for f-orbital occupancy with a few exceptions.⁴³ Alternatively, modern computational methods provide a complemental approach to study molecular actinide science.^44–46 In particular, ab initio valence bond (VB) methods have the capability to perform either single or multi-reference calculations,^47–50 and thus are promising to unravel the nature of the chemical bonding in molecular actinides.

In this study, we characterized actinide nitrides, including experimentally identified compounds containing a U₂N₂ motif and theoretically modelled An₂N₂ (An = Pa, Th, Ac) clusters, as a new family of double Möbius aromatic compounds. Different from the exemplary Pa₂B₂,⁴² the double Möbius aromaticity in An₂N₂ assists the unpaired electrons on metal centers to exhibit multiconfigurational characters. This bonding model is described as an “aromaticity-assisted multiconfiguration” to establish a bridge between aromaticity and multiconfiguration. Its unique feature lies in that the multiconfiguration characteristics of the unpaired electrons on actinides are mainly assisted by the aromatic skeleton, and the unpaired electrons have no significant effect on the aromaticity.

Computational details

Geometry optimizations were performed with the PBE0 ⁵¹ functional augmented with Grimme's D3 dispersion corrections⁵² in Gaussian 16.⁵³ In terms of basis sets, a small-core fully relativistic effective core potential (ECP60MDF)⁵⁴ and associated segmented valence basis sets were adopted for actinides and the def2-TZVP basis set was used for main group elements. In the following discussion, the combination of these basis sets is simply labelled as ECP60MDF.

Molecular orbital (MO) based multi-reference methods, including complete active space self-consistent field (CASSCF) and corrections from second-order perturbation theory (CASPT2) along with multi-state CASPT2 (MS-CASPT2),^55–57 were performed with the all-electron basis set ANO-RCC^58,59 and the OpenMolcas software.⁶⁰ The scalar relativistic effect was considered through the Douglas–Kroll–Hess (DKH) Hamiltonian,^61,62 while the spin–orbit (SO) coupling was added as a posteriori correction to the MS-CASPT2 energy. Since the scalar relativistic effect can be introduced by relativistic effective core potentials, we also performed CASSCF/CASPT2/MS-CASPT2 calculations with the ECP60MDF basis set. The energy trends obtained with the ANO-RCC basis set together with the DKH correction are completely identical to those with the ECP60MDF basis set (see details in Table S1†). Consequently, the VB self-consistent field (VBSCF)⁶³ calculations and corrections from the second-order perturbation theory (VBPT2)⁶⁴ were performed with the ECP60MDF basis set by using the XMVB software.^65,66 The data listed in the following section are taken from the calculations at the MS-CASPT2/ANO-RCC level unless specified.

It should be noted that the AdNDP, QTAIM and MCI analyses in this work were performed at the PBE0/ECP60MDF theoretical level for the highest spin states, as the DFT analyses yielded identical results with the multi-reference CASSCF method. As for the NICS and current density analyses, we can only perform PBE0/ECP60MDF calculations at this stage. Since the results for the singlet states are comparable to those for the high-spin state in U₂N₂, Pa₂N₂ and Th₂N₂, it is reliable to assess the aromaticity for An₂N₂ systems at the DFT level. In all DFT calculations, a tight SCF convergence criterion was imposed.

Results and discussion

Multiconfigurational nature of actinide nitrides

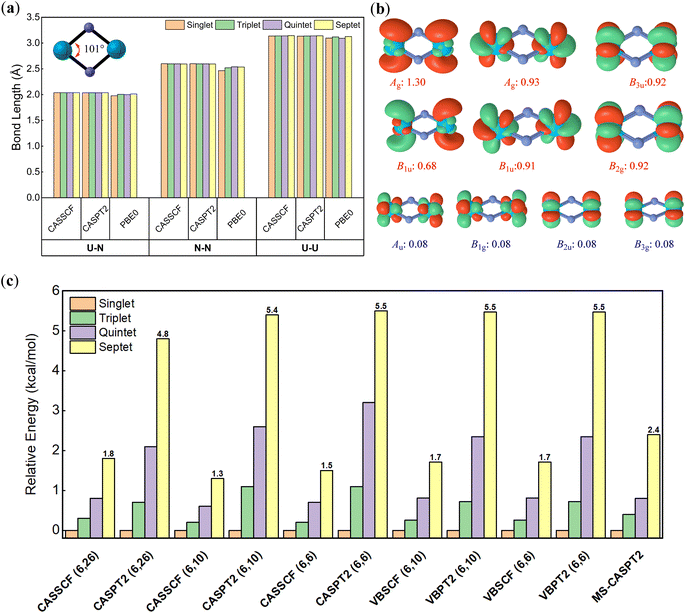
The optimal naked U₂N₂ (structural data in Table 1) exhibits a rhombic structure with D_2h symmetry as illustrated in Fig. 2a, in accordance with previous experimental and computational findings.^30,67 Furthermore, we observed a noteworthy resemblance between the geometry of U₂N₂ and the double Möbius aromatic species Pa₂B₂, where the total 16 valence electrons form four identical localized Pa–B covalent bonds, two delocalized σ bonds and two delocalized π bonds. For the neutral U₂N₂ with 22 valence electrons, we anticipate that 16 valence electrons engage in the same bonding pattern as Pa₂B₂, while the remaining 6 electrons are localized on two uranium atoms. The ground state of U₂N₂ is predicted to be a septet³⁰ or quintet⁶⁷ at the DFT level, but experimental observations indicate that antiferromagnetic U₂N₂ nitrides should have a singlet ground state.^29,68 This discrepancy may arise from the multiconfigurational nature of U₂N₂.

Table 1 Optimal bond lengths (in Å) for An₂N₂ at the PBE0/ECP60MDF level and their Wiberg bond order. The italic data are obtained from the XRD experiments

Species	Bond lengths				Wiberg bond order
	An–N	An–N	An–An	N–N	An–N	An–N	An–An	N–N
U2N2	2.013	2.013	3.126	2.536	2.206	2.206	1.391	0.138
Pa2N2	2.029	2.029	3.145	2.563	2.164	2.164	1.606	0.130
Th2N2	2.069	2.069	3.179	2.648	2.064	2.064	1.424	0.113
Ac2N2	2.177	2.177	3.325	2.811	2.025	2.025	1.574	0.078
[U2N2]^+	1.996	1.996	3.087	2.531	1.921	1.906	1.210	0.073
Mol I	2.051	2.058	3.288	2.466	2.032	2.001	1.009	0.108
	2.077	2.098	3.355	2.485
Mol II	2.006	2.080	3.252	2.476	2.249	1.904	1.053	0.108
	2.023	2.101	3.296	2.479
Mol III	2.140	2.179	3.381	2.688	1.763	1.617	0.683	0.069
	2.152	2.208	3.404	2.725

---

Fig. 2 (a) Key bond lengths for optimal U₂N₂ with D_2h symmetry; (b) ten major active orbitals used in multi-reference calculations and their occupation numbers for the state ¹A_g; (c) relative energies for each spin multiplicity.

To identify the multiconfigurational nature, we resorted to high-level multi-reference methods, in which the 6 valence electrons on metal centres were chosen as the active electrons according to previous theoretical studies.³⁰ Standard CASSCF and CASPT2 calculations with 26 active orbitals were first performed for each spin multiplicity and space symmetry. As shown in Fig. 2b, only ten orbitals have occupation numbers higher than 0.01, in which six of them are prominent for all cases. Subsequently, we continued to run the CASSCF and CASPT2 calculations with (6, 10) and (6, 6) active spaces. The computed absolute and relative energies from these two small active spaces are nearly identical and comparable to those from the large (6, 26) active space. Furthermore, multi-state CASPT2 (MS-CASPT2) calculations are conducted based on CASSCF(6, 10) wavefunctions averaged over the first ten states. Remarkably, all multi-reference methods consistently suggest that the ground state of U₂N₂ is a singlet, though the energy gaps to the triplet (0.4 kcal mol⁻¹), quintet (0.8 kcal mol⁻¹) and septet (2.4 kcal mol⁻¹) states are trivial, and excitations can easily occur under ambient conditions. For each spin multiplicity, the lowest-lying electronic states are ¹A_g, ³B_1u, ⁵A_g and ⁷B_1u, respectively, with similar electronic configurations for active space. In particular, the six major orbitals have occupation numbers close to unity, primarily originating from 7s and 5f atomic orbitals of uranium. Moreover, the spin–orbital coupling induced by the six active electrons was computed as negligible. Thus, it can be concluded that the six active electrons are spin-free and strictly localized on metal centres, resulting in the multiconfigurational nature of U₂N₂.

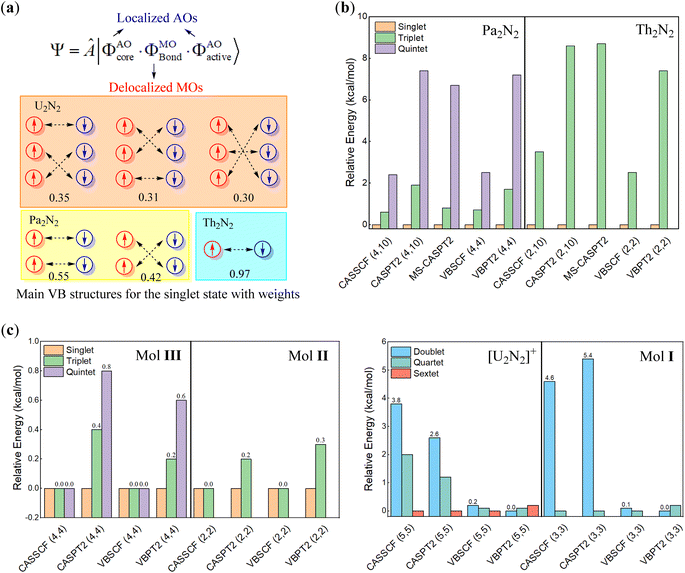
We further conducted VBSCF and VBPT2 calculations within the (6, 10) and (6, 6) active spaces with the ECP60MDF basis set as a supplement. As depicted in Fig. 3a, the VB wavefunction comprises three components, including the core and active orbitals which are expressed with pure atomic orbitals (AOs), and the bonding orbitals which are molecular orbitals (MOs) delocalizing over the whole system. Thus, the above MO- and present VB-based calculations differ in active orbitals. However, the energy gaps from the VBSCF (6, 6)/(6, 10) computations are even closer to those from CASSCF(6, 26) than those from CASSCF(6, 6)/(6, 10), further confirming that the active electrons prefer to localize on metal centres. In VBSCF calculations, the most important VB structure typically involves electron pairings between compatible atomic orbitals, when any chemical bonding is forged between metal centres in U₂N₂. However, the major VB structures in the singlet ground state reveal that the active electrons even pair crossing d or f atomic orbitals with different symmetries (as seen in Fig. 3a), indicating that the active electrons are essentially independent of any meaningful bonding between metal centres. Consequently, the active electrons are oriented in opposite directions on each metal centre, giving rise to open-shell singlet ground states. This obviously explains the insignificant energy gaps among different spin states.

Fig. 3 (a) The definition of the VBSCF wavefunction and computed structural weights for major VB structures, and relative energies for (b) theoretically modelled An₂N₂ (An = Pa, Th) and (c) [U₂N₂]⁺ and experimentally identified compounds I–III with reduced numbers of active electrons and orbitals.

As a single-reference method, conventional DFT obviously predicts a septet ground state for U₂N₂ with significantly exaggerated energy gaps to the singlet (65.1 kcal mol⁻¹), triplet (35.0 kcal mol⁻¹) and quintet (25.7 kcal mol⁻¹) states at the PBE0/ANO-RCC-DKH level, respectively. Despite the much large energy gaps compared to multi-reference methods, DFT produces nearly identical optimal geometries for each spin multiplicity (see Fig. 2a), suggesting that the arrangement of the spin-free electrons has little impact on the framework of U₂N₂. This is further validated by the consistent optimal geometries for each spin multiplicity using either CASSCF/CASPT2(6, 10) or (6, 6) methods. Given that DFT methods can provide convincing geometry for the highest spin multiplicity, the PBE0/ECP60MDF level was employed to optimize the geometries for the remaining studied molecules for the sake of efficiency.

The multiconfigurational character of U₂N₂ is also observed both in experimentally identified compounds I–III and theoretically modelled [U₂N₂]⁺ and An₂N₂ (An = Pa, Th and Ac) clusters. There is no doubt that the optimal geometries for I–III are well consistent with their solid-state molecular structures (C_i symmetry) determined by X-ray diffraction. Therefore, multi-reference calculations were performed for An₂N₂ (An = Pa, Th) with D_2h symmetry, while [U₂N₂]⁺ and compounds I–III adopted C_i symmetry in calculations. Due to the high computational costs associated with compounds II and III, multi-reference calculations were performed on model systems, where t-butyl groups and Pr_i³ groups were replaced with hydrogens. It should be noted that the model systems were also optimized at the PBE0/ECP60MDF level with the U₂N₂ core fixed at their crystal structures.

As depicted in Fig. 3c, computational results reveal an open-shell singlet ground state for Pa₂N₂, Th₂N₂, and compounds II and III, confirming the antiferromagnetic nature of II and III.^29,68 Even closed-shell singlet Ac₂N₂ also exhibits the rhombic structural geometry albeit without any spin-free electrons. In sharp contrast, the ground state of [U₂N₂]⁺ and I are found to be sextet and quartet states by CASSCF, VBSCF and CASPT2 methods, while the VBPT2 computations showed that the low spin states are more stable. It is interesting that the energy gaps among different states are less than 1 kcal mol⁻¹ for [U₂N₂]⁺ and compounds I–III, even lower than the respective gaps for the neutral An₂N₂ cluster. It is also worth noting that the energy gaps for the U₂N₂ core of I–III, i.e. [U₂N₂]³⁺, [U₂N₂]⁴⁺ and [U₂N₂]²⁺ are nearly identical to those for their parents.

Double Möbius aromaticity in actinide nitrides

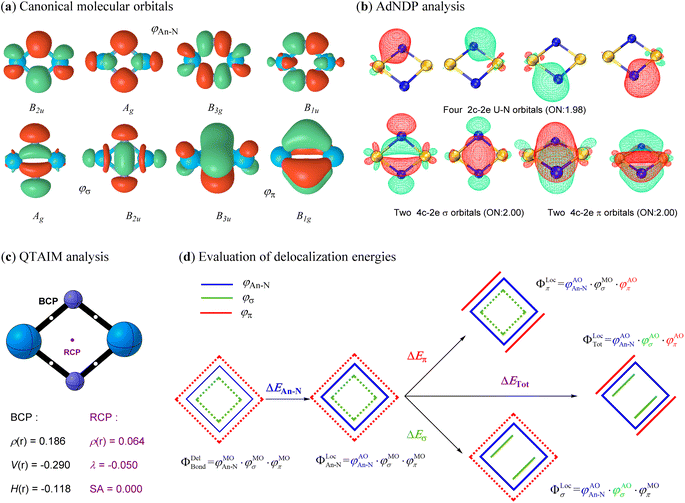
The above analyses demonstrate that all studied actinide nitrides share a similar planar geometry with equivalent An–N bonds, implying an intrinsic bonding pattern for the An₂N₂ rings. In addition to the 6, 4, 2 and 0 active electrons on the metal centers of U, Pa, Th and Ac, respectively, the other 16 valence electrons collectively form eight identical canonical molecular orbitals (CMOs) for each spin multiplicity of all studied An₂N₂ clusters (Fig. 4a for U₂N₂ and Fig. S1–S7† for the remaining systems). In other words, the bonding orbitals essentially remain invariant despite variations in the number and orientation of the spin-free electrons. The adaptive natural density partitioning (AdNDP)⁶⁹ method provides further insights. Four of the CMOs are found to be a linear combination of four identical 2c–2e An–N covalent bonds, while the remaining CMOs represent two delocalized 4c–2e σ bonds and two delocalized π bonds. It should be noted that there is one delocalized MO with Hückel topology (B_2u and B_3u) and one with Möbius topology (A_g and B_1g) for both σ and π systems, indicating a hybrid Hückel–Möbius character.^70–72 However, the four-membered 4σ/4π An₂N₂ with equivalent An–N bonds obviously satisfy the 4n Möbius rule, predominantly demonstrating the double Möbius aromaticity. This is also consistent with the well-identified 4π Möbius aromatic ReB₄.⁷³ Furthermore, the various aromaticity criteria investigated in the following section further endorsed the double Möbius aromaticity in An₂N₂.

Fig. 4 (a) Valence canonical molecular orbitals (CMOs) with an isovalue of 0.05 a.u.; (b) AdNDP analysis showing four localized 2c–2e U–N covalent bonds and four delocalized 4c–2e aromatic bonds along with their occupation numbers (ONs); (c) QTAIM analysis including the electron density ρ(r), potential energy density V(r), electron energy density H(r), electron density curvature (λ) and Shannon aromaticity (SA) at BCP (3, −1) or RCP (3, +1) for U₂N₂; (d) evaluation of delocalization energies for the chemical bonding of interest.

It becomes clear that the unprecedent double Möbius aromaticity strongly stabilizes the framework of actinide nitrides, allowing the unpaired electrons to be spin-free and either localize on metal centres or bond with ligands. Since the unpaired electrons do not form any bonding interactions among themselves, they do not contribute to the bond orders. Therefore, the Wiberg bond orders (see Table 1) for An–N (ca. 2), An–An (ca. 1–1.5) and N–N (ca. 0.1) primarily come from the bonding orbitals. According to the AdNDP analysis, however, the bond order for An–N should be around 3, while chemical bonding is absent between two actinide atoms. This disagreement may result from the cyclic delocalization in actinide nitrides. To further validate the cyclic delocalization, we employed the quantum theory of atoms in molecules (QTAIM) method⁷⁴ to identify the critical points among bound atoms. As expected, four identical bond critical points (BCPs) are found between adjacent actinide and nitrogen atoms, representing the four localized An–N covalent bonds. In addition, a ring critical point (RCP) precisely at the ring centre suggests that the An–An bonding interaction originates from the cyclic electron delocalization rather than the direct An⋯An communication. Furthermore, the presence of aromaticity in actinide nitrides is supported by the positive electron density, negative electron density curvature and zero Shannon aromaticity value at RCP. We also calculated the multicenter index (MCI)⁷⁵ and found one four-center bond with a MCI (4) value of around 0.5. Besides, there are also four three-center bonds with a MCI (3) value up to 0.7. The MCI results provide support for the presence of the aromaticity in An₂N₂.

In pursuit of an improved understanding of the bonding nature, we applied ab initio VB methods to quantify the energetics from the electron delocalization effect of the bonding orbitals. In Fig. 4d and the following definition, only the Φ_Bond components are depicted, while the core and active orbitals remain the same as in the previous definition. We first constructed a localized state (Φ^Loc_An–N) with the four An–N covalent bonds strictly localized on the corresponding atoms. The energy change (ΔE_An–N) from this localized state to the delocalized ψ^Bond_Del state measures the degree of electron delocalization among the four An–N covalent bonds. Subsequently, strictly σ- and π-localized states (ψ^Loc_σ and ψ^loc_π) were established by further localizing two σ and two π orbitals on two adjacent actinide and nitrogen atoms separately. Finally, all eight chemical bonds including four An–N covalent bonds, two delocalized σ bonds and two delocalized π bonds, were localized as in the previous definition to construct a completely localized state (ψ^Tot_Loc). As a result, the electron delocalization induced by σ and π orbitals, and their combined effect was evaluated based on the energy differences of the σ-, π-, or totally localized states with reference to the Φ^Loc_An–N state, respectively. This comprehensive energy analysis offers a thorough examination of the electron delocalization effects in the bonding interactions of interest.

The computational delocalization energies with the VBSCF and VBPT2 methods are identical for each spin multiplicity of actinide nitrides (see Table S2†), again indicating the insignificant effect of active electrons on the planar framework. Therefore, we only collect the data for their ground states at the VBSCF level in Table 2 and VBPT2 level in Table S2.† The minor values of ΔE_An–N confirm that the four An–N covalent bonds are inherently localized. Remarkably, the energetic gains for the delocalized σ and π components reaches up to around 40 and 30 kcal mol⁻¹, respectively, while the total gains amount to 70 kcal mol⁻¹. For Ac₂N₂, we can also conduct block-localized wavefunction (BLW) computations at the PBE0 level, which is the simplest variant of VB theory and incorporates the efficiency of MO theory.^76–79 The computed delocalized energies at the PBE0 level are very close to those with the VBSCF method. The high delocalization energies for bonding orbitals are fully consistent with the AdNDP and QTAIM analysis, confirming the delocalization nature of two σ and two π orbitals.

Table 2 Computed delocalization energies and extra cyclic resonance energies (ECRE) at the VBSCF level (kcal mol⁻¹), the NICS(1)_zz values (in ppm), the multicenter index (MCI) and integrated induced ring-current (J^int, in nA/T) passing the An–N bond by PBE0/ECP60MDF for the highest spin state

Species	ΔEAn–N	ΔEπ	ΔEσ	ΔETot	ECREπ	ECREσ	ECRETot	NICS(1)zz	MCI (4)	MCI (3)	J ^int,
a The data in parenthesis are obtained with the BLW method at the PBE0 level. b The data in parenthesis refer to the singlet state.
U2N2	2.0	41.9	32.9	77.0	41.5	32.5	76.3	−84.7	0.485	0.687	26.4 (23.7)
Pa2N2	1.9	42.6	33.3	77.9	42.3	33.0	77.3	−46.0	0.478	0.693	23.8 (30.4)
Th2N2	1.9	40.5	30.2	72.7	40.2	29.9	72.1	−8.9	0.445	0.697	12.6 (13.6)
Ac2N2^a	2.0 (2.5)	30.2 (35.0)	21.6 (25.7)	53.1 (61.5)	29.9 (34.5)	21.3 (25.2)	52.6 (60.4)	−9.9	0.382	0.684	10.0
[U2N2]^+	2.2	45.8	35.4	83.7	45.4	35.1	82.9	−97.6	0.478	0.680	36.9
Mol I	3.0	49.8	38.4	90.9	49.6	38.2	90.4	−35.7	0.491	0.653	—
Mol II	3.7	45.7	34.4	81.8	45.4	34.1	81.0	−53.7	0.507	0.726	—
Mol III	1.8	45.2	32.4	80.1	45.0	32.2	79.7	−20.1	0.439	0.701	—

---

However, we understood that aromaticity refers to the “extra” stability in a cyclic system relative to non-cyclic systems. In this regard, extra cyclic resonance energy (ECRE), defined as the delocalization energy difference between a cyclic compound and its appropriate acyclic reference, serves as a convincing criterion for assessing the aromaticity.^80,81 Specifically, the value of positive ECRE indicates the magnitude of aromaticity. Herein, linear [An–N–An–N] and [H₂N–An–N–An–NH] were considered as the acyclic references to evaluate ECRE values, as they possess the same number of delocalized electrons compared to cyclic An₂N₂. Besides, linear An₂N₂ has the same number of atoms as cyclic An₂N₂, while An₂N₃H₃ has the same number of An–N bonds as cyclic An₂N₂. Linear An₂N₂ is obviously less stable than cyclic An₂N₂ due to the loss of one An–N bond and the linear constraint, but this is not an issue here. Notably, the delocalization energies for both acyclic references are negligible, e.g. 0.4 kcal mol⁻¹ for each component and 0.7 kcal mol⁻¹ for the total contribution in U₂N₃H₃. This is also reflected by the CMOs in linear systems (see Fig. S8†), where the canonical σ and π orbitals in the cyclic system become relatively localized on the adjacent actinide and nitrogen atoms. In other words, the concerned An–N bonds in linear systems can be viewed as triple bonds like in acetylene. Accordingly, the ECREs relative to An₂N₃H₃ are listed in Table 2. The significant positive ECREs strongly authenticate that the actinide nitrides represent a new family of double Möbius aromatic compounds.

We further calculated the nuclear-independent chemical shift (NICS)⁸² values to examine the magnetic shielding effects of the delocalized electrons, and the zz component of NICS above the ring center is considered in this work because it was believed to be a more suitable choice for assessing aromaticity for planar rings.⁸³ The negative NICS(1)_zz values are consistent with the positive ECREs, confirming the aromaticity in An₂N₂.

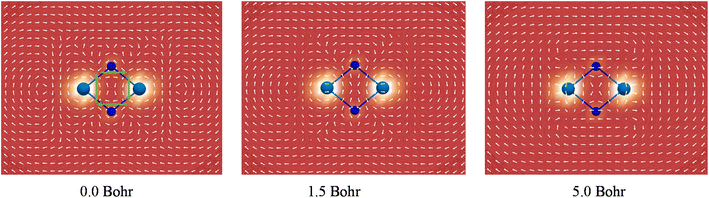
It has been well recognized that the NICS has limitations for assessing aromaticity in heavy metal clusters^84–88 and even in organic molecules.⁸⁹ In this regard, the negative NICS values for Ac₂N₂ may just be a coincidence. In contrast, the global diamagnetic induced ring-current is believed to be a more reliable criterion for aromaticity in heavy metal clusters,^90–93 and has been well-validated in a comprehensive theoretical work by Orozco-Ic et al. very recently.⁹⁴ Therefore, we performed rigorous ring-current analyses. Fig. 5 depicts the line integral convolution visualization of the induced currents by the gauge including magnetically induced current (GIMIC) method^95–97 for U₂N₂ (see Fig. S9† for other systems). There are diatropic ring-currents inside and outside of the ring, which become much clearer at 5.0 Bohr above the molecular plane. It is also obvious that the paramagnetic currents induced by core electrons on metal centers have a significant effect on the inner and outer ring-currents in U₂N₂, in agreement with the findings by Orozco-Ic et al.⁹⁴ In order to eliminate the effect of core electrons, we calculated the induced current by setting the end point of the crossing plane at the midpoint of the An–N bond,⁹⁸ which can better reflect the strength of the inner ring-current. As listed in Table 2, the results indicate that An₂N₂ is magnetically aromatic, which is comparable to and even stronger than the aromaticity in benzene with a J^int value of around 12 nA/T. Besides, the isosurfaces of anisotropy of the induced current density (ACID)^99,100 generated by all CMOs, two delocalized π and two delocalized σ, provide further support for the presence of diatropic inner ring-currents in An₂N₂ (see Fig. S10†).

Fig. 5 The strength and direction of the induced current of U₂N₂ at 0.0, 1.5 and 5.0 Bohr above the molecular plane calculated by the GIMIC program. Clockwise currents represented by green arrows in the inner of U₂N₂ ring are diatropic and indicate aromaticity.

Conclusions

In conclusion, comprehensive chemical bonding analyses show that the framework of actinide nitrides (An₂N₂) adopts a planar geometry with four delocalized σ and four delocalized π electrons, satisfying the 4n Möbius aromaticity rule. Furthermore, the presence of double Möbius aromaticity supports actinide nitrides to exhibit multiconfigurational character due to the unpaired electrons on metal centers, namely the “aromaticity-assisted multiconfiguration” (AAM) bonding model. Since the unpaired electrons are spin-free to strictly localize on the metal centers or form chemical bonding with ligands, the energy gaps between different spin states are remarkably minor. Nevertheless, the actinide nitrides always have an open-shell singlet ground state, except when the number of unpaired electrons is odd.

Author contributions

X. H. L., Y. R. M. and W. W. directed the project. X. H. L. conceived the idea, and designed, and performed the calculations. X. H. L. and Y. R. M. wrote the manuscript. X. X. L. conducted the ring current analysis. All authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are thankful for the support from the National Natural Science Foundation of China (Grant No. 22103064, 21973077, and 22373077). This work was performed in part at the Joint School of Nanoscience and Nanoengineering, a member of the Southeastern Nanotechnology Infrastructure Corridor (SENIC) and National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (Grant ECCS-2025462). We are grateful for resources from the High Performance Computing Center of Central South University.

Notes and references

1. P. Schwerdtfeger, O. R. Smits and P. Pyykkö, The periodic table and the physics that drives it, Nat. Rev. Chem, 2020, 4, 359–380.
2. A. Pichon, Bonding with actinides, Nat. Chem., 2017, 9, 832.
3. C. J. Burns, Bridging a Gap in Actinide Chemistry, Science, 2005, 309, 1823–1824.
4. J. Riedhammer, D. P. Halter and K. Meyer, Nonaqueous Electrochemistry of Uranium Complexes: A Guide to Structure–Reactivity Tuning, Chem. Rev., 2023, 123, 7761–7781.
5. C. Ekberg, D. Ribeiro Costa, M. Hedberg and M. Jolkkonen, Nitride fuel for Gen IV nuclear power systems, J. Radioanal. Nucl. Chem., 2018, 318, 1713–1725.
6. M. Falcone, L. Chatelain, R. Scopelliti, I. Živković and M. Mazzanti, Nitrogen reduction and functionalization by a multimetallic uranium nitride complex, Nature, 2017, 547, 332–335.
7. M. Falcone, L. Barluzzi, J. Andrez, F. Fadaei Tirani, I. Zivkovic, A. Fabrizio, C. Corminboeuf, K. Severin and M. Mazzanti, The role of bridging ligands in dinitrogen reduction and functionalization by uranium multimetallic complexes, Nat. Chem., 2019, 11, 154–160.
8. R. K. Thomson, T. Cantat, B. L. Scott, D. E. Morris, E. R. Batista and J. L. Kiplinger, Uranium azide photolysis results in C–H bond activation and provides evidence for a terminal uranium nitride, Nat. Chem., 2010, 2, 723–729.
9. L. Barluzzi, F.-C. Hsueh, R. Scopelliti, B. E. Atkinson, N. Kaltsoyannis and M. Mazzanti, Synthesis, structure, and reactivity of uranium(vi) nitrides, Chem. Sci., 2021, 12, 8096–8104.
10. C. T. Palumbo, R. Scopelliti, I. Zivkovic and M. Mazzanti, C–H Bond Activation by an Isolated Dinuclear U(III)/U(IV) Nitride, J. Am. Chem. Soc., 2020, 142, 3149–3157.
11. F. Haber, Über die synthetische Gewinnung des Ammoniaks, Angew. Chem., 1914, 27, 473–477.
12. P. L. Arnold, T. Ochiai, F. Y. T. Lam, R. P. Kelly, M. L. Seymour and L. Maron, Metallacyclic actinide catalysts for dinitrogen conversion to ammonia and secondary amines, Nat. Chem., 2020, 12, 654–659.
13. X. Xin, I. Douair, Y. Zhao, S. Wang, L. Maron and C. Zhu, Dinitrogen cleavage and hydrogenation to ammonia with a uranium complex, Natl. Sci. Rev., 2022, 10, nwac144.
14. L. Petit, L. Joubert, P. Maldivi and C. Adamo, A Comprehensive Theoretical View of the Bonding in Actinide Molecular Complexes, J. Am. Chem. Soc., 2006, 128, 2190–2191.
15. N. H. Anderson, J. Xie, D. Ray, M. Zeller, L. Gagliardi and S. C. Bart, Elucidating bonding preferences in tetrakis(imido)uranate(VI) dianions, Nat. Chem., 2017, 9, 850–855.
16. E. Lu, B. E. Atkinson, A. J. Wooles, J. T. Boronski, L. R. Doyle, F. Tuna, J. D. Cryer, P. J. Cobb, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, N. Kaltsoyannis and S. T. Liddle, Back-bonding between an electron-poor, high-oxidation-state metal and poor π-acceptor ligand in a uranium(v)–dinitrogen complex, Nat. Chem., 2019, 11, 806–811.
17. G. W. C. Silva, C. B. Yeamans, A. P. Sattelberger, T. Hartmann, G. S. Cerefice and K. R. Czerwinski, Reaction Sequence and Kinetics of Uranium Nitride Decomposition, Inorg. Chem., 2009, 48, 10635–10642.
18. L. Barluzzi, R. Scopelliti and M. Mazzanti, Photochemical Synthesis of a Stable Terminal Uranium(VI) Nitride, J. Am. Chem. Soc., 2020, 142, 19047–19051.
19. D. M. King, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Isolation and characterization of a uranium(VI)–nitride triple bond, Nat. Chem., 2013, 5, 482–488.
20. S. S. Rudel, H. L. Deubner, M. Müller, A. J. Karttunen and F. Kraus, Complexes featuring a linear [N≡U≡N] core isoelectronic to the uranyl cation, Nat. Chem., 2020, 12, 962–967.
21. X. Xin, I. Douair, T. Rajeshkumar, Y. Zhao, S. Wang, L. Maron and C. Zhu, Photochemical Synthesis of Transition Metal-Stabilized Uranium(VI) Nitride Complexes, Nat. Commun., 2022, 13, 3809.
22. D. M. King, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Synthesis and Structure of a Terminal Uranium Nitride Complex, Science, 2012, 337, 717–720.
23. W. Su, S. Pan, X. Sun, S. Wang, L. Zhao, G. Frenking and C. Zhu, Double dative bond between divalent carbon(0) and uranium, Nat. Commun., 2018, 9, 4997.
24. J. Li, B. E. Bursten, B. Liang and L. Andrews, Noble Gas-Actinide Compounds: Complexation of the CUO Molecule by Ar, Kr, and Xe Atoms in Noble Gas Matrices, Science, 2002, 295, 2242–2245.
25. B. M. Gardner, G. Balázs, M. Scheer, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Triamidoamine uranium(IV)–arsenic complexes containing one-, two- and threefold U–As bonding interactions, Nat. Chem., 2015, 7, 582–590.
26. M. Keener, L. Maria and M. Mazzanti, Progress in the chemistry of molecular actinide-nitride compounds, Chem. Sci., 2023, 14, 6493–6521.
27. I. Korobkov, S. Gambarotta and G. P. A. Yap, A Highly Reactive Uranium Complex Supported by the Calix[4]tetrapyrrole Tetraanion Affording Dinitrogen Cleavage, Solvent Deoxygenation, and Polysilanol Depolymerization, Angew. Chem., Int. Ed., 2002, 41, 3433–3436.
28. C. Camp, J. Pécaut and M. Mazzanti, Tuning Uranium–Nitrogen Multiple Bond Formation with Ancillary Siloxide Ligands, J. Am. Chem. Soc., 2013, 135, 12101–12111.
29. D. M. King, B. E. Atkinson, L. Chatelain, M. Gregson, J. A. Seed, A. J. Wooles, N. Kaltsoyannis and S. T. Liddle, Uranium–nitride chemistry: uranium–uranium electronic communication mediated by nitride bridges, Dalton Trans., 2022, 51, 8855–8864.
30. B. Vlaisavljevich, L. Andrews, X. Wang, Y. Gong, G. P. Kushto and B. E. Bursten, Detection and Electronic Structure of Naked Actinide Complexes: Rhombic-Ring (AnN)2 Molecules Stabilized by Delocalized π-Bonding, J. Am. Chem. Soc., 2016, 138, 893–905.
31. L. Gagliardi and B. O. Roos, Quantum chemical calculations show that the uranium molecule U2 has a quintuple bond, Nature, 2005, 433, 848–851.
32. G. Feng, M. Zhang, D. Shao, X. Wang, S. Wang, L. Maron and C. Zhu, Transition-metal-bridged bimetallic clusters with multiple uranium–metal bonds, Nat. Chem., 2019, 11, 248–253.
33. S. Knecht, H. J. A. Jensen and T. Saue, Relativistic quantum chemical calculations show that the uranium molecule U2 has a quadruple bond, Nat. Chem., 2019, 11, 40–44.
34. D. P. Mills, F. Moro, J. McMaster, J. van Slageren, W. Lewis, A. J. Blake and S. T. Liddle, A delocalized arene-bridged diuranium single-molecule magnet, Nat. Chem., 2011, 3, 454–460.
35. A. R. Eulenstein, Y. J. Franzke, N. Lichtenberger, R. J. Wilson, H. L. Deubner, F. Kraus, R. Clérac, F. Weigend and S. Dehnen, Substantial π-aromaticity in the anionic heavy-metal cluster [Th@Bi12]4⁻, Nat. Chem., 2021, 13, 149–155.
36. J. K. Pagano, J. Xie, K. A. Erickson, S. K. Cope, B. L. Scott, R. Wu, R. Waterman, D. E. Morris, P. Yang, L. Gagliardi and J. L. Kiplinger, Actinide 2-metallabiphenylenes that satisfy Hückel's rule, Nature, 2020, 578, 563–567.
37. A. C. Tsipis, C. E. Kefalidis and C. A. Tsipis, The Role of the 5f Orbitals in Bonding, Aromaticity, and Reactivity of Planar Isocyclic and Heterocyclic Uranium Clusters, J. Am. Chem. Soc., 2008, 130, 9144–9155.
38. G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Aromaticity: Quo Vadis, Chem. Sci., 2023, 14, 5569–5576.
39. M. Solà, Aromaticity rules, Nat. Chem., 2022, 14, 585–590.
40. J. T. Boronski, J. A. Seed, D. Hunger, A. W. Woodward, J. van Slageren, A. J. Wooles, L. S. Natrajan, N. Kaltsoyannis and S. T. Liddle, A crystalline tri-thorium cluster with σ-aromatic metal–metal bonding, Nature, 2021, 598, 72–75.
41. X. Lin and Y. Mo, On the Bonding Nature in the Crystalline Tri-Thorium Cluster: Core-Shell Syngenetic σ-Aromaticity, Angew. Chem., Int. Ed., 2022, 61, e202209658.
42. X. Lin, W. Wu and Y. Mo, Planar Four-Membered Diboron Actinide Compound with Double Möbius Aromaticity, J. Am. Chem. Soc., 2023, 145, 8107–8113.
43. A. Formanuik, A.-M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. McInnes and D. P. Mills, Actinide covalency measured by pulsed electron paramagnetic resonance spectroscopy, Nat. Chem., 2017, 9, 578–583.
44. L. Gagliardi and B. O. Roos, Multiconfigurational quantum chemical methods for molecular systems containing actinides, Chem. Soc. Rev., 2007, 36, 893–903.
45. T. K. Todorova, L. Gagliardi, J. R. Walensky, K. A. Miller and W. J. Evans, DFT and CASPT2 Analysis of Polymetallic Uranium Nitride and Oxide Complexes: How Theory Can Help When X-Ray Analysis Is Inadequate, J. Am. Chem. Soc., 2010, 132, 12397–12403.
46. J. Su, E. R. Batista, K. S. Boland, S. E. Bone, J. A. Bradley, S. K. Cary, D. L. Clark, S. D. Conradson, A. S. Ditter, N. Kaltsoyannis, J. M. Keith, A. Kerridge, S. A. Kozimor, M. W. Löble, R. L. Martin, S. G. Minasian, V. Mocko, H. S. La Pierre, G. T. Seidler, D. K. Shuh, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, Energy-Degeneracy-Driven Covalency in Actinide Bonding, J. Am. Chem. Soc., 2018, 140, 17977–17984.
47. S. S. Shaik and P. C. Hiberty, A chemist's guide to valence bond theory, John Wiley & Sons, 2007.
48. W. Wu, P. Su, S. Shaik and P. C. Hiberty, Classical Valence Bond Approach by Modern Methods, Chem. Rev., 2011, 111, 7557–7593.
49. D. Cooper, Valence bond theory, Elsevier, 2002.
50. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 3rd edn, 1960.
51. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170.
52. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Wallingford, CT, 2016.
54. A. Weigand, X. Cao, T. Hangele and M. Dolg, Relativistic Small-Core Pseudopotentials for Actinium, Thorium, and Protactinium, J. Phys. Chem. A, 2014, 118, 2519–2530.
55. B. O. Roos, Adv. Chem. Phys., 1987, 399–445.
56. K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, Second-order perturbation theory with a CASSCF reference function, J. Phys. Chem., 1990, 94, 5483–5488.
57. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299–306.
58. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set, J. Phys. Chem. A, 2004, 108, 2851–2858.
59. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, New Relativistic ANO Basis Sets for Transition Metal Atoms, J. Phys. Chem. A, 2005, 109, 6575–6579.
60. G. Li Manni, I. F. Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. Carvalho Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. De Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov, L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krośnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. López Ríos, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel, D. Padula, R. Pandharkar, Q. M. Phung, F. Plasser, G. Raggi, E. Rebolini, M. Reiher, I. Rivalta, D. Roca-Sanjuán, T. Romig, A. A. Safari, A. Sánchez-Mansilla, A. M. Sand, I. Schapiro, T. R. Scott, J. Segarra-Martí, F. Segatta, D.-C. Sergentu, P. Sharma, R. Shepard, Y. Shu, J. K. Staab, T. P. Straatsma, L. K. Sørensen, B. N. C. Tenorio, D. G. Truhlar, L. Ungur, M. Vacher, V. Veryazov, T. A. Voß, O. Weser, D. Wu, X. Yang, D. Yarkony, C. Zhou, J. P. Zobel and R. Lindh, The OpenMolcas Web: A Community-Driven Approach to Advancing Computational Chemistry, J. Chem. Theory Comput., 2023, 19, 6933–6991.
61. B. A. Hess, Applicability of the no-pair equation with free-particle projection operators to atomic and molecular structure calculations, Phys. Rev. A, 1985, 32, 756–763.
62. M. Douglas and N. M. Kroll, Quantum electrodynamical corrections to the fine structure of helium, Ann. Phys., 1974, 82, 89–155.
63. J. H. van Lenthe and G. G. Balint-Kurti, The valence-bond self-consistent field method (VB–SCF): Theory and test calculations, J. Chem. Phys., 1983, 78, 5699–5713.
64. Z. Chen, J. Song, S. Shaik, P. C. Hiberty and W. Wu, Valence Bond Perturbation Theory. A Valence Bond Method That Incorporates Perturbation Theory, J. Phys. Chem. A, 2009, 113, 11560–11569.
65. Z. Chen, F. Ying, X. Chen, J. Song, P. Su, L. Song, Y. Mo, Q. Zhang and W. Wu, XMVB 2.0: A new version of Xiamen valence bond program, Int. J. Quantum Chem., 2015, 115, 731–737.
66. L. Song, Y. Mo, Q. Zhang and W. Wu, XMVB: A program for ab initio nonorthogonal valence bond computations, J. Comput. Chem., 2005, 26, 514–521.
67. P. Zhang, W.-L. Zou, P. Zhang and S.-X. Hu, Electronic Structures and Properties of Actinide-Bimetal Compounds An2O2 (An = Th to Cf) and U2E2 (E = N, F, S), Eur. J. Inorg. Chem., 2021, 2021, 3926–3937.
68. L. Barluzzi, L. Chatelain, F. Fadaei-Tirani, I. Zivkovic and M. Mazzanti, Facile N-functionalization and strong magnetic communication in a diuranium(v) bis-nitride complex, Chem. Sci., 2019, 10, 3543–3555.
69. D. Y. Zubarev and A. I. Boldyrev, Developing paradigms of chemical bonding: adaptive natural density partitioning, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
70. D. W. Szczepanik and M. Solà, Electron Delocalization in Planar Metallacycles: Hückel or Möbius Aromatic?, ChemistryOpen, 2019, 8, 219–227.
71. M. Solà, Connecting and combining rules of aromaticity. Towards a unified theory of aromaticity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1404.
72. L. F. Cheung, J. Czekner, G. S. Kocheril and L.-S. Wang, ReB6–: A Metallaboron Analog of Metallabenzenes, J. Am. Chem. Soc., 2019, 141, 17854–17860.
73. L. F. Cheung, G. S. Kocheril, J. Czekner and L.-S. Wang, Observation of Möbius Aromatic Planar Metallaborocycles, J. Am. Chem. Soc., 2020, 142, 3356–3360.
74. R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928.
75. M. Giambiagi, M. S. de Giambiagi, C. D. dos Santos Silva and A. P. de Figueiredo, Multicenter bond indices as a measure of aromaticity, Phys. Chem. Chem. Phys., 2000, 2, 3381–3392.
76. Y. Mo and S. D. Peyerimhoff, Theoretical analysis of electronic delocalization, J. Chem. Phys., 1998, 109, 1687–1697.
77. Y. Mo, L. Song and Y. Lin, Block-Localized Wavefunction (BLW) Method at the Density Functional Theory (DFT) Level, J. Phys. Chem. A, 2007, 111, 8291–8301.
78. Y. Mo, in The Chemical Bond, 2014, pp. 199–232.
79. Y. Mo, H. Zhang, C. Wang and X. Lin, in Comprehensive Computational Chemistry, ed. M. Yáñez and R. J. Boyd, Elsevier, Oxford, 1st edn, 2024, pp. 481–500.
80. Y. Mo and P. v. R. Schleyer, An Energetic Measure of Aromaticity and Antiaromaticity Based on the Pauling–Wheland Resonance Energies, Chem.–Eur. J., 2006, 12, 2009–2020.
81. W. Wu, B. Ma, J. I-Chia Wu, P. v. R. Schleyer and Y. Mo, Is Cyclopropane Really the σ-Aromatic Paradigm?, Chem.–Eur. J., 2009, 15, 9730–9736.
82. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe, J. Am. Chem. Soc., 1996, 118, 6317–6318.
83. H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Which NICS Aromaticity Index for Planar π Rings Is Best?, Org. Lett., 2006, 8, 863–866.
84. C. Foroutan-Nejad, Is NICS a reliable aromaticity index for transition metal clusters?, Theor. Chem. Acc., 2015, 134, 8.
85. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, All-Metal Aromaticity: Revisiting the Ring Current Model among Transition Metal Clusters, J. Chem. Theory Comput., 2013, 9, 4789–4796.
86. R. Islas, G. Martínez-Guajardo, J. O. C. Jiménez-Halla, M. Solà and G. Merino, Not All That Has a Negative NICS Is Aromatic: The Case of the H-Bonded Cyclic Trimer of HF, J. Chem. Theory Comput., 2010, 6, 1131–1135.
87. J. J. Torres, R. Islas, E. Osorio, J. G. Harrison, W. Tiznado and G. Merino, Is Al2Cl6 Aromatic? Cautions in Superficial NICS Interpretation, J. Phys. Chem. A, 2013, 117, 5529–5533.
88. M. Solà, F. Feixas, J. O. C. Jiménez-Halla, E. Matito and J. Poater, A Critical Assessment of the Performance of Magnetic and Electronic Indices of Aromaticity, Symmetry, 2010, 2, 1156–1179.
89. M. Orozco-Ic, L. Soriano-Agueda, S. Escayola, D. Sundholm, G. Merino and E. Matito, Understanding Aromaticity in [5]Helicene-Bridged Cyclophanes: A Comprehensive Study, J. Org. Chem., 2024, 89, 2459–2466.
90. Z.-L. Wang, T.-T. Chen, W.-J. Chen, W.-L. Li, J. Zhao, X.-L. Jiang, J. Li, L.-S. Wang and H.-S. Hu, The smallest 4f-metalla-aromatic molecule of cyclo-PrB2− with Pr–B multiple bonds, Chem. Sci., 2022, 13, 10082–10094.
91. S. Das, S. Sinha, G. Roymahapatra, M. Orozco-Ic, G. Chandra De and S. Giri, Understanding the bonding and aromaticity of [Au3{C4H4(X)4E}3]− (X = CF3, CN, BO; E = Si, Ge): trinuclear gold superhalogens, New J. Chem., 2024, 48, 4765–4771.
92. M. Orozco-Ic, N. D. Charistos, A. Muñoz-Castro, R. Islas, D. Sundholm and G. Merino, Core-electron contributions to the molecular magnetic response, Phys. Chem. Chem. Phys., 2022, 24, 12158–12166.
93. R. J. F. Berger, M. Dimitrova, R. T. Nasibullin, R. R. Valiev and D. Sundholm, Integration of global ring currents using the Ampère–Maxwell law, Phys. Chem. Chem. Phys., 2022, 24, 624–628.
94. M. Orozco-Ic, L. Soriano-Agueda, D. Sundholm, E. Matito and G. Merino, Core-electron contributions to the magnetic response of molecules with heavy elements and their significance in aromaticity assessments, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-8293t.
95. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, The gauge including magnetically induced current method, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
96. S. Taubert, D. Sundholm and J. Jusélius, Calculation of spin-current densities using gauge-including atomic orbitals, J. Chem. Phys., 2011, 134.
97. M. Rauhalahti, S. Taubert, D. Sundholm and V. Liégeois, Calculations of current densities for neutral and doubly charged persubstituted benzenes using effective core potentials, Phys. Chem. Chem. Phys., 2017, 19, 7124–7131.
98. D. Sundholm, H. Fliegl and R. J. F. Berger, Calculations of magnetically induced current densities: theory and applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
99. R. Herges and D. Geuenich, Delocalization of Electrons in Molecules, J. Phys. Chem. A, 2001, 105, 3214–3220.
100. D. Geuenich, K. Hess, F. Köhler and R. Herges, Anisotropy of the Induced Current Density (ACID), a General Method To Quantify and Visualize Electronic Delocalization, Chem. Rev., 2005, 105, 3758–3772.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01549e

---