Metadynamics simulations reveal alloying-dealloying processes for bimetallic PdGa nanoparticles under CO₂ hydrogenation

Abstract

Supported bimetallic nanoparticles (NPs) often display improved catalytic performances (activity and/or selectivity). Yet, structure–activity relationships are difficult to derive due to the multitude of possible compositions, interfaces and alloys. This is notably true for bimetallic NPs used in the selective hydrogenation of CO₂ to methanol, where the NPs respond dynamically to the chemical potential of the reactants and products. Herein, we use a combined computational and experimental approach that leverages ab initio Molecular Dynamics (AIMD) and Metadynamics (MTD) in conjunction with in situ X-ray absorption spectroscopy, chemisorption and CO-IR, to explore the dynamic structures and interactions with adsorbates under various CO₂ hydrogenation conditions in highly active and selective silica-supported PdGa NPs. We find that PdGa alloying generates isolated Pd sites at the NP surface, changing the dominant binding modes of relevant adsorbates compared to pure Pd NPs: CO molecules mainly occupy atop sites and hydrides switch from mainly internal to atop and bridge sites. Under more oxidizing conditions, akin to CO₂ hydrogenation, Ga is partially oxidized, forming a GaO_X layer on the NP surface, with a partially dealloyed PdGa core and some remaining isolated Pd surface sites. Overall, these bimetallic NPs show high structural dynamics and a variable extent of alloying depending on the adsorbates relevant to CO₂ hydrogenation. This work highlights that AIMD/MTD is a powerful approach to elucidate structural dynamics at a single particle level in complex catalytic systems.

---

Introduction

Supported metal nanoparticles (NPs) constitute one of the largest classes of catalysts, covering a broad range of applications, from selective hydrogenation to reforming and hydrocracking technologies.¹ Among them, bimetallic NPs, composed of two transition metals or a combination of a transition metal and a main group or post-transition metal element, frequently display improved catalytic performances (activity, selectivity and/or stability) due to synergistic effects between the two elements, making them particularly interesting systems to investigate in both academia and industry.² These supported bimetallic catalysts are inherently complex: besides classical particle size effects, bimetallic systems can differ in compositions, the type of interfaces, as well as their structures, which can form various alloys, e.g. core–shell, Janus-type, intermetallic, etc. Moreover, the chemical state of the active catalyst can respond dynamically to the composition and individual partial pressures of reactants and products, i.e. their chemical potentials.^3,4 This complexity poses a significant challenge for elucidating the distribution and nature of active sites, even when using advanced in situ/operando spectroscopic techniques and state-of-the-art computational modelling.⁵

For instance, state-of-the-art bimetallic NP catalysts for the selective hydrogenation of CO₂ to methanol exemplify the complexity of dynamic alloying processes as a function of chemical potential or reaction conditions (Fig. 1a). Despite years of research in this area, the reaction mechanism remains unclear: multiple active sites/states have been proposed across bimetallic systems, that include interfacial sites, surface alloys,⁶ active site defects,⁷ and oxide overlayers.^8,9

Fig. 1 (a) State-of-the-art CO₂ hydrogenation catalyst based on a PdGa alloy supported on a dehydroxylated silica support and its complex alloying-dealloying behaviour under reaction conditions. (b) Combined computational and experimental approach of this work to elucidate the atomic level structure of (de)alloying, as well as particle-support and particle–adsorbate interactions.

To study these complex systems, recent efforts from our group have shown that confronting ab initio molecular dynamics (AIMD),¹⁰ in combination with metadynamics (MTD) for enhanced structural space exploration,^11–16 with experimental data on well-defined model catalysts can help to resolve the minimal free energy structures of small mono-and bimetallic NPs, while also providing insights into the influence of chemical potential, the role of supports, and the dominant binding modes of specific adsorbates (Fig. 1b).^17,18 In particular, the AIMD/MTD approach can access the high-energy surfaces, edges and local defects of small nanoparticles which contribute significantly to the structure and reactivity of active supported catalysts, and which cannot be captured effectively using slab models that are normally used for periodic calculations in heterogeneous catalysis.

In this work, we used this combined approach to study the active structure of supported bimetallic PdGa NPs under a range of conditions (reducing and oxidizing), related to those expected during CO₂ hydrogenation. Suitable well-defined model systems containing small, size-homogeneous bimetallic NPs with controllable interfaces and composition, in the absence of bulk metal/oxide were previously obtained using Surface Organometallic Chemistry (SOMC).^19,20 PdGa NPs supported on a Ga(III)-doped silica are highly active and selective catalysts for the hydrogenation of CO₂ to methanol, displaying a distinct reactivity compared to the monometallic equivalent.²⁰ In this catalyst, Pd and Ga form an alloy in the as-prepared catalysts, as shown by X-ray absorption spectroscopy (XAS). Notably, the Pd K-edge Extended X-ray Absorption Fine Structure (EXAFS) shows a significantly lower Pd–Pd path degeneracy in PdGa@SiO₂ compared with the monometallic Pd@SiO₂ analogue, indicating the dilution of Pd with Ga. Furthermore, analysis of the Ga K-edge X-ray Absorption Near Edge Spectroscopy (XANES) suggests that predominantly reduced Ga is present, alloyed with Pd, while some Ga(III) is retained. Under CO₂ hydrogenation conditions, the alloyed Ga is partially re-oxidized (dealloying), while Pd remains metallic. In addition to this dealloying, chemisorption experiments show that the PdGa system exhibits distinct adsorption properties towards H₂ and CO compared to the monometallic system (Pd@SiO₂), while the distribution of adsorbed CO species differs markedly in the presence of Ga, as shown by infrared (IR) spectroscopy.

While a dynamic alloying-dealloying was observed on a single particle level, these observations raise questions regarding (i) the structure of the alloy at an atomic level (distribution of Ga in Pd), (ii) the influence of the support on such structures, (iii) how alloying affects the adsorption properties of probe molecules such as H₂ and CO and, (iv) how such alloys structurally evolve under CO₂ hydrogenation conditions, which correspond to rather oxidizing conditions compared to these under CO hydrogenation (Fig. 1b).^4,21

To answer these questions, we confront experimental observations (XAS, chemisorption, CO-adsorption IR) on this well-defined SOMC-derived catalyst with simulations to explore the structural space of PdGa NPs around the free energy minimum under various reactive environments. We first refine the structure of PdGa NPs and study the influence of the SiO₂ support on their structure, before addressing the morphological changes of PdGa NPs under different reactive gas atmospheres–H₂, CO, and oxidizing conditions that correspond to CO₂ hydrogenation. Finally, we discuss the broader implications of these results on the structure, reactivity, and stability of bimetallic NPs under reaction conditions.

Results and discussion

Experimental systems and structure of pristine PdGa nanoparticles

To gain insights into the distribution of Ga and Pd in the particles, we use AIMD/MTD to refine the structure of the as-synthesised catalyst by first exploring the most stable structures of PdGa NPs. We first investigate a PdGa NP containing a total of 38 atoms, in the absence of the support, with Pd/Ga ratio of ca. 1 : 1 (0.8 nm, 18 Pd atoms, 20 Ga atoms, compare Fig. 2b(i)), close to the experimental particle size and composition.²⁰ The Pd and Ga coordination numbers (CN_Pd–Pd, CN_Pd–Ga, and CN_Ga–Ga, see computational methods for definition) are used as collective variables (CVs) to explore the free energy surface (FES) for all MTD simulations. These CVs are chosen since they allow us to distinguish various alloyed and segregated structures possible for the NPs.

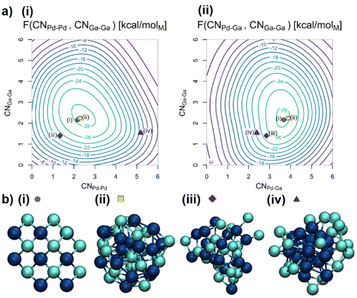Fig. 2 (a) Free energy surfaces (FES) of the Pd₁₈Ga₂₀ NP in vacuum in kcal mol_M⁻¹ based on (i) CN_Pd–Pd and CN_Ga–Ga as well as (ii) CN_Pd–Ga and CN_Ga–Ga with the minimum located at CN_Pd–Pd = 2.5, CN_Pd–Ga = 3.7 and CN_Ga–Ga = 2.3. (b) Structures of the Pd₁₈Ga₂₀ NP in vacuum visited during the trajectory including (i) starting guess, (ii) structure closest to the free energy minimum, (iii) statistically mixed structure and (iv) structure with a Pd-core. Pd: dark blue; Ga: brighter blue. See the ESI for in-depth treatment of the trajectory (Fig. S6–S11†).

The conformational space of the NP was explored by MTD (Fig. S6†). Both segregated and alloyed structures are sampled over the course of the simulation, as evidenced by the selected structure snippets (Fig. 2b(ii)–(iv)). CN_Pd–Pd varies rapidly between 0.8 and 5.2, whereas CN_Pd–Ga varies between 1.8 and 4.2, and CN_Ga–Ga varies between 0.7 and 4.8 (Fig. S6†). The free energy minimum corresponds to an alloyed structure located at CN_Pd–Pd = 2.5, CN_Pd–Ga = 3.7, and CN_Ga–Ga = 2.3. This structure features mainly isolated Pd sites surrounded by an average of four Ga atoms, similar to the starting guess, i.e. a well-mixed alloy, indicating that segregation of the two metals, either as a Janus particle or a core–shell structure, is energetically disfavoured. Fig. 2b(ii) shows the structure during the trajectory closest to the free energy minimum, which is a representation of the ensemble of particles with these exact values for the CVs. No crystalline structures are observed, likely due to increased particle dynamics associated with the small particle size.²² Thus, these particles are best described as disordered alloys.

The shape of the FES as shown in Fig. 2a indicates that CN_Pd–Ga is not easily changed while both CN_Pd–Pd and CN_Ga–Ga have more shallow minima in the FES. The shallow FES for some of the CVs allows efficient exploration of different structures, including core–shell structures with a Ga-enriched shell (Fig. 2b(iv)). Interestingly, only one distinct minimum was found on the FES, which indicates that the particles are distributed around a single minimum rather than having different phases. Thus, the structure of the small PdGa NP can be described as inherently disordered and highly dynamic.

Alloying is likely driven by two factors. First, alloying increases the mixing entropy. This mixing entropy can be evaluated using the Cowley Short Range Order Parameter (see ESI† for an in-depth discussion of the Cowley Short Range Order Parameter²³). Note that, if mixing entropy was the only driving force for PdGa alloying, a statistical alloy with Cowley short range order parameters of α_Pd–Ga = α_Ga–Pd = 0 (Fig. 2b(iii)) would be obtained. Yet, α_Ga–Pd = −0.24 (α_Pd–Ga = −0.14) deviates significantly from 0, indicating that there must also be an additional enthalpic factor that disfavours a purely statistical distribution. Previous computational studies have found that among the three bond combinations, Pd–Ga bonds are the strongest and significantly shorter than individual monometallic bonds.²⁴ Hence, short-range Pd–Ga interactions are maximized while weaker Ga–Ga and Pd–Pd bonds are broken. The strong preference for Pd–Ga bonds is confirmed by the CN_Pd−Ga of around 4. In contrast, Pd–Pd and Ga–Ga bonds are readily interconverted without changing the overall free energy of the structure significantly due to their low formation enthalpies. Such weaker bonds also partially account for the higher fluxionality of PdGa NPs compared to pure Pd. Overall, PdGa alloying implies that Pd atoms are diluted in the structure compared to pure Pd NPs, an observation that is overall consistent with EXAFS fits (vide infra), suggesting that Pd atoms are well-dispersed at the surface and in the bulk of the NPs.

Impact of SiO₂-surface on the structure of PdGa

Next, we explore the influence of the support onto the PdGa NPs, since such support effects can influence the coordination environment of the elements in the particle, as recently shown for PtGa and PtMn NPs supported on dehydroxylated silica.^17,18 Thus, we took a pre-optimised structure of a PdGa NP and placed it onto a model surface of dehydroxylated amorphous silica, used to synthesise the PdGa NPs.^20,25 CN_Pd–O and CN_Ga–O were added as CVs to model interactions between the PdGa NP and the SiO₂ surface (Fig. S12†).

The FES (Fig. S20†) indicates that the minimum free energy structure deviates from the PdGa NP in vacuum, with CN_Pd–Pd decreasing from 2.5 to 1.8, CN_Pd–Ga decreasing from 3.6 to 3.0, and CN_Ga–Ga increasing from 2.3 to 2.6. While this demonstrates a clear interaction between NP and SiO₂ surface, CN_Pd–O and CN_Ga–O are close to 0, indicating that no covalent bonds are formed between the support and the NP.

As a result, the overall structure of the bimetallic NP supported on the SiO₂ surface does not change significantly. Contrary to what was observed for PtGa particles supported on partially dehydroxylated silica surfaces, no insertion of Pt or Ga atoms in distorted Si–O bonds could be observed¹⁶ Comparing the unsupported PdGa NPs with the SiO₂-supported system shows that qualitative features like alloying and Pd site isolation are successfully reproduced in both models. As a first approximation, the support can be considered as mostly innocent. Therefore, subsequent modelling utilizes the unsupported Pd₁₈Ga₂₀ NP model.

Structure of adsorbed COs on PdGa catalysts

Next, we modelled both PdGa and Pd NPs with adsorbed CO* in order to better understand the significant differences between the adsorption of CO on the bimetallic PdGa@SiO₂ compared to that observed for the monometallic Pd@SiO₂. The CO coverage was chosen in accordance with the experimentally observed values from CO chemisorption (0.55 and 0.93 CO per Pd for Pd₁₈Ga₂₀ and Pd₃₈, respectively).²⁰ 10 CO molecules were placed on the surface of a pre-optimised Pd₁₈Ga₂₀ NP, and the particle was evolved using MTD. A pure Pd NP with 35 CO* was also considered for comparison. CN_Pd–C and CN_Ga–C were used as additional CVs to model interactions between the PdGa NP with the CO molecules. The structures closest to the free energy minima are shown in Fig. 3a. The FES, the initial guess, and the evolution of the CVs during the MTD simulations can be found in Fig. S21–S27.†

Fig. 3 (a) Structures closest to the free energy minimum for (i) Pd₁₈Ga₂₀(CO)₁₀ NP and (ii) Pd₃₈(CO)₃₅ NP in vacuum obtained from metadynamics. Pd: dark blue, Ga: brighter blue, C: black, and O: red (trajectories and FES can be found in Fig. S21–S38†). (b) Proportion of different CO coordination modes of the Pd₁₈Ga₂₀(CO)₁₀ and Pd₃₈(CO)₃₅ NP obtained from AIMD simulations. (c) (i) Simulated IR spectra from the AIMD simulations of the Pd₁₈Ga₂₀(CO)₁₀ and Pd₃₈(CO)₃₅ NP. (ii) Experimental CO-IR for Pd@SiO₂ and PdGa@SiO₂ (background subtracted).

In both Pd₃₈(CO)₃₅ NP and Pd₁₈Ga₂₀(CO)₁₀ NP, CO molecules are exclusively bound to the surface. In the case of the alloy, CO are preferentially coordinated to Pd with a CN_Pd–C = 0.6 with limited coordination to Ga with CN_Ga–C = 0.2 (Fig. 3a and S27†). The dominant binding modes of adsorbed CO also change, as indicated by the simulated and experimental CO adsorption IR (Fig. 3c): for the Pd₃₈(CO)₃₅ NP, a significant amount of surface CO is coordinated in a bridged fashion between multiple Pd atoms. In contrast, the adsorbed CO for Pd₁₈Ga₂₀(CO)₁₀ are predominantly occupying atop sites. The core of Pd₁₈Ga₂₀ itself undergoes significant structural changes. The formation of a Pd-core within the NP leads to an increased CN_Pd–Pd from 2.5 to 3.6 (α_Ga–Pd = −0.35 and α_Pd–Ga = 0.18). Meanwhile, the migration of Ga to the surface is evidenced by decreased CN_Pd–Ga from 3.7 to 2.8 and decreased CN_Ga–Ga from 2.3 to 1.4. (compare Fig. 2vs.3a and S27†). The dealloying of Ga to the NP surface is further evidenced by the larger mean distance of Ga to the centre of mass (4.4 Å) compared to Pd (3.2 Å). Importantly, some Pd surface sites are retained and responsible for CO adsorption. The separation of surface Pd atoms by Ga is consistent with CO adsorption IR, which shows no contiguous domains of metallic Pd at the NP surface.^20,26

To better understand the proportion of different CO binding modes on the surface, AIMD was used to simulate the structure of the particles closest to the minima in the FES. In the simulation, the adsorbates transition rapidly between different coordination environments indicating low activation energies for the transition (Fig. S43†). Pd₁₈Ga₂₀(CO)₁₀ and Pd₃₈(CO)₃₅ exhibit radically different distributions of the main coordination modes (Fig. 3b and Table S5†). Pd₁₈Ga₂₀(CO)₁₀ shows only atop CO, while a mixture of atop and bridged CO is present in Pd₃₈(CO)₃₅. Neither particle shows CO adsorbed on hollow sites for the selected cut-off distance of 2.3 Å.

To compare these results to experimental CO adsorption IR spectra, the IR spectra of the AIMD runs were calculated by Fourier transforming the molecular dipole autocorrelation function along the simulation trajectory, as implemented in the TRAVIS program package (Fig. 3c(i)).^27,28 The simulated spectrum (Fig. 3c(i)) of Pd₃₈(CO)₃₅ consists of two dominant absorption bands centred at 2010 and 1870 cm⁻¹, which are attributed to atop and bridged carbonyls, respectively. This is consistent with the experimental CO-adsorption IR of Pd@SiO₂ (Fig. 3(ii)), where two dominant bands are also observed. The maxima of these peaks are found at ca. 2090 and 1960 cm⁻¹. The simulated spectrum for Pd₁₈Ga₂₀(CO)₁₀ consists of a single symmetrical band at ca. 1970 cm⁻¹, which, based on the observation of CO exclusively occupying atop sites in the simulation (Fig. 3b), and previous assignments, is attributed to atop Pd–CO species. The experimental spectrum for PdGa@SiO₂ is dominated by a symmetrical peak at 2080 cm⁻¹, with smaller contributions from a broad peak at ca. 1950 cm⁻¹, attributed to bridging carbonyl species. This disparity between calculation and experiment (i.e. the observation of some bridged species experimentally) may arise from inhomogeneity of the sample, however, the trends in both experiment and simulation are consistent. To summarize, the IR spectra confirm the interaction between CO and PdGa is dominated by atop CO sites, whereas two frequencies are observed for the Pd NP, corresponding to atop and bridged CO respectively, which is consistent with the experimental CO adsorption IR.²⁰

Structure of hydrides on PdGa catalysts

Equally important for both reactivity and characterization, but much harder to probe experimentally, are the coordination modes of hydrides during CO₂ hydrogenation and the subsequent structural changes of the NPs. From an experimental perspective, bulk Pd is known to form a sub-surface PdH_X alloy phase, which makes interpretation of H₂ chemisorption challenging in terms of adsorption stoichiometry.^29,30 Since the simulation of Pd₁₈Ga₂₀ and Pd₃₈ NPs with adsorbed CO successfully reproduced the CO adsorption IR spectra, we reason that placing H* onto the NPs could help us understand the binding mode of chemisorbed H*, and the disparities between particle sizes (from TEM) and H₂ uptake (chemisorption). H₂ chemisorption data suggests the coverage is equal to 1.1H and 1.25H per Pd for the PdGa and Pd NPs, respectively. Thus, 20H* and 48H* atoms were placed on the surface of pre-optimized Pd₁₈Ga₂₀ NP and Pd₃₈ NP, respectively. The evolution of the particles was followed by MTD. CN_Pd–H, and CN_Ga–H were used as additional CVs to model interactions between the PdGa NP and H* atoms.

For the Pd₁₈Ga₂₀H₂₀ NP, all CNs decrease slightly in the most stable structure (CN_Pd–Pd from 2.5 to 1.9, CN_Pd–Ga from 3.7 to 2.7 and CN_Ga–Ga from 2.3 to 1.6, α_Ga–Pd = – 0.36 and α_Pd–Ga = 0.07, Fig. 4 and S44–S50†). The decrease in CN is attributed to a particle expansion in the presence of hydrides,³¹ and is further evidenced by the increased distance of metal atoms to the centre of mass of the NP (3.7 Å vs. 3.9 Å, Fig. S47†). Contrary to the simulations with CO, no dealloying is observed for the PdGa NP with H* (compare Fig. 3vs.4). In Pd₁₈Ga₂₀H₂₀ NPs, H* atoms are preferentially bound to Pd (CN_Pd–H = 1.0) but also to Ga (CN_Ga–H = 0.8) (Fig. 4 and S50†), and the overall coordination number of adsorbed H* is lower than for the pure Pd NP. Conversely, the Pd NP has significant amounts of subsurface hydrides, explaining the high H/Pd stoichiometry. This is well documented for Pd, which is known to adsorb hydrogen to form a bulk PdH_X alloy.^29,30

Fig. 4 Ga K-edge XANES of PdGa@SiO₂ under reaction conditions. (a) Before and after introduction of CO₂, (b) pure spectral components obtained from a 2-component MCR fit tracking introduction of CO₂ into the gas phase, and (c) MCR component profiles tracking influence of introduction of CO₂ to the reactive gas mixture.

Subsequent AIMD simulations confirm that H* atoms are generally less coordinated in Pd₁₈Ga₂₀H₂₀ compared to the Pd₃₈H₄₈ NP (Fig. 4 and Table S7†), reminiscent of the simulations with CO. Pd₁₈Ga₂₀H₂₀ shows mainly bridged hydrides with a significant number of hydrides on atop sites and a small number of hydrides in three-fold hollow sites. In contrast, on the Pd₃₈H₄₈ NP, very few atop hydrides are observed, with bridging hydrides and hydrides in hollow sites dominating. Moreover, in both cases H* rapidly exchange between different coordination environments, indicating low activation energies for the transition between binding sites and binding modes (Fig. S66†).

Influence of oxygen chemical potential and implications for PdGa NPs under CO₂ hydrogenation conditions

Next, we assess how switching to more oxidising (CO₂ hydrogenation) conditions affects the distribution of Ga and Pd within the particle. As recently shown, CO₂ hydrogenation conditions are significantly more oxidising than the equivalent CO hydrogenation conditions, mainly due to the large quantity of water produced.⁹

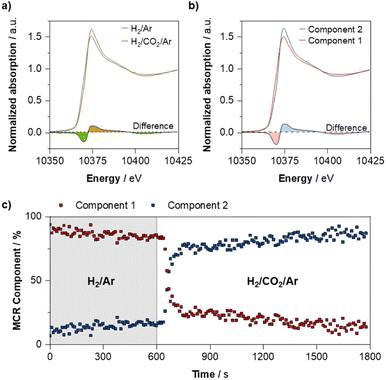
In fact, the Ga K-edge XANES shows that the CO₂ hydrogenation conditions (H₂ : Ar : CO₂ (3 : 1 : 1)) promote partial oxidation of Ga (0) from the alloyed PdGa NP (Fig. 5a), as illustrated by the increase in white line intensity (10 375 eV) after switching, as well as the depletion of the feature at ca. 10 368 eV that is indicative of Ga (0).²⁰ Further analysis of the time-resolved process, by means of multivariate curve resolution alternating least squares (MCR-ALS) analysis suggest that this oxidation process occurs rapidly upon introduction of CO₂ (Fig. 5b and c). We note that small differences between the before/after spectra and the MCR-resolved components arise from the fact that when using MCR-ALS, the experimental spectrum is reproduced as a weighted sum of the two pure spectral components that are obtained from analysis of all scans, while the before/after spectra represent an average of a smaller number of spectra. Meanwhile, the average Ga–Pd path degeneracy obtained from fitting of the Ga K-edge EXAFS decreases from 0.7 ± 0.2 to 0.3 ± 0.1 after reaction, while the Ga–O path degeneracy increases from 2.9 ± 0.4 to 3.5 ± 0.3–indicating that a proportion of the reduced Ga found in the alloyed NPs indeed partially oxidises upon exposure to reaction conditions (Fig. S1–S4 and Tables S1–S3†).

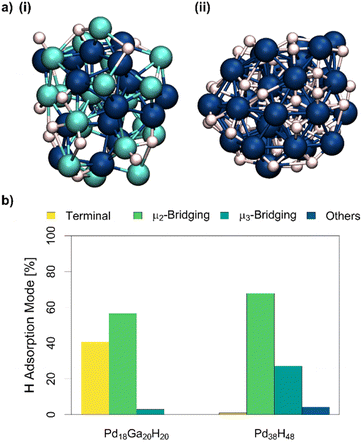Fig. 5 (a): Structure of (i) Pd₁₈Ga₂₀H₂₀ NP and (ii) Pd₃₈H₄₈ NP in vacuum obtained from metadynamics. Pd: dark blue, Ga: brighter blue, and H: white (trajectories and FES can be found in Fig. S44–S61†). (b): Proportion of different hydride coordination modes of the Pd₁₈Ga₂₀H₂₀ and Pd₃₈H₄₈ NP obtained from AIMD simulations.

We thus next evaluate the influence of the more “oxidizing” conditions on the structure of the alloy by adding O* atoms that would arise from the reaction of CO₂ or H₂O (Fig. S67†). Different Pd₁₈Ga₂₀O_X NPs were simulated with various O* contents (X = 10, 20, and 30; 0.5, 1.0, and 1.5 relative to Ga) to gain insights into general structural trends. CN_Pd–O and CN_Ga–O were used as additional CVs.

For all three O* contents, CN_Pd–Ga and CN_Ga–Ga decrease in the presence of O* while CN_Pd–O and CN_Ga–O increase (Fig. 6, Table 1 and Fig. S68–S89†). While CN_Pd–Pd does not vary significantly with different stoichiometries of O*, it increases compared to the pristine PdGa NP. These two observations combined indicate partial dealloying of the NP, regardless of the exact O* coverage. The large distance of Ga to the centre of mass of the Pd₁₈Ga₂₀O₁₀ NP (4.5 Å) compared to Pd (3.3 Å) once again indicates that Ga is extruded to the surface upon exposure to more oxidizing conditions and that a Pd-rich core is present, causing the increase in CN_Pd–Pd.

Fig. 6 Structure closest to the free energy minima for the (i) Pd₁₈Ga₂₀O₁₀ NP, (ii) Pd₁₈Ga₂₀O₂₀ NP, and (iii) Pd₁₈Ga₂₀O₃₀ NP. The FES, the initial guess for each structure, and the analysis of the trajectories can be found in Fig. S67–S89.†

Table 1 CN_Pd–Pd, CN_Pd–Ga, CN_Ga–Ga, CN_Pd–O and CN_Ga–O at the minima of the FES of Pd₁₈Ga₂₀, Pd₁₈Ga₂₀@SiO₂, Pd₁₈Ga₂₀O₁₀, Pd₁₈Ga₂₀O₂₀ and Pd₁₈Ga₂₀O₃₀ NPs

	Pd18Ga20	Pd18Ga20O10	Pd18Ga20O20	Pd18Ga20O30
CNPd–Pd	2.5	3.6	3.4	3.3
CNPd–Ga	3.7	2.5	2.5	2.1
CNGa–Ga	2.3	1.1	1.3	1.3
CNPd–O	—	0.4	0.6	1.1
CNGa–O	—	0.7	1.1	1.8

---

While oxygen is coordinated to both Pd and Ga, a slightly higher CN_Ga–O of ca. 0.5 compared to CN_Pd–O is observed for all O* contents, indicating that Ga is preferentially oxidised in these systems, which is consistent with observations from in situ XAS experiments (Fig. 5). However, some Ga remains in close contact with Pd (i.e. CN_Pd–Ga > 0), which suggests that complete oxidation and, therefore, complete dealloying does not occur, even where the oxygen stoichiometry is sufficient to allow full oxidation of Ga into Ga₂O₃ (1.5 O* per Ga). Instead, the competing interaction of Pd with Ga (Ga(0) or Ga^III) is likely strong enough to retain some Pd–Ga interaction and prevents the complete oxidation of Ga. These observations are consistent with experimental observations for PdGa@SiO₂, where analysis of Ga K-edge XANES illustrates that upon introduction of CO₂, appreciable oxidation of Ga occurs.

Conclusions

In this work, AIMD/MTD simulations in combination with XAS were used to elucidate the structure of small PdGa NPs under CO₂ hydrogenation conditions on an atomic level. Alloying of the PdGa NP results in the dilution of Pd sites on the NP surface, and in contrast to other systems explored using similar approaches, no significant change in terms of particle structure or shape is observed when the NPs interact with silica.

To confront observations from chemisorption, AIMD/MTD simulations were used to explore the dominant binding modes of different molecules at realistic adsorbate coverages. The simulations confirm that CO occupies isolated atop Pd sites almost exclusively in the PdGa alloy, while bridging CO molecules are observed on pure Pd, consistent with experimental findings. Furthermore, the presence of Ga modifies the dominant binding modes of H*, promoting the formation of atop and bridged H* vs. bridged and hollow H* in the monometallic system. It is also shown that under more oxidizing conditions, such as those expected during CO₂ hydrogenation, the PdGa NPs partially dealloy in the presence of O*, leading to the formation of a Pd-rich core and a partially oxidised GaO_X shell, reconciling previous observations from in situ XAS. Yet, the complete oxidation of Ga to Ga₂O₃ is not observed, even at high oxygen coverage. This indicates strong interaction of the partially oxidised GaO_X with Pd, reminiscent of strong metal-support interaction.³²

Overall, these results demonstrate that the structures of alloyed PdGa NPs are highly sensitive to the surrounding atmosphere, likely resulting in rapid changes and (de)alloying under reducing and oxidizing conditions. This work also highlights that MTD is a powerful approach to elucidate structural dynamics at a single particle level, such as the dynamics of adsorbed hydrides, which static computations with slab models or small clusters would not capture. We are further investigating the implications of these results and how they can be generalised to other catalytic systems and reaction conditions.

Methods

Models for Pd and PdGa NPs (0.8 nm, 38 atoms) were constructed, which have a size comparable to the synthesised NPs (1.6 ± 0.4 nm).²⁰ The crystalline PdGa NP was constructed by cutting the bcc-PdGa bulk structure at different low-index facets and used as a starting guess (Fig. 1b(i), Pd is shown in dark blue while Ga is shown in brighter blue). Surface interactions were captured by using a model surface of dehydroxylated amorphous SiO_2-700 (silica model with an OH-density similar to silica dehydroxylated at 700 °C, which used to synthesise the PdGa NPs)²⁰ previously developed.²⁵

Calculations were carried out with the CP2K package.³³ Periodic Kohn–Sham Density-Functional Theory (DFT) was used with the exchange-correlation functional of Perdew, Burke, and Ernzerhof (PBE) in the rev-PBE implementation which was chosen for its reliable prediction of adsorption energies.³⁴ Additional Grimme dispersion corrections with Beckett-Johnson damping function (D3-BJ) were employed.³⁵ A Gaussian plane wave (GPW) basis set on the DZVP level was employed.^36,37 Goedecker–Teter–Hutter (GTH) pseudopotentials were chosen to model core electrons.³⁸ The SiO_2-700 support was modelled using an SZV GPW basis set.^36,37

AIMD was used in the Born-Oppenheimer variant to explore the conformational space of the NPs.^10,39 All calculations were carried out in an NVT (canonical) ensemble held at 503 K, the temperature typically used for CO₂ hydrogenation.¹⁹ The temperature was imposed using the canonical sampling through velocity rescaling thermostat with a time constant of 100 fs.⁴⁰ Hydrogen was replaced by deuterium to avoid artificial bond breaking due to the fast motion of H. The AIMD time steps were chosen as 1 fs. For simulations of the SiO₂ surface, atoms from the lower half of the support were frozen.

MTD was employed with the Lagrangian formulation to accelerate the AIMD runs and explore the conformational space of the PdGa NP more efficiently.^12–16 Gaussian-shaped potentials (hills) were deposited along the CVs every 20 steps (every 20 fs) with a height of 0.01 Hartree (Ha). The width was chosen as 0.15 times the range of the CVs. This compromise minimizes the overall error on the FES made between deposited Gaussian size and simulation time.^16,41 Simulations for the conformational analysis of the NPs (unsupported and supported, with and without adsorbates) were run for 20 ps.

The correct choice of CVs is very important for MTD. It is required for them to distinguish between all intermediates to map them on the FES unambiguously. The coordination number between two elements X and Y (CN_X–Y) is commonly chosen as a CV, as shown in eqn (1).⁴²

Here, r⁰_X–Y is the cut-off distance, r_iX,jY is the distance between the atoms i_X and j_Y and the exponents nn_X–Y and nd_X–Y determine the steepness of the cut-off. Coordination numbers were selected as collective variable since they can be straightforwardly extracted from fitting of the experimental EXAFS spectra. To find the optimum values, the trajectory of the PdGa NP was analysed with r⁰ values ranging from r⁰_X–Y = 1.0 Å to 5.0 Å, nn values ranging from nn_X–Y = 5 to 20 and nd values ranging from nn_X–Y = 10 to 25 (Fig. S5†). It was found that the qualitative results are not strongly dependent on the exact choices of the parameters of the CVs, as long as the values are in a reasonable range around the optimal values, as claimed by Valsson et al.⁴³ For the simulations, nn_X–Y = 6 and nd_X–Y = 12 were chosen for all CN values since they provide a good trade-off between sharp transitions at the cut-off distance and smooth CN values. The coordination number of Pd to Pd (CN_Pd–Pd, r⁰_Pd−Pd = 3.0 Å) and Ga (CN_Pd–Ga, r⁰_Pd−Ga = 2.8 Å) as well as Ga to Ga (CN_Ga–Ga, r⁰_Ga−Ga = 2.8 Å) were used to explore the conformational space of the PdGa NPs. For subsequent Metadynamics simulations, the coordination to C (from CO) (CN_M–C, r⁰_M–C = 2.1 Å), to D (as a replacement to H) (CN_M–D, r_M–⁰_D = 1.9 Å) and to O (CN_M–O, r_M–⁰_O = 2.0 Å) with M = Ga, Pd were considered as well. The cut-off distances r_X–⁰_Y were chosen to be around 1.3 times the sum of the Van-der-Waals radii of the individual atoms and allow good differentiation between bound atom pairs (r_iX,jY < r⁰_X–Y), unbound atom pairs (r_iX,jY > r⁰_X–Y) and intermediate states (r_iX,jY ≈ r⁰_X–Y). All CVs were added to the extended Lagrangian with λ = 0.5 and restricted to positive values by a quartic wall at 0 to prevent negative, non-physical CNs.

For a better understanding of the specific properties of the trajectories, such as the movement of particular atoms in the particle or the connectivity of surface adsorbates to compare AIMD and MTD, the trajectories were post-treated with the PLUMED library.⁴⁴ For the analysis of the AIMD trajectories in the presence of adsorbates, CNs of adsorbates (X = C, H) to the metal atom (CN_X–M, M = Pd, Ga) were recorded and categorized into terminal (0.5 < CN_X–M < 1.5), μ₂-bridging (1.5 < CN_X–M < 2.5), μ₃-bridging (2.5 < CN_X–M < 3.5) and subsurface (internal) (3.5 < CN_X–M). Cut-off distances of r⁰_H–M = 2.1 Å and of r⁰_C–M = 2.3 Å were chosen to categorize the CN_X–M. Analysis of various cut-off distances indicated that while the relative amounts of the different categories depend on the cut-off distance, the overall trends between Pd and PdGa NP are independent of the cut-off distance as long as the cut-off distances are not too short (r⁰_C–M > 2.1 Å and r⁰_H–M > 1.7 Å, compare Fig. S39, S42, S62 and S65†).

The IR-spectra were calculated using TRAVIS (TRajectory Analyzer and VISualizer), a free program package for analysing and visualising Monte Carlo and molecular dynamics trajectories.^27,28 The dipole moments were calculated using the Voronoi tessellation, as implemented in CP2K, and exported as BQB files, which are produced using an efficient lossless compression algorithm for trajectories of atom positions and volumetric data.⁴⁵

In addition to the previously mentioned coordination number, we also investigated different CVs to better distinguish different states. We first evaluated the influences of the three primary parameters on the CNs (nn, nd, and r⁰). The chosen parameters are sufficiently close to the ideal values since small changes in the parameters have a somewhat limited influence on the CVs. We refer the reader to the SI for the complete analysis (Fig. S5†). We also looked at other CVs for the trajectories. This includes the CNs of each atom (to specific elements and to all other atoms), the interatomic distances, the distance to the C–O–M (Centre of Mass), and the cluster size of each metal in the NPs with and without oxygen/hydrogen using contact matrices, where the CNs are used as switching functions. The hills of the MTD run were also summed up using PLUMED to generate the FES. For better comparison of the MTD runs, the FES were normalised; the total free energy of one NP is divided by the number of metal atoms in the NP to obtain the free energy per mole of metal in the NP, denoted as kcal mol_M⁻¹.

The MTD runs were visualised using Visual Molecular Dynamics (VMD), a molecular visualization program for displaying, animating, and analysing larger large biomolecular systems or particles.⁴⁶ It is available free of charge (including source code) on their website. The images were exported using the Tachyon ray tracing library built into VMD.⁴⁷

The materials described (PdGa@SiO₂ and Pd@SiO₂) were prepared according to a reported procedure.²⁰ Fitting of the Ga K-edge EXAFS was performed on previously published data.²⁰ For Ga K-edge EXAFS, the amplitude reduction factor (S₀²) was not specifically extracted, meaning that coordination numbers will be systematically underestimated, but trends across EXAFS fitting will be consistent within the series of measurements. The program package Demeter was used for fitting of EXAFS.⁴⁸ Time-resolved XAS at the Ga K-edge was measured at the SuperXAS beamline (X10DA) at the Swiss Light Source (SLS, PSI, Villigen, Switzerland), operating in top-up mode at a 2.4 GeV electron energy and a current of 400 mA. Calibration of the monochromator energy at the Ga K-edge was achieved using a Zn foil (9659 eV) as an in-line reference, placed between the second and third ion chambers. The incident photon beam was selected by a liquid nitrogen-cooled Si (111) quick-EXAFS monochromator, and the rejection of higher harmonics and focusing were achieved by a rhodium-coated collimating mirror. The beam size on the sample was approximately 2000 μm × 500 μm. During measurement, the quick XAS monochromator was rotating (1 Hz, 2.5° angular range) and spectra were collected in transmission mode using ionization chambers specially developed for quick data collection.

For in situ XAS experiments, the air-exposed powder sample (ca. 20 mg, 250–400 μm SiO₂ aggregates) was packed into quartz capillary (3 mm Ø_outer, 2.8 mm Ø_inner, bed length ca. 1 cm) which was integrated to a pressurisable gas flow system consisting of 2 parallel arrays, each consisting of 3 mass flow controllers (MFCs, Bronkhorst), while the total pressure was maintained by a back-pressure regulator (Bronkhorst EL-Press). Switching between the two systems (i.e. switching the MFC array that was feeding the capillary) was performed using a remote controlled 6-port 2-way switching valve (VICI, Valco) that could be operated from outside the experimental hutch. While one gas mixture was flowing to the cell, the other was directed via a bypass to the exhaust. Samples were heated using a custom-built infrared heater (Elstein-Werk M. Steinmetz GmbH & Co. KG (Germany), 30 mm length, with two heating elements – one above and one below sample capillary), and temperature was monitored/maintained using a 0.3 mm K-type thermocouple placed in direct contact with the catalyst bed. Ar and H₂ were purified by passing through a trap containing molecular sieves and Q5 catalyst prior to introduction to the XAS quartz cell. CO₂ was purified by passing through a trap containing molecular sieves.

In the in situ experiment, Ar (10 sccm, 1 bar) was flowed over the over the catalyst for 10 minutes while the spectra were recorded. The gas flow was then changed to H₂ (10 sccm, 1 bar), and the sample was heat-treated to 300 °C with a ramp of 5 °C min⁻¹, before cooling to 230 °C. Spectra were recorded continuously during the hydrogen treatment. The gas composition was then switched to H₂/Ar (3 : 2, 10 sccm), and subsequently pressurized to 11 bar. At the point at which pressure stabilized, acquisition was started, and the sample was measured continuously for 30 minutes. After 10 minutes of acquisition, the gas composition was switched, under isobaric conditions, using the 6-port valve, to H₂/Ar/CO₂ (3 : 1 : 1, 10 sccm), to capture any changes upon introduction of CO₂ to the reaction gas. The delay between switching of the gas compositions and CO₂ reaching the catalyst bed was estimated to be approximately 40 seconds, based on the reduced absorption of the beam (drop in baseline of spectrum prior to normalization) upon replacing a fraction of the Ar in the feed with less-absorbing CO₂, using a strategy similar to that described by Lomachenko, et al.⁴⁹ Multivariate curve resolution alternating least-squares (MCR-ALS) analysis is a chemometric method that enables the extraction of the concentration profiles of pure components of complex mixtures on the basis of their kinetic behaviour (i.e. a response to an applied stimulus).⁵⁰ Thus, it is well-suited to tracking the distribution of kinetically-distinct species during in situ experiments.⁵¹ MCR-ALS algorithm is used to decompose a series of experimental spectra (D) into pure contributions, consisting of concentration profiles (C) and the corresponding spectra (S) of different chemical compounds, based on the equation D = CS^T + E, where S^T is the transpose of matrix S and E corresponds to the residual. For this purpose, the in-built MCR feature of the ProQEXAFS software was used.⁵² For the analysis, an energy range of 10 300–10 450 eV was used for the Ga K-edge. Spectra were first normalized and cut to include only the relevant range for further analysis.

Data availability

All the data supporting this article have been included in the main text and the ESI.†

Author contributions

J. F. B. and A. M. performed the calculations. S. R. D. performed XAS analysis. The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research is supported by the Sinergia Project of the Swiss National Science Fonds (SNSF fond number: CRSII5_183495). C.C. and S.R.D. acknowledge the Swiss National Science Foundation (grants 200021_169134, and 200020B_192050) Aleix Comas-Vives thanks the Spanish “Ministerio de Ciencia, Innovación y Universidades” (PID2021-128416NB-I00). We thank Quentin Pessemesse for help with the data visualisation, imaging of the NPs and calculating the IR-spectra. We acknowledge the Swiss Light Source for beamtime (SuperXAS beamline (X10DA) (Proposal No. 20210709)) and thank Dr Olga Safonova and Ilia Sadykov for support during the beamtime, as well as members of the Copéret group for their support during these experiments.

Notes and references

1. (a) I. Fechete, Y. Wang and J. C. Védrine, Catal. Today, 2012, 189, 2; (b) L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981; (c) C. Adams, Top. Catal., 2009, 52, 924; (d) W. Bonrath and T. Netscher, Appl. Catal., A, 2005, 280, 55.
2. (a) H. Liao, A. Fisher and Z. J. Xu, Small, 2015, 11, 3221; (b) T. Dang-Bao, D. Pla, I. Favier and M. Gómez, Catalysts, 2017, 7; (c) K. Loza, M. Heggen and M. Epple, Adv. Funct. Mater., 2020, 30, 1909260; (d) R. Wei, N. Tang, L. Jiang, J. Yang, J. Guo, X. Yuan, J. Liang, Y. Zhu, Z. Wu and H. Li, Coord. Chem. Rev., 2022, 462, 214500; (e) N. G. Dlamini, A. K. Basson and V. S. R. Pullabhotla, Applied Nano, 2023, 4, 1; (f) X. Liu, Q. Gu, Y. Zhang, X. Xu, H. Wang, Z. Sun, L. Cao, Q. Sun, L. Xu, L. Wang, S. Li, S. Wei, B. Yang and J. Lu, J. Am. Chem. Soc., 2023, 145, 6702.
3. (a) H. Frey, A. Beck, X. Huang, J. A. van Bokhoven and M. G. Willinger, Science, 2022, 376, 982; (b) A. Beck, M. Zabilskiy, M. A. Newton, O. Safonova, M. G. Willinger and J. A. van Bokhoven, Nat. Catal., 2021, 4, 488; (c) A. Urakawa, Nat. Catal., 2021, 4, 447.
4. A. Müller, A. Comas-Vives and C. Copéret, Chem. Sci., 2022, 13, 13442.
5. R. Schlögl, Angew. Chem., Int. Ed., 2015, 54, 3465.
6. (a) J. Nakamura, Y. Choi and T. Fujitani, Top. Catal., 2003, 22, 277; (b) S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjær, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969.
7. M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893.
8. T. Lunkenbein, J. Schumann, M. Behrens, R. Schlögl and M. G. Willinger, Angew. Chem., Int. Ed., 2015, 54, 4544.
9. S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296.
10. R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471.
11. (a) K. Rossi and F. Baletto, Phys. Chem. Chem. Phys., 2017, 19, 11057; (b) L. Pavan, K. Rossi and F. Baletto, J. Chem. Phys., 2015, 143, 184304.
12. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562.
13. M. Iannuzzi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 238302.
14. A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601.
15. G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200.
16. A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826.
17. P.-A. Payard, L. Rochlitz, K. Searles, L. Foppa, B. Leuthold, O. V. Safonova, A. Comas-Vives and C. Copéret, JACS Au, 2021, 1, 1445.
18. L. Rochlitz, Q. Pessemesse, J. W. A. Fischer, D. Klose, A. H. Clark, M. Plodinec, G. Jeschke, P.-A. Payard and C. Copéret, J. Am. Chem. Soc., 2022, 144, 13384.
19. (a) J. D. A. Pelletier and J.-M. Basset, Acc. Chem. Res., 2016, 49, 664; (b) C. Copéret, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Núñez-Zarur and P. A. Zhizhko, Chem. Rev., 2016, 116, 323; (c) C. Copéret, A. Fedorov and P. A. Zhizhko, Catal. Lett., 2017, 147, 2247; (d) M. K. Samantaray, E. Pump, A. Bendjeriou-Sedjerari, V. D'Elia, J. D. A. Pelletier, M. Guidotti, R. Psaro and J.-M. Basset, Chem. Soc. Rev., 2018, 47, 8403; (e) C. Copéret, Acc. Chem. Res., 2019, 52, 1697; (f) S. R. Docherty and C. Copéret, J. Am. Chem. Soc., 2021, 143, 6767; (g) S. R. Docherty, L. Rochlitz, P.-A. Payard and C. Copéret, Chem. Soc. Rev., 2021, 50, 5806; (h) E. Lam, G. Noh, K. W. Chan, K. Larmier, D. Lebedev, K. Searles, P. Wolf, O. V. Safonova and C. Copéret, Chem. Sci., 2020, 11, 7593; (i) E. Lam, G. Noh, K. Larmier, O. V. Safonova and C. Copéret, J. Catal., 2021, 394, 266; (j) G. Noh, E. Lam, D. T. Bregante, J. Meyet, P. Šot, D. W. Flaherty and C. Copéret, Angew. Chem., Int. Ed., 2021, 60, 9650; (k) S. R. Docherty, O. V. Safonova and C. Copéret, J. Am. Chem. Soc., 2023, 145, 13526.
20. S. R. Docherty, N. Phongprueksathat, E. Lam, G. Noh, O. V. Safonova, A. Urakawa and C. Copéret, JACS Au, 2021, 1, 450.
21. P. Amann, B. Klötzer, D. Degerman, N. Köpfle, T. Götsch, P. Lömker, C. Rameshan, K. Ploner, D. Bikaljevic, H.-Y. Wang, M. Soldemo, M. Shipilin, C. M. Goodwin, J. Gladh, J. Halldin Stenlid, M. Börner, C. Schlueter and A. Nilsson, Science, 2022, 376, 603.
22. (a) P. R. Couchman and W. A. Jesser, Nature, 1977, 269, 481; (b) P. Puri and V. Yang, J. Phys. Chem. C, 2007, 111, 11776; (c) H. Jiang, K. Moon, H. Dong, F. Hua and C. P. Wong, Chem. Phys. Lett., 2006, 429, 492.
23. (a) J. M. Cowley, Phys. Rev., 1950, 77, 669; (b) J. M. Cowley, Phys. Rev., 1960, 120, 1648; (c) J. M. Cowley, Phys. Rev., 1965, 138, A1384–A1389; (d) A. I. Frenkel, Q. Wang, S. I. Sanchez, M. W. Small and R. G. Nuzzo, J. Chem. Phys., 2013, 138, 64202.
24. I. Kaul and P. Ghosh, Chem. Phys., 2017, 487, 87.
25. A. Comas-Vives, Phys. Chem. Chem. Phys., 2016, 18, 7475.
26. (a) K. Kovnir, M. Armbrüster, D. Teschner, T. V. Venkov, L. Szentmiklósi, F. C. Jentoft, A. Knop-Gericke, Y. Grin and R. Schlögl, Surf. Sci., 2009, 603, 1784; (b) Q. Sun, B. W. J. Chen, N. Wang, Q. He, A. Chang, C.-M. Yang, H. Asakura, T. Tanaka, M. J. Hülsey, C.-H. Wang, J. Yu and N. Yan, Angew. Chem., Int. Ed., 2020, 59, 20183.
27. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105.
28. M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007.
29. L. L. Jewell and B. H. Davis, Appl. Catal., A, 2006, 310, 1.
30. Z. Zhao, X. Huang, M. Li, G. Wang, C. Lee, E. Zhu, X. Duan and Y. Huang, J. Am. Chem. Soc., 2015, 137, 15672.
31. (a) A. L. Bugaev, A. A. Guda, K. A. Lomachenko, V. V. Srabionyan, L. A. Bugaev, A. V. Soldatov, C. Lamberti, V. P. Dmitriev and J. A. van Bokhoven, J. Phys. Chem. C, 2014, 118, 10416; (b) C. Mager-Maury, G. Bonnard, C. Chizallet, P. Sautet and P. Raybaud, ChemCatChem, 2011, 3, 200; (c) M. W. Tew, J. T. Miller and J. A. van Bokhoven, J. Phys. Chem. C, 2009, 113, 15140.
32. (a) S. J. Tauster, S. C. Fung and R. L. Garten, J. Am. Chem. Soc., 1978, 100, 170; (b) B. Han, Y. Guo, Y. Huang, W. Xi, J. Xu, J. Luo, H. Qi, Y. Ren, X. Liu, B. Qiao and T. Zhang, Angew. Chem., Int. Ed., 2020, 59, 11824; (c) T. Uchijima, Catal. Today, 1996, 28, 105; (d) C. Wu, D. Cheng, M. Wang and D. Ma, Energy Fuels, 2021, 35, 19012.
33. (a) J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103; (b) J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15; (c) A. Heinecke, G. Henry, M. Hutchinson and H. Pabst, in SC '16: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 2016, pp. 981–991; (d) A. Marek, V. Blum, R. Johanni, V. Havu, B. Lang, T. Auckenthaler, A. Heinecke, H.-J. Bungartz and H. Lederer, J. Phys.: Condens. Matter, 2014, 26, 213201; (e) U. Borštnik, J. VandeVondele, V. Weber and J. Hutter, Parallel Comput., 2014, 40, 47; (f) M. Frigo and S. G. Johnson, Proc. IEEE, 2005, 93, 216; (g) J. Kolafa, J. Comput. Chem., 2004, 25, 335; (h) T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
34. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396; (c) S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921; (d) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 415; (e) Y. Zhang and W. A. Yang, Phys. Rev. Lett., 1998, 80, 890.
35. (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
36. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
37. G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477.
38. (a) P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953; (b) G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758; (c) S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B, 1996, 54, 1703; (d) C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B, 1998, 58, 3641; (e) M. Krack, Theor. Chem. Acc., 2005, 114, 145.
39. T. D. Kühne, M. Krack, F. R. Mohamed and M. Parrinello, Phys. Rev. Lett., 2007, 98, 66401.
40. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 14101.
41. A. Laio, A. Rodriguez-Fortea, F. L. Gervasio, M. Ceccarelli and M. Parrinello, J. Phys. Chem. B, 2005, 109, 6714.
42. G. Fiorin, M. L. Klein and J. Hénin, Mol. Phys., 2013, 111, 3345.
43. O. Valsson, P. Tiwary and M. Parrinello, Annu. Rev. Phys. Chem., 2016, 67, 159.
44. (a) T. P. consortium, Nat. Methods, 2019, 16, 670; (b) G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604.
45. (a) M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608; (b) M. Thomas, M. Brehm and B. Kirchner, Phys. Chem. Chem. Phys., 2015, 17, 3207; (c) M. Brehm, H. Weber, M. Thomas, O. Hollóczki and B. Kirchner, ChemPhysChem, 2015, 16, 3271; (d) M. Brehm and M. Thomas, Molecules, 2021, 26; (e) M. Brehm and M. Thomas, J. Chem. Inf. Model., 2018, 58, 2092; (f) C. H. Rycroft, Chaos, 2009, 19, 41111.
46. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.
47. J. Stone, Master thesis, Computer Science Department, University of Missouri-Rolla, 1998.
48. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537.
49. K. A. Lomachenko, A. Y. Molokova, C. Atzori and O. Mathon, J. Phys. Chem. C, 2022, 126, 5175.
50. (a) A. de Juan, J. Jaumot and R. Tauler, Anal. Methods, 2014, 6, 4964; (b) R. Tauler and D. Barceló, Trends Anal. Chem., 1993, 12, 319.
51. (a) A. H. Clark, R. J. G. Nuguid, P. Steiger, A. Marberger, A. W. Petrov, D. Ferri, M. Nachtegaal and O. Kröcher, ChemCatChem, 2020, 12, 1429; (b) S. B. Varandili, D. Stoian, J. Vavra, K. Rossi, J. R. Pankhurst, Y. T. Guntern, N. López and R. Buonsanti, Chem. Sci., 2021, 12, 14484.
52. A. H. Clark, J. Imbao, R. Frahm and M. Nachtegaal, J. Synchrotron Radiat., 2020, 27, 551.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00484a

‡ These authors contributed equally to this work.

---