Reversible and irreversible reaction mechanisms of Li–CO₂ batteries

Abstract

Li–CO₂ batteries are considered a versatile solution for CO₂ utilization. However, their development, including reversibility and efficiency, is impeded by an inadequate understanding of Li–CO₂ electrochemistry, particularly the decomposition of carbon and the generation of by-product O₂. Here, using typical Ru(0001) (reversible) and Ir(111) (irreversible) as model catalysts and employing state-of-the-art first-principles calculations, the rechargeable/reversible reaction mechanisms of Li–CO₂ batteries are disclosed. We find that electrolyte, often neglected or oversimplified in Li–CO₂ modelling, plays an essential role in CO₂ activation and C–C coupling affects the generation pathways of discharge intermediates due to the sluggish kinetics. The results rationalize experimental observations, which are also examined by constant-potential modelling. Specifically, by exploring the kinetics of the charging process, we discover that the reversibility of Ru(0001) is attributed to its ability to suppress O–O coupling while co-oxidizing Li₂CO₃ and carbon. In contrast, Li₂CO₃ decomposition on Ir(111) preferentially produces O₂, during which carbon can only be partially decomposed. These findings solve long-standing questions and highlight the necessity of describing the explicit solvent effect in modelling, which can promote further studies on Li–CO₂ batteries.

---

Introduction

Li–CO₂ batteries have garnered extensive attention from the scientific community owing to their high potential for CO₂ fixation while simultaneously enabling energy storage with a theoretical energy density of 1876 W h kg⁻¹.^1–3 In contrast to Li-ion batteries, their performance is governed by Li–CO₂ electrochemistry, which operates according to the following reaction: 4Li + 3CO₂ ↔ 2Li₂CO₃ + C (E₀ = 2.8 V vs. Li/Li⁺).^4–7 However, CO₂ reduction during the discharging process is kinetically sluggish, which results in large discharging overpotentials, and a high charge voltage is also required to decompose the discharge product, Li₂CO₃, due to its wide bandgap of 5.03 eV and high thermodynamic stability (ΔG_f = −1132.1 kJ mol⁻¹).^8,9 The inadequate decomposition of the discharge product carbon limits energy efficiency and leads to an irreversible reaction (e.g., 2Li₂CO₃ → 4Li⁺ + 4e⁻ + 2CO₂ + O₂).^10–12 Moreover, the passivation of catalyst surfaces and instability of electrolytes affect the cycle performance of Li–CO₂ batteries. Such issues pose massive challenges to the practical applications of Li–CO₂ batteries, thereby inspiring the rational design of catalysts that demonstrate high reversibility and low overpotentials.^13–15

Uncovering the underlying mechanisms can facilitate the design of efficient catalysts.^16–21 Based on experimental characterization and theoretical calculations, much effort has been expended to reveal the reaction pathway on the catalysts, which directly determines the reversibility of Li–CO₂ electrochemistry.^22–25 For the discharging process, C–C coupling, such as the dimerization of *CO₂ (* indicates an adsorption site) and the reaction of *Li₂CO₂ and *CO₂, was regarded as the essential steps for Li₂CO₃ formation.^12,18,26 However, the dominant coupling step and reaction pathway are still controversial. Another important issue is that the oxidative decomposition mechanism of Li₂CO₃ and carbon remains quite ambiguous. For example, in principle, the as-formed O species can react with carbon, but in the case of most catalysts, such as Au(111) and Ir(111), only the decomposition of Li₂CO₃ has been observed; both O₂ and CO₂ were found to evolve concomitantly during the charging process.^3,26–30 Note that the generated O₂ may contain aggressive singlet oxygen (¹O₂), which can attack battery components and cause severe parasitic reactions.^13,31 In the cases of Ru-based metal catalysts, Li₂CO₃ and carbon disappear together and only CO₂ is released, corresponding to a reversible process.³ However, to date, no satisfactory explanation for such phenomena exists. It is of great significance to gain a mechanistic understanding of Li–CO₂ electrochemistry.

Herein, we investigate the underlying mechanisms of Li–CO₂ electrochemistry by conducting comprehensive first-principles calculations to provide fundamental insights into the reversibility with a focus on the initial charge and discharge processes. Ru(0001) and Ir(111) are selected as model catalysts because the former has been extensively reported to achieve good reversibility in Li–CO₂ electrochemistry, while the latter suffers from irreversibility issues. The modelling results show that the electrolyte can facilitate the activation of CO₂, and the disproportionation of *CO₂ corresponds to the predominant kinetic barrier for the discharging process. The two catalysts exhibit different CO₂ charging processes. Ru(0001) can suppress O–O coupling to form O₂ while co-oxidizing carbon and Li₂CO₃ to generate CO₂, thereby ending a complete battery cycle. By contrast, in the case of Ir(111), Li₂CO₃ decomposes and releases both CO₂ and O₂, and carbon can only be partially decomposed into small fragments.

Results and discussion

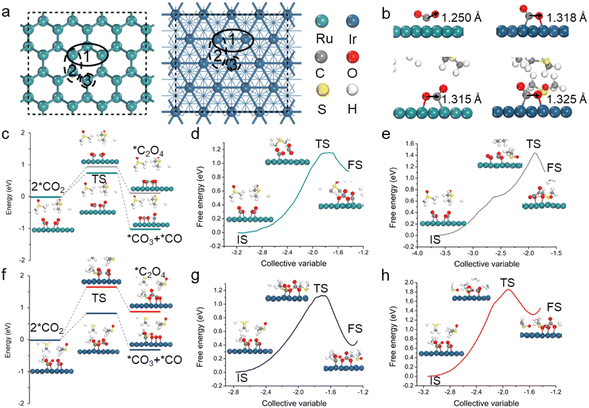
To explore rechargeable/reversible mechanisms of Li–CO₂ batteries, the Ru(0001) and Ir(111) surfaces were constructed (Fig. 1a). We first investigated the discharge process with a focus on the CO₂ activation (forming *CO₂) and subsequent C–C coupling that are crucial steps in the Li–CO₂ electrochemistry. Note that the interactions between reaction intermediates and solvent molecules can be strong, thereby affecting the discharge pathways; for example, prior experiments have indicated that the addition of DMSO can induce the generation of oxalate intermediates.^32,33 However, the solvent effect is often neglected or oversimplified in Li–CO₂ electrochemistry modelling. Hence, an explicit description of the solvent effect was conducted, where DMSO was chosen as a demonstration.

Fig. 1 (a) Structures and possible adsorption sites of the Ru(0001) (left) and Ir(111) (right) surfaces. (b) The most stable CO₂ adsorption configurations of Ru(0001) and Ir(111) in a vacuum (upper) and DMSO solvent (bottom). C, O, S, H, Ru, and Ir are represented by gray, red, yellow, white, green, and dark cyan spheres, respectively. (c and f) Energy barriers of C–C coupling on (c) Ru(0001) and (f) Ir(111), in which the DESW and CBD methods are employed. The insets show geometric structures of the initial state (IS), transition state (TS), and final state (FS). (d and e) Free energy profiles of the (d) CO₂ disproportionation and (e) dimerization pathways on Ru(0001). (g and h) Free energy profiles of the (g) CO₂ disproportionation and (h) dimerization pathways on Ir(111).

Different CO₂ adsorption sites on the two surfaces were investigated. Fig. 1b shows the lowest-energy structure of *CO₂ in which the CO₂ molecule is chemically adsorbed onto Ru(0001) and Ir(111) with a dual-site adsorption configuration. The adsorption free energies are −0.35 eV for Ru(0001) and −0.30 eV for Ir(111). It is worth mentioning that the solvent effect has resulted in an extension of the C–O bond length with respect to both the Ru(0001) and Ir(111) surfaces, with an increase from 1.250 Å to 1.315 Å for the former and 1.318 Å to 1.325 Å for the latter, indicating an overall stronger CO₂ adsorption in both cases (Fig. 1b). The dual-site adsorption presents a longer C–O bond length, which may facilitate bond breaking in the subsequent disproportionation reaction. Please also note that in the case of Ru, the configuration of *CO₂ changes from single-site adsorption (forming a Ru–C bond) to dual-site adsorption (forming Ru–O and Ru–C bonds) after considering the solvent effect. These results highlight the essential role of electrolytes in the activation of CO₂ and demonstrate the necessity of describing the explicit solvent effect in Li–CO₂ electrochemistry modelling.

The activated *CO₂ species can undergo direct dimerization to form oxalate or carbonate intermediates, and they are also available to be coupled with the lithiated intermediates, including *LiCO₂ and *Li₂CO₂. After adsorbing the first CO₂ molecule, the second CO₂ molecule is also activated; the adsorption energies are −0.31 and −0.20 eV for Ru(0001) and Ir(111), respectively. To find the most likely reaction path, we performed a kinetic analysis using the double-ended surface walking (DESW) and constrained Broyden dimer (CBD) approaches.^34,35 Note that the methods can determine a low-energy pathway linking two minima even without iterative optimization of the path, from which the transition state (TS) can be located readily. As shown in Fig. S1 and S2,† *CO₂ is more favourable to disproportionate into *CO₃ and *CO for both Ru(0001) and Ir(111). However, the coupling of *Li₂CO₂ and *CO₂ on Ru(0001) tends to generate oxalates, while in the case of Ir(111), the formation of carbonates is still predominant. As mentioned above, polar electrolytes have a significant impact on the formation of discharge intermediates. Therefore, ab initio molecular dynamics (AIMD) simulations were performed to obtain explicit DMSO structures for the Ru(0001) and Ir(111) surfaces (Fig. S3†),³⁶ and both reaction pathways under solvent conditions were further analysed.

The kinetic results involving the solvation effect shown in Fig. 1c and f indicate that the disproportionation pathway (2*CO₂ → *CO₃ + *CO) is more energetically favourable than the dimerization pathway (2*CO₂ → *C₂O₄). For the disproportionation pathway, the energy barriers of Ru(0001) and Ir(111) are 0.76 and 0.83 eV, respectively, which are lower than those of the dimerization pathway (0.96 and 1.65 eV). In addition, to further catch the solvent network, the slow-growth method was also employed to sample the energy change of the aforementioned optimal reaction pathway; multiple independent slow-growth samplings for each step were conducted (Fig. 1d, e, g, h and S4†). The results prove that *CO₂ on the catalysts has a higher propensity towards undergoing disproportionation to form *CO₃ and *CO, which is consistent with the above kinetic results (Fig. 1c and f). Note that we also conducted slow-growth simulations up to 50 ps and found similar results. This is not surprising as highly polar electrolytes do not directly participate in the Li–CO₂ reactions, which is different from typical aqueous electrochemical reactions (e.g., the hydrogen evolution reaction and the reduction of CO₂ and H₂O to CH₃OH). On a different note, the competing coupling of *Li₂CO₂ and *CO₂ to form *Li₂C₂O₄ in DMSO also exhibits a high energy barrier on the Ru(0001) surface (Fig. S5†). Therefore, the disproportionation of *CO₂ to form *CO₃ and *CO is the dominant pathway for Ru(0001) and Ir(111).

The Li₂CO₃ and carbon formation processes were subsequently investigated using the constant charge method (Fig. 2).^2,12,24 The relative free energy changes (ΔG) are summarized in Table S1.† Please also note that the modelling of the Li–CO₂ reaction still faces many challenges, such as accurately describing the formation process of Li₂CO₃; currently, one common strategy is to simplify it to a Li₂CO₃ moiety, which successfully explains the reaction processes and operation potentials.^{2,11,12,22,24,25} This strategy was adopted in this work. It was found that after the disproportionation of *CO₂, *CO₃ can convert to *Li₂CO₃via two-step lithiation reactions, which are both thermodynamically spontaneous for the Ru(0001) and Ir(111) surfaces (Fig. 2). Subsequently, *Li₂CO₃ desorbs to produce the first Li₂CO₃ species, whereas the previously generated *CO remains on the catalyst surface.

Fig. 2 Free energy diagrams of CO₂ reduction (discharging process) on the (a) Ru(0001) and (b) Ir(111) surfaces. Insets display geometric structures of free slabs, adsorbates, and key transition states that are highlighted by dashed boxes. The structures of transition states are shown in Fig. S6 and S7.†

The remaining question is whether CO undergoes disproportionation or participates in subsequent lithiation reactions. According to our calculations, *CO lithiation to form *LiOC is an exothermic reaction, with respective ΔG values of −1.43 eV for Ru(0001) and −1.54 eV for Ir(111); in accordance with our expectations, the kinetic barriers of such a lithiation step are small (less than 0.3 eV). By contrast, the disproportionation of *CO to form *C and *CO₂ is considerably endothermic, and the kinetic barriers are as high as 1.92 and 2.98 eV for Ru(0001) and Ir(111), respectively. We also calculated the coupling of *CO and *CO₂ to form *CO₃ and *C but found that the relative kinetic barriers are very high (2.31 and 3.28 eV). These results suggest that the two reactions are difficult to occur. Moreover, the lithiation of *LiOC to *Li₂OC is exothermic, and the as-formed *Li₂OC can react with CO₂ to form *Li₂C₂O₃ and then decompose into *Li₂CO₃ and *C species. Such a decomposition step is slightly endothermic by 0.07 eV for Ru(0001) and 0.66 eV for Ir(111).

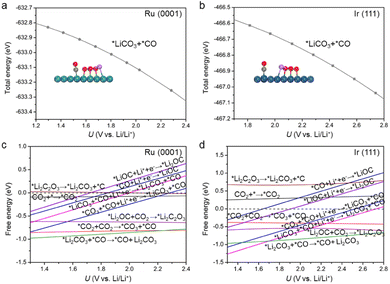
The theoretical limiting potential (U_L) is an important indicator to bridge the experimental activity, such as discharge potential. Based on the free-energy diagrams in Fig. 2, U_L was identified to be 1.43 V for Ru(0001) and 1.54 V for Ir(111). To better simulate electrochemical environments, we performed constant potential modelling, which can describe the effects of the surface charge of catalysts on electrochemical reactions.^37–40 The total energy of each reaction intermediate as a function of potential is fitted (Figs. S8 and S9†), and Fig. 3a and b show the fitting results for *LiCO₃ and *CO intermediates on Ru(0001) and Ir(111), respectively. We found that the U_L values of Ru(0001) and Ir(111) obtained based on the constant potential method are close to the above constant charge results (Fig. 3c and d), and these values are in agreement with experimental observations.⁴¹ These results demonstrate the rationality of our proposed discharge mechanism. Considering the computational cost, the constant charge method was used in subsequent calculations.

Fig. 3 (a and b) Total energy of the absorbed *LiCO₃ and *CO species of (a) Ru(0001) and (b) Ir(111) as a function of potential. (c and d) Free energy changes of discharge elementary reactions of (c) Ru(0001) and (d) Ir(111) based on the constant potential method.

Compared with the discharge reaction, the charging mechanism is relatively complex and ambiguous. According to whether the discharge products Li₂CO₃ and carbon can be completely decomposed, the charging process can be divided into reversible and irreversible reactions.^3,25,27–29 Please note that the reversibility can be influenced by many aspects, such as discharge product-caused passivation of catalyst surfaces, instability of electrolytes, and the incomplete decomposition of discharge products that directly determines the reversibility of Li–CO₂ reactions. In this modelling work, we focused on the decomposition of discharge products during the charging process.

It was previously reported that both chemical and electrochemical pathways may exist for the decomposition of Li₂CO₃.^42,43 For most reported catalysts, only the decomposition of Li₂CO₃ was observed during the charging process while carbon was partially decomposed.^3,12–15 Meanwhile, for exceptional catalysts such as Ru, no satisfactory explanation of the underlying mechanism of the oxidation of Li₂CO₃ and carbon has been provided. In this regard, we proposed two possible mechanisms and performed corresponding calculations, as discussed later.

The discharge product carbon is a complex system; in principle, its decomposition is the gradual transformation of large fragments into small fragments. According to our calculations, the decomposition of carbon on Ru(0001) is much more energetically favourable than that on Ir(111), and as the number of C atoms in the carbon fragments decreases, the energy barrier for removing C atoms typically increases. For example, we investigated the kinetics of removing a C atom from C₁₃ and C₆ clusters (Fig. S10†). The results show that the decomposition barrier of the C₁₃ cluster is 0.38 and 0.94 eV for Ru(0001) and Ir(111), respectively. In the case of the C₆ cluster, the barriers are significantly higher, being 1.45 eV for Ru(0001) and 1.98 eV for Ir(111). Note that after the carbon six-membered ring is broken, the subsequent barrier is moderate; for instance, the barrier of removing a C atom from a C₅ cluster is 1.05 eV for Ru(0001) and 1.21 eV for Ir(111).

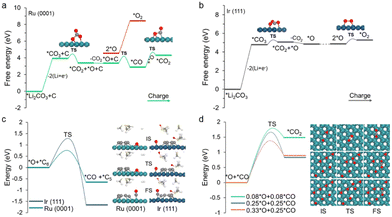
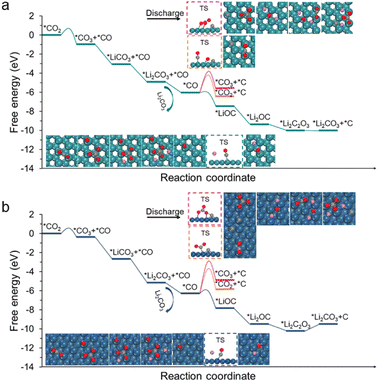
However, the decomposition of carbon and Li₂CO₃ might not be simply oxidized separately but is a co-oxidation process.²⁷ Thus, we further include the contributions from Li₂CO₃ in carbon decomposition. Herein, the C₆ cluster is adopted as the representative model because its decomposition exhibits the largest energy barrier compared with other carbon fragments (Fig. S10†). For the charging process, *Li₂CO₃ first loses two Li and then generates *CO₃via two delithiation steps (Fig. 4a and b), and the kinetic barriers are 0.67 and 0.83 eV for Ru(0001) and Ir(111), respectively (Fig. S11†). The relative free energy changes are summarized in Tables S2 and S3.† These steps are relatively easy to occur on both Ru(0001) and Ir(111) by applying moderate charging voltage. The further decomposition of *CO₃ to *CO₂ and *O is also energetically favourable, displaying a moderate barrier of 0.51 eV and 0.50 eV on Ru(0001) and Ir(111), respectively.

Fig. 4 (a and b) Calculated energetic profiles of the charging process of (a) Ru(0001) and (b) Ir(111). (c) Energy barriers for the oxidative decomposition of a C₆ cluster to form *C₅ and *CO on Ru(0001) and Ir(111). (d) Energy barriers for *CO oxidation under different *CO and *O coverages.

The remaining question is how *O is oxidized. Two possible reaction pathways for *O oxidation were studied. In the first pathway, *O species couple with one another to generate O₂, corresponding to the irreversible charge; in the second pathway, *O attacks carbon to form carbon oxides, which enables a complete battery cycle. It was found that the as-formed *O species can facilitate the carbon decomposition on both the Ru(0001) and Ir(111) surfaces (Fig. S12†). Meanwhile, in accordance with our expectations, the reaction of *O with the C₆ cluster to form *CO and *C₅ on Ru(0001) exhibits a moderate energy barrier (0.86 eV), whereas in the case of Ir(111), the value is as high as 1.60 eV (Fig. S12†). To further investigate the oxidative decomposition of carbon, the reaction energy barriers with respect to the DMSO solvent were also computed (Fig. 4c). A slight decline in the respective energy barriers was observed, validating the feasibility (infeasibility) of oxidative decomposition of carbon on Ru (Ir).

Finally, the adsorbed CO species over Ru(0001) can react with another *O to form *CO₂. Although the energy barrier of the *CO oxidation reaction is slightly high, it becomes more favourable as the coverage of *O and *CO increases (Fig. 4d). This is also consistent with previous reports that CO oxidation on Ru will be more active under high gas pressure.^44,45 On a different note, the dimerization of *O to form O₂ on Ru(0001) is virtually impossible on account of the massive changes in a free energy of 3.90 eV (Fig. 4a). In the case of Ir(111), the *O intermediate preferentially couples with another *O species to generate O₂, which is attributed to a moderate kinetic barrier (0.53 eV). Note that high O coverage reduces the energy barrier of O–O coupling on Ir(111), and while a similar situation occurs in Ru(0001), the energy barrier is still very high (Fig. S13†). Overall, the above modelling results demonstrate that Li₂CO₃ and carbon can be co-oxidized on Ru to conclude a complete battery cycle, while Ir(111) can only partially decompose carbon into small fragments together with oxidizing Li₂CO₃ into CO₂ and O₂. Therefore, our observations are in good agreement with the aforementioned experimental phenomena.^3,28

To gain a fundamental understanding of the difference in the oxidation of carbon on Ru(0001) and Ir(111), the surface charge distributions of *C adsorbed on the two metal surfaces were assessed through a Bader charge analysis. As shown in Fig. S14,† a considerable amount of electronic charge is transferred from both metal surfaces to the *C species. The electron transfer value of the Ru(0001) surface (1.39e) significantly exceeds that of the Ir(111) surface (1.02e), corresponding to a substantially stronger Coulomb interaction between C and Ru(0001). In addition, the continuous formation of the *O intermediate on the Ru(0001) surface results in the former being widely distributed on the latter, which also facilitates reactions between *O and *C to generate CO₂.

Conclusions

In conclusion, using comprehensive first-principles calculations, the complete reversible and irreversible mechanism pathways of Li–CO₂ batteries were disclosed for the first time. The modelling results highlighted that the electrolyte may play an essential role in the activation of CO₂; both Ru(0001) and Ir(111) prefer to undergo the direct disproportionation of *CO₂ to *CO₃ and *CO during the discharge process. The constant-potential calculations verified the rationality of our reaction mechanism. Moreover, we elucidated the reversible co-oxidation process of the discharge products carbon and Li₂CO₃ on Ru(0001) as well as the rationale for the partial decomposition of carbon and the generation of O₂ on Ir(111). Our findings provide a solution to long-standing questions and impart ample guidance in the development of reversible Li–CO₂ batteries.

Methods

First-principles calculations

All first-principles calculations were performed using the Vienna ab initio simulation package (VASP) with the projector augmented wave method and Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation exchange-correlation functional.^46–48 The cutoff energy was set to 400 eV after a series of tests, and the criteria were set as 10⁻⁵ eV for energy and 0.05 eV Å⁻¹ for force. The Brillouin zone was sampled using a Monkhorst–Pack 3 × 3 × 1 k-point grid, and the Grimme-D3 approach was applied to describe the dispersion interactions.⁴⁹ The reaction pathways and transition states were located using the double-ended surface walking (DESW) and constrained Broyden dimer (CBD) methods, as implemented in the LASP software.^34,35 All transition states have been verified by using vibrational frequency calculations (only one imaginary frequency). Note that these methods can determine a low-energy pathway linking two minima even without iterative optimization of the path, from which the transition state (TS) can be located readily.

Structure models

The lattice parameters of bulk Ru and Ir are optimized to be a = b = 2.719 Å, c = 4.297 Å, and a = b = c = 3.872 Å, respectively, which are consistent with experimental values. Two typical metal surfaces, i.e., Ru(0001) and Ir(111), were constructed using 2 × 4 × 1 supercells. A vacuum region of 15 Å thickness along the z direction was chosen to eliminate the interactions between neighbouring surfaces. Specifically, to better describe the reactions in the electrode interface, we considered the solvent effect and potential effect, which are often neglected or oversimplified in the Li–CO₂ electrochemistry modelling. A typical electrolyte, DMSO, was adopted to describe the solvent effect on reaction pathways as a demonstration; five explicit DMSO molecules fill the vacuum gap to provide an experimental density of ρ = 1.1 g cm⁻³.³⁶ Note here that other electrolytes (e.g., TEGDME) were not considered because they have negligible influence on reversibility. The top layer, the adsorbates, and all DMSO molecules are allowed to relax while the remaining atoms are fixed during the calculations. For the Ru(0001) and Ir(111) surfaces, we first performed 10 ps AIMD simulations to obtain explicit DMSO structures. Then, adsorbates were placed on the metal surfaces for further study of the CO₂ electrochemical processes.

Slow-growth simulations

The slow-growth method was used to sample the free-energy change during the disproportionation reaction.^50,51 Nose–Hoover thermostat was adopted to keep temperature at 300 K.⁵² The corresponding increment speed of the CV was within the range between 0.0003 and 0.0004 CV per step, and the simulation time ranged from 5 to 10 ps depending on the length of the reaction pathways. We performed multiple independent slow-growth simulations for each step, and all results revealed that the disproportionation pathway (2*CO₂ → *CO₃ + *CO) is more energetically favourable than the dimerization pathway (2*CO₂ → *C₂O₄). In addition, we also conducted slow-growth simulations up to 50 ps and found no impact on determining the dominant pathway.

Free energy calculations

The free energy change (ΔG) for each elemental step was calculated using

ΔG = ΔE + ΔE_ZPE - TΔS (1)

where ΔE, ΔE_ZPE and ΔS are the total electronic energy difference, zero-point energy difference and entropy change (T = 298 K), respectively. For adsorbates, all 3N degrees of freedom were treated as harmonic vibrations, while the contributions from the catalyst surfaces were neglected. For CO₂, the adsorption energy can be calculated according to the following equation:

E_ads = E_total − E_slab − E_adsorbate (2)

where E_total represents the electronic energy of the total system, E_slab is the energy of the adsorbate-free slab, and E_adsorbate represents the energy of the adsorbate moiety.

Data availability

The computational data supporting the findings can be found in the article and ESI,† and are available from the authors upon reasonable request.

Author contributions

Y. L. designed the research, X. Z. and Y. W. demonstrated the initial idea and collected all the data. X. Z., Y. W. and Y. L. wrote the paper and all authors commented on it.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

We are grateful for funding support from the National Key R&D Program of China (2019YFA0308000), the Natural Science Foundation of China (No. 22173048 and 22203044), the Jiangsu Specially Appointed Professor Plan and the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References

1. J. Zou, G. Liang, F. Zhang, S. Zhang, K. Davey and Z. Guo, Adv. Mater., 2023, 35, 2210671.
2. B. Chen, D. Wang, J. Tan, Y. Liu, M. Jiao, B. Liu, N. Zhao, X. Zou, G. Zhou and H.-M. Cheng, J. Am. Chem. Soc., 2022, 144, 3106–3116.
3. Y. Qiao, J. Yi, S. Wu, Y. Liu, S. Yang, P. He and H. Zhou, Joule, 2017, 1, 359–370.
4. A. Ahmadiparidari, R. E. Warburton, L. Majidi, M. Asadi, A. Chamaani, J. R. Jokisaari, S. Rastegar, Z. Hemmat, B. Sayahpour, R. S. Assary, B. Narayanan, P. Abbasi, P. C. Redfern, A. Ngo, M. Voros, J. Greeley, R. Klie, L. A. Curtiss and A. Salehi-Khojin, Adv. Mater., 2019, 31, 1902518.
5. Z. Zhang, Q. Zhang, Y. Chen, J. Bao, X. Zhou, Z. Xie, J. Wei and Z. Zhou, Angew. Chem., Int. Ed., 2015, 54, 6550–6553.
6. X. Zhang, Q. Zhang, Z. Zhang, Y. Chen, Z. Xie, J. Wei and Z. Zhou, Chem. Commun., 2015, 51, 14636–14639.
7. Y. Jiao, J. Qin, H. M. K. Sari, D. Li, X. Li and X. Sun, Energy Storage Mater., 2021, 34, 148–170.
8. L. Qie, Y. Lin, J. W. Connell, J. Xu and L. Dai, Angew. Chem., Int. Ed., 2017, 56, 6970–6974.
9. P. D. James Speight, Lange's Handbook of Chemistry, Mcgraw-Hill Education, New York, 16th edn, 2005.
10. X. Sun, X. Mu, W. Zheng, L. Wang, S. Yang, C. Sheng, H. Pang, W. Li, C.-H. Li, P. He and H. Zhou, Nat. Commun., 2023, 14, 536.
11. C. Guo, F. Zhang, X. Han, L. Zhang, Q. Hou, L. Gong, J. Wang, Z. Xia, J. Hao and K. Xie, Adv. Mater., 2023, 35, 2302325.
12. Z. Zhao, L. Pang, Y. Su, T. Liu, G. Wang, C. Liu, J. Wang and Z. Peng, ACS Energy Lett., 2022, 7, 624–631.
13. X. Mu, H. Pan, P. He and H. Zhou, Adv. Mater., 2020, 1903790.
14. B. Liu, Y. Sun, L. Liu, J. Chen, B. Yang, S. Xu and X. Yan, Energy Environ. Sci., 2019, 12, 887–922.
15. Z. Zhang, W.-L. Bai, K.-X. Wang and J.-S. Chen, Energy Environ. Sci., 2020, 13, 4717–4737.
16. S. Yang, Y. Qiao, P. He, Y. Liu, Z. Cheng, J.-J. Zhu and H. Zhou, Energy Environ. Sci., 2017, 10, 972–978.
17. C. Ling, Y. Ouyang, L. Shi, S. Yuan, Q. Chen and J. Wang, ACS Catal., 2017, 7, 5097.
18. Y. Wang, T. Liu and Y. Li, Chem. Sci., 2022, 13, 6366–6372.
19. J. Zhou, T. Wang, L. Chend, L. Liao, Y. Wang, S. Xie, B. Chen, T. Lin, Q. Zhang, C. Ye, X. Zhou, Z. Guan, L. Zhai, Z. He, G. Wang, J. Wang, J. Yua, Y. Ma, P. Lu, Y. Xiong, S. Lu, Y. Chen, B. Wang, C.-S. Leea, J. Cheng, L. Gu, T. Zhao and Z. Fan, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2204666119.
20. J. Li, L. Wang, Y. Zhao, S. Li, X. Fu, B. Wang and H. Peng, Adv. Funct. Mater., 2020, 30, 2001619.
21. X. Zhi, Y. Jiao, Y. Zheng, A. Vasileff and S. Z. Qiao, Nano Energy, 2020, 71, 104601.
22. Y. Liu, S. Zhao, D. Wang, B. Chen, Z. Zhang, J. Sheng, X. Zhong, X. Zou, S. P. Jiang, G. Zhou and H.-M. Cheng, ACS Nano, 2022, 16, 1523–1532.
23. D. Guan, X. Wang, M. Li, F. Li, L. Zheng, X. Huang and J. Xu, Angew. Chem., Int. Ed., 2020, 59, 19518–19524.
24. C. Yang, K. Guo, D. Yuan, J. Cheng and B. Wang, J. Am. Chem. Soc., 2020, 142, 6983–6990.
25. J. Hu, C. Yang and K. Guo, J. Mater. Chem. A, 2022, 10, 14028–14040.
26. L. Fan, H. Shen, D. Ji, Y. Xing, L. Tao, Q. Sun and S. Guo, Adv. Mater., 2022, 34, 2204134.
27. D. Cao, C. Tan and Y. Chen, Nat. Commun., 2022, 13, 4908.
28. C. Wang, Q. Zhang, X. Zhang, X. Wang, Z. Xie and Z. Zhou, Small, 2018, 14, 1800641.
29. Y. Xing, Y. Yang, D. Li, M. Luo, N. Chen, Y. Ye, J. Qian, L. Li, D. Yang, F. Wu, R. Chen and S. Guo, Adv. Mater., 2018, 30, 1803124.
30. C. Tan, A. Wang, D. Cao, F. Yu, Y. Wu, X. He and Y. Chen, Adv. Energy Mater., 2023, 13, 2204191.
31. N. Mahne, S. E. Renfrew, B. D. Mccloskey and S. A. Freunberger, Angew. Chem., Int. Ed., 2018, 57, 5529.
32. Y.-F. Wang, G.-J. Ji, L.-N. Song, X.-X. Wang and J.-J. Xu, ACS Energy Lett., 2023, 8, 1026–1034.
33. Z. Zhao, E. Wang, J. Wang, C. Liu and Z. Peng, J. Mater. Chem. A, 2021, 9, 3290–3296.
34. C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2010, 6, 1136–1144.
35. X. Zhang, C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 5745–5753.
36. Z. Jiang and A. M. Rappe, J. Am. Chem. Soc., 2022, 144, 22150–22158.
37. J.-S. Filhol and M. Neurock, Angew. Chem., Int. Ed., 2006, 45, 402–406.
38. Y.-H. Fang and Z.-P. Liu, J. Am. Chem. Soc., 2010, 132, 18214–18222.
39. D. Kim, J. Shi and Y. Liu, J. Am. Chem. Soc., 2018, 140, 9127–9131.
40. Y. Wang, L. You and K. Zhou, Chem. Sci., 2021, 12, 14065–14073.
41. X. Xiao, Z. Zhang and P. Tan, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2217454120.
42. L. A. Kaufman and B. D. McCloskey, Chem. Mater., 2021, 33, 4170–4176.
43. A. T. S. Freiberg, J. Sicklinger, S. Solchenbach and H. A. Gasteiger, Electrochim. Acta, 2020, 346, 136271.
44. A. Tetenoire, J. I. Juaristi and M. Alducin, J. Phys. Chem. C, 2021, 125, 12614–12627.
45. C. H. F. Peden, D. W. Goodman, M. D. Weisel and F. M. Hoffmann, Surf. Sci., 1991, 253, 44–58.
46. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
48. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
49. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
50. T. P. Straatsma, H. Berendsen and J. Postma, J. Chem. Phys., 1986, 85, 6720–6727.
51. E. A. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Chem. Phys. Lett., 1989, 156, 472–477.
52. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00383g

---