Electronic Lieb lattice signatures embedded in two-dimensional polymers with a square lattice

Abstract

Exotic band features, such as Dirac cones and flat bands, arise directly from the lattice symmetry of materials. The Lieb lattice is one of the most intriguing topologies, because it possesses both Dirac cones and flat bands which intersect at the Fermi level. However, the synthesis of Lieb lattice materials remains a challenging task. Here, we explore two-dimensional polymers (2DPs) derived from zinc-phthalocyanine (ZnPc) building blocks with a square lattice (sql) as potential electronic Lieb lattice materials. By systematically varying the linker length (ZnPc-xP), we found that some ZnPc-xP exhibit a characteristic Lieb lattice band structure. Interestingly though, fes bands are also observed in ZnPc-xP. The coexistence of fes and Lieb in sql 2DPs challenges the conventional perception of the structure–electronic structure relationship. In addition, we show that manipulation of the Fermi level, achieved by electron removal or atom substitution, effectively preserves the unique characteristics of Lieb bands. The Lieb Dirac bands of ZnPc-4P shows a non-zero Chern number. Our discoveries provide a fresh perspective on 2DPs and redefine the search for Lieb lattice materials into a well-defined chemical synthesis task.

---

Introduction

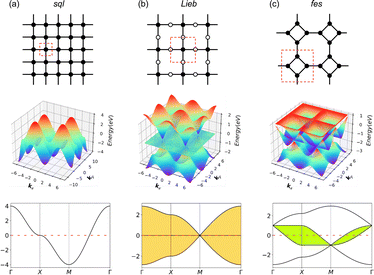
Exotic electronic structures, exemplified by Dirac cones and flat bands, have emerged as a focal point in contemporary research due to their unique electronic properties, including exotic charge carrier mobilities and the induction of topological effects.^1,2 An ample example of these exotic electronic structures is the Dirac cones in a honeycomb (hcb) lattice, which were first predicted theoretically and only later gained importance with the discovery of graphene.^3,4 Since then, graphene has found many applications in electronic devices, high-speed transistors, spintronics, photonics and optoelectronics.⁵ All these applications are possible thanks to the Dirac cone, characterized by crossing bands with linear dispersion intersecting at the K point of the Brillouin zone. This implies the existence of massless electrons from a non-relativistic perspective, consequently leading to exceedingly high electron mobility and topological effects.^4,6 On the other hand, flat (dispersionless) bands are characterized by electrons with extraordinarily large effective masses and energies that are independent of the carrier momentum.^2,7,8 Partially filled flat bands can then result in novel phases of matter, such as superconductivity, magnetism, and metal–insulator transitions.⁹

The relationship between the hcb lattice and Dirac cones can be generalized to a statement that electronic structure features arise directly from the lattice symmetry of the materials.¹⁰ Notably, many of the distinctive electronic features are shared between very different lattices, with Dirac cones appearing, e.g., in kagome (kgm), hcb, fes¹¹ and Lieb¹² lattices, and flat bands, e.g., in kgm and Lieb.^10,13 Among these, the Lieb lattice signature electronic structure is a very interesting one because it contains flat bands exactly crossing the Dirac cone (denoted as “Lieb bands” in the remaining paper) (Fig. 1).⁷ Another related lattice derived from square symmetry is the fes lattice, containing square and octahedral pores (Fig. 1c). Its characteristic band structure (denoted as fes bands in the remaining manuscript) has two high-symmetry crossing points (Γ and M), with one locally flat band intersecting a Dirac cone.^10,14

Fig. 1 Schematic models and band structures of (a) sql, (b) Lieb and (c) fes lattices in the tight-biding model, considering only 1st-neighbor interactions, the next-nearest neighbor interactions are set to zero. The red dashed lines indicate the unit cells. Yellow and green areas indicate Lieb and fes bands, respectively.

Lieb bands may be interesting from the viewpoint of electronic topology due to the effect of spin–orbit coupling (SOC), since the Dirac bands in an ideal Lieb lattice (the corner and edge sites are in the same energy, dE = 0) can have a non-zero Chern number and the contact between them and the flat bands is protected by the real-space topology. When dE ≠ 0, where the corner and edge sites are in different energies, the flat band shows a non-zero Chern number, while one of the Dirac bands shows a zero Chern number with a band gap between it and the flat band being opened.^10,15,16 Theoretical predictions using the Tight-Binding (TB) model show that Lieb bands require ideal lattice symmetry and strict conditions on state energies.^15,17,18 Because of these very strict criteria, the electronic Lieb lattice has rarely been achieved experimentally.

So far, the Lieb lattice has been investigated mainly by using optical lattices,¹⁹ or by surface deposition of small molecules.²⁰ A recently synthesized two-dimensional (2D) sp² carbon-conjugated covalent organic framework (COF)²¹ was theoretically demonstrated to have Lieb bands.^15,18 Soon after, the ZnPc-1P polymer, an analogue to the experimentally achievable FePc polymer,²² with zinc-phthalocyanine as the lattice center and benzene ring as the linker, was predicted to have Lieb bands, which remain topologically non-trivial after chemical substitution or physical strain engineering.¹⁷ However, while the ZnPc-1P band structure was identified as a Lieb lattice in the original paper, it much more resembles that of the fes lattice, which has been in depth studied in ref. 14 and 23.

Zhou et al. reported the intriguing finding that structural and electronic lattices can differ as is the case of hexagonal (hxl) sd² graphene displaying a kgm electronic structure.²⁴ While similar results have been found in other materials,²⁵ commonly between hxl and kgm lattices, to date there has been no exploration of the sql vs. Lieb/fes scenario.

In this study, we have investigated a series of hypothetical two-dimensional polymer (2DP) structures derived from the zinc-phthalocyanine (ZnPc) 2DP as model sql polymers. These derivatives, denoted as ZnPc-xP, feature linkers with varying lengths, where x represents the number of aromatic rings in the linker (ranging from 1 to 5, Fig. 2). Interestingly, the band structure of the ZnPc-xP 2DPs, while structurally having a simple sql lattice, exhibits an evolution from fes bands to Lieb bands, depending on the linker chain length. In particular, the Lieb bands of the ZnPc-4P material are in perfect agreement with the TB model of the Lieb lattice, including their topological properties. We have also shown that the features of the Lieb bands are preserved when the Fermi level is shifted by both simple electron removal or atom substitution, thereby transforming the challenge of Lieb lattice search into a well-defined chemical synthesis task.

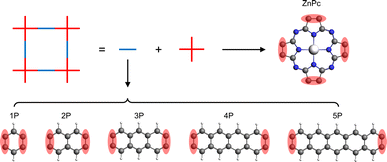Fig. 2 Schematic representation of the ZnPc-xP 2DP series structures. The red shaded area indicates the shared atoms between the center and linker molecules.

Results

The basic building units of the 2DPs of interest in this study are the ZnPc molecule and acenes (benzene, naphthalene, anthracene, tetracene, and pentacene, denoted as 1P, 2P, 3P, 4P, and 5P, respectively). These building blocks assemble into flat 2D sheets with square pores, forming ZnPc-xP 2DPs, where x = 1, 2, …, 5 represents the number of aromatic rings in the linker. The ZnPc-xP 2DP family, although only hypothetical structures, are mechanically stable based on their phonon dispersion (Fig. SI-1†) and represent a very interesting case study into the lattice structure and electronic properties relationship. From the structural point of view, common in experimental/synthetic materials community, they would be considered as sql. However, in a deeper look, Lieb and fes lattices can also be formally projected on the ZnPc-xP geometries (Fig. 3). This is confirmed by the reported band structure of ZnPc-1P, 2P and 3P by Pham et al.,²⁶ and 4P, 5P by Raptakis et al.,²⁷ which show emerging Lieb bands. In order to explain this interesting finding, herein we investigate the relationship between ZnPc-xP 2DP structures and electronic properties, particularly considering them as possible materials possessing Lieb bands.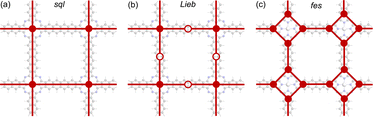

Fig. 3 Possible topologies (a) sql, (b) Lieb and (c) fes lattices projectable on the ZnPc-xP 2DPs. ZnPc-4P is shown as an example.

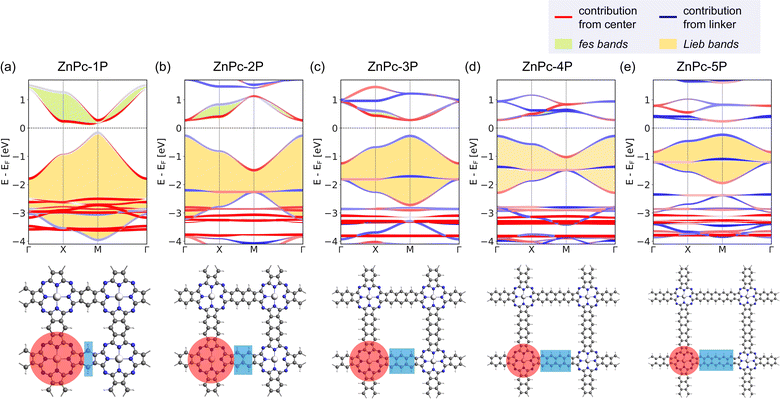
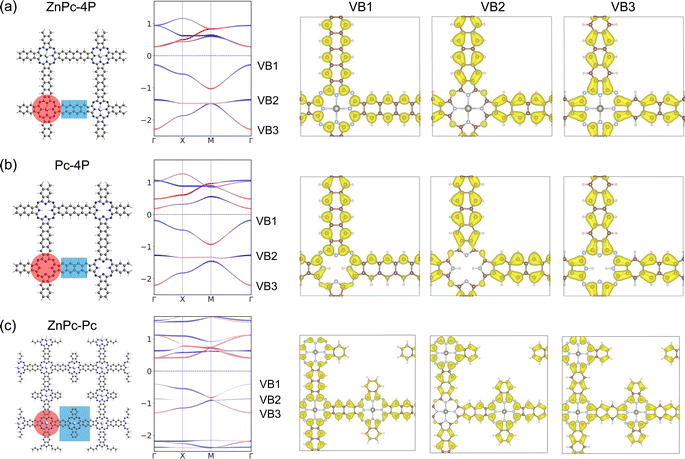
Indeed, the band structures of ZnPc-xP 2DPs shown in Fig. 4 include both fes band and Lieb band features. The fes bands are obviously present in the band structure of ZnPc-1P 2DP, the feature becomes weaker as the linker length increases, as indicated by the green area. The Lieb bands can also be observed below the Fermi level (set to 0) with a distorted flat band located at about −2.5 eV. With increasing linker length, the (almost) flat band gradually approaches the Fermi level, as indicated by the yellow area in Fig. 4. It is noteworthy that the position of the Dirac cone in ZnPc-xP 2DPs alternates between the Γ point for x = 1, 3, 5, and M point for x = 2, 4 (Fig. 4) while keeping all features of Lieb bands intact. This behavior of the 2DP electronic structures has recently been reported in the same material by Raptakis et al.²⁷ and attributed to the parity of the symmetry. Upon further investigation, we found that the same behavior can be observed in other classes of square polymers, as shown in the model structures in Fig. SI-2.†

Fig. 4 Band structure and the top view of the ZnPc-xP 2DPs of (a) ZnPc-1P, (b) ZnPc-2P, (c) ZnPc-3P, (d) ZnPc-4P, and (e) ZnPc-5P. The red and blue bands indicate the orbital contribution from the center/linker, respectively, which are also highlighted in the crystal structure using the same color scheme. fes band and Lieb band features are highlighted with green and yellow backgrounds in the band structures.

The contribution of the center/linker to the band structure of ZnPc-xP 2DPs is shown in Fig. 4 (center defined as a porphyrin molecule equivalent and linker as the connector in between). The flat band contributes from both the linker and the center, while the bands forming the Dirac cone originate from both the center and the linker. The fes bands in ZnPc-1P are dominated by the center with a partial contribution from the linker. The contribution varies depending on the definition of the center/linker region in the 2DP structures, as shown in Fig. SI-3,† but shows the same trend: as the linker length increases, the contribution of the linker to the Dirac cone bands gradually increases, while the fes lattice features become less pronounced.

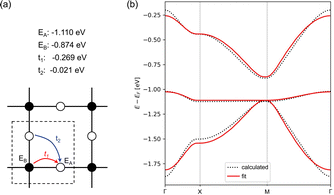
To further verify that ZnPc-xP 2DPs can be regarded electronically as a Lieb lattice, we have fitted the band structure to a TB model of a Lieb lattice to reproduce the electronic structure of ZnPc-4P. The TB model has four parameters: on-site energies for the edge and center sites, and hopping parameters amongst the nearest neighbors and next-nearest neighbors. The parameters of the model were optimized to fit the Lieb bands of ZnPc-4P. Our analysis shows an excellent match between the band structures from the TB model and the bands from full ZnPc-4P (Fig. 5).

Fig. 5 (a) Lieb lattice with four parameters, the center site E_A, the corner site E_B, the nearest neighbor hopping t₁ and the next-nearest neighbor hopping t₂. (b) The TB fitting of DFT calculated band structures.

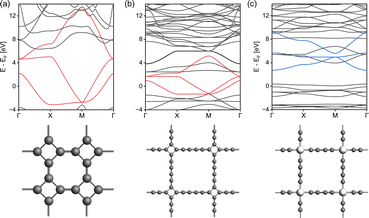
In order to understand how the electronic topology originates from the atomistic structure, we have constructed three simplistic, full-atomic hypothetical carbon allotrope models featuring fes and sql/Lieb lattices similar to the TB lattice models. The first model (Fig. 6a), T-graphene,²⁸ constitutes exactly the fes lattice, and produces nearly ideal fes bands. The electronic features of the fes lattice are preserved in T-graphtriyne²⁹ (Fig. 6b), which incorporates an extended linker between the rhombic nodes. If the rhombic center of T-graphtriyne is substituted with a single Zn atom forming Zn-diyne (Fig. 6c), which would traditionally be considered an sql lattice, distorted Lieb bands emerge instead of the sql bands.¹⁰ These simple models confirm that the sql TB model is too simplistic to describe square-pore 2DP systems, since even a simple D_4h symmetry structure as in Fig. 6c contains Lieb bands. The reason for this is that the electronic structure is defined by the topology of the scalar field of electron density rather than by simple geometry, which means that the lattice of the material cannot be simply mapped by its atomistic structure.

Fig. 6 Band structures and the top view of model structures connected by (a) T-graphene, (b) T-graphtriyne, and (c) Zn-diyne. Features of fes and Lieb in the band are colored in red and blue, respectively.

We have evaluated the topological properties of the ZnPc-xP materials by calculating their Chern numbers, taking into account SOC. The Chern numbers of the three Lieb bands are (−1 1 0) from the bottom band to the top band. The fitted TB model for ZnPc-4P shows the same Chern numbers. The topological properties often depend on the strength of the SOC effect structure, which can be modulated, e.g., by incorporating heavy metal atoms into the structure. We have investigated this on the fitted TB model of ZnPc-4P by scanning the effect of artificially set SOC values. Under heavy SOC effects, robust edge states can emerge in the electronic structure (Fig. SI-4 and 5†).

The primary limitation of the studied 2DPs lies in the positioning of the Lieb bands below the Fermi level. Achieving non-trivial structural properties in these bands thus requires shifting the Fermi level while preserving the Lieb bands. To address this, we first conducted an analysis of the atom contributions to the charge density within the Lieb bands (VB1, VB2, and VB3) using ZnPc-4P 2DP as a model system (Fig. 7a and SI-6†). The primary contribution to the Lieb bands comes from the linker (tetracene) π-electrons, which contribute to all VB1-3, although the carbons in the phthalocyanine center also partially contribute to the Dirac bands VB1 and VB3 (Fig. 7).

Fig. 7 Structure, band structure, and charge density distribution of the upper three VB bands of (a) ZnPc-4P with Zn atom, (b) Pc-4P without Zn atom, (c) ZnPc–ZnPc 2DP. The red and blue bands indicate the orbital contribution from the center/linker, with the center–linker partitioning highlighted in the crystal structure using the same color scheme.

The contribution of the metal atom to the Lieb bands is only minimal. This is also confirmed using a structure without a metal atom in the phthalocyanine center (Pc-4P), which gives almost identical Lieb bands to ZnPc-4P (Fig. 7). However, the fes features in conduction bands collapse after the removal of the metal atom.

Additionally, we have designed a hypothetical reference porphyrin polymer characterized by an “ideal atomic Lieb lattice” structure ZnPc–ZnPc 2DP (Fig. 7c and SI-7†). Both fes features in conduction bands and Lieb bands in valence bands are present with only minor changes. Lieb bands again contain the full π-system of the linker, despite its bigger size. This suggests that the well-ordered conjugated π-system is important for achieving high quality Lieb electronic materials.

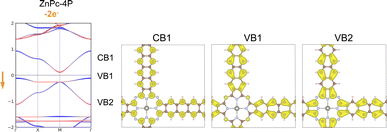
We have investigated the modulation of the Fermi level position by two different methods: the direct removal of electrons from the system and atomic substitution.³⁰ The removal of two electrons per unit cell effectively shifts the Fermi level toward the flat band. This adjustment results in a slight increase in the dispersion of the flat band, but leaves the fundamental Lieb bands intact (Fig. 8). The charge density contributions from the Lieb bands show identical features to those observed in the pristine structure. The Chern number of flat band VB1 is −1, while it is 0 for Dirac bands.

Fig. 8 Band structure and charge density distribution of the three Lieb bands of ZnPc-4P with two electrons removed (two holes introduced) per unit-cell. The red and blue bands indicate the orbital contribution from the center/linker.

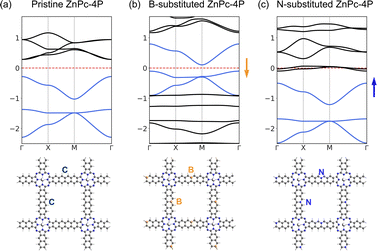
The charge density analysis of VB1-3 (Fig. 7) shows that in order to access the flat band, electrons should be removed from the aromatic system of the linkers, especially in the edge atoms of the linker. We have tested replacing individual carbons (2 atoms per UC, one per linker) in the linker with boron atoms, shifting the Fermi level to the flat band; and with nitrogen, shifting the Fermi level to the fes bands (Fig. 9). In the B-substituted structure, the Fermi level shifts to the Lieb bands, and most of the band structure features are preserved, although the dispersion of the “flat band” is stronger. The two Dirac bands of the Lieb bands show a non-zero Chern number. In the N-substituted structure, the Lieb bands are also preserved. These substituted model structures, although not easily achieved chemically, could provide a general guide how Lieb bands could be accessed in other square pore 2DPs with more suitable structures for substitution.

Fig. 9 Band structures, and top view of the structures of (a) pristine (b) B-substituted, (c) N-substituted ZnPc-4P. Lieb bands are colored in blue. The arrow indicates the Fermi level shift direction.

Conclusions

We have investigated the ZnPc-xP 2DPs as a model system for electronic structure topology of square pore 2DPs. While these materials are traditionally considered to have an sql topology well known from TB models, our results challenge this oversimplified view. We found that ZnPc-xP 2DPs exhibit both fes bands and Lieb bands while completely lacking the expected sql features. This is because the electronic structure of these materials is governed by the topology of the electron density, rather than by simple atomic geometry. Furthermore, the flat band and bottom Dirac band of the Lieb bands possess a non-zero Chern number. Unfortunately, the Lieb bands in the ZnPc-xP 2DPs are located below the Fermi level, as well as in most other model materials studied here. However, we have shown that shifting the Fermi level by controlling the number of electrons in the system via gating or substitution preserves the Lieb bands including their topological character. The challenge of finding Lieb lattice structures thus turns into a well-defined chemical synthesis task. This opens up the possibility of designing materials with unique properties, such as Chen semiconductors. We hope that our work will stimulate further experimental exploration of Lieb-lattice-based topological materials.

Methods

The geometries were optimized using the self-consistent-charge density functional based tight binding (SCC-DFTB)³¹ method as implemented in the Amsterdam Modelling Suite (AMS) ADF 2019.³² The 3ob-3-1 parameter set³³ was used for systems with X–Y element pair interaction (X, Y = =C, H, Zn), and the matsci-0-3 parameter set was applied for systems including boron.³⁴ Band structure calculations were performed employing FIH-aims with a TIER1 basis set with a 4 × 4 × 1 k-mesh grid,³⁵ using DFT with the Heyd–Scuseria–Ernzerhof 2006 functional.³⁶. The key parameter “tight” regarding computational accuracy was used to control all integration grids, and the accuracy of the Hartree potential. The scalar relativistic effects were involved by using the atomic zeroth order regular approximation (ZORA) level of theory. Tight-binding models were built using PythTB,³⁷ under consideration of both nearest-neighbor and next-nearest neighbor interactions, as well as SOC. The topological properties were simulated based on the Haldane model. The Berry curvature and the intrinsic anomalous Hall conductivity were performed using the WANNIER90 package.³⁸ Calculations of edge states and the Chern number were carried out using the WannierTools package.³⁹ SOC and spin polarization were taken into account in the topological calculations. Phonon dispersions were calculated using Phonopy & DFTB+ with a 4 × 4 × 1 supercell.⁴⁰

Data availability

The geometries and corresponding band structures for all systems investigated in this work are available at the NOMAD repository as a dataset under DOI: https://doi.org/10.17172/NOMAD/2023.11.26-1.

Author contributions

Y. Z. and S. Z. performed calculations and theoretical analysis. M. P. and T. H. supervised the study. Y. Z. wrote the manuscript with contributions of all authors, and all authors have given approval for the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Y. Z. acknowledges Tsai-Jung Liu, Florian Arnold and Dr Hongde Yu for fruitful discussions. Y. Z. acknowledges the China Scholarship Council. S. Z. and T. H. acknowledge funding of the DFG priority program SPP 2244. M. P. is supported by project EMPIR 20FUN03 COMET; this project has received funding from the EMPIR programme co-financed by the Participating States. All authors thank Deutsche Forschungsgemeinschaft for support within CRC 1415. All authors thank for computational resources provided by the NHR centers ZIH Dresden and PC².

References

1. (a) N. J. Ghimire and I. I. Mazin, Nat. Mater., 2020, 19, 137; (b) M. Li, Q. Wang, G. Wang, Z. Yuan, W. Song, R. Lou, Z. Liu, Y. Huang, Z. Liu, H. Lei, Z. Yin and S. Wang, Nat. Commun., 2021, 12, 3129.
2. Z. Li, J. Zhuang, L. Wang, H. Feng, Q. Gao, X. Xu, W. Hao, X. Wang, C. Zhang, K. Wu, S. X. Dou, L. Chen, Z. Hu and Y. Du, Sci. Adv., 2018, 4, eaau4511.
3. Y. Otsuka, S. Yunoki and S. Sorella, Phys. Rev. X, 2016, 6, 11029.
4. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
5. (a) W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Nat. Nanotechnol., 2014, 9, 794; (b) B. Sun, J. Pang, Q. Cheng, S. Zhang, Y. Li, C. Zhang, D. Sun, B. Ibarlucea, Y. Li, D. Chen, H. Fan, Q. Han, M. Chao, H. Liu, J. Wang, G. Cuniberti, L. Han and W. Zhou, Adv. Mater. Technol., 2021, 6; (c) Application of Graphene to High-Speed Transistors: Expectations and Challenges - CORE, https://core.ac.uk/works/71637028, accessed 23 October 2023; (d) F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611.
6. (a) E. Tang, J.-W. Mei and X.-G. Wen, Phys. Rev. Lett., 2011, 106, 236802; (b) S. Thomas, H. Li, C. Zhong, M. Matsumoto, W. R. Dichtel and J.-L. Bredas, Chem. Mater., 2019, 31, 3051.
7. X. Ni, H. Li, F. Liu and J.-L. Brédas, Mater. Horiz., 2022, 9, 88.
8. (a) A. Bhattacharya and B. Pal, Phys. Rev. B, 2019, 100, 235145; (b) Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43.
9. (a) H. Tian, X. Gao, Y. Zhang, S. Che, T. Xu, P. Cheung, K. Watanabe, T. Taniguchi, M. Randeria, F. Zhang, C. N. Lau and M. W. Bockrath, Nature, 2023, 614, 440; (b) J.-X. Yin, S. S. Zhang, G. Chang, Q. Wang, S. S. Tsirkin, Z. Guguchia, B. Lian, H. Zhou, K. Jiang, I. Belopolski, N. Shumiya, D. Multer, M. Litskevich, T. A. Cochran, H. Lin, Z. Wang, T. Neupert, S. Jia, H. Lei and M. Z. Hasan, Nat. Phys., 2019, 15, 443; (c) Y. Kim, T. Čadež, A. Andreanov and S. Flach, Phys. Rev. B, 2023, 107, 17; (d) Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori and P. Jarillo-Herrero, Nature, 2018, 556, 80.
10. M. A. Springer, T.-J. Liu, A. Kuc and T. Heine, Chem. Soc. Rev., 2020, 49, 2007.
11. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782.
12. E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201.
13. F. Crasto de Lima, G. J. Ferreira and R. H. Miwa, Phys. Chem. Chem. Phys., 2019, 21, 22344.
14. T.-J. Liu, M. A. Springer, N. Heinsdorf, A. Kuc, R. Valentí and T. Heine, Phys. Rev. B, 2021, 104, 205419.
15. B. Cui, X. Zheng, J. Wang, D. Liu, S. Xie and B. Huang, Nat. Commun., 2020, 11, 66.
16. S. Banerjee and A. Saxena, Phys. Rev. B, 2021, 103, 235125.
17. W. Jiang, S. Zhang, Z. Wang, F. Liu and T. Low, Nano Lett., 2020, 20, 1959.
18. W. Jiang, H. Huang and F. Liu, Nat. Commun., 2019, 10, 2207.
19. (a) S. Mukherjee, A. Spracklen, D. Choudhury, N. Goldman, P. Öhberg, E. Andersson and R. R. Thomson, Phys. Rev. Lett., 2015, 114, 245504; (b) R. A. Vicencio, C. Cantillano, L. Morales-Inostroza, B. Real, C. Mejía-Cortés, S. Weimann, A. Szameit and M. I. Molina, Phys. Rev. Lett., 2015, 114, 245503.
20. (a) M. R. Slot, T. S. Gardenier, P. H. Jacobse, G. C. P. van Miert, S. N. Kempkes, S. J. M. Zevenhuizen, C. M. Smith, D. Vanmaekelbergh and I. Swart, Nat. Phys., 2017, 13, 672; (b) R. Drost, T. Ojanen, A. Harju and P. Liljeroth, Nat. Phys., 2017, 13, 668.
21. E. Jin, M. Asada, Q. Xu, S. Dalapati, M. A. Addicoat, M. A. Brady, H. Xu, T. Nakamura, T. Heine, Q. Chen and D. Jiang, Science, 2017, 357, 673.
22. M. Abel, S. Clair, O. Ourdjini, M. Mossoyan and L. Porte, J. Am. Chem. Soc., 2011, 133, 1203.
23. L. H. C. M. Nunes and C. M. Smith, Phys. Rev. B, 2020, 101, 224514.
24. M. Zhou, Z. Liu, W. Ming, Z. Wang and F. Liu, Phys. Rev. Lett., 2014, 113, 236802.
25. (a) S. Paavilainen, M. Ropo, J. Nieminen, J. Akola and E. Räsänen, Nano Lett., 2016, 16, 3519; (b) J. Jung and Y.-H. Kim, Phys. Rev. B, 2022, 105, 85138.
26. H. Q. Pham, D. Q. Le, N.-N. Pham-Tran, Y. Kawazoe and D. Nguyen-Manh, RSC Adv., 2019, 9, 29440.
27. A. Raptakis, A. Croy, A. Dianat, R. Gutierrez and G. Cuniberti, RSC Adv., 2022, 12, 12283.
28. Y. Liu, G. Wang, Q. Huang, L. Guo and X. Chen, Phys. Rev. Lett., 2012, 108, 225505.
29. S. Jana, A. Bandyopadhyay and D. Jana, Phys. Chem. Chem. Phys., 2019, 21, 13795.
30. (a) Y. Jing and T. Heine, J. Am. Chem. Soc., 2019, 141, 743; (b) T. Saha, L. Petaccia, B. Ressel, P. R. Ribič, G. Di Santo, W. Zhao and G. de Ninno, Phys. Rev. B, 2022, 106, 75148; (c) R. Habibpour, E. Kashi and R. Vazirib, Russ. J. Phys. Chem., 2018, 92, 532.
31. M. Elstner and G. Seifert, Philos. Trans.: Math., Phys. Eng. Sci., 2014, 372, 20120483.
32. R. Rüger, A. Yakovlev, P. Philipsen, S. Borini, P. Melix, A. F. Oliveira, M. Franchini, T. van Vuren, T. Soini, M. de Reus, M. Ghorbani Asl, T. Q. Teodoro, D. McCormack, S. Patchkovskii and T. Heine, Amsterdam Modeling Suite Making Computational Chemistry Work For You, SCM, Vrije Universiteit, Amsterdam, The Netherlands, 2019.
33. M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2012, 7, 931.
34. J. Frenzel, A. F. Oliveira, N. Jardillier, T. Heine and G. Seifert, Zeolites, 2004, 2, 7.
35. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175.
36. (a) J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101; (b) J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
37. Python Tight Binding (PythTB)—PythTB 1.8.0 documentation, https://www.physics.rutgers.edu/pythtb/index.html, accessed 13 February 2024.
38. (a) A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685; (b) X. Wang, J. R. Yates, I. Souza and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195118.
39. Q. Wu, S. Zhang, H.-F. Song, M. Troyer and A. A. Soluyanov, Comput. Phys. Commun., 2018, 224, 405.
40. (a) A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1; (b) B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc06367d

---