 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure and dynamics of liquid water from ab initio simulations: adding Minnesota density functionals to Jacob's ladder†
Justin
Villard
 a,
Martin P.
Bircher
a,
Martin P.
Bircher
 b and
Ursula
Rothlisberger
b and
Ursula
Rothlisberger
 *a
*a
aLaboratory of Computational Chemistry and Biochemistry, Institute of Chemical Sciences and Engineering, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, CH-1015, Switzerland. E-mail: ursula.roethlisberger@epfl.ch
bComputational and Soft Matter Physics, Universität Wien, Wien, A-1090, Austria
First published on 15th February 2024
Abstract
The accurate representation of the structural and dynamical properties of water is essential for simulating the unique behavior of this ubiquitous solvent. Here we assess the current status of describing liquid water using ab initio molecular dynamics, with a special focus on the performance of all the later generation Minnesota functionals. Findings are contextualized within the current knowledge on DFT for describing bulk water under ambient conditions and compared to experimental data. We find that, contrary to the prevalent idea that local and semilocal functionals overstructure water and underestimate dynamical properties, M06-L, revM06-L, and M11-L understructure water, while MN12-L and MN15-L overdistance water molecules due to weak cohesive effects. This can be attributed to a weakening of the hydrogen bond network, which leads to dynamical fingerprints that are over fast. While most of the hybrid Minnesota functionals (M06, M08-HX, M08-SO, M11, MN12-SX, and MN15) also yield understructured water, their dynamical properties generally improve over their semilocal counterparts. It emerges that exact exchange is a crucial component for accurately describing hydrogen bonds, which ultimately leads to corrections in both the dynamical and structural properties. However, an excessive amount of exact exchange strengthens hydrogen bonds and causes overstructuring and slow dynamics (M06-HF). As a compromise, M06-2X is the best performing Minnesota functional for water, and its D3 corrected variant shows very good structural agreement. From previous studies considering nuclear quantum effects (NQEs), the hybrid revPBE0-D3, and the rung-5 RPA (RPA@PBE) have been identified as the only two approximations that closely agree with experiments. Our results suggest that the M06-2X(-D3) functionals have the potential to further improve the reproduction of experimental properties when incorporating NQEs through path integral approaches. This work provides further proof that accurate modeling of water interactions requires the inclusion of both exact exchange and balanced (non-local) correlation, highlighting the need for higher rungs on Jacob's ladder to achieve predictive simulations of complex biological systems in aqueous environments.
1 Introduction
Liquid water is a ubiquitous and essential component of life, playing a critical role in a wide variety of chemical and biological processes.1–4 A comprehensive understanding of water at the atomic scale is vital for advancing research in diverse domains such as aqueous chemistry,5–8 biochemistry,9,10 atmospheric science,11,12 and environmental engineering.13,14 Furthermore, unraveling the intricate behavior of water molecules enables deeper insights into solvation dynamics,15,16 water–materials interactions,17,18 protein folding,19–22 enzymatic reactions,23,24 and the properties of biological membranes,25,26 ultimately contributing to the development of innovative technologies and therapeutics. Deceivingly simply at first sight, it is well known that liquid water shows anomalous properties that have been extensively observed and documented like the density anomaly,2,27,28 high heat capacity,10,25,29 high boiling and melting points,3,30 high surface tension,31,32 high dielectric constant,33,34 and high viscosity.35,36 Despite substantial advances in the understanding of the behavior of water, the origins of these anomalies are not yet entirely elucidated neither by experiments nor theory, although it has been widely recognized that the structural characteristics of the hydrogen bond network under thermal fluctuations play a pivotal role for these unique features.4,37–41Significant challenges exist in conclusively capturing atomic-scale phenomena in water through experiments like NMR,42–52 IR,53 X-ray54,55 or neutron55–58 spectroscopy for which measurement interpretations often rely on theoretical models. Although a variety of computationally efficient and relatively accurate empirical force fields have been developed,59–63 such as those from the TIPnP family,64,65 those remain intrinsically incapable of describing bond breaking in chemical reactions. Therefore, the quantitative understanding of condensed phase water, in particular its reactivity, and role as a universal solvent can only fully emerge from the development of accurate ab initio molecular dynamics (AIMD) simulations.66–68 These simulations need to faithfully represent both electronic reorganization and nuclear quantum effects (NQEs) associated with hydrogen bonding but, at present, such a comprehensive predictive quantum picture at ambient conditions remains quite elusive. In addition, the cost of most accurate wavefunction-based approaches such as post-Hartree–Fock69,70 (e.g., MP2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 or RPA72–75), coupled cluster (CCSD(T)),76,77 or configuration interaction (CI)78,79 hinders their potential application across the entire water phase diagram.
71 or RPA72–75), coupled cluster (CCSD(T)),76,77 or configuration interaction (CI)78,79 hinders their potential application across the entire water phase diagram.
Balancing accuracy and computational feasibility, Kohn–Sham (KS)80 density functional theory (DFT)81 has become the go-to quantum-chemical method for time propagation of molecular systems and computation of statistical averages when combined with molecular dynamics (MD) or Monte-Carlo (MC) engines.63,82 Although the ground-state energy and electron density are formally exact within DFT, their universal mapping remains unknown, necessitating the use of approximations in the KS formalism. In this approach, many-body interactions are accounted for and incorporated into the approximate exchange–correlation (XC) functional.
Over the past several decades, hundreds of XC functionals have been developed with the aim to capture all relevant physics and achieve chemical accuracy over a broad range of molecules, materials, and organometallic systems.83 To classify the growing number of functionals, John P. Perdew and Karla Schmidt proposed a hierarchy called Jacob's ladder,84 which organizes functionals based on their complexity. The ladder consists of five rungs: (1) Local Density Approximations (LDA) depend only on the electron density at a given point in space and offer computational efficiency but often lack accuracy.85,86 (2) Generalized Gradient Approximations (GGA) functionals incorporate the (local) electron density and its gradient.87–89 (3) Meta-GGA functionals account for the electron density, its gradient, and the kinetic energy density.90–94 (4) Hybrid functionals mix a portion of exact exchange‡ from Hartree–Fock (HF) theory with XC terms from DFT,95–99 and (5) double-hybrid and RPA-based functionals (rung-5), the highest rung on the ladder, combine a hybrid functional with post-HF correlation corrections, e.g., within second-order perturbation theory (MP2)71,100–106 or non-local correlation based on the random phase approximation (RPA).107–111 As one moves up the ladder, the functionals globally tend to provide better descriptions of electronic interactions and improve the overall predictive accuracy.84,112–116 This is primarily attributed to the introduction of orbital-dependent terms at the meta-GGA rung 3 level, which enables the XC potential to become non-local in what is known as generalized KS-DFT, in contrast to traditional KS-DFT, where the XC potential remains local. However, this comes at the price of an increasingly higher computational cost: for instance, the cost of hybrids is roughly two orders of magnitude the one of GGA functionals.115,117–119
While DFT with refined density functional approximations has demonstrated impressive success in the examination of structures, properties, and reactivities for a wide range of molecules and materials, the prominent challenge persists in identifying the appropriate XC functional for a specific problem, as the performance of a functional can vary significantly depending on the system under study.120 For liquid water, no local (LDA) or semilocal (GGA, meta-GGA) DFT simulation has yet achieved a conclusive replication of experimental observations, covering both structural and dynamical properties simultaneously. For example, it was established that most of the GGA functionals, like PBE89 and BLYP,87,88 provide a more pronounced dip after the first peak of the oxygen–oxygen pair correlation function, thus an overstructured description of water, and dynamical figures that are too slow, therefore not completely remedying the glassy behavior observed with the LDA.121–125 Furthermore, GGA and (even) hybrid levels can underestimate the equilibrium density of liquid water, leading to the incorrect prediction that ice sinks in water.41,126
DFT approximations encounter difficulties when describing condensed water due to the intricate nature of concurrent competing interactions that are involved in covalent bonds, hydrogen bonds, and van der Waals (vdW) forces. Hydrogen bonds, though one order of magnitude weaker than intramolecular O–H covalent bonds, remain locally strong and directionally attractive. Another order of magnitude weaker, vdW dispersion forces play a non-negligible role at larger distances, with an attractive and isotropic character.127 The interplay between varying interaction strengths, length scales, and directionalities makes water a highly sensitive test system for the design and assessment of XC functionals. Indeed, even slight imprecision in the XC description is likely to disrupt the complex balance of interactions, ultimately impacting the H-bond network that is responsible for many of water's properties.125,128
While local and semilocal functionals fail to capture intermediate to long-range vdW forces,125 AIMD simulations have demonstrated that GGAs enhanced with vdW representations typically lead to a softer structure of bulk water where peak maxima and minima in the radial distribution functions are less pronounced, accompanied by increased mobility that aligns more closely with experimental measurements.124 This improvement is achieved by incorporating dispersion-corrected atom-centered potentials (DCACPs),124,129,130 empirical dispersion corrections (e.g., Grimme's D2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 131 and D3
131 and D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132), or non-local correlation terms (e.g., (r)VV10,133–135 vdW-DF,136 TS-vdW127,137). However, the performance of such corrections relies on the original GGA to which the combination may not always improve, or may even deteriorate properties.124,138 Other studies pointed out the necessity of including a fraction of exact exchange, thus resorting to rung-4 hybrids, to effectively describe hydrogen bonding but without reaching a perfect agreement with the experiment.125,139–143
132), or non-local correlation terms (e.g., (r)VV10,133–135 vdW-DF,136 TS-vdW127,137). However, the performance of such corrections relies on the original GGA to which the combination may not always improve, or may even deteriorate properties.124,138 Other studies pointed out the necessity of including a fraction of exact exchange, thus resorting to rung-4 hybrids, to effectively describe hydrogen bonding but without reaching a perfect agreement with the experiment.125,139–143
Altogether, attaining a reliable description of the structural and dynamical properties of liquid water through lower rung (1–3) DFT models remains an issue. The goal of this work is consequently to contribute further understanding to this endeavor by incorporating the popular Minnesota density functionals92,144–153 into the array of approximations tested on water at ambient conditions. While having demonstrated success for molecular systems, previous investigations of the performance of Minnesota functionals on condensed water are, to our knowledge, limited to the work of Del Ben et al. who ran MC simulations on water with the M06-L-D3, M06-D3, and M06-2X-D3 functionals,154 and the work of Pestana et al. that focuses on MD with M06-L-D3.143 Our work thus fills a gap in the evaluation of the performance of DFT functionals for liquid water. Gaining insights from the performance of various functionals not only helps demystify their promise and limitations for water, but also on a wider range of systems exhibiting a similar delicate balance of interactions such as e.g., in large biomolecules,155,156 heterogeneous catalysts,157,158 aqueous solutions7,159,160 and molecules on surfaces.161 For this reason, we have made an effort, albeit not exhaustive, to compile in this document previously calculated quantities from DFT-based MC and AIMD. Our aim is to establish a common ground for comparing various studies found in the literature and confront them with experimental measurements.
Information on higher-rung approximations, such as double-hybrids, is limited in this assessment due to their exorbitant computational overhead and infrequent implementation in MD software packages.154 The substantial cost of hybrid functionals also poses a significant challenge for obtaining extensive results in MD simulations,140,162 in particular in the context of plane wave based approaches. To tackle this issue, the emergence of machine learning (ML)-based interaction models has shown the potential to attain a similar level of accuracy at a fraction of the cost.163–165 Nevertheless, the effectiveness of such ML potentials primarily depends on their reliability across the entire phase (configurational) space sampled during MD (MC) simulations.
Hereafter, we present structural properties (in terms of radial distribution functions, coordination numbers, density, number of H-bonds and angular distributions) and dynamical characteristics (quantified via diffusion coefficients and rotational correlation times) obtained with AIMD and all the later generation Minnesota functionals. Those include some of the most employed meta-GGAs and hybrid meta-GGAs in computational chemistry.115,166,167 Meta-GGAs are investigated with Car–Parrinello MD (CPMD), while the much more computationally expensive hybrid meta-GGAs have been run with Born–Oppenheimer MD (BOMD), thanks to the crucial acceleration of a recent ML-aided multiple time step scheme that preserves the target DFT level description by construction.119,168,169 Both CPMD and BOMD employ classical propagation of nuclei; however, capturing a comprehensive picture of water including nuclear quantum effects (NQEs) requires more sophisticated and considerably costlier (approximately two orders of magnitude117) ab initio path integral MD (PIMD) approaches.63,170 Alternatively, NQEs can be qualitatively evaluated based on very recent studies that employ DFT/ML-based PIMD methods.40,163,164 This allows an identification of the most promising XC functionals worth further investigation in conjunction with quantum nuclei.
In this regard, this article provides benchmarks for the widely-used Minnesota density functionals in simulating liquid water, and places them in the context of existing knowledge of other DFT approximations as well as experimental measurements. Anticipating our results, it turns out that M06-2X is not only the best of all Minnesota functionals tested, but also rivals the currently most promising functionals reported overall, especially if combined with dispersion corrections (M06-2X-D3), and considered in the light of NQEs.
2 Theory and methods
2.1 Minnesota density functionals
Since 2005, the Minnesota theoretical chemistry group led by Donald Truhlar has focused on the development of post-GGA functionals capable of capturing the chemistry of main group elements as well as transition metals including activation barriers as well as non-covalent interactions. The excellent “across-the-board” performance of these functionals has made them one of the most widely used XC approximations in computational chemistry.7,115,166,167 The Minnesota functionals are semi-empirical in nature, with functional forms that have been fitted against extensive datasets of reference absolute and relative energies, as well as eventual structures and lattice constants. For brevity's sake, Table 1 provides a summary of the XC approximations studied in this work, along with a global overview of their functional components. Interested readers are referred to the corresponding references for more technical and mathematical details.| Functional | Classb | X [%] | E DFTx | E DFTc | # | UEG | Ref. |
|---|---|---|---|---|---|---|---|
| a SR stands for short-range, LR for long-range. LSDA is the local spin density approximation,171,172 PBE the Perdew, Burke, Ernzerhof functional,89 RPBE the secondly revised PBE functional,173 and N12 Truhlar's non-separable density gradient functional.174 b L stands for local, RSL for range-separated local, GH for global hybrid, RSH for range-separated hybrid and NGA for non-separable gradient approximation. | |||||||
| Meta-GGA | |||||||
| M06-L | L meta-GGA | 0 | M05 + VSXC | M05 + VSXC | 34 | ✓ | 92 |
| revM06-L | L meta-GGA | 0 | M05 + VSXC | M05 + VSXC | 31 | × only | 144 |
| M11-L | RSL meta-GGA | 0 | SR/LR: LSDA(PBE + RPBE) | LSDA + PBE | 44 | ✓ | 145 |
| MN12-L | L meta-NGA | 0 | N12 | N12 + (LSDA + PBE) | 58 | × | 146 |
| MN15-L | L meta-NGA | 0 | N12 | N12 + (LSDA + PBE) | 58 | × | 147 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Hybrid meta-GGA | |||||||
| M06 | GH meta-GGA | 27 | M05 + VSXC | M05 + VSXC | 33 | ✓ | 148 |
| M06-HF | GH meta-GGA | 100 | M05 + VSXC | M05 + VSXC | 32 | ✓ | 149 |
| M06-2X | GH meta-GGA | 54 | M05 | M05 + VSXC | 29 | ✓ | 148 |
| M08-HX | GH meta-GGA | 52.23 | LSDA(PBE + RPBE) | LSDA + PBE | 47 | ✓ | 150 |
| M08-SO | GH meta-GGA | 56.79 | LSDA(PBE + RPBE) | LSDA + PBE | 44 | ✓ | 150 |
| M11 | RSH meta-GGA | 42.8–100 | SR: LSDA(PBE + RPBE) | LSDA + PBE | 40 | ✓ | 151 |
| MN12-SX | RSH meta-NGA | 25–0 | N12 | N12 + (LSDA + PBE) | 58 | × | 152 |
| MN15 | GH meta-NGA | 44 | N12 | N12 + (LSDA + PBE) | 59 | × | 153 |
The generation of the 2006 functionals was ingeniously crafted by merging the characteristics of the earlier M05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 and VSXC176 functionals (in turn designed from modifications of the PBE and LSDA functionals for the exchange). These include M06, a versatile hybrid meta-functional that boasts consistent accuracy for main group thermochemistry, barrier heights, medium-range correlation energies, and transition metals. M06-2X, another hybrid meta-GGA, excels in main group chemistry and barrier heights, accurately predicts valence and Rydberg electronic excitation energies, and π–π stacking interactions, while its performance falters in the realm of transition metals. M06-L, a local functional devoid of Hartree–Fock exchange, was skillfully tailored as a cost-effective choice for numerous demanding applications associated with extensive systems. It excels for transition metals, yet its accuracy for barrier heights does not match that of M06 and M06-2X. Finally, M06-HF was designed primarily for spectroscopy, demonstrating good performance for valence, Rydberg, and charge transfer excited states with little compromise on ground-state accuracy. An important point to note is that M06-2X and M06-HF that differ in the amount of exact exchange (54 vs. 100%) share the same training set, which was expanded with transition metals with respect to the one used for the parameterization of the M06 functional. revM06-L, on the other hand, was developed later using an even larger database and additional smoothness restraints to ensure better numerical stability, smoother potential energy curves, and overall improved accuracy compared to M06-L.
175 and VSXC176 functionals (in turn designed from modifications of the PBE and LSDA functionals for the exchange). These include M06, a versatile hybrid meta-functional that boasts consistent accuracy for main group thermochemistry, barrier heights, medium-range correlation energies, and transition metals. M06-2X, another hybrid meta-GGA, excels in main group chemistry and barrier heights, accurately predicts valence and Rydberg electronic excitation energies, and π–π stacking interactions, while its performance falters in the realm of transition metals. M06-L, a local functional devoid of Hartree–Fock exchange, was skillfully tailored as a cost-effective choice for numerous demanding applications associated with extensive systems. It excels for transition metals, yet its accuracy for barrier heights does not match that of M06 and M06-2X. Finally, M06-HF was designed primarily for spectroscopy, demonstrating good performance for valence, Rydberg, and charge transfer excited states with little compromise on ground-state accuracy. An important point to note is that M06-2X and M06-HF that differ in the amount of exact exchange (54 vs. 100%) share the same training set, which was expanded with transition metals with respect to the one used for the parameterization of the M06 functional. revM06-L, on the other hand, was developed later using an even larger database and additional smoothness restraints to ensure better numerical stability, smoother potential energy curves, and overall improved accuracy compared to M06-L.
The next generation functionals M08-HX and M08-SO resulted from exploring a more flexible functional form, with different formal constraints; while M08-SO respects the exact gradient expansion for slowly varying density up to the second order (SO) and the uniform electron gas (UEG) limit, M08-HX only respects the latter. Both functionals of the M08 generation were found to modestly improve on M06-2X for main-group thermochemistry, kinetics, and non-covalent interactions. The even more recent M11, on the other hand, is a range-separated version177 of the M08 functionals, with the same correlation component. The percentage of exact exchange of 100% at large inter-electronic distance reduces to 42.8% at short range. The second-order density gradient expansion is also correct by construction in M11, and good across-the-board accuracy was shown thanks to the use of a further extended training set. A bit later, the M11-L functional was designed as the local analogue of M11, mainly for cost-efficiency and improved accuracy for multi-reference systems. M11-L replaces the exact exchange by a long-range meta-GGA exchange functional, that has different spatial extent and parameters than the exchange at short range.
In 2012, a new functional form called N12 was developed that pushes the limits of local functionals, providing simultaneous accuracy on energetic and structural properties of both solids and molecules.174 Unlike traditional GGAs, the N12 functional is a non-separable approximation (NGA) between the density and its (reduced) gradient that embodies both exchange and correlation effects, and can be seen as a generalization of the dual-range M11-L. By adding a dependence on the kinetic energy density, and the M08/M11 correlation term, Peverati and Truhlar designed the MN12-L meta-non-separable gradient approximation to obtain even broader accuracy with a local functional. With the inclusion of 25% of short-range exact exchange (that is screened at large distances), the MN12-SX functional yields better results than MN12-L for most chemical properties, and is notably more successful in calculating semiconductor band gaps.152 Finally, re-optimization of MN12-L using a larger training database and additional smoothness restraints on the functional form resulted in the most recent MN15-L local meta-NGA functional. This latter shows better performance for transition metals and is generally recommended over MN12-L.147 Its hybrid version, called MN15, was trained using a combination of single-reference chemical data (barrier heights), as well as diverse multi-reference transition-metal bond energies and atomic excitation energies that are challenging to describe with KS-DFT. As a result, it provides broad accuracy for both multi-reference and single-reference systems, and at the same time has demonstrated outstanding performance in describing noncovalent interactions.153 Note that we include NGAs in the category of GGAs in the rest of the text for simplicity's sake. Also, we emphasize that explicit dispersion corrections to the Minnesota density functionals were not considered in the present work.
2.2 Simulations
AIMD simulations were carried out using the CPMD code178 with PBE Troullier–Martins norm-conserving pseudopotentials.179 We observed that this universal choice has a negligible effect when comparing the optimization of a water molecule with Minnesota functionals and PBE pseudopotentials/plane waves to all-electron Gaussian basis set calculations. When convergence limits and integration grids are tight, and basis sets large, the difference between all-electron and pseudopotential/plane-wave calculations becomes negligible, a reassuring conclusion that has also been observed recently on Hartree–Fock and correlation energies.180 The plane-wave wavefunction cutoff energy was set to 80 Ry for all systems. We used a finer integration mesh with a density cutoff energy set to 640 Ry (dual of 8) to ensure proper convergence of the Minnesota functionals with planes waves,167 therefore affecting the usual computational cost by a factor of 2. The convergence threshold for the DIIS181 wavefunction optimization was set to 10−6 a.u. on the residual gradient on occupied orbitals, except for the M06 functional that is harder to converge to such a low criterion and for which 5 × 10−6 a.u. was used instead.A first equilibration phase was performed for each functional. Starting with a pre-equilibrated structure at the classical level, systems were first heated up to 400 K with velocity rescaling for about 1 ps until reaching a stable average temperature. Then, systems were cooled down to 330 K during another picosecond, and the temperature was again decreased more slowly to 300 K during a time interval of about half a picosecond.
After the first initial equilibration, systems were further thermalized with a Nosé–Hoover thermostat on the ions at 300 K for several picoseconds with a coupling frequency of 1500 cm−1 before finally switching to the NVE ensemble for the production runs for at least 10 ps. Configurations were saved every 50 steps for analysis. More information about the lengths of the trajectories, time steps and energy conservation are reported in Table S1 of the ESI.†
The OQML185,186 kernel method is used to infer force differences ΔFPBE0-LDAML from the aSLATM187 representations of chemical environments. The training set for the OQML model was generated by running PBE0 trajectories on condensed water and small water clusters. Both energies and forces were used in the training. The model demonstrated an out-of-sample mean absolute error of around 0.3 kcal (mol−1 Å−1) on |ΔFPBE0-LDAML|, as well as a mean absolute error of 0.7° on force directions, based on a test set of 4800 atomic forces.
Starting from a PBE0 pre-equilibrated configuration, all systems were first thermalized in the NVT ensemble with the ML-MTS acceleration method and a Nosé–Hoover thermostat with a coupling frequency of 1500 cm−1 at 300 K for at least 5 ps. After this initial equilibration process, NVE runs were conducted during the production phase, sampling configurations for at least 6 ps. The lengths of the trajectories, time step ratios, and energy conservation are reported in the ESI (Table S1†).
2.3 Analysis
Here, we provide information on how the properties were calculated from AIMD trajectories. As the production runs were conducted in the NVE ensemble, the average temperature of each simulation slightly differs. To ensure comparability, care was taken to renormalize the properties either by considering temperature or box volume differences.We note that the average structural properties are similar in the NVT and NVE ensembles.184 Additionally, the replacement of hydrogen atoms with deuterium has little effect on structural properties when the ionic motion is treated classically.121,139 However, the use of deuterated water can affect dynamical properties, such as the diffusion coefficient. Therefore, it is important to rely on heavy water data when validating D2O simulations against experimental results.
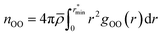 | (1) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) is the molecular number density. For consistency with experimental reference data, the value of
is the molecular number density. For consistency with experimental reference data, the value of 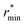 is set as the position of the first minimum in the actual integrand r2gOO(r), rather than the first minimum of gOO(r). For comparison, we also report the coordination number
is set as the position of the first minimum in the actual integrand r2gOO(r), rather than the first minimum of gOO(r). For comparison, we also report the coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OO calculated up to the first minimum of gOO(r) in the ESI (Table S3†).
OO calculated up to the first minimum of gOO(r) in the ESI (Table S3†).
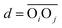 between the respective oxygen atoms. According to the experimental O–O RDF (cf.Fig. 1), neighboring oxygen atoms in the first coordination shell are located at distances between 2.4 and 3.4 Å. To reflect this, a smoothed rectangle function is defined by the following polynomial approximation
between the respective oxygen atoms. According to the experimental O–O RDF (cf.Fig. 1), neighboring oxygen atoms in the first coordination shell are located at distances between 2.4 and 3.4 Å. To reflect this, a smoothed rectangle function is defined by the following polynomial approximation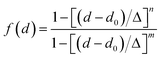 | (2) |
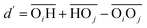 (with the donor oxygen Oi and its covalently-bound hydrogen H, and the distance
(with the donor oxygen Oi and its covalently-bound hydrogen H, and the distance 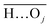 to the corresponding acceptor oxygen Oj). This latter metric increases in particular when the donor-hydrogen direction is tilted. As d′ increases, the probability of hydrogen bonding gradually decreases to zero. This is described by the second function
to the corresponding acceptor oxygen Oj). This latter metric increases in particular when the donor-hydrogen direction is tilted. As d′ increases, the probability of hydrogen bonding gradually decreases to zero. This is described by the second function 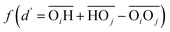 (eqn (2)) with d0 = 0, Δ = 0.4 Å, n = 4 and m = 8. With such parameters, f(d′) equals 1 at 0 Å, and rapidly decays to 0 when the argument exceeds 0.5 Å. Here again, the results do not differ significantly even if the smoothing parameters n and m are chosen somewhat differently. With this, an H-bond is finally counted if the product of the two functions exceeds 0.5, and not otherwise. The presence or absence of an H-bond is facilitated because the product of these analytical functions is predominantly either close to 0 or to 1. In practice, it is defined whether H is covalently bound to either molecule i or j in order to ensure the correct counting with periodic boundary conditions. We have observed, like others,189 that this counting is qualitatively comparable to conventional criteria that involve both the
(eqn (2)) with d0 = 0, Δ = 0.4 Å, n = 4 and m = 8. With such parameters, f(d′) equals 1 at 0 Å, and rapidly decays to 0 when the argument exceeds 0.5 Å. Here again, the results do not differ significantly even if the smoothing parameters n and m are chosen somewhat differently. With this, an H-bond is finally counted if the product of the two functions exceeds 0.5, and not otherwise. The presence or absence of an H-bond is facilitated because the product of these analytical functions is predominantly either close to 0 or to 1. In practice, it is defined whether H is covalently bound to either molecule i or j in order to ensure the correct counting with periodic boundary conditions. We have observed, like others,189 that this counting is qualitatively comparable to conventional criteria that involve both the 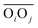 distance and the angle between the OiOj and OiH directions.139
distance and the angle between the OiOj and OiH directions.139
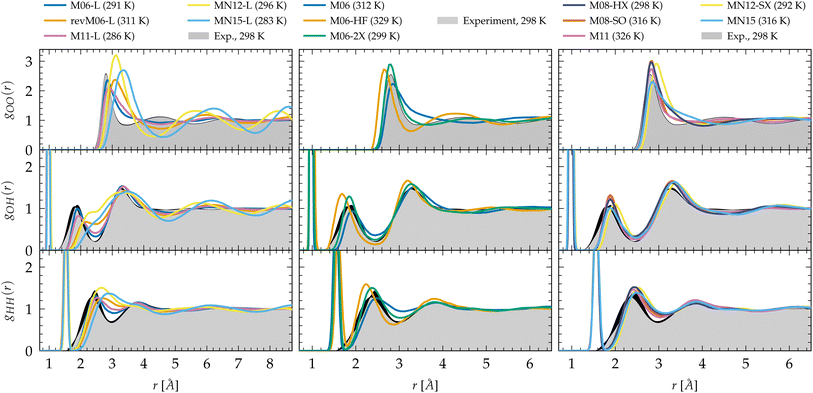 | ||
Fig. 1 Oxygen–oxygen (gOO), oxygen–hydrogen (gOH) and hydrogen–hydrogen (gHH) radial distribution functions of liquid water predicted by Minnesota density functionals. The experimental reference for gOO comes from X-ray diffraction54,55 interpolated at 298 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 and joint X-ray/neutron diffraction experiments were used for gOH and gHH.58 Black areas represent experimental uncertainties. 197 and joint X-ray/neutron diffraction experiments were used for gOH and gHH.58 Black areas represent experimental uncertainties. | ||
To compute the H-bond angular distributions, we took into account all the molecules present in the first coordination shell of the reference molecule, i.e. we restricted our analysis to angles for which the donor–acceptor distance is less than 3.4 Å, and the hydrogen-acceptor distance is less than 2.5 Å, based on the experimental RDFs.54,55
 | (3) |
Since DL is calculated from the simulation of a L3 cubic water box, finite size effects are corrected via191
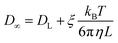 | (4) |
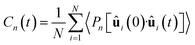 | (5) |
3 Results and discussion
3.1 Structural properties
The hybrid functionals of the M06 family are shown in the center panel of Fig. 1. Interestingly, M06 predicts RDFs that are very similar to its M06-L sister. M06-L therefore appears as a good local functional fit for the 27%-hybrid M06, but both fail at reproducing the intermolecular structure of water at long range.155 In contrast, the increase of exact exchange to 100% in M06-HF noticeably over-accentuates the structure and shifts the first and second gOO peaks to too short intermolecular distances. This increased cohesive effect that was missing for the local functionals is also observed in the gOH and gHH RDFs.
As a compromise between M06 and M06-HF, M06-2X, with 54% of exact exchange, remarkably improves the agreement of the RDFs with experiments. Despite the first minimum of gOO being a bit right-shifted by ∼0.3 Å, M06-2X shows better peak positions and an improved second coordination shell according to the second peak in gOO. As observed, the agreement with experimental data is not a trivial matter, as the structure of water is the result of the complex interplay between covalent bonds, hydrogen bonds, and vdW interactions. Many-body effects among hydrogen-bonded water molecules can be observed in the first peak of gOO and the second peak of gOH. The region between the first and second peaks of gOO mainly consists of non-hydrogen-bonded water molecules that occupy the intershell space between the hydrogen-bonded neighbors. The increased number of water molecules in these intershell regions can partly be attributed to the attractive, non-directional vdW interactions.41,143 Therefore, achieving a balance between exact exchange and vdW dispersion at an intermediate length scale is essential for accurately reproducing the densely packed and disordered structure in the intershell regions. As demonstrated by the RDFs, M06-2X captures these correlations with the highest accuracy and is thus capable of describing both hydrogen bonding and dispersion effects. M06-2X was specifically designed with the absence of transition metals in its training set, and focuses on the description of the electron correlation of the main group elements which could be one of the reasons why it performs so well on water compared to M06 for which transition metals were included. M06-HF lacks an adequate amount of correlation to counterbalance the full exact exchange: the second coordination shell has a higher population of water molecules that are not sufficiently drawn out to the intershell region by vdW forces.
The newer generation Minnesota hybrid functionals do not improve the structural description any further (Fig. 1, right panel). While possessing nearly the same amount of exact exchange as M06-2X, the new functional form introduced in M08-HX (52%) and M08-SO (57%) does not outperform M06-2X. MN12-SX is both range-separated and non-separable, with 25% of exact exchange at short range that decreases to 0% at long range. This functional has the lowest proportion of exact exchange. Notably, it is also the one where the first gOO and the second gOH peaks are shifted to the right, i.e. to longer intermolecular distances, presumably due to an elongation (weakening) of the intermolecular hydrogen bonds, or a lack of vdW cohesive forces202 (the analysis of the dynamical properties in Section 3.2 confirms the second hypothesis). In general, it is observed that the inclusion of a fraction of exact exchange leads to clearly visible improvements in the gOH and gHH RDFs over local functionals, and the addition of an appropriate amount of exact exchange can also enhance the agreement for gOO. This is particularly the case for M11, MN12-SX and MN15 that improve the second peak of gOH significantly over M11-L, MN12-L and MN15-L, respectively. Moreover, although not perfect, these functionals clearly improve the position and shape of the first gOO peak compared to their local counterparts. Consequently, this emphasizes the crucial importance of exact exchange in accurately describing the hydrogen bond network in general, supporting the notion that hybrid functionals and higher rungs of Jacob's ladder are indeed the most accurate approaches for depicting complex interactions with KS-DFT.
To evaluate the performance of Minnesota functionals in the broader context of DFT approximations, we compiled a comprehensive dataset from the literature (Table S2 of the ESI†). As various functionals were employed at different temperatures, the position and height of the first gOO peak, as well as the first gOO minimum, were rescaled to a common reference point at 298 K based on empirical interpolations fitted to experimental data (Fig. S2†). The differences between simulated and experimental values are depicted in Fig. 2. As can be seen, KS-DFT coupled to a classical propagation of the nuclei have the tendency to generally overestimate the height of the first peak and underestimate the first minimum, resulting in an overstructured prediction of liquid water. This is a well-known result for approximations lacking vdW interactions, such as purely local GGAs.124,143,154 Although dispersion corrections generally represent a step in the right direction, i.e. a less overstructured RDF, their effect depends on the specific functional and correction employed. For instance, BLYP is improved when supplemented with either D3 and DCACP corrections, while PBE is only improved with the D3 correction and deteriorates with DCACP (which was attributed to the presence of artificial dispersion effects in PBE124). Notably, the rVV10 non-local functional is also overstructured. In summary, BLYP-DCACP and revPBE-D3 are the best GGA functionals reported so far for the structure of liquid water.
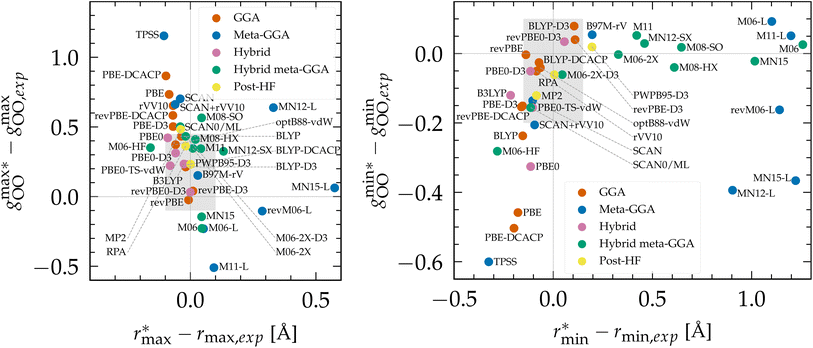 | ||
Fig. 2 (Left) Difference between the rescaled position 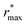 and height and height 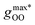 of the first gOO maximum and the experimental values at 298 K. (Right) Difference between the rescaled position of the first gOO maximum and the experimental values at 298 K. (Right) Difference between the rescaled position 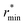 and height and height 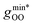 of the first gOO minimum and the experimental values at 298 K. Values for non-Minnesota functionals were extracted from ref. 40, 117, 124, 138, 140, 143, 154, 162, 164 and 165 and are reported in Table S2 of the ESI.† Rescaled values were obtained through empirical interpolation of experimental data.55 The grey areas represent a visual estimate of the potential deviations resulting from the neglect of nuclear quantum effects as well as statistical and experimental uncertainties (cf. Section 3.1.2). of the first gOO minimum and the experimental values at 298 K. Values for non-Minnesota functionals were extracted from ref. 40, 117, 124, 138, 140, 143, 154, 162, 164 and 165 and are reported in Table S2 of the ESI.† Rescaled values were obtained through empirical interpolation of experimental data.55 The grey areas represent a visual estimate of the potential deviations resulting from the neglect of nuclear quantum effects as well as statistical and experimental uncertainties (cf. Section 3.1.2). | ||
The importance of a sensitive tweaking of non-local dispersion effects is likely the primary reason why meta-GGA functionals do not exhibit improvement over the best dispersion-corrected GGAs. Compared to all functionals, the local Minnesota are the worst, as they cause substantial right-shifting and broadening of the first gOO peak. In contrast, the SCAN functional appears to capture the intermediate-ranged vdW interactions which seem to help locating the gOO maximum and minimum at good distance,41 but SCAN remains overstructured. The difference in results between SCAN and its augmentation with the rVV10 non-local correlation functional (SCAN + rVV10) is negligible.138 However, this add-on does help the B97M-rV functional to become the best meta-GGA reported.
Based on the available data, hybrids provide a good approximation of the first maximum of gOO, which is consistent with our previous observation that the inclusion of exact exchange in Minnesota functionals improves the accuracy of both the position and height of the first peak. This can be attributed to the fraction of exact exchange that mitigates the self-interaction error in local and semilocal XC functionals, which has been correlated with an artificial strengthening of the H2O tetrahedral structure and the delocalization of protons.164 Although PBE0 still yields overly structured water, its D3 and TS-vdW variants provide better agreement with experimental data. The most accurate hybrid functional appears to be revPBE0-D3, which is also the best approximation over all functionals for which data on water has been reported (vide infra).
Moving on to hybrid meta-GGAs, indications of the performance of SCAN0, the hybridized version of SCAN, has been obtained from simulations based on a deep neural network potential (SCAN0/ML) which indicate that SCAN0 is still overstructured. With the exception of M06-HF with 100% exact exchange, the hybrid Minnesota functionals are generally accurate in predicting the height of the first minimum, but they fail to accurately predict its position (Fig. 2, right). However, Del Ben et al. discovered that M06-2X, which appears to be the best performing Minnesota functional for water overall, further improves when coupled with the D3 correction.154 In general, the first minimum 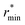 is shifted to a smaller intermolecular distance when there is either an excessive amount of exchange (M06-HF) or when the correlation effects overestimate vdW interactions. This highlights the remarkable sensitivity between (exact) exchange and correlation, both of which tend to compress or augment the first coordination peak instead of having compensatory effects. Achieving an accurate description of liquid water with DFT therefore requires finding the correct balance between these two quantum effects. This quest has motivated the refinement of XC functionals, where the occupied and virtual KS orbitals contribute to non-local correlation just as the occupied orbitals contribute to the non-local exact exchange. From Fig. 2, the RPA, which consists of exact exchange plus the RPA correlation, appears as the most promising rung-5 (post-HF) DFT approach in this direction, e.g., yielding very good structural properties outperforming MP2.154,165
is shifted to a smaller intermolecular distance when there is either an excessive amount of exchange (M06-HF) or when the correlation effects overestimate vdW interactions. This highlights the remarkable sensitivity between (exact) exchange and correlation, both of which tend to compress or augment the first coordination peak instead of having compensatory effects. Achieving an accurate description of liquid water with DFT therefore requires finding the correct balance between these two quantum effects. This quest has motivated the refinement of XC functionals, where the occupied and virtual KS orbitals contribute to non-local correlation just as the occupied orbitals contribute to the non-local exact exchange. From Fig. 2, the RPA, which consists of exact exchange plus the RPA correlation, appears as the most promising rung-5 (post-HF) DFT approach in this direction, e.g., yielding very good structural properties outperforming MP2.154,165
According to this comprehensive comparison, the most accurate functionals for describing the structure of water with classical nuclei are: revPBE-D3, BLYP-DCACP (GGA), B97M-rV (meta-GGA), revPBE0-D3 (hybrid), M06-2X-D3 (hybrid meta-GGA) and the RPA (rung-5).
As expected, the general trend observed in PIMD simulations is that NQEs tend to soften the structure of liquid water: for BLYP,203 SCAN/ML,40,163 PBE0-D3,154 SCAN0/ML,164 RPA/ML165 and MP2/ML,206 less structured RDFs were found when including NQEs. For other functionals like SCAN,184 B97M-rV117 and revPBE0-D3,117,204 O–O RDFs remain almost unchanged, while the O–H and H–H RDFs become less structured. O–H and H–H RDFs are also less structured for BLYP-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 and revPBE-D3,204 that however have a slight decrease in the O–O first minimum (by ∼0.1) when adding NQEs, with no impact on the first maximum. However, overall NQEs seem to have a marginal influence on the positions of the maxima and minima of the distribution functions. Hence, classical RDFs tend to be either too structured or very similar to their quantum analogues. This is in agreement with experimental isotope studies between heavy and light water that also showed that NQEs soften the structure of liquid water.40,162,207 Hence, NQEs partially explain why in Fig. 2 most DFT functionals tend to overstructure water compared to the experimental results. The gray areas plotted in this figure account for possible deviations due to the neglect of NQEs. These are based on the previously-cited PIMD references, potential discrepancies between experimental measurements,54,55,58 and the variance of the rescaling procedure to 298 K. These areas therefore enclose the most promising XC functionals to be predictive when including NQEs.
184 and revPBE-D3,204 that however have a slight decrease in the O–O first minimum (by ∼0.1) when adding NQEs, with no impact on the first maximum. However, overall NQEs seem to have a marginal influence on the positions of the maxima and minima of the distribution functions. Hence, classical RDFs tend to be either too structured or very similar to their quantum analogues. This is in agreement with experimental isotope studies between heavy and light water that also showed that NQEs soften the structure of liquid water.40,162,207 Hence, NQEs partially explain why in Fig. 2 most DFT functionals tend to overstructure water compared to the experimental results. The gray areas plotted in this figure account for possible deviations due to the neglect of NQEs. These are based on the previously-cited PIMD references, potential discrepancies between experimental measurements,54,55,58 and the variance of the rescaling procedure to 298 K. These areas therefore enclose the most promising XC functionals to be predictive when including NQEs.
According to previous studies, the best functionals tested so far for describing the atomic structure of water with NQEs are: revPBE-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204 (GGA), B97M-rV117 (meta-GGA), revPBE0-D3
204 (GGA), B97M-rV117 (meta-GGA), revPBE0-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117,204 (hybrid), SCAN0/ML164 (hybrid meta-GGA) and RPA/ML165 (rung-5). However, good agreement with experiment was only obtained for revPBE0-D3 and the RPA (from insights with ML potentials). The other levels of theory still overstructure water when considering NQEs, except for B97M-rV that remains understructured. Therefore, from Fig. 2, other XC approximations that would be worth investigating with PIMD simulations would be: optB88-vdW, BLYP-DCACP (GGA), PBE0-D3(TS-vdW) (hybrid) and M06-2X(-D3) (hybrid meta-GGA). Running PIMD calculations with rung-5 XCs like the RPA, without the aid of ML, would be of interest but their cost currently prevents such endeavors.
117,204 (hybrid), SCAN0/ML164 (hybrid meta-GGA) and RPA/ML165 (rung-5). However, good agreement with experiment was only obtained for revPBE0-D3 and the RPA (from insights with ML potentials). The other levels of theory still overstructure water when considering NQEs, except for B97M-rV that remains understructured. Therefore, from Fig. 2, other XC approximations that would be worth investigating with PIMD simulations would be: optB88-vdW, BLYP-DCACP (GGA), PBE0-D3(TS-vdW) (hybrid) and M06-2X(-D3) (hybrid meta-GGA). Running PIMD calculations with rung-5 XCs like the RPA, without the aid of ML, would be of interest but their cost currently prevents such endeavors.
Finally, we note that NQEs influence the balance between covalent and hydrogen bond interactions. Indeed, PIMD simulations showed that NQEs broaden the covalent peak of the O–H RDF, meaning that more fluctuations occur for the hydrogen atoms, accompanied by a weakening of the covalent bonds. In turn, such a delocalization of the protons seems to strengthen the hydrogen bond network by forming statistically more H-bond interactions, which slows down dynamical properties.117,154,163,184,204 Thus, counterintuitively, the disordering due to NQEs smoothes out the structure of water by destabilizing molecules in the intershell region of the O–O RDF, while simultaneously reducing diffusion and rotational times due to stronger hydrogen bonds. Such findings are crucial in order to analyze dynamical properties in light of NQEs (Section 3.2).
 | ||
| Fig. 3 Structural and dynamical properties of liquid water from DFT-based ab initio simulations, compared to experimental values.51,54,55,192,208,209 (a) Coordination number, (b) equilibrium density, (c) average number of H-bonds per water molecule (*upper bound from the integration of gOH instead of geometric criteria), (d) finite-size diffusion coefficient. Results for non-Minnesota functionals were extracted from ref. 40, 41, 117, 124, 138, 140, 143, 154, 162–165, 184 and 197 and reported in Tables S3 and S4 of the ESI.† | ||
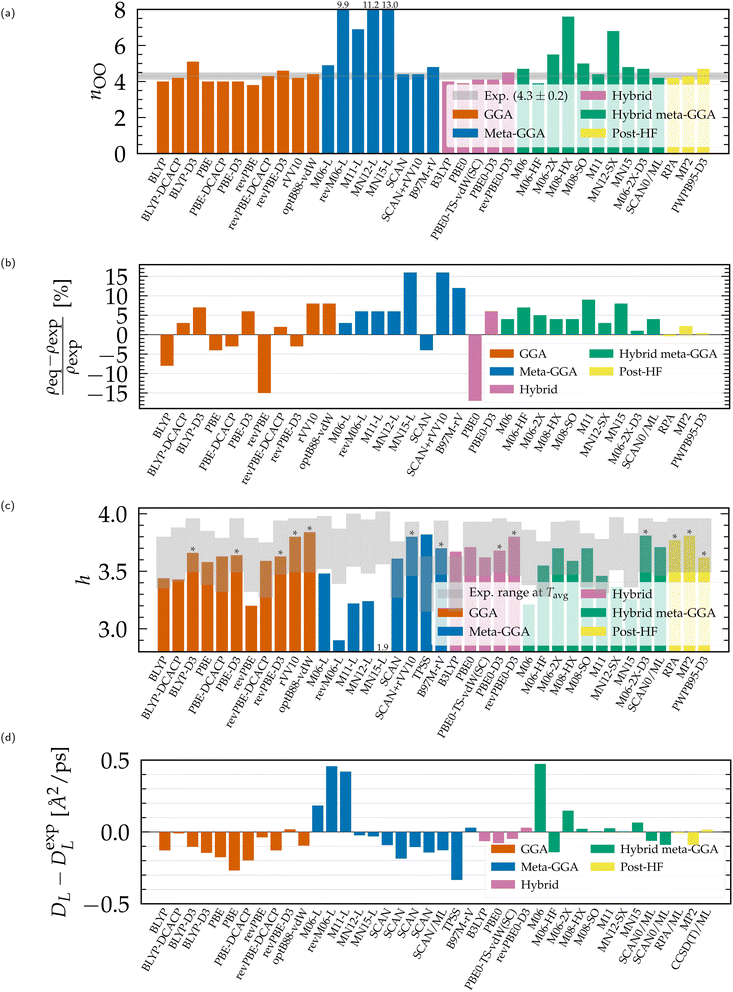
Linked to the fact that Minnesota meta-GGAs are not providing accurate descriptions of the structure of water (Fig. 1), being either understructured (M06-L, revM06-L, M11-L) or biasing the orientation between neighboring molecules (MN12-L, MN15-L), they are also unable to properly account for hydrogen bonds. Their angular distribution in Fig. 4a further shows that semilocal Minnesota functionals are incapable of capturing the full details of the hydrogen bond network of water, that is too fluid.
 | ||
| Fig. 4 Distribution P(β) of the H-bonding angle β, compared to experimental values.210 (a) Meta-GGA Minnesota functionals, (b) hybrid meta-GGA Minnesota functionals. Distributions of the complementary angle α are provided in the ESI (Fig. S3†). | ||
The hydrogen bond network of water is composed of a combination of short, straight, and robust bonds as well as longer, weak, and bent interactions. The strength of a hydrogen bond is consequently highly correlated with its length and angular orientation. At finite temperature, the elongation of the H-bonds competes with the cohesive effects of vdW interactions, which explains why the h number is in general higher and in better agreement with experimental data with dispersion corrections without altering significantly the angular distribution.124 In contrast, both h and the angular distribution vary when considering different fractions of exact exchange; Fig. 3c shows that h increases for M06-HF (100%), M06-2X (54%), M08-HX (52%), M08-SO (57%), while it is too low for M06 (27%), M11 (43–100%), MN12-SX (25–0%) and MN15 (44%). At the same time, H-bonds become shorter (Fig. 1, gOH) and straighter (Fig. 4b) when augmenting the fraction of exact exchange from M06 (27%) to M06-2X (54%) to M06-HF (100%). Hydrogen bonds are therefore particularly more sensitive to exchange effects than to correlation ones. Incorporating more exact exchange strengthens the hydrogen bonds and results in a more rigid structure of water.
Of all the structural properties analyzed, and taking also potential variations due to NQEs into account, we conclude that the functionals that provide results closest to experiments are: revPBE-D3, optB88-vdW, BLYP-DCACP (GGA), B97M-rV (meta-GGA), revPBE0-D3, PBE0-D3 (hybrid), M06-2X-D3, SCAN0 (hybrid meta-GGA) and the RPA (rung-5). Satisfactory agreement with experimental results, while directly accounting for NQEs, has only been demonstrated for revPBE0-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117,204 and the RPA.165 The revPBE-D3,204 PBE0-D3
117,204 and the RPA.165 The revPBE-D3,204 PBE0-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 154 and SCAN0
154 and SCAN0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 164 functionals overstructure water with NQEs, while B97M-rV117 understructures. From a structural perspective, the remaining optB88-vdW and BLYP-DCACP GGAs emerge as intriguing candidates to investigate also in the presence of NQEs. The rung-4 M06-2X-D3 functional is even more promising, as it is slightly overstructured without NQEs and offers accurate density and hydrogen bond characteristics.
164 functionals overstructure water with NQEs, while B97M-rV117 understructures. From a structural perspective, the remaining optB88-vdW and BLYP-DCACP GGAs emerge as intriguing candidates to investigate also in the presence of NQEs. The rung-4 M06-2X-D3 functional is even more promising, as it is slightly overstructured without NQEs and offers accurate density and hydrogen bond characteristics.
3.2 Dynamical properties
 | ||
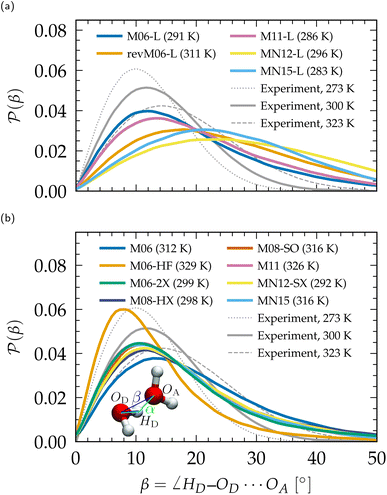
| Fig. 5 (a) Diffusion coefficient rescaled to infinite size for heavy (left) and light (right) water. Experimental data points were compiled from ref. 47–49, 51, 211 and 212 and fitted according to ref. 51. (b) Qualitative comparison of the orientational relaxation times τμ2 and τOH2 with experimental results.42,46,50,52,198–201,213 CCSD(T)/ML values are from PIMD simulations including NQEs,197 and extend through the range of experiments. Non-Minnesota results were extracted from ref. 40, 41, 117, 124, 140, 143, 154, 162–165, 184 and 204 and reported in Tables S4 and S5 of the ESI.† | ||
The dynamics predicted by DFT functionals depends on their ability to account for hydrogen bond strength as well as directionality. Diffusion and rotational movements are determined by the dynamic breaking and formation of H-bonds under thermal fluctuations. Therefore, if the description of H-bonds is too strong, it significantly slows down the dynamical properties. Local and semilocal functionals suffer from the self-interaction error that promotes a delocalization of the protons.143,164 This delocalization facilitates the formation of H-bonds when the proton moves toward the acceptor and thus contributes to the H-bond strengthening, in an analogous manner to the NQEs (Section 3.1.2). As an illustration, the diffusion coefficient is too low for most GGA and meta-GGA functionals, in agreement with their tendency to overstructure. For example, optB88-vdW yields slightly overstructured water (Fig. 2), and diffuses too slowly (Fig. 5a). BLYP-DCACP and revPBE have higher diffusion coefficients, more in line with experiment, but this originates from their underestimation of the number of hydrogen bonds (Fig. 3c).
For GGAs, both BLYP-DCACP and revPBE-D3 functionals have a diffusion coefficient and relaxation times very close to the experiment, which is also true for the diffusion modelled by the B97M-rV meta-GGA. In contrast to the statement that the self-interaction error slows down the dynamics of liquid water, we have found that the M06-L, revM06-L and M11-L semilocal functionals exhibit a complete opposite trend, generally leading to faster dynamics. This is obviously due to their distortion of the hydrogen bonding network (Fig. 4) and incorrect structuring (Fig. 1). The diffusion coefficients predicted by MN12-L and MN15-L functionals appear to be in good agreement with experimental values (Fig. 5a), but this is fortuitously caused by an error compensation between the lack of hydrogen bonds (Fig. 3c) and their overly strong (incorrect) structure (Fig. 1). Their rotational dynamics is indeed significantly faster than observed experimentally (Fig. 5b).
As explained earlier, NQEs tend to strengthen H-bonds and slow down the dynamical properties. This was seen in all PIMD calculations with BLYP-D3,184 revPBE-D3,204 SCAN,40,163,184 B97M-rV,117 revPBE0-D3,117,204 and RPA/ML.165 The diffusion coefficients, in the absence of NQEs, should therefore be seen as overestimated, and relaxation times as underestimated. The diffusion with GGAs would therefore become even slower with NQEs. From the available data, hybrid and hybrid meta-GGA functionals generally give faster diffusion than GGAs, which indicates that the exact exchange is a key ingredient towards achieving accuracy for the dynamics, in the same way as for the structural properties. The revPBE0-D3 functional can be considered as the most effective hybrid in this regard. Other functionals like PBE0 or SCAN0 are likely to remain too slow even upon inclusion of NQEs.
Except for M06-HF, hybrid Minnesota functionals lead either to too fast diffusion or are in good agreement with the reference values. Thus, incorporating NQEs could potentially bring them closer to experimental results. Consistent with the understructuring tendency of M06 (with 27% of exact exchange) and the overstructuring of M06-HF (with 100%) (Fig. 1), the M06 family shows once again that the amount of exact exchange tightly regulates the precision of the functional: dynamical properties are too slow for M06-HF due to the shortening of stronger H-bonds, while M06 is too fast. The balanced M06-2X (54%) is giving results that are inbetween and therefore closer to experimental values. From a first estimation based on ML potentials, the dynamics of the rung-5 RPA description resembles closely the one revPBE-D3 and is thus highly consistent with the experimental data.
Overall, considering the possible influence of NQEs on the analyzed structural and dynamical properties, the functionals that most closely align with experiments are: revPBE-D3 and BLYP-DCACP (GGA), B97M-rV (meta-GGA), revPBE0-D3 (hybrid), M06-2X(-D3), SCAN0 (hybrid meta-GGA) and the RPA (rung-5). Satisfactory agreement for both structural and dynamical properties while accounting for NQEs has only been demonstrated with revPBE0-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117,204 and RPA/ML.165 revPBE-D3
117,204 and RPA/ML.165 revPBE-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204 and SCAN0/ML164 descriptions tend to overstructure water yielding too slow dynamics, even when accounting for NQEs, while B97M-rV117 understructures and slightly accelerates diffusion. Based on our extensive analysis, BLYP-DCACP124 (GGA) and M06-2X(-D3)154 (hybrid meta-GGA) functionals therefore emerge as promising competitors to revPBE0-D3
204 and SCAN0/ML164 descriptions tend to overstructure water yielding too slow dynamics, even when accounting for NQEs, while B97M-rV117 understructures and slightly accelerates diffusion. Based on our extensive analysis, BLYP-DCACP124 (GGA) and M06-2X(-D3)154 (hybrid meta-GGA) functionals therefore emerge as promising competitors to revPBE0-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117,204, and the RPA,154,165 and warrant further investigation with PIMD approaches.
117,204, and the RPA,154,165 and warrant further investigation with PIMD approaches.
4 Conclusions
Water is the most abundant substance on Earth, and its liquid properties are distinct from those of other fluids, posing a challenge for in silico simulations not only of condensed water but also of aqueous chemistry. In this work, we explored the performance of Minnesota meta-GGA and hybrid meta-GGA density functionals in describing the structure and dynamics of liquid water via ab initio molecular dynamics simulations. Contrary to the prevailing belief that local and semilocal functionals overstructure water, leading to underestimation of dynamical properties, the non-hybrid Minnesota meta-GGAs exhibit the opposite trend. M06-L, revM06-L, and M11-L lead to understructuring of water, while MN12-L and MN15-L lack cohesive effects, resulting in increased intermolecular distances. This behavior can be attributed to the weakening of the hydrogen bond network causing dynamical fingerprints that are far too fast. On the other hand, while most of the hybrid Minnesota functionals remain understructured (M06, M08-HX, M08-SO, M11, MN12-SX, MN15), their dynamical properties generally improve over those obtained with local and semilocal functionals (e.g., M06-L, revM06-L, M11-L, MN12-L, MN15-L). The inclusion of exact exchange was identified as a key ingredient for the correct description of hydrogen bonds leading to improved structural and dynamical properties. In contrast, we found that an excessive amount of exact exchange (M06-HF) shortens and strengthens the hydrogen bonds between molecules, thus giving water properties that are too glassy.M06-2X turns out to be the best Minnesota functional tested for liquid water and one of the best DFT functionals reported so far for this system overall. Its D3 dispersion corrected version shows very good agreement for structural properties. Describing the complete picture of water from small to larger clusters, to the condensed phase, is highly non-trivial with DFT, because functionals showing good performance in the gas phase do not necessarily perform well in the liquid phase and vice versa.124,125 Very encouragingly, M06-2X has also been identified as one of the most accurate functionals for relative energies of water hexamers214 and binding energies of 16-mers and 17-mers.215 Furthermore, from the thorough benchmark by Goerigk and Grimme, M06-2X-D3 was found to be the best among 23 hybrid functionals for general main group thermochemistry, kinetics, and noncovalent interactions.112
Previous studies considering explicit NQEs in water, have identified the hybrid revPBE0-D3, and the rung-5 RPA (EXX + RPA, RPA@PBE) with the help of machine learning potentials, as the only two approximations that agree closely with experiments so far. This therefore encourages the investigation of the performance of M06-2X(-D3) functionals with NQEs via path integral approaches. Although it is unfortunate that this involves drastic computational overheads, our work provides further evidence that both exact exchange and appropriate (non-local) correlation are essential for accurately describing water interactions. This, in turn, suggests that well-balanced XC functionals from higher rungs of the Jacob's ladder are required for simulating complex biological systems in water with predictive accuracy. In this regard, determining whether M06-2X(-D3) are indeed one of the best functionals would avoid the resort to the significantly more expensive fifth rung of the Jacob's ladder.
Data availability
Data and analysis scripts are provided on Zenodo at https://doi.org/10.5281/zenodo.7933087.Author contributions
Conceptualization: J. V., M. P. B., U. R.; methodology: J. V., M. P. B., U. R.; software: J. V., M. P. B.; formal analysis: J. V., U. R.; investigation: J. V., M. P. B., U. R.; resources: U. R.; data curation: J. V.; writing – original draft preparation: J. V., U. R.; writing – review & editing: J. V., M. P. B., U. R.; visualization: J. V., M. P. B.; supervision: U. R.; project administration: J. V., U. R.; funding acquisition: U. R.Conflicts of interest
There are no conflicts to declare.Acknowledgements
U. R. acknowledges funding from the Swiss National Science Foundation via individual grant No. 200020_185092 and the NCCR MUST, as well as computing time provided by the Swiss National Supercomputing Centre (CSCS). J. V. would like to thank Nicholas J. Browning and Pablo Baudin for implementing the ML-MTS scheme with CPMD.References
- F. Franks, Water: A Matrix of Life, Royal Society of Chemistry, Cambridge, 2nd edn, 2000 Search PubMed.
- D. Eisenberg and W. Kauzmann, The Structure and Properties of Water, Oxford University Press, Oxford, 1st edn, 1969 Search PubMed.
- P. Atkins and J. de Paula, Physical Chemistry: Thermodynamics, Structure, and Change, W. H. Freeman, New York, 10th edn, 2014 Search PubMed.
- M. F. Chaplin, Structure and Properties of Water in its Various States, John Wiley & Sons, New York, 2019 Search PubMed.
- W. P. Jencks, Chem. Rev., 1972, 72, 705–718 CrossRef CAS.
- P. L. Geissler, C. Dellago, D. Chandler, J. Hutter and M. Parrinello, Science, 2001, 291, 2121–2124 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Rev. Mineral. Geochem., 2010, 71, 19–37 CrossRef CAS.
- M. Chen, L. Zheng, B. Santra, H.-Y. Ko, R. A. DiStasio Jr, M. L. Klein, R. Car and X. Wu, Nat. Chem., 2018, 10, 413–419 CrossRef CAS PubMed.
- I. D. Kuntz, K. Chen, K. A. Sharp and P. A. Kollman, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9997–10002 CrossRef CAS PubMed.
- P. Ball, Chem. Rev., 2008, 108, 74–108 CrossRef CAS PubMed.
- S. Manabe and R. T. Wetherald, J. Atmos. Sci., 1967, 24, 241–259 CrossRef CAS.
- V. Ramanathan, R. D. Cess, E. F. Harrison, P. Minnis, B. R. Barkstrom, E. Ahmad and D. Hartmann, Science, 1989, 243, 57–63 CrossRef CAS PubMed.
- S. C. Chapra, Surface Water-Quality Modeling, Waveland Press, Long Grove, 2008 Search PubMed.
- M.-O. Simon and C.-J. Li, Chem. Soc. Rev., 2012, 41, 1415–1427 RSC.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 6221–6239 CrossRef CAS.
- S. K. Pal, J. Peon, B. Bagchi and A. H. Zewail, J. Phys. Chem. B, 2002, 106, 12376–12395 CrossRef CAS.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608 CrossRef CAS PubMed.
- J. R. Werber, C. O. Osuji and M. Elimelech, Nat. Rev. Mater., 2016, 1, 16018 CrossRef CAS.
- C. Tanford, Science, 1978, 200, 1012–1018 CrossRef CAS PubMed.
- R. Zhou, X. Huang, C. J. Margulis and B. J. Berne, Science, 2004, 305, 1605–1609 CrossRef CAS PubMed.
- C. Camilloni, D. Bonetti, A. Morrone, R. Giri, C. M. Dobson, M. Brunori, S. Gianni and M. Vendruscolo, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- R. L. Baldwin and G. D. Rose, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12462–12466 CrossRef CAS PubMed.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- A. Warshel and R. P. Bora, J. Chem. Phys., 2016, 144, 180901 CrossRef PubMed.
- M. Chaplin, Nat. Rev. Mol. Cell Biol., 2006, 7, 861–866 CrossRef CAS PubMed.
- S. J. Marrink, V. Corradi, P. C. T. Souza, H. I. Ingólfsson, D. P. Tieleman and M. S. P. Sansom, Chem. Rev., 2019, 119, 6184–6226 CrossRef CAS PubMed.
- P. G. Debenedetti, J. Phys.: Condens. Matter, 2003, 15, R1669 CrossRef CAS.
- G. S. Kell, J. Chem. Eng. Data, 1975, 20, 97–105 CrossRef CAS.
- A. Nilsson and L. G. M. Pettersson, Chem. Phys., 2011, 389, 1–34 CrossRef CAS.
- F. H. Stillinger, Science, 1980, 209, 451–457 CrossRef CAS PubMed.
- D. Fennell Evans and H. Wennerström, The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, Wiley-VCH, Weinheim, 2nd edn, 1999 Search PubMed.
- A. W. Adamson and A. P. Gast, Physical Chemistry of Surfaces, John Wiley & Sons, New York, 6th edn, 1997 Search PubMed.
- J. B. Hasted, Aqueous Dielectrics, Chapman and Hall, London, 1973 Search PubMed.
- U. Kaatze, J. Chem. Eng. Data, 1989, 34, 371–374 CrossRef CAS.
- P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. M. Pettersson, Chem. Rev., 2016, 116, 7463–7500 CrossRef CAS PubMed.
- K. Ni, H. Fang, Z. Yu and Z. Fan, J. Mol. Liq., 2019, 278, 234–238 CrossRef CAS.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832–835 CrossRef CAS PubMed.
- G. N. I. Clark, C. D. Cappa, J. D. Smith, R. J. Saykally and T. Head-Gordon, Mol. Phys., 2010, 108, 1415–1433 CrossRef CAS.
- J. Teixeira, Mol. Phys., 2012, 110, 249–258 CrossRef CAS.
- C. Herrero, M. Pauletti, G. Tocci, M. Iannuzzi and L. Joly, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, 1–8 CrossRef PubMed.
- M. Chen, H. Y. Ko, R. C. Remsing, M. F. Calegari Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein, J. P. Perdew and X. Wu, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10846–10851 CrossRef CAS PubMed.
- J. A. Glasel, Proc. Natl. Acad. Sci. U. S. A., 1967, 58, 27–33 CrossRef CAS PubMed.
- J. Jonas, T. DeFries and D. J. Wilbur, J. Chem. Phys., 1976, 65, 582–588 CrossRef CAS.
- K. Krynicki, C. D. Green and D. W. Sawyer, Faraday Discuss. Chem. Soc., 1978, 66, 199–208 RSC.
- J. R. C. van der Maarel, D. Lankhorst, J. de Bleijser and J. C. Leyte, Chem. Phys. Lett., 1985, 122, 541–544 CrossRef CAS.
- R. P. Struis, J. De Bleijser and J. C. Leyte, J. Phys. Chem., 1987, 91, 1639–1645 CrossRef CAS.
- W. S. Price, H. Ide and Y. Arata, J. Phys. Chem. A, 1999, 103, 448–450 CrossRef CAS.
- M. Holz, S. R. Heil and A. Sacco, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- W. S. Price, H. Ide, Y. Arata and O. Söderman, J. Phys. Chem. B, 2000, 104, 5874–5876 CrossRef CAS.
- D. Lankhorst, J. Schriever and J. C. Leyte, Ber. Bunsenges. Phys. Chem., 1982, 86, 215–221 CrossRef CAS.
- E. H. Hardy, A. Zygar, M. D. Zeidler, M. Holz and F. D. Sacher, J. Chem. Phys., 2001, 114, 3174–3181 CrossRef CAS.
- J. Ropp, C. Lawrence, T. C. Farrar and J. L. Skinner, J. Am. Chem. Soc., 2001, 123, 8047–8052 CrossRef CAS PubMed.
- C. P. Lawrence and J. L. Skinner, J. Chem. Phys., 2003, 118, 264–272 CrossRef CAS.
- L. B. Skinner, C. Huang, D. Schlesinger, L. G. Pettersson, A. Nilsson and C. J. Benmore, J. Chem. Phys., 2013, 138, 074506 CrossRef PubMed.
- L. B. Skinner, C. J. Benmore, J. C. Neuefeind and J. B. Parise, J. Chem. Phys., 2014, 141, 214507 CrossRef CAS PubMed.
- A. K. Soper, J. Chem. Phys., 1994, 101, 6888–6901 CrossRef.
- A. K. Soper, Chem. Phys., 2000, 258, 121–137 CrossRef CAS.
- A. K. Soper, ISRN Phys. Chem., 2013, 2013, 1–67 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. R. Errington and P. G. Debenedetti, Nature, 2001, 409, 318–321 CrossRef CAS PubMed.
- M. Matsumoto, S. Saito and I. Ohmine, Nature, 2002, 416, 409–413 CrossRef CAS PubMed.
- X. Teng, B. Liu and T. Ichiye, J. Chem. Phys., 2020, 153, 104510 CrossRef CAS PubMed.
- M. E. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, Oxford University Press, Oxford, 1st edn, 2010 Search PubMed.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- C. Vega and J. L. F. Abascal, Phys. Chem. Chem. Phys., 2011, 13, 19663–19688 RSC.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- M. E. Tuckerman, J. Phys.: Condens. Matter, 2002, 14, R1297 CrossRef CAS.
- D. R. Hartree, Math. Proc. Cambridge Philos. Soc., 1928, 24, 89–110 CrossRef CAS.
- V. Fock, Z. Phys., 1930, 61, 126–148 CrossRef.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- D. Bohm and D. Pines, Phys. Rev., 1951, 82, 625–634 CrossRef CAS.
- D. Pines and D. Bohm, Phys. Rev., 1952, 85, 338–353 CrossRef CAS.
- D. Bohm and D. Pines, Phys. Rev., 1953, 92, 609–625 CrossRef CAS.
- H. Eshuis and F. Furche, J. Chem. Phys., 2012, 136, 084105 CrossRef PubMed.
- J. Čížek, J. Chem. Phys., 1966, 45, 4256–4266 CrossRef.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- P.-O. Löwdin, Phys. Rev., 1955, 97, 1474–1489 CrossRef.
- C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, John Wiley & Sons, Chichester, 2nd edn, 2004 Search PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, Cambridge, 1st edn, 2009 Search PubMed.
- S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- D. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett., 1999, 82, 2544–2547 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 3–6 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 36402 CrossRef PubMed.
- J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, Z. Yang, A. Paul, U. Waghmare, X. Wu, M. L. Klein and J. P. Perdew, Nat. Chem., 2016, 8, 831–836 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- K. Burke, M. Ernzerhof and J. P. Perdew, Chem. Phys. Lett., 1997, 265, 115–120 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. Görling and M. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13105–13113 CrossRef PubMed.
- A. Görling and M. Levy, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 4493–4499 CrossRef PubMed.
- E. Engel and R. M. Dreizler, J. Comput. Chem., 1999, 20, 31–50 CrossRef CAS.
- M. Ernzerhof, Chem. Phys. Lett., 1996, 263, 499–506 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- L. Goerigk and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 576–600 CAS.
- D. C. Langreth and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 5469–5493 CrossRef.
- F. Furche, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195120 CrossRef.
- M. Fuchs and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 235109 CrossRef.
- F. Furche, J. Chem. Phys., 2008, 129, 114105 CrossRef PubMed.
- X. Ren, P. Rinke, C. Joas and M. Scheffler, J. Mater. Sci., 2012, 47, 7447–7471 CrossRef CAS.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- R. Peverati and D. G. Truhlar, Philos. Trans. R. Soc., A, 2014, 372, 20120476 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- P. Verma and D. G. Truhlar, Tends Chem., 2020, 2, 302–318 CAS.
- M. Bursch, J. Mewes, A. Hansen and S. Grimme, Angew. Chem., 2022, 134, e202205735 CrossRef.
- L. R. Pestana, O. Marsalek, T. E. Markland and T. Head-Gordon, J. Phys. Chem. Lett., 2018, 9, 5009–5016 CrossRef PubMed.
- M. P. Bircher and U. Rothlisberger, J. Phys. Chem. Lett., 2018, 9, 3886–3890 CrossRef CAS PubMed.
- F. Mouvet, J. Villard, V. Bolnykh and U. Rothlisberger, Acc. Chem. Res., 2022, 55, 221–300 CrossRef CAS PubMed.
- D. Rappoport, N. R. M. Crawford, F. Furche and K. Burke, Approximate Density Functionals: Which Should I Choose?, John Wiley & Sons, New York, 2009 Search PubMed.
- J. C. Grossman, E. Schwegler, E. W. Draeger, F. Gygi and G. Galli, J. Chem. Phys., 2004, 120, 300–311 CrossRef CAS PubMed.
- M. J. McGrath, J. I. Siepmann, I. F. W. Kuo, C. J. Mundy, J. Vandevondele, J. Hutter, F. Mohamed and M. Krack, ChemPhysChem, 2005, 6, 1894–1901 CrossRef CAS PubMed.
- J. Schmidt, J. VandeVondele, I.-F. W. Kuo, D. Sebastiani, J. I. Siepmann, J. Hutter and C. J. Mundy, J. Phys. Chem. B, 2009, 113, 11959–11964 CrossRef CAS PubMed.
- I. C. Lin, A. P. Seitsonen, I. Tavernelli and U. Rothlisberger, J. Chem. Theory Comput., 2012, 8, 3902–3910 CrossRef CAS PubMed.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- A. P. Gaiduk, F. Gygi and G. Galli, J. Phys. Chem. Lett., 2015, 6, 2902–2908 CrossRef CAS PubMed.
- A. Tkatchenko, R. A. Distasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- T. Morawietz, A. Singraber, C. Dellago and J. Behler, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8368–8373 CrossRef CAS PubMed.
- O. A. Von Lilienfeld, I. Tavernelli, U. Rothlisberger and D. Sebastiani, Phys. Rev. Lett., 2004, 93, 1–4 CrossRef PubMed.
- I. C. Lin, A. P. Seitsonen, M. D. Coutinho-Neto, I. Tavernelli and U. Rothlisberger, J. Phys. Chem. B, 2009, 113, 1127–1131 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 132, 164113 CrossRef PubMed.
- R. Sabatini, T. Gorni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 4–7 CrossRef.
- G. Miceli, S. De Gironcoli and A. Pasquarello, J. Chem. Phys., 2015, 142, 034501 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 22–25 CrossRef PubMed.
- N. Ferri, R. A. Distasio, A. Ambrosetti, R. Car and A. Tkatchenko, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- J. Wiktor, F. Ambrosio and A. Pasquarello, J. Chem. Phys., 2017, 147, 2016–2018 CrossRef PubMed.
- P. H. Sit and N. Marzari, J. Chem. Phys., 2005, 122, 204510 CrossRef PubMed.
- T. Todorova, A. P. Seitsonen, J. Hutter, I. F. W. Kuo and C. J. Mundy, J. Phys. Chem. B, 2006, 110, 3685–3691 CrossRef CAS PubMed.
- M. Guidon, F. Schiffmann, J. Hutter and J. Vandevondele, J. Chem. Phys., 2008, 128, 214104 CrossRef PubMed.
- H. S. Lee and M. E. Tuckerman, J. Chem. Phys., 2007, 126, 164501 CrossRef PubMed.
- L. Ruiz Pestana, N. Mardirossian, M. Head-Gordon and T. Head-Gordon, Chem. Sci., 2017, 8, 3554–3565 RSC.
- Y. Wang, X. Jin, H. S. Yu, D. G. Truhlar and X. He, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8487–8492 CrossRef CAS PubMed.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 117–124 CrossRef CAS.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 13171–13174 RSC.
- H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 16187–16191 RSC.
- H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293 CrossRef CAS PubMed.
- M. Del Ben, J. Hutter and J. VandeVondele, J. Chem. Phys., 2015, 143, 054506 CrossRef PubMed.
- N. Marom, A. Tkatchenko, M. Rossi, V. V. Gobre, O. Hod, M. Scheffler and L. Kronik, J. Chem. Theory Comput., 2011, 7, 3944–3951 CrossRef CAS PubMed.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- A. Dorcier, P. J. Dyson, C. Gossens, U. Rothlisberger, R. Scopelliti and I. Tavernelli, Organometallics, 2005, 24, 2114–2123 CrossRef CAS.
- B. Thapa and H. B. Schlegel, J. Phys. Chem. A, 2016, 120, 5726–5735 CrossRef CAS PubMed.
- U. F. Röhrig, I. Frank, J. Hutter, A. Laio, J. VandeVondele and U. Rothlisberger, ChemPhysChem, 2003, 4, 1177–1182 CrossRef PubMed.
- A. Tkatchenko, L. Romaner, O. T. Hofmann, E. Zojer, C. Ambrosch-Draxl and M. Scheffler, MRS Bull., 2010, 35, 435–442 CrossRef CAS.
- R. A. Distasio, B. Santra, Z. Li, X. Wu and R. Car, J. Chem. Phys., 2014, 141, 084502 CrossRef PubMed.
- Y. Yao and Y. Kanai, J. Chem. Phys., 2020, 153, 044114 CrossRef CAS PubMed.
- C. Zhang, F. Tang, M. Chen, J. Xu, L. Zhang, D. Y. Qiu, J. P. Perdew, M. L. Klein and X. Wu, J. Phys. Chem. B, 2021, 125, 11444–11456 CrossRef CAS PubMed.
- Y. Yao and Y. Kanai, J. Phys. Chem. Lett., 2021, 12, 6354–6362 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 4303–4325 CrossRef CAS PubMed.
- M. P. Bircher, P. López-Tarifa and U. Rothlisberger, J. Chem. Theory Comput., 2019, 15, 557–571 CrossRef CAS PubMed.
- N. J. Browning, PhD thesis, EPFL, Lausanne, 2019.
- M. E. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001 CrossRef CAS.
- M. E. Tuckerman, Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms, John von Neumann Institute for Computing, Jülich, 2002, vol. 10, pp. 269–298 Search PubMed.
- P. A. M. Dirac, Math. Proc. Cambridge Philos. Soc., 1930, 26, 376–385 CrossRef CAS.
- G. L. Oliver and J. P. Perdew, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 397–403 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- R. Peverati and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 2310–2319 CrossRef CAS PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Phys., 2005, 123, 161103 CrossRef PubMed.
- T. Van Voorhis and G. E. Scuseria, J. Chem. Phys., 1998, 109, 400–410 CrossRef CAS.
- J. Toulouse, F. Colonna and A. Savin, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 62505 CrossRef.
- IBM-MPI-CPMD, Car-Parrinello Molecular Dynamics code, 2019, http://www.cpmd.org Search PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- J. Villard, M. P. Bircher and U. Rothlisberger, J. Chem. Theory Comput., 2023, 19, 9211–9227 CrossRef CAS PubMed.
- J. Hutter, H. P. Lüthi and M. Parrinello, Comput. Mater. Sci., 1994, 2, 244–248 CrossRef CAS.
- E. Liberatore, R. Meli and U. Rothlisberger, J. Chem. Theory Comput., 2018, 14, 2834–2842 CrossRef CAS PubMed.
- R. P. Steele, J. Chem. Phys., 2013, 139, 011102 CrossRef PubMed.
- C. Li, F. Paesani and G. A. Voth, J. Chem. Theory Comput., 2022, 18, 2124–2131 CrossRef CAS PubMed.
- A. S. Christensen, F. A. Faber and O. A. von Lilienfeld, J. Chem. Phys., 2019, 150, 064105 CrossRef PubMed.
- A. S. Christensen, L. A. Bratholm, F. A. Faber and O. Anatole Von Lilienfeld, J. Chem. Phys., 2020, 152, 044107 CrossRef CAS PubMed.
- B. Huang and O. A. von Lilienfeld, Nat. Chem., 2020, 12, 945–951 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- P. Raiteri, A. Laio and M. Parrinello, Phys. Rev. Lett., 2004, 93, 6–9 CrossRef PubMed.
- T. Giorgino, J. Open Source Softw., 2019, 4, 1698 CrossRef.
- I. C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- E. W. Lemmon, I. H. Bell, M. L. Huber and M. O. McLinden, NIST Chemistry webbook, NIST Standard reference database, National Institute of Standards and Technology, Gaithersburg MD, 20899, USA, 1998, vol. 69 Search PubMed.
- K. Lee, J. Yu and Y. Morikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–5 Search PubMed.
- D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 14230–14242 CrossRef CAS PubMed.
- D. M. Wilkins, D. E. Manolopoulos, S. Pipolo, D. Laage and J. T. Hynes, J. Phys. Chem. Lett., 2017, 8, 2602–2607 CrossRef CAS PubMed.
- T. F. Miller and D. E. Manolopoulos, J. Chem. Phys., 2005, 123, 154504 CrossRef PubMed.
- J. Daru, H. Forbert, J. Behler and D. Marx, Phys. Rev. Lett., 2022, 129, 226001 CrossRef CAS PubMed.
- D. W. G. Smith and J. G. Powles, Mol. Phys., 1966, 10, 451–463 CrossRef CAS.
- M. S. Sansom, I. D. Kerr, J. Breed and R. Sankararamakrishnan, Biophys. J., 1996, 70, 693–702 CrossRef CAS PubMed.
- H. J. Bakker, Y. L. Rezus and R. L. Timmer, J. Phys. Chem. A, 2008, 112, 11523–11534 CrossRef CAS PubMed.
- H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498–1517 CrossRef CAS PubMed.
- L. Goerigk, J. Phys. Chem. Lett., 2015, 6, 3891–3896 CrossRef CAS PubMed.
- J. A. Morrone and R. Car, Phys. Rev. Lett., 2008, 101, 017801 CrossRef PubMed.
- O. Marsalek and T. E. Markland, J. Phys. Chem. Lett., 2017, 8, 1545–1551 CrossRef CAS PubMed.
- R. P. Feynman, A. R. Hibbs and D. F. Styer, Quantum Mechanics and Path Integrals, Dover Publications, New York, 2010 Search PubMed.
- J. Lan, D. M. Wilkins, V. V. Rybkin, M. Iannuzzi and J. J. Hutter, ChemRxiv, 2021, preprint, DOI:10.26434/chemrxiv-2021-n32q8-v2.
- A. K. Soper and C. J. Benmore, Phys. Rev. Lett., 2008, 101, 65502 CrossRef CAS PubMed.
- M. Chaplin, Hydrogen Bonding in Water, 2023, https://water.lsbu.ac.uk/water/water_hydrogen_bonding.html Search PubMed.
- A. Rastogi, A. K. Ghosh and S. J. Suresh, Thermodynamics – Physical Chemistry of Aqueous Systems, IntechOpen, London, 1st edn, 2011, ch. 13, pp. 351–364 Search PubMed.
- K. Modig, B. G. Pfrommer and B. Halle, Phys. Rev. Lett., 2003, 90, 075502 CrossRef PubMed.
- R. Mills, J. Phys. Chem., 1973, 77, 685–688 CrossRef CAS.
- A. J. Easteal, W. E. Price and L. A. Woolf, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 1091–1097 RSC.
- A. Rahman and F. H. Stillinger, J. Chem. Phys., 1971, 55, 3336–3359 CrossRef CAS.
- E. E. Dahlke, R. M. Olson, H. R. Leverentz and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 3976–3984 CrossRef CAS PubMed.
- H. R. Leverentz, H. W. Qi and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 995–1006 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc05828j |
| ‡ As emphasized by a reviewer, the nomenclature of exact exchange refers herein to the single-determinant exchange evaluated from the Fock integral of orbitals coming from hybrid functionals. This term should therefore not be confused with the exact KS exchange, obtained by evaluating the Fock form with the KS determinant, in association with the exact and local KS potential. |
| This journal is © The Royal Society of Chemistry 2024 |
