 Open Access Article
Open Access ArticleMolecular mechanism of α-synuclein aggregation on lipid membranes revealed†
Alexander J.
Dear
a,
Xiangyu
Teng
a,
Sarah R.
Ball
a,
Joshua
Lewin
a,
Robert I.
Horne
a,
Daniel
Clow
a,
Alisdair
Stevenson
bc,
Natasha
Harper
a,
Kim
Yahya
a,
Xiaoting
Yang
 a,
Suzanne C.
Brewerton
a,
John
Thomson
a,
Thomas C. T.
Michaels
bc,
Sara
Linse
ad,
Tuomas P. J.
Knowles
ef,
Johnny
Habchi
*a and
Georg
Meisl
a,
Suzanne C.
Brewerton
a,
John
Thomson
a,
Thomas C. T.
Michaels
bc,
Sara
Linse
ad,
Tuomas P. J.
Knowles
ef,
Johnny
Habchi
*a and
Georg
Meisl
 *a
*a
aWaveBreak Therapeutics Ltd, Chemistry of Health, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: georg.meisl@googlemail.com
bDepartment of Biology, Institute of Biochemistry, ETH Zurich, Otto Stern Weg 3, 8093 Zurich, Switzerland
cBringing Materials to Life Initiative, ETH Zurich, Switzerland
dBiochemistry and Structural Biology, Lund University, Lund, Sweden
eYusuf Hamied Department of Chemistry, University of Cambridge, Cambridge, UK
fCavendish Laboratory, University of Cambridge, Cambridge, UK
First published on 22nd April 2024
Abstract
The central hallmark of Parkinson's disease pathology is the aggregation of the α-synuclein protein, which, in its healthy form, is associated with lipid membranes. Purified monomeric α-synuclein is relatively stable in vitro, but its aggregation can be triggered by the presence of lipid vesicles. Despite this central importance of lipids in the context of α-synuclein aggregation, their detailed mechanistic role in this process has not been established to date. Here, we use chemical kinetics to develop a mechanistic model that is able to globally describe the aggregation behaviour of α-synuclein in the presence of DMPS lipid vesicles, across a range of lipid and protein concentrations. Through the application of our kinetic model to experimental data, we find that the reaction is a co-aggregation process involving both protein and lipids and that lipids promote aggregation as much by enabling fibril elongation as by enabling their initial formation. Moreover, we find that the primary nucleation of lipid–protein co-aggregates takes place not on the surface of lipid vesicles in bulk solution but at the air–water and/or plate interfaces, where lipids and proteins are likely adsorbed. Our model forms the basis for mechanistic insights, also in other lipid–protein co-aggregation systems, which will be crucial in the rational design of drugs that inhibit aggregate formation and act at the key points in the α-synuclein aggregation cascade.
Introduction
The aggregation of α-synuclein has been linked to the emergence of a range of neurodegenerative disorders,1–3 the synucleinopathies, the most prominent of which is Parkinson's disease. Thus, α-synuclein aggregation is a promising target for drug development and significant efforts have been made to discover inhibitors of this process.4–7 A key requirement for the successful development of small molecule aggregation inhibitors is the availability of a reliable, predictive in vitro assay, which often relies on a purified protein drug target, to evaluate compound potency. While this parallels drug discovery strategies for other targets, the search for aggregation inhibitors is additionally complicated by the complexity of the aggregation reaction: several different steps contribute to the overall aggregate formation reaction,8,9 and all are potential targets for slowing in vitro aggregation. However, targeting some of these different steps is unlikely to elicit the desired in vivo responses.10–12 A detailed mechanistic understanding of the aggregation mechanism and its inhibition is thus required for the accurate interpretation and utilisation of in vitro data.13In recent decades, mechanistic work has shown that the aggregation of most purified proteins into large fibrillar aggregates in vitro involves at least 3 classes of processes:15,16 primary nucleation, which leads to the formation of new aggregates directly from monomeric protein without the involvement of existing aggregates, elongation, which is the linear growth of existing aggregates by addition of monomeric protein to the fibril ends, and secondary processes, which lead to the formation of new aggregates from existing aggregates. The two most important secondary processes are fibril fragmentation, and secondary nucleation (the binding of monomeric protein to a fibril surface, which then catalyzes their nucleation into new fibrils). By applying the framework of chemical kinetics,8 these mechanisms can be turned into rate laws to then be fitted to experimental data.13 Application of these rate laws to measurements of the aggregation of purified protein in vitro has been very successful in elucidating the detailed mechanisms of aggregate formation for a wide range of proteins,16 in particular Aβ,17–19 but to some extent also α-synuclein under different conditions.20,21 However, the more complex mechanism that describes the aggregation of a mixture of purified protein and lipid vesicles has remained elusive to date. Here, we build such a mechanistic description and show that it can describe the aggregation of α-synuclein and 1,2-dimyristoyl-sn-glycero-3-phospho-L-serine (DMPS) lipid vesicles, globally, across lipid and protein concentrations.
At neutral pH, supersaturated solutions of purified α-synuclein may be kinetically stable for extended periods of time, generally requiring vigorous agitation or the introduction of preformed seed fibrils to trigger the aggregation process.20,22 This apparent resistance of α-synuclein to aggregation is likely due to the low rate of primary nucleation. The barrier to nucleation is high, meaning monomeric α-synuclein is kinetically stable, but agitation, likely by introducing shearing forces and increasing turnover at the air–water interface can significantly increase its rate.23 Introduction of preformed aggregates increases the speed of aggregation considerably, further supporting the idea that a slow primary nucleation step is the main reason for the aggregation resistance of α-synuclein.20 Lowering the pH20,21 or using high salt concentrations24 are other ways to induce aggregation, likely by reducing electrostatic repulsion between the aggregating proteins.25,26
An alternative method to initiate the aggregation at neutral pH is the introduction of lipids,27 usually in the form of small unilamellar vesicles (SUVs),28 see Fig. 1. This induces formation of aggregates without extended lag-times, however the aggregates formed are quite different to those formed in the absence of lipids. Here we focus on lipid vesicles made from DMPS lipids, because they have been commonly used as a model system for lipid-induced α-synuclein aggregation. However, similar effects have been observed with a range of lipid compositions, suggesting a general behaviour.27,29 DMPS lipids have short saturated acyl chains and its membranes have a melting temperature above 37 °C.30 Although not found in biological membranes,31 DMPS in the form of SUVs efficiently triggers α-synuclein aggregation at near neutral pH (6.5) and may therefore serve as a useful system for mechanistic in vitro studies, such as inhibitor screening.
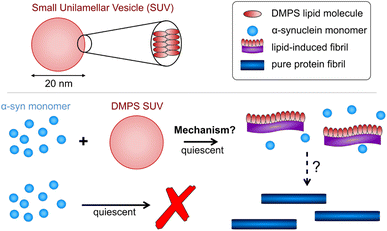 | ||
| Fig. 1 Schematic of α-synuclein aggregates w/o lipids. In the presence of lipid vesicles α-synuclein forms mixed protein–lipid aggregates. In the absence of lipids, monomeric α-synuclein is much more stable and biased against aggregation, however, the formation of pure protein fibrils can be triggered e.g. by agitation. Lipidic fibrils can similarly be triggered to convert to the structures reminiscent of those seen in pure protein aggregation e.g. by heating the reaction mixture.14 Lipids may still be present in those structures but, unlike for lipidic fibrils, do not limit their formation. | ||
In vivo, α-synuclein is believed to be associated with lipid membranes, potentially as part of both its biological function and its pathology.32–36 The introduction of lipid vesicles thus not only allows formation of aggregates under quiescent conditions in vitro, but it also provides a simple in vitro model for the interaction of α-synuclein with membranes. The interaction of α-synuclein with lipid-vesicles and their effect on the kinetics of aggregation has been investigated in detail.14,27,28,33,35–41 It was thus established, using model membranes, that α-synuclein adsorbs in an α-helical conformation42 in the head group area and upper acyl layer43,44 and that protein aggregation is triggered only in situations of protein excess.28,29,45 However, to date no mechanistic model has been able to globally describe the observed aggregation kinetics and thus establish how and at which microscopic step(s) lipid vesicles promote the aggregation of α-synuclein.
While DMPS lipid vesicles efficiently trigger the aggregation of α-synuclein, the fibrils formed under those conditions differ considerably from those formed by seeding or through agitation14 and crucially contain both protein and lipids. Cryo-EM images reveal that the aggregates formed in the presence of DMPS30 are again different from those formed in the presence of other lipids such as DOPC-DOPS mixtures46 and DOPC-GM1 mixtures,47 although lipids appear to decorate the fibrils in all cases. The fibrils formed in the presence of DMPS lipids are sometimes referred to as protofibrils with those formed without lipids referred to as mature fibrils. Similarly, elongated oligomers of protein alone are also commonly called protofibrils. To minimise the potential for misinterpretation, we here refer to the fibrils formed with DMPS as lipidic fibrils (or lipid–protein co-aggregates) and those formed from protein alone as pure protein fibrils. While pure protein fibrils form long, straight structures, the lipidic fibrils appear more flexible in microscopy.14,28 The term mature fibrils is here used to refer simply to any structures that resemble long, straight fibrils, without indicating their composition. There is strong evidence that lipidic fibrils are in fact co-aggregates of both α-synuclein and lipids,28,30 not just for DMPS but across different lipid systems,46 with some recent work providing high resolution structures of such mixed fibrils.48 Another strong piece of evidence in favour of lipidic fibrils containing both lipid and protein comes from the fact that the amount of lipidic fibrils formed is limited not only by the amount of available protein, but also by the amount of available lipid, see Fig. 4A.28 It has been shown that the structures for lipidic and pure protein fibrils may, however, be not entirely unrelated: heating of lipidic fibrils can induce formation of structures reminiscent of pure protein fibrils by microscopy, which use up the remaining free protein in solution, indicating that the lipidic fibrils are a thermodynamically less stable form.14. (Note: as lipidic fibrils may thus be precursors to more mature fibrils, lipid-induced aggregation is sometimes loosely referred to as a primary nucleation process for mature fibrils. However, we feel that referring to the entirety of the formation, growth and conversion of lipidic fibrils as a “primary nucleation” step is stretching the definition of nucleation beyond its generally accepted meaning, so will not be using this terminology.) This observation has also given rise to the hypothesis that some protein–lipid co-aggregates represent the precursors to mature aggregates in disease, prompting our research into therapeutic molecules to target this process. Therefore, a mechanistic understanding of the exact role of lipids in the formation of these co-aggregates is crucial both to evaluate the translatability of in vitro lipid-induced experiments to in vivo systems and to establish which processes in this aggregation reaction are rate-limiting and therefore should be the focus of drug development efforts. In this work, we focus on DMPS lipids and present a new kinetic model that is able to globally fit the aggregation kinetics, across monomer and DMPS lipid concentrations, and thus yields new insights into the ways in which lipid vesicles promote α-synuclein aggregation.
Results and discussion
First, we clarify the terminology used here: in the presence of DMPS lipids, the lipidic fibrils formed contain lipids as well as proteins, thus the processes that give rise to these lipidic fibrils, i.e. their nucleation, growth and potentially fragmentation/secondary nucleation, necessarily involve both proteins and lipids (although they may not contribute to a rate-limiting step). In the context of this work, the central question is, what mechanistic roles do lipids play in each step in the formation of lipidic fibrils, and what therefore are the implications for designing inhibitors of this process? We will now examine these processes in turn and build a model to globally fit the aggregation kinetics across lipid and protein concentrations.Thermodynamics of lipid-induced aggregation
Before a kinetic description of fibril formation is possible, it is necessary to determine which species are formed over the course of the reaction. Initially, only DMPS vesicles and monomeric α-synuclein are present. However, monomeric α-synuclein binds tightly to the vesicles, a process that is believed to be faster than the tens of hours it takes for lipidic fibrils to form, see Fig. 2A.28,32,39 We therefore make the simplifying approximation of pre-equilibrium for α-synuclein monomer-vesicle binding, i.e. assume this equilibrium has already been attained by t = 0, which allows the calculation of the free monomer concentration, mf(t), based on the previously measured equilibrium constant, KD28 (details see Methods). Under the conditions used in this work, α-synuclein is sufficiently in excess that the majority is in solution at early reaction times even after application of pre-equilibrium. In addition to the species present in bulk solution, both lipid and protein may also be found adsorbed at the air–water and/or plate interfaces.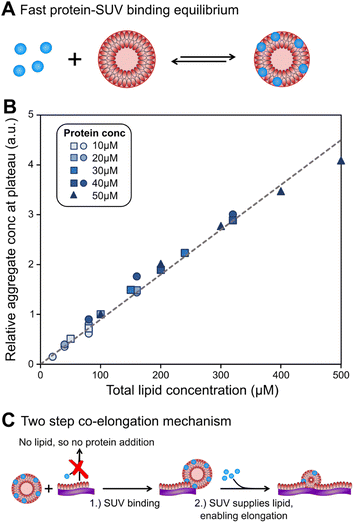 | ||
| Fig. 2 Lipids can be limiting factor in co-elongation of fibrils. (A) Schematic of protein binding to DMPS SUVs. (B) Amounts of fibril at plateau of aggregation curves, as reported by ThT intensity, scale linearly with lipid amounts, regardless of protein concentration. Several datasets, at a range of different protein concentrations, were combined to generate this plot. Circles and squares are new data, triangles are the data from Galvagnion et al.28 To account for differences in the absolute values of ThT fluorescence between the three datasets, within each set the data were normalised to the ThT intensity at 100 μM (80 μM for circles) lipid. (C) Schematic of lipid–protein co-elongation reaction. | ||
At the end of the aggregation reaction, there is an equilibrium of lipidic fibrils, monomeric α-synuclein, free vesicles and vesicle-bound α-synuclein. However, at concentrations used in the study the yield of fibrils is always lipid-limited and not dependent on the initial monomeric α-synuclein concentration, see Fig. 2B. Thus the free monomer concentration is considerably larger than the equilibrium constant at all times during aggregation, and we can approximate the concentration of vesicles not covered in protein as zero at all times.
Finally, to complete the picture, the stoichiometry χ of lipid to protein molecules at the end of the reaction, in the lipidic fibrils, needs to be estimated. A careful examination of the data suggest that this stoichiometry is somewhat flexible, with slightly more lipids per protein at higher lipid to protein ratios, r(0) (details see Methods). This may indicate that the interactions between lipids and protein in these co-aggregates are not as specific as the interactions between proteins, allowing for some flexibility in the stoichiometry to achieve the global free energy minimum at different protein and lipid concentrations. Under the conditions used here, a stoichiometry of χ = 10.5 is consistent across datasets, and we thus use this value for the remainder of the work (details see Methods).
Presence of lipid is crucial for elongation of lipidic fibrils
To understand how DMPS lipids affect the kinetics of aggregate formation, it is crucial to appreciate how essential fibril elongation is for the observation of any aggregate formation in an amyloid forming system: while primary nucleation, and in some systems secondary nucleation, are responsible for the formation of new fibrils from monomeric protein, these new fibrils are usually orders of magnitude smaller than the average fibril size observed at the end of the reaction. Fibrils generally contain thousands to tens of thousands of protein monomers, whereas newly nucleated fibrils likely contain only up to tens of monomers. Thus, for every nucleation event thousands of elongation events take place, and the elongation rate always affects the overall rate of aggregate formation.13,15,16 Fibrils formed in the presence of DMPS vesicles are co-aggregates of protein and lipids. Moreover, the availability of lipid limits the overall fibril yield. Given these observations, we can conclude that elongation involves addition of both protein and lipids to the growing fibril. Therefore, no such aggregate formation can happen without lipids, regardless of the role of lipids during nucleation.With these insights, we can now build a mechanistic model for lipidic fibril growth as follows: First, a lipid vesicle (concentration cS) binds to the surface of a fibril adjacent to the growing end. Vesicles were determined in ref. 28 to consist of V ≃ 6000 DMPS lipid molecules on average. Since the lipidic fibrils contain fewer lipids per protein than the vesicles, intramolecular rearrangement of the protein-coated SUV cannot supply sufficient protein on its own to permit fibril elongation. Instead, this requires the sequential addition of y > 0 free protein monomers on average to the growing end, where y is related to the lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein stoichiometries in the SUVs (n) and in the lipidic fibrils (χ). Once the y-th protein monomer has been added, a new vesicle must bind adjacent to the newly positioned growing end before any further elongation by protein addition may occur, see Fig. 2B. Since there is a large excess of protein and χ < n, this also implies detachment from vesicles is never a significant source of monomeric α-synuclein, and the kinetics of free protein, mf(t > 0), depends purely on its loss by assembly into lipidic fibrils. These considerations lead to the following rate laws for fibril mass (the concentration M(t) of α-synuclein that has been incorporated into fibrils), for monomeric α-synuclein, and for SUVs (derived in Methods):
protein stoichiometries in the SUVs (n) and in the lipidic fibrils (χ). Once the y-th protein monomer has been added, a new vesicle must bind adjacent to the newly positioned growing end before any further elongation by protein addition may occur, see Fig. 2B. Since there is a large excess of protein and χ < n, this also implies detachment from vesicles is never a significant source of monomeric α-synuclein, and the kinetics of free protein, mf(t > 0), depends purely on its loss by assembly into lipidic fibrils. These considerations lead to the following rate laws for fibril mass (the concentration M(t) of α-synuclein that has been incorporated into fibrils), for monomeric α-synuclein, and for SUVs (derived in Methods):
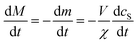 | (1a) |
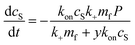 | (1b) |
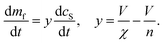 | (1c) |
Behaviour in lipid concentration limited regime confirms elongation co-aggregation mechanism
This model makes a very specific testable prediction: above a critical initial lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratio (rc) the vesicle binding rate (koncSP) exceeds the rate of addition of the corresponding number of protein monomers (k+mfP/y), i.e. the rate-limiting step changes. From the structure of eqn (1) it can be seen that the contribution of vesicle binding to the overall kinetics is then predicted to become negligible. Instead, protein monomer addition will become rate-limiting; consequently, the overall rate of fibril elongation will then depend primarily on protein concentration, not on lipid concentration. Conversely at lipid
protein ratio (rc) the vesicle binding rate (koncSP) exceeds the rate of addition of the corresponding number of protein monomers (k+mfP/y), i.e. the rate-limiting step changes. From the structure of eqn (1) it can be seen that the contribution of vesicle binding to the overall kinetics is then predicted to become negligible. Instead, protein monomer addition will become rate-limiting; consequently, the overall rate of fibril elongation will then depend primarily on protein concentration, not on lipid concentration. Conversely at lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratios below rc, i.e. when r(0) ≪ rc, vesicle binding becomes the rate-limiting step for overall fibril elongation since koncS ≪ k+mf/y. Elongation then depends predominantly on lipid not protein concentration. Crucially it is not the absolute concentrations of protein, m(0), and lipid, L(0), that governs the overall concentration-dependence of elongation, but their relative concentration, r(0). There is no readily conceivable explanation of such behaviour other than co-aggregation in elongation.
protein ratios below rc, i.e. when r(0) ≪ rc, vesicle binding becomes the rate-limiting step for overall fibril elongation since koncS ≪ k+mf/y. Elongation then depends predominantly on lipid not protein concentration. Crucially it is not the absolute concentrations of protein, m(0), and lipid, L(0), that governs the overall concentration-dependence of elongation, but their relative concentration, r(0). There is no readily conceivable explanation of such behaviour other than co-aggregation in elongation.
We test this prediction experimentally to confirm co-aggregation in elongation. We find that below a DMPS lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratio of 2, the rate of aggregation is reduced significantly when lipid concentration is reduced, see Fig. 3A, while at higher DMPS ratios the rate is constant, see Fig. 3B. This observation holds across different datasets and protein concentrations, as shown in Fig. 3C, where the half time of aggregation (the time at which half of the plateau aggregate mass is formed) is plotted against the lipid
protein ratio of 2, the rate of aggregation is reduced significantly when lipid concentration is reduced, see Fig. 3A, while at higher DMPS ratios the rate is constant, see Fig. 3B. This observation holds across different datasets and protein concentrations, as shown in Fig. 3C, where the half time of aggregation (the time at which half of the plateau aggregate mass is formed) is plotted against the lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratio. The data acquired at different protein concentrations are collapsed onto one plot by rescaling the half times to the half time at a lipid
protein ratio. The data acquired at different protein concentrations are collapsed onto one plot by rescaling the half times to the half time at a lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratio of 2 (this is the condition shared across datasets). At ratios below 2, the half time decreases with increasing lipid concentration, i.e. the reaction speeds up with increasing lipid, which we refer to as regime 1. At ratios above 2, in regime 2, the half time increases with increasing lipid, see Fig. 3D for a mechanistic illustration. Note that the reaction is not slower in absolute terms in regime 2. This increase in half time simply results from the fact that the plateau increases with increasing lipid but the reaction proceeds at the same absolute speed, meaning it takes longer to reach the half way point between baseline and the now higher plateau.
protein ratio of 2 (this is the condition shared across datasets). At ratios below 2, the half time decreases with increasing lipid concentration, i.e. the reaction speeds up with increasing lipid, which we refer to as regime 1. At ratios above 2, in regime 2, the half time increases with increasing lipid, see Fig. 3D for a mechanistic illustration. Note that the reaction is not slower in absolute terms in regime 2. This increase in half time simply results from the fact that the plateau increases with increasing lipid but the reaction proceeds at the same absolute speed, meaning it takes longer to reach the half way point between baseline and the now higher plateau.
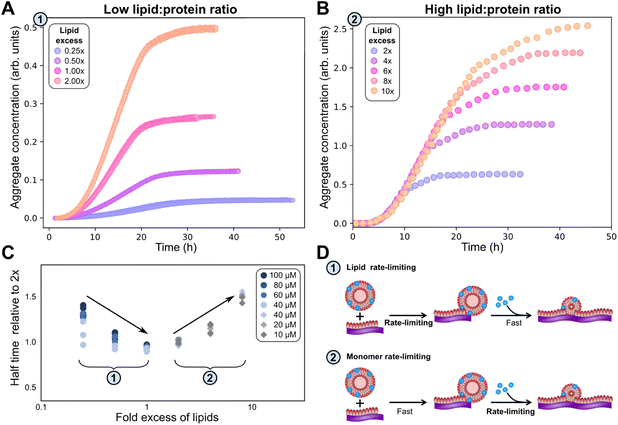 | ||
Fig. 3 Lipid concentration limits rate at low lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratios. (A) At lipid protein ratios. (A) At lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratios below 2, both the plateau height and the rate of aggregate formation depend on the lipid concentration (new data). (α-synuclein monomer concentration is 100 μM here.) (B) By contrast, at higher lipid protein ratios below 2, both the plateau height and the rate of aggregate formation depend on the lipid concentration (new data). (α-synuclein monomer concentration is 100 μM here.) (B) By contrast, at higher lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratios the rate is independent of the lipid concentration (data from Fig. 1 of Galvagnion et al.28). (C) The half time of aggregation (time to reach half of the plateau aggregate concentration) is plotted against lipid protein ratios the rate is independent of the lipid concentration (data from Fig. 1 of Galvagnion et al.28). (C) The half time of aggregation (time to reach half of the plateau aggregate concentration) is plotted against lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratio. A number of different protein concentrations (both new and previously published data) are collapsed onto the same curve by normalising the half times to that of the lipid protein ratio. A number of different protein concentrations (both new and previously published data) are collapsed onto the same curve by normalising the half times to that of the lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratio of 2. Two regions in the data are clear from the half time plots, in which either the lipid or the protein is rate limiting. (D) Schematic mechanisms in the two regimes. protein ratio of 2. Two regions in the data are clear from the half time plots, in which either the lipid or the protein is rate limiting. (D) Schematic mechanisms in the two regimes. | ||
These observations clearly confirm that lipid is involved at the elongation step, rather than being added after fibrils have already formed, consistent with the earlier conclusion based on plateau heights. However, they also allow us to rule out another possible mechanism, that of lipids attaching to growing fibrils as lipid monomers from solution, rather than as vesicles. While solubility of lipid monomers is low, some will be present in solution, in equilibrium with the more stable vesicle forms. Paralleling the behaviour in micelle formation, the initial lipid monomer concentration in solution is expected to be constant at lipid concentrations where vesicles are stable. As DMPS vesicles are stable at all lipid concentrations investigated here, we expect that the initial concentration of DMPS monomers in solution is independent of the total DMPS lipid concentration. The fact that we observe the reaction rate to be dependent on lipid concentration at the low lipid to monomer ratios is therefore in disagreement with a model where lipid addition proceeds by addition of lipid monomers from solution (for fits of these data to the complete model that is built in the next section, see Fig. 4 and S3†).
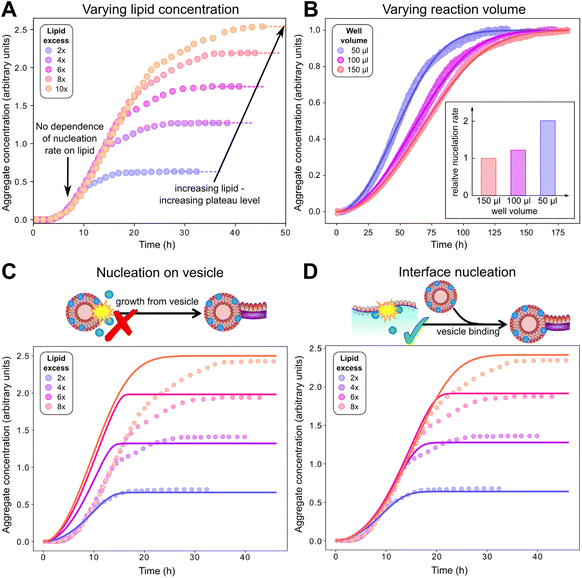 | ||
| Fig. 4 Behaviour at varying lipid concentration, and varying reaction volumes indicates that primary nucleation does not occur on vesicles in solution. (A): Careful inspection of kinetic data from Galvagnion et al.28 shows that aggregation rates of α-synuclein (50 μM) are independent of lipid concentration before the plateauing of aggregation curves. (B): Aggregation experiments (20 μM α-synuclein + 40 μM DMPS) with varying surface area to volume ratio show that primary nucleation rates increase with this ratio (fits to eqn (1)–(3)), indicating that primary nucleation is a heterogeneous process taking place on plate or air water interfaces. (C and D): Fits of the data in A to a model assuming nucleation on lipid vesicles in solution (C) or on interfaces (D). Parameters: kon/k+ = 8.3, χ = 10.5 (determined a priori, see text and Methods), nc = 0.6, n2 = 0 (fitted), with k+kn = 1.7, 2.1, 3.4 × 10−5 μM−nc h−1, k+k2 = 2.5 × 10−12 μM−1 h−1 (fitted, panel B) or k+kn = 5.6 × 10−4 μM−nc h−1, k+k2 = 1.5 × 10−3 μM−1 h−1 (fitted, panel D). In both B and D ncS = 0 to model surface catalysed nucleation, whereas in C ncS = 1 to model nucleation on vesicles in solution. As C is a misfit the other parameters are not meaningful. | ||
Primary nucleation of lipid–protein co-aggregates takes place on interfaces, not lipid vesicles in bulk solution
To complete our mechanistic model for protein–lipid co-aggregation we require a rate law for the concentration of growing fibril ends P(t). Primary nucleation (rate constant kn), the formation of aggregates directly from monomers, is always obligatory in unseeded reactions for the initiation of any aggregation. While this process can take place via homogeneous nucleation in bulk solution, the dominant pathway is in most cases via heterogeneous nucleation on surfaces present in the reaction vessel, such as air–water or reaction vessel interfaces. Furthermore, in our co-aggregation system, care needs to be taken to clearly define this process: a number of different protein only and protein–lipid clusters may be present in solution during nucleation. However, while these clusters may be on-path species of the nucleation process, the actual nucleus is defined as the first species that resembles the aggregates and can grow rapidly by further addition of monomers (lipid and protein). As we consider the formation of co-aggregates, this nucleus necessarily has to be a co-aggregate and thus nucleation has to involve both protein and lipids (although they may not both be involved in rate-limiting steps).An additional type of process producing fibril ends that is believed to be key in many pathological aggregating system is fibril self-replication.16 That is any processes by which new fibrils are formed from existing fibrils, such as fragmentation or secondary nucleation. Their presence gives rise to self-replication of aggregated structures and characteristic kinetic curves with a pronounced lag phase.16 In our system, the rate of self-replication can be written as k2mf(t)n2M(t)cS(t)n2S, where k2 is the rate constant and n2 and n2S the reaction orders with respect to free protein and vesicles and cS is the lipid vesicle concentration. This term can describe both fragmentation (n2 = n2S = 0) or secondary nucleation (n2, n2S ≥ 0). The importance of this contribution in our system, if present, is minor as explored in the ESI, Fig. S1.† These considerations lead to the following generic rate law for fibril ends (as usual, we neglect filament annealing and dissociation as processes with negligible rates on the aggregation timescale49):
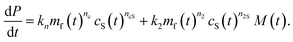 | (2) |
We can now investigate the role of vesicles in the formation of new lipidic fibrils. If primary nucleation (or secondary nucleation, if present) were a simple heterogeneous nucleation process on the surface of lipid vesicles in bulk solution, with or without the involvement of both lipid bound and free protein, the data would be expected to display a number of key features. Most importantly one would expect the rate of nucleation to depend on the concentration of lipid vesicles present. In this model the vesicle surface serves as a catalytic site for nucleation, so the dependence of the rate on vesicle concentration would be linear (ncS = 1) as an increase in the vesicle concentration simply corresponds to an increase in catalytic surface area. However, in reality, no such dependence of the rate on lipid concentration is observed, implying ncS = 0, as demonstrated in Fig. 4A, where the aggregation reaction at a constant initial α-synuclein concentration and varying DMPS lipid concentrations is monitored (note: while in these data the free protein concentration after SUV coverage has reached equilibrium also differs between curves, these differences are minor and the dominant factor is a change in lipid concentration; detailed calculation see Methods). In this experiment, the kinetic curves at different lipid concentrations overlap perfectly until the plateau phase is approached. Approaching the plateau phase, enough vesicles have been depleted for elongation to become lipid-limited, leading to deviation of the curves and to plateaus of different heights.
If primary nucleation does not occur on vesicles, the remaining possibilities are that it is a homogeneous process occurring in solution, or that it is a heterogeneous process occurring on the air–water interface or the plate surface, with the former being the more likely scenario. It is well-known that lipids in aqueous solution adsorb to the air–water interface, therefore nucleation at this interface would likely have a ready supply of lipids. To further experimentally evaluate the importance of interface effects, we monitored aggregation reactions with the same starting protein and lipid concentrations, but with different solution volumes of 50, 100 and 150 μl, to alter the surface to volume ratio (Fig. 4B). If nucleation occurs on an interface, then the number of nucleation events per unit time is proportional to its area. So, the resultant rate of increase in the concentration of new nuclei (i.e. nucleation events per unit volume per unit time) is proportional to the surface area to volume ratio. We observed a significant increase in the rate of aggregation as the volume decreased (and thus the surface area to volume ratio increased), consistent with primary nucleation of lipid–protein co-aggregates being a heterogeneous, surface catalysed process. While other effects of the volume change, such as altered evaporation, cannot be ruled out, this behaviour is exactly as expected for a surface catalysed reaction and thus in agreement with the remainder of the data. It is also in line with the general observation that heterogeneous, rather than homogeneous, primary nucleation is the more common process in most aggregating systems.23,50,51
To confirm whether a surface catalysed nucleation mechanism can describe the full kinetics, we have globally fitted13,15 the mechanistic model comprised of eqn (1)–(3) to published data (Fig. 4C and D) as well as to two more extensive new independent kinetic experiments, each featuring multiple initial protein and lipid concentrations, see Fig. 5 (see Fig. S2† for fits of aggregation kinetics in the presence of preformed fibrils). We tested both nucleation on vesicles in solution (ncS = 1) and nucleation on interfaces (ncS = 0) but allowed the other parameters kn, k2, kon/k+, nc and n2 to vary freely. We always find that n2 = n2S = 0, consistent with any possible secondary process being either saturated secondary nucleation or fragmentation. The latter seems more likely given the known propensity for these fibrils to fragment.28 Importantly, we find that a reasonable fit can be obtained only using ncS = 0, implying nucleation on interfaces, with nucleation on vesicle surfaces (ncS = 1) being clearly inconsistent with the data. We provide further confirmation by testing these two models against additional published data in Fig. S4;† again, modelling nucleation as occurring on interfaces yields better fits than modelling nucleation as occurring on vesicles in bulk solution. As the two models have the same number of fitting parameters, they differ only in the value chosen for ncS. The improved performance of one over the other therefore cannot be a result of a different number of degrees of freedom.
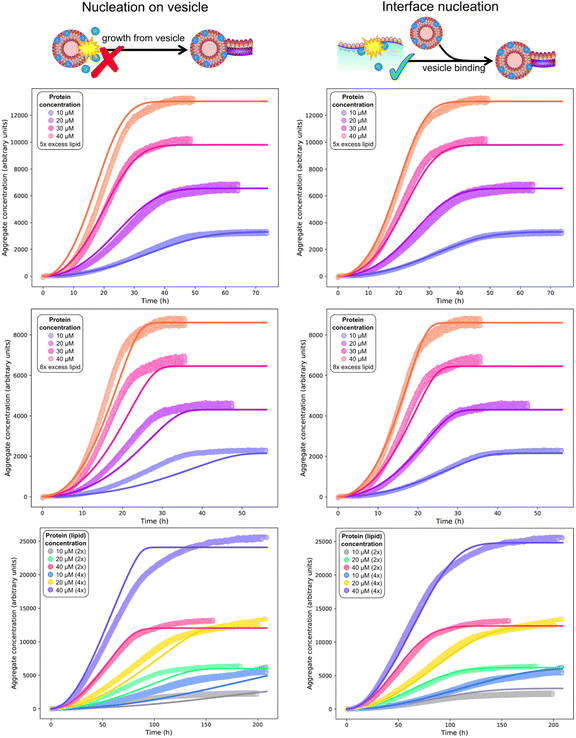 | ||
| Fig. 5 Global (mis)fits of kinetic models across protein and lipid concentrations. Top and middle rows: single experiment featuring 10 (blue), 20 (purple), 30 (pink), 40 (orange) μM protein, and 5× (top row) or 8× (middle row) DMPS concentrations. The data at 5× and 8× DMPS is fitted globally, but shown in separate panels for clarity. Bottom row: separate experiment featuring 10, 20, 40 μM protein and 2× or 4× lipid concentration. Global fits of a model assuming nucleation on vesicles in solution (left column) or on an interface (right column), using eqn (1)–(3) with ncS = 1 or ncS = 0, respectively. The identity of the fitted parameters is the same in both cases. As evident across datasets (see also fits to the published data in Fig. 4C and D), a kinetic model featuring primary nucleation on vesicles in solution cannot fit the data, whereas a model featuring primary nucleation on reaction vessel interfaces, with the same number of fitting parameters, can fit the data well throughout. Fitted parameter values (right column): k+kn = 3.6 × 10−4 μM−nc h−1, k+k2 = 1.5 × 10−3 μM−1 h−1, nc = 0.6, n2 = 0 (top 2 rows), k+kn = 1.2 × 10−5 μM−nc h−1, k+k2 = 4.4 × 10−13 μM−1 h−1, nc = 0.79, n2 = 0 (bottom row), χ = 10.5, kon/k+ = 8.3 (determined a priori, see text). In the left column ncS = 1 to model nucleation on vesicles in solution whereas in the right column ncS = 0 to model surface catalysed nucleation. As the left column are a misfit the other parameters are not meaningful and thus not given. | ||
For the vesicle-independent nucleation model (ncS = 0), we are able to fit all datasets with the same stoichiometry χ = 10.5 determined above, and the same kon/k+ value (= 8.3). Given the experiments were performed by different people in different years and using different equipment and reagent preparations, there is no reason to expect that rate constants will remain exactly the same, so this is a remarkable level of consistency. We allowed the nucleation rate constants kn and k2 to differ from dataset to dataset. We found that kn values are broadly in line with those determined from less complete kinetic models from earlier studies.
We also found that the rate of secondary processes is never much larger than that of primary nucleation. Consequently we tested a version of the model excluding secondary processes against the data (see Fig. S1†). The decrease in fit quality was relatively minor given the decreased complexity of the model. This tells us that in this lipid-induced assay, secondary nucleation or fragmentation, if present at all, only has a relatively minor effect on the overall aggregation kinetics. Given the small effect on the kinetics, we cannot rule out that other extensions of the primary nucleation only model lead to a equally good fits as the addition of self-replication. This finding is in line with previous work showing that a different set of conditions was generally required to enable significant secondary nucleation.20,22,24
Consistency with earlier studies and implications for other work
Based on the deeper mechanistic understanding of the co-aggregation mechanism gained in the above analysis, we now re-examine some of the related previous work by us and others. A common interpretation of the obligate role of DMPS lipid vesicles in α-synuclein aggregation at pH 6.5 is that they trigger primary nucleation.28 Since without primary nucleation, no aggregation is observed, this is a seemingly obvious conclusion. Indeed, by definition lipids must play a role in the formation of new lipidic fibril nuclei. However, care needs to be taken when interpreting this: lipidic fibrils are different species to pure protein fibrils. DMPS therefore cannot be regarded as simply accelerating primary nucleation of pure protein fibrils; instead, it facilitates an entirely different aggregation reaction, with a different product and a different primary nucleation step, as we demonstrate in this work. In other words, the presence of DMPS allows the formation of lipid–protein co-aggregates, which have a low barrier to nucleation, whereas pure protein fibrils have a high barrier to nucleation.Our finding that primary nucleation does not occur predominantly on DMPS lipid vesicles in bulk solution may at first seem at odds with previous findings of lipid identity affecting nucleation. However, we know that vesicles are involved at the elongation step, which is sufficient to explain their effect on the overall aggregation rate. Moreover, lipid involvement during nucleation, without the direct involvement of vesicles in bulk solution is mechanistically straightforward to account for: Lipid-containing aqueous solutions usually form a lipid monolayer at the air water interface, known as a Langmuir film, with the head group facing the water and the acyl chains the air (illustrated in Fig. 4D). A similar monolayer may also form on the plate surface. Assuming such a layer is also present in our experiments, nucleation at these surfaces would thus have a ready supply of lipid. The altered structure of the lipid layer compared to that in the vesicles, as well as the potential for proteins to arrange at the air–water interface, could explain the increased rate of nucleation at these interfaces. Such a scenario would be consistent with both the lack of a lipid concentration dependence and the sensitivity to the surface to volume ratio, if such monolayers fully cover the interface on which heterogeneous nucleation takes place. While Langmuir layers are a well known phenomenon, it cannot be ruled out that rather than a lipid monolayer, intact vesicles bind to the interfaces in our experiments: provided this binding is not rate-limiting this would also be consistent with all available data.
It should be emphasized that our finding of a surface dependent nucleation process simply means that under these experimental conditions, nucleation on the surface dominates over other nucleation processes. Under conditions where no such catalytic surface is present, for example in micro-droplets, other, slower mechanisms such as bulk vesicle-induced primary nucleation may become relevant.
Partial mechanistic models have previously been developed (by several of the authors of this work), that have not included lipid addition in the elongation step, and have treated primary nucleation as vesicle-dependent.6,7,28 These have been broadly successful at fitting data and have allowed quantification of effective rates, but are only valid across relatively narrow ranges of protein and lipid concentrations and only allow fitting of the initial part of the aggregation curves. In Perni et al. and Brown et al.,6,7 only one DMPS lipid concentration was used, thus the fact that the model neglected the lipid scaling of the kinetics was irrelevant. Using only one lipid concentration also allowed the protein concentration scaling of the kinetics to be described by a traditional elongation-saturation step in the model employed. Although data with multiple lipid concentrations were successfully partially fitted to such a model in Fig. 6b of Galvagnion et al.,28 these fitted curves had relatively low r(0) values between 0.4 and 4. Our model predicts full loss of lipid dependence only at r(0) ≳ 4. Since nucleation and elongation rates affect the kinetics as a product, vesicle-dependent elongation when r(0) is sufficiently far below 4 is indistinguishable from vesicle-dependent nucleation. A closer examination of these older fits confirms that the lipid scaling was indeed captured more accurately at the lower r(0) values. Data with r(0) ≥ 4 were collected in this study, but could not be fitted, presumably in part due to the impossibility of reproducing the lipid scaling of the kinetics with the partial mechanistic models used. Our model is now complete enough to successfully globally fit all of these data as well (Fig. 4). In summary, our new model, which explicitly includes co-aggregation, is able to match all aspects of the data (protein dependence, lipid dependence, plateau heights) and can provide detailed rates of individual processes, rather than effective rates from simpler previous models, giving insights into the rate limiting steps during nucleation and elongation.
In Perni et al. and Brown et al.,6,7 inhibitors were also investigated using this in vitro assay in conjunction with these partial mechanistic models. The more complete mechanistic understanding we have developed here should not affect the key conclusions of these papers regarding inhibitors, namely that molecules capable of binding to vesicles and displacing α-synuclein should inhibit amyloid formation. This was rationalized as being due to these molecules reducing the rate of primary nucleation. This remains true in light of our more complete mechanistic understanding, but another cause can be identified: the fibril yield should be reduced, and given enough inhibitor an inhibitory effect on elongation should also appear.
Going forward, we envision that application of our model will allow more detailed investigation of which processes are affected by alterations of the protein, such as mutations or acetylation37,38,52 or the determination of inhibitor mechanisms of action.7
Implications for the design of inhibitors of aggregation
Having established the detailed mechanism of formation of lipidic fibrils, the key question is how this process can be inhibited most effectively, and which mode of action is most promising in the context of developing a drug against Parkinson's disease.10,13,53 Compounds targetting the initial formation of aggregates can be effective in vitro, for example by blocking the interfaces on which nucleation takes place, but are unlikely to translate to the in vivo situation where such interfaces may not be present in the same form.12 Much more promising are compounds that inhibit aggregation by interacting with those processes expected to be relevant in vivo, in this case the incorporation of lipids or proteins into a growing fibril.More generally, targetting fibrils is the more promising strategy for designing aggregation inhibitors for a number of reasons. Binding to fibril surfaces can inhibit fibril proliferation by preventing the formation of new fibrils via secondary nucleation, but it can also stop the production of toxic oligomeric species, directly and swiftly.11,54 Furthermore, it may constitute the safer approach in terms of avoiding inhibitor mechanism-based (i.e. “on target”) toxicity. The aggregated structures are products of a disease process and appear to be greatly enriched in disease.2,55 Thus, binding to them is less likely to have deleterious effects when compared with binding to other targets that are known to be present and fulfill potentially important functions in healthy individuals, such as lipids or monomeric protein. This strategy is analogous to directly and specifically targeting the invading pathogens in an infectious disease.
Our models show that, in the context of DMPS vesicle-induced aggregation of α-synuclein, targetting the incorporation of either protein or lipid into the growing fibril are promising strategies for inhibiting aggregation in vitro. The above considerations highlight the fibril as the most suitable target for small molecules to inhibit this process and maximise chances of translatability. By contrast, given the negligible effect on the kinetics in this particular in vitro assay of any secondary processes that may be present, their inhibition will have little effect on the aggregation speed, and instead different conditions should be used to investigate this process.20,22,24
Conclusions
At neutral pH, in the absence of lipids, α-synuclein is kinetically stable, biased against aggregation for many hours due to the slow formation of pure protein aggregates. The observation that the introduction of lipid vesicles triggers formation of aggregates has led to the assumption that vesicles simply promote primary nucleation. However, our findings in this work reveal that an explicit description of protein–lipid co-aggregation is required to properly interpret the kinetic effect of DMPS vesicles on α-synuclein aggregation. In particular, lipid participation in the elongation step, rather than just during nucleation, is crucial to explain the observed data. Quantitatively accounting for this formation of lipid–protein co-aggregates is sufficient to describe the observed kinetics, including the dependence of the aggregation rate on both protein and lipid concentrations. Although primary nucleation of these lipidic fibrils must by definition involve lipids, it does not predominantly take place on the surface of DMPS lipid vesicles, and we instead find that in this in vitro system, primary nucleation occurs on the air–water or plate interfaces, although lipids may also be present at these interfaces. The finding that primary nucleation takes place on these assay-dependent surfaces is an important point to consider when translating in vitro findings between assays and drawing conclusions for the behaviour in living systems.While the findings in this work are based on the behaviour of a specific lipid, DMPS, we expect that several aspects of it will translate to other lipids. In particular, protein–lipid co-aggregates are formed as the predominant species, with a range of other lipids.30,46,47,56 In those systems, just as in the system analysed here, both protein and lipids are likely involved in the elongation step, therefore the minimal mechanism of co-elongation we propose here is likely to also be relevant in those systems, although the values of the rate constants and identity of rate-limiting steps may differ. Indeed, previous work has shown that the identity of the lipid strongly affects the kinetics of aggregation, indicating its involvement in the rate limiting steps of aggregate formation and thus requiring a co-aggregation model such as the one we develop here.56 Regarding the primary nucleation step, while our model is general and can also describe bulk nucleation, the air water interface or plate interfaces are found to be sites for primary nucleation across different proteins and experimental setups,23,57 so our finding of interface-catalysed nucleation may be equally general.
Beyond improving our mechanistic understanding, our findings highlight several key implications for the use of lipid-induced aggregation in the investigation of synucleinopathies and potential therapeutics: we show how lipidic fibrils differ from pure protein fibrils not only in their structure but also in their mechanism of formation. As both types of structure may be of relevance in disease, care needs to be taken when investigating mechanistic effects in vitro: potential therapeutic molecules should be capable of delaying fibril formation under both pure protein and lipid-induced conditions, to maximise their efficacy potential. The most robust way to achieve such dual pharmacology is to target the species that is key in both processes, the fibril surface: this is where oligomeric species are formed in pure protein fibrils and where lipid vesicles interact with growing fibrils in the lipidic system. Moreover, we find that the DMPS vesicles provide lipid for the growth of lipidic fibrils, but they do not serve as nucleation sites, which instead takes place at air–water or plate interfaces, likely involving both protein and lipid adsorbed at these interfaces. Thus, care needs to be taken when interpreting the readouts of this assay to ensure that the focus is on processes that retain in vivo translatability, and not on processes that involve air–water or plate interfaces.
In conclusion, the model we present here enables the quantitative analysis of DMPS α-synuclein co-aggregation, across protein and lipid concentrations. It is the first model of this kind and can serve as the basis for developing and expanding similar models in other systems where lipid–protein co-aggregation occurs. This mechanistic understanding of α-synuclein lipid co-aggregation will allow more targetted design of inhibitors of aggregation, that efficiently prevent the formation of both lipidic and pure protein fibrils and thus attack the formation of pathological aggregates at multiple points in the aggregation cascade.
Methods
Aggregation assay and protein purification
Wild-type α-syn was expressed and purified as previously described.20,28,58 Briefly, after the final size exclusion chromatography run (20 mM phosphate buffer, pH 6.5), the protein was lyophilized in 1 mL aliquots and stored at −80 °C. Aliquots were resuspended in MQW and used directly. The lipids (Avanti Polar Lipids, Inc.) were dissolved in 20 mM phosphate buffer, pH 6.5 and stirred at 45 °C for 2 h. The solution was then frozen and thawed five times using dry ice and a water bath at 45 °C. The preparation of SUVs was done using extrusion through membranes with a 100 nm pore diameter at 45 °C. The lipid-induced aggregation assay was monitored in low-binding, clear-bottomed half-area 96-well plates (Corning) and ran at 30 °C and pH 6.5. Lipid and protein concentrations vary and are specified at the relevant places in the text.Calculating free protein concentration and vesicle coverage
The stoichiometry n of lipid to α-synuclein within DMPS vesicles, and corresponding dissociation constant KD, were previously determined to be n = 28 and KD = 0.38 μM under the conditions used here.28 We use these values throughout to calculate the effective initial monomeric α-synuclein concentration mf(0) from the total non-fibrillar α-synuclein concentration m(t) at t = 0, by adapting eqn (6) from ref. 28: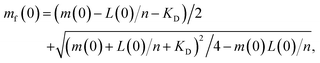 | (3) |
| mf(0) ≃ m(0)(1 − r(0)/n) | (4) |
Calculating lipid stoichiometry in fibrils at equilibrium
The preferred stoichiometry of α-synuclein and DMPS in lipidic fibrils can be inferred from measurements of fibril formation at a fixed m(0) but varying r(0). As shown previously,28 the yield of lipidic fibrils, as reported by the height of the plateau of the kinetic curves, reaches a maximum at r(0) ≃ 15 (see also Fig. S5†), implying that the optimal stoichiometry of lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein in lipidic fibrils is approximately 15. This can be rationalized as follows. If the optimal lipid
protein in lipidic fibrils is approximately 15. This can be rationalized as follows. If the optimal lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein stoichiometry in the fibrils is χ*, then when r(0) < χ*, as fibril formation progresses the ratio of lipid
protein stoichiometry in the fibrils is χ*, then when r(0) < χ*, as fibril formation progresses the ratio of lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein outside the fibrils r(t) decreases as the lipid is used up faster in relative terms. Thus the yield is ultimately lipid-limited. The inverse argument applies when r(0) > χ*, where r(t) increases as fibril formation progresses, and the yield is limited by protein concentration. Thus, the ratio of initial protein and lipid concentrations at the maximum yield gives the optimal stoichiometry in the lipidic fibrils as χ* = r0 ≃ 15. Given n = 28 this implies that if the majority of lipids ultimately end up in fibrils the concentration of protein in these fibrils is approximately double that initially bound to vesicles, consistent with findings in ref. 28. Interestingly, the yield deviates from the expected approximate linearity in r(0) when r(0) ≤ χ* as r(0) increases, particularly once r(0) > 8. For instance, reducing r(0) from 15 to 10 reduces fibril yield by far less than a third, despite the yield for r(0) ≤ χ* ≃ 15 being lipid-limited (Fig. S5†). This implies that lipidic fibrils with lower, less thermodynamically favourable lipid
protein outside the fibrils r(t) decreases as the lipid is used up faster in relative terms. Thus the yield is ultimately lipid-limited. The inverse argument applies when r(0) > χ*, where r(t) increases as fibril formation progresses, and the yield is limited by protein concentration. Thus, the ratio of initial protein and lipid concentrations at the maximum yield gives the optimal stoichiometry in the lipidic fibrils as χ* = r0 ≃ 15. Given n = 28 this implies that if the majority of lipids ultimately end up in fibrils the concentration of protein in these fibrils is approximately double that initially bound to vesicles, consistent with findings in ref. 28. Interestingly, the yield deviates from the expected approximate linearity in r(0) when r(0) ≤ χ* as r(0) increases, particularly once r(0) > 8. For instance, reducing r(0) from 15 to 10 reduces fibril yield by far less than a third, despite the yield for r(0) ≤ χ* ≃ 15 being lipid-limited (Fig. S5†). This implies that lipidic fibrils with lower, less thermodynamically favourable lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein stoichiometry will form when there is a shortage of lipid, with the free energy penalty being outweighed by the resultant higher fibril yield and lower concentration of energetically unfavourable monomeric protein at equilibrium. However, once r(0) ≤ 8, approximate linearity in the yield is restored (as also demonstrated in Fig. 2A for several different experiments, at a wide range of protein concentrations), implying that we have approached a minimum favourable stoichiometry χ. Its value can be estimated by the value r(0) at which this linearity intercepts the maximum yield at r(0) = χ*, giving χ ≃ 10.5 (Fig. S5†). We will use this stoichiometry throughout the rest of the paper.
protein stoichiometry will form when there is a shortage of lipid, with the free energy penalty being outweighed by the resultant higher fibril yield and lower concentration of energetically unfavourable monomeric protein at equilibrium. However, once r(0) ≤ 8, approximate linearity in the yield is restored (as also demonstrated in Fig. 2A for several different experiments, at a wide range of protein concentrations), implying that we have approached a minimum favourable stoichiometry χ. Its value can be estimated by the value r(0) at which this linearity intercepts the maximum yield at r(0) = χ*, giving χ ≃ 10.5 (Fig. S5†). We will use this stoichiometry throughout the rest of the paper.
We also note that excluding the r(0) = 8 yield from Fig. 4d in ref. 28, which is an outlier as the reaction has not completed fully, the slope implies the yield of fibrils is approximately 2.4 times the initial bound protein concentration. If we assume full conversion of vesicles into fibrils, the yield should equal n/χ × L(0)/n ≃ 2.7L(0)/n, which is very close to this, both giving orthogonal confirmation of our stoichiometry estimates and confirming that the majority of lipid ends up in fibrils at these initial concentrations.
Derivation of rate equation for fibril mass
Let cS(t) be the concentration of protein monomer-coated SUVs, and let y be the number of free protein monomers (concentration mf(t)) that add to the growing fibril by elongation on average each time an SUV binds to the fibril. y > 0 because the lipid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein ratio is lower in fibrils than in SUVs. Let us define the fibril mass concentration as M(t) = m(0) − m(t), i.e. the concentration of monomeric protein subunits aggregated into fibrils. We can then express the aggregation reaction yield as M(∞) = m(0) − m(∞).
protein ratio is lower in fibrils than in SUVs. Let us define the fibril mass concentration as M(t) = m(0) − m(t), i.e. the concentration of monomeric protein subunits aggregated into fibrils. We can then express the aggregation reaction yield as M(∞) = m(0) − m(∞).
Since we know elongation involves lipid, and this is essentially entirely in the form of protein-coated SUVs, and since y > 0, we must model both protein-addition and SUV-binding steps. Writing Pi as the concentration of fibril ends formed by i successive additions of free protein monomer subunits (not counting intramolecular redistribution of protein from the shrinking SUV), we now take a mean field approach to modelling. In this model, more than y free protein monomers cannot bind to fibril ends without addition of a new SUV, and SUVs can only bind to fibril ends after y free protein monomer addition events, or to the ends of freshly nucleated fibrils (concentration P*). We also assume that protein monomers bind with the same rate to all fibril ends with SUVs bound closer than y subunits away. Thus,
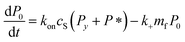 | (5) |
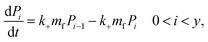 | (6) |
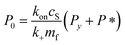 | (7) |
| Pi = Pi−1 0 < i < y | (8) |
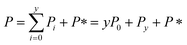 | (9) |
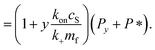 | (10) |
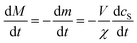 | (11) |
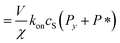 | (12) |
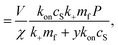 | (13) |
It remains only to determine the number of free protein monomers y added to the growing fibril per SUV. The total number of protein monomers added per SUV is y + V/n. Per lipid this becomes y/V + 1/n protein monomers, which we can equate to the inverse of the fibril stoichiometry 1/χ. Rearranging gives us:
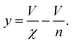 | (14) |
It should be fairly clear from the form of this equation that either protein or lipid addition become rate-limiting depending on the relative values of mf and cS. The cross-over between these regimes occurs at k+mf = ykoncS = ykonL/V. We can rearrange this into the following constraint on rate constants:
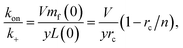 | (15) |
We also have:
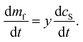 | (16) |
Note we can put the above rate equation into more convenient units L instead of cS by noting L = VcS:
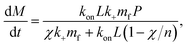 | (17) |
The derivation of the rate equation for the nucleation terms, eqn (2), is much more straightforward. As has been done previously, we coarse-grain both primary nucleation and the secondary processes into a single step.59 We allow for explicit dependence on the free solution concentrations of monomer, mf(t), and vesicles, cS(t), with reaction orders ncS and n2S, respectively. This is a simple and versatile representation that will be able to capture a range of behaviours. When nucleation occurs on interfaces, and does not involve vesicles in solution, we use ncS = 0. This description is accurate when the surface on which nucleation takes place is fully saturated, so the dependence on the concentration of species in solution disappears (at the high lipid and protein concentrations in this study we are likely always in this regime). The constant parameters, such as the concentration of catalytic surface, are subsumed into the rate constant. In situations where they are changed, for example when the volume is changed, thus changing the concentration of catalytic surface, this is reflected in a change of the rate constant, as shown in Fig. 4.
Kinetic analysis
Kinetic analysis is performed by numerically integrating the differential rate equations given above and using a least squares algorithm to fit the data. The data processing follows closely the procedure detailed in Meisl et al.13Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
Conceptualization: AJD, TCTM, TPJK, SL, JH, GM. Data curation: XT, SRB, JL, RIH, DC, XY. Formal Analysis: AJD. Methodology: AJD, XT, SL, GM. Project administration: JT, JH, GM. Resources: NH, KY. Software: AJD, GM. Supervision: XY, SCB, SL, JH, GM. Visualization: AJD, GM. Writing – original draft: AJD, GM. Writing – review and editing: AJD, SRB, RIH, AS, TCTM, SL, SCB, JT, JH, GM.Conflicts of interest
All authors except AS were, at the time of their contribution, employees, founders or consultants of WaveBreak Therapeutics.Acknowledgements
We thank Patrick Connelly for discussions about the thermodynamics and kinetics of aggregate formation and Celine Galvagnion and Alexander Buell for their insightful feedback and their help in refining the presentation of our results. We would like to acknowledge funding from the European Research Council through the ERC grant DiProPhys (agreement ID 101001615) and the Swedish Research Council, grant number VR 2015-00143.References
- M. G. Spillantini, M. L. Schmidt, V. M. Lee, J. Q. Trojanowski, R. Jakes and M. Goedert, Nature, 1997, 388, 839–840 CrossRef CAS PubMed.
- F. Chiti and C. M. Dobson, Annu. Rev. Biochem., 2006, 75, 333–366 CrossRef CAS PubMed.
- H. McCann, C. H. Stevens, H. Cartwright and G. M. Halliday, Park. Relat. Disord., 2014, 20, S62–S67 CrossRef PubMed.
- B. Dehay, M. Bourdenx, P. Gorry, S. Przedborski, M. Vila, S. Hunot, A. Singleton, C. W. Olanow, K. M. Merchant, E. Bezard, G. A. Petsko and W. G. Meissner, Lancet Neurol., 2015, 14, 855–866 CrossRef CAS PubMed.
- H. G. Jasutkar, S. E. Oh and M. M. Mouradian, Pharmacol. Rev., 2022, 74, 207–237 CrossRef CAS PubMed.
- J. W. P. Brown, A. K. Buell, T. C. T. Michaels, G. Meisl, J. Carozza, P. Flagmeier, M. Vendruscolo, T. P. J. Knowles, C. M. Dobson and C. Galvagnion, Sci. Rep., 2016, 6, 36010 CrossRef CAS PubMed.
- M. Perni, C. Galvagnion, A. Maltsev, G. Meisl, M. B. D. Müller, P. K. Challa, J. B. Kirkegaard, P. Flagmeier, S. I. A. Cohen, R. Cascella, S. W. Chen, R. Limbocker, P. Sormanni, G. T. Heller, F. A. Aprile, N. Cremades, C. Cecchi, F. Chiti, E. A. A. Nollen, T. P. J. Knowles, M. Vendruscolo, A. Bax, M. Zasloff and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E1009–E1017 CrossRef CAS PubMed.
- T. P. J. Knowles, C. A. Waudby, G. L. Devlin, S. I. A. Cohen, A. Aguzzi, M. Vendruscolo, E. M. Terentjev, M. E. Welland and C. M. Dobson, Science, 2009, 326, 1533–1537 CrossRef CAS PubMed.
- S. I. Cohen, M. Vendruscolo, C. M. Dobson and T. P. Knowles, J. Mol. Biol., 2012, 421, 160–171 CrossRef CAS PubMed.
- P. Arosio, M. Vendruscolo, C. M. Dobson and T. P. Knowles, Trends Pharmacol. Sci., 2014, 35, 127–135 CrossRef CAS PubMed.
- S. I. A. Cohen, P. Arosio, J. Presto, F. R. Kurudenkandy, H. Biverstal, L. Dolfe, C. Dunning, X. Yang, B. Frohm, M. Vendruscolo, J. Johansson, C. M. Dobson, A. Fisahn, T. P. J. Knowles and S. Linse, Nat. Struct. Mol. Biol., 2015, 22, 207–213 CrossRef CAS PubMed.
- G. Meisl, T. P. J. Knowles and D. Klenerman, Front. Neurosci., 2022, 16 DOI:10.3389/fnins.2022.909861.
- G. Meisl, J. B. Kirkegaard, P. Arosio, T. T. C. Michaels, M. Vendruscolo, C. M. Dobson, S. Linse and T. P. J. Knowles, Nat. Protoc., 2016, 11, 252–272 CrossRef CAS PubMed.
- J. W. P. Brown, G. Meisl, T. P. J. Knowles, A. K. Buell, C. M. Dobson and C. Galvagnion, Chem. Commun., 2018, 54, 7854–7857 RSC.
- S. I. A. Cohen, M. Vendruscolo, M. E. Welland, C. M. Dobson, E. M. Terentjev and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 065105 CrossRef PubMed.
- G. Meisl, C. K. Xu, J. D. Taylor, T. C. T. Michaels, A. Levin, D. Otzen, D. Klenerman, S. Matthews, S. Linse, M. Andreasen and T. P. J. Knowles, Sci. Adv., 2022, 8, eabn6831 CrossRef CAS PubMed.
- S. I. A. Cohen, S. Linse, L. M. Luheshi, E. Hellstrand, D. A. White, L. Rajah, D. E. Otzen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9758–9763 CrossRef CAS PubMed.
- G. Meisl, X. Yang, E. Hellstrand, B. Frohm, J. B. Kirkegaard, S. I. A. Cohen, C. M. Dobson, S. Linse and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9384–9389 CrossRef CAS PubMed.
- X. Yang, G. Meisl, B. Frohm, E. Thulin, T. P. J. Knowles and S. Linse, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E5849–E5858 CrossRef CAS PubMed.
- A. K. Buell, C. Galvagnion, R. Gaspar, E. Sparr, M. Vendruscolo, T. P. J. Knowles, S. Linse and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7671–7676 CrossRef CAS PubMed.
- R. Gaspar, G. Meisl, A. K. Buell, L. Young, C. F. Kaminski, T. P. J. Knowles, E. Sparr and S. Linse, Q. Rev. Biophys., 2017, 50, E6 CrossRef PubMed.
- C. K. Xu, G. Meisl, E. Andrzejewska, G. Krainer, A. J. Dear, M. C. Cruz, S. Turi, R. Jacquat, W. E. Arter, M. Vendruscolo, S. Linse and T. P. Knowles, bioRxiv, 2023, preprint, DOI:10.1101/2023.05.28.542651.
- F. Grigolato, C. Colombo, R. Ferrari, L. Rezabkova and P. Arosio, ACS Nano, 2017, 11, 11358–11367 CrossRef CAS PubMed.
- R. I. Horne, M. A. I. Metrick, W. Man, D. J. Rinauro, Z. F. Brotzakis, S. Chia, G. Meisl and M. Vendruscolo, ACS Chem. Neurosci., 2023, 14, 3125–3131 CrossRef CAS PubMed.
- A. K. Buell, P. Hung, X. Salvatella, M. E. Welland, C. M. Dobson and T. P. Knowles, Biophys. J., 2013, 104, 1116–1126 CrossRef CAS PubMed.
- G. Meisl, X. Yang, C. M. Dobson, S. Linse and T. P. J. Knowles, Chem. Sci., 2017, 8, 4352–4362 RSC.
- M. Grey, S. Linse, H. Nilsson, P. Brundin and E. Sparr, J. Parkinson's Dis., 2011, 1, 359–371 CAS.
- C. Galvagnion, A. K. Buell, G. Meisl, T. C. T. Michaels, M. Vendruscolo, T. P. J. Knowles and C. M. Dobson, Nat. Chem. Biol., 2015, 11, 229–234 CrossRef CAS PubMed.
- C. Galvagnion, J. Parkinson's Dis., 2017, 7, 433–450 CAS.
- C. Galvagnion, D. Topgaard, K. Makasewicz, A. K. Buell, S. Linse, E. Sparr and C. M. Dobson, J. Phys. Chem. Lett., 2019, 10, 7872–7877 CrossRef CAS PubMed.
- A. A. Spector and M. A. Yorek, J. Lipid Res., 1985, 26, 1015–1035 CrossRef CAS.
- G. Fusco, A. De Simone, T. Gopinath, V. Vostrikov, M. Vendruscolo, C. M. Dobson and G. Veglia, Nat. Commun., 2014, 5, 3827 CrossRef CAS PubMed.
- A. Iyer and M. M. Claessens, Biochim. Biophys. Acta, Proteins Proteomics, 2019, 1867, 468–482 CrossRef CAS PubMed.
- M. Kiechle, V. Grozdanov and K. M. Danzer, Front. Cell Dev. Biol., 2020, 8 DOI:10.3389/fcell.2020.562241.
- K. Makasewicz, S. Wennmalm, B. Stenqvist, M. Fornasier, A. Andersson, P. Jönsson, S. Linse and E. Sparr, ACS Chem. Neurosci., 2021, 12, 2099–2109 CrossRef CAS PubMed.
- K. Makasewicz, S. Wennmalm, S. Linse and E. Sparr, QRB Discovery, 2022, 3, e10 CrossRef PubMed.
- P. Flagmeier, G. Meisl, M. Vendruscolo, T. P. J. Knowles, C. M. Dobson, A. K. Buell and C. Galvagnion, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10328–10333 CrossRef CAS PubMed.
- R. Bell, M. Castellana-Cruz, A. Nene, R. J. Thrush, C. K. Xu, J. R. Kumita and M. Vendruscolo, J. Mol. Biol., 2023, 435, 167825 CrossRef CAS PubMed.
- G. Šneideriene, M. A. Czekalska, C. K. Xu, A. Jayaram, G. Krainer, W. E. Arter, Q. Peter, M. Castellana-Cruz, K. L. Saar, A. Levin, T. Mueller, S. Fiedler, S. R. A. Devenish, H. Fiegler, J. R. Kumita and T. P. J. Knowles, bioRxiv, 2023, preprint, DOI:10.1101/2023.03.21.533646.
- C. Galvagnion, A. Barclay, K. Makasewicz, F. R. Marlet, M. Moulin, J. Devos, S. Linse, A. Martel, L. Porcar, E. Sparr, M. C. Pedersen, F. Roosen-Runge, L. Arleth and A. K. Buell, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-6hsh2.
- K. Makasewicz, S. Linse and E. Sparr, JACS Au, 2024 DOI:10.1021/jacsau.3c00579.
- C. M. Pfefferkorn, Z. Jiang and J. C. Lee, Biochim. Biophys. Acta, Proteins Proteomics, 2012, 1818, 162–171 CAS.
- C. Pfefferkorn, F. Heinrich, A. Sodt, A. Maltsev, R. Pastor and J. Lee, Biophys. J., 2012, 102, 613–621 CrossRef CAS PubMed.
- E. Hellstrand, M. Grey, M.-L. Ainalem, J. Ankner, V. T. Forsyth, G. Fragneto, M. Haertlein, M.-T. Dauvergne, H. Nilsson, P. Brundin, S. Linse, T. Nylander and E. Sparr, ACS Chem. Neurosci., 2013, 4, 1339–1351 CrossRef CAS PubMed.
- R. Gaspar, M. Lund, E. Sparr and S. Linse, QRB Discovery, 2020, 1, e2 CrossRef PubMed.
- E. Hellstrand, A. Nowacka, D. Topgaard, S. Linse and E. Sparr, PLoS One, 2013, 8, 1–10 CrossRef PubMed.
- R. Gaspar, I. Idini, G. Carlström, S. Linse and E. Sparr, Front. Cell Dev. Biol., 2021, 9 DOI:10.3389/fcell.2021.622764.
- B. Frieg, L. Antonschmidt, C. Dienemann, J. A. Geraets, E. E. Najbauer, D. Matthes, B. L. de Groot, L. B. Andreas, S. Becker, C. Griesinger and G. F. Schröder, Nat. Commun., 2022, 13, 6810 CrossRef CAS PubMed.
- T. C. T. Michaels, G. A. Garcia and T. P. J. Knowles, J. Chem. Phys., 2014, 140, 194906 CrossRef PubMed.
- A. J. Dear, G. Meisl, T. C. T. Michaels, M. R. Zimmermann, S. Linse and T. P. J. Knowles, J. Chem. Phys., 2020, 152, 045101 CrossRef CAS PubMed.
- S. Campioni, G. Carret, S. Jordens, L. Nicoud, R. Mezzenga and R. Riek, J. Am. Chem. Soc., 2014, 136, 2866–2875 CrossRef CAS PubMed.
- R. Bell, R. J. Thrush, M. Castellana-Cruz, M. Oeller, R. Staats, A. Nene, P. Flagmeier, C. K. Xu, S. Satapathy, C. Galvagnion, M. R. Wilson, C. M. Dobson, J. R. Kumita and M. Vendruscolo, Biochemistry, 2022, 61, 1743–1756 CrossRef CAS PubMed.
- T. C. T. Michaels, D. Qian, A. Šarić, M. Vendruscolo, S. Linse and T. P. J. Knowles, Nat. Rev. Phys., 2023, 5, 379–397 CrossRef CAS.
- C. Mansson, P. Arosio, R. Hussein, H. H. Kampinga, R. M. Hashem, W. C. Boelens, C. M. Dobson, T. P. J. Knowles, S. Linse and C. Emanuelsson, J. Biol. Chem., 2014, 289, 31066–31076 CrossRef PubMed.
- F. Chiti and C. M. Dobson, Annu. Rev. Biochem., 2017, 86, 27–68 CrossRef CAS PubMed.
- C. Galvagnion, J. W. P. Brown, M. M. Ouberai, P. Flagmeier, M. Vendruscolo, A. K. Buell, E. Sparr and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7065–7070 CrossRef CAS PubMed.
- C. L. L. Pham, A. Rey, V. Lo, M. Soulès, Q. Ren, G. Meisl, T. P. J. Knowles, A. H. Kwan and M. Sunde, Sci. Rep., 2016, 6, 25288 CrossRef CAS PubMed.
- W. Hoyer, T. Antony, D. Cherny, G. Heim, T. M. Jovin and V. Subramaniam, J. Mol. Biol., 2002, 322, 383–393 CrossRef CAS PubMed.
- G. Meisl, L. Rajah, S. A. I. Cohen, M. Pfammatter, A. Saric, E. Hellstrand, A. K. Buell, A. Aguzzi, S. Linse, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Chem. Sci., 2017, 8, 7087–7097 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc05661a |
| This journal is © The Royal Society of Chemistry 2024 |
