Open Access Article
Open Access ArticleCoeffNet: predicting activation barriers through a chemically-interpretable, equivariant and physically constrained graph neural network†
Sudarshan
Vijay
 ab,
Maxwell C.
Venetos
ab,
Evan Walter Clark
Spotte-Smith
ab,
Maxwell C.
Venetos
ab,
Evan Walter Clark
Spotte-Smith
 ab,
Aaron D.
Kaplan
b,
Mingjian
Wen
c and
Kristin A.
Persson
*ad
ab,
Aaron D.
Kaplan
b,
Mingjian
Wen
c and
Kristin A.
Persson
*ad
aDepartment of Materials Science and Engineering, University of California, Berkeley, 210 Hearst Memorial Mining Building, Berkeley, CA, 94720 USA. E-mail: kristinpersson@berkeley.edu
bMaterials Science Division, Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA, 94720 USA
cDepartment of Chemical and Biomolecular Engineering, University of Houston, Houston, Texas 77204, USA
dThe Molecular Foundry, Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA, 94720 USA
First published on 22nd January 2024
Abstract
Activation barriers of elementary reactions are essential to predict molecular reaction mechanisms and kinetics. However, computing these energy barriers by identifying transition states with electronic structure methods (e.g., density functional theory) can be time-consuming and computationally expensive. In this work, we introduce CoeffNet, an equivariant graph neural network that predicts activation barriers using coefficients of any frontier molecular orbital (such as the highest occupied molecular orbital) of reactant and product complexes as graph node features. We show that using coefficients as features offer several advantages, such as chemical interpretability and physical constraints on the network's behaviour and numerical range. Model outputs are either activation barriers or coefficients of the chosen molecular orbital of the transition state; the latter quantity allows us to interpret the results of the neural network through chemical intuition. We test CoeffNet on a dataset of SN2 reactions as a proof-of-concept and show that the activation barriers are predicted with a mean absolute error of less than 0.025 eV. The highest occupied molecular orbital of the transition state is visualized and the distribution of the orbital densities of the transition states is described for a few prototype SN2 reactions.
I. Introduction
Activation barriers computed using ab initio methods have greatly facilitated mechanistic understanding of reactions occurring in battery electrolytes,1–4 catalysis,5–8 organic synthesis9 and many other fields of chemistry.10,11 The activation barrier is determined as the energy difference between a first-order saddle point (a transition state) and a local minimum of the potential energy surface (a reactant or product), which provides insight into the likelihood of a reactant converting into a product. A large activation barrier implies that the reaction is sluggish, while fast chemical reactions have small activation barriers.Activation barriers are often computed using electronic structure methods like density functional theory (DFT). In practice, these computations are usually not straightforward to perform. They can be time-consuming, requiring multiple gradient evaluations for an optimizer to identify a first-order saddle point. They are also difficult to automate, as transition state optimizations are very sensitive to the choice of the initial guessed structure. Even when an optimization successfully converges, it frequently produces an unwanted transition state.12
Several models have been proposed to approximate the activation barrier to circumvent the need for explicitly performing transition-state finding calculations. A fundamental assumption of these models is that the activation barrier can be expressed as a function of a handful of variables determined from the electronic structure of the reactants and products alone. The simplest such model is the Brønsted–Evans–Polanyi (BEP) relation,13–16 which assumes a linear relationship between the activation barrier and energy difference between reactants and products. More complex models consider other potential energy surface (PES) complexities, such as solvent reorganization in Marcus theory.17–21 While these models work well for a narrow chemical space and are chemically interpretable, they need to be re-parameterized for even the slightest change to the chemistry and conditions, such as for example, different ligands around a fixed reaction centre.
Machine learning models offer an alternative to determining activation barriers without relying on assumptions about the PES, such as in BEP and Marcus-theory-based models.22 Current machine-learning models used to determine activation barriers range from methods using active-learning routines,23 to one-shot kernel-methods24 or neural network25–27 predictions. Active learning routines require iteratively performed DFT calculations, and one-shot predictions require a significant number (between 2000 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) of DFT calculations as a part of their training data sets. In general, these approaches lack chemical interpretability in their outputs.
000) of DFT calculations as a part of their training data sets. In general, these approaches lack chemical interpretability in their outputs.
In this work, we introduce CoeffNet, a graph-neural network (GNN) that is capable of predicting both the activation energies and the frontier orbitals, such as the highest-occupied molecular orbital (HOMO) of the transition state. Inputs to the model are the coefficients of any frontier molecular orbitals of reactant and product complexes which are outputs of any localized-basis electronic structure code. Our approach of using coefficients of molecular orbitals offers three advantages: (1) inductive bias in the form of an idealized description of the variation of the electronic structure from reactant to transition state, which is a common feature of theoretical models enabling accurate activation barrier predictions (2) physical constraints imposed on the features used to parameterize the GNN allowing the model to learn within a fixed numerical range, and (3) chemical interpretability of the predicted output, which is any molecular orbital of the transition state. A key use-case of CoeffNet is to accurately predict activation barriers and offer chemical interpretability when applied to a fixed class of reactions. When applied to a diverse database of reactions, it acts as a pre-sieving tool to provide a coarse estimate of the activation barrier such that only those reactions with chemically interesting activation barriers may be computed using computationally intensive transition state search DFT calculations. This manuscript is organized as follows: in Section II, we discuss the features of the coefficients of frontier orbitals and how they incorporate inductive bias when used as features in CoeffNet. In Section III, we describe the architecture of CoeffNet. As a proof-of-concept, we apply it to predict activation barriers and the HOMO for selected SN2 reactions. Finally, in Section IV, we show that the model outputs align with chemical intuition.
II. Coefficients of frontier orbitals serve as a gauge of reactivity
In this section, we motivate our choice of coefficients of a molecular orbital as features for CoeffNet. We briefly describe how these coefficients are defined in the context of DFT and how they change for different molecular orbitals as a function of the rotation of a molecule and along a reaction path from reactant to transition state to product. We note that the example of analysing the orbitals of water is a simple one, where we illustrate the interpretive role that coefficients provide. We defer more chemically relevant examples to Section S3† and Section IV of this manuscript.Localized-basis DFT codes compute a chosen molecular orbital, ψi, through a linear combination of all multiple atom-centred atomic orbitals, ϕj consisting of s, p, d, and higher basis functions. Cij contains the relative weights of atomic orbital j in a molecular orbital with index i,
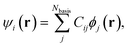 | (1) |
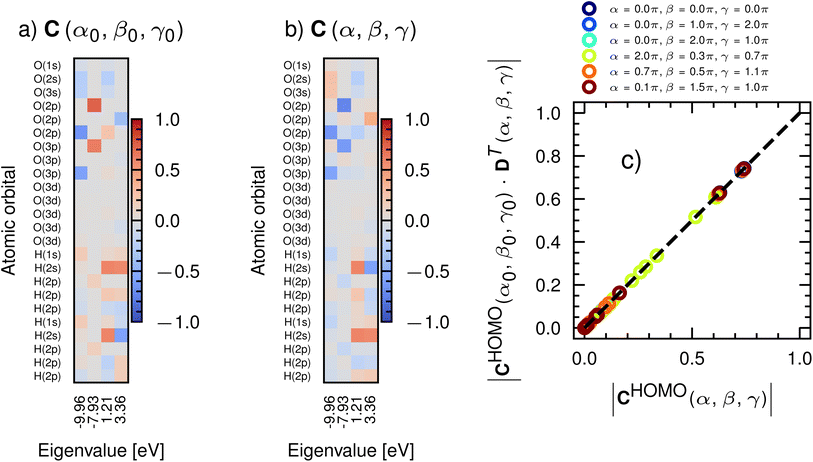
For a given ψi, we think of Cij as informing us as to what ϕj, and hence what atoms are reactive. Consider Cij for selected molecular orbitals of water shown in Fig. 1a. For the HOMO (column corresponding to an x-axis value of −7.93 eV, i.e. the least negative x-axis value), we find that the largest value of |Cij| (in red) appears for oxygen p-orbitals and hydrogen p-orbitals (polarization functions). This result matches our expectations on the reactivity of water; the oxygen lone-pairs (composed of p-orbitals), as well as additional hydrogen-bond-forming orbitals of hydrogen, are likely to be the most reactive. All ψ's that are lower in energy, such as those corresponding to an eigenvalue of −9.96 eV, include deeply buried ϕj, such as the s-functions of oxygen and hydrogen, which are less reactive. Unoccupied molecular orbitals (where the x-axis is positive) are largely made up of polarization functions. Passing this information to CoeffNet will inform it of orbital-level, environment-specific reactivity. In Section S3† we discuss the case where multiple molecular orbitals might be needed to correctly represent reactivity through the example of coefficients of the molecular orbital of pyridine, where a combination of HOMO and the eigenstate below the HOMO are needed to properly represent the reactive centers of the molecule.29
A. Numerical properties of C
A useful property of Cij is that it can take values strictly between −1 to 1 when determined in orthonormal basis and for real-valued functions (see Section S1† for converting from non-orthonormal to orthonormal basis). Furthermore,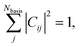 | (2) |
While C provides intuitive molecular-orbital level information, as well as constraints on attainable numerical values, it is sensitive to both rotation and sign change. Fig. 1b shows C for water at a different orientation than shown in Fig. 1a (denoted by an Euler angle change α0 → α, β0 → β and γ0 → γ with a rotation matrix defined through an extrinsic rotation about the origin of cartesian coordinates). Note that both absolute values and signs are altered by this rotation. C is an eigenvector and hence accurate only up to a sign change (multiplying the eigenvalue problem ±1 has no effect on the solution) and rotation changes the relative weights of px, py, pz, dxy, dyz, dzx, d3z2−r2 and dx2−y2 contributions to ψ. However, it is known that C rotates predictably, i.e.
| C(α, β, γ) = C(α0, β0, γ0)·DT(α, β, γ), | (3) |
B. Variation of C from reactant to transition state to product
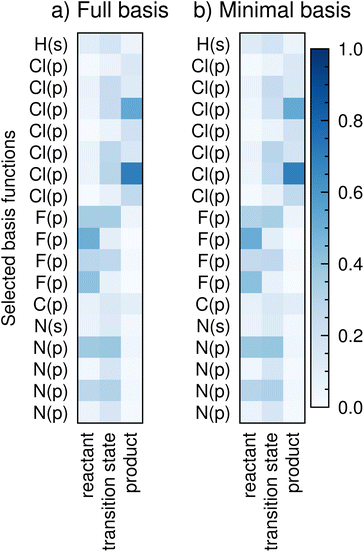
A final useful property of C is that it changes expectedly with chemical intuition along a reaction path. Fig. 2a shows selected basis functions of atomic orbitals (y-axis) for the HOMO of reactant, transition state and product species for a prototype SN2 reaction taken from ref. 31. The reaction follows the template| A + X− → B + Y− | (4) |
In this particular SN2 reaction, the chlorine atom (X−) moves towards the carbon atom, while the fluorine atom (Y−) leaves with a charge of −1. Nitrogen and hydrogen atoms are close to the reaction centre. Matching chemical intuition, the p-orbitals of chlorine have a higher weight in the product state (i.e. these orbitals contribute significantly to the HOMO and hence are involved in the bonding state of the species), while the p-orbitals of fluorine have a higher weight in the reactant state; the transition state has an intermediate weight between chlorine and fluorine p-orbitals. As expected through chemical intuition, bystander atoms nitrogen (p-orbitals) and hydrogen (s-orbital) have intermediate weight throughout the reaction.
C. Constructing a smaller representation of C
Most modern basis sets contain several polarization and diffuse functions (extra basis functions with higher angular quantum numbers, l, such as d, f, g and h functions for small organic molecules, where only s and p functions are needed to fill all electrons). These extra basis functions are likely to render an intuitive understanding of C less straightforward. While they may provide more information to CoeffNet, they will also lead to a model that is more expensive to train. To explore the effect of reduction in the number of atomic orbitals a posteriori of a DFT calculation, we construct a smaller, minimal basis set from the full basis by the direct-projection method.32 As an illustration of this idea, we select all s and p functions to constitute a minimal basis representation, ϕmj, which constitutes of a subset of basis functions present in ϕj. This choice of minimal-basis set is consistent with the classes of molecules tested in this work (small organics with halogens) and can be tuned to include or exclude any atomic orbitals. If the number of basis functions in the minimal set is Mbasis(<Nbasis), then we define a rectangular matrix projection, P = 〈ϕmj|ψi〉 with dimensions Mbasis × Nbasis. This projection is used to determine a minimal-basis Hamiltonian matrix, Fm = PεPT which is diagonalized to get the coefficients and eigenvalues in the minimal-basis representation. Fig. 2b shows C in a minimal-basis representation for the same SN2 reaction shown in Fig. 2a. Both Fig. 2a and b convey the same information for the relevant atoms, with only minor changes in numerical values for the minimal basis representation compared to the full basis representation. Thus, choosing a smaller basis set leads to a minimal loss of information (apart from the atomic orbitals that have purposefully been removed) for the examples we consider in this manuscript, allowing us to work with a smaller representation.In summary, molecular orbitals represented through C present a chemically intuitive representation of reactivity, which we use as features in a graph neural network to learn quantities such as the activation barrier. C can also be converted to a smaller, minimal-basis representation without much information loss, allowing for a simpler learning process. In the next section, we discuss how CoeffNet uses C as a feature to learn activation barriers and molecular orbitals.
III. Equivariant graph-neural network to predict activation barriers
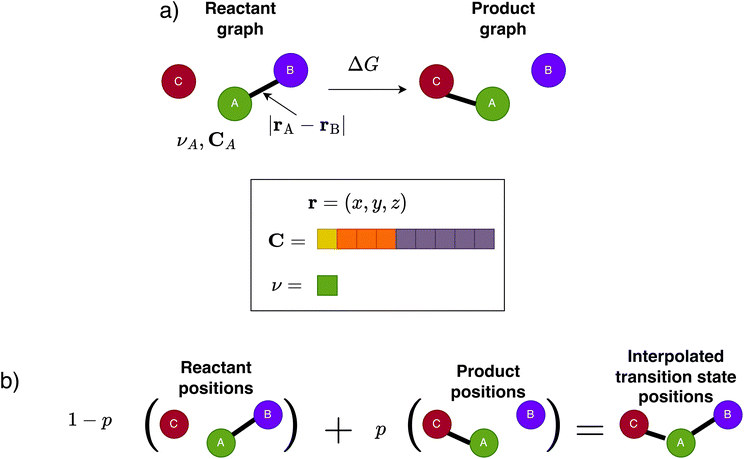
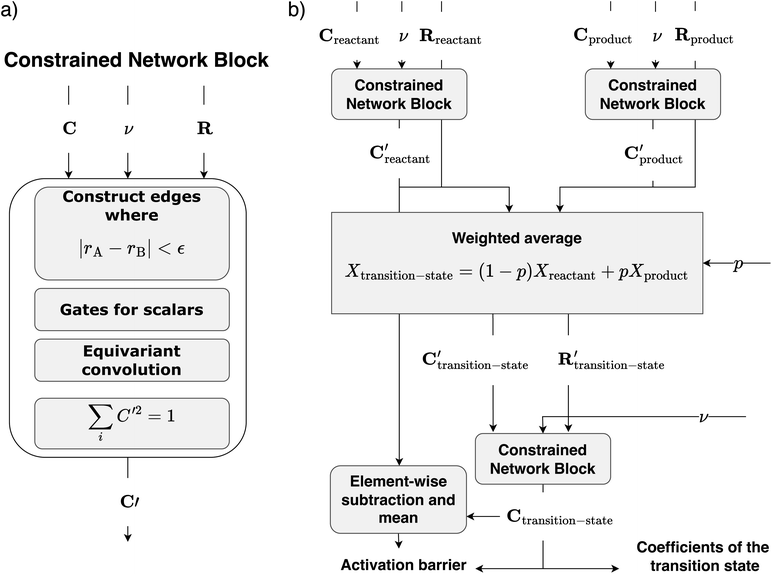
In this section, we describe the architecture of CoeffNet, and, as a proof-of-concept, we test its performance on the SN2 reaction dataset.31 We discuss how inputs are pre-processed to be amenable to use with commonly available graphs neural network architectures. We illustrate how learnt weights of the model allow it to predict both the activation barrier and C for a particular molecular orbital of the transition state.Fig. 3a shows a schematic of the required inputs to CoeffNet, which are the geometry optimized positions (r), atomic numbers (ν), C for reactant and product complexes and the free energy difference, ΔG, of the reaction going from reactant to product. Note that all inputs are readily obtained from DFT calculations on reactant and product complexes.
A. Pre-processing of inputs to node and edge attributes and features
We begin by generating graphs for both reactant and product complexes. The nodes of each graph represent atoms in a complex, and the edges represent the connectivity between these atoms. We choose to express this connectivity through a fixed cutoff, i.e. an atom in a complex is connected to all other atoms in its neighbourhood up to a fixed cutoff distance (which is left as a hyperparameter). We determine the distance between any two nodes, A and B, as the norm of the vector of their relative positions, |rA − rB| (see schematic in Fig. 3a).After creating the graphs for the reactant and product, we parameterize it with attributes using inputs illustrated in Fig. 3a. These attributes are fundamental properties of the node and edges they describe and are not altered by learnt weights. Each node is represented by a one-hot encoding of its atomic number. Each edge is parameterized by a normalized soft one-hot encoding33 of the edge length. In practice, the edge length is expanded on a grid based on a fixed number of Gaussian basis functions.
We use C to generate node features which are to be modified by learnt weights. Since each atom has a different number of atomic orbitals, we need to pre-process C before it can be used as node features. This pre-processing is required as we use a graph with the same dimension of node features for all nodes and edge features for all edges. We split C into different atom-wise chunks based on which atom the atomic-orbital is centred on. These chunks are then normalized to be of the same dimension for all atoms by padding smaller chunks with zeros in an orbital-wise fashion. For example, in the case of a minimal basis representation of H2O, the oxygen node will have the largest number of orbitals (two s functions with l = 0 and three p functions, with l = 1 for a total dimension of five). The hydrogen node features would have exactly one s orbital; the other four dimensions (remaining one s and three p functions) are padded with zeros to make a total dimension of five.
B. Interpolation scheme to generate approximate transition state graphs and features
Having generated reactant and product graphs and parameterized them with node features, we now discuss how we generate transition state graphs and their associated node features. Generating this information is a necessary intermediate step to CoeffNet. Note that we cannot use the same method of graph generation as described in the previous section for reactant and product states, as we do not have access to the structure of the transition state as an input.We use linear interpolation to generate an approximate representation of the transition state quantities from reactant and product quantities (see Fig. 3b for a schematic of this interpolation). For any quantity X,
| Xtransition-state = (1 − p)Xreactant + pXproduct. | (5) |
We note that our objective through this interpolation scheme is not to predict accurate transition state structures or C (the latter is an output of CoeffNet) but to incorporate as much useful information as possible into an approximate transition state graph.
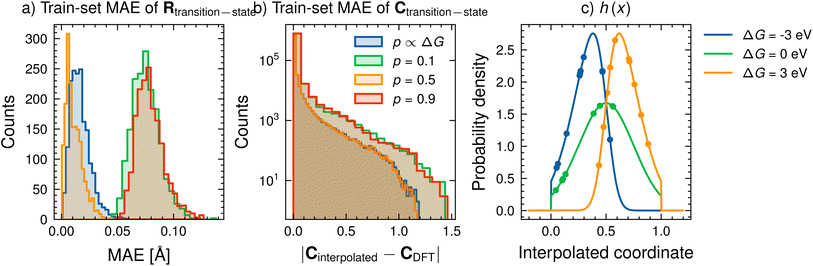
We start by assessing the feasibility of using a constant value of p. To test this method, we compare the mean absolute error (MAE) between Rtransition-state obtained through eqn (5) and from DFT. Fig. 4a shows the MEA for different values of p for the training dataset for p = 0.1 (green), p = 0.5 (yellow) and p = 0.9 (red). We report the performance on the training dataset as the choice of p is made before training and kept fixed throughout training and inference. For our chosen proof-of-concept dataset, all values of p perform suitably well, with only minor differences in MAE of positions (less than 0.15 Å). Fig. 4b compares the absolute error between the interpolated and DFT computed C for the same values of p as in Fig. 4a. Several elements already have negligibly small errors prior to any learning, implying that this linear interpolation strategy to determine transition state C from reactant and product C's is a sufficient pre-processing step to the model.
While a constant value of p performs well for this dataset, it might be advantageous to incorporate further inductive bias into an approximated transition state structure. We propose an alternative interpolation scheme, which considers the reaction's ΔG to generate interpolated R and C at the transition state. The motivation for this interpolation scheme is Hammond's postulate34 for organic reactions, which states that endergonic reactions have transition states that are product-like, while exergonic reactions have transition states that are reactant-like.
To encode Hammond's postulate into a model to generate p, we create a skewed normal distribution Φ(x) = 2f(x)g(x), where,
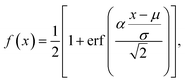 | (6) |
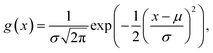 | (7) |
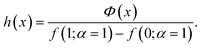 | (8) |
Fig. 4c (lines) shows the behaviour of h for three different values of α(=ΔG). At a very endergonic ΔG = 3 eV (orange line), h is centred close to 1, indicating a high probability for the structure being product-like. Conversely, at a very exergonic ΔG = −3 eV (blue line), h is centred close to 0, indicating a high probability of the structure being reactant-like; this behaviour is in line with Hammond's postulate. Finally, p is determined by taking a mean of a few randomly sampled points of h(x) (coloured points in the distribution of Fig. 4c). Note that we sample this distribution to determine p, as opposed to, say, taking a moment of h(x), to allow us to deal with varied reaction environments, which may be better described by several h(x) functions instead of just one as we do here.
Fig. 4a and b (blue lines, p ∝ ΔG) shows the performance of this Hammond's postulate-inspired interpolation scheme in comparison to a constant value of p. Overall, the performance for R (Fig. 4a) is comparable to that of p = 0.5, with most structures having an MAE lower than 0.05 Å. Interpolations of C (Fig. 4b) yield similar performance as well. Since we are interested in predicting activation barriers and coefficient matrix elements (and not the transition state structure), we use fixed hyperparameter values of μ = 0.5, σ = 0.25 and α = 1 with ten randomly sampled points throughout this work. Further analysis of this method of determining an approximate transition state is performed in Section S3† and illustrated in Fig. S9† for a more diverse dataset. However, the influence of the value of p may be reduced in such a comparison as significantly more input parameters (such as more coefficients) are used in the model.
C. CoeffNet architecture
We modify the equivariant network as implemented in ref. 33 to incorporate the constraints of C described in Section II. Fig. 5a shows a schematic of the constrained-network block that we use as a building block throughout CoeffNet. The inputs to the block are C, ν and R and the outputs are node features (C′) modified by weights, with the same dimensions of C. The first three operations (in red and blue) are consistent with ref. 33, where the edges are constructed based on a fixed cutoff, non-linearities are applied to the scalar quantities (gates), and convolutions are performed. The last block (in green) ensures that (1) entries in node features that come from padding to make the dimension of the node features equal are masked (i.e. set to zero and serve no role in the model), (2) this masked output is normalized such that its sum of squares is exactly one (both in line with the properties discussed in Section II).To ensure that the network is equivariant with respect to rotations of the orbitals that make C, we generate appropriate irreducible representations to be fed into the network. The irreducible representation of the inputs is given by the maximum number of s, p, d and higher functions that are present in each node feature. For example, if every node feature has one s, p and d function, the irreducible representation would consist of one l = 0 function with even parity, one l = 1 function with odd parity and one l = 2 function with even parity, in that order.
Fig. 5b shows a schematic of the architecture of CoeffNet. We start by supplying {C, ν, R} for reactants and products into two separate constrained network blocks. The outputs of these reactant and product blocks ( and
and  respectively) are averaged using (1 − p) (reactant weight) and p (product weight) to generate an output for an interpolated transition state,
respectively) are averaged using (1 − p) (reactant weight) and p (product weight) to generate an output for an interpolated transition state,  . Interpolated transition state positions,
. Interpolated transition state positions,  are generated through eqn (5).
are generated through eqn (5).  , ν and
, ν and  are passed to another constrained network block to obtain the coefficients of the transition state, Ctransition-state. To obtain the activation barrier from this output, we elementwise subtract Ctransition-state with
are passed to another constrained network block to obtain the coefficients of the transition state, Ctransition-state. To obtain the activation barrier from this output, we elementwise subtract Ctransition-state with  and take the mean along the feature dimension. This subtraction is done to stay consistent with the definition of an activation barrier as the difference between the transition state and reactant energies.
and take the mean along the feature dimension. This subtraction is done to stay consistent with the definition of an activation barrier as the difference between the transition state and reactant energies.
D. Loss function
We use an MAE loss function for the task of predicting the activation energy and a custom unsigned-MAE loss function for the task of predicting C. We define this unsigned-MAE loss function as, | (9) |
E. Model performance: activation barriers
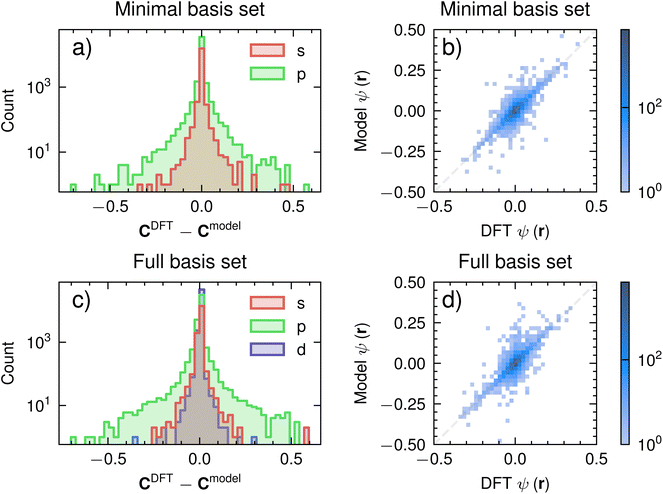
We now report the performance of CoeffNet on the task of predicting the activation barrier on the SN2 dataset computed with the def2-SVP basis set.35 To demonstrate the working of CoeffNet, we choose this proof-of-concept dataset of SN2 reactants taken from ref. 31 (see Section VI for further description and Section S4† for hyperparameter testing, Section S5† for information about data-splits and Section S8† for corresponding plot for the def2-TZVP basis set). Our motivation for using this dataset as a basis for testing the performance of CoeffNet stems from the need for high-accuracy activation barrier prediction for a specific type of chemical reaction with limited number of elements.Fig. 6a and b show the results of the activation barrier prediction task on both minimal basis and full basis representations, respectively, for the test set. Both models accurately predict the activation barrier computed with DFT calculations (x-axis) to within an accuracy of 0.025 eV (the mean activation barrier for the test dataset is 0.29 eV, see Fig. S4† for further information).
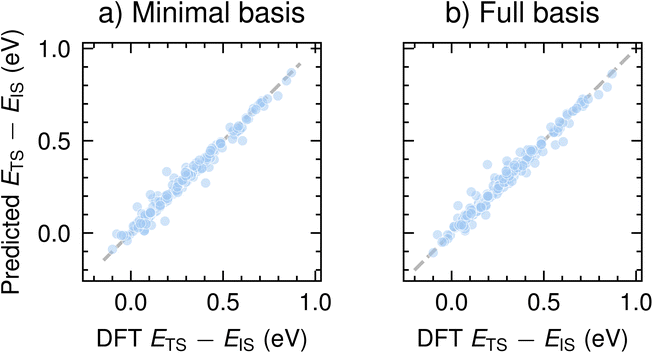 | ||
| Fig. 6 Comparison of predicted activation barriers and DFT computed barriers on the test set for (a) minimal-basis representation (i.e. only s and p basis functions), and (b) full-basis (i.e. as computed with DFT) for the def2-SVP basis set. See Fig. S7† for a corresponding plot for barriers computed with the def2-TZVP basis set. | ||
Table 1 shows the performance of the model with two different basis sets def2-SVP and def2-TZVP; the latter contains more basis functions than the former. To compare our results with a baseline, we fit a linear model between the activation barrier and the difference between the product and reactant energies (a form of BEP relations). Note that the baseline test does not learn the barriers very well (see Section S6† for further details); the relatively small numeric value of the error has to do with the range of activation energies considered in this dataset (most values are between 0 and 0.5 eV). Kernel-based machine learning models as in ref. 36 trained on a similar dataset has a mean absolute error of ∼0.25 eV. Recent implementations of message-passing neural networks using simpler and easier to obtain descriptors obtain an MAE of ∼0.11 eV.37
| Basis set | Basis set type | Error |
|---|---|---|
| def2-SVP | Full | 0.022 eV |
| def2-SVP | Minimal | 0.021 eV |
| def2-TZVP | Full | 0.023 eV |
| def2-TZVP | Minimal | 0.021 eV |
| Baseline | — | 0.152 eV |
Both minimal and full basis models predict activation barriers for the SN2 with low MAE. Applying a larger basis sets (def2-SVP → def2-TZVP) does not change errors in prediction significantly (0.022 vs. 0.023 eV). As expected, employing a larger basis set while operating on a minimal basis does not change the mean absolute error significantly (only changes beyond the third decimal place). Given that the performance of all models, irrespective of the basis set, is nearly identical (around 0.02 eV), it is preferable to use a minimal basis representation as it is much cheaper to train and requires fewer parameters during inference for the SN2. Note that the prediction errors are distinct from those associated with differences in computed and experimental transition states. However, the errors from CoeffNet for this dataset are smaller than those between experiment and DFT calculations (∼0.08 eV for similar reactions with the B3LYP functional),38 indicating that errors between our model and experiment are of similar orders of magnitude as between DFT calculations and experiments. We achieve this level of accuracy while training on the coefficients of a single eigenvalue (i.e. the HOMO) and hence do not need to add more parameters by using the coefficients of multiple eigenvalues as input. Furthermore, we note that CoeffNet has been tested only on a specific reaction class (i.e. the SN2 reaction) and will most likely require further modifications before being applied to more diverse datasets. It is also likely that there might be reactions involving more complex species, such as organometallic compounds, which might require an input to CoeffNet consisting of a combination of multiple eigenstates to accurately predict their activation barriers.
Finally, we briefly discuss the performance of CoeffNet on a diverse dataset, consisting of several different reaction classes (as opposed to just a single reaction class, such as the SN2 dataset discussed in this section). Note that the objective of training CoeffNet on a diverse dataset is to use its results as a pre-sieving strategy for high-throughput study of large reaction networks. For example, if CoeffNet predicts an activation barrier that is too large to be of chemical interest (typically >1 eV for reactions at room temperature) it is removed from further consideration in the reaction network. Conversely, if it predicts an activation barrier that indicates that the reaction is likely to occur, then the conventional computationally-intensive transition state search approaches are employed to determine the correct value of the activation barrier.
In order for CoeffNet to perform this pre-sieving role for high-throughput reaction networks, it must predict reasonably accurate transition state barriers with a small spread (i.e. a small standard deviation of the errors). We train CoeffNet on the dataset generated by ref. 25 and 39 (see Section S10† for a detailed discussion). We find that the MAE is 0.42 eV on a dataset which spans ≈10 eV, similar to the MAE of obtained with the SLATM(2)d kernel and nearly double that of a trained directed message-passing neural network for slightly different dataset splits.40 We do not perform extensive hyperparameter tests, instead we use the same parameters as listed in Section VI; while out of the scope of our current work, we expect that further hyperparameter and model tuning to be beneficial to reduce the mean absolute error for this dataset. Furthermore, we find that the standard deviation of the error to be 0.68 eV (corresponding to a root-mean-square error of 0.65 eV), well within the margin of error expected to accurately predict reactions of interest which can then undergo computationally intensive DFT and transition state finding calculations.
F. Model performance: predicting HOMO on a grid
Fig. 7 shows the model's performance in predicting the HOMO of the transition state. Fig. 7a and c show the signed error between the coefficients of the HOMO determined by DFT (CDFT) and those that are output from the model (Cmodel) for the minimal and full basis set respectively. Most errors are between −0.2 and 0.2, indicating that the model learns the relative importance of each atomic orbital in the HOMO. There are a few select p-functions (less than 20 elements out of a possible approx. 6000 elements) that have considerable errors of less than −0.4 and more than 0.4 for both minimal and full basis representations. This large error in a small percentage of points likely stems from incorrectly learnt polarization functions (largely composed of p-orbitals). If highly accurate coefficients are needed, we suggest excluding polarization functions in the minimal basis representation or incorporating further constrained network blocks (cf.Fig. 5) to learn core and polarization functions separately. Given that our purposes are largely for interpretation (see Section IV), we suggest that this level of accuracy, from a relatively small dataset, is sufficient.We now discuss the model's performance after using its output coefficients to generate the HOMO on a grid through eqn (1). Fig. 7b and d shows a parity plot between the predicted and DFT ψ for the HOMO of the transition state for the minimal and full basis set, respectively. We generate a uniform grid of 4 × 4 × 4 around the molecule to determine this ψ. Overall, we find that the test set predictions faithfully represent the DFT outputs on the grid for most of the points (darker colours in Fig. 7b and d represent a larger concentration of points). In the next section, we use this predicted HOMO to gain insight into SN2 reactions and compare this insight with conventional chemical intuition.
IV. Model output coefficients of frontier orbitals are interpretable
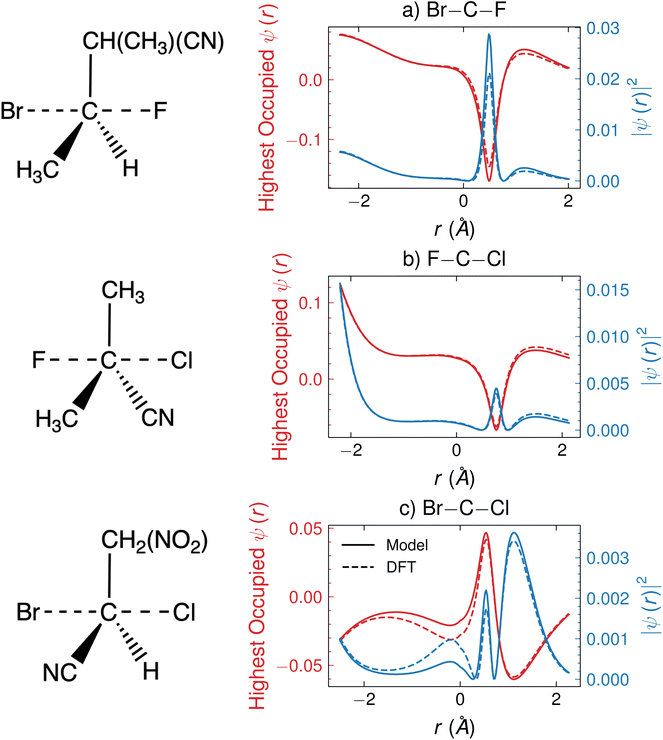
In this section, we analyze the predicted HOMO for a few specific SN2 reactions to illustrate the interpretive qualities of the outputs of CoeffNet. Fig. 8 shows ψ (in red) along a one-dimensional channel for three arbitrarily chosen reactions in the test dataset, F attacking and Br leaving in Fig. 8a (transition states are visualized to the left of the plot), Cl attacking and F leaving in Fig. 8b and Cl attacking and Br leaving in Fig. 8c; all occurring via a commonly bound carbon atom, which is bound to different species (such as H, CN, CH3 and NO2). The corresponding orbital densities, |ψ|2, are shown in blue. The x-axis indicates the relative positions of the leaving group (left) to the attacking group (right) at the transition state structure, centred around the carbon atom (i.e. the carbon atom centre is at zero on the x-axis). In the reactant state, the attacking group has a charge of −1, and leaving group is bound to the carbon atom, while in the product state, leaving group has a charge of −1, and the attacking group is attached to the carbon atom. At the transition state, the attacking and leaving groups are at an intermediate distance from the carbon atom. Dashed lines indicate outputs from DFT, while solid lines indicate the outputs from CoeffNet. Consistent with the tests of Fig. 7b and d the model predicted and DFT ψ are very similar (i.e. the dashed and solid lines nearly overlap for all r).We observe a peak in the orbital densities for the HOMO for all reactions shown in Fig. 8 between the central carbon atom at the attacking group (between 0 and 1 Å on the x-axis). This peak indicates the formation of a negatively charged substituent and is present irrespective of the character of the attacking group or the surrounding reaction environment around the carbon atom. Furthermore, certain reactions, such as in Fig. 8c, have peaks present near the attacking group atom (∼1.5 Å on the x-axis), which is likely due to a large anionic character present on the chlorine atom at the transition state. Smaller secondary peaks are observed in Fig. 8a and b, indicating a weaker anionic character of these incoming substituents at this particular transition state. Anionic character is present in the leaving group as well; all reactions in Fig. 8 show an increase in the orbital density at the attacking group atom centre (∼−2 Å), though their relative magnitude is given by their electronegativity (larger for fluorine in Fig. 8b and smaller for Br in Fig. 8a and c).41 Note that the complexities of the task of predicting the activation barrier are represented by the lack of clear trends in orbital densities in Fig. 8, i.e. a combination of factors, such as electronegativity and incoming and leaving groups and steric effects of ligands appear to influence chemical reactivity (and hence the barrier).
As CoeffNet facilitates predictions of activation barriers as well as ψ, we suggest that it can lead to interpretive arguments about patterns of chemical bonding present in a large dataset. We hypothesize that predictions of ψ can be used to determine if the model is incorrectly learning attributes of a certain reaction, thus offering checks and balances on the predicted activation barriers. Overall, we find that using C as a feature to CoeffNet allows us to interpret our model predictions in the context of known chemical bonding patterns, leading to more robust and interpretable predictions for a given class of reactions. Furthermore, we suggest that predictions of C could lead to easy initialization of a DFT calculation, allowing for a direct link to active-learning procedures to reduce the number of optimizer steps required to determine a transition state.
V. Conclusion
In this work, we introduce CoeffNet, an interpretable, equivariant and physically constrained graph neural network. CoeffNet uses the coefficients of a chosen molecular orbital of reactants and products to predict activation barriers as well as coefficients for the same molecular orbital of the transition state. We illustrate the different components of CoeffNet, starting with the interpolation routine to predict interpolated transition state quantities based on Hammond's postulate and the constraints to ensure that its node features can always be interpreted as coefficients. As a proof-of-concept, we test our model on an SN2 dataset and show that the predicted activation barriers are accurate with respect to DFT calculations. Based on the SN2 dataset, we show that the output molecular orbitals allow for chemically intuitive interpretations. Overall, we find that by using the coefficients of a molecular orbital as features, we gain accurate transition state predictions and an interpretive understanding of the chemical reactions in a dataset.VI. Computational methods
Localized-basis density functional theory calculations were performed using the Q-Chem42 (v5.4) software package. Workflows to perform these calculations were taken from the atomate43 Python package and were facilitated through the fireworks44 package. Parsing of all energies, Hamiltonian matrices, overlap matrices and coefficient matrices from Q-Chem output files were performed using pymatgen.45The SN2 dataset was taken directly from ref. 31. As these structures were computed with a different electronic structure code and transition states were determined using numerical frequencies, we recomputed the frequencies for all provided transition state structures. We re-optimized the transition states for all structures that did not have exactly one imaginary frequency using the FrequencyFlatteningTransitionStateFW implemented in atomate,43 which computes the transition state structure and iteratively checks if exactly one imaginary frequency is present. We take all structures that contain one imaginary frequency (2178 total entries). We note that the dataset in ref. 31 does not contain complexes in the product state. To determine these end states, transition state structures are perturbed along the eigenvectors scaled by −0.5 and 0.5. Constraints on atoms are used in line with ref. 31 to ensure that the halogen atoms do not abstract hydrogen atoms away from the carbon skeleton. After determining the structures, a single point with the different basis sets used in this study, i.e. def2-SVP and def2-TZVP,35,46 were performed. Note that the def2 family of basis sets requires the use of effective core potentials (ECPs) for atoms heavier than Kr. No reactions using an ECP were included in the training set. While the inclusion of ECPs should change only the Kohn–Sham effective potential in the Hamiltonian, application of CoeffNet to reactions using heavier element ECPs may require further training. All calculations were performed with the B3LYP47,48 functional in spin-restricted mode. The purecart = 1111 option was used to ensure that all calculations were performed in a spherical basis.
CoeffNet is written entirely in Python using the pytorch-geometric framework. Equivariant networks, consisting of convolution, activation (of scalars) and aggregation, were performed using the e3nn package. All training was performed on NVIDIA A100 GPUs. Further details on hyperparameter testing are shown in Section S4.† Tests were conducted on the SN2 dataset using a random split of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 train/validation/test set. Model parameters were optimized on the training set, hyperparameters are selected based on model performance on the validation set, and errors are reported using the test set unless otherwise stated. The Adam optimizer with a batch size of 8 with an initial learning rate of 0.001 was adopted. The learning rate is altered through the training process by a factor of 0.5 each time the learning rate plateaus for more than 10 epochs through the ReduceLROnPlateau function implemented in the torch python library.
10 train/validation/test set. Model parameters were optimized on the training set, hyperparameters are selected based on model performance on the validation set, and errors are reported using the test set unless otherwise stated. The Adam optimizer with a batch size of 8 with an initial learning rate of 0.001 was adopted. The learning rate is altered through the training process by a factor of 0.5 each time the learning rate plateaus for more than 10 epochs through the ReduceLROnPlateau function implemented in the torch python library.
Data availability
CoeffNet is freely available at https://github.com/sudarshanv01/coeffnet. Hamiltonian matrices, overlap matrices, coefficient matrices, eigenvalues and structures for all SN2 reactions used in this work are available at https://doi.org/10.5281/zenodo.10530180.Author contributions
Sudarshan Vijay: conceptualization, data curation, formal analysis, methodology, software, validation, visualization, writing – original draft, writing – review & editing. Maxwell Venetos: formal analysis, writing – review & editing. Evan Walter Clark Spotte-Smith: conceptualization, writing – review & editing. Aaron Kaplan: formal analysis, writing – review & editing. Mingjian Wen: formal analysis, writing – review & editing. Kristin Persson: conceptualization, funding acquisition, resources, writing – original draft, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support by the Silicon Consortium Project directed by Brian Cunningham under the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of Vehicle Technologies of the U.S. Department of Energy, Contract No. DE-AC02-05CH11231. E. W. C. S.-S. was supported by the Kavli Energy NanoScience Institute Philomathia Graduate Student Fellowship. Additional support was provided by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under contract no. DE-AC02-05-CH11231 (Materials Project program KC23MP). Data described in this study were produced using computational resources provided by the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility under Contract No. DE-AC02-05CH11231 and the Eagle and Swift HPC systems at the National Renewable Energy Laboratory (NREL).References
- L. Xing and O. Borodin, Oxidation induced decomposition of ethylene carbonate from DFT calculations - importance of explicitly treating surrounding solvent, Phys. Chem. Chem. Phys., 2012, 14, 12838–12843 RSC.
- E. W. C. Spotte-Smith, T. B. Petrocelli, H. D. Patel, S. M. Blau and K. A. Persson, Elementary decomposition mechanisms of lithium hexafluorophosphate in battery electrolytes and interphases, ACS Energy Lett., 2023, 8, 347–355 CrossRef CAS.
- E. W. C. Spotte-Smith, S. M. Blau, D. Barter, N. J. Leon, N. T. Hahn, N. S. Redkar, K. R. Zavadil, C. Liao and K. A. Persson, Chemical reaction networks explain gas evolution mechanisms in mg-ion batteries, J. Am. Chem. Soc., 2023, 145(22), 12181–12192 CrossRef CAS PubMed.
- J. L. Tebbe, T. F. Fuerst and C. B. Musgrave, Degradation of ethylene carbonate electrolytes of lithium ion batteries via ring opening activated by licoo2 cathode surfaces and electrolyte species, ACS Appl. Mater. Interfaces, 2016, 8, 26664–26674 CrossRef CAS PubMed.
- M. D. Wodrich, M. Busch and C. Corminboeuf, Accessing and predicting the kinetic profiles of homogeneous catalysts from volcano plots, Chem. Sci., 2016, 7, 5723–5735 RSC.
- J. Lym, G. R. Wittreich and D. G. Vlachos, A Python Multiscale Thermochemistry Toolbox (pMuTT) for thermochemical and kinetic parameter estimation, Comput. Phys. Commun., 2020, 247, 106864 CrossRef CAS.
- E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Density functional theory calculations for the hydrogen evolution reaction in an electrochemical double layer on the Pt(111) electrode, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250 RSC.
- E. D. Hermes, A. N. Janes and J. R. Schmidt, Micki: a python-based object-oriented microkinetic modeling code, J. Chem. Phys., 2019, 151, 014112 CrossRef PubMed.
- J. Andersen and J. Mack, Mechanochemistry and organic synthesis: from mystical to practical, Green Chem., 2018, 20, 1435–1443 RSC.
- T. Nakayoshi, K. Kato, S. Fukuyoshi, O. Takahashi, E. Kurimoto and A. Oda, Comparison of the activation energy barrier for succinimide formation from α-and β-aspartic acid residues obtained from density functional theory calculations, Biochim. Biophys. Acta, Proteins Proteomics, 2018, 1866, 759–766 CrossRef CAS PubMed.
- X. Li, Z. Cai and M. D. Sevilla, Investigation of proton transfer within dna base pair anion and cation radicals by density functional theory (dft), J. Phys. Chem. B, 2001, 105, 10115–10123 CrossRef CAS.
- H. B. Schlegel, Exploring potential energy surfaces for chemical reactions: an overview of some practical methods, J. Comput. Chem., 2003, 24, 1514–1527 CrossRef CAS PubMed.
- J. Bronsted, Acid and basic catalysis, Chem. Rev., 1928, 5, 231–338 CrossRef CAS.
- R. P. Bell, The theory of reactions involving proton transfers, Proc. R. Soc. London, Ser. A, 1936, 154, 414–429 Search PubMed.
- M. G. Evans and M. Polanyi, Some applications of the transition state method to the calculation of reaction velocities, especially in solution, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- P. N. Plessow and F. Abild-Pedersen, Examining the linearity of transition state scaling relations, J. Phys. Chem. C, 2015, 119, 10448–10453 CrossRef CAS.
- A. O. Cohen and R. A. Marcus, Slope of free energy plots in chemical kinetics, J. Phys. Chem., 1968, 72, 4249–4256 CrossRef CAS.
- M. M. Melander, Grand Canonical Rate Theory for Electrochemical and Electrocatalytic Systems I: General Formulation and Proton-coupled Electron Transfer Reactions, J. Electrochem. Soc., 2020, 167, 116518 CrossRef CAS , ISBN: 192.38.90.123..
- S. M. Brown, M. J. Orella, Y. W. Hsiao, Y. Roman-Leshkov, Y. Surendranath, M. Z. Bazant, and F. Brushett, Electron Transfer Limitation in Carbon Dioxide Reduction Revealed by Data-Driven Tafel Analysis, ChemRxiv, 2020, preprint, DOI:10.26434/chemrxiv.13244906.v1.
- S. Gosavi and R. A. Marcus, Nonadiabatic Electron Transfer at Metal Surfaces, J. Phys. Chem. B, 2000, 104, 2067–2072 CrossRef CAS.
- S. Choi, Prediction of transition state structures of gas-phase chemical reactions via machine learning, Nat. Commun., 2023, 14, 1168 CrossRef CAS PubMed.
- T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Machine learning activation energies of chemical reactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 12(4), e1593 Search PubMed.
- J. A. Garrido Torres, P. C. Jennings, M. H. Hansen, J. R. Boes and T. Bligaard, Low-Scaling Algorithm for Nudged Elastic Band Calculations Using a Surrogate Machine Learning Model, Phys. Rev. Lett., 2019, 122, 156001 CrossRef CAS PubMed.
- S. Heinen, G. F. von Rudorff and O. A. von Lilienfeld, Toward the design of chemical reactions: machine learning barriers of competing mechanisms in reactant space, J. Chem. Phys., 2021, 155, 064105 CrossRef CAS PubMed.
- C. A. Grambow, L. Pattanaik and W. H. Green, Deep Learning of Activation Energies, J. Phys. Chem. Lett., 2020, 11, 2992–2997 CrossRef CAS PubMed.
- K. A. Spiekermann, L. Pattanaik and W. H. Green, Fast Predictions of Reaction Barrier Heights: Toward Coupled-Cluster Accuracy, J. Phys. Chem. A, 2022, 126, 3976–3986 CrossRef CAS PubMed.
- R. Jackson, W. Zhang and J. Pearson, Tsnet: predicting transition state structures with tensor field networks and transfer learning, Chem. Sci., 2021, 12, 10022–10040 RSC.
- W. Yang, Direct calculation of electron density in density-functional theory, Phys. Rev. Lett., 1991, 66, 1438 CrossRef CAS PubMed.
- T. Stuyver and S. Shaik, Unifying conceptual density functional and valence bond theory: the hardness–softness conundrum associated with protonation reactions and uncovering complementary reactivity modes, J. Am. Chem. Soc., 2020, 142, 20002–20013 CrossRef CAS PubMed.
- E. P. Wigner, Gruppentheorie und ihre anwendung auf die quantenmechanik der atomspektren, 1931 Search PubMed.
- G. F. von Rudorff, S. N. Heinen, M. Bragato and O. A. von Lilienfeld, Thousands of reactants and transition states for competing e2 and s2 reactions, Mach. Learn.: Sci. Technol., 2020, 1, 045026 Search PubMed.
- L. A. Agapito, S. Ismail-Beigi, S. Curtarolo, M. Fornari and M. B. Nardelli, Accurate tight-binding hamiltonian matrices from ab initio calculations: minimal basis sets, Phys. Rev. B, 2016, 93, 035104 CrossRef.
- M. Geiger and T. Smidt, e3nn, Euclidean Neural Networks, arXiv, 2022, preprint, arXiv:2207.09453 [cs], DOI:10.48550/arXiv.2207.09453.
- G. S. Hammond, A correlation of reaction rates, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for h to rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Heinen, G. F. von Rudorff and O. A. von Lilienfeld, Transition state search and geometry relaxation throughout chemical compound space with quantum machine learning, J. Chem. Phys., 2022, 155(22), 221102 CrossRef PubMed.
- E. Heid, K. P. Greenman, Y. Chung, S.-C. Li, D. E. Graff, F. H. Vermeire, H. Wu, W. H. Green, and C. J. McGill, Chemprop: a machine learning package for chemical property prediction, 2023 Search PubMed.
- A. D. Kaplan, C. Shahi, P. Bhetwal, R. K. Sah and J. P. Perdew, Understanding density-driven errors for reaction barrier heights, J. Chem. Theory Comput., 2023, 19, 532–543 CrossRef CAS PubMed.
- C. A. Grambow, L. Pattanaik and W. H. Green, Reactants, products, and transition states of elementary chemical reactions based on quantum chemistry, Sci. Data, 2020, 7, 137 CrossRef CAS PubMed.
- K. A. Spiekermann, T. Stuyver, L. Pattanaik and W. H. Green, Comment on ‘physics-based representations for machine learning properties of chemical reactions’, Mach. Learn.: Sci. Technol., 2023, 4, 048001 Search PubMed.
- A. P. Bento and F. M. Bickelhaupt, Nucleophilicity and leaving-group ability in frontside and backside sn2 reactions, J. Org. Chem., 2008, 73, 7290–7299 CrossRef CAS PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Advances in molecular quantum chemistry contained in the Q-Chem 4 program package, Mol. Phys., 2015, 113, 184–215, DOI:10.1080/00268976.2014.952696.
- K. Mathew, J. H. Montoya, A. Faghaninia, S. Dwarakanath, M. Aykol, H. Tang, I.-h. Chu, T. Smidt, B. Bocklund and M. Horton, et al., Atomate: a high-level interface to generate, execute, and analyze computational materials science workflows, Comput. Mater. Sci., 2017, 139, 140–152 CrossRef.
- A. Jain, S. P. Ong, W. Chen, B. Medasani, X. Qu, M. Kocher, M. Brafman, G. Petretto, G.-M. Rignanese and G. Hautier, et al., Fireworks: a dynamic workflow system designed for high-throughput applications, Concurr. Comput. Pract. Exp., 2015, 27, 5037–5059 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): a robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- F. Weigend, F. Furche and R. Ahlrichs, Gaussian basis sets of quadruple zeta valence quality for atoms h–kr, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- A. Becke, Density-functional thermochemistry. iii. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04411d |
| This journal is © The Royal Society of Chemistry 2024 |