Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational insights into steady-state and dynamic Joule-heated reactors†
Arnav
Mittal
a,
Marianthi
Ierapetritou
ab and
Dionisios G.
Vlachos
 *ab
*ab
aDepartment of Chemical and Biomolecular Engineering, University of Delaware, 150 Academy St., Newark, DE 19716, USA. E-mail: vlachos@udel.edu
bDelaware Energy Institute, University of Delaware, 221 Academy St., Newark, DE 19716, USA
First published on 10th June 2024
Abstract
Joule-heated reactors could drive high-temperature endothermic reactions without heat transfer limitations to the catalyst and with high energy efficiency and fast dynamics under suitable conditions. We use 3D computational fluid dynamics (CFD) to investigate the power distribution, temperature field, and flow patterns in continuous steady-state and rapid-pulse Joule heated reactors with carbon fiber paper as the heating element. The model is in good agreement with published experimental data. We demonstrate flow recirculation under typical conditions and derive criteria for their suppression. We showcase rapid (seconds or shorter) and uniform heating to very high temperatures (>1500 °C) with minimal heating of the flowing gas, which could reduce undesired gas-phase chemistry. A simple energy model indicates that a high applied voltage and heating elements of high electrical conductivity and low volumetric heat capacity accelerate heating. We report heat transfer enhancement during rapid pulsing, a form of process intensification enabled by dynamic operation.
1. Introduction
Manufacturing is the world's largest energy-consuming sector and the third-largest source of greenhouse gas emissions.1–3 Process heating of chemical manufacturing accounts for 36% of the total energy consumption of the manufacturing sector.1–4 This underscores an urgent need to develop and deploy scalable and sustainable technologies that decouple economic growth from greenhouse gas emissions to decarbonize the industrial sector using renewable electricity.5 An effective decarbonization approach involves developing new processes for chemical production that replace fossil fuels with energy from wind and solar sources.1 Electrification methods that convert electricity into heat, such as microwave heating,6–9 induction heating,10 and Joule heating,11–16 are such technologies. Among these, Joule heating is the only one that directly transforms electrical energy into thermal energy.17Recent studies proposed that reactor internal Joule heating elements can eliminate heat transfer limitations from the reactor wall to the catalyst and save 2× the energy compared to a furnace for high-temperature endothermic reactions, such as ammonia decomposition, methane reforming, high-temperature pyrolysis, alkane dehydrogenation, and plastics recycling.18,19 Our previous work used a carbon fiber paper (CFP) heating element and achieved very high heating rates (∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 °C s−1) and a near-isothermal catalyst surface.18 Other studies20–24 used different geometries to understand the reactor's dynamics, gas temperature contours, and the effect of reactor size on heat transfer. Despite advances, the spatiotemporal flow and temperature fields in Joule-heated reactors are hard to obtain experimentally but are crucial for efficient reactor operation.25 Computational fluid dynamics (CFD) can be employed to provide temperature and flow fields non-intrusively, insights into operation, and transients with unprecedented spatiotemporal resolution.7,16,26,27
000 °C s−1) and a near-isothermal catalyst surface.18 Other studies20–24 used different geometries to understand the reactor's dynamics, gas temperature contours, and the effect of reactor size on heat transfer. Despite advances, the spatiotemporal flow and temperature fields in Joule-heated reactors are hard to obtain experimentally but are crucial for efficient reactor operation.25 Computational fluid dynamics (CFD) can be employed to provide temperature and flow fields non-intrusively, insights into operation, and transients with unprecedented spatiotemporal resolution.7,16,26,27
In our study, we first compare CFD simulations with experimental data and then examine flow and temperature patterns in Joule reactors under steady state, transient, and rapid pulse heating operation. We found that carbon heating elements can achieve high, uniform temperatures, crucial for efficient catalyst use, and localize hot zones near the element to mitigate unwanted gas-phase reactions. We observed reverse flows influenced by the element's steady-state temperature. Strategies to reduce reverse flows and prevent dead zones are proposed. Heat transfer between the element and gas results in low Nusselt numbers. We also showed that rapid pulse Joule heating enhances heat transfer, essential for industrial applications. The voltage, heating element length, and the element's electrical conductivity and volumetric heat capacity enable ultra-fast heating and a short time to attain steady state. We have also developed an analytical model to describe the system's dynamics and timescales crucial for designing reactors.
This article is structured as follows. First, we present the computational methodology and system schematics employed in analyzing flow and temperature profiles in Joule heating reactors. This is followed by a description of the parameters for assessing the performance of the Joule heating reactor. In the results and discussion, we provide experimental validation for the CFD model, present steady-state results for a continuous Joule heated reactor and discuss transient behavior and rapid pulsing with insights from a 0D model. The conclusions highlight the key findings.
2. System description and computational methods
2.1 System description
Scheme 1 shows the geometry of the Joule heating reactor, where V1 represents the surface connection to the positive terminal and V0 represents the ground connection (0 V). We model a carbon fiber paper (length (L) = 38 mm, width (Lw) = 8 mm, and thickness (Lth) = 0.21 mm, refer to Table 1 for material properties) contained within a quartz tube (radius (r) = 11 mm, length (Lt) = 80 mm) in continuous gas flow. A constant voltage V is applied across the carbon fiber paper.| Material property | Carbon fiber paper values |
|---|---|
| Thermal conductivity [W m−1 K−1]28,29 | 400 |
| Density [kg m−3]30 | 452.38 |
| Heat capacity [J kg−1 K−1]31 | 2253 + 0.038 × T − 3.8 × 105/T |
| Electrical conductivity [S m−1]18 | 1/[0.00021 × [0.76 − 0.000113 × (T − 273.15)]] |
| Relative permittivity [1]32 | 4960 |
| Emissivity (this work with data from ref. 18) | 0.68 |
| Effective voltage (this work with data from ref. 18) | 0.97 × V |
2.2 Models and computational methods
We solve the electric current, fluid dynamics, and heat-transfer equations. The current density J in the carbon fiber paper is described using the Maxwell–Ampere law33,34 | (1) |
| E = −∇V | (2) |
| ∇·J = 0 | (3) |
 | (4) |
 . The dissipated power serves as a heat generation term in the energy balance equation (eqn (5)).33
. The dissipated power serves as a heat generation term in the energy balance equation (eqn (5)).33 | (5) |
 | (6) |
 | (7) |
Scheme 2 illustrates the boundary conditions of the model. All Joule heating element surfaces except the terminals are electrically insulated. At the carbon paper–gas interface, the tangential component of the electric field and the normal component of electric displacement are considered continuous. Heat loss due to natural convection is imposed outside the quartz tube. We also consider radiation loss from all surfaces of the carbon fiber paper to the environment. The initial temperature is 20 °C. The temperature at the inlet (Ting) is 20 °C, and a zero gradient boundary condition is applied at the outlet. A zero gradient for pressure and no-slip boundary condition for velocity are imposed at the tube wall. A zero gradient and constant velocity are used for the pressure and velocity at the inlet, respectively. At the outlet, the velocity has zero gradient, the backflow is suppressed, and the pressure is constant (atmospheric). A mesh dependency was performed to ensure discretization-independent results (Fig. S1†). We have utilized a fine general physics mesh for the heating tape and normal for the quartz tube and the fluid dynamics. The emissivity and effective voltage faced by the element were adjusted by matching the predicted temperature and current to our previous experiments (see also below and Table 1).18
Flow dynamics is primarily influenced by interfacial, viscous, and gravitational (buoyant) forces. To understand the relevant forces, we compared nitrogen (N2) and helium (He) as a carrier gas (see Table 2 for gas properties calculated at 20 °C using the in-built COMSOL material module). These gases share similar volumetric heat capacity (density × heat capacity) but the density, mass-based specific heat, thermal conductivity, and viscosity differ substantially. To assess the presence of reverse flow, we use the criterion of Visser et al.36,37 Reverse flow exists when the axial component of the velocity (uz) falls below −0.1 times the average axial velocity (uavg). In dimensionless form, reverse flows are prevented when the ratio of the Grashof number (Gr) to the Reynolds number (Re) (refer to ESI† for definitions, eqn (S1) and (S2)),36,38 is smaller than αcrit. αcrit can be determined by increasing the inlet flow rate for given conditions until no reverse flow occurs.
| Property (20 °C)35 | Helium (He) | Nitrogen (N2) |
|---|---|---|
| Density (kg m−3) | 0.16 | 1.16 |
| Viscosity (Pa s) | 1.95 × 10−5 | 3.805 × 10−5 |
| Thermal conductivity (W m−1 K−1) | 0.15 | 0.06 |
| Heat capacity (J kg−1 K−1) | 5195 | 1040 |
| Volumetric heat capacity (J m−3 K−1) | 852.0 | 1206.4 |
To investigate the axial variation of heat transfer from the element to the gas, we calculated the Nusselt number (Nu, eqn (8)) along the heating element in the wide dimension (x-direction in the ZX plane, refer to Scheme 1) using eqn (9).37–39
 | (8) |
 | (9) |
 was evaluated using a 3 point forward finite difference scheme with a step size of 0.105 mm by metanalysis of the CFD data.
was evaluated using a 3 point forward finite difference scheme with a step size of 0.105 mm by metanalysis of the CFD data.
To support insights regarding flow and heat transfer, we estimated the carbon tape heating and cooling rates (upon turning the power off), the time to reach steady state, and the steady state temperature (refer to Fig. S2† for details).  is the carbon tape spatial average steady state temperature. Steady state is achieved when
is the carbon tape spatial average steady state temperature. Steady state is achieved when  , where
, where ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) e is the temperature spatial average over the volume of the heating element and Δt is the time step. tss corresponds to the time elapsed to reach the steady state temperature. The heating rate is the slope of the fit from the initial temperature to
e is the temperature spatial average over the volume of the heating element and Δt is the time step. tss corresponds to the time elapsed to reach the steady state temperature. The heating rate is the slope of the fit from the initial temperature to  . The cooling rate is determined similarly when the temperature decreases upon turning the power off.
. The cooling rate is determined similarly when the temperature decreases upon turning the power off.
The temperature uniformity of the element at steady state is evaluated using the coefficient of variance (CV).40 CFD also solves the heat equation inside the heating element. As both faces of the element are symmetric, the temperature profile for one of the surfaces (Ts) is used to calculate the CV.
 | (10) |
To gain insights, a simple 0-D model for an isothermal element is also derived below. The validity of the assumption is discussed in the Results and discussion section. The element's temperature, Te, evolution is described using a simple energy balance across the element volume:
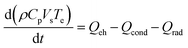 | (11) |
 | (12) |
| Qcond = hA(Te − Ta) | (13) |
| Qrad = eΣA(Te4 − Ta4) | (14) |
3. Results and discussion
3.1 Comparison to experimental data
Experiments from previous work18 was used to validate our CFD model. The experiments consist of a vertical tubular reactor made of quartz with gas flowing from top to bottom. The CFP element is held by two stainless steel clamps and four copper plates, and a DC power supply provides the current for Joule heating. We compared our predictions with the CFP element's steady state temperature under continuous operation at various voltages with He flowing at 90 mL min−1 using the infrared (IR) camera (Optris PI 1M or PI640). CFD temperatures for continuous Joule-heated reactors at various voltages are in excellent agreement with experimental data (Fig. 1a), with a relative deviation of <0.5%. The insets show an IR camera image highlighting the experimental element temperature uniformity. Experiments shows that the heating element remains stable experimentally over days of operation. Longer time on stream data will be valuable. Under adiabatic conditions, one would expect high wall temperatures and materials stability would need attention.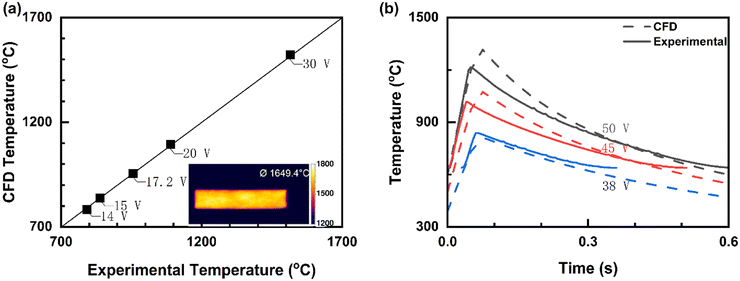 | ||
| Fig. 1 Comparison of CFD and published experimental data.18 (a) Average steady-state element's surface temperature for continuous Joule-heated reactors at various voltages with He, flowing at 90 mL min−1 (element's length = 38 mm, width = 8 mm, and thickness = 0.21 mm). The inset shows IR data indicating the temperature uniformity. (b) Transient data for rapid pulse Joule-heated reactors (50 ms of heating and 950 ms of cooling. The IR camera detects down to 638.5 °C and thus, cooling-phase transient data below this temperature is not shown). | ||
Fig. 1b compares our prediction with the element surface temperatures for transient operation with the voltage turned on and then off for three settings. The IR camera had a lower detection limit (the solid lines are truncated at long times). Additional validation data is shown in Table S1.† Given that the properties of the materials are not as accurately known, especially their temperature dependence, the model predictions are satisfactory.
3.2 Steady-state flow and temperature in continuous Joule-heated reactors
The majority of the literature Joule-heated reactors operate at steady state (a continuous Joule-heated reactor).42,43 Thus, we first investigate the Joule heated reactor's temperature followed by flow at steady state.Highly endothermic reactions, such as propane dehydrogenation or methane reforming, need high temperatures, which can also trigger undesired gas phase reactions. Joule heated reactors using a CFP element can provide high temperatures while minimizing undesirable reactions.18,20 For example, how localized the temperature field is near the heating element is unclear. We analyze the temperature field without reactions to provide insights. Fig. 2a–d shows isotherm contours on two planes (ZX and ZY) parallel to the z-axis at various He flow rates. The gas temperature remains high only near the heating element. It decreases with increasing distance (x and y-axis distance) from the heating element. Lower inlet gas flow rates (Fig. 2a–c) result in the incoming gas being heated near the entrance of the reactor, due to heat transfer upstream, whereas higher inlet flow rates (Fig. 2d) result in heating of the gas after a certain distance from the entrance. Fig. 2e depicts the temperature contours for the element, showing negligible change with increasing inlet flow rate. The temperature of >80% of the surface is within 15 K (1805–1790 K). The edges, especially near the entrance, are slightly colder (∼1770 K) than the center (∼1805 K). Overall, the temperature gradient along the surface is small (<2% of the maximum temperature and the coefficient of variance (CV) < 0.1%), i.e., the surface is almost isothermal despite the very high temperature. Unlike temperature gradients in other Joule-heated reactors, e.g., external wall-heated, the carbon heating tape leads to very efficient and uniform catalyst utilization.18
The radial distance between isotherms in the gas is constant, implying a roughly constant spatial temperature gradient. The gas temperature profile between the element and the quartz tube remains similar when changing the inlet flow rate, and the reactor has fixed hot and cold regions at steady state. High temperatures happen on the catalyst and a hot zone contained only near the element; the gases experience rapid cooling away from the heating element (at ∼5 mm axially and ∼8 mm radially, the temperature has dropped from 1700 K to 600 K). This localized hot zone confined to the element, as seen in Fig. 2, aligns with prior hypothesis that the gas remains cold. The CPF behaves unlike Wismann et al.23 FeCrAl element, who found significant temperature gradients across it due to its lower thermal conductivity. This rapid cooling significantly reduces the likelihood of undesirable gas phase side reactions. The rapid quenching of the gas phase and reduced coking by gas chemistry, consistent with experiments,20 is a novel characteristic of the heating tape.
As the gas inlet flow rate increases, the gas heat-carrying capacity increases, shifting the isotherms downwards (along the + z-axis). The z-distance between the isotherms upstream of the element decreases. Conversely, the z-distance between contours downstream of the element increases, i.e., as the inlet flow rate increases, the distance required for cooling downstream becomes greater. The gas cools and heats faster with increasing inlet flow rate.
Here we assess the effect of increasing inlet gas flow rate on both the outlet gas temperature  and element's average temperature
and element's average temperature  (Fig. 3a) for the two gases. The tape temperature is very high despite the relatively low voltage applied and the heat losses (discussed next). Clearly, one can achieve catalyst temperatures unachievable by conventional means. Surprisingly, despite the high heating element temperature, the exit gas temperature is hardly above room temperature. As the inlet flow rate increases,
(Fig. 3a) for the two gases. The tape temperature is very high despite the relatively low voltage applied and the heat losses (discussed next). Clearly, one can achieve catalyst temperatures unachievable by conventional means. Surprisingly, despite the high heating element temperature, the exit gas temperature is hardly above room temperature. As the inlet flow rate increases,  increases gradually for He and
increases gradually for He and 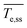 increases slightly. This aligns with the increase in the gas expansion observed with increasing inlet flow rate. For N2,
increases slightly. This aligns with the increase in the gas expansion observed with increasing inlet flow rate. For N2,  is higher by approximately 100 °C and
is higher by approximately 100 °C and  is slightly comparable to He.
is slightly comparable to He. 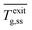 increases with an increase in the inlet gas flow rate as the gas removes more energy from the element.
increases with an increase in the inlet gas flow rate as the gas removes more energy from the element.
We analyze the energy dissipation to understand the low outlet temperature despite the element's high temperatures. Most of the power supplied is lost through radiation (Fig. 3b). A small fraction is lost through conduction from the element surface to the gas, which is then convected and conducted toward the quartz tube. This energy is eventually carried away by the air circulating outside the quartz tube. The quartz tube power loss through radiation is negligible, due to its low temperature (∼20 °C). The remainder of the power supplied is carried by the outlet gas (this is a very small fraction). Owing to the low thermal conductivity of N2, the power transferred to the quartz tube is reduced. This results in diminished power loss to the environment as compared to He (6% vs. 21.8%), consistent with the results in Fig. 3a. The data highlights a potential strategy for enhancing power efficiency by minimizing radiative power loss through radiation reflection (Fig. S3† shows the element's temperature profile when we trap radiation). At these high heating elements temperatures, radiation dominates heat losses, as expected, the heat transfer to the gas is slow, and the heat losses from such a microsystem are huge that the exit gas is hardly warm.
A similar analysis was conducted for  ∼ 1000 °C and 600 °C, with N2 flowing, as shown in Fig. S4.† At 1000 °C (methane reforming temperatures), radiation remains the primary power loss mechanism, accounting for about 70% of the total, but is now comparable in magnitude to the conduction power loss. At 600 °C (propane and ethane dehydrogenation temperature), radiation and conductive power losses are comparable. The reduction in the radiation power loss (and the corresponding increase in the conduction power loss) as
∼ 1000 °C and 600 °C, with N2 flowing, as shown in Fig. S4.† At 1000 °C (methane reforming temperatures), radiation remains the primary power loss mechanism, accounting for about 70% of the total, but is now comparable in magnitude to the conduction power loss. At 600 °C (propane and ethane dehydrogenation temperature), radiation and conductive power losses are comparable. The reduction in the radiation power loss (and the corresponding increase in the conduction power loss) as 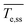 decreases is attributed to the T4 dependency of the radiation term. This highlights the significance of employing an adiabatic system. At these temperatures,
decreases is attributed to the T4 dependency of the radiation term. This highlights the significance of employing an adiabatic system. At these temperatures,  changes negligibly (<1%) with increasing gas flow rate.
changes negligibly (<1%) with increasing gas flow rate.
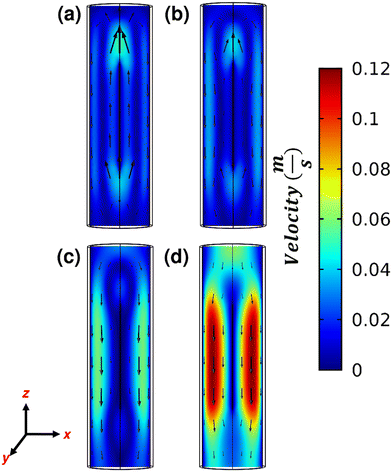
The temperature profile of the gas influences the velocity profile (and vice versa). This interplay between temperature and velocity results in different flow patterns that can either improve or hinder reactor performance. In Joule heated reactors, we observe reverse flow facilitated by buoyant forces due to the cool gas entering the reactor and contacting the hot element, inducing a density difference. These buoyant forces are countered by the inertial and viscous forces. This is illustrated in Fig. 4 which shows the axial velocity on the ZY plane at various inlet flow rates. Positive velocity means an upward gas flow; negative implies downward motion. Fig. 4a–c indicates reverse flow. As inertial and viscous forces become strong, no reverse flow is seen at higher inlet flow rates, e.g., 720 mL min−1 (Fig. 4d).
 | ||
| Fig. 4 Axial velocity on the ZY plane of the heating element with 30 V applied and He inlet flow rate of (a) 90 mL min−1, (b) 180 mL min−1, (c) 360 mL min−1, and (d) 720 mL min−1. | ||
Reverse flow affects the vertical velocity (z-component), altering the flow's overall magnitude and direction. Fig. 5 illustrates the velocity magnitude on the plane perpendicular to the heating element (XZ plane) at various inlet flow rates. Fig. S5† shows the velocity magnitude in ZY plane. Low inlet flow rates result in reverse flows, with the maximum velocity magnitude seen above the element. Comparatively, a lower velocity magnitude occurs below the element (Fig. 5a). A minimum velocity magnitude occurs near the walls. As inertial and viscous forces increase with increasing inlet flow rate, the velocity magnitude builds up around the element and decreases above and below the element. Hence at high flow rates (Fig. 5d), a significantly higher velocity is seen around the element, whereas a minimum is seen above the element and near walls. Fig. 5a–c also shows vortices above and below the element because of the reverse flow. Despite minimal reverse flow in Fig. 5c, most of the gas flows near the walls avoiding the reverse flow near the element. A forward flow is seen in Fig. 5d.
We compare the axial location of maximum velocity magnitude for various flow rates in Fig. 5. Fig. 5 presents the maximum velocity magnitude within the XY plane (refer to Scheme 1), perpendicular to the reactor axis, versus position at steady state. The expected maximum velocity profile in the XY plane typically shows an increase from the inlet up to the element, followed by a region where the velocity remains constant over the element, and then a decrease toward the outlet. This pattern is attributed to the flow dividing into two distinct streams when it encounters the element. Fig. 6 reveals this expected trend only when the inlet flow rate exceeds 360 mL min−1, i.e., under minimal reverse flow. For lower inlet flow rates, there is a peak in velocity before reaching the heating element (vortices formation), followed by a region of nearly constant velocity over the element. Remarkably, at low inlet flow rates, such as 90 mL min−1, a secondary peak in velocity appears after the element.
 | ||
| Fig. 6 Maximum velocity magnitude vs. axial position from reactor top to bottom. Shaded region represents the space parallel to the element. 30 V was applied for various He flow rates. | ||
Reverse flows have been observed when high-temperature elements interact with gas flows, such as horizontal and vertical metal–organic chemical vapor deposition (MOCVD) reactors. It has been found that reverse flow significantly affects the reactor temperature uniformity.44,45 In MOCVD reactors, a cold gas finger at specific velocities was seen and attributed to reverse flows, a phenomenon also influenced by gas properties. For instance, a stable flow was observed above 80 cm s−1 for He and hydrogen (H2) while N2 and argon (Ar) consistently exhibit unstable flows.45 Reverse flow leads to instability in laminar flow profile, causing entrance effects.46,47 Furthermore, they create dead zones and minimize yield in chemical reactors.36,38 In MOCVD reactors, the heating element is typically placed near the reactor wall, and transient operations have not been studied.
As mentioned above, the onset of reverse flow is often characterized by αcrit, which depends on the heating rate (Fig. S6† shows αcrit for various heating rates) due to its effect on the thermal boundary layer, indirectly influencing the buoyant force and the amount of gas traveling backwards. We regressed αcrit at various voltages for He, yielding eqn (15), where Rh stands for the heating rate and αcrit is the critical value at a given heating rate.
αcrit = 8.145 × Rh + 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 206 206 | (15) |
Fig. 7 shows the variation of the Nu number along the length of the heating element for varying inlet flow rate. We observe an asymmetric U-shaped profile for all inlet flow rates, with high Nu values ∼4.5 at the start and ∼3.8 near the end of the element, possibly due to vortex formation leading to faster heating of the gas than the middle of the element. A constant value of ∼1.4 is observed over most of the element. Interestingly, the inlet flow rate has no obvious effect on the Nu number. This occurs when the heat transfer between the element and the gas is dominated by free convection, manifested with a high Richardson number  .48,49 This also means that the thermal boundary layer is governed by the buoyant force and gas expansion (variables such as gas properties and
.48,49 This also means that the thermal boundary layer is governed by the buoyant force and gas expansion (variables such as gas properties and  ) rather than the inertial or viscous forces. A constant Nu reflects a fully developed laminar flow and a low Gr number.48
) rather than the inertial or viscous forces. A constant Nu reflects a fully developed laminar flow and a low Gr number.48
 | ||
| Fig. 7 Impact of inlet flow rate on the Nu number vs. distance from the leading edge of the heating element at steady state. 30 V applied to CFP. | ||
A similar analysis for an incompressible flow gave an average Nu ∼ 2 (results shown in Fig. S8†). This implies that compressibility has some effect on heat transfer.38 When Ri ≫ 1, the empirical correlation (eqn (16)) for a hot vertical plate can be used49 for a Rayleigh number Ra ≤ 108
 | (16) |
 is 1.23 compared to 1.4 shown in Fig. 7.48
is 1.23 compared to 1.4 shown in Fig. 7.48
3.3 Dynamic joule heating
Time scales play a crucial role in the design of continuous and pulsed Joule-heated reactors. Each CFD simulation takes 6–12 h computing time using 36 CPU's (Intel E5-2695 V4) on a high-performance computing cluster to obtain a solution of a given pulse. Here, we exploit an analytical, dynamic, spatially homogeneous (0D) model for rapidly predicting the temperature of the Joule heating element, the time to reach steady state, and the heating and cooling rates. The model is grounded on the isothermicity of the element due to its high thermal conductivity. The heating time scale for the gas is discussed in the ESI.† In evaluating the results of CFD and this simple model, one should keep in mind the element material's physical constraints, e.g., the melting temperature, and use realistic physical parameters.Our model predicts the heating rate (Rh), the temperature at steady state (Te,ss), and the time to reach steady state (tss) within 15% of the CFD data (refer to Fig. S9† for parity plots).
We can get further insights by introducing the dimensionless temperature, the catalyst residence time based on the inlet velocity (Uin), and the associated dimensionless time.
 | (17) |
 | (18) |
 | (19) |
 | (20) |
 | (21) |
 | (22) |
 | (23) |
 where tcond is the heat conduction time scale, tconv is the heat convection time scale, and r is the radius of the tube), and Bo is the Boltzmann number (
where tcond is the heat conduction time scale, tconv is the heat convection time scale, and r is the radius of the tube), and Bo is the Boltzmann number ( with the dimension of time, in s).50
with the dimension of time, in s).50
α, β, and γ represent the dimensionless rate of Joule heating and losses due to gas conduction/convection and radiation, respectively. α includes the key physical properties of the element (electrical conductivity and volumetric heat capacity), its geometric length, and the voltage. The strongest dependence of α is on the voltage, V2. As one changes variables while keeping a constant residence time, the dependence on the heating element length L is also strong, L−2. Without such a constrain, the dependence of α on physical properties and length is linear or inverse linear. One can increase the Joule heating rate by increasing the voltage, selecting a heating element material with high electric conductivity and low volumetric heat capacity, and a short length.
β includes the ratio of the thermal conduction rate to the thermal convection rate (Pe), the ratio of convective to conductive heat transfer across the boundary of the element and the fluid (Nu), the ratio of the tube's radius squared to geometric features of the heating element, r2/(L × Lth), and the ratio of the gas' volumetric heat capacity to that of the element. Increasing the heat transfer coefficient (h) or the element's length leads to increased heat loss to the gas (β). Increasing the element's volumetric heat capacity and element's thickness (Lth) leads to a decreased heat loss to the gas. Increasing the element's emissivity (e) and decreasing the element's thickness (Lth) or volumetric heat capacity (ρCp) leads to increased γ (radiative losses). These dimensionless constants exhibit distinct order of magnitude, with α ∼ 10–102, α ∼ 10−3 for gases and ∼10 for liquids, and γ ∼ 10−2. For this work, the geometric factor is r2/(L × Lth) ∼ 15. Since θ > 1, the last term in eqn (20) can attain values of ∼10−1 at high temperatures. The dominance of α in eqn (20) highlights the importance of the element's material selection and design (length).
Eqn (20) can be simplified for endothermic reactions essential for production of chemicals into four temperature ranges, as shown in Table 3. We utilized the 0D model to estimate the maximum power required by the CFP to achieve the desired temperature range, using the maximum temperature as the input to the model. We provide derivations in the ESI.† The table provides an estimate of the steady state temperature, the heating time scale (tH) that is the characteristic time scale for the response of the system (see ESI†), and implicitly the time to steady state (5tH) assuming constant material properties.
Temperature range I includes reactions related to biomass processing, such as fructose dehydration. Such processes frequently involve liquids (for e.g. water, ethyl acetate, methyl isobutyl ketone)51,52 that are typically governed by forced convective heat transfer from the element to the fluid due to the liquid's smaller kinetic viscosity compared to gas (water ∼10−6 m2 s−1 and gas ∼10−5 m2 s−1; free convection case also discussed in the ESI†). Also, liquids like water typically exhibit higher Nu ∼ 10–53 and Pe ∼ 0.3–10 compared to gases (Nu ∼ 4 and Pe ∼ 0.05 for He, see the ESI† for details). Despite  being an order of magnitude smaller for liquids compared to gases, liquids' β is higher due to the ratio of the volumetric heat capacities being 3–4 magnitudes larger. For, θ < 1.5 and <10 W, radiation is negligible as α, β ≫ γ, and eqn (20) is linear in θ and dependent only on α and β. Solving eqn (20) gives an estimate of the heating time scale for the element (tH ∼ 1.5 s for temperature range I for water assuming r = 11 mm, Uin = 30 ml min−1). For ranges II–III, which involve gas-phase chemistry, we can only ignore the conduction to the gas (dependence on α and γ). For range IV, eqn (20) is also only dependent on α and γ but the input power is high, making α ≫ γ. For instance, when 170 W is applied to the carbon fiber element, tH = 0.46 s and tss = 2.3 s.53 Similarly, in temperature ranges III and II, tH ∼ 1 s and ∼ 6 s, assuming 35 W and 14 W, respectively. All analytical equations in Table 3 agree well with CFD with average error ∼25% (refer to Fig. S9† for parity plots). Overall, these relatively short times indicate the ability of the system to respond fast to transient operations.
being an order of magnitude smaller for liquids compared to gases, liquids' β is higher due to the ratio of the volumetric heat capacities being 3–4 magnitudes larger. For, θ < 1.5 and <10 W, radiation is negligible as α, β ≫ γ, and eqn (20) is linear in θ and dependent only on α and β. Solving eqn (20) gives an estimate of the heating time scale for the element (tH ∼ 1.5 s for temperature range I for water assuming r = 11 mm, Uin = 30 ml min−1). For ranges II–III, which involve gas-phase chemistry, we can only ignore the conduction to the gas (dependence on α and γ). For range IV, eqn (20) is also only dependent on α and γ but the input power is high, making α ≫ γ. For instance, when 170 W is applied to the carbon fiber element, tH = 0.46 s and tss = 2.3 s.53 Similarly, in temperature ranges III and II, tH ∼ 1 s and ∼ 6 s, assuming 35 W and 14 W, respectively. All analytical equations in Table 3 agree well with CFD with average error ∼25% (refer to Fig. S9† for parity plots). Overall, these relatively short times indicate the ability of the system to respond fast to transient operations.
Similar conclusions can be derived from the element's steady state temperature. It increases with an increase in element's electrical conductivity, thickness, and voltage, and decreases with an increase in the element's length. The voltage and element's length are the dominant parameters. For temperature range I, the steady state temperature increases as h decreases. For temperature ranges II–IV, emissivity is a key parameter; a decrease in emissivity leads to an increase in temperature.
3.4 Pulsed Joule-heated reactors
Rapid pulse Joule-heated reactors have recently been proposed for higher energy efficiency and performance.18,20 The element is subjected to cycles of heating (voltage on) followed by cooling (voltage off). This process generates an oscillatory temperature profile, referred to as a ‘pulse’.Fig. S10† shows the voltage pulse applied to the element and the associated temperature profile at the element's center point. The temperature rapidly increases during heating due to the resistive power supplied (∼500 W). The radiative loss increases, explaining the decreasing heating rate at higher temperatures (a decreasing slope or effective heating rate). During cooling, the temperature gradually decreases as cooling due to conduction and radiative losses from the element. The reduction in radiation leads to a slower cooling rate with time. The conductive loss to the gas remains approximately constant throughout the cycle. As the voltage V increases, the resistive power also rises, following  , which in turn elevates the peak temperature. The duration of heating and cooling parts of the cycle (duty) also affects the temperature.
, which in turn elevates the peak temperature. The duration of heating and cooling parts of the cycle (duty) also affects the temperature.
As detailed in Fig. S11,† isotherms shift downwards as the element's temperature increases and upwards as the element's temperature decreases, following the same trend as discussed in continuous Joule-heated reactors.
Fig. 8 shows the maximum velocity vs. axial position at various times (detailed in Fig. S12†) of a given pulse. During heating, the velocity keeps on increasing due to continuous heating as the gas flows over the element. Small peaks in the velocity before the element, indicative of reverse flow, are also observed. During cooling, the velocity decreases, leading to a pressure increase and upward flow. This behavior is ascribed to substantial reverse flows (refer to Fig. S13 and S14† for axial flow velocity). The significant variations in the maximum velocity suggest changes in the residence time, which will affect chemical reactions.
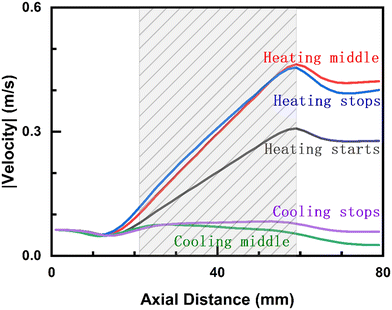 | ||
| Fig. 8 Maximum velocity normal to the reactor axis vs. axial position at 90 mL min−1 during a pulse. The shaded region denotes the heating element. | ||
The thermal boundary expands during heating and contracts during cooling, as seen in Fig. S15.† These results align with the isotherms reported by Dong et al.20 The impact of dynamics on the Nu number is shown in Fig. 9. Nu declines gradually during heating and part of the cooling until a minimum before start rising again. Fig. 9 indicates that pulsing enhances heat transfer from the element to the gas due to increased Nu number. This may have to do with the dynamic nature of the thermal boundary layer and manifests how dynamic operation intensifies the heat transfer rate.
4. Conclusions
We developed a CFD model for a Joule-heated reactor consisting of carbon fiber paper heated by an externally applied voltage. The model is in excellent agreement with experimental data. High and uniform temperatures of the CFP can be achieved with a low power input due to its high thermal and electric conductivity. Most of the power is radiated away from the element in this configuration, and the gas flowing by is hot only near the heating element. This implies that undesired gas phase chemistry can be suppressed in this configuration. At typical laboratory scales, we found flow recirculation induced by buoyancy. The reverse flow influences the temperature isotherms. Above a minimum velocity, the reverse flows are suppressed. The Nu for the heat transfer from the heating element to the gas reveals a U-shaped trend with a low magnitude indicative of free convection and enhanced transport near the leading and trailing edges of the element due to recirculation.We also developed a 0D energy balance model to predict the various timescales rapidly. The model is in decent agreement with the CFD model. Analytical expressions were derived under certain assumptions for the steady state temperature and time scale controlling heating. These reveal the dependency on various design parameters. We have identified the voltage and the element's length, electrical conductivity, and thermal conductivity as the dominant design factors. The volumetric heat capacity and the thermal conductivity of the fluid influence the heating rate and time to reach a steady state in low-temperature reactions involving liquids. Joule-heated reactors showcase high heating rates and a short time (seconds or shorter) to steady state and, thus, are suitable for fast transient operation. Finally, rapid pulsing enhances the heat transfer and tunes the residence time due to strong reverse flows.
Conflicts of interest
There are no conflicts of interest.Acknowledgements
This work was supported by the National Science Foundation under Grant No. 2134471.References
- D. S. Mallapragada, Y. Dvorkin, M. A. Modestino, D. V. Esposito, W. A. Smith, B.-M. Hodge, M. P. Harold, V. M. Donnelly, A. Nuz, C. Bloomquist, K. Baker, L. C. Grabow, Y. Yan, N. N. Rajput, R. L. Hartman, E. J. Biddinger, E. S. Aydil and A. D. Taylor, Joule, 2023, 7, 23–41 CrossRef CAS.
- J. E. T. Bistline and G. J. Blanford, Energy Clim. Change, 2021, 2, 100045 CrossRef CAS.
- J. DeAngelo, I. Azevedo, J. Bistline, L. Clarke, G. Luderer, E. Byers and S. J. Davis, Nat. Commun., 2021, 12, 6096 CrossRef CAS PubMed.
- E. Worrell, D. Phylipsen, D. Einstein and N. Martin, Energy use and energy intensity of the U.S. chemical industry, Report LBNL--44314, 773773, 2000 Search PubMed.
- P. R. Shukla, J. Skea, R. Slade, A. Al Khourdajie, R. van Diemen, D. McCollum, M. Pathak, S. Some, P. Vyas and R. Fradera, Climate Change 2022 - Mitigation of Climate Change, Working Group III Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 2023 Search PubMed.
- V. Palma, D. Barba, M. Cortese, M. Martino, S. Renda and E. Meloni, Catalysts, 2020, 10, 246 CrossRef CAS.
- A. Malhotra, W. Chen, H. Goyal, P. J. Plaza-Gonzalez, I. Julian, J. M. Catala-Civera and D. G. Vlachos, Ind. Eng. Chem. Res., 2021, 60, 6835–6847 CrossRef CAS.
- M. Baker-Fales, T.-Y. Chen and D. G. Vlachos, Chem. Eng. J., 2023, 454, 139985 CrossRef CAS.
- H. Goyal, Chem. Eng. Process., 2022, 178, 109026 CrossRef CAS.
- W. Wang, G. Tuci, C. Duong-Viet, Y. Liu, A. Rossin, L. Luconi, J.-M. Nhut, L. Nguyen-Dinh, C. Pham-Huu and G. Giambastiani, ACS Catal., 2019, 9, 7921–7935 CrossRef CAS.
- X. Mei, X. Zhu, Y. Zhang, Z. Zhang, Z. Zhong, Y. Xin and J. Zhang, Nat. Catal., 2021, 4, 1002–1011 CrossRef CAS.
- A. V. Porsin, A. V. Kulikov, Y. I. Amosov, V. N. Rogozhnikov and A. S. Noskov, Theor. Found. Chem. Eng., 2014, 48, 397–403 CrossRef CAS.
- V. M. Shekunova, Y. A. Aleksandrov, E. I. Tsyganova and S. V. Filofeev, Pet. Chem., 2017, 57, 446–451 CrossRef CAS.
- F. Liu, Z. Zhao, Y. Ma, Y. Gao, J. Li, X. Hu, Z. Ye, Y. Ling and D. Dong, J. Adv. Ceram., 2022, 11, 1163–1171 CrossRef CAS.
- M. Rieks, R. Bellinghausen, N. Kockmann and L. Mleczko, Int. J. Hydrogen Energy, 2015, 40, 15940–15951 CrossRef CAS.
- M. Ambrosetti, Chem. Eng. Process., 2022, 182, 109187 CrossRef CAS.
- I. Dincer, Comprehensive energy systems, Elsevier, Amsterdam, 2018 Search PubMed.
- K. Yu, C. Wang, W. Zheng and D. G. Vlachos, ACS Energy Lett., 2023, 8, 1050–1057 CrossRef CAS.
- E. Selvam, Y. Luo, M. Ierapetritou, R. F. Lobo and D. G. Vlachos, Catal. Today, 2023, 418, 114124 CrossRef CAS.
- Q. Dong, Y. Yao, S. Cheng, K. Alexopoulos, J. Gao, S. Srinivas, Y. Wang, Y. Pei, C. Zheng, A. H. Brozena, H. Zhao, X. Wang, H. E. Toraman, B. Yang, I. G. Kevrekidis, Y. Ju, D. G. Vlachos, D. Liu and L. Hu, Nature, 2022, 605, 470–476 CrossRef CAS.
- S. T. Wismann, J. S. Engbæk, S. B. Vendelbo, W. L. Eriksen, C. Frandsen, P. M. Mortensen and I. Chorkendorff, Ind. Eng. Chem. Res., 2019, 58, 23380–23388 CrossRef CAS.
- Q. Zhang, M. Nakaya, T. Ootani, H. Takahashi, M. Sakurai and H. Kameyama, Int. J. Hydrogen Energy, 2007, 32, 3870–3879 CrossRef CAS.
- S. T. Wismann, J. S. Engbæk, S. B. Vendelbo, W. L. Eriksen, C. Frandsen, P. M. Mortensen and I. Chorkendorff, Chem. Eng. J., 2021, 425, 131509 CrossRef CAS.
- L. Liu, A. Bhowmick, S. Cheng, B. H. Blazquez, Y. Pan, J. Zhang, Y. Zhang, Y. Shu, D. T. Tran, Y. Luo, M. Ierapetritou, C. Zhang and D. Liu, Cell Rep. Phys. Sci., 2023, 4, 101692 CrossRef CAS.
- M. Ambrosetti, A. Beretta, G. Groppi and E. Tronconi, Front. Chem. Eng., 2021, 3, 747636 CrossRef.
- M. Maestri and A. Cuoci, Chem. Eng. Sci., 2013, 96, 106–117 CrossRef CAS.
- S. T. Wismann, J. S. Engbæk, S. B. Vendelbo, F. B. Bendixen, W. L. Eriksen, K. Aasberg-Petersen, C. Frandsen, I. Chorkendorff and P. M. Mortensen, Science, 2019, 364, 756–759 CrossRef CAS.
- L. Zhang, K.-k. Deng, K.-b. Nie, C.-j. Wang, C. Xu, Q.-x. Shi, Y. Liu and J. Wang, iScience, 2023, 26, 106505 CrossRef CAS PubMed.
- P. Bhatt and A. Goe, Mater. Sci. Res. India, 2017, 14, 52–57 CAS.
- Fuel cell store. Freudenberg Carbon Paper GDL Properties Sheet, www.fuelcellstore.com/freudenberg-h2315, (accessed January 2024).
- A. T. D. Butland and R. J. Maddison, J. Nucl. Mater., 1973, 49, 45–56 CrossRef CAS.
- A. A. Eddib and D. D. L. Chung, Carbon, 2019, 143, 475–480 CrossRef CAS.
- AC/DC Module User's Guide, COMSOL Multiphysics ® v. 5.4, COMSOL AB, Stockholm, Sweden, 2022 Search PubMed.
- A. Kovetz, The principles of electromagnetic theory, Cambridge University Press, Cambridge [England], New York, 1990 Search PubMed.
- COMSOL Multiphysics v. 5.4, www.comsol.com, COMSOL AB, Stockholm, Sweden, 2022 Search PubMed.
- E. P. Visser, C. R. Kleijn and C. A. M. Govers, J. Cryst. Growth, 1989, 94, 929–946 CrossRef CAS.
- S. Kieda, D. Fotiadis and K. F. Jensen, J. Cryst. Growth, 1990, 102, 441–470 CrossRef.
- H. Moffat and K. F. Jensen, J. Cryst. Growth, 1986, 77, 108–119 CrossRef CAS.
- D. I. Fotiadis, M. Boekholt, K. F. Jensen and W. Richter, J. Cryst. Growth, 1990, 100, 577–599 CrossRef.
- H. Goyal, A. Mehdad, R. F. Lobo, G. D. Stefanidis and D. G. Vlachos, Ind. Eng. Chem. Res., 2020, 59, 2516–2523 CrossRef CAS.
- R. R. Ratnakar and V. Balakotaiah, Int. J. Hydrogen Energy, 2023, S0360319923039034 Search PubMed.
- V. Balakotaiah and R. R. Ratnakar, AIChE J., 2022, 68, e17542 CrossRef CAS.
- L. Zheng, M. Ambrosetti, A. Beretta, G. Groppi and E. Tronconi, Chem. Eng. J., 2023, 466, 143154 CrossRef CAS.
- L. Stock and W. Richter, J. Cryst. Growth, 1986, 77, 144–150 CrossRef CAS.
- L. J. Giling, J. Electrochem. Soc., 1982, 129, 634–644 CrossRef CAS.
- J. Van De Ven, G. M. J. Rutten, M. J. Raaijmakers and L. J. Giling, J. Cryst. Growth, 1986, 76, 352–372 CrossRef CAS.
- J. Ouazzani and F. Rosenberger, J. Cryst. Growth, 1990, 100, 545–576 CrossRef.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport phenomena, J. Wiley, New York, 2002 Search PubMed.
- T. Bergman, A. Lavine, F. Incropera and D. DewWitt, Fundamentals of heat and mass transfer, Wiley, Hoboken, NJ, 6th edn, 2007 Search PubMed.
- I. Zlatsman, A-to-Z Guide to Thermodynamics, Heat and Mass Transfer, and Fluids Engineering: AtoZ, Begellhouse, 2006 Search PubMed.
- P. Desir, B. Saha and D. G. Vlachos, Energy Environ. Sci., 2019, 12, 2463–2475 CAS.
- A. Mittal, S. Bhattacharyya, M. Marino, T.-Y. Chen, P. Desir, M. Ierapetritou and D. G. Vlachos, Ind. Eng. Chem. Res., 2023, 62, 15006–15017 CAS.
- A. Frymoyer, in Infectious Disease and Pharmacology, Elsevier, 2019, pp. 123–139 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Definition of dimensionless number, temperature profiles, flow and temperature heat maps, derivation, derivation of analytical solutions, heating time scale for the gas, and parity plots for 0-D model. See DOI: https://doi.org/10.1039/d4re00114a |
| This journal is © The Royal Society of Chemistry 2024 |