Open Access Article
Open Access ArticleUnderstanding heterogeneous growth mechanisms at graphene edges: a theoretical study on acetylene deposition and mechanistic analysis†
C.
Giudici
 a,
G.
Contaldo
a,
G.
Contaldo
 b,
M.
Ferri
b,
M.
Ferri
 b,
L.
Pratali Maffei
b,
L.
Pratali Maffei
 a,
M.
Bracconi
a,
M.
Bracconi
 b,
M.
Pelucchi
b,
M.
Pelucchi
 *a and
M.
Maestri
*a and
M.
Maestri
 *b
*b
aCRECK Modeling Laboratory, Dipartimento di Chimica, Materiali e Ingegneria Chimica, Politecnico di Milano, Piazza L. Da Vinci 32, Milan, Italy. E-mail: matteo.pelucchi@polimi.it
bLaboratory of Catalysis and Catalytic Processes, Dipartimento di Energia, Politecnico di Milano, via La Masa 34, 20156, Milano, Italy. E-mail: matteo.maestri@polimi.it
First published on 20th June 2024
Abstract
This study aims to bridge significant knowledge gaps in the understanding of graphene growth mechanisms. We enhance current kinetic models through a detailed investigation of C2H2 deposition processes on solid graphene surfaces. These processes represent key elementary reaction steps in the complex heterogeneous network responsible for pyrocarbon formation during chemical vapor deposition and infiltration processes. Unlike previous methodologies that relied on analogies with gas-phase systems, our research meticulously explored the actual system, providing a comprehensive overview of the reactions involved in graphene growth at both armchair and zigzag edges. Utilizing transition state theory, we calculate accurate, temperature-dependent rate constants for all elementary reactions in graphene edge growth. This sheds light on the mechanisms and kinetics of pyrocarbon growth, including the potential for structural defect formation. Findings are compared with analogous gas-phase reactions responsible for soot particle formation, assessing the impact of surface interactions. A lumping technique is applied to reduce the complexity of species and reactions while preserving the accuracy of the chemical description. As such, this approach offers valuable insights into relevant pathways paving the way towards a deep understanding of the chemistry of the pyrolysis of hydrocarbons aiming to produce nanomaterials with targeted properties.
1. Introduction
Hydrocarbon pyrolysis processes hold tremendous promise as highly efficient methods for fabricating value-added carbon (VAC) materials, along with the concomitant production of hydrogen, often referred to as “turquoise hydrogen”.1–3 Overall, the synthesis of graphene, pyrolytic carbon, carbon/carbon composites, carbon nanotubes, and fullerenes, among others, from hydrocarbons may enable a key material/energy nexus by fixating the carbon content of the starting feedstock into usable and durable materials, while producing hydrogen, a carbon free energy carrier that can be used for energy production avoiding CO2 emissions. VACs exhibit exceptional mechanical, electrical, and thermal properties, rendering them highly promising for a wide range of applications, including the substitution of energy-intensive materials (e.g., metals, aluminum, etc.) or a variety of other uses in the automotive, electronics or aerospace industries.4–8 However, their widespread utilization faces challenges due to the limited understanding of the underlying chemical and physical phenomena governing their growth during hydrocarbon pyrolysis. Chemical vapor deposition (CVD) and chemical vapor infiltration (CVI) represent two widely employed techniques for VAC production.9 In these processes, hydrocarbons undergo pyrolysis at high temperatures (∼800–1500 K) and low to atmospheric pressure (∼1–100 kPa) leading to the deposition of carbon atoms on a surface (CVD) or to the infiltration in a preform (CVI).10 This gradual growth or densification of the starting carbon preform enhances the thermal, mechanical, and chemical properties of the resulting material. Contextually, depending on the feedstock and on the operating conditions, H2 is produced either directly through gas-phase reactions or via gas/surface interactions (e.g., by H-atom abstractions from the surface) further valorizing the process product. This also leads to the formation of various intermediates, including low molecular weight hydrocarbons such as ethylene (C2H4), acetylene (C2H2), and propyne (C3H4), as well as aromatic compounds like benzene, toluene, fulvene, polycyclic aromatic hydrocarbons (PAHs), and amorphous carbon, commonly referred to as particulate matter, or soot. Therefore, it is of primary importance to control the selectivity towards H2 and solid materials with the desired quality and nanostructure minimizing the formation of lower value byproducts in the gas phase including amorphous carbon. To achieve this goal, the theoretical exploration of heterogeneous reaction channels and the development of predictive chemistry models are essential since they allow us to understand the underlying chemistry and to establish correlations between the starting feedstock, process conditions and process outputs (i.e., gas-phase composition, nanostructure of the solid material, H2 yield, etc.).Several heterogeneous kinetic models have been proposed in the literature to model the growth of graphene layers in both CVD and CVI processes.10–12 Among these models, the hydrogen abstraction carbon addition (HACA) mechanism has received significant attention. This is primarily due to its pivotal role in the formation and growth of polycyclic aromatic hydrocarbons (PAHs) and soot through homogeneous gas-phase reactions under conditions similar to those employed in CVD/CVI processes (i.e., low pressure and temperatures ranging from 1000 to 1500 K) as discussed in ref. 13–15. The HACA mechanism involves the formation of a σ radical via H-atom abstraction reactions by a radical species in the gas phase (e.g., Ṙ = Ḣ, ĊH3, Ċ2H3, etc.), followed by the addition of an unsaturated gas-phase intermediate (CxHy = C2H4, C2H2, etc.) on the surface radical active sites, and subsequent growth at the edges through H transfer and ring-closure reactions. A schematic of these three steps of the HACA mechanism on zigzag and armchair graphene edges is provided in Fig. 1.
Recent studies16,17 have mechanistically investigated the H-atom abstraction reactions and provided semi-empirical approaches to estimate rate constants. In particular, Ding et al.16 performed theoretical calculations for H-atom abstraction reactions by Ḣ, major alkyl and alkenyl radicals at graphene edges using density functional theory (DFT). Serse et al.17 derived empirical correlations between gas-phase reactions and gas/solid reactions from calculations of analogous reactions occurring on relatively large PAHs (phenanthrene, anthracene, tetracene) having zigzag and/or armchair configuration. The findings were then implemented in a detailed mechanistic model that was validated over a wide range of experimental targets.11,12,18–20 Nevertheless, no similar study was performed for the carbon addition step of the HACA mechanism.
Besides the inaccuracy of the currently implemented HACA kinetic parameters for gas/solid deposition mechanisms as they are largely based on direct analogies with gas-phase growth of aromatics, existing models also lack in the capability of predicting the formation of nanostructural defects such as graphene sheet curvature due to the formation of 5- or 7-membered rings, void bays, and the sp3/sp2 hybridization ratio of surface carbon. Quantifying the presence of such defects is crucial, as they significantly influence the degree of optical anisotropy and, consequently, the properties of the final material. However, existing models10–12,17 primarily focus on rather macroscopic quantities such as carbon deposition rates and deposited mass, for which some experimental data are available across a relatively wide range of kinetically controlled conditions.
Aiming to extend our recent kinetic model for pyrocarbon deposition17 to comprehensively represent the dependence of nanostructure on reactor operating conditions (temperature, pressure, surface to volume ratio, residence time), we herein present an a priori investigation of acetylene (C2H2) deposition on zigzag and armchair graphene edges in the form of activated radical sites (i.e., carbon addition step in the HACA mechanism). The selected system is representative of typical C1–C3 hydrocarbon pyrolysis, where acetylene deposition typically plays a key role in the growth of PAHs, soot and deposited pyrocarbon.13–15 Armchair and zigzag edges are selected as representatives of two different types of growth sites. The potential energy surfaces (PESs) and temperature-dependent reaction rates for C2H2 addition to the two selected sites are determined. Then, semi-quantitative validation of the findings is performed by comparison with analogous chemical pathways observed in gas-phase molecular growth processes.13,21–27 This comparison also serves to reveal the similarities to the homogeneous molecular growth of aromatics in the gas phase. A rigorous automated lumping methodology extended from gas-phase master equation calculations is finally employed (i.e., MEL),28 to better highlight dominant pathways out of a quite complex network of reactions and to simplify the implementation of these growth mechanisms in existing kinetic models by reducing the overall number of species and reactions needed to describe the edge growth processes. Overall, this study proposes a workflow that can be extended to other relevant reaction pathways in CVD chemistry, supporting the development of higher accuracy mechanistic kinetic models.
The article is organized as follows: section 2 provides a detailed description of the adopted theoretical methodology. Results are presented in section 3, starting with the exploration of the potential energy surfaces (PES) in section 3.1 for the growth of armchair edges (section 3.1.1) and zigzag edges (section 3.1.2) with the addition of C2H2. Then, in section 3.2, the temperature-dependent rate constants of the observed elementary steps are discussed in comparison with available rate constants from analogous gas-phase reactions. Section 3.3 presents the proposed final kinetic mechanism, derived through the adopted lumping methodology. Finally, section 4 summarizes the main findings, and highlights the positive implications and future perspectives of the presented study.
2. Methods
The reactivity of graphene edge growth by addition of C2H2 was investigated using density functional theory-based methods implemented in the Quantum-Espresso package.29 Electronic and geometrical properties are derived using the generalized gradient approximation proposed by Perdew–Burke–Ernzerhof (GGA-PBE30) along with periodic plane waves and ultrasoft pseudopotentials. This method has been employed to accurately describe the properties of carbon-based materials and has been widely employed in graphene-related studies.16,31–34 The plane wave cut-off was set to 40 Ry, and the contribution of long-range van der Waals interactions was accounted for by applying the Grimme-D3 scattering correction.35,36 The orthorhombic unit cells adopted for the armchair and zigzag configurations are reported in Fig. 2. The corresponding Brillouin zone has been sampled with a 5 × 1 × 1 grid. In the armchair edge unit cell, the 6-membered ring repeats three times along the x direction and five times along the z direction. For the zigzag configuration, the width of the unit cell corresponds to four and three benzene rings along the x and z direction, respectively. All of the dangling carbon bonds are saturated with hydrogen atoms, apart from one that results in the σ radical site of C2H2 addition. Thus, the resulting unit cells consist of 50 carbon atoms and 9 hydrogen atoms. To avoid interactions among the periodic replicated images, we accounted for a vacuum region with dimensions of 8.5 Å and 9.8 Å perpendicular to the armchair and zigzag graphene planes (i.e., y direction), respectively. The detailed assessment of computational parameters obtained through the convergence tests can be found in the ESI† (Fig. S5–S7).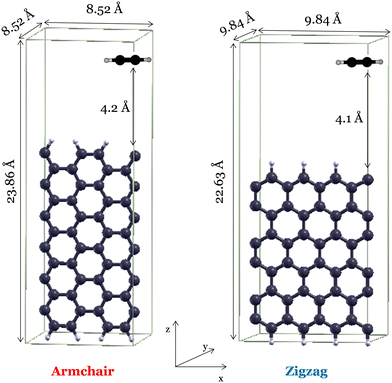 | ||
| Fig. 2 Selected unit cells for the armchair and zigzag site configurations in the presence of C2H2. Orthorhombic unit cell dimensions are reported in angstrom. | ||
The zigzag edge model was treated as antiferromagnetic, following previous studies.16,37 The climbing-image nudged elastic band (CI-NEB) methodology38 was employed to determine the transition state (TS) of each elementary reaction. We used a 16-image path sampling with a final force convergence threshold of 0.05 eV Å−1. For all local minima and transition states, the vibrational frequencies and zero-point energy (ZPE) corrections were calculated using the finite difference approximation of the Hessian matrix, as implemented in the Atomic Simulation Environment (ASE).39 TS structures were verified by visual inspection of the imaginary normal mode corresponding to the reaction coordinate.
The temperature-dependent rate constants of each elementary step on the potential energy surfaces were calculated using the harmonic transition state theory (HTST) in the mean-field approximation (MFA).40,41 Direct and reverse reaction rate constants were evaluated explicitly for each reaction j (kj) with molecularity m using the following relation:
 | (1) |
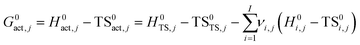 | (2) |
The temperature-dependent rate constants were then fitted according to the modified Arrhenius equation (eqn (3)) by considering a temperature range of 800–1800 K.
 | (3) |
3. Results
3.1. Investigation of reaction pathways and potential energy surfaces
Fig. 3 and 5 show the potential energy surfaces describing acetylene addition on armchair and zigzag graphene edges, respectively. Electronic energies of intermediates and TSs are reported relative to the bimolecular reactants. The relative energies of the initial states (IS) and final states (FS) used in the CI-NEB calculations of steps involving bimolecular reactants/products are also provided for completeness. Fig. 3 and 5 also report analogous energetics from literature calculations of gas-phase acetylene addition on PAHs with armchair (i.e., 4-phenanthrenyl) and zigzag (pentacyl and 1-naphthyl) edges, respectively reported in ref. 13. These values serve as benchmarks for our comparative analysis between homogeneous and heterogeneous kinetics of the HACA process. It should be noted that the reference gas-phase values exclude ZPE for a more coherent alignment with our solid-phase findings, thus facilitating a consistent and insightful juxtaposition of results. In other words the comparison is restrained to purely electronic energies. ZPE corrections, total energies, and the Cartesian atomic coordinates of the unit cell of each reactant, intermediate, product, and transition state can be found in Tables S3–S5 of the ESI.†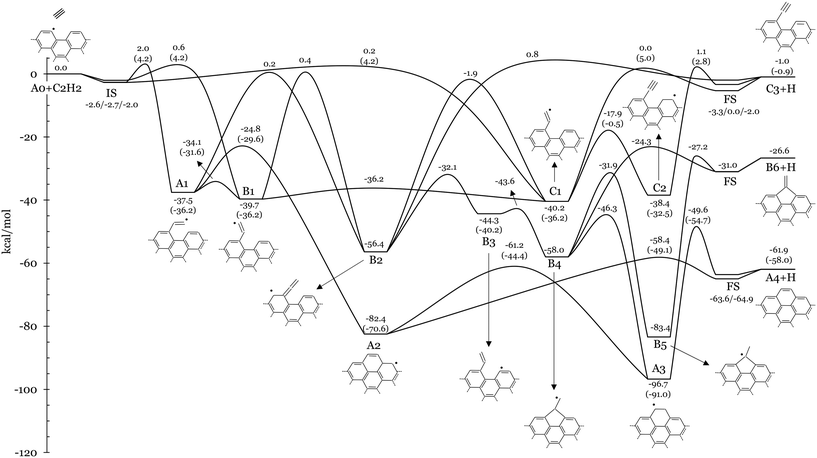 | ||
| Fig. 3 Potential energy surface of the addition of acetylene to the radical site at the armchair edge of graphene (A0 + C2H2). Electronic energies relative to A0 + C2H2 are reported in kcal mol−1. Energy values of analogous TSs and intermediates from the gas-phase C14H9 + C2H2 PES13 are also shown in brackets. ZPE corrections are not considered. A schematic graphical representation of the investigated intermediates is also provided. | ||
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, where R represents the saturated surface site), and finally B6+H, presenting a pentagonal carbon structure at the edge (Fig. 4a). These products can be formed through a series of steps that mainly involve isomerization, H-transfer, ring closure, and H-elimination reactions.
CH, where R represents the saturated surface site), and finally B6+H, presenting a pentagonal carbon structure at the edge (Fig. 4a). These products can be formed through a series of steps that mainly involve isomerization, H-transfer, ring closure, and H-elimination reactions.
 | ||
| Fig. 4 Unit cells of the bimolecular products (a) and of the three intermediates carrying an ethynyl function (b) reported in the armchair PES of Fig. 3. | ||
Deposition of C2H2 at the radical site of A0 results in the exothermic formation of an ethenyl group at the edge (R–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ĊH). Specifically, the three stereoisomers A1, B1 and C1 (Fig. 4b) are formed through barriers below 2 kcal mol−1 (i.e., EA0+C2H2⇔A1,B1,C1 = 2, 0.6, 0.2 kcal mol−1, respectively). A1 is located 37.5 kcal mol−1 below the entrance channel and the ethenyl fragment is parallel to the edge direction (see the red dashed line in Fig. 4b). Meanwhile, the ethenyl fragment lies at 120° with respect to the edge direction in B1 and C1, with hydrogen atoms in cis- and trans-configurations, respectively. The more stable C1 (EC1 = −40.2 kcal mol−1) and B1 (EB1 = −39.7 kcal mol−1) are equilibrated through a very low energy barrier (EC1⇔B1 = 4.0 kcal mol−1). Similar energetic values are reported for the addition of C2H2 to the radical site of 4-phenanthrenyl13 (i.e., C16H11 PES) with a slightly higher addition barrier of 4.2 kcal mol−1 (values in brackets in Fig. 3). The torsion of the fragment in A1
ĊH). Specifically, the three stereoisomers A1, B1 and C1 (Fig. 4b) are formed through barriers below 2 kcal mol−1 (i.e., EA0+C2H2⇔A1,B1,C1 = 2, 0.6, 0.2 kcal mol−1, respectively). A1 is located 37.5 kcal mol−1 below the entrance channel and the ethenyl fragment is parallel to the edge direction (see the red dashed line in Fig. 4b). Meanwhile, the ethenyl fragment lies at 120° with respect to the edge direction in B1 and C1, with hydrogen atoms in cis- and trans-configurations, respectively. The more stable C1 (EC1 = −40.2 kcal mol−1) and B1 (EB1 = −39.7 kcal mol−1) are equilibrated through a very low energy barrier (EC1⇔B1 = 4.0 kcal mol−1). Similar energetic values are reported for the addition of C2H2 to the radical site of 4-phenanthrenyl13 (i.e., C16H11 PES) with a slightly higher addition barrier of 4.2 kcal mol−1 (values in brackets in Fig. 3). The torsion of the fragment in A1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B1 involves a barrier of 3.4 kcal mol−1, very similar to the values of the analogous gas molecule (i.e., 4.6 kcal mol−1 (ref. 13)). Details about the hindered rotor analysis and results are reported in the ESI† (Fig. S8 and S9).
B1 involves a barrier of 3.4 kcal mol−1, very similar to the values of the analogous gas molecule (i.e., 4.6 kcal mol−1 (ref. 13)). Details about the hindered rotor analysis and results are reported in the ESI† (Fig. S8 and S9).
A hydrogen transfer from Cα to Cβ of the fragment moiety in A1 or B1 (R–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ĊH
ĊH  Ṙ
Ṙ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2) results in the formation of a radical site on the surface (B2) via energy barriers of 37.7 and 40.1 kcal mol−1, respectively. These isomerization reactions show similarities with previously investigated gas phase reactions in the C6H5 + C2H2 (ref. 21) and C16H11 (ref. 22) PESs. Tokmakov et al.21 reported an energy barrier of 45 kcal mol−1 for the smaller system, while a barrier of 42 kcal mol−1 is observed for the larger one by Li et al. B2 has the unpaired electron delocalized over the entire π-electronic system, thus justifying the higher stability of B2 compared to the gas-phase prototypes. As a result, the reactions A1
CH2) results in the formation of a radical site on the surface (B2) via energy barriers of 37.7 and 40.1 kcal mol−1, respectively. These isomerization reactions show similarities with previously investigated gas phase reactions in the C6H5 + C2H2 (ref. 21) and C16H11 (ref. 22) PESs. Tokmakov et al.21 reported an energy barrier of 45 kcal mol−1 for the smaller system, while a barrier of 42 kcal mol−1 is observed for the larger one by Li et al. B2 has the unpaired electron delocalized over the entire π-electronic system, thus justifying the higher stability of B2 compared to the gas-phase prototypes. As a result, the reactions A1  B2 and B1
B2 and B1  B2 are more exothermic (18.9 and 16.7 kcal mol−1, respectively) than their gas-phase counterparts (10.6 kcal mol−1 (ref. 21) and 7.2 kcal mol−1 (ref. 22)). However, A1 preferentially undergoes ring closure via a smaller energy barrier of 12.7 kcal mol−1 (gas (i.e., EA1⇔A2 = −24.8 kcal mol−1) and forms A2, which is located 82.4 kcal mol−1 below the reactants. Then A2 rapidly forms A4+H with a barrier of 24.0 kcal mol−1 (EA2⇔A4+H = −58.4 kcal mol−1). Alternatively, A2 undergoes H-migration to A3 via a barrier of 21.2 kcal mol−1 (i.e., EA2⇔A3 = −61.2 kcal mol−1), which also forms A4+H with a larger barrier of 47.1 kcal mol−1. This two-step channel formation of A4+H is however less favourable due to the significant resonance stabilization of A3 (EA3 = −96.7 kcal mol−1). Analogous reactions are found in the C14H9 + C2H2 PES,13 where the energy barriers of the corresponding A1
B2 are more exothermic (18.9 and 16.7 kcal mol−1, respectively) than their gas-phase counterparts (10.6 kcal mol−1 (ref. 21) and 7.2 kcal mol−1 (ref. 22)). However, A1 preferentially undergoes ring closure via a smaller energy barrier of 12.7 kcal mol−1 (gas (i.e., EA1⇔A2 = −24.8 kcal mol−1) and forms A2, which is located 82.4 kcal mol−1 below the reactants. Then A2 rapidly forms A4+H with a barrier of 24.0 kcal mol−1 (EA2⇔A4+H = −58.4 kcal mol−1). Alternatively, A2 undergoes H-migration to A3 via a barrier of 21.2 kcal mol−1 (i.e., EA2⇔A3 = −61.2 kcal mol−1), which also forms A4+H with a larger barrier of 47.1 kcal mol−1. This two-step channel formation of A4+H is however less favourable due to the significant resonance stabilization of A3 (EA3 = −96.7 kcal mol−1). Analogous reactions are found in the C14H9 + C2H2 PES,13 where the energy barriers of the corresponding A1  A2, A2
A2, A2  A4+H, A2
A4+H, A2  A3 and A3
A3 and A3  A4+H pathways are 6.6, 21.5, 26.2 and 36.3 kcal mol−1, respectively. In the studied solid-state system, the resonant effect is increased by the periodicity of the graphene structure. Consequently, the A2 well is deeper than its gas-phase counterpart by about 10 kcal mol−1. Conversely, the stability of intermediate A3 and of the product A4+H is closer to their gas-phase analogues, with discrepancies below 5.7 kcal mol−1.
A4+H pathways are 6.6, 21.5, 26.2 and 36.3 kcal mol−1, respectively. In the studied solid-state system, the resonant effect is increased by the periodicity of the graphene structure. Consequently, the A2 well is deeper than its gas-phase counterpart by about 10 kcal mol−1. Conversely, the stability of intermediate A3 and of the product A4+H is closer to their gas-phase analogues, with discrepancies below 5.7 kcal mol−1.
The formation of A3 can also occur through a multi-step pathway from B2. In particular, electron delocalization over the surface facilitates H-transfer in B2 from the sheet to the Ṙ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 moiety, forming a closed shell vinyl function in B3 (Ṙ–CH
CH2 moiety, forming a closed shell vinyl function in B3 (Ṙ–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2) through a relatively low energy barrier of 24.3 kcal mol−1. Subsequently, ring closure at the Cα in B3 forms a 5-membered ring (B4) through a notably low energy barrier of 0.7 kcal mol−1. B4 can ultimately undergo ring expansion to A3 through an energy barrier of 11.7 kcal mol−1 (EB4⇔A3 = −46.3 kcal mol−1). This channel competes with the direct H-loss, forming B6+H via an energy barrier of 33.7 kcal mol−1 (EB4⇔B6+H = −24.3 kcal mol−1). However, B6+H is mainly formed through a 2-step process starting with a 1–2 H-shift in B4, leading to B5 through a lower energy barrier of 26.1 kcal mol−1, followed by H-loss (EB5⇔B6+H = −27.2 kcal mol−1). B2 can also access additional higher energy pathways. 1–2 H-transfer from Cβ to Cα of the Ṙ
CH2) through a relatively low energy barrier of 24.3 kcal mol−1. Subsequently, ring closure at the Cα in B3 forms a 5-membered ring (B4) through a notably low energy barrier of 0.7 kcal mol−1. B4 can ultimately undergo ring expansion to A3 through an energy barrier of 11.7 kcal mol−1 (EB4⇔A3 = −46.3 kcal mol−1). This channel competes with the direct H-loss, forming B6+H via an energy barrier of 33.7 kcal mol−1 (EB4⇔B6+H = −24.3 kcal mol−1). However, B6+H is mainly formed through a 2-step process starting with a 1–2 H-shift in B4, leading to B5 through a lower energy barrier of 26.1 kcal mol−1, followed by H-loss (EB5⇔B6+H = −27.2 kcal mol−1). B2 can also access additional higher energy pathways. 1–2 H-transfer from Cβ to Cα of the Ṙ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 moiety leads to C1 via a barrier of 54.5 kcal mol−1 (i.e., EB2⇔C1 = −1.9 kcal mol−1), which is almost identical to the analogous gas-phase isomerization reaction.13 Successively, C1 can form C3+H via a 40.2 kcal mol−1 barrier (EC1⇔C3+H = 0.0 kcal mol−1), which is very similar to the reported analogous gas-phase prototype reaction forming phenyl-acetylene (41.2 kcal mol−1 energy barrier13). C1 can also isomerize via H-transfer to form C2, which presents an ethynyl function (Ṙ–C
CH2 moiety leads to C1 via a barrier of 54.5 kcal mol−1 (i.e., EB2⇔C1 = −1.9 kcal mol−1), which is almost identical to the analogous gas-phase isomerization reaction.13 Successively, C1 can form C3+H via a 40.2 kcal mol−1 barrier (EC1⇔C3+H = 0.0 kcal mol−1), which is very similar to the reported analogous gas-phase prototype reaction forming phenyl-acetylene (41.2 kcal mol−1 energy barrier13). C1 can also isomerize via H-transfer to form C2, which presents an ethynyl function (Ṙ–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH) and a secondary surface radical. The C1
CH) and a secondary surface radical. The C1  C2 pathway occurs with an energy barrier of 22.3 kcal mol−1, which is about 10 kcal mol−1 lower than the analogous gas-phase reaction on the C16H11 PES (i.e., 35.7 kcal mol−1 (ref. 13)). C2 can finally decompose into C3+H with a barrier of 39.5 kcal mol−1 (EC2⇔C3+H = 1.1 kcal mol−1), slightly higher than the analogous gas-phase reaction (i.e., 35.3 kcal mol−1). Different from the gas phase systems, we observed that a single elementary step was not sufficient to describe the connections A1
C2 pathway occurs with an energy barrier of 22.3 kcal mol−1, which is about 10 kcal mol−1 lower than the analogous gas-phase reaction on the C16H11 PES (i.e., 35.7 kcal mol−1 (ref. 13)). C2 can finally decompose into C3+H with a barrier of 39.5 kcal mol−1 (EC2⇔C3+H = 1.1 kcal mol−1), slightly higher than the analogous gas-phase reaction (i.e., 35.3 kcal mol−1). Different from the gas phase systems, we observed that a single elementary step was not sufficient to describe the connections A1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B3 and B3
B3 and B3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B5 and thus these reactions are not accounted for in the presented study.
B5 and thus these reactions are not accounted for in the presented study.
 | ||
| Fig. 5 Potential energy surface (PES) of the addition of acetylene to the radical site at the zigzag edge of graphene (Z0 + C2H2). Electronic energies relative to the bimolecular reactants are reported in kcal mol−1. Energy values of analogous TSs and intermediates from the gas-phase pentacyl + C2H2 and naphthyl-1 + C2H2 PESs13 are also shown in round and square brackets, respectively. ZPE corrections are not included. A schematic graphical representation of the investigated intermediates is also provided. | ||
Acetylene adds to the radical site on the zigzag ring, forming Z1 or Y1 with low barriers of EZ0+C2H2⇔Z1 = 1.5 kcal mol−1 and EZ0+C2H2⇔Y1 = 1.6 kcal mol−1, and exothermicities of 43.1 and 45.1 kcal mol−1. Z1 and Y1 exhibit the H atoms of the ethenyl fragment in the cis and trans configuration, respectively, and they are equilibrated through a low-energy barrier. In the analogous gas-phase systems, the addition of C2H2 to the radical centre of pentacyl and 1-naphthyl has similar energy barriers (1.3 and 41.4 kcal mol−1, respectively) and exothermicities (2.3 and 42.3 kcal mol−1, respectively).13 Z1 can undergo a five-membered ring closure, forming Z2 via a 4 kcal mol−1 energy barrier (i.e., EZ1⇔Z2 = −39.3 kcal mol−1), which is smaller by ∼10 kcal mol−1 than the gas analogues in the C24H15 and C12H9 systems13 due to the stronger resonance stabilization of the product. Then, H-transfer in Z2 leads to species Z3 via a barrier of 15.2 kcal mol−1 (i.e., EZ2⇔Z3 = −85.6 kcal mol−1). As anticipated, Z2 and Z3 are 12–14 and 32–37 kcal mol−1 deeper than the corresponding gas-phase intermediates in the C24H15 and C12H9 PESs, respectively, due to the additional aromatic stabilization (see Fig. 5).13 The formation of Z3 can also occur through a second pathway: Y1 undergoes H transfer from the ring to the β carbon of the R–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ĊH fragment via a low barrier of 6.2 kcal mol−1 (EY1⇔X1 = −38.9 kcal mol−1), forming a vinyl group in X1. Next, this Ṙ–CH
ĊH fragment via a low barrier of 6.2 kcal mol−1 (EY1⇔X1 = −38.9 kcal mol−1), forming a vinyl group in X1. Next, this Ṙ–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 moiety in X1 closes to Z3 via a barrier of 0.6 kcal mol−1 (i.e., EX1⇔Z3 = −44.8 kcal mol−1). Z3 finally undergoes an H-elimination reaction, forming the pentagonal aromatic ring in Z4+H with a very high energy barrier of 70.4 kcal mol−1 (EZ3⇔Z4+H = −43.3 kcal mol−1). Due to the higher resonance stabilization, this barrier is higher than that of the analogous gas phase step in the C24H15 PES (i.e., 61.0), which in turn exceeds that in the C12H9 PES (i.e., 46.0 kcal mol−1).13 The formation of the second investigated product is globally exothermic by 9 kcal mol−1, similar to the formation of the analogous ethynyl pentacene and acenaphthylene in ref. 13. Y3+H can be produced via H-loss from the α carbon of the ethenyl moiety in Y1 via a 44.2 kcal mol−1 barrier, which is slightly higher than the analogous gas-phase reactions (i.e., 38.7 and 41.9 kcal mol−1 in the C24H15 and C12H9 PESs, respectively13). Alternatively, a hydrogen transfer from Cα to Cβ within the ethenyl fragment in Y1 leads to intermediate Y2 (R–CH
CH2 moiety in X1 closes to Z3 via a barrier of 0.6 kcal mol−1 (i.e., EX1⇔Z3 = −44.8 kcal mol−1). Z3 finally undergoes an H-elimination reaction, forming the pentagonal aromatic ring in Z4+H with a very high energy barrier of 70.4 kcal mol−1 (EZ3⇔Z4+H = −43.3 kcal mol−1). Due to the higher resonance stabilization, this barrier is higher than that of the analogous gas phase step in the C24H15 PES (i.e., 61.0), which in turn exceeds that in the C12H9 PES (i.e., 46.0 kcal mol−1).13 The formation of the second investigated product is globally exothermic by 9 kcal mol−1, similar to the formation of the analogous ethynyl pentacene and acenaphthylene in ref. 13. Y3+H can be produced via H-loss from the α carbon of the ethenyl moiety in Y1 via a 44.2 kcal mol−1 barrier, which is slightly higher than the analogous gas-phase reactions (i.e., 38.7 and 41.9 kcal mol−1 in the C24H15 and C12H9 PESs, respectively13). Alternatively, a hydrogen transfer from Cα to Cβ within the ethenyl fragment in Y1 leads to intermediate Y2 (R–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ĊH
ĊH  Ṙ
Ṙ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2) followed by H-elimination. The contribution of the latter pathway is constrained due to the high stability of intermediate Y2 (i.e., EY2 = −83.8 kcal mol−1), and the very high energy barrier of 73.9 kcal mol−1 in the H-loss step (i.e., EY2⇔Y3+H = −9.9 kcal mol−1).
CH2) followed by H-elimination. The contribution of the latter pathway is constrained due to the high stability of intermediate Y2 (i.e., EY2 = −83.8 kcal mol−1), and the very high energy barrier of 73.9 kcal mol−1 in the H-loss step (i.e., EY2⇔Y3+H = −9.9 kcal mol−1).
To illustrate the similarities and differences between the studied solid systems and their respective gas-phase analogs, Fig. 6a shows the relative energy of intermediates (solid squares) and transition states (empty triangles) for the A0 + C2H2 PES in comparison to the corresponding intermediates and transition states in the 4-phenanthrenyl + C2H2.13Fig. 6b provides a similar comparison for Z0 + C2H2 with the pentacyl + C2H2 system.13 Additional correlations for prototype gas-phase deposition reactions over armchair and zigzag sites are reported in Fig. S1 and S2 of the ESI.†
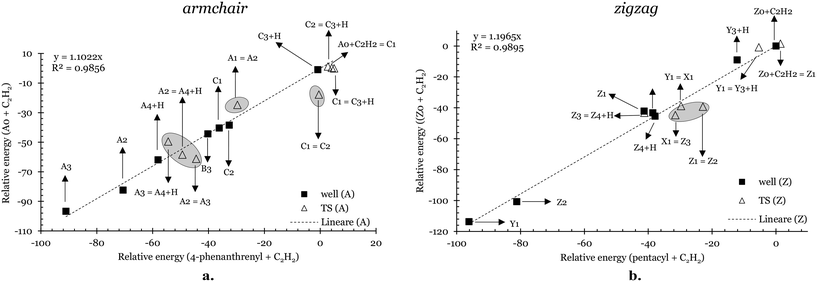 | ||
| Fig. 6 Relative energies of the intermediates (solid squares) and transition states (empty triangles) compared to those observed in PESs of analogous gas phase prototypes from ref. 13 for the C2H2 deposition on armchair (a.) and zigzag (b.) sites. TSs with larger deviations from the linear correlations found are highlighted by circles. | ||
Notably, we observe a strong linear correlation for both armchair and zigzag edges. The relative energies in the solid system are increased compared to their gas-phase counterparts by factors of 1.1 and 1.2 for the armchair and zigzag systems, respectively. However, significant deviations from the linear correlation are noted in the energy values of transition states associated with solid species exhibiting enhanced stability (e.g., A2, A3, C2, Z2, and Z3), as indicated by the circles in the graphs in Fig. 6.
3.2. Rate constants and product distribution
Modified Arrhenius fits for the rate constants of each reaction channel identified in the armchair and zigzag PESs are reported in Tables S1 and S2 of the ESI;† herein, we discuss the rate constants of the relevant channels. Theoretically estimated high pressure limit rate constants of the analogous gas-phase processes previously mentioned are also compared with our results. It is indeed expected that the surface undergoes fast vibrational relaxation (i.e., energy dissipation through the bulk) upon collision thanks to the availability of numerous vibrational levels preventing the dependence of the rate constants on pressure.The individual rate constants for the C2H2 addition reactions (i.e., A0 + C2H2 C1 and Z0 + C2H2
C1 and Z0 + C2H2 Z1) are depicted in Fig. 7a. The formation of C1 at the armchair edge occurs at a rate of 1.2 × 1011–5 × 1011 cm3 mol−1 s as the temperature rises from 900 to 1800 K (solid red line). This behavior is akin to the high-pressure limit of C2H2 addition to 4-phenanthrenyl13 (red dashed line), where the temperature dependence is enhanced by the higher activation energy. Carbon deposition on the zigzag edge is slightly more favored, with the rate constant for the formation of the more stable isomer (Z1) significantly varying from 3 × 1011 to 1.3 × 1012 cm3 mol−1 s within the 900–1800 K range (solid blue line). Kinetics up to almost one order of magnitude faster are instead observed for C2H2 deposition reactions on gas-phase phenyl,42 1-naphthyl,13 and pentacyl13 (black dash-dotted line, blue dashed line, and blue dash-dotted line, respectively), with the latter reaction exhibiting the highest rate. Reverse reactions of C2H2 elimination from both armchair and zigzag edges have similar rates approaching those of similar gas-phase steps (Fig. 7b). Both the rates of C2H2 addition and reverse elimination adopted in CVD models in the literature11 (black dotted lines) differ significantly from those found in this study and would therefore lead to different predictions of growth rates through the HACA mechanism.
Z1) are depicted in Fig. 7a. The formation of C1 at the armchair edge occurs at a rate of 1.2 × 1011–5 × 1011 cm3 mol−1 s as the temperature rises from 900 to 1800 K (solid red line). This behavior is akin to the high-pressure limit of C2H2 addition to 4-phenanthrenyl13 (red dashed line), where the temperature dependence is enhanced by the higher activation energy. Carbon deposition on the zigzag edge is slightly more favored, with the rate constant for the formation of the more stable isomer (Z1) significantly varying from 3 × 1011 to 1.3 × 1012 cm3 mol−1 s within the 900–1800 K range (solid blue line). Kinetics up to almost one order of magnitude faster are instead observed for C2H2 deposition reactions on gas-phase phenyl,42 1-naphthyl,13 and pentacyl13 (black dash-dotted line, blue dashed line, and blue dash-dotted line, respectively), with the latter reaction exhibiting the highest rate. Reverse reactions of C2H2 elimination from both armchair and zigzag edges have similar rates approaching those of similar gas-phase steps (Fig. 7b). Both the rates of C2H2 addition and reverse elimination adopted in CVD models in the literature11 (black dotted lines) differ significantly from those found in this study and would therefore lead to different predictions of growth rates through the HACA mechanism.
 | ||
| Fig. 7 Individual channel rate constants of the armchair (red) and zigzag (blue) PESs. a. C2H2 addition to armchair and zigzag edges; b. reverses of reactions in a.; c. ring closure reactions with formation of a pentagonal or hexagonal carbon ring; d. reverses of reactions in c.; dotted and dash-dotted lines represent high-pressure limit kinetic constants of analogous gas-phase reactions in C2H2 + PAH with armchair (phenanthryl) and zigzag (1-naphthyl and pentacyl) edges,13 respectively. The black dash-dotted lines in a. and b. represent high-pressure limit kinetic constants of analogous reactions in the C2H2 + phenyl system.42 Rate constants adopted in CVD models in the literature11 are reported with dotted black lines in a. and b. | ||
The ring closure reactions and their reverse ring opening steps are presented in Fig. 7c and d, respectively. The low energy barrier for the pentagonal ring closure reaction on the zigzag graphene edge (Z1  Z2) and the high stability of the intermediate Z2, as discussed in section 3.1.2., result in a rate constant for Z1
Z2) and the high stability of the intermediate Z2, as discussed in section 3.1.2., result in a rate constant for Z1  Z2 (solid blue line) of three orders of magnitude higher than the gas-phase counterpart (dotted and dash-dotted blue lines).13 Furthermore, this reaction is faster than the ring closure on the graphene armchair edge through A1
Z2 (solid blue line) of three orders of magnitude higher than the gas-phase counterpart (dotted and dash-dotted blue lines).13 Furthermore, this reaction is faster than the ring closure on the graphene armchair edge through A1  A2 affecting a higher energy barrier, thus reversing their relative behavior with respect to gas-phase reactions. Meanwhile, the reverse ring opening processes (Fig. 7d) display very similar rate constants for both armchair and zigzag graphene edges (3–1.9 × 108 s−1 at 800–1800 K), thus indicating a stronger preference for the formation of the 5-membered ring on the zigzag edge compared to the 6-membered ring on the armchair edge through this step.
A2 affecting a higher energy barrier, thus reversing their relative behavior with respect to gas-phase reactions. Meanwhile, the reverse ring opening processes (Fig. 7d) display very similar rate constants for both armchair and zigzag graphene edges (3–1.9 × 108 s−1 at 800–1800 K), thus indicating a stronger preference for the formation of the 5-membered ring on the zigzag edge compared to the 6-membered ring on the armchair edge through this step.
The rate constants of the H-loss channels of the investigated PESs are depicted in Fig. 8. Fig. 8a illustrates the rate constants for H-elimination reactions leading to the formation of a new aromatic ring at the graphene edge (pentagonal in Z4 and hexagonal in A4), as well as the analogous gas-phase steps. A2  A4+H displays the fastest kinetics (solid orange line), with a rate constant of 1.2 × 1011–9 × 1011 s−1 at 800–1800 K (about 4 times faster than the analogous gas-phase pyrene formation). The rate constant of the A3
A4+H displays the fastest kinetics (solid orange line), with a rate constant of 1.2 × 1011–9 × 1011 s−1 at 800–1800 K (about 4 times faster than the analogous gas-phase pyrene formation). The rate constant of the A3  A4+H reaction (solid red line) shows lower kinetics (from 7.5 × 102 to 1.4 × 109 s−1 from 800 to 1800 K) due to its higher energy barrier. The formation of the five-membered ring (Z4+H) through the elimination of H in the intermediate Z3 involves a very high energy barrier and thus has a significantly lower rate constant (solid blue line).
A4+H reaction (solid red line) shows lower kinetics (from 7.5 × 102 to 1.4 × 109 s−1 from 800 to 1800 K) due to its higher energy barrier. The formation of the five-membered ring (Z4+H) through the elimination of H in the intermediate Z3 involves a very high energy barrier and thus has a significantly lower rate constant (solid blue line).
 | ||
Fig. 8 Rate constants of the H-loss channels in the armchair (red and orange) and zigzag (blue) PESs: a. H-elimination with formation of R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH fragment in Y3 and C3; b. reverses of reactions in a.; c. H-elimination leading to the new pentagonal or hexagonal aromatic carbon ring at the edge; d. reverses of reactions in c.; e. H-elimination leading to species B6; f. reverses of reactions in e. Dotted and dash-dotted lines (red, blue, orange) are high-pressure limit rate constants of analogous gas-phase reactions in the C2H2 + phenanthryl/1-naphthyl/pentacyl systems13 (a.–d.) or in the methylcyclopentadienyl decomposition PES23 (e. and f.). The black dash-dotted lines represent high-pressure limit kinetic constants of analogous reactions in the phenyl + C2H2 PES.23,42 Rate constant adopted in CVD models in the literature11 is reported in a. with a dotted black line. CH fragment in Y3 and C3; b. reverses of reactions in a.; c. H-elimination leading to the new pentagonal or hexagonal aromatic carbon ring at the edge; d. reverses of reactions in c.; e. H-elimination leading to species B6; f. reverses of reactions in e. Dotted and dash-dotted lines (red, blue, orange) are high-pressure limit rate constants of analogous gas-phase reactions in the C2H2 + phenanthryl/1-naphthyl/pentacyl systems13 (a.–d.) or in the methylcyclopentadienyl decomposition PES23 (e. and f.). The black dash-dotted lines represent high-pressure limit kinetic constants of analogous reactions in the phenyl + C2H2 PES.23,42 Rate constant adopted in CVD models in the literature11 is reported in a. with a dotted black line. | ||
This latter is also lower than both the analogous gas-phase steps, where the formation of acenaphthylene (dash-dotted blue line) has the highest values. The rate constants of the reverse H-addition reactions are shown in Fig. 8b. H-addition to the pentagonal aromatic ring at the graphene zigzag edge (Z4+H  Z3 solid blue line) involves energy barriers similar to those of the analogous gas-phase steps, hence similar rate constants are observed (dashed and dash-dotted lines for H-addition to acepentacene and acenaphthylene, respectively), with values around 1 × 1014 cm3 mol−1 s. The H-additions to the hexagonal edge (leading to A2 and A3, solid red and orange lines, respectively) are slower. In particular, A4+H
Z3 solid blue line) involves energy barriers similar to those of the analogous gas-phase steps, hence similar rate constants are observed (dashed and dash-dotted lines for H-addition to acepentacene and acenaphthylene, respectively), with values around 1 × 1014 cm3 mol−1 s. The H-additions to the hexagonal edge (leading to A2 and A3, solid red and orange lines, respectively) are slower. In particular, A4+H  A3 shows the lowest values (ranging from 5.5 × 109 to 6.5 × 1011 cm3 mol−1 s in the 800–1800 K range) that are about two orders of magnitude lower than the analogous H-addition to pyrene (dashed red line in Fig. 8d), which in fact involves a higher energy barrier. Similar values are instead found for the A4+H
A3 shows the lowest values (ranging from 5.5 × 109 to 6.5 × 1011 cm3 mol−1 s in the 800–1800 K range) that are about two orders of magnitude lower than the analogous H-addition to pyrene (dashed red line in Fig. 8d), which in fact involves a higher energy barrier. Similar values are instead found for the A4+H  A2 reaction and the analogous gas-phase step (solid and dashed orange lines in Fig. 8b, respectively) where very similar barriers are observed (i.e., only 0.1 kcal mol−1 difference).
A2 reaction and the analogous gas-phase step (solid and dashed orange lines in Fig. 8b, respectively) where very similar barriers are observed (i.e., only 0.1 kcal mol−1 difference).
The rate constants for the H loss channels to form the ethynyl fragment (R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH) at the armchair and zigzag edges (in C3 and Y3, respectively) are shown in Fig. 8c and d for the direct and reverse reactions, respectively. Reaction Y2
CH) at the armchair and zigzag edges (in C3 and Y3, respectively) are shown in Fig. 8c and d for the direct and reverse reactions, respectively. Reaction Y2  Y3+H has the lowest rate ranging from 9 × 103 to 2.3 × 109 s−1 at 800–1800 K (solid blue line in Fig. 8c). The rate constants of the gas-phase counterparts, presenting lower barriers, show a similar temperature dependence and values higher by a factor of 2 and 3 for the formation of ethynylpentacene (dashed blue line) and ethynylnaphthalene (dash-dotted blue line), respectively. H-elimination reactions at the armchair edge (i.e., C1
Y3+H has the lowest rate ranging from 9 × 103 to 2.3 × 109 s−1 at 800–1800 K (solid blue line in Fig. 8c). The rate constants of the gas-phase counterparts, presenting lower barriers, show a similar temperature dependence and values higher by a factor of 2 and 3 for the formation of ethynylpentacene (dashed blue line) and ethynylnaphthalene (dash-dotted blue line), respectively. H-elimination reactions at the armchair edge (i.e., C1  C3+H and C2
C3+H and C2  C3+H indicated by the solid red and orange lines, respectively) are faster and closely resemble their gas-phase counterparts. The inverse H-addition reactions leading to intermediates C1 and C2 (solid red and orange lines in Fig. 8d, respectively) exhibit similar kinetics to each other and to the analogous gas-phase reactions of H-addition to ethynylphenanthrene (dashed red and orange lines, respectively). Conversely, the addition of H to the Y3 intermediate on the zigzag edge (blue solid line) displays a lower rate constant than its gas-phase counterpart (dashed and dash-dot blue lines for H-addition to ethynylpentacene and ethynylnaphthalene, respectively).
C3+H indicated by the solid red and orange lines, respectively) are faster and closely resemble their gas-phase counterparts. The inverse H-addition reactions leading to intermediates C1 and C2 (solid red and orange lines in Fig. 8d, respectively) exhibit similar kinetics to each other and to the analogous gas-phase reactions of H-addition to ethynylphenanthrene (dashed red and orange lines, respectively). Conversely, the addition of H to the Y3 intermediate on the zigzag edge (blue solid line) displays a lower rate constant than its gas-phase counterpart (dashed and dash-dot blue lines for H-addition to ethynylpentacene and ethynylnaphthalene, respectively).
The rate constants related to the exit channel of B6+H on the armchair PES are depicted in Fig. 8e (B4/B5  B6+H) and Fig. 8f (B6+H
B6+H) and Fig. 8f (B6+H  B4/B5). The reaction involving the highest energy barrier is the formation of B6 from the more stable species B5 (solid orange line), which is approximately two orders of magnitude lower than B4
B4/B5). The reaction involving the highest energy barrier is the formation of B6 from the more stable species B5 (solid orange line), which is approximately two orders of magnitude lower than B4  B6+H (solid red line). Strong similarity is observed with the analogous gas-phase reactions leading to fulvene (i.e., C5H5CH2-5/C5H4CH3
B6+H (solid red line). Strong similarity is observed with the analogous gas-phase reactions leading to fulvene (i.e., C5H5CH2-5/C5H4CH3 FULVENE+H in ref. 31 indicated by dashed red and orange lines, respectively). Conversely, concerning the reverse H-addition channel to B6 (Fig. 8f), higher values are observed for B6+H
FULVENE+H in ref. 31 indicated by dashed red and orange lines, respectively). Conversely, concerning the reverse H-addition channel to B6 (Fig. 8f), higher values are observed for B6+H  B5 (solid red line) compared to the H-addition to B4 (i.e., B6+H
B5 (solid red line) compared to the H-addition to B4 (i.e., B6+H  B4, solid orange line). Also in this case, strong resemblance is observed with the analogous gas-phase steps of H-addition to fulvene (i.e., FULVENE+H
B4, solid orange line). Also in this case, strong resemblance is observed with the analogous gas-phase steps of H-addition to fulvene (i.e., FULVENE+H  C5H5CH2-5/C5H4CH3 in ref. 31 indicated by dashed red and orange lines, respectively).
C5H5CH2-5/C5H4CH3 in ref. 31 indicated by dashed red and orange lines, respectively).
3.3. Chemical lumping and mechanistic analysis
Fig. 9a and b illustrate the lumped scheme for C2H2 deposition on armchair and zigzag graphene edge sites, respectively, better highlighting the dominating pathways of C2H2 deposition.As described in section 2, the MEL approach28 enables us to automatically lump the reactivity of the investigated multi-well potential energy surfaces effectively reducing the overall number of species and reactions. C2H2 deposition on the armchair edge involves a network of 14 intermediate species and 42 irreversible reactions. MEL was able to reduce this complexity to a smaller model of only 5 pseudospecies (delimited by red boxes in Fig. 9a) and 10 reactions (red arrows in Fig. 9a). In this refined mechanism, three closely reactive intermediates B1, C1, and C2 were lumped as single pseudospecies  . The isomer pool composition was determined through iterative isothermal 0-D batch reactor simulations of the full PES reactivity, as elucidated in ref. 28. The final composition is consistent with the relative stability of the isomers manifesting as 11–18% C2, 32–36% B1, and 55–46% C1 across the 800–1900 K temperature range (see Fig. 10). Comparison between the performances of the detailed and lumped models for both zigzag and armchair graphene edge growth by acetylene deposition is reported in Fig. S3 and S4 of the ESI,† respectively.
. The isomer pool composition was determined through iterative isothermal 0-D batch reactor simulations of the full PES reactivity, as elucidated in ref. 28. The final composition is consistent with the relative stability of the isomers manifesting as 11–18% C2, 32–36% B1, and 55–46% C1 across the 800–1900 K temperature range (see Fig. 10). Comparison between the performances of the detailed and lumped models for both zigzag and armchair graphene edge growth by acetylene deposition is reported in Fig. S3 and S4 of the ESI,† respectively.
Intermediate A3 can also accumulate significantly, and it was thus treated as a single pseudo-species  . The primary products, A4+H and C3+H, were also considered as single lumped pseudo-species, represented by
. The primary products, A4+H and C3+H, were also considered as single lumped pseudo-species, represented by  and
and  , respectively.
, respectively.
Conversely, the formation of B6+H was omitted from the consolidated mechanism, as the generation of B6 from all other pseudo-species is negligible (e.g., cB6+H/ctot < 0.05) under the considered conditions (i.e., 800–1900 K). The remaining seven intermediates showed negligible accumulation across all temperatures and were excluded from the lumped mechanism pseudospecies set but only considered implicitly in the reactivity. In conclusion, similar to what happens in gas-phase PAH systems with armchair bays,13 the higher resonance stabilization on the graphene sheet favors the formation of the additional 6-membered ring over that of a fulvene-like structure, to the point that the latter can be neglected from a macroscopic standpoint. However, considering the global reactivity, it can be expected that the main limiting step of the reaction remains the acetylene addition channel, which was found to be faster than the gas-phase counterparts; the higher stability of intermediates involving resonance stabilization with the graphene sheet (A3 in particular) might lead to a larger accumulation of these species, possibly suggesting the need to investigate further growth from these wells.
In the lumped zigzag system, the most thermodynamically stable intermediate, Z3, is the sole accumulating intermediate. Y3+H was excluded from the stable pseudospecies for reasons analogous to the exclusion of B6+H in the armchair system. Consequently, the simplified lumped zigzag model encompasses only 3 species,  ,
,  and
and 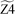 (blue rectangles in Fig. 9b) and 4 irreversible reactions (blue arrows in Fig. 9b). This approach significantly simplifies the zigzag network, which previously comprised 9 species and 22 reactions.
(blue rectangles in Fig. 9b) and 4 irreversible reactions (blue arrows in Fig. 9b). This approach significantly simplifies the zigzag network, which previously comprised 9 species and 22 reactions.
The final set of lumped rate constants for 12 reactions that occur among the 8 pseudospecies in the final lumped scheme is presented in Table 1. When implementing such findings in a semi-detailed kinetics framework, successive reactivity of A4 can be assimilated to that of a pure armchair edge thus leading to the formation of intermediates that, upon H-abstraction, are structurally equivalent to A0 consequently leading to further growth through deposition channels here investigated or through other channels (e.g. recombination, ipso-substitutions, etc.17) that are outside the scope of this study. This assumption is justified by analogous bond dissociation energies13 and by the need of simplifying the description of a complex heterogeneous network of reactions thus limiting the number of isomer intermediates.
4. Conclusions
We provide a detailed analysis of graphene growth mechanisms at both armchair and zigzag edges. The use of advanced methodologies, including density functional theory calculations and the CI-NEB technique, enabled us to construct intricate potential energy surfaces for C2H2 deposition. This allowed us to elucidate favored growth pathways extending the analysis to the formation of structural irregularities, such as the formation of five-membered rings during zigzag edge growth. The meticulous derivation of rate constants for each reactive step undertaken in this study establishes the foundation for a comprehensive kinetic framework capable of capturing the inherent complexities within graphene growth dynamics. A detailed comparison with analogous gas-phase reactions occurring along the armchair and zigzag edges of PAHs has underscored remarkable parallels between graphene growth chemistry and that of gas-phase aromatics. Conversely, significant peculiarities of the solid system investigated here have also come to light, particularly the stabilization effect resulting from a broader radical resonance within the graphene sheet, as opposed to the fewer rings of PAHs. The final kinetic mechanism, derived through the MEL approach, significantly reduces the number of species from 23 (i.e., 14 for armchair and 9 for zigzag) to 8 lumped pseudo-species (5 for armchair and 3 for zigzag) and the number of reactions from 64 (42 for armchair and 22 for zigzag) to 16 (10 for armchair, and 6 for zigzag). This makes it perfectly integrable into current models, enhancing the accuracy of representing the chemical dynamics governing the synthesis of pyrocarbons via CVD and CVI, without introducing undue complexities for simulation purposes. Such revisions can be realized through adjusting the kinetic constants of pre-existing reactions and incorporating the chemistry leading to the introduction of structural irregularities, thereby influencing the structure of the final material.As a whole, this exploration of interactions between acetylene and graphene sheet edges has highlighted potential gaps, biases and weaknesses in current models, predominantly derived from gas-phase pathways thus pointing to the necessity of more accurate derivation of kinetic constants, particularly for reactions involving the formation of resonant π-radicals throughout the structure. In addition, it emphasized the critical importance of studying further reactions involving highly stable structures that can accumulate during the process and subsequently interact with other gas-phase species or nearby edge structures. Consequently, the forthcoming focus should be devoted to investigating the deposition of other intermediates (e.g., methyl radical, propene, propyne, allene and related radicals such as propargyl) on stable species highlighted in this study, such as C3, A3, or Z3.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge financial support from the Carbon Hub and from Brembo S.p.A. M. M. and L. P. M. acknowledge funding from the National Recovery and Resilience Plan (NRRP), mission 4 component 2 investment 1.3 – Call for tender No. 1561 of 11.10.2022 of Ministero dell'Università e della Ricerca (MUR); funded by the European Union – NextGenerationEU (Award Number: Project code PE0000021, Concession Decree No. 1561 of 11.10.2022 adopted by Ministero dell'Università e della Ricerca (MUR), CUP – D43C22003090001, according to attachment E of Decree No. 1561/2022, Project title “Network 4 Energy Sustainable Transition – NEST”). The authors are thankful to Matilde Russo for her support with the DFT calculations conducted during her Master's thesis at Politecnico di Milano. We also acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support.References
- M. McConnachie, M. Konarova and S. Smart, Literature review of the catalytic pyrolysis of methane for hydrogen and carbon production, Int. J. Hydrogen Energy, 2023, 48, 25660–25682, DOI:10.1016/j.ijhydene.2023.03.123
.
- N. Sánchez-Bastardo, R. Schlögl and H. Ruland, Methane Pyrolysis for Zero-Emission Hydrogen Production: A Potential Bridge Technology from Fossil Fuels to a Renewable and Sustainable Hydrogen Economy, Ind. Eng. Chem. Res., 2021, 60, 11855–11881, DOI:10.1021/acs.iecr.1c01679
.
- N. Sánchez-Bastardo, R. Schlögl and H. Ruland, Methane Pyrolysis for CO2-Free H2 Production: A Green Process to Overcome Renewable Energies Unsteadiness, Chem. Ing. Tech., 2020, 92, 1596–1609, DOI:10.1002/cite.202000029
.
- N. Anzar, R. Hasan, M. Tyagi, N. Yadav and J. Narang, Carbon nanotube - A review on Synthesis, Properties and plethora of applications in the field of biomedical science, Sens. Int., 2020, 1, 100003, DOI:10.1016/j.sintl.2020.100003
.
- L. S. Porto, D. N. Silva, A. E. F. de Oliveira, A. C. Pereira and K. B. Borges, Carbon nanomaterials: synthesis and applications to development of electrochemical sensors in determination of drugs and compounds of clinical interest, Rev. Anal. Chem., 2019, 38, 20190017, DOI:10.1515/revac-2019-0017
.
- Q. Wu, W. Miao, Y. Zhang, H. Gao and D. Hui, Mechanical properties of nanomaterials: A review, Nanotechnol. Rev., 2020, 9, 259–273, DOI:10.1515/ntrev-2020-0021
.
- V. B. Mbayachi, E. Ndayiragije, T. Sammani, S. Taj, E. R. Mbuta and A. Ullah Khan, Graphene synthesis, characterization and its applications: A review, Results Chem., 2021, 3, 100163, DOI:10.1016/j.rechem.2021.100163
.
- P. Bhakta and B. Barthunia, Fullerene and its applications: A review, J. Indian Acad. Oral Med. Radiol., 2020, 32, 159, DOI:10.4103/jiaomr.jiaomr_191_19
.
- P. Delhaes, Chemical vapor deposition and infiltration processes of carbon materials, Carbon, 2002, 40, 641–657, DOI:10.1016/S0008-6223(01)00195-6
.
- G. L. Vignoles, F. Langlais, C. Descamps, A. Mouchon, H. L. Poche, N. Reuge and N. Bertrand, CVD and CVI of pyrocarbon from various precursors, Surf. Coat. Technol., 2004, 188–189, 241–249, DOI:10.1016/j.surfcoat.2004.08.036
.
- R. Lacroix, R. Fournet, I. Ziegler-Devin and P.-M. Marquaire, Kinetic modeling of surface reactions involved in CVI of pyrocarbon obtained by propane pyrolysis, Carbon, 2010, 48, 132–144, DOI:10.1016/j.carbon.2009.08.041
.
- I. Ziegler, R. Fournet and P.-M. Marquaire, Pyrolysis of propane for CVI of pyrocarbon: Part II. Experimental and modeling study of polyaromatic species, J. Anal. Appl. Pyrolysis, 2005, 73, 231–247, DOI:10.1016/j.jaap.2005.03.007
.
- M. Frenklach, R. I. Singh and A. M. Mebel, On the low-temperature limit of HACA, Proc. Combust. Inst., 2019, 37, 969–976, DOI:10.1016/j.proci.2018.05.068
.
- M. Frenklach and H. Wang, Detailed modeling of soot particle nucleation and growth, Symp. (Int.) Combust., 1991, 23, 1559–1566, DOI:10.1016/S0082-0784(06)80426-1
.
- M. Frenklach, D. W. Clary, W. C. Gardiner and S. E. Stein, Detailed kinetic modeling of soot formation in shock-tube pyrolysis of acetylene, Symp. (Int.) Combust., 1985, 20, 887–901, DOI:10.1016/S0082-0784(85)80578-6
.
- Z.-B. Ding, E. D. Marco, M. Pelucchi, T. Faravelli and M. Maestri, First-principles assessment of the analogy between gas-phase and gas-solid H-abstraction reactions at graphene edges, Chem. Eng. J., 2019, 377, 119691, DOI:10.1016/j.cej.2018.08.077
.
- F. Serse, Z. Ding, M. Bracconi, M. Maestri, A. Nobili, C. Giudici, A. Frassoldati, T. Faravelli, A. Cuoci and M. Pelucchi, A comprehensive kinetic framework for solid carbon deposition and hydrogen production from
the pyrolysis of light hydrocarbons streams, Carbon Trends, 2023, 11, 100263, DOI:10.1016/j.cartre.2023.100263
.
- I. Ziegler-Devin, R. Fournet, R. Lacroix and P. M. Marquaire, An interpretation of the hydrogen inhibiting effect on chemical vapor deposition of pyrocarbon, J. Anal. Appl. Pyrolysis, 2015, 115, 299–306, DOI:10.1016/j.jaap.2015.08.009
.
- I. Ziegler-Devin, R. Fournet and P.-M. Marquaire, Influence of surface on chemical kinetic of pyrocarbon deposition obtained by propane pyrolysis, J. Anal. Appl. Pyrolysis, 2005, 73, 107–115, DOI:10.1016/j.jaap.2004.12.004
.
- W. Zhang and K. J. Huettinger, Influence of initial surface area/volume ratio of the fiber preform on kinetics of chemical vapor infiltration and texture of infiltrated carbon, Materials China, 2013, 32, 646–654, DOI:10.7502/j.issn.1674-3962.2013.11.02
.
- I. V. Tokmakov and M. C. Lin, Reaction of Phenyl Radicals with Acetylene: Quantum Chemical Investigation of the Mechanism and Master Equation Analysis of the Kinetics, J. Am. Chem. Soc., 2003, 125, 11397–11408, DOI:10.1021/ja0301121
.
- Z. Li, P. Liu, P. Zhang, H. He, S. H. Chung and W. L. Roberts, Theoretical Study of PAH Growth by Phenylacetylene Addition, J. Phys. Chem. A, 2019, 123, 10323–10332, DOI:10.1021/acs.jpca.9b09450
.
- B. Hanamirian, A. Della Libera, L. Pratali Maffei and C. Cavallotti, Investigation of Methylcyclopentadiene Reactivity: Abstraction Reactions and Methylcyclopentadienyl Radical Unimolecular Decomposition, J. Phys. Chem. A, 2023, 127, 1314–1328, DOI:10.1021/acs.jpca.2c08028
.
- V. V. Kislov, N. I. Islamova, A. M. Kolker, S. H. Lin and A. M. Mebel, Hydrogen Abstraction Acetylene Addition and Diels−Alder Mechanisms of PAH Formation: A Detailed Study Using First Principles Calculations, J. Chem. Theory Comput., 2005, 1, 908–924, DOI:10.1021/ct0500491
.
- V. V. Kislov, A. I. Sadovnikov and A. M. Mebel, Formation Mechanism of Polycyclic Aromatic Hydrocarbons beyond the Second Aromatic Ring, J. Phys. Chem. A, 2013, 117, 4794–4816, DOI:10.1021/jp402481y
.
- L. Zhao, R. I. Kaiser, B. Xu, U. Ablikim, M. Ahmed, D. Joshi, G. Veber, F. R. Fischer and A. M. Mebel, Pyrene synthesis in circumstellar envelopes and its role in the formation of 2D nanostructures, Nat. Astron., 2018, 2, 413–419, DOI:10.1038/s41550-018-0399-y
.
- L. Zhao, S. Doddipatla, R. I. Kaiser, W. Lu, O. Kostko, M. Ahmed, L. B. Tuli, A. N. Morozov, A. H. Howlader, S. F. Wnuk, A. M. Mebel, V. N. Azyazov, R. K. Mohamed and F. R. Fischer, Gas-phase synthesis of corannulene – a molecular building block of fullerenes, Phys. Chem. Chem. Phys., 2021, 23, 5740–5749, 10.1039/D0CP06537D
.
- L. P. Maffei, M. Pelucchi, C. Cavallotti, A. Bertolino and T. Faravelli, Master equation lumping for multi-well potential energy surfaces: A bridge between ab initio based rate constant calculations and large kinetic mechanisms, Chem. Eng. J., 2021, 422, 129954, DOI:10.1016/j.cej.2021.129954
.
- P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. De Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, Q UANTUM ESPRESSO toward the exascale, J. Chem. Phys., 2020, 152, 154105, DOI:10.1063/5.0005082
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/PhysRevLett.77.3865
.
- H. Shu, X. Chen, X. Tao and F. Ding, Edge Structural Stability and Kinetics of Graphene Chemical Vapor Deposition Growth, ACS Nano, 2012, 6, 3243–3250, DOI:10.1021/nn300726r
.
- T. Ma, W. Ren, X. Zhang, Z. Liu, Y. Gao, L.-C. Yin, X.-L. Ma, F. Ding and H.-M. Cheng, Edge-controlled growth and kinetics of single-crystal graphene domains by chemical vapor deposition, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20386–20391, DOI:10.1073/pnas.1312802110
.
- W. Zhang, X. Yu, E. Cahyadi, Y.-H. Xie and C. Ratsch, On the kinetic barriers of graphene homo-epitaxy, Appl. Phys. Lett., 2014, 105, 221607, DOI:10.1063/1.4903485
.
- X. Zhang, L. Wang, J. Xin, B. I. Yakobson and F. Ding, Role of Hydrogen in Graphene Chemical Vapor Deposition Growth on a Copper Surface, J. Am. Chem. Soc., 2014, 136, 3040–3047, DOI:10.1021/ja405499x
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465, DOI:10.1002/jcc.21759
.
- L. Pisani, J. A. Chan, B. Montanari and N. M. Harrison, Electronic structure and magnetic properties of graphitic ribbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064418, DOI:10.1103/PhysRevB.75.064418
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904, DOI:10.1063/1.1329672
.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002, DOI:10.1088/1361-648X/aa680e
.
- G. H. Vineyard, Frequency factors and isotope effects in solid state rate processes, J. Phys. Chem. Solids, 1957, 3, 121–127, DOI:10.1016/0022-3697(57)90059-8
.
- H. Eyring, The Activated Complex and the Absolute Rate of Chemical Reactions, Chem. Rev., 1935, 17, 65–77, DOI:10.1021/cr60056a006
.
- A. M. Mebel, Y. Georgievskii, A. W. Jasper and S. J. Klippenstein, Temperature- and pressure-dependent rate coefficients for the HACA pathways from benzene to naphthalene, Proc. Combust. Inst., 2017, 36, 919–926, DOI:10.1016/j.proci.2016.07.013
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4re00096j |
| This journal is © The Royal Society of Chemistry 2024 |











![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456.60
456.60