Open Access Article
Open Access ArticleCoupling catalytic bed fluidization with impeller rotation for improved hydrodynamic characterization of Berty reactors†
Mengmeng
Cui
a,
Shekhar R.
Kulkarni
a,
Yacoub-Yousef
Abu-Naaj
b,
Stefan
Wagner
b,
Claudia
Berger-Karin
b,
Jan Lennart
Weber
b,
Anton
Nagy
b and
Pedro
Castaño
 *ac
*ac
aMultiscale Reaction Engineering, KAUST Catalysis Center (KCC), King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia. E-mail: pedro.castano@kaust.edu.sa
bILS – Integrated Lab Solutions GmbH, 12489 Berlin, Germany
cChemical Engineering Program, Physical Science and Engineering (PSE) Division, King Abdullah University of Science and Technology, Saudi Arabia
First published on 30th April 2024
Abstract
We developed an integrated modeling framework to capture the gas–solid mixing patterns in internal circulating Berty reactors operating under batch fluidized mode. Our framework combines computational fluid dynamics for the gas phase with impeller rotation and computational particle fluid dynamics for solid fluidization in the catalyst basket. We proposed several key hydrodynamic indicators for the Berty-type reactor and compared the prediction results from the integrated simulation strategy with previous settings without considering the actual bed fluidization. Deviations in bed velocity, gas–solid contact time, and recirculation rate underscored the necessity of employing accurate hydrodynamic characteristics when designing Berty-type reactors. The consistent impeller relationships under various fluidization conditions suggested that the hydrodynamics in internal circulating Berty reactors are predominantly influenced by impeller rotation, irrespective of bed status. In this context, we introduced a fluidized bed expansion correlation to the impeller relationship, offering a more reliable hydrodynamic explanation for the Berty fluidized bed reactor in batch mode. This can also serve as a design foundation for internal recycling reactors.
1. Introduction
With the advantages of superior mass and heat transfer characteristics, continuous movement of particles, and high gas–solid throughput,1 fluidized beds have been favored in industrial applications for highly exothermic, endothermic, or explosive catalytic reactions, especially where catalysts deactivate in minutes or seconds.2,3 Such applications include fluid catalytic cracking,4–7 biomass gasification,8,9 and chemical looping combustion.10,11 Effective laboratory-scale testing units are required to utilize fluidization technology for new feedstocks, catalysts, or processes, and they must clearly explain transport phenomena and flow patterns approaching the intrinsic reaction kinetic regime.12Equipped with a stationary catalyst basket in the middle and a rotating impeller at the top,13 the Berty reactor functions as a continuous stirred tank reactor (CSTR) with perfect mixing. It offers convenience for kinetic and deactivation studies,14–17 providing an ideal contact pattern. This reactor is known for achieving mass and heat transfer characteristics similar to commercial operations. It has been utilized to screen catalysts at high conversion levels under the fixed bed and in continuous operating mode.13,18–24 The Berty-type reactor was adapted to fluid catalytic cracking in the batch fluidized bed mode in the 1980s and 1990s at the Chemical Reactor Engineering Centre (CREC), University of Western Ontario,25,26 for a laboratory catalytic testing unit called the riser simulator, which has been widely used for catalyst evaluation, development, kinetic modeling, and catalyst characterization.12,26–32 Two metallic porous plates are set in the catalyst basket to retain the solid and distribute the gas flow homogeneously. In this process, reactants are injected into the vessel and circulated through the catalyst basket by an impeller until the desired end time. The contents are then rapidly evacuated and analyzed. As an internal recycle reactor, the Berty-type reactor mirrors the regime in commercial units, maintaining identical mass velocity over the same-sized catalyst under the same heat and mass transfer conditions and the same partial pressure of reactants, products, and inert substances, ensuring identical diffusional and kinetic rates.13
A better depiction of the mixing pattern in laboratory internal recycle reactors has been a continuous research pursuit for gas–solid catalytic studies, which can be assessed using pressure drop,18 temperature drop measurements across the bed,33 mass transfer coefficient estimations,34 or transient responses of tracer injections.16,34 One of the most significant outcomes from the mixing pattern of the Berty reactor in batch fluidized bed operations is to evaluate when and whether fluidization can be achieved. Pekediz et al.35 adopted a hot-film anemometer sensor placed in the annulus region between the catalyst basket and the reactor wall to gauge gas velocities. It used fiber optic measurements within the catalytic basket to examine the particle fluidization based on a reactor made of Plexiglas. However, presuming a consistent velocity distribution throughout the annulus section introduced uncertainties about the actual recirculation rate.
Computational fluid dynamics (CFD) is a powerful method for investigating mixing patterns in this type of reactor concerning their hydrodynamic performances.16,32,36–40 Ahmed et al.32 verified the CFD simulations using experimental data and mass balance calculations by a model with pressure drop assigned to the particle bed and basket grids for the CREC riser simulator and compared the mixing patterns of reactor designs with and without baffles. Cui et al.36 validated the CFD simulations, assuming the catalyst bed as a porous media zone. We demonstrated that a fluidized bed can be maintained in the catalyst basket of the Integrated Lab Solutions (ILS) Berty reactor under a certain rotation rate and catalyst loading, which was anticipated from Berty's experiments several decades earlier.13 Tracer fraction contours and the F curve displayed that the ILS Berty reactor approaches perfect mixing as a CSTR in the catalytic bed.13 However, previous simulation studies could not accurately depict bed expansion from fluidization, which may lead to malfunctioning of the desired fluidization system or inappropriate design modifications.32,36,41–44 A comprehensive understanding of the complex hydrodynamics, which combines fluidization with rotation, is essential to utilizing the benefits of Berty-type reactors in representing industrial riser conditions. This understanding is also pivotal for establishing design criteria for internal recycle reactors. Towards this target, we attempted to propose an improved simulation strategy by coupling catalytic bed fluidization with impeller rotation to characterize the hydrodynamics of Berty reactors.
The CFD-DEM (discrete element method) approach can couple fluidization with the rotating zone, but it requires significant computational resources to maintain particles between the two screens on the top and bottom of the catalytic bed.45–51 Based on the Eulerian–Lagrangian scheme, computational particle fluid dynamics (CPFD) offers competitive advantages due to reduced computational costs across multiple scales for systems with gas–particle interactions.52–57 Yet, reproducing the impeller rotation is a challenge. Thankfully, the basket velocity is relatively consistent, with the screen set at the bottom functioning as a gas distributor.36 This results in an independent fluidization system in the catalytic bed. Therefore, a combined CFD/CPFD approach leads to a more accurate hydrodynamic characterization in the Berty reactor.
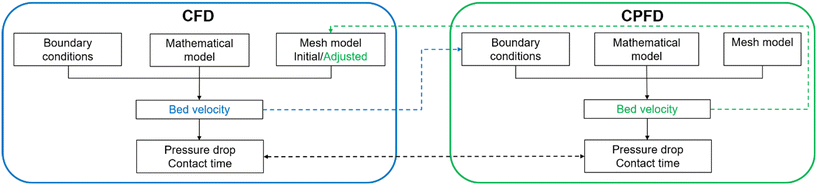
In this study, we developed a simulation framework to explore the hydrodynamics of a Berty fluidized bed reactor by combining CFD with the CPFD method using the ILS Berty reactor as an example. We obtained the bed velocity by treating the catalytic bed as a porous zone and incorporating the rotating recycled fluid flow in CFD. This velocity was used as the boundary condition for CPFD to determine bed expansion and particle volume fraction at various rotation rates. The observed bed properties were then incorporated into CFD simulations using modified mesh models. We introduced several key hydrodynamic indicators for the Berty-type reactor and compared the predictive results from CFD to those from the combined CFD/CPFD method. Lastly, we integrated the bed expansion correlation with the impeller relationship to shed light on the hydrodynamics of the ILS Berty reactor.
2. Methodology
2.1. Simulation framework
We combined the capabilities of CFD using ANSYS Fluent, which couples the porous zone setting with the multiple reference frame (MRF) to represent both the catalytic basket and the rotator, with CPFD by Barracuda, which analyzes the fluidization behavior in the catalytic bed. We used the ILS Berty fluidized bed reactor (Fig. 1) to investigate the hydrodynamics of internal circulating Berty reactors operating in batch mode. Details of the ILS Berty reactor and validations with experiments (Fig. S1†) can be found in our previous publication.36The proposed modeling framework is depicted in Fig. 2, and the operating conditions are detailed in Table 1. We considered the entire catalytic bed between the two screens a uniform porous media zone. The viscous and inertial resistance factors are derived from the Gidaspow equation (eqn (1) and (2)).58–62 The CFD simulation was conducted using the initial mesh model under uniform bed porosities (Fig. S2a†), wherein the MRF model was integrated to simulate the rotating zone. This enabled the acquisition of gas velocity and pressure drop across the bed between gas and solids. Owing to the well-mixing behavior characteristic of a CSTR system, bed fluidization can be examined as an individual system using the CPFD approach.36 Here, the bed velocity from the CFD was used as the boundary condition, offering a detailed description of the fluidization status. Drawing on the bed expansion and particle volume fraction data from CPFD, we adjusted the CFD mesh model to incorporate different layers of porosities (Fig. S2b†) for a subsequent simulation round.
 | (1) |
 | (2) |
| Condition | Item | CFD | CPFD | |
|---|---|---|---|---|
| Temperature (°C) | 700 | Inlet | NA, change to wall | Flow boundary condition |
| Pressure (bar) | 1 | Outlet | NA, change to wall | Pressure boundary condition |
| Particle diameter (μm) | 66 | Turbulent model | SST k–ω | Large eddy simulation |
| Particle density (kg m−3) | 1500 | Energy model | No | No |
| Packed bed porosity | 0.47 | Transient state | No | Yes |
| Hastelloy mesh porosity | 0.7 | Multiphase | No | Yes |
| Catalyst loading (g) | ∼5.6 | |||
| Rotation rate (min−1) | 4000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|||
Since hydrodynamics under various feed mixtures can be modified by the corrected physical properties in batch mode, we simplified our work using the inert gas argon (Table 2) at the reaction condition (700 °C, 1 bar).36 Argon was fully introduced into the reactor at the outset with the desired physical properties. We simulated a batch operation by converting the inlet and outlet to wall boundaries. By setting the porous zone of the catalytic bed, calculations could be simplified to a single gas phase. The SST k–ω turbulent model with low-Reynold corrections was chosen to capture the flow transition from laminar to turbulent regimes. We used the standard solid properties of fluid catalytic cracking catalysts, which are 66 μm and 1500 kg m−3. The steady-state isothermal CFD simulation was conducted using ANSYS Fluent with other default settings at rotation rates ranging from 4000 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. An initial catalyst of approximately 5.6 g was loaded into the reactor, assuming a catalytic bed with a uniform porosity of 0.7. Subsequently, we conducted the CPFD simulation of the catalytic basket depicted in Fig. 1 using Barracuda. This had a flow boundary condition at the bottom and a pressure boundary condition at the top, allowing us to investigate the gas–solids interactions concerning bed fluidization behaviors in terms of expansion, particle volume fraction, and pressure drop.
000 rpm. An initial catalyst of approximately 5.6 g was loaded into the reactor, assuming a catalytic bed with a uniform porosity of 0.7. Subsequently, we conducted the CPFD simulation of the catalytic basket depicted in Fig. 1 using Barracuda. This had a flow boundary condition at the bottom and a pressure boundary condition at the top, allowing us to investigate the gas–solids interactions concerning bed fluidization behaviors in terms of expansion, particle volume fraction, and pressure drop.
| Gas | Density (kg m−3) | Heat capacity (kJ kg−1 K−1) | Thermal conductivity (W m−1 K−1) | Viscosity (cP) | Molecular weight (g mol−1) |
|---|---|---|---|---|---|
| Argon | 0.494 | 0.521 | 4.17 × 10−2 | 5.70 × 10−2 | 39.95 |
2.2. CFD approach
ANSYS Fluent, a commercial CFD package, was employed for the 3D, steady-state, and isothermal computations in the ILS Berty reactor, employing the MRF model for the rotating domain.36,63 The catalyst bed was treated as one or several homogeneous porous zones,41,64 where the viscous and inertial loss coefficients were determined using the Gidaspow equation (eqn (1) and (2)),58–62,65,66 considering uniform particle diameters and designated porosities. The SST k–ω model with low-Reynolds corrections was chosen as the turbulence model.64,67 The governing equations (eqn (3)–(11)) for the CFD approach are presented in Table 3.In this study, two types of CFD mesh models for the ILS Berty reactor are illustrated in Fig. 1. The first is based on the homogeneous porous zone assumption for the entire bed (Fig. S2a†),36 while the second adjusts bed porosity and expansion according to the particle volume fraction distribution derived from CPFD simulations (Fig. S2b†). Both mesh models were developed using ANSYS Workbench, where rotationally periodic boundaries were applied to emulate computational efforts based on a 60° slice model (representing 1/6 of the reactor volume).32,68,69 A mesh independence check was performed under each condition to balance computation time and prediction accuracy. Consequently, a mesh model comprising approximately 150k cells was selected. The CFD simulation was validated with pressure drop measurements and further details can be referenced in previous work.36
2.3. CPFD approach
In the CPFD simulation, the Eulerian approach is employed to solve the governing equations for the fluid phase, treating it as a continuum. Meanwhile, particles are considered to be in the dispersed phase and are described using the Lagrangian method. The continuity and momentum equations for gas flow can be found in eqn (12) and (13).70–72 | (12) |
 | (13) |
 | (14) |
The particle acceleration is modeled using the Lagrangian method, as presented in eqn (15), and the Liouville equation (eqn (16)) is used to determine particle positions.71
 | (15) |
 | (16) |
Before proceeding with the numerical simulations, a mesh independence study was conducted to estimate the minimum number of cells needed to capture the operational physics of the geometry. This amounted to roughly 50k cells for the catalytic basket in the CPFD simulation.
2.4. Key hydrodynamic indicators for Berty-type reactors
The top impeller generates compression and suction when operating the Berty-type reactor in batch fluidized bed mode. This facilitates fluid circulation upwards through the center and then downwards into the outer annulus region. In this context, we proposed several key hydrodynamic indicators for the Berty-type reactor, emphasizing the catalytic bed and the reactor itself.The fluidization regime is classified based on the superficial gas velocity, given specific gas/solid properties.2 This classification determines the mass, momentum, and heat transfer behaviors of the gas–solid flow structure and its contact pattern. The particle volume fraction illustrates the fluidization status, ranging from dense packing to the dilute transport zone. Consequently, we selected the superficial gas velocity and particle volume fraction in the catalytic bed to characterize its fluidization status. Ensuring a uniform velocity distribution in the catalytic bed,36 we adjusted the recirculation rate (eqn (17)) based on the approach from Pekediz et al.35 This rate represents the gas flow ratio within the catalytic bed to the entire reactor volume. Similarly, the single-round gas–solid contact time (eqn (18)) can be deduced from the ratio of the bed height to the superficial gas velocity.
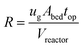 | (17) |
 | (18) |
Additionally, the pressure drop (eqn (19)) has been identified as an important parameter for the Berty-type reactor in previous experimental and simulation investigations,20,36 and it is correlated with the rotation speed and gas density.
 | (19) |
We defined the effectiveness factor ε and the momentum loss factor lm in eqn (20) and (21) to evaluate the overall hydrodynamic performance of the Berty-type reactor.
 | (20) |
| lm = 1 − ε | (21) |
3. Results
3.1. CFD simulation with homogeneous basket porosity
We conducted the CFD simulation of the ILS Berty reactor with a homogeneous basket porosity of 0.7 at rotation rates of 4000, 5500, 7000, 8500, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, using the detailed conditions presented in Tables 1 and 2. Fig. 3 displays the pressure and velocity contours for one representative surface from the entire revolving geometry. To better illustrate the pressure distribution, we presented the relative static pressure compared to the operating condition.
000 rpm, using the detailed conditions presented in Tables 1 and 2. Fig. 3 displays the pressure and velocity contours for one representative surface from the entire revolving geometry. To better illustrate the pressure distribution, we presented the relative static pressure compared to the operating condition.
 | ||
Fig. 3 Pressure (a–e) and velocity (f–j) contours of the ILS Berty reactor from CFD with a homogeneous basket porosity of 0.7: (a and f) rotation rate: 4000 min−1; (b and g) rotation rate: 5500 min−1; (c and h) rotation rate: 7000 min−1; (d and i) rotation rate: 8500 min−1; (e and j) rotation rate: 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 min−1. All the contours are displayed at one representative surface of the revolving geometry, and the simulation conditions are shown in Tables 1 and 2. 000 min−1. All the contours are displayed at one representative surface of the revolving geometry, and the simulation conditions are shown in Tables 1 and 2. | ||
Fig. 3a–e depict analogous hydrodynamic behaviors in pressure and velocity distributions across various rotating rates. Similar low-pressure areas are evident in the rotating zone, the volume of which diminishes with increasing rotation rates. This suggests a reduction in the dead volume in the spinning section. The primary pressure drop in the stationary section originates from the Hastelloy meshes and the intervening catalytic bed. A consistent decrease in pressure from the bottom to the top is a characteristic behavior for catalytic beds. Fig. 3f–j reveal a velocity increment with rising rotation rates due to the increased momentum imparted by the impeller. However, the rotation rate does not markedly impact the fluid domain's velocity distribution, especially in the stationary section. Here, the velocity across the bed remains relatively low for most of the stationary area compared to the rotating linear velocity generated by the impeller. This suggests a significant momentum loss in the circulation section without velocity contour lines. Fig. S3† shows the area-averaged velocities of the bottom and top surfaces and the mass-averaged velocity of the entire catalyst bed zone under the batch-packed bed mode. The uniform basket porosity setting demonstrates ideal mixing behavior with a consistent velocity distribution. Although the reactor simulation was in batch mode, the catalytic bed operated similarly to a CSTR, featuring a uniform velocity profile and continuous gas movement. The horizontally distributed pressure contour lines (Fig. 3a–e) and the uniform velocity (Fig. S3†) within the catalytic bed highlight a distinct gas–solid interaction system, validating the reliability of the combined CFD/CPFD approach.
3.2. CPFD simulation for bed fluidization
We adopted the volume-average basket velocity obtained from the CFD simulation in section 3.1 as the superficial gas velocity at the bottom of the catalytic bed to investigate fluidization behavior using CPFD. With a Hastelloy mesh serving as the gas distributor in the reactor, the assumption of a uniform bed velocity from the bottom is reasonable. This assumption was further validated by the simulated basket velocity distribution (Fig. 3f–j and S3†).36The major characteristics of gas–solid fluidization are in the fluidization regime, which varies with gas and solid properties and is classified by the superficial gas velocity.2,73 As illustrated in Fig. S3,† the bed velocity reaches the minimum fluidization velocity at a rotation rate of 4600 rpm under the conditions presented in Tables 1 and 2. However, it remains well below the terminal velocity (∼60 mm s−1) under all conditions, suggesting a dense fluidization regime.73 We utilized the particle volume fraction contour at a rotation rate of 4000 rpm (Fig. 4f) from the CPFD simulation to elucidate bed expansion behavior. The bed consists of layers with varying particle volume fractions. A decrease in these fractions along the horizontal direction results in a packed bed at the bottom and smooth fluidization at the surface, creating a dynamic velocity distribution in the catalytic bed. This differs from the CFD simulation, which assumed a homogeneous basket porosity.
 | ||
Fig. 4 Bed fluidization behavior obtained by CPFD based on the simulated CFD velocity with a homogeneous basket porosity of 0.7: (a) a catalytic bed with different layers of particle volume fraction; (a and b) rotation rate: 4000 min−1; (c) rotation rate: 5500 min−1; (d) rotation rate: 7000 min−1; (e) rotation rate: 8500 min−1; (f) rotation rate: 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 min−1. Detailed simulation conditions are presented in Tables 1 and 2. 000 min−1. Detailed simulation conditions are presented in Tables 1 and 2. | ||
We positioned 20 equidistantly distributed planes along the vertical direction to capture bed expansion characteristics (Fig. 4f). From these planes, the area-averaged pressure, particle volume fraction, and gas velocity are depicted in Fig. 4a–e. We segmented the bed in Fig. 4f into several zones based on particle volume fraction distribution, the average of which is also highlighted in Fig. 4a. Gas velocity fluctuates with bed fluidization status; a packed bed (with a higher particle volume fraction) results in an elevated gas velocity due to mass balance. As a result, the gas velocity profile shifts synchronously with the particle volume fraction curve. Pressure maintains a linear relationship along the bed height, which is also characteristic of fluidized catalytic beds.
As rotation rates increase, bed fluidization becomes more uniform with fewer layers of varied particle volume fraction. For instance, the bed achieves uniform fluidization with a particle volume fraction of 0.42 at a rotation rate of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. The evolving particle volume fraction indicates the progression of fluidization from the surface to the transition zone and eventually throughout the entire bed. While the bed status changes with different superficial gas velocities and rotation rates, similar patterns of a linear pressure drop profile and a synchronous gas velocity curve are observed under all conditions. However, the bed pressure drop remains consistent in an individual fluidization system, a finding that diverges from the CFD simulation results assuming a homogeneous basket porosity.36
000 rpm. The evolving particle volume fraction indicates the progression of fluidization from the surface to the transition zone and eventually throughout the entire bed. While the bed status changes with different superficial gas velocities and rotation rates, similar patterns of a linear pressure drop profile and a synchronous gas velocity curve are observed under all conditions. However, the bed pressure drop remains consistent in an individual fluidization system, a finding that diverges from the CFD simulation results assuming a homogeneous basket porosity.36
3.3. CFD simulation with adjusted basket porosity
Considering bed expansion under various superficial gas velocities, we conducted another round of CFD simulations on the ILS Berty reactor, adjusting for basket porosities. These simulations were run at rotation rates of 4000, 5500, 7000, 8500, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm based on the conditions presented in Tables 1 and 2. The bed expansion and particle volume fraction data were sourced from the CPFD simulation detailed in section 3.2, with more information provided in Fig. 4. Pressure and velocity contours for one representative surface from the entire revolving geometry are depicted in Fig. 5. To better illustrate the pressure distribution, we displayed the relative static pressure in relation to the operating condition.
000 rpm based on the conditions presented in Tables 1 and 2. The bed expansion and particle volume fraction data were sourced from the CPFD simulation detailed in section 3.2, with more information provided in Fig. 4. Pressure and velocity contours for one representative surface from the entire revolving geometry are depicted in Fig. 5. To better illustrate the pressure distribution, we displayed the relative static pressure in relation to the operating condition.
 | ||
Fig. 5 Pressure (a–e) and velocity (f–j) contours of the ILS Berty reactor from the CFD simulation with adjusted basket porosity from the CPFD fluidization results: (a and f) rotation rate: 4000 min−1; (b and g) rotation rate: 5500 min−1; (c and h) rotation rate: 7000 min−1; (d and i) rotation rate: 8500 min−1; (e and j) rotation rate: 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 min−1. All contours are displayed on a representative surface of the revolving geometry, and the simulation conditions can be found in Tables 1 and 2. 000 min−1. All contours are displayed on a representative surface of the revolving geometry, and the simulation conditions can be found in Tables 1 and 2. | ||
Fig. 5 depicts analogous behaviors of the simulated hydrodynamic characteristics, including pressure and velocity distributions, when the basket porosity is adjusted in homogeneous settings. Even though the bed height with an adjusted basket porosity is approximately 2/3 of that with a homogeneous basket porosity, the main pressure drop in the stationary part (as seen in Fig. 5a–e) from the Hastelloy meshes and the interposed catalytic bed remains consistent under each rotation rate, as compared to Fig. 3a–e. This consistency is evident in both the distribution and the pressure drop within the stationary zone. Fig. 5f–j present similar low bed velocities and momentum loss in the circulation part, suggesting a direction for optimizing reactor geometry for batch fluidized bed operations by minimizing the recirculation zone. The nearly identical pressure distributions under various bed expansion statuses indicate that bed fluidization has minimal impact on the overall pressure drop in the Berty-type reactor. However, it significantly influences the gas velocity in the catalytic bed.
3.4. Comparison
We compared the hydrodynamic characteristics of the ILS Berty reactor using different simulation settings (Fig. 6a–c). We focused on three key hydrodynamic indicators related to fluidization, mixing, and the impeller: superficial gas velocity in the catalytic bed, single-round gas–solid contact time, and pressure drop. Fig. 6 presents the results from the CFD simulation (model I) with a homogeneous basket porosity of 0.7, the CPFD simulation (model II) based on the volume-average basket velocity from model I, and the CFD simulation (model III) with adjusted basket porosities accounting for bed fluidization behaviors. Fig. 6d illustrates the impeller relationships under models I and III, including profiles without frits. The single-round contact time is simplified by summing up the bed height to gas velocity ratio in each bed layer, as described in eqn (18). Results from the CPFD simulation did not account for impeller rotation and are listed for reference. The primary aim is to compare results between the homogeneous and adjusted basket porosity settings.The pressure and velocity contours for both homogeneous and adjusted basket porosities suggest that bed fluidization significantly impacts the gas velocity in the catalytic bed, a finding corroborated by Fig. 6a. The simulated gas velocity with the adjusted basket porosity is lower than that with the homogeneous setting. This is due to a denser bed with reduced height given the same catalyst loading. As the rotation rate increases, the deviation becomes more pronounced. However, the single-round gas–solid contact time (Fig. 6b) becomes more consistent across different porosity settings because of the reduced bed height and decreased gas velocity. This indicates that the assumption and simplification of homogeneous basket porosity for the Berty-type reactor remain valid concerning contact time when the rotation rate exceeds 7000 rpm.
We observed deviations in the key hydrodynamic indicators related to fluidization status and mixing pattern due to the bed velocity and single-round gas–solid contact time between the two simulation approaches. Moreover, the recirculation rate (eqn (17)) has a linear relationship with the superficial gas velocity. This relationship results in differences ranging from 2 to 5.5 times between the uniform and adjusted porosity settings, highlighting the importance of employing accurate hydrodynamic characteristics when designing a Berty-type reactor.
The agreement in bed pressure drop (Fig. 6c) across different bed expansions and particle volume fractions indicates that the hydrodynamics in the Berty-type reactor are predominantly influenced by impeller rotation, which determines bed fluidization behavior. The CPFD simulation of an individual fluidization system with increased superficial gas velocity is depicted in Fig. 6c for reference. This figure displays a typical characteristic of fluidized beds: a stable pressure drop once fluidized. However, our results suggest that the pressure drop determines fluidization and gas velocity in the catalytic bed of a Berty-type reactor. This conclusion is supported by the impeller relationship shown in Fig. 6d and the experimental observations from Berty.18 The pressure drop experienced across the catalyst basket correlates directly with the pressure generated by the impeller, which depends on rotation speed and fluid density. Any minor deviation in the impeller relationship without frits (considering only the bed behavior) disappears when accounting for the pressure drop from the frits. This is confirmed by the pressure distributions observed with varying basket porosities in Fig. 3a–e and 5a–e. The good match with the well-known features of the Berty-type reactor verified the feasibility and effectiveness of our simulation approach. However, disparities were spotted in the bed velocity, singular-round gas–solid contact duration, and the recirculation rate between the previous model and the improved one proposed in this paper. This underscores the imperative of incorporating precise hydrodynamic attributes during the design phase of the Berty-type reactor.
4. Discussion
The simulation results, under different porosity settings, confirmed that the pressure drop in the stationary part of the Berty-type reactor follows the impeller relationship (eqn (22)–(24)). In this relationship, the pressure drop is determined by both the rotation rate and the flow medium, independent of the fluidization status. However, the gas velocity in the catalytic bed is influenced by the fluidization behavior during bed expansion and particle volume fraction distribution. We introduced two additional equations (eqn (25) and (26)) to augment the hydrodynamic characteristics of the ILS Berty fluidized bed reactor when operated in batch mode. These equations can also be applied to other internal recycle reactors. Eqn (25) is a simplified version adapted from tapered fluidized bed systems,74 while eqn (26) is rooted in particle mass balance, assuming a uniform particle volume fraction. | (22) |
 | (23) |
 | (24) |
 | (25) |
 | (26) |
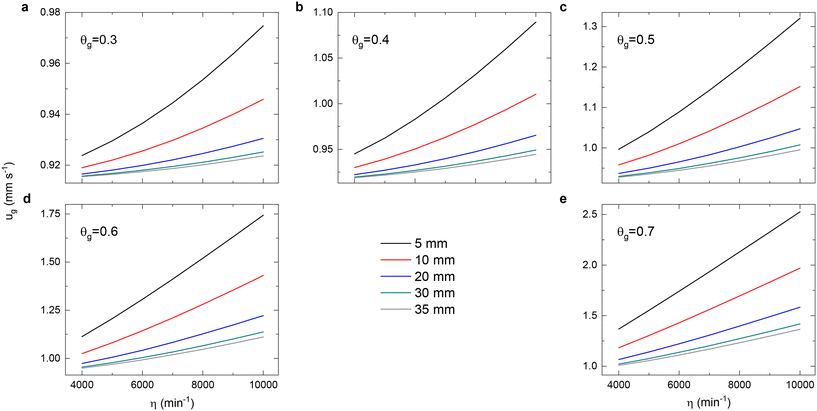
A solution to these equations is obtained using Mathematica v12.0, which yields a numerical relationship between gas velocity as a function of the solid volume fraction and the initial bed height. Fig. 7, along with the contour plots in the ESI† (Fig. S4–S8), showcases these velocities in the catalytic basket relative to the impeller rotation rate. Due to more efficient momentum transfer between gas and solid at smaller initial bed heights (5 mm), the velocities are at their highest, potentially leading to better fluidization of the solids. When increasing the solids loading through a larger h0 in the basket at constant impeller rotation speeds, gas velocities decrease. This reduction effect is more pronounced the higher the initial solids loading. As bed packing intensifies, momentum transfer becomes less effective, evidenced by the nearly unchanged velocities for perfectly packed beds.
From the obtained superficial gas velocities under various rotation rates and solid loadings, we can determine the operating conditions based on the hydrodynamic performances of the ILS Berty reactor for fluidization status and single-round gas–solid contact time. The recirculation rate (eqn (17)) and effectiveness factor (eqn (20)) can be compared across different designs. Various feedstocks and operating conditions can be explored to verify fluidization by adjusting the fluid property. The detailed hydrodynamic characterization facilitates proper and convenient data interpretation and design modification, which can be applied to other internal recycle reactors.
5. Conclusions
To harness the benefits of Berty-type reactors in mimicking industrial riser conditions, we devised a combined CFD/CPFD simulation framework to investigate the complex hydrodynamics of the ILS Berty fluidized bed reactor during batch operation. CFD, which integrates the porous zone setting with MRF to depict the catalytic basket and rotator, was amalgamated with CPFD to encapsulate the fluidization behavior in the catalytic bed.By treating the catalytic bed as a porous zone and incorporating the rotated recycling fluid flow in CFD, we discerned the pressure and velocity distributions with a consistent basket porosity of 0.7 under rotation rates ranging from 4000 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. Even though the reactor was simulated in batch mode, the catalytic bed operates akin to a CSTR, showcasing a uniform velocity profile and continuous gas motion. The uniformly distributed pressure contour lines and the consistent velocity within the catalytic bed unveil a distinct system of gas–solid interactions, underscoring the reliability of the integrated CFD/CPFD approach.
000 rpm. Even though the reactor was simulated in batch mode, the catalytic bed operates akin to a CSTR, showcasing a uniform velocity profile and continuous gas motion. The uniformly distributed pressure contour lines and the consistent velocity within the catalytic bed unveil a distinct system of gas–solid interactions, underscoring the reliability of the integrated CFD/CPFD approach.
As deduced from CFD, the bed velocity served as the boundary condition for CPFD, guiding bed expansion and particle volume fraction across diverse rotating rates. The discerned bed characteristics were subsequently employed in CFD simulations within revised mesh models. Comparatively subdued bed velocities and momentum loss in the circulation section underscore an optimization direction for the reactor's geometry—trimming the stationary zone for enhanced fluidization. The pressure distributions amid various bed expansions insinuate that the overarching pressure drop is virtually indifferent to the fluidization status, though it profoundly influences the gas velocity in the catalytic bed.
We posited several pivotal hydrodynamic indicators for the Berty-type reactor and juxtaposed the predictive outcomes from CFD against those from the combined CFD/CPFD method. Disparities were spotted concerning fluidization status and mixing pattern by the bed velocity, singular-round gas–solid contact duration, and the recirculation rate between consistent and modulated porosity setups. This underscores the imperative of incorporating precise hydrodynamic attributes during the design phase of the Berty-type reactor.
Given that the pressure drop is governed by both the rotation rate and the flow medium, irrespective of the fluidization status, we integrated the bed expansion correlation with the impeller relationship. This was done to characterize the hydrodynamics of the ILS Berty reactor concerning superficial gas velocity under varying impeller rotation rates.
Nomenclature
| A | Impeller constant of the Berty reactor |
| A bed | Is the cross-sectional area of the catalytic bed |
| B | Intercept constant |
| C 2 | Inertial resistance factor |
| C D | Drag coefficient |
| d | Diameter |
| D | Drag force |
| f | Function of the particle location |
| F | Gas-to-particle momentum transfer rate per unit volume |
| F i | External body forces |
| g | Gravitational acceleration |
| h | Bed height |
| J | Diffusion flux of the species |
| k | Turbulence kinetic energy |
| l m | Momentum loss factor |
| m | Mass |
| p | Pressure |
| Δp | Pressure drop obtained between the inlet and outlet of the ILS Berty reactor |
| R | Recirculation rate |
| r blade | Radius of impeller blade |
| S | Other source items |
| t | Time |
| t op | Operating time |
| t c | Single-round gas-solid contact time |
| u | Velocity |
| g | Gas phase |
| u r | The velocity of the moving frame relative to the inertial reference frame |
| V reactor | Reactor volume |
| v a | Absolute velocity viewed from the stationary frame |
| v r | Relative velocity viewed from the moving frame |
| Y i | Local mass fraction of each species |
Symbols
| ρ | Density |
| τ | Stress tensor |
| α | Viscous resistance factor |
| θ | Volume fraction |
| ω r | Angular velocity with/without the direction vector â |
| ω | Specific dissipation rate |
| τ D | Particle collision damping time |
| μ | Viscosity |
| η | Rotation rate |
| ε | Effectiveness factor |
Subscripts
| s | Solid phase |
Abbreviations
| CFD | Computational fluid dynamics |
| CFPD | Computational particle fluid dynamics |
| CREC | Chemical Reactor Engineering Centre |
| CSTR | Continuous stirred tank reactor |
| DEM | Discrete element method |
| ILS | Integrated Lab Solutions |
| MRF | Multiple reference frame |
Author contributions
Mengmeng Cui: methodology; investigation; data curation; software; visualization; writing – original draft. Shekhar R. Kulkarni: investigation; analysis; writing – review and editing. Yacoub-Yousef Abu-Naaj, Stefan Wagner, Claudia Berger-Karin, Jan Lennart Weber: investigation; visualization, validation. Anton Nagy: resources; supervision. Pedro Castaño: conceptualization; methodology; funding acquisition; supervision; project administration; writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is based upon work supported by the King Abdullah University of Science and Technology (KAUST) under Award No. TTO-RTF4-2022-5401. The authors acknowledge the KAUST Supercomputing Laboratory (KSL) for providing high-performance computational resources. The authors are also thankful to the CPFD support team.References
- R. Cocco, S. B. Reddy and K. T. Knowlton, Chem. Eng. Prog., 2014, 21–29 Search PubMed.
- M. Menéndez, J. Herguido, A. Bérard and G. S. Patience, Can. J. Chem. Eng., 2019, 97, 2383–2394 CrossRef.
- T. Cordero-Lanzac, A. T. Aguayo, A. G. Gayubo, P. Castaño and J. Bilbao, Chem. Eng. J., 2020, 379, 122260 CrossRef CAS.
- A. Corma, E. Corresa, Y. Mathieu, L. Sauvanaud, S. Al-Bogami, M. S. Al-Ghrami and A. Bourane, Catal. Sci. Technol., 2017, 7, 12–46 RSC.
- A. Usman, M. A. B. Siddiqui, A. Hussain, A. Aitani and S. Al-Khattaf, Chem. Eng. Res. Des., 2017, 120, 121–137 CrossRef CAS.
- F. M. Alotaibi, S. González-Cortés, M. F. Alotibi, T. Xiao, H. Al-Megren, G. Yang and P. P. Edwards, Catal. Today, 2018, 317, 86–98 CrossRef CAS.
- M. Alabdullah, A. Rodriguez-Gomez, T. Shoinkhorova, A. Dikhtiarenko, A. D. Chowdhury, I. Hita, S. R. Kulkarni, J. Vittenet, S. M. Sarathy, P. Castaño, A. Bendjeriou-Sedjerari, E. Abou-Hamad, W. Zhang, O. S. Ali, I. Morales-Osorio, W. Xu and J. Gascon, Nat. Catal., 2021, 4, 233–241 CrossRef CAS.
- N. Hanchate, S. Ramani, C. S. Mathpati and V. H. Dalvi, J. Cleaner Prod., 2021, 280, 123148 CrossRef.
- D. Kong, K. Luo, S. Wang, J. Yu and J. Fan, Chem. Eng. J., 2022, 428, 131847 CrossRef CAS.
- X. Chen, J. Ma, X. Tian, J. Wan and H. Zhao, Int. J. Greenhouse Gas Control, 2019, 90, 102800 CrossRef CAS.
- A. Lyngfelt, D. Pallarès, C. Linderholm, F. Lind, H. Thunman and B. Leckner, Energy Fuels, 2022, 36, 9588–9615 CrossRef CAS.
- P. M. Witt and D. A. Hickman, AIChE J., 2022, 68, e17803 CrossRef CAS.
- J. M. Berty, Chem. Eng. Prog., 1974, 70, 78–84 CAS.
- K. Ountaksinkul, S. Wannakao, P. Praserthdam and S. Assabumrungrat, RSC Adv., 2020, 10, 36667–36677 RSC.
- G. D. Wehinger, B. Kreitz, A. Nagy and T. Turek, Chem. Eng. J., 2020, 389, 124342 CrossRef CAS.
- K. Ountaksinkul, S. Sripinun, P. Bumphenkiattikul, S. Bubphacharoen, A. Vongachariya, A. Jantharasuk, P. Praserthdam and S. Assabumrungrat, React. Chem. Eng., 2022, 7, 361–375 RSC.
- H. Kreuder, C. Müller, J. Meier, U. Gerhards, R. Dittmeyer and P. Pfeifer, Catal. Today, 2015, 242, 211–220 CrossRef CAS.
- J. M. Berty, Catal. Rev.: Sci. Eng., 1979, 20, 75–96 CrossRef CAS.
- J. M. Berty, Plant/Oper. Prog., 1984, 3, 163–168 CrossRef CAS.
- J. M. Berty, Experiments in Catalytic Reaction Engineering, Elsevier B.V., Amsterdam, 1999 Search PubMed.
- F. S. Ramos, A. M. D. De Farias, L. E. P. Borges, J. L. Monteiro, M. A. Fraga, E. F. Sousa-Aguiar and L. G. Appel, Catal. Today, 2005, 101, 39–44 CrossRef CAS.
- A. S. Al-Dughaither and H. De Lasa, Fuel, 2014, 138, 52–64 CrossRef CAS.
- R. Jara, M. Lawoko and A. van Heiningen, Can. J. Chem. Eng., 2019, 97, 649–661 CrossRef CAS.
- B. Kreitz, G. D. Wehinger, C. F. Goldsmith and T. Turek, ChemCatChem, 2022, e202200570 CrossRef CAS.
- H. de Lasa, US10220363B2, 2019.
- H. De Lasa, Catalysts, 2022, 12, 888 CrossRef CAS.
- Reactor Engineering and Catalytic Technologies Inc, CREC Riser Simulator, 2006 Search PubMed.
- T. El Solh, K. Jarosch and H. De Lasa, Ind. Eng. Chem. Res., 2003, 42, 2507–2515 CrossRef CAS.
- J. A. Atias and H. De Lasa, Chem. Eng. Sci., 2004, 59, 5663–5669 CrossRef CAS.
- F. Passamonti, G. de la Puente, W. Gilbert, E. Morgado and U. Sedran, Chem. Eng. J., 2012, 183, 433–447 CrossRef CAS.
- S. Lopez-Zamora, A. Alkhlel and H. de Lasa, Chem. Eng. Sci., 2018, 192, 788–802 CrossRef CAS.
- I. Ahmed, S. Rostom, A. Lanza and H. de Lasa, Powder Technol., 2017, 316, 641–649 CrossRef CAS.
- J. A. Mahoney, J. Catal., 1974, 32, 247–253 CrossRef CAS.
- L. Caldwell, Appl. Catal., 1983, 8, 199–213 CrossRef CAS.
- A. Pekediz, D. W. Kraemer, J. Chabot and H. I. Lasa, in Chemical Reactor Technology for Environmentally Safe Reactors and Products, Springer, Netherlands, Dordrecht, 1992, pp. 133–146 Search PubMed.
- M. Cui, S. R. Kulkarni, S. Wagner, C. Berger-Karin, A. Nagy and P. Castaño, ACS Eng. Au, 2022, 2, 103–117 CrossRef CAS.
- C. Zhang, B. Lu, W. Wang, M. Liu, C. Lu and M. Ye, Chem. Eng. J., 2022, 446, 136849 CrossRef CAS.
- J. Shabanian and J. Chaouki, Chem. Eng. J., 2017, 313, 580–590 CrossRef CAS.
- V. Santos-Moreau, L. Brunet-Errard and M. Rolland, Chem. Eng. J., 2012, 207–208, 596–606 CrossRef CAS.
- S. D. Anderson, B. Kreitz, T. Turek and G. D. Wehinger, Ind. Eng. Chem. Res., 2022, 61, 10790–10803 CrossRef CAS.
- Y. Yang, Y. Xiang, Y. Li, G. Chu, H. Zou, M. Arowo and J. Chen, Can. J. Chem. Eng., 2015, 93, 1138–1148 CrossRef CAS.
- X. Lu, P. Xie, D. B. Ingham, L. Ma and M. Pourkashanian, Chem. Eng. Sci., 2018, 189, 123–134 CrossRef CAS.
- X. Lu, P. Xie, D. B. Ingham, L. Ma and M. Pourkashanian, Chem. Eng. Sci., 2019, 199, 302–318 CrossRef CAS.
- Y. Yang, Y. Ouyang, N. Zhang, Q. Yu and M. Arowo, J. Chem. Technol. Biotechnol., 2019, 94, 1017–1031 CrossRef CAS.
- X. Gao, J. Yu, L. Lu, C. Li and W. A. Rogers, Chem. Eng. J., 2021, 420, 127654 CrossRef CAS.
- A. Di Renzo and F. P. Di Maio, Chem. Eng. Sci., 2007, 62, 116–130 CrossRef CAS.
- Y. Gu, A. Ozel and S. Sundaresan, Powder Technol., 2016, 296, 17–28 CrossRef CAS.
- A. Bakshi, M. Shahnam, A. Gel, T. Li, C. Altantzis, W. Rogers and A. F. Ghoniem, Powder Technol., 2018, 338, 519–537 CrossRef CAS.
- R. Uglietti, D. Micale, D. La Zara, A. Goulas, L. Nardi, M. Bracconi, J. R. van Ommen and M. Maestri, React. Chem. Eng., 2023, 8, 2029–2039 RSC.
- R. Uglietti, M. Bracconi and M. Maestri, React. Chem. Eng., 2020, 5, 278–288 RSC.
- R. Uglietti, M. Bracconi and M. Maestri, React. Chem. Eng., 2018, 3, 527–539 RSC.
- F. Zafiryadis, A. Degn Jensen, W. Lin, S. Clausen, E. Akoh Hove, M. Boberg Larsen and H. Wu, Chem. Eng. J., 2023, 461, 141952 CrossRef CAS.
- C. Chen, J. Werther, S. Heinrich, H. Y. Qi and E. U. Hartge, Powder Technol., 2013, 235, 238–247 CrossRef CAS.
- Q. Wang, H. Yang, P. Wang, J. Lu, Q. Liu, H. Zhang, L. Wei and M. Zhang, Powder Technol., 2014, 253, 822–828 CrossRef CAS.
- J. C. Bandara, R. Thapa, H. K. Nielsen, B. M. E. Moldestad and M. S. Eikeland, Part. Sci. Technol., 2019, 39, 223–236 CrossRef.
- Q. Tu, Z. Luo and H. Wang, Chem. Eng. J., 2021, 421, 129835 CrossRef CAS.
- M. Cui, A. Dikhtiarenko, S. R. Kulkarni, T. Shoinkhorova, I. Al Aslani, M. Alabdullah, J. Mazumder, R. M. Flores, A. Alahmadi, L. Alfilfil, I. M. Osorio, K. Almajnouni, J. Gascon and P. Castaño, Powder Technol., 2024, 438, 119573 CrossRef CAS.
- S. Kraft, F. Kirnbauer and H. Hofbauer, Particuology, 2018, 36, 70–81 CrossRef.
- Z. Wan, S. Yang, J. Hu, G. Bao and H. Wang, Energy, 2022, 243, 122974 CrossRef CAS.
- Y. Liang, Y. Zhang, T. Li and C. Lu, Powder Technol., 2014, 263, 121–134 CrossRef CAS.
- Q. Wang, H. Yang, P. Wang, J. Lu, Q. Liu, H. Zhang, L. Wei and M. Zhang, Powder Technol., 2014, 253, 814–821 CrossRef CAS.
- S. Yang, S. Wang and H. Wang, Chem. Eng. J., 2021, 421, 127787 CrossRef CAS.
- J. Q. Wang, Y. Ouyang, W. L. Li, A. Esmaeili, Y. Xiang and J. F. Chen, Chem. Eng. J., 2020, 385, 123812 CrossRef CAS.
- K. Mohammadpour, A. Alkhalaf and E. Specht, Comput. Part. Mech., 2019, 6, 157–162 CrossRef.
- H. Jin, Z. Wu, L. Guo and X. Su, Heat Transfer Eng., 2018, 39, 1596–1607 Search PubMed.
- A. Nabizadeh, H. Hassanzadeh, M. Asadieraghi, A. Hassanpour, D. Moradi, M. Keshavarz Moraveji and M. Hozhabri Namin, Chem. Eng. Res. Des., 2020, 156, 13–22 CrossRef CAS.
- P. Xie, X. Lu, X. Yang, D. Ingham, L. Ma and M. Pourkashanian, Chem. Eng. Sci., 2017, 172, 216–229 CrossRef CAS.
- H. Larsson, P. A. Schjøtt Andersen, E. Byström, K. V. Gernaey and U. Krühne, Ind. Eng. Chem. Res., 2017, 56, 3853–3865 CrossRef CAS.
- S. R. Kulkarni, A. González Quiroga, P. Perreault, H. Sewani, G. J. Heynderickx, K. M. Van Geem and G. B. Marin, in Chemical Engineering Transactions, 2018, vol. 65 Search PubMed.
- I. Ahmed and H. De Lasa, Ind. Eng. Chem. Res., 2020, 59, 6900–6913 CrossRef CAS.
- S. Rostom and H. de Lasa, Chem. Eng. Process., 2019, 137, 87–99 CrossRef CAS.
- Y. Wu, X. Shi, C. Wang, J. Gao and X. Lan, Energy Fuels, 2019, 33, 12295–12307 CrossRef CAS.
- J. R. Grace, Essentials of Fluidization Technology, John Wiley & Sons, Ltd, 2020 Search PubMed.
- D. C. Sau, S. Mohanty and K. C. Biswal, Chem. Eng. Process., 2010, 49, 418–424 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4re00074a |
| This journal is © The Royal Society of Chemistry 2024 |





![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif)