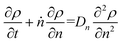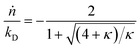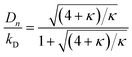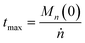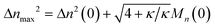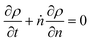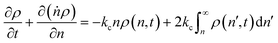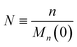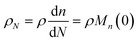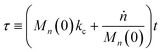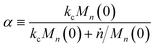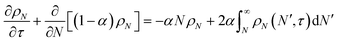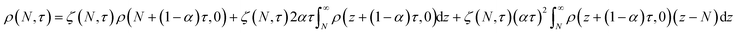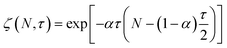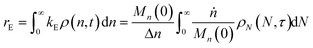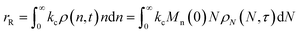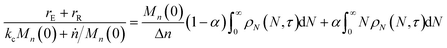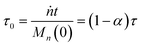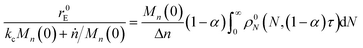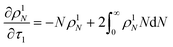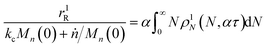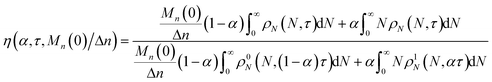Quantifying synergy for mixed end-scission and random-scission catalysts in polymer upcycling†
Received
21st July 2023
, Accepted 25th September 2023
First published on 26th September 2023
Abstract
The environmental consequences of plastic waste are driving research into many chemical and catalytic recycling strategies. The isomerizing ethenolysis strategy for polyethylene upcycling combines three catalysts to affect two different actions: non-processive scission at chain ends, and scission at random interior points. We show that population balance equations (PBEs) based on the local density approximation (LDA) accurately describe the end-scission chemistry. We further show that the model can be simplified to a first-order PBE when started from a realistic molecular weight distribution. The simplification enables formulation and solution of a model that includes both end-scission and random-scission modalities. The mixture of catalysts (in theory) can exhibit a quantitative synergy, e.g., with the total number of cuts for the catalyst mixture exceeding that for the sum of its separate component catalyst actions. We develop equations to predict and optimize the synergistic acceleration.
Introduction
Over 300 million tons of plastics are produced every year, yet less than 10% is recycled.1–3 Most is incinerated, landfilled, or discarded into the natural environment. Chemical recycling processes, especially with catalysts to guide selectivity, have the potential to create high value chemicals from plastic waste.4–17 Different catalysts for polymer upcycling operate in different ways: end scission or random scission, heterogeneous or homogeneous, processive or non-processive, etc. Processes that use a mixture of catalysts may even exploit synergies between different catalyst modalities.18–26
Current research in catalytic polymer upcycling is mainly empirical,27–40 with only a small fraction of studies attempting theoretical analysis of the underlying reaction mechanisms and reaction progress.41–49 Based on an extrapolation from other branches of catalysis,50–62 theoretical models and calculations will likely have a major impact on polymer upcycling, from understanding the chemistry, to developing new catalysts, to industrial process design. However, polymer upcycling presents several unique challenges for theory and computation.49 The polymer mixture typically contains chains with millions of different molecular weights having different degrees and types of functionalization.
Population balance equations (PBEs) are analogous to the more familiar species balance equations (often called rate equations), but PBEs describe a continuous distribution rather than a short discrete list of reagents.63,64 Several recent studies have used PBEs to model the evolution of molecular weight distributions (MWDs) and generation of products during catalytic polymer upcycling processes.45,49
This study is motivated by recent experiments that combine polyethylene with excess ethylene and three catalysts: a double-bond isomerization catalyst, a metathesis catalyst, and a dehydrogenation catalyst.18,20 The first two catalysts cooperate to affect end-scission via a complex isomerizing ethenolysis reaction. In brief, this reaction uses ethylene to excise CH2 units from the ends of vinyl terminated polyethylene chains, leaving a propylene product and a shortened chain. Prior to the experimental works, Guironnet and Peters described the mechanism and modeled the double-bond isomerization and metathesis kinetics in isomerizing ethenolysis.45 In the subsequent experiments, the third dehydrogenation catalyst was added to create double bonds at random interior locations.18,20 The double bonds allow the chain to also be cut at random locations upon metathesis with ethylene. The random-scission events should result in more chains with double bonds at both ends, and thereby accelerate the isomerizing ethenolysis reaction.
At present, the isomerizing ethenolysis and dehydrogenation catalysts do not work together as intended.18,20 However, end scission and random scission are common catalysis motifs, and nature has already combined them. For example, fungi use a cocktail of cellulases to depolymerize cellulose, with random scission by the endocellulases creating new chain ends which are then attacked by exocellulases. In the cellulase literature, the synergy between these enzymes was anticipated in many studies65–68 and several works modeled the enzymatic reactions with discrete rate equations and population balance equations.69–72 One population balance study demonstrated the synergy between end-scission and random-scission enzymes, although no recipe for the synergy calculation was provided.72
In this work, we revisit the second-order PBE developed by Guironnet and Peters.45 Using numerical solutions to the complete set of double-bond isomerization and metathesis rate equations as a standard, we show that the full PBE, as well as a simplified first-order version of the PBE, both yield accurate solutions for realistic initial MWDs. Then we combine the first-order model for end scission with birth and death terms in the PBE for random scission. We provide a new analytic solution to the combined PBE for end scission and random scission and predict the synergistic acceleration due to the combination of random-scission and end-scission catalysts. Finally, we discuss how these results might be used to optimize the catalyst mixture to achieve the maximum acceleration.
Revisiting the isomerizing ethenolysis model
Guironnet and Peters presented a kinetic model for polymer upcycling with tandem double bond isomerization and olefin metathesis catalysts.45 They started with rate equations for all olefin species, and used pseudo-steady state approximations (PSSAs) and local density approximations (LDAs), to convert the massive ODE system into one Fokker–Planck-type equation:| | 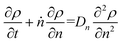 | (1) |
with| | 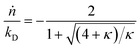 | (2) |
and| | 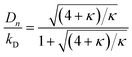 | (3) |
Here κ is the ratio of the metathesis rate over the isomerization rate and kD is the isomerization rate, i.e., the frequency at which a double bond changes position on the olefin chain. In eqn (2) and (3), ṅ represents the chain shortening rate, and Dn represents the rate at which dispersity grows in the polymer distribution. Eqn (1) is different from typical PBEs because it does not invoke the coefficients as adjustable phenomenological parameters. Rather, the coefficients are expressions derived from details of the underlying mechanism. Detailed derivations of (1)–(3) as well as the starting rate equations, can be found in Guironnet and Peters.
There are several methods for modeling end-scission depolymerizations, including numerical methods and analytic solutions44 for discrete rate equations73,74 and for PBEs.75–77 Guironnet and Peters compared numerical solutions for the complete set of double-bond isomerization and ethene metathesis rate equations to analytic solutions from the simplified PBE in eqn (1)–(3).
Guironnet and Peters focused on a sharp monodisperse initial MWD. They found that the PBE yielded highly accurate solutions for κ > 1, but less accurate solutions for κ < 1. In Fig. 1 we similarly compare numerical solutions to (analytic) PBE solutions, but we start with a more realistic polydisperse initial MWD. Note that the calculated MWDs from eqn (1) do not include the propylene products.
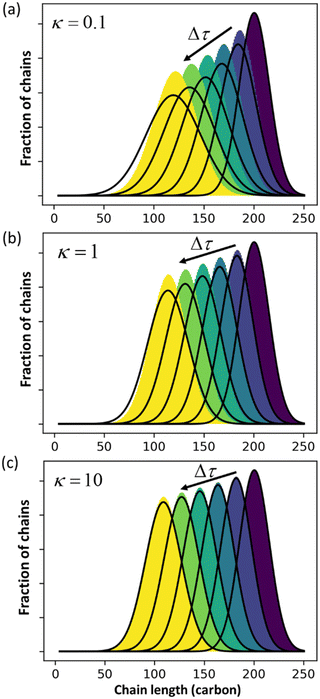 |
| | Fig. 1 Comparison between exact solution from rate equations and solutions of eqn (1) for (a) κ = 0.1; (b) κ = 1 (c) κ = 10. | |
The accuracy of eqn (1) decreases when olefin metathesis is slower than double bond isomerization, i.e., when κ < 1. In the derivation of eqn (1), the LDA ignores gradient [∂ρ/∂n] terms when applying the PSSA to the distribution of double bond positions. If we include gradient terms when applying the PSSA equations, the resulting PBE becomes nonlinear and no longer admits analytical solutions.
An analysis of error contributions suggests that the average “drift velocity” term, i.e., that containing ṅ, contributes negligible errors. The inaccuracies for κ < 1 are entirely due to an exaggerated increase in polydispersity, i.e., from an overestimation of Dn.
We can estimate the importance of polydispersity errors as follows. The predicted variance in the MWD over time can be calculated by the mean square displacement: Δn2(t) = Δn2(0) + 2Dnt,78,79 where Δn2(t) is the variance of the MWD at time t. The time required to consume chains of an average initial length Mn(0) is:
| | 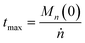 | (4) |
Therefore, we have Δ
nmax2 = Δ
n2(0) + 2
DnMn(0)/
ṅ where both
Dn and
ṅ can be written in terms of
κ using
eqn (2) and
(3). The result gives an estimate for the variance in the MWD as the reaction approaches completion:
| | 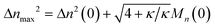 | (5) |
When the added variance from the second derivative term [((4 +
κ)/
κ)
1/2Mn(0)] is smaller than the initial variance [Δ
n2(0)], it makes little difference whether the second derivative term is included or neglected. That is, for the ratio [Δ
nmax2/Δ
n2(0)], when it is close to 1, the dispersion term does not affect the results, and when it is much larger than 1, then the dispersion term becomes very important to the PBE. Indeed, for realistic initial MWDs the second derivative term may be omitted entirely. We illustrate this in
Table 1:
Table 1 Inaccuracies emerging from the second order (2°) term in the LDA-derived PDE. The 2°-term is important for small initial molecular weights, but inconsequential for realistic PE materials with broad MWDs
|
|
Parameters |
Δnmax2/Δn2(0) |
Dispersion from 2°-term |
|
Fig. 1a
|
M
n
(0) = 200 |
6.78 |
Very important. Small errors matter |
| Δn(0) = 15 |
|
κ = 0.1 |
|
Fig. 1c
|
M
n
(0) = 200 |
2.04 |
Moderately important. OK to make small errors |
| Δn(0) = 15 |
|
κ = 10 |
| Conk et al. |
M
n
(0) = 3276 |
1.00 |
Unimportant. Can entirely omit 2°-term |
| Δn(0) = 2000 |
|
κ = 0.1 |
Note that the MWD can be scaled with the mass of CH2 to recover the distribution of chain concentrations, and that all calculations in Table 1 are performed in the number of carbons instead of Daltons for simplicity. The analysis in Table 1 suggests that, for initial MWDs like those from commercial plastics, the second-order term in eqn (1) can be entirely neglected.
In Fig. 2 we let ρ0(n) be the initial MWD from the experiments of Conk et al. on isomerizing ethenolysis of polyethylene.20Fig. 2a solves the equation using the LDA-derived PBE as written in eqn (1). Fig. 2b presents the solution for the same initial conditions and same PBE, but with the second-order term omitted. In this case, the PBE becomes:
| | 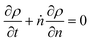 | (6) |
and the solution (
e.g., from the method of characteristics) is:
Note that the mass is not conserved because the propylene products are not included in
ρ(
n,
t).
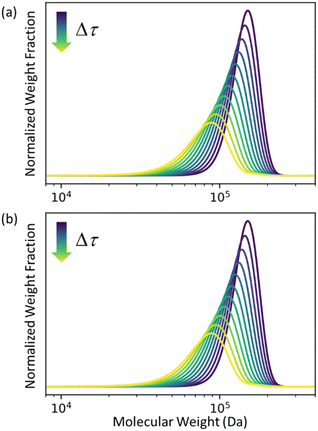 |
| | Fig. 2 (a) Predicted MWD evolving with time according to eqn (1) with κ = 1. (b) Predicted MWD evolving with time from eqn (6) with κ = 1. | |
There is no apparent difference between Fig. 2a and b, which confirms our prediction that the first order term in the LDA-derived PBE is sufficient for predicting the MWD evolution with realistic initial MWDs. We emphasize that this conclusion should be generally applicable to any end-scission upcycling mechanism, and not specific to isomerizing ethenolysis.
Tandem end scission and random scission
In this section, we build a model for tandem end-scission and random-scission catalysts. End scission results in a new chain of length that is slightly smaller than that of the parent chain. Because the changes in molecular weight from end scission are small, the result is a gradual drift-like term in the PBE. In contrast, random scission results in new chains of completely different lengths from the parent chain. Thus, random scission must be modeled using birth and death terms.80 The combined result of both end scission and random scission is the PBE:| | 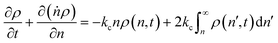 | (8) |
Here ṅ is the rate of chain shortening on the end as in eqn (2), and thus will be a negative value. And kc is the rate of random scission per carbon–carbon bond. The birth and death terms on the right-hand side of eqn (8) are explained in the references.49,80 The combined equation was also obtained in work on end-scission and random-scission by cellulases.72
To enable a systematic analysis of synergy, we pursue a nondimensionalization that balances end-scission and random-scission contributions. First, we nondimensionalize chain length using the initial mean chain length of the polymer, that is:
| | 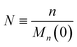 | (9) |
We refer to
N as the relative chain length throughout the remainder of the manuscript. Correspondingly, we have:
| | 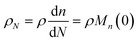 | (10) |
Then, we define the nondimensional time as the real time multiplied by the sum of two contributions: the frequency of new chain creation by a random scission and the frequency of entire chain digestion
via end scission:
| | 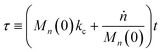 | (11) |
Now, we define a new term
α:
| | 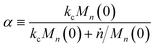 | (12) |
which can be interpreted as the fraction of chains at the initial average length that get cut at a random location before complete digestion from the end.
With these definitions, the nondimensional form of eqn (8) becomes:
| | 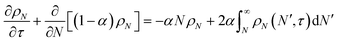 | (13) |
We solved
eqn (13) numerically over nondimensional time
τ by first converting the equations into a series of ODEs. Then, using a normal distribution as the initial condition, we use Scipy v1.4.1 (ref.
81) to solve the initial value problem. The backward differentiation formula (BDF) is chosen as the ODE solver for stability and convergence. The solutions are shown in
Fig. 3a and b for the limiting cases where there is only random scission (
ṅ = 0 and
α = 1) and only end scission (
kc = 0 and
α = 0), respectively.
Fig. 3c shows the solutions for a case where both catalysts work together at ratio
α = 0.95. The effects of random cuts are most pronounced when nearly all chains get randomly cut before they are consumed by end-scission.
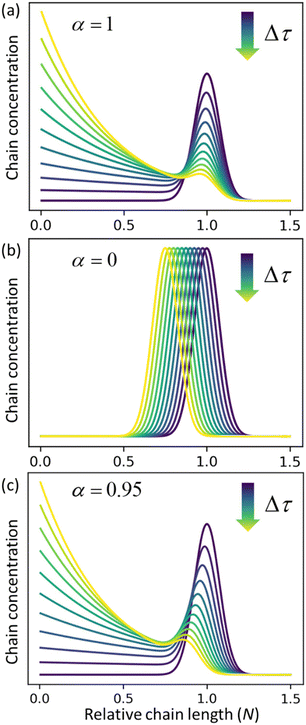 |
| | Fig. 3 Time evolution of the relative chain length distribution for three cases. (a) Only random-scission, i.e., α = 1; (b) only end-scission, i.e., α = 0; (c) both end- and random-scission with α = 0.95. All three calculations begin from a normal distribution in relative chain length N with a mean of 1.0 and standard deviation of 0.075. | |
We also developed an analytical solution for eqn (13) using the strategy from Ziff and McGrady,82
| | 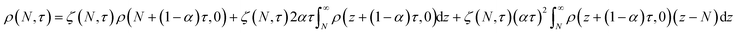 | (14) |
where
| | 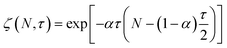 | (15) |
To check the derivation, we confirmed that the analytic solution matches the numerical solutions. See ESI
† for detailed derivations and results.
The solutions in Fig. 3 resemble those from analysis of combined end-scission and random-scission of cellulose by cellulase enzymes. In the following section, we exploit the non-dimensionalization to provide an expression that quantifies synergy of the end-scission and random-scission catalysts.
Quantifying synergy with cutting rates
When both end-scission and random-scission rates are nonzero, the number of chain ends will increase with time due to random scission. If excess end-scission catalyst is available, the overall rate of conversion should increase with time. To quantify the number of cuts, we first decompose ṅ as:where kE is the number of end-scission events per time per chain, and Δn is the segment size per end scission. For isomerizing ethenolysis, Δn = 1. The rate of end scission is:| | 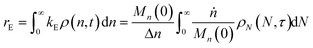 | (17) |
Similarly, the rate of random scission is:| | 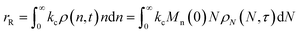 | (18) |
rE and rR can be normalized by kcMn(0) + ṅ/Mn(0) and then written in terms of the dimensionless α. With these simplifications, the total (normalized) scission rate, with both random- and end-scission events occurring at the same time, is:| | 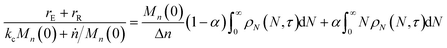 | (19) |
Now to quantify the synergistic acceleration of the mixed catalyst system, we compare the rate in eqn (17) to that for limiting cases with end scission or random scission occurring separately.
For a system with only end scission, at the same physical time t, define the nondimensional time τ0 as:
| | 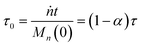 | (20) |
Then we solve
| |  | (21) |
to predict the time evolution of the molecular weight distribution
ρ0N(
N,
τ0) with only end scission. Note that we are not actually changing the rate parameters for end or random scission relative to those in
eqn (17). Rather, we are solving for the molecular weight evolution and scission rates as though the two scission mechanisms are occurring separately.
For end scission alone, the normalized scission rate is:
| | 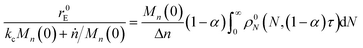 | (22) |
For the system with only random scission, we define
τ1 as:
Then we solve
| | 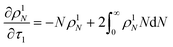 | (24) |
to predict the time evolution of the molecular weight distribution
ρ1N(
N,
τ1) with only random scission. Now the normalized rate with random scission alone is
| | 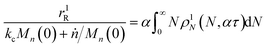 | (25) |
To compare the rate with both catalysts operating simultaneously (
eqn (17)) to the rates of their separate actions, we add the rates in
eqn (22) and
(23). In other words, we can directly compare
rE +
rR to
r0E +
r1R.
We define the synergistic acceleration as η(α, τ) = (rE + rR)/(r0E + r1R). From eqn (19), (22), and (25), the synergistic acceleration is a function of α, τ, and Mn(0)/Δn.
| | 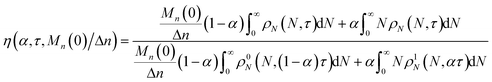 | (26) |
When
α = 0.0 or
α = 1.0, the synergistic acceleration factor
η → 1.0. For all intermediate values it initially climbs to a value larger than unity. At long times, as the reaction completes, the acceleration factor drops below unity because the mixed catalyst system more rapidly reaches a point where all chains have been cut to propylene and butadiene.
Note that derivations from eqn (16)–(26) assume cutting rates are only determined by the number of chains and C–C bonds with no limitation on the catalyst amount. Situations where the rate of end scission becomes limited by the availability of catalyst will require additional analysis.
Fig. 4 plots η as a function of dimensionless time and for three different values of the initial chain length parameter Mn(0)/Δn. The first initial chain length parameter, Mn(0)/Δn = 40, corresponds approximately to the lengths of chains at the onset of isomerizing ethenolysis in the work of Conk et al.20 The chains are unusually short because they are randomly dehydrogenated before the isomerizing ethenolysis step. Therefore, the chains of Conk et al. undergo metathesis with ethane to give short chains very early in the isomerizing ethenolysis process.
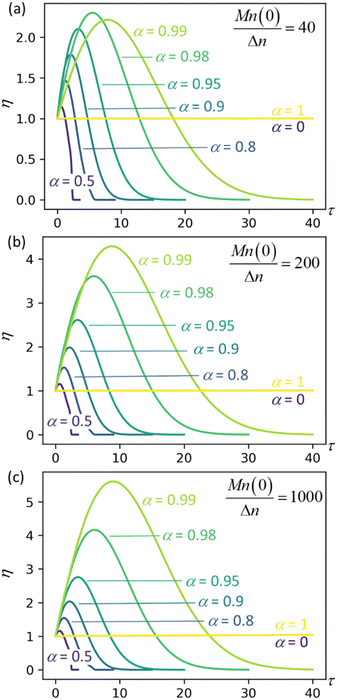 |
| | Fig. 4 Synergistic acceleration η vs. dimensionless time at different α values with (a) Mn(0)/Δn = 40; (b) Mn(0)/Δn = 200; (c) Mn(0)/Δn = 1000. | |
Results for the other initial chain length parameters in Fig. 4, Mn(0)/Δn = 200 and Mn(0)/Δn = 1000, show that the synergistic acceleration becomes a relatively weak function of chain length for long chains.
We can see that all mixtures of end-scission and random-scission catalysts initially accelerate beyond the rate of the limiting cases (α = 0 and α = 1). η first increases due to the newly generated chain ends from random scissions, and all the new chains are longer than the minimal cutting length. Then, as these chains reach the minimum length, η starts to decrease, ultimately dropping to 0, which indicates the complete consumption of chains.
The results in Fig. 4 allow us to design the depolymerization process by varying α to maximize the cutting rate. Interestingly, the α value that maximizes the synergistic acceleration seems to be related to Mn(0)/Δn. For Mn(0)/Δn = 40, the maximum synergy occurs for α = 0.98. For Mn(0)/Δn = 200, the maximum synergy occurs for α = 0.995, as shown in the ESI.† For Mn(0)/Δn = 1000, the maximum synergy occurs for α = 0.999, as shown in the ESI.† In each case, the value of α that maximizes the synergy is approximately α = 1 − Δn/Mn(0). This design rule should be regarded as a conjecture, because as yet we cannot say whether it remains valid for all values of Mn(0)/Δn nor provide a justification for its validity.
Conclusion
For realistic initial molecular weight distributions (MWDs), this paper shows that a previous kinetic model for isomerizing ethenolysis by Guironnet and Peters can be dramatically simplified to the form of a first-order population balance equation (PBE). Motivated by recent experiments, which demonstrated the isomerizing ethenolysis chemistry and also explored the effects of an additional dehydrogenation catalyst, we extended the kinetic model to cases with mixed end-scission and random-scission catalysts.
A dimensionless parameter α that emerges from the model quantifies the relative rates of end scission and random scission. We provided an analytic solution to the combined end-scission and random-scission equation for any α. We compare results from the two limiting cases of random-scission and end-scission to intermediate cases where both catalysts are working together. We show that, given sufficient end-scission catalyst, random scission causes a proliferation of new chain ends and thereby accelerates the overall depolymerization progress.
We developed a mathematical expression for the synergistic acceleration factor (η), i.e., the rate relative to the combined rate from the two independently occurring processes. η depends on the initial average molecular weight, on the reaction time, and on the value of α, i.e. the fraction of chains at the initial average length that get cut at a random location before they are completely digested from the chain ends. As time advances, η begins at 1.0 (no acceleration), and gradually climbs to a maximum value that depends on α and the initial molecular weight. The results should be useful in understanding and optimizing the mixture of catalysts to achieve the maximum acceleration. Specifically, our analysis suggests that the value of α (and accordingly the catalyst mixture) that maximizes the synergy is approximately α = 1 − Δn/Mn(0).
Author contributions
ZC was responsible for writing – original draft and editing, methodology, computational work, and data analysis. EE developed the analytical solution of PBE. BP was responsible for conceptualization, funding acquisition, project administration, supervision, and writing – review and editing.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
We thank members of the iCOUP team, Charles Sing, and Damien Guironnet for helpful discussions. This work was supported by the Institute for Cooperative Upcycling of Plastics (iCOUP), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, via subcontract from Ames National Laboratory. Ames National Laboratory is operated for the DOE by Iowa State University under Contract No. DE-AC02-07CH11358.
References
- R. Geyer, J. R. Jambeck and K. L. Law, Production, use, and fate of all plastics ever made, Sci. Adv., 2017, 3, e1700782 CrossRef PubMed.
- Y. Liang, Q. Tan, Q. Song and J. Li, An analysis of the plastic waste trade and management in Asia, Waste Manage., 2021, 119, 242–253 CrossRef PubMed.
- D. K. Barnes, F. Galgani, R. C. Thompson and M. Barlaz, Accumulation and fragmentation of plastic debris in global environments, Philos. Trans. R. Soc., B, 2009, 364, 1985–1998 CrossRef CAS.
- S. C. Kosloski-Oh, Z. A. Wood, Y. Manjarrez, J. P. de Los Rios and M. E. Fieser, Catalytic methods for chemical recycling or upcycling of commercial polymers, Mater. Horiz., 2021, 8, 1084–1129 RSC.
- H. Chen, K. Wan, Y. Zhang and Y. Wang, Waste to Wealth: Chemical Recycling and Chemical Upcycling of Waste Plastics for a Great Future, ChemSusChem, 2021, 14, 4123–4136 CrossRef CAS PubMed.
- B. M. Stadler and J. G. de Vries, Chemical upcycling of polymers, Philos. Trans. R. Soc., A, 2021, 379, 20200341 CrossRef CAS.
- C. Jehanno, J. W. Alty, M. Roosen, S. De Meester, A. P. Dove, E. Y. Chen, F. A. Leibfarth and H. Sardon, Critical advances and future opportunities in upcycling commodity polymers, Nature, 2022, 603, 803–814 CrossRef CAS.
- X. Zhao, M. Korey, K. Li, K. Copenhaver, H. Tekinalp, S. Celik, K. Kalaitzidou, R. Ruan, A. J. Ragauskas and S. Ozcan, Plastic waste upcycling toward a circular economy, Chem. Eng. J., 2022, 428, 131928 CrossRef CAS.
- L. T. J. Korley, T. H. Epps, , 3rd, B. A. Helms and A. J. Ryan, Toward polymer upcycling-adding value and tackling circularity, Science, 2021, 373, 66–69 CrossRef CAS.
- X. Li, J. Wang, T. Zhang, S. Yang, M. Sun, X. Qian, T. Wang and Y. Zhao, Sustainable catalytic strategies for the transformation of plastic wastes into valued products, Chem. Eng. Sci., 2023, 276, 118729 CrossRef CAS.
- Z. R. Hinton, M. R. Talley, P. A. Kots, A. V. Le, T. Zhang, M. E. Mackay, A. M. Kunjapur, P. Bai, D. G. Vlachos and M. P. Watson,
et al., Innovations Toward the Valorization of Plastics Waste, Annu. Rev. Mater. Sci., 2022, 52, 249–280 CrossRef CAS.
- M.-Q. Zhang, M. Wang, B. Sun, C. Hu, D. Xiao and D. Ma, Catalytic strategies for upvaluing plastic wastes, Chem, 2022, 8, 2912–2923 CAS.
- J. Bidange, C. Fischmeister and C. Bruneau, Ethenolysis: A Green Catalytic Tool to Cleave Carbon-Carbon Double Bonds, Chemistry, 2016, 22, 12226–12244 CrossRef CAS.
- K. Faust, P. Denifl and M. Hapke, Recent Advances in Catalytic Chemical Recycling of Polyolefins, ChemCatChem, 2023, 15, e202300310 CrossRef CAS.
- J. Wei, J. Liu, W. Zeng, Z. Dong, J. Song, S. Liu and G. Liu, Catalytic hydroconversion processes for upcycling plastic waste to fuels and chemicals, Catal. Sci. Technol., 2023, 13, 1258–1280 RSC.
- T. Tan, W. Wang, K. Zhang, Z. Zhan, W. Deng, Q. Zhang and Y. Wang, Upcycling Plastic Wastes into Value-Added Products by Heterogeneous Catalysis, ChemSusChem, 2022, 15, e202200522 CrossRef CAS.
- P. A. Kots, B. C. Vance and D. G. Vlachos, Polyolefin plastic waste hydroconversion to fuels, lubricants, and waxes: a comparative study, React. Chem. Eng., 2022, 7, 41–54 RSC.
- N. M. Wang, G. Strong, V. DaSilva, L. Gao, R. Huacuja, I. A. Konstantinov, M. S. Rosen, A. J. Nett, S. Ewart and R. Geyer,
et al., Chemical Recycling of Polyethylene by Tandem Catalytic Conversion to Propylene, J. Am. Chem. Soc., 2022, 144, 18526–18531 CrossRef CAS.
- F. Zhang, M. Zeng, R. D. Yappert, J. Sun, Y.-H. Lee, A. M. LaPointe, B. Peters, M. M. Abu-Omar and S. L. Scott, Polyethylene upcycling to long-chain alkylaromatics by tandem hydrogenolysis/aromatization, Science, 2020, 370, 437–441 CrossRef CAS.
- R. J. Conk, S. Hanna, J. X. Shi, J. Yang, N. R. Ciccia, L. Qi, B. J. Bloomer, S. Heuvel, T. Wills and J. Su,
et al., Catalytic deconstruction of waste polyethylene with ethylene to form propylene, Science, 2022, 377, 1561–1566 CrossRef CAS PubMed.
- R. Ahuja, S. Kundu, A. S. Goldman, M. Brookhart, B. C. Vicente and S. L. Scott, Catalytic ring expansion, contraction, and metathesis-polymerization of cycloalkanes, Chem. Commun., 2008, 253–255 RSC.
- A. Tennakoon, X. Wu, A. L. Paterson, S. Patnaik, Y. C. Pei, A. M. LaPointe, S. C. Ammal, R. A. Hackler, A. Heyden and I. I. Slowing,
et al., Catalytic upcycling of high-density polyethylene via a processive mechanism, Nat. Catal., 2020, 3, 893–901 CrossRef CAS.
- D. S. Achilias, C. Roupakias, P. Megalokonomos, A. A. Lappas and E. V. Antonakou, Chemical recycling of plastic wastes made from polyethylene (LDPE and HDPE) and polypropylene (PP), J. Hazard. Mater., 2007, 149, 536–542 CrossRef CAS PubMed.
- H. Zhou, Y. Wang, Y. Ren, Z. Li, X. Kong, M. Shao and H. Duan, Plastic Waste Valorization by Leveraging Multidisciplinary Catalytic Technologies, ACS Catal., 2022, 12, 9307–9324 CrossRef CAS.
- S. Martínez and P. Dydio, Multicatalysis enables turning plastic waste into chemical commodities, Trends Chem., 2023, 5, 249–251 CrossRef.
- J. E. Rorrer, A. M. Ebrahim, Y. Questell-Santiago, J. Zhu, C. Troyano-Valls, A. S. Asundi, A. E. Brenner, S. R. Bare, C. J. Tassone and G. T. Beckham,
et al., Role of Bifunctional Ru/Acid Catalysts in the Selective Hydrocracking of Polyethylene and Polypropylene Waste to Liquid Hydrocarbons, ACS Catal., 2022, 12, 13969–13979 CrossRef CAS.
- S. Chen, A. Tennakoon, K.-E. You, A. L. Paterson, R. Yappert, S. Alayoglu, L. Fang, X. Wu, T. Y. Zhao and M. P. Lapak,
et al., Ultrasmall amorphous zirconia nanoparticles catalyse polyolefin hydrogenolysis, Nat. Catal., 2023, 6, 161–173 CrossRef CAS.
- G. Zichittella, A. M. Ebrahim, J. Zhu, A. E. Brenner, G. Drake, G. T. Beckham, S. R. Bare, J. E. Rorrer and Y. Roman-Leshkov, Hydrogenolysis of Polyethylene and Polypropylene into Propane over Cobalt-Based Catalysts, JACS Au, 2022, 2, 2259–2268 CrossRef CAS.
- J. E. Rorrer, G. T. Beckham and Y. Roman-Leshkov, Conversion of Polyolefin Waste to Liquid Alkanes with Ru-Based Catalysts under Mild Conditions, JACS Au, 2021, 1, 8–12 CrossRef CAS PubMed.
- J. E. Rorrer, C. Troyano-Valls, G. T. Beckham and Y. Román-Leshkov, Hydrogenolysis of Polypropylene and Mixed Polyolefin Plastic Waste over Ru/C to Produce Liquid Alkanes, ACS Sustainable Chem. Eng., 2021, 9, 11661–11666 CrossRef CAS.
- J. Du, L. Zeng, T. Yan, C. Wang, M. Wang, L. Luo, W. Wu, Z. Peng, H. Li and J. Zeng, Efficient solvent- and hydrogen-free upcycling of high-density polyethylene into separable cyclic hydrocarbons, Nat. Nanotechnol., 2023, 772–779 CrossRef CAS.
- J. Z. Tan, C. W. Hullfish, Y. Zheng, B. E. Koel and M. L. Sarazen, Conversion of polyethylene waste to short chain hydrocarbons under mild temperature and hydrogen pressure with metal-free and metal-loaded MFI zeolites, Appl. Catal., B, 2023, 338, 123028 CrossRef CAS.
- S. S. Borkar, R. Helmer, S. Panicker and M. Shetty, Investigation into the Reaction Pathways and Catalyst Deactivation for Polyethylene Hydrogenolysis over Silica-Supported Cobalt Catalysts, ACS Sustainable Chem. Eng., 2023, 11, 10142–10157 CrossRef CAS.
- J. N. Hancock and J. E. Rorrer, Hydrogen-free catalytic depolymerization of waste polyolefins at mild temperatures, Appl. Catal., B, 2023, 338, 123071 CrossRef CAS.
- B. C. Vance, P. A. Kots, C. Wang, Z. R. Hinton, C. M. Quinn, T. H. Epps, L. T. J. Korley and D. G. Vlachos, Single pot catalyst strategy to branched products via adhesive isomerization and hydrocracking of polyethylene over platinum tungstated zirconia, Appl. Catal., B, 2021, 299, 120483 CrossRef CAS.
- B. C. Vance, P. A. Kots, C. Wang, J. E. Granite and D. G. Vlachos, Ni/SiO2 catalysts for polyolefin deconstruction via the divergent hydrogenolysis mechanism, Appl. Catal., B, 2023, 322, 122138 CrossRef CAS.
- Z. R. Hinton, P. A. Kots, M. Soukaseum, B. C. Vance, D. G. Vlachos, T. H. Epps and L. T. J. Korley, Antioxidant-induced transformations of a metal-acid hydrocracking catalyst in the deconstruction of polyethylene waste, Green Chem., 2022, 24, 7332–7339 RSC.
- P. A. Kots, P. A. Doika, B. C. Vance, S. Najmi and D. G. Vlachos, Tuning High-Density Polyethylene Hydrocracking through Mordenite Zeolite Crystal Engineering, ACS Sustainable Chem. Eng., 2023, 11, 9000–9009 CrossRef CAS.
- S. Liu, P. A. Kots, B. C. Vance, A. Danielson and D. G. Vlachos, Plastic waste to fuels by hydrocracking at mild conditions, Sci. Adv., 2021, 7, eabf8283 CrossRef CAS.
- P. A. Kots, S. Liu, B. C. Vance, C. Wang, J. D. Sheehan and D. G. Vlachos, Polypropylene Plastic Waste Conversion to Lubricants over Ru/TiO2 Catalysts, ACS Catal., 2021, 11, 8104–8115 CrossRef CAS.
- G. Madras and B. J. McCoy, Numerical and similarity solutions for reversible population balance equations with size-dependent rates, J. Colloid Interface Sci., 2002, 246, 356–365 CrossRef CAS PubMed.
- B. J. McCoy and G. Madras, Discrete and continuous models for polymerization and depolymerization, Chem. Eng. Sci., 2001, 56, 2831–2836 CrossRef CAS.
- B. J. McCoy and G. Madras, Analytical solution for a population balance equation with aggregation and fragmentation, Chem. Eng. Sci., 2003, 58, 3049–3051 CrossRef CAS.
- M. Kostoglou, Mathematical analysis of polymer degradation with chain-end scission, Chem. Eng. Sci., 2000, 55, 2507–2513 CrossRef CAS.
- D. Guironnet and B. Peters, Tandem Catalysts for Polyethylene Upcycling: A Simple Kinetic Model, J. Phys. Chem. A, 2020, 124, 3935–3942 CrossRef CAS.
- C. F. Chang and S. Rangarajan, Machine Learning and Informatics Based Elucidation of Reaction Pathways for Upcycling Model Polyolefin to Aromatics, J. Phys. Chem. A, 2023, 127, 2958–2966 CrossRef CAS PubMed.
- J. B. P. Soares and T. F. L. McKenna, A conceptual multilevel approach to polyolefin reaction engineering, Can. J. Chem. Eng., 2022, 100, 2432–2474 CrossRef CAS.
- T. Xie, G. R. Wittreich and D. G. Vlachos, Multiscale modeling of hydrogenolysis of ethane and propane on Ru(0001): Implications for plastics recycling, Appl. Catal., B, 2022, 316, 121597 CrossRef CAS.
- R. Yappert and B. Peters, Population balance models for polymer upcycling: signatures of the mechanism in the molecular weight evolution, J. Mater. Chem. A, 2022, 10, 24084–24095 RSC.
- F. Keil, Diffusion and reaction in porous networks, Catal. Today, 1999, 53, 245–258 CrossRef CAS.
- F. J. Keil, Multiscale modelling in computational heterogeneous catalysis, Top. Curr. Chem., 2012, 307, 69–107 CrossRef CAS.
- J. K. Norskov, T. Bligaard, B. Hvolbaek, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, The nature of the active site in heterogeneous metal catalysis, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC.
- A. J. Medford, M. R. Kunz, S. M. Ewing, T. Borders and R. Fushimi, Extracting Knowledge from Data through Catalysis Informatics, ACS Catal., 2018, 8, 7403–7429 CrossRef CAS.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier principle to a predictive theory of transition-metal heterogeneous catalysis, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- M. Boudart, Heterogeneous catalysis by metals, J. Mol. Catal., 1985, 30, 27–38 CrossRef CAS.
-
M. Boudart, Catalysis by Supported Metals, in Adv. Catal., ed. D. D. Eley, H. Pines and P. B. Weisz, Academic Press, 1969, vol. 20, pp. 153–166 Search PubMed.
- B. Hinnemann and J. K. Nørskov, Catalysis by Enzymes: The Biological Ammonia Synthesis, Top. Catal., 2006, 37, 55–70 CrossRef CAS.
- M. Meirow and E. Luijten, Coarse-Grained Modeling of Polymer Cleavage within a Porous Catalytic Support, ACS Macro Lett., 2023, 12, 189–194 CrossRef CAS PubMed.
- L. J. Broadbelt and R. Q. Snurr, Applications of molecular modeling in heterogeneous catalysis research, Appl. Catal., A, 2000, 200, 23–46 CrossRef CAS.
- L. J. Broadbelt, S. M. Stark and M. T. Klein, Computer Generated Pyrolysis Modeling: On-the-Fly Generation of Species, Reactions, and Rates, Ind. Eng. Chem. Res., 2002, 33, 790–799 CrossRef.
- A. J. Yanez, P. Natarajan, W. Li, R. Mabon and L. J. Broadbelt, Coupled Structural and Kinetic Model of Lignin Fast Pyrolysis, Energy Fuels, 2018, 32, 1822–1830 CrossRef CAS.
- R. E. Harmon, G. SriBala, L. J. Broadbelt and A. K. Burnham, Insight into Polyethylene and Polypropylene Pyrolysis: Global and Mechanistic Models, Energy Fuels, 2021, 35, 6765–6775 CrossRef CAS.
-
D. Ramkrishna, Population balances : theory and applications to particulate systems in engineering, Academic Press, San Diego, CA, 2000 Search PubMed.
-
E. Renshaw, Stochastic population processes : analysis, approximations, simulations, Oxford University Press, Oxford, 2011 Search PubMed.
- C. M. Payne, B. C. Knott, H. B. Mayes, H. Hansson, M. E. Himmel, M. Sandgren, J. Stahlberg and G. T. Beckham, Fungal cellulases, Chem. Rev., 2015, 115, 1308–1448 CrossRef CAS PubMed.
- D. C. Irwin, M. Spezio, L. P. Walker and D. B. Wilson, Activity studies of eight purified cellulases: Specificity, synergism, and binding domain effects, Biotechnol. Bioeng., 1993, 42, 1002–1013 CrossRef CAS PubMed.
- B. K. Barr, Y. L. Hsieh, B. Ganem and D. B. Wilson, Identification of two functionally different classes of exocellulases, Biochemistry, 1996, 35, 586–592 CrossRef CAS.
- B. Nidetzky, W. Steiner, M. Hayn and M. Claeyssens, Cellulose hydrolysis by the cellulases from Trichoderma reesei: a new model for synergistic interaction, Biochem. J., 1994, 298(Pt 3), 705–710 CrossRef CAS.
- S. A. Hosseini and N. Shah, Enzymatic hydrolysis of cellulose part II: Population balance modelling of hydrolysis by exoglucanase and universal kinetic model, Biomass Bioenergy, 2011, 35, 3830–3840 CrossRef CAS.
- S. A. Hosseini and N. Shah, Modelling enzymatic hydrolysis of cellulose part I: Population balance modelling of hydrolysis by endoglucanase, Biomass Bioenergy, 2011, 35, 3841–3848 CrossRef CAS.
-
P. Engel, B. Bonhage, D. Pernik, R. Rinaldi, P. Schmidt, H. Wulfhorst and A. C. Spiess, Population balance modelling of homogeneous and heterogeneous cellulose hydrolysis, in Computer Aided Chemical Engineering, ed. E. N. Pistikopoulos, M. C. Georgiadis and A. C. Kokossis, Elsevier, 2011, vol. 29, pp. 1316–1320 Search PubMed.
- N. Lebaz, A. Cockx, M. Spérandio and J. Morchain, Population balance approach for the modelling of enzymatic hydrolysis of cellulose, Can. J. Civ. Eng., 2015, 93, 276–284 CAS.
- J. Wang, T.-T. Wang, Z.-H. Luo and Y.-N. Zhou, Simulation of irreversible and reversible degradation kinetics of linear polymers using sectional moment method, Chem. Eng. Sci., 2023, 275, 118711 CrossRef CAS.
- J. Wang, T. T. Wang, Z. H. Luo and Y. N. Zhou, Analytical and numerical simulations of depolymerization based on discrete model: A chain-end scission scenario, AIChE J., 2022, 69, e17854 CrossRef.
- J. J. Stickel and A. J. Griggs, Mathematical modeling of chain-end scission using continuous distribution kinetics, Chem. Eng. Sci., 2012, 68, 656–659 CrossRef CAS.
- Y. K. Ho, P. Doshi, H. K. Yeoh and G. C. Ngoh, Modeling chain-end scission using the Fixed Pivot technique, Chem. Eng. Sci., 2014, 116, 601–610 CrossRef CAS.
- G. Madras and B. J. McCoy, Time evolution to similarity solutions for polymer degradation, AIChE J., 1998, 44, 647–655 CrossRef CAS.
-
A. Nitzan, Chemical dynamics in condensed phases : relaxation, transfer and reactions in condensed molecular systems, Oxford University Press, New York, 2006 Search PubMed.
-
W. Coffey and Y. P. Kalmykov, The Langevin equation : with applications to stochastic problems in physics, chemistry, and electrical engineering, World Scientific Publishing, Hackensack, New Jersey, 4th edn, 2017 Search PubMed.
- B. J. McCoy, A population balance framework for nucleation, growth, and aggregation, Chem. Eng. Sci., 2002, 57, 2279–2285 CrossRef CAS.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser and J. Bright,
et al., SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- R. M. Ziff and E. D. McGrady, The kinetics of cluster fragmentation and depolymerisation, J. Phys. A: Math. Gen., 1985, 18, 3027–3037 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Emmanuel
Ejiogu
a and
Baron
Peters
*ab
a,
Emmanuel
Ejiogu
a and
Baron
Peters
*ab