Open Access Article
Open Access ArticleHeat and mass transfer of water flow in graphene nanochannels: effect of pressure and interfacial interaction
Xiong Pana,
Hanhui Jin *ab,
Xiaoke Kuab,
Yu Guo
*ab,
Xiaoke Kuab,
Yu Guo ab and
Jianren Fanb
ab and
Jianren Fanb
aSchool of Aeronautics and Astronautics, Zhejiang University, Hangzhou, 310027, China. E-mail: enejhh@emb.zju.edu.cn
bState Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou, 310027, China
First published on 12th September 2024
Abstract
The low-resistance transport of water within graphene nanochannels makes it promising for electronic cooling applications. However, how the water pressure and the water–graphene interaction strength affect the flow field and the thermal transfer, including velocity slip, friction coefficient, Nusselt number, temperature slip, interfacial thermal resistance, and variation of physical properties, is still not clearly understood. In this paper, we employ molecular dynamics (MD) simulations to investigate qualitatively the heat transfer of water flow in graphene nanochannels. Our results reveal that the water peak density near the wall increases approximately linearly with water pressure and water–graphene interaction strength. The water peak density near the water–graphene interface is a key factor in regulating interfacial flow and heat transfer characteristics. Under constant inlet temperature, the relationship between velocity slip length and peak density follows a consistent power function, simply modifying the pressure or the interaction strength doesn't bring a specific effect. The Nusselt number and interfacial thermal resistance are not solely dependent on water peak density; at the same water peak density, increasing interaction strength results in lower interfacial thermal resistance compared to increasing pressure. Increasing pressure improves both interfacial heat transfer and internal heat transfer of water. Furthermore, the convection heat transfer coefficient increases approximately linearly with flow resistance when pressure and interaction strength vary moderately. Finally, we notice that pressure and interaction strength hardly affect the variation range of viscosity and thermal conductivity at a channel height of 10–12 nm. These qualitative insights could lead to the development of more efficient cooling systems for electronic devices.
Introduction
The demands for heat dissipation have increased with the rapid development of Integrated Circuits (ICs) and Micro/Nano-Electro-Mechanical Systems (MEMS/NEMS) in recent decades.1–3 For instance, the thermal design power of the AMD TR 3970X chip reaches 280 W, with heat flux exceeding 220 W cm−2 under peak load conditions.3 The failure rate of micro/nano-electronic components doubles for every 10 °C increase in temperature.4–6 Therefore, implementing high-efficiency cooling techniques is crucial for enhancing these components' reliability and service life.7–10 In 1981, Tuckerman and Pease11 first introduced a forced liquid cooling microchannel heat sink, demonstrating superior cooling performance. Notably, the cooling performance improves as the channel diameter decreases, although a significant rise in flow resistance accompanies this increase. Consequently, reducing flow resistance is critical when channel diameter reduces to the nanoscale. Fast water transport in graphitic nanoconduits like carbon nanotubes and graphene nanochannels exhibit low flow resistance. Holt et al.12 and Majumder et al.13 studied the slip flow of water in carbon nanotube films with the diameters of 1.6 nm and 7 nm, respectively. The measured water flow rates exceeded values predicted by the Hagen–Poiseuille relationship14 with the no-slip boundary condition by more than two to five orders of magnitude. This low-resistance water transport within graphene nanochannels opens up exciting possibilities for electronic cooling applications, inspiring further research.When the characteristic scale of the flow field is reduced to the molecular mean free path (Knudsen number is greater than 0.01), the effects of size and surface become more pronounced at the nanoscale, where molecular behavior at the fluid–solid interface profoundly affects the momentum and energy transport. Many studies have shown that structure evolution,15,16 variation of physical properties (especially the viscosity),17–19 velocity slip,20–23 and temperature slip24 occur in fluids near the fluid–solid interface. Heslot et al.15 observed strong, dynamic structuring of the simple fluid near the solid surface. X-ray reflectivity measurements of water adjacent to a mica surface revealed that the first-layer water exhibited a strong interaction with the oxide surface and an oxygen density twice as high as the bulk water.16 Chiu et al.17 found that viscous shear force in nanoconfined water was larger than in bulk water and they decreased greatly when the interaction strength between water with confining surfaces was reduced. Similarly, Nazari et al.18 showed that the increase in interfacial viscosity of the liquid near the confining surfaces led to slowdown in capillary motion. In 2018, Xie et al.20 studied the hydraulic resistance and slippage of single-layer graphene/SiO2 mixed rectangular nanochannels using capillary flow. The obtained slip lengths ranged from 0.5 to 200 nm and were independent of the height of the nanochannel. In 2021, Keerthi et al.21 studied the slip flow of water in graphite nanochannels with a width of 130 nm and a height range of 0.68–8.5 nm, and the calculated slip length was approximately 60 nm. In 2022, Chen et al.22 a developed 3D capillary flow model to analyze the slip flow of water in a graphene rectangular nanochannel with a depth of 45 nm and width of 5 mm, measuring slip lengths of about 30–40 nm. They also reevaluated slip lengths from previous literature, determining values of 30 nm for literature20 and 47 nm for literature.21 Li et al.23 studied the dependence of the slip length of water on the type of supporting substrates and the number of graphene layers. They found that different supporting substrates' slip lengths gradually converged to the graphite value (4.3 ± 3.5 nm) with the few-layer graphene increasing to 3–4 layers.
Despite the rapid progress in new experimental technologies, conducting experimental studies at the nanoscale is still difficult, and the accuracy of many theories is also challenged.24 Molecular dynamics (MD) simulations have become an effective alternative for studying nanoscale fluid flow and heat transfer.25–32 Kannam et al.25 used equilibrium MD (EMD) and non-equilibrium MD (NEMD) simulations to quantify the velocity slip length in a planar graphene nanochannel. Their results showed that the NEMD method has significant statistical errors in obtaining the velocity profile. Wagemann et al.26 used NEMD simulations to study the dependence of velocity slip length on shear stress in graphene nanochannels and they found that the velocity slip length converged to 50 nm under low shear stress. Song et al.27 used NEMD simulations to analyze the effects of different types of ordered rough surfaces on heat transfer and fluid flow. Their results showed that as surface roughness increased, both thermal slip length and velocity slip length decreased, while the Nusselt number increased. Yao et al.28 employed NEMD simulations to investigate the effects of solid–liquid interaction strength on flow and heat transfer characteristics. They found that as the solid–liquid interaction strength increased, the slip length decreased and the friction factor increased. Additionally, Sun et al.29 used NEMD simulations to explore the convective heat transfer mechanism of a nano heat exchanger, finding that the heat transfer performance of the nano heat exchanger could be enhanced by increasing the solid–liquid interaction strength. Marable et al.30 evaluated the effects of channel height, wall temperature, water–graphene interaction strength, and water flow velocity on the convective heat transfer of water in graphene nanochannels. They observed the velocity and thermal slip at the interface and found that thermal slip dominated convective heat transfer. Alexeev et al.31 also used NEMD simulations to study the interfacial thermal resistance at the water/few-layer graphene (FLG) interface. They pointed out that the interfacial thermal resistance was seriously affected by the number of FLG layers and the peak density of water at the water/FLG interface.
Previous studies have shown that water on graphene exhibits low interfacial flow resistance and high interfacial thermal resistance. The thermal and flow resistance of the solid–liquid interface can be adjusted by modifying the pressure and the interface interaction strength.24 However, the effect of pressure on momentum and heat transport processes during water flow through graphene nanochannels has not been reported yet. Meanwhile, a comprehensive evaluation of the influence of the pressure and the water–graphene interaction strength on the thermal and flow field, such as the viscosity, the thermal conductivity, the flow resistance and the heat transfer performance, is still needed. In this paper, we aim to numerically explore the convective heat transfer of water in graphene nanochannels under various circumstance, especially focusing on inlet temperatures, pressures, and interface interaction strengths. The comprehensive effects of these conditions on the heat and mass transfer characteristics, including velocity slip, friction coefficient, Nu, temperature slip, and interfacial thermal resistance, are carefully discussed.
Methodology
Computational model
Fig. 1 shows the MD simulation system configuration, which consists of water and graphene nanochannel with a length Lx = 40 nm, a width Ly = 5 nm, and a height Lz = 12 nm. Each wall of the nanochannel is composed of five-layer graphene. A vacuum space of 2 nm is introduced to avoid wall–wall interactions across the z-axis boundary. During the system construction process, the water molecules are initially assigned in a simple cubic lattice, which will become from solid to fluid during simulations. The unit cell length of 3.107 A provides a density of 998 kg m−3. Each graphene layer has a honeycomb crystal lattice of carbon atoms arranged two-dimensionally in a hexagon, with a C–C bond length of 1.42 A. The interlayer equilibrium spacing is established at 3.35 A. The optimized Tersoff potential33 models the interaction of graphene's intralayer carbon atoms. The ML-BOP potential,34 a machine-learning coarse-grained potential of water molecules with the same potential expression as the optimized Tersoff potential, is used to mimic liquid water at system sizes and times that current common AA models do not cover. In calculating the thermal conductivity of water, the ML-BOP potential is only 5% less accurate than the SPC/E and TIP4P models,35 while incurring a computational cost that is two orders of magnitude lower than that of the SPC/E and TIP4P models.36The Lennard-Jones (L-J) 12–6 potential models interlayer carbon interactions and carbon–water interactions. The functional form of the L-J potential is defined as:
 | (1) |
The timestep in all simulations is 1.0 fs. Atoms of the outermost layer of the nanochannel wall are frozen by zeroing the force of each atom during the simulations. After performing energy minimization, the system is initialized to an equilibrated state under isothermal–isobaric conditions (NPT) at the specified pressure and temperature for 1.0 ns. Subsequently, the system's thermodynamic properties are investigated under the microcanonical ensemble condition (NVE). The simulations are performed 10 ns to ensure a steady velocity and temperature profile across the system. During the NVE simulations, the convective heat transfer process is fulfilled by the thermal pump method. As shown in Fig. 1, the fluid domain is divided into three separate regions: the forcing region, the cold thermostat region, and the data collection region. In the forcing region, water molecules are driven by a constant body force fx between 0.0 nm and 2.0 nm along the x-direction. Then, after removing the velocity bias, the water temperature is reset in the 2 nm–4 nm region by implementing a Langevin thermostat39 in the cold thermostat region. In addition, the data collection region can monitor the convective heat transfer process. The periodic boundary conditions are imposed in all directions to ensure that water molecules re-enter the forcing region after flowing out of the data collection region. However, along the boundary in the z direction, there is no particle exchange or interaction between particles due to the presence of a vacuum layer and the cutoff distance for the L-J potential. In the nanochannel wall domain, the atoms of the outermost layer of the nanochannel wall are in a fixed position, and the second outer layer keeps a constant temperature of 420 K by implementing a Langevin thermostat. The three layers inside ensure that the graphene layer that interacts with water is not directly thermostated, which can potentially avoid molecular movement distortions and the reduction of data accuracy. The above simulation settings remain the same in all simulation cases. The Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package40 performs all MD simulations.
We evaluate the water flow and heat transfer characteristics in graphene nanochannels under varying inlet water temperatures Tin, water pressures P, and water–graphene interaction strengths ε. The water's velocity, inlet temperature, and pressure can be controlled by the body force fx, thermostat parameters, and barostat parameters. The L-J potential parameter ε adjusts the interface interaction strength between water and graphene. Here, the inlet temperature increases from 280 K to 320 K, the pressure rises from 1 bar to 5000 bar, and the interaction strength escalates up to 2.5 times, from 0.003992 eV to 0.008782 eV. Additionally, fx in each simulation is continuously adjusted to appropriate value to maintain relatively consistent flow velocities across all simulations. Table 2 summarizes the relevant control parameters.
| Case | Thermostat Tin (K) | fx (eV A–1) | Pressure P (bar) | Interaction strength ε (eV) | |
|---|---|---|---|---|---|
| Water temperatures | Case 1 | 280 K | 0.00005 | 1.0 | 0.003992 |
| Case 2 | 300 K | 0.00005 | 1.0 | 0.003992 | |
| Case 3 | 320 K | 0.00005 | 1.0 | 0.003992 | |
| Water pressures | Case 4 | 280 K | 0.00006 | 1000 | 0.003992 |
| Case 5 | 280 K | 0.00007 | 2000 | 0.003992 | |
| Case 6 | 280 K | 0.000085 | 3000 | 0.003992 | |
| Case 7 | 280 K | 0.00012 | 5000 | 0.003992 | |
| Water–graphene interaction strengths | Case 8 | 280 K | 0.00006 | 1.0 | 0.004790 |
| Case 9 | 280 K | 0.00009 | 1.0 | 0.005988 | |
| Case 10 | 280 K | 0.00013 | 1.0 | 0.007984 | |
| Case 11 | 280 K | 0.00015 | 1.0 | 0.008782 |
Definition of physical quantities
The no-slip boundary condition, which assumes that the velocity of the liquid at the solid–liquid interface is equal to that of the solid, is one of the most fundamental assumptions in fluid mechanics. However, at the molecular scale, liquid molecules may slip along the solid surface, leading to a discrepancy between the velocities of the liquid and the solid at the solid–liquid interface. These phenomena are quantified by velocity slip length. According to the Navier's model,41 the local velocity slip length can be defined as follows:
 | (2) |
 is the velocity gradient of the fluid at the fluid–solid interface. Analogously, the local temperature slip length is given by:24
is the velocity gradient of the fluid at the fluid–solid interface. Analogously, the local temperature slip length is given by:24
 | (3) |
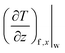 is the fluid temperature gradient at the fluid–solid interface. Temperature slip length is also known as the thickness of the interfacial thermal resistance or Kapitza resistance Rk:24
is the fluid temperature gradient at the fluid–solid interface. Temperature slip length is also known as the thickness of the interfacial thermal resistance or Kapitza resistance Rk:24
 | (4) |
In addition, interfacial thermal resistance Rk,i can also be define as:24
 | (5) |
The analytical solution of non-dimensional velocity distribution for 2D plate Poiseuille flow with velocity slip is given by:42
 | (6) |
The analytical solution of the friction coefficient of the 2D plate Poiseuille flow with velocity slip is:43
 | (7) |
 | (8) |
The wall shear stress τw,i can also be obtained by the driving body force fx:
 | (9) |
The convective heat transfer process is characterized through the non-dimensional Nusselt number (Nu),45 Nux, at the x-direction position:
 | (10) |
 | (11) |
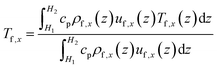 | (12) |
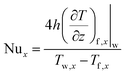 | (13) |
Thermal conductivity and viscosity of the ML-BOP model
We first use EMD to determine the thermal conductivity and viscosity of liquid water described by the ML-BOP model at different temperatures and pressures. A cube containing 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules is built for EMD simulations. The system first equilibrates at specific temperatures and pressures under the NPT ensemble. Subsequently, the thermodynamic properties, including thermal conductivity and viscosity, are calculated under the NVE ensemble condition. The system's average thermal conductivities and viscosities under the identical simulation conditions are obtained by 30 independent simulations.
000 water molecules is built for EMD simulations. The system first equilibrates at specific temperatures and pressures under the NPT ensemble. Subsequently, the thermodynamic properties, including thermal conductivity and viscosity, are calculated under the NVE ensemble condition. The system's average thermal conductivities and viscosities under the identical simulation conditions are obtained by 30 independent simulations.
Tables 3 and 4 present the simulated and experimental thermal conductivity and viscosity values. The average deviations among the simulated thermal conductivities and viscosities are 0.8% and 0.5%, respectively. The experimental values used for comparison are sourced from the NIST database. Although the simulated values are not in good agreement with the experimental values, the errors are within an acceptable level. The average errors between the simulated and experimental thermal conductivity and viscosity are 28.2% and 26.1%, respectively. The largest error between the simulated and experimental thermal conductivity occurs at 1 bar and 360 K, where the simulated value is approximately 40% lower than the experimental value. Similarly, the most significant error between the experimental and simulated viscosity values is at 5000 bar and 280 K, with the simulated viscosity value only about one-third of the experimental value. At 1 bar and within the temperature range of 300 K to 360 K, the simulated viscosity value aligns relatively closely with the experimental value.
| κ (W mK−1) | 1 bar | 2000 bar | 3000 bar | 5000 bar | ||||
|---|---|---|---|---|---|---|---|---|
| MD | EXP | MD | EXP | MD | EXP | MD | EXP | |
| 280 K | 0.446 ± 0.003 | 0.572 | 0.581 ± 0.003 | 0.665 | 0.597 ± 0.003 | 0.690 | 0.710 ± 0.010 | 0.725 |
| 300 K | 0.442 ± 0.003 | 0.609 | 0.554 ± 0.002 | 0.694 | 0.580 ± 0.006 | 0.722 | 0.648 ± 0.002 | 0.764 |
| 320 K | 0.426 ± 0.003 | 0.637 | 0.516 ± 0.002 | 0.721 | 0.573 ± 0.007 | 0.753 | 0.596 ± 0.003 | 0.803 |
| 340 K | 0.412 ± 0.002 | 0.657 | 0.499 ± 0.004 | 0.745 | 0.540 ± 0.002 | 0.780 | 0.579 ± 0.006 | 0.839 |
| 360 K | 0.394 ± 0.002 | 0.671 | 0.472 ± 0.003 | 0.765 | 0.494 ± 0.004 | 0.804 | 0.560 ± 0.003 | 0.871 |
| 380 K | — | — | 0.442 ± 0.005 | 0.780 | 0.510 ± 0.004 | 0.823 | 0.550 ± 0.005 | 0.897 |
| μ (Pa s) | 1 bar | 2000 bar | 3000 bar | 5000 bar | ||||
|---|---|---|---|---|---|---|---|---|
| MD | EXP | MD | EXP | MD | EXP | MD | EXP | |
| 280 K | (8.02 ± 0.02) × 10−4 | 1.43 × 10−3 | (6.05 ± 0.03) × 10−4 | 1.39 × 10−3 | (5.70 ± 0.03) × 10−4 | 1.47 × 10−3 | (5.36 ± 0.03) × 10−4 | 1.75 × 10−3 |
| 300 K | (6.37 ± 0.04) × 10−4 | 8.54 × 10−4 | (5.38 ± 0.02) × 10−4 | 8.91 × 10−4 | (4.81 ± 0.04) × 10−4 | 9.40 × 10−4 | (4.62 ± 0.02) × 10−4 | 1.10 × 10−3 |
| 320 K | (5.38 ± 0.02) × 10−4 | 5.77 × 10−4 | (4.57 ± 0.02) × 10−4 | 6.30 × 10−4 | (4.38 ± 0.03) × 10−4 | 6.70 × 10−4 | (4.14 ± 0.02) × 10−4 | 7.70 × 10−4 |
| 340 K | (4.86 ± 0.04) × 10−4 | 4.22 × 10−4 | (4.08 ± 0.02) × 10−4 | 4.77 × 10−4 | (4.01 ± 0.02) × 10−4 | 5.10 × 10−4 | (3.71 ± 0.03) × 10−4 | 5.87 × 10−4 |
| 360 K | (4.10 ± 0.02) × 10−4 | 2.83 × 10−4 | (3.81 ± 0.02) × 10−4 | 3.80 × 10−4 | (3.51 ± 0.02) × 10−4 | 4.08 × 10−4 | (3.49 ± 0.02) × 10−4 | 4.70 × 10−4 |
| 380 K | — | — | (3.25 ± 0.01) × 10−4 | 3.13 × 10−4 | (3.03 ± 0.02) × 10−4 | 3.39 × 10−4 | (3.00 ± 0.02) × 10−4 | 3.93 × 10−4 |
The Prandtl number (Pr)46 can provide further insight into the influence of fluid physical properties on the convective heat transfer process. It is defined as the ratio of momentum diffusivity to thermal diffusivity and is given by:
 | (14) |
Fig. 2 compares the numerical Pr results with the experimental data. For macroscopic laminar convection heat transfer, the Nu is a function of the Pr. Within the simulated temperature range, the Pr range obtained from the simulation is a part of experimental values. It indicates that the ML-BOP potential can reasonably represent the momentum and heat transport processes within the water well. Additionally, our following research demonstrates that the ML-BOP potential can also effectively simulate flow and heat transfer resistance at the interface.
Results and discussion
Flow characteristics
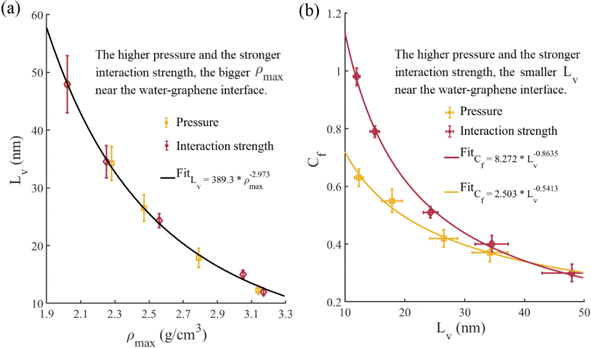
Propelled by water molecules in the forcing region, a hydrodynamic flow field is established throughout the entire channel. Once the flow field stabilizes, the local velocity slip length Lv,x within the whole channel is computed using eqn (2), as depicted in Fig. 3a. At the inlet part, the local velocity slip length changes with the x-coordinate due to alterations in the velocity distribution affected by the driving body and random forces when water molecules pass through the forcing region and the cold thermostat region. As the water molecules move away from the inlet part, the local velocity slip length gradually stabilizes, indicating a relatively stable velocity distribution in this area and the onset of the flow fully-developed segment. The periodic boundary also influences the velocity distribution in the outlet part, causing the slip length to change with the x-coordinate again. We utilize the flow fully-developed segment to calculate the velocity distribution, the average flow velocity um, and the velocity slip length Lv. The non-dimensional velocity distribution u/um of the fully-developed segment is illustrated in Fig. 3b. Subsequently, the obtained velocity slip length is incorporated into eqn (6), and the analytical solution of the non-dimensional velocity distribution is also plotted in Fig. 3b. The results show that the predictions from the analytical solution agree with the non-dimensional velocity distributions measured by MD simulations. Therefore, the correctness of the velocity slip length calculation is confirmed. Based on the average water temperature and pressure, we employ linear interpolation to derive the viscosity from Table 3 and then compute the friction coefficient Cf by eqn (7).Fig. 4a illustrates the oscillated density distribution of water near the water–graphene interface, a common phenomenon similar to previous findings in ref. 31 and 47. Further from the water–graphene interface, water density fluctuation decays and converges to the average bulk value. Since pressure is applied to the entire fluid, the interfacial interaction only acts on the fluid at the interface. Accordingly, bulk density increases with rising pressure, while interaction strength does not affect bulk density. Fig. 4b displays the simulated (average water temperature Tf from Table 5) and experimental (345 K) values of bulk density at different pressures, showing nearly no difference between simulated and experimental density values. Fig. 4c demonstrates the peak density of water ρmax at the interface under varying pressures and interaction strengths. The water peak density increases roughly linearly with pressure and interaction strength. Water molecules are captured to the graphene nanochannel wall and form the relatively ordered liquid layers, significantly affecting interfacial flow and heat transfer characteristics.
| Tf (K) | Um (m s−1) | ρmax (g cm−3) | Lv (nm) | Cf | |
|---|---|---|---|---|---|
| Case 1 | 337.58 | 64.37 | 2.02 | 47.94 ± 4.98 | 0.30 ± 0.03 |
| Case 2 | 347.61 | 67.03 | 2.01 | 43.90 ± 3.83 | 0.29 ± 0.02 |
| Case 3 | 357.77 | 70.14 | 1.95 | 42.18 ± 4.25 | 0.26 ± 0.02 |
| Case 4 | 343.12 | 61.14 | 2.28 | 34.24 ± 2.97 | 0.37 ± 0.03 |
| Case 5 | 346.12 | 60.61 | 2.47 | 26.51 ± 2.29 | 0.42 ± 0.03 |
| Case 6 | 348.94 | 61.76 | 2.79 | 17.88 ± 1.68 | 0.55 ± 0.04 |
| Case 7 | 351.85 | 64.42 | 3.14 | 12.31 ± 0.75 | 0.63 ± 0.03 |
| Case 8 | 339.25 | 63.14 | 2.25 | 34.52 ± 2.78 | 0.40 ± 0.03 |
| Case 9 | 345.12 | 67.20 | 2.56 | 24.30 ± 1.23 | 0.51 ± 0.02 |
| Case 10 | 350.33 | 64.94 | 3.05 | 14.98 ± 0.79 | 0.79 ± 0.02 |
| Case 11 | 351.23 | 64.87 | 3.17 | 11.96 ± 0.56 | 0.98 ± 0.03 |
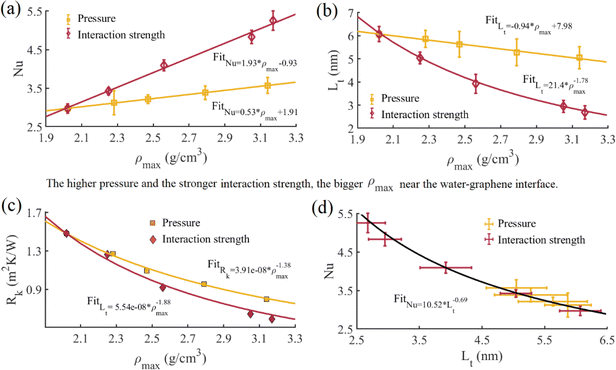
We present a comprehensive analysis of flow characteristics within the nanochannel under various simulation conditions in Table 5. The second and third columns represent the average water temperatures and flow velocities. To avoid the influence of water velocity, we maintain the average flow velocity Um of all cases between 60 and 70 m s−1. The velocity slip length and friction coefficient slightly decrease with inlet temperature. With the increase in inlet temperature from 280 K to 320 K, the velocity slip length and friction coefficient decrease by 12% and 13.3%, respectively. At the primitive water–graphene interaction and atmospheric pressure, the velocity slip length is about 44 nm, aligning with the experimental value measured by capillary flow in the experiment.20,21 Increasing the inlet temperature causes the average water temperature to rise. This decrease in velocity slip length is attributed to the increase in average water temperature, which leads to stronger collisions between the water molecules and the nanochannel wall.48 On the other hand, water viscosity decreases with the average temperature, reducing the friction coefficient. This reduction in friction coefficient leads to an increase in average water velocity under the same driving force, as shown in Table 5. The velocity slip length decreases, and the friction coefficient increases with pressure and interaction strength. The velocity slip length at 5000 bar decreases by 74.3% compared with that at 1 bar, the corresponding friction coefficient increases by 110%. Similarly, the velocity slip length under the condition of ε = 0.008782 eV decreases by 75.1% compared with that under the condition of ε = 0.003992 eV, and the corresponding friction coefficient increases by 227%. As shown previously, the water peak density increases with pressure and interaction strength, which allows more water molecules to attach to the wall, thereby suppressing velocity slip. Fig. 5a illustrates the variation of velocity slip length with water peak density under different simulation conditions. At the same inlet temperature, we observed a consistent power function relationship between velocity slip length and water peak density. The velocity slip length is influenced by all three simulation variations, but the two physical properties, velocity slip length and the peak density value are directly related under the same inlet temperature. We calculate the potential energy in water adjacent to water–graphene interface along the height of the channel and plot the potential energy distribution in Fig. 6a. The circular markers in the Fig. 6a indicate the locations of the peak density in the potential energy distribution. Fig. 6b shows the values of the potential energy at the peak density points under different simulation conditions. As the interaction strength and pressure increase, the potential energy at the peak density decreases, leading to a more stable molecular structure at the fluid–solid interface, which reduce velocity slip. Fig. 6c shows the potential energy gradient along the height of the channel at peak density points, reflecting the force on water molecules in this direction. Similarly, as the interaction strength and pressure increase, the force on water molecules along the height of the channel increases, causing them to collide with the wall more frequently, which also reduces velocity slip. Moreover, it is observed that increasing interaction strength more easily stabilizes the molecular structure at the fluid–solid interface compared to increasing pressure, while increasing pressure tends to make fluid molecules impact the nanochannel wall more readily than increasing interaction strength. These two factors together lead to that the velocity slip length decreases with the increase of water peak density in the form of power law function. Fig. 5b shows the friction coefficient as a function of the velocity slip length. As shown in eqn (7), the friction coefficient increases continuously as the velocity slip length decreases. However, water viscosity also affects the friction coefficient, resulting in the friction coefficient showing an inconsistent trend with velocity slip length for different pressures and interaction strengths.
Heat transfer characteristics
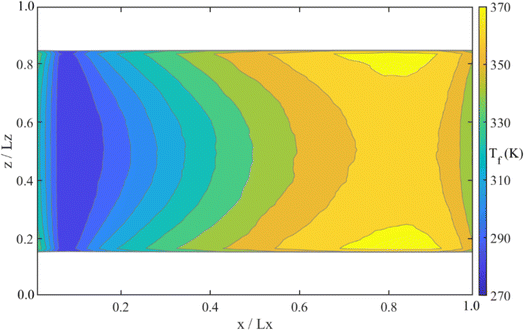
The temperature distribution is a vital indicator of the thermal development process within the nanochannel. Fig. 7 illustrates the water temperature distribution in Case 1. Following the fluid temperature reset at the cold thermostat region, water molecules are heated as they flow through the high-temperature nanochannel wall. This leads to a continuous rise in water temperature along the flow direction. However, the reverse axial heat conduction induced by the periodic boundary prompts the water temperature to decrease again in the outlet part. Since the reverse axial heat conduction does not occur in actual applications, only the data from the area of increased water temperature along the flow direction is used for calculations of the Nu and temperature slip length.49 Fig. 8a–c depict the local water temperature, wall temperature, and water-wall temperature difference along the flow direction under varying inlet temperatures. Compared to the local water temperature, the temperature profile for the nanochannel wall is relatively uniform due to the high in-plane thermal conductivity of graphene, with the maximum local temperature difference on nanochannel wall being about 1 K. So, the water-wall temperature difference primarily depends on the local water temperature. The largest local water-wall temperature difference is observed within the fluid cold thermostat region (enclosed in the dotted box). Fig. 8d presents the temperature gradient at the water–graphene interface along the flow direction. Under the largest local water-wall temperature, the temperature gradient in the fluid cold thermostat region is significantly lower than in the surrounding area. This indicates that the fluid cold thermostat greatly influences the water temperature gradient at the water–graphene interface, leading to inaccurate calculations of physical quantities related to the temperature gradient in this area. Fig. 8e and f display the local Nu and local temperature slip length along the flow direction. Far from the fluid cold thermostat region and reverse axial heat conduction region, the Nu and temperature slip length exhibit stable values, as shown in the dotted box. The stable Nu also indicates that it reaches the thermal-fully developed segment. We calculate the Nu and temperature slip length by averaging the stable values within the dashed box.Additionally, we also calculate the interfacial thermal resistance according to eqn (5). Compared to temperature slip length, the interfacial thermal resistance can more intuitively reflect interfacial heat transfer resistance because of a change in interfacial thermal conductivity. To assess the impact of convection behavior on the interfacial thermal resistance, we conduct a simulation scheme excluding convection, as depicted in Fig. 9a. Langevin thermostats are applied at the nanochannel wall and the center of the water, and the system pressure is maintained at 1 bar.
Fig. 9b illustrates a temperature profile of the system without convection along the z-direction. The noticeable temperature difference across the graphene–water interface indicates the presence of significant interfacial thermal resistance. By comparing the interfacial thermal resistances, including convection and excluding convection at varying water temperatures (Fig. 9c), we observe that convection behavior with an average flow velocity of 60–70 m s−1 has little effect on the interfacial thermal resistance, which can be attributed to macro velocities drastically less than thermal velocities on the order of 640 m s−1 for simulated water temperatures. The interfacial thermal resistance value of 1.45 m2 K W−1 is close to the previously published MD result using the SPC/E water model.47 The interfacial thermal resistance slightly decreases as the water temperature increases. Similar to the velocity slip length, the enhancement of collisions between water molecules and the wall at higher water temperatures also reduces interfacial heat transfer resistance,50–52 allowing for more efficient heat diffusion from the nanochannel wall into the water.
We present a comprehensive analysis of heat transfer characteristics within the nanochannel under various simulation conditions in Table 6. The Nu increases while the temperature slip length and interfacial thermal resistance decrease with the rise in inlet temperature, water pressure, and water–graphene interaction strength. However, the inlet temperature, water pressure, and water–graphene interaction strength affect these crucial parameters in heat transfer differently. The inlet temperature has a minimal effect on interfacial heat transfer characteristics compared with pressure and interaction strength. When the inlet temperature increases from 280 K to 320 K, the Nu increases by 5.4%, and the temperature slip length and interfacial thermal resistance decrease by 6.3% and 4.1%, respectively. Fig. 10a and c show the variation of the Nu and interfacial thermal resistance with water peak density at the water–graphene interface. As the pressure and interaction strength change, the Nu increases linearly with the water peak density, and the interfacial thermal resistance power-law decreases with the water peak density. Although the Nu and the interfacial thermal resistance have the same functional form with respect to the water peak density, the effect of the interaction strength is more significant than that of the pressure, especially for the Nu. For instance, at 5000 bar, the Nu increases by 20.2% compared with that at 1 bar; and the corresponding interfacial thermal resistance decreases by 46.3%. Similarly, under the condition of ε = 0.008782 eV, the Nu increases by 76.8% compared with that at ε = 0.003992 eV; with the corresponding interfacial thermal resistance decreasing by 60.1%. The slower increase in the Nu with pressure is attributed to the increase in thermal conductivity with pressure, leading to a smaller temperature gradient at the interface and thus reducing the Nu. At the same flow velocity, although Case 11 has a higher Nu, the interfacial heat flux is smaller than that of Case 7. This is mainly because Case 7 has higher bulk thermal conductivity under higher pressure, which is more conducive to internal heat transfer within the water. Therefore, increasing interaction strengths to improve interfacial heat transfer for smaller channel heights is crucial. For higher channel heights, increasing the pressure can not only improve the interfacial heat transfer but also help enhance the internal heat transfer within water. For the same peak density, increasing the interaction results in a relatively small interfacial thermal resistance compared to increasing the pressure. It indicates that increasing interaction strength is more beneficial to the heat transfer between channel and fluid at the interface than increasing pressure. This indicates that interface heat transfer not only depends on water peak density but also has a stronger correlation with the coupling between water molecules and wall atoms. Compared to velocity slip, the origin of interfacial thermal resistance is very complicated, involving vibrational modes and phonon transport.24 A previous report31 indicates the interfacial thermal resistance has an inverse proportionality relationship to the water peak density. The difference in results may be due to the different thermostat methods used. Fig. 10b shows the variation of the temperature slip length with water peak density at the water–graphene interface. When the pressure changes, the temperature slip length decreases linearly with the water peak density; while the interaction strength changes, the temperature slip length follows a power-law decrease with the water peak density. Fig. 10d shows that the Nu and temperature slip length approximate a power function relationship, which is consistent with a previous report.29
| ρmax (g cm−3) | Nu | Lt (nm) | J (eV ps−1) | Rk,i (m2 K W−1) | |
|---|---|---|---|---|---|
| Case 1 | 2.02 | 2.97 ± 0.12 | 6.07 ± 0.33 | 7.54 | 1.48 × 10−8 |
| Case 2 | 2.01 | 3.03 ± 0.17 | 5.72 ± 0.42 | 6.30 | 1.45 × 10−8 |
| Case 3 | 1.95 | 3.13 ± 0.19 | 5.69 ± 0.56 | 5.06 | 1.42 × 10−8 |
| Case 4 | 2.28 | 3.12 ± 0.31 | 5.87 ± 0.37 | 7.91 | 1.27 × 10−8 |
| Case 5 | 2.47 | 3.21 ± 0.11 | 5.63 ± 0.55 | 8.44 | 1.09 × 10−8 |
| Case 6 | 2.79 | 3.38 ± 0.18 | 5.28 ± 0.58 | 8.96 | 9.53 × 10−9 |
| Case 7 | 3.14 | 3.57 ± 0.21 | 5.05 ± 0.48 | 10.14 | 7.95 × 10−9 |
| Case 8 | 2.25 | 3.42 ± 0.10 | 5.04 ± 0.25 | 7.91 | 1.26 × 10−8 |
| Case 9 | 2.56 | 4.09 ± 0.14 | 3.92 ± 0.41 | 9.14 | 9.18 × 10−9 |
| Case 10 | 3.05 | 4.83 ± 0.17 | 2.95 ± 0.26 | 9.83 | 6.42 × 10−9 |
| Case 11 | 3.17 | 5.25 ± 0.25 | 2.68 ± 0.28 | 10.05 | 5.90 × 10−9 |
Variation of physical properties
Water's viscosity and thermal conductivity at the water–graphene interface also exhibit a non-homogenous profile, just like density. To assess the effect of variation of overall viscosity and thermal conductivity of pressure and interaction strength at our simulated channel height, we compare the wall shear stress τw following eqn (7) according to the bulk viscosity μ obtained from EMD simulation in Table 4 and actual wall shear stress τw,i following eqn (9), respectively. Meanwhile, the interfacial thermal resistance Rk as follows eqn (4) according to the temperature slip length LT and bulk value of thermal conductivity k from EMD simulation in Table 3 and the actual interfacial thermal resistance Rk,i as follows eqn (5) are also compared. As the pressure and interaction strength increase, the wall shear stress increases and the interfacial thermal resistance decreases. Fig. 11a and b show the wall shear stress and interfacial thermal resistance obtained by the above equations. represents the ratio of the bulk viscosity μ obtained by EMD simulation in Table 4 to the viscosity μi in the actual flow, and
represents the ratio of the bulk viscosity μ obtained by EMD simulation in Table 4 to the viscosity μi in the actual flow, and  means the ratio of the bulk thermal conductivity k obtained by EMD simulation in Table 3 to the interfacial thermal conductivity ki in the actual convection heat transfer. It can be observed that the
means the ratio of the bulk thermal conductivity k obtained by EMD simulation in Table 3 to the interfacial thermal conductivity ki in the actual convection heat transfer. It can be observed that the 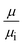 and
and 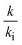 under different simulation conditions exhibit a linear relationship. This indicates that pressure and interaction strength hardly affect the change range of the viscosity and the thermal conductivity at our simulated channel height.
under different simulation conditions exhibit a linear relationship. This indicates that pressure and interaction strength hardly affect the change range of the viscosity and the thermal conductivity at our simulated channel height.
 | ||
| Fig. 11 (a) Wall shear stress obtained by eqn (7) and (9), (b) interfacial thermal resistance obtained by eqn (4) and (5), (c) convective heat transfer coefficient as a function of wall shear stress under different water temperature (ε = 0.003992 eV, P = 1 bar), pressures (Tin = 280 K, ε = 0.003992 eV) and interaction strengths (Tin = 280 K, P = 1 bar). | ||
Finally, we plot the convective heat transfer coefficient as a function of actual wall shear stress, as shown in Fig. 11c. The convective heat transfer coefficient is computed by eqn (13). As shown in the fitting curve, as the pressure and interaction strength increase, the convective heat transfer coefficient increases slower than the wall shear stress. However, when pressure and interaction strength vary moderately, the convection heat transfer coefficient approximately exhibits a linear relationship with wall shear stress. This shows that the benefits of increasing moderately pressure and interaction strength on convective heat transfer are relatively high.
Conclusions
In this study, we utilize the MD method to numerically investigate the convection heat transfer of water flow in graphene nanochannel under different circumstance conditions, such as the inlet temperature, environmental pressure and interfacial interaction strength. Both heat and mass transfer performances influenced by the circumstance conditions are then studied, including velocity slip and friction coefficient, temperature slip and Nu, and interfacial thermal resistance, as well as the variation of physical properties. The microscopic mechanisms of inlet temperatures, water pressures, and water–graphene interaction strengths that influence flow and heat transfer characteristics are analyzed.(1) As the inlet temperature increases, the velocity slip, friction coefficient, temperature slip, and interfacial thermal resistance reduce slightly, while the Nu rises somewhat. Pressure and interfacial interaction strength have the similar effect on interfacial thermal and flow characteristics. With the increase of pressure and interfacial interaction strength, the velocity slip, temperature slip, and interfacial thermal resistance reduce obviously, while the friction coefficient, Nu significantly rise.
(2) The water peak density at the water–graphene interface is a key factor in regulating interfacial flow and heat transfer characteristics. Under constant inlet temperature, the water peak density adjacent to the interface increases approximately linearly with pressure and interaction strength. The velocity slip length shows the same power function relationship with water peak density, simply modifying the pressure or the interaction strength doesn't bring specific effect. However, the Nu, temperature slip length and interfacial thermal resistance are not solely dependent on water peak density; at the same water peak density, increasing interaction strength results in lower interfacial thermal resistance compared to increasing pressure.
(3) Increasing interfacial interactions is crucial for improving interfacial heat transfer in smaller channel heights. For larger channel heights, increasing pressure not only improves interfacial heat transfer but also enhances the internal heat transfer within water.
(4) Pressure and interaction strength hardly impact the variation range of viscosity and thermal conductivity at a channel height of 10–12 nm. The convection heat transfer coefficient increases roughly linearly with flow resistance when pressure and interaction strength vary moderately.
Data availability
The data that support the findings of this study are available on request from the corresponding author, Hanhui Jin, upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Natural Science Fund of China (Grant No. U2341283, 52236002), the Ningbo 2025 Key R&D Project (2023Z223), and technical support from the Information Technology Center and State Key Lab of CAD&CG, Zhejiang University.References
- A. L. Moore and L. Shi, Emerging challenges and materials for thermal management of electronics, Mater. Today, 2014, 17(4), 163–174 CrossRef CAS.
- E. Pop, Energy dissipation and transport in nanoscale devices, Nano Res., 2010, 3, 147–169 CrossRef CAS.
- B. Ramakrishnan, H. Alissa, I. Manousakis, R. Lankston, R. Bianchini, W. Kim, R. Baca, P. A. Misra, I. Goiri, M. Jalili and A. Raniwala, CPU overclocking: A performance assessment of air, cold plates, and two-phase immersion cooling, IEEE Trans. Compon., Packag., Manuf. Technol., 2021, 11(10), 1703–1715 CAS.
- B. Ozmat, Interconnect technologies and the thermal performance of MCM, IEEE Trans. Compon. Packag. Technol., 1992, 15(5), 860–869 Search PubMed.
- M. Mahalingam, Thermal management in semiconductor device packaging, Proc. IEEE, 1985, 73(9), 1396–1404 Search PubMed.
- G. P. Peterson and A. Ortega, Thermal control of electronic equipment and devices, in Advances in Heat Transfer, 1990, vol. 20, pp. 181–314 Search PubMed.
- M. K. Sung and I. Mudawar, CHF determination for high-heat flux phase change cooling system incorporating both micro-channel flow and jet impingement, Int. J. Heat Mass Transfer, 2009, 52(3–4), 610–619 CrossRef CAS.
- J. Koo and C. Kleinstreuer, Laminar nanofluid flow in microheat-sinks, Int. J. Heat Mass Transf., 2005, 48(13), 2652–2661 CrossRef CAS.
- A. Koşar and Y. Peles, Boiling heat transfer in a hydrofoil-based micro pin fin heat sink, Int. J. Heat Mass Transfer, 2007, 50(5–6), 1018–1034 CrossRef.
- L. W. Da Silva and M. Kaviany, Micro-thermoelectric cooler: interfacial effects on thermal and electrical transport, Int. J. Heat Mass Transfer, 2004, 47(10–11), 2417–2435 CrossRef CAS.
- D. B. Tuckerman and R. F. Pease, High-performance heat sinking for VLSI, IEEE Elect Device Lett., 1981, 2(5), 126–129 Search PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Fast mass transport through sub-2-nanometer carbon nanotubes, Science, 2006, 312(5776), 1034–1037 CrossRef CAS PubMed.
- M. Majumder, N. Chopra, R. Andrews and B. J. Hinds, Enhanced flow in carbon nanotubes, Nature, 2005, 438(7064), 44 CrossRef CAS PubMed.
- G. G. Stokes, On the theories of internal friction of fluids in motion, Trans. Cambridge Philos. Soc., 1845, 8, 287–305 Search PubMed.
- F. Heslot, N. Fraysse and A. M. Cazabat, Molecular layering in the spreading of wetting liquid drops, Nature, 1989, 338(6217), 640–642 CrossRef CAS.
- L. Cheng, P. Fenter, K. L. Nagy, M. L. Schlegel and N. C. Sturchio, Molecular-scale density oscillations in water adjacent to a mica surface, Phys. Rev. Lett., 2001, 87(15), 156103 CrossRef CAS PubMed.
- D. Ortiz-Young, H. C. Chiu, S. Kim, K. Voïtchovsky and E. Riedo, The interplay between apparent viscosity and wettability in nanoconfined water, Nat. Commun., 2013, 4(1), 2482 CrossRef PubMed.
- M. Nazari, A. Davoodabadi, D. Huang, T. Luo and H. Ghasemi, On interfacial viscosity in nanochannels, Nanoscale, 2020, 12(27), 14626–14635 RSC.
- C. Bakli and S. Chakraborty, Capillary filling dynamics of water in nanopores, Appl. Phys. Lett., 2012, 101(15), 153112 CrossRef.
- Q. Xie, M. A. Alibakhshi, S. Jiao, Z. Xu, M. Hempel, J. Kong, H. G. Park and C. Duan, Fast water transport in graphene nanofluidic channels, Nat. Nanotechnol, 2018, 13(3), 238–245 CrossRef CAS PubMed.
- A. Keerthi, S. Goutham, Y. You, P. Iamprasertkun, R. A. Dryfe, A. K. Geim and B. Radha, Water friction in nanofluidic channels made from two-dimensional crystals, Nat. Commun., 2021, 12(1), 3092 CrossRef CAS PubMed.
- K. T. Chen, Q. Y. Li, T. Omori, Y. Yamaguchi, T. Ikuta and K. Takahashi, Slip length measurement in rectangular graphene nanochannels with a 3D flow analysis, Carbon, 2022, 189, 162–172 CrossRef CAS.
- H. Li, Z. Xu, C. Ma and M. Ma, Translucency and negative temperature-dependence for the slip length of water on graphene, Nanoscale, 2022, 14(39), 14636–14644 RSC.
- J. Chen, X. Xu, J. Zhou and B. Li, Interfacial thermal resistance: Past, present, and future, Rev. Mod. Phys., 2022, 94(2), 025002 CrossRef CAS.
- K. S. Kumar, B. D. Todd, J. S. Hansen and P. J. Daivis, Slip length of water on graphene: Limitations of non-equilibrium molecular dynamics simulations, J. Chem. Phys., 2012, 136(2), 024705 CrossRef PubMed.
- E. Wagemann, E. Oyarzua, J. H. Walther and H. A. Zambrano, Slip divergence of water flow in graphene nanochannels: the role of chirality, Phys. Chem. Chem. Phys., 2017, 19(13), 8646–8652 RSC.
- Z. Song, Z. Cui, Q. Cao, Y. Liu and J. Li, Molecular dynamics study of convective heat transfer in ordered rough nanochannels, J. Mol. Liq., 2021, 337, 116052 CrossRef CAS.
- H. Sun, F. Li, M. Wang, G. Xin and X. Wang, Molecular dynamics study of convective heat transfer mechanism in a nano heat exchanger, RSC Adv., 2020, 10(39), 23097–23107 RSC.
- S. Yao, J. Wang, S. Jin, F. Tan and S. Chen, Atomistic insights into the microscope mechanism of solid–liquid interaction influencing convective heat transfer of nanochannel, J. Mol. Liq., 2023, 371, 121105 CrossRef CAS.
- D. C. Marable, S. Shin and A. Y. Nobakht, Investigation into the microscopic mechanisms influencing convective heat transfer of water flow in graphene nanochannels, Int. J. Heat Mass Transfer, 2017, 109, 28–39 CrossRef CAS.
- D. Alexeev, J. Chen, J. H. Walther, K. P. Giapis, P. Angelikopoulos and P. Koumoutsakos, Kapitza resistance between few-layer graphene and water: liquid layering effects, Nano Lett., 2015, 15(9), 5744–5749 CrossRef CAS PubMed.
- M. E. Suk and N. R. Aluru, Molecular and continuum hydrodynamics in graphene nanopores, RSC Adv., 2013, 3(24), 9365–9372 RSC.
- L. Lindsay and D. A. Broido, Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(20), 205441 CrossRef.
- H. Chan, M. J. Cherukara, B. Narayanan, T. D. Loeffler, C. Benmore, S. K. Gray and S. K. Sankaranarayanan, Machine learning coarse grained models for water, Nat. Commun., 2019, 10(1), 379 CrossRef CAS PubMed.
- X. Pan, H. Jin, X. Ku, Y. Guo and J. Fan, Coupling at the molecular scale between the graphene nanosheet and water and its effect on the thermal conductivity of the nanofluid, Phys. Chem. Chem. Phys., 2024, 26(3), 2402–2413 RSC.
- T. W. Sirk, S. Moore and E. F. Brown, Characteristics of thermal conductivity in classical water models, J. Chem. Phys., 2013, 138(6), 061101 CrossRef PubMed.
- L. A. Girifalco, M. Hodak and R. S. Lee, Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(19), 13104 CrossRef CAS.
- K. K. Bejagam, S. Singh and S. A. Deshmukh, Development of non-bonded interaction parameters between graphene and water using particle swarm optimization, J. Comput. Chem., 2018, 39(12), 721–734 CrossRef CAS PubMed.
- R. L. Davidchack, R. Handel and M. V. Tretyakov, Langevin thermostat for rigid body dynamics, J. Chem. Phys., 2009, 130(23), 234101 CrossRef PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen and R. Shan, LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- L. M. Navier, Mémoire sur les lois du mouvement des fluides, Mem. Acad. R. Sci., 1822, 6, 389–440 Search PubMed.
- A. C. Yunus, Fluid Mechanics: Fundamentals and Applications (Si Units), Tata McGraw Hill Education Private Limited; 2010 Search PubMed.
- S. Yao, J. Wang and X. Liu, Role of wall-fluid interaction and rough morphology in heat and momentum exchange in nanochannel, Appl. Energy, 2021, 298, 117183 CrossRef CAS.
- N. Rott, Note on the history of the Reynolds number, Annu. Rev. Fluid. Mech., 1990, 22(1), 1–2 CrossRef.
- A. Bejan, Convection Heat Transfer, John wiley & sons, 2013 Search PubMed.
- R. Verzicco and R. Camussi, Prandtl number effects in convective turbulence, J. Fluid Mech., 1999, 383, 55–73 CrossRef.
- S. Alosious, S. K. Kannam, S. P. Sathian and B. D. Todd, Kapitza resistance at water–graphene interfaces, J. Chem. Phys., 2020, 152(22), 224703 CrossRef CAS PubMed.
- A. A. Pahlavan and J. B. Freund, Effect of solid properties on slip at a fluid-solid interface, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83(2), 021602 CrossRef PubMed.
- Y. W. Gu, S. Ge and M. Chen, A molecular dynamics simulation of nanoscale convective heat transfer with the effect of axial heat conduction, Mol. Phys., 2016, 114(12), 1922–1930 CrossRef CAS.
- S. Murad and I. K. Puri, Thermal transport across nanoscale solid-fluid interfaces, Appl. Phys. Lett., 2008, 92(13), 133105 CrossRef.
- R. J. Stoner and H. J. Maris, Kapitza conductance and heat flow between solids at temperatures from 50 to 300 K, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(22), 16373 CrossRef CAS PubMed.
- M. Barisik and A. Beskok, Temperature dependence of thermal resistance at the water/silicon interface, Int. J. Therm. Sci., 2014, 77, 47–54 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |