Open Access Article
Open Access ArticleTunable photoelectric properties of monolayer Mo1−xWxTe2 alloys: a first-principles study
Mohan Gao ,
Zhenhua Wang
,
Zhenhua Wang *,
Jinchao Ma,
Haowen Jiang
*,
Jinchao Ma,
Haowen Jiang ,
Yuanyuan Fu,
Suifeng Huo,
Hui Zhang,
Chen Wu
,
Yuanyuan Fu,
Suifeng Huo,
Hui Zhang,
Chen Wu ,
Kan Chai and
Guangju Ji
,
Kan Chai and
Guangju Ji
Department of Physics, School of Science, Harbin University of Science and Technology, Harbin 150080, P.R. China. E-mail: wzhua@hrbust.edu.cn
First published on 30th September 2024
Abstract
Monolayer MoTe2 and WTe2 within the two-dimensional transition metal dichalcogenides (TMDCs) material family exhibit broad potential for application in optoelectronic devices owing to their direct band gap characteristics. In this work, upon alloying these materials into a monolayer system denoted as Mo1−xWxTe2, intriguing alterations are observed in the electronic and optoelectronic properties. The photoelectric attributes of these alloys can be tailored by manipulating the respective ratios of molybdenum to tungsten (Mo/W). This investigation employs first-principles calculations based on density functional theory (DFT) to assess physical traits of two-dimensional monolayered structures composed from varying compositions of Mo1−xWxTe2. Our findings reveal that while maintaining a direct band gap characteristic across all compositions studied, there is also a reduction observed in electron effective mass near the Fermi level. Moreover, changing in the Mo/W ratio allows gradual adjustments in electronic properties such as density of states (DOS), work function, dielectric function, absorptivity, and reflectivity. Phonon dispersion curves further demonstrate the stability of Mo1−xWxTe2 systems. Notably, Mo0.5W0.5Te2 exhibits lower polarizability and reduced band gap when compared against MoTe2 and WTe2 counterparts. This research underscores how alloying processes enable customizable modifications in the electronic and optoelectronic properties of Mo1−xWxTe2 monolayer materials which is essential for enhancing nanoscale electronic and optoelectronic device design.
Introduction
Two-dimensional transition metal dichalcogenides (TMDCs) with graphene-like structures break through the zero-band gap limit of graphene,1,2 and have been extensively studied in recent years for various practical applications of nano-electronic devices. TMDC materials exhibit a direct band gap due to quantum confinement effects,3 which fosters pronounced photoexcitation. Due to their optical transition and photocatalysis,4,5 high specific surface area,6,7 abundant active catalytic sites,8 and high electron–hole separation rate,9 TMDCs offer vast potential for applications in broadband photonic devices.10 Among TMDCs, monolayer MoTe2 and WTe2 (ref. 11) exhibit novel electronic12 and thermoelectric properties.13 A series of strain-driven topological phase transitions have been found in monolayer MoTe2, which indicates possible experimental implementations of different topological semi-metallic phases.14 Particularly, it is discovered that topological Fermi arc15 and new semi-metallic states16 emerge in orthogonal monolayer MoTe2 and WTe2. Furthermore, valley splitting in monolayer MoTe2 can be continuously regulated by rotating the substrate magnetization,17 which can be applied to exploring valley electron nanodevices. However, due to the limitation of monolayer MoTe2 and WTe2 structures, it is relatively difficult to study the continuous band gap regulation and physical properties of future 2D optoelectronic devices. Therefore, continuous adjustment of the band gap in monolayer MoTe2 and WTe2 is a major challenge to the applications of these two materials as semiconductor devices.Currently, alloying has emerged as a crucial technique for fine-tuning the photoelectric properties of TMDCs,18–20 particularly for precise adjustment of the band gap. Afrid et al. verified in their calculations that alloyed monolayer Mo1−xWxSe2 materials achieve the purpose of band gap regulation while keeping the lattice structure unchanged.21 Previously, the band structure and carrier transport characteristics of Mo1−xWxS2 (ref. 22) and MoSxSe2−x23 alloys have been modulated. The stability of TMD alloys is predicted.24 Subsequently, Mo0.91W0.09Te2 alloy was successfully prepared in the experiment, showing potential applications in optoelectronics, and therefore have wide application prospects in the field of optoelectronics and photonics.25 However, there is limited research on the alloying of monolayer MoTe2 and WTe2, particularly regarding the impact of Mo–W alloy composition on its band structure, dynamic stability, electron state density, and optical properties. Further investigation is required to clarify these aspects.
At present, the effect of different alloying degrees of monolayer MoTe2 and WTe2 on their photoelectric properties has not been widely studied, so the alloying system is worthy of further exploration. In this paper, based on monolayer MoTe2, W with similar atomic radius and valence electron structure as Mo is alloyed and modified, and the band structure, state density, work function, and optical properties of Mo1−xWxTe2 system at x = 0, 0.25, 0.5, 0.75, 1 are studied by first-principles calculation method. Our study shows the potential application of the Mo1−xWxTe2 system with a band gap as low as 1.082 eV at x = 0.5, for high-sensitivity photodetectors. The phonon dispersion curve shows that all the alloyed materials can exist stably. In particular, the lattice constant after alloying has little change, which provides a new idea for exploring the band gap change of TMDC materials, excluding the influence of structure, and realizing continuous band gap regulation.
Computing approach and modeling
Construction of alloys
The growth of monolayer Mo1−xWxTe2 films involves deposition and tellurization processes. The deposition of the transition metal films is prepared at the customized magnetron sputter containing a load lock chamber (base pressure <0.5 Pa) and a sputter chamber (base pressure <9−5 Pa). The required high purity (>99.95%) metal targets are standard, and the sapphire substrate is annealed at 300 °C under vacuum (<9−5 Pa) in the sputter chamber before sputtering. The process parameters of the sputtering are conducted under the following conditions: RF power source of 30 W, Ar introducing of 100 sccm, substrate temperature of 100 °C, constant chamber pressure of 10 Pa, and deposition rate of 0.2 Å s−1. Thus, the thickness of the metal film can be well controlled by the sputtering time. As shown in Fig. 1, the typical tellurization process is performed under atmospheric pressure, where Te (>99.9%) is placed in low-temperature zone (Te at 400 °C) upstream, and the Mo1−xWx metal films are heated to 500 °C at a heating speed of 50 °C min−1 and held at 500 °C for 30 min to complete the in high-temperature zone downstream. The Ar–H2 gas mixture with a flow rate for both Ar and H2 of 100 standard cubic centimeters per minute is used to obtain the Mo1−xWxTe2 films under a reductive atmosphere. All samples are annealed under an ultrahigh vacuum (approximately 10−6 Pa) at 300 °C for 0.5 h, and these samples are then brought down to room temperature and stored in a vacuum for subsequent characterizations. | ||
| Fig. 1 Preparation diagram of monolayer Mo1−xWxTe2 system and structure diagram of Mo1−xWxTe2 system at x = 0, 0.25, 0.5, 0.75, 1. | ||
Computational details
MoTe2 possesses various crystal structures at room temperature, including the 1T phase, 2H phase, and 3R phase. This study focuses on stable 2H–MoTe2 with space group P63/mmc. The modeling system was constructed based on a 4 × 4 × 1 supercell of monolayer MoTe2. The supercell contains a total of 48 atoms, including 16 Mo atoms and 32 Te atoms. In Fig. 1, it is shown that in monolayer MoTe2, the W atom achieves alloying model construction at x = 0.25, 0.5, 0.75 by replacing the Mo atom. The geometric configuration of the supercell system was optimized before and after alloying, and the performance improvements were assessed using single-point energy calculations. The calculations involve the following valence electron arrangements 4d55s1, 5d46s2 and 5s25p4 for Mo, W, and Te, respectively.In this study, all first-principles calculations were performed using density functional theory (DFT) with the Cambridge Sequential Total Energy Package (CASTEP),26 and the interaction between ions and valence electrons was described by the ultra-soft pseudopotential (USPP) method. The exchange–correlation function based on the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) is adopted. The GGA-PBE method has been proven to be highly effective for surface analyses.27 In this study, we employed the semi-empirical Tkatchenko–Scheffler (TS)28 dispersion correction method to calculate the van der Waals forces. Using ultra-soft pseudopotentials to calculate electronic and optical properties. We introduced a vacuum layer with a thickness of 20 Å in the (c)-direction. We conducted convergence testing and used Broyden, Fletcher, Goldfarb, and Shanno's (BFGS) algorithm26 for the geometric optimization and the calculations of electronic structure. According to the Monkhorst Pack scheme, the cutoff energy of the plane wave basis is set to 500 eV, and the k-grid is selected as 4 × 4 × 1. The self-consistent accuracy SCF is set to 5.0 × 10−6 eV per atom, and the maximum stress is set to 0.02 GPa. The maximum displacement is less than 5 × 10−4 Å, and the convergence accuracy of the interatomic force field is 0.01 eV Å−1.
Results and discussion
Electronic property
The optimized structure of the Mo1−xWxTe2 system is depicted in Fig. 2(a), all exhibiting a hexagonal structure and belonging to the C2V point group. As illustrated in Fig. 2(b), the phonon dispersion curves of monolayer MoTe2 and WTe2 confirm their inherent dynamic stability, with no virtual frequency observed. The crystal parameters after optimization for MoTe2 and WTe2 are determined to be 3.539 and 3.546 respectively, showing small errors compared to the results of previous studies,29,30 indicating the reliability of the calculation method used in this study. Additionally, Fig. 2(b) displays the phonon dispersion curves of the Mo1−xWxTe2 system at different alloying degrees when x = 0.25, 0.5, 0.75, with no virtual frequency observed. The lattice constants measured as 3.541, 3.544, and 3.546 respectively. The slight changes in crystal parameters after different degrees of alloying can be attributed to the similar valence electron structure between the Mo atom and the W atom. It has the basis of stable existence in synthesis.The work function is a crucial parameter for elucidating the charge transfer and field emission characteristics of materials. As delineated in eqn (1), the work function is defined as the minimum energy necessary for an electron to transition from the Fermi level to the vacuum layer.
| Φ = Evac − EF | (1) |
To investigate the charge transfer properties of the monolayer Mo1−xWxTe2 systems before and after alloying, we calculated their work functions at different compositions. Where Φ, Evac, and EF denote the work function, vacuum energy level, and Fermi energy level, respectively. The work functions of the monolayer Mo1−xWxTe2 system are 4.751 eV, 4.568 eV, 4.666 eV, 4.617 eV, and 4.62 eV at x values of 0, 0.25, 0.5, 0.75, and 1, respectively. These values can be modulated through alloying ratios to alter the field emission performance of monolayer Mo1−xWxTe2. A decrease in the work function of the system enhances electron emission efficiency, improving electron transition capabilities across the semiconductor interface. Moreover, variations in band gap and work function suggest potential methods for modulating Schottky barrier heights, which is one of the critical bottlenecks in the application of two-dimensional transition metal dichalcogenides (TMDCs) in semiconductor technologies. After analyzing, it is evident that the work function of the monolayer Mo1−xWxTe2 system is lower than that of monolayer MoTe2 and WTe2 when x = 0.25, 0.5, 0.75. This effectively reduces the energy required for electron escape from the interior to the semiconductor surface, demonstrating superior electronic transition capabilities. In the Mo1−xWxTe2 system, variations in the band gap and work function also indicate that the Schottky barrier height can be sensitively adjusted when creating a heterogeneous structure with other materials, potentially offering a novel approach to modulating the Schottky barrier height (Table 1).31–34
| Type | Crystal parameters (Å) | Work function (eV) |
|---|---|---|
| MoTe2 | 3.539549 | 4.751 |
| Mo0.75W0.25Te2 | 3.5415825 | 4.568 |
| Mo0.5W0.5Te2 | 3.544767 | 4.666 |
| Mo0.25W0.75Te2 | 3.546017 | 4.617 |
| WTe2 | 3.5461095 | 4.62 |
Fig. 3 illustrates the band structures of Mo1−xWxTe2 of various x values in the energy range of −3 to +3 eV. The Fermi level was set to 0 eV. As shown in Fig. 3(a), the minimum conduction band (CBM) and maximum valence band (VBM) are both located at the high symmetry point k, with a band gap of 1.107 eV. The monolayer WTe2 band structure is shown in Fig. 3(e), with a band gap of 1.1 eV. It can be seen from the figure that the band structures of MoTe2 and WTe2 are both direct band gaps, this result is consistent with previous reports.35,36 On the other hand, the monolayer Mo1−xWxTe2 maintains a direct band gap across varying degrees of alloying without transitioning from a semiconductor to a metallic phase. The Mo1−xWxTe2 band structures show no significant change in the interlayer spatial inversion symmetry under different degrees of alloying. The interlayer built-in electric field caused by this has not been reflected. Mo0.5W0.5Te2, bears a band gap of 1.082 eV which is the narrowest among all the studying compositions. The calculated band structure of Mo1−xWxTe2 reveals no new impurity levels compared to the original band gap in MoTe2, and the VBM remains largely unchanged. The modulation of the band gap can be attributed to the interaction of d-orbital electrons between Mo and W, which alleviates the degeneracy of the original CBM and exhibits a general downward trend with varying degrees of alloying. Therefore, by varying the proportion of Mo–W content, the band gap can be continuously tuned while retaining the macroscopic physical properties and basic band structure of MoTe2 or WTe2 materials nearly unchanged.
Band analysis of various Mo1−xWxTe2 monolayer structures reveals band gap values of 1.107 eV, 1.09 eV, 1.082 eV, 1.094 eV, and 1.1 eV at x values of 0, 0.25, 0.5, 0.75, and 1, respectively. The CBM and VBM exhibit the lowest energies at x = 0.5. For 0 < x < 0.5, the band gap decreases as x increases, whereas for 0.5 < x < 1, the band gap increases with increasing x. When 0 < x < 0.5, the decrease in band gap with increasing x indicates an effective reduction in the energy required for electron transition which improves the overall electron mobility. Owing to the comparable sizes and valence electron configurations between Mo and W atoms, hybridization of the d and p states at the Fermi level alters the conduction band's bottom structure, as depicted in the energy band diagram. The change of band gap decreases first and then increases under visible light exposure, this structure facilitates electron transitions between the valence and conduction bands, generating photon-induced electron–hole pairs and enhancing light absorption. Electron transitions to the conduction band for Mo0.5W0.5Te2 are the most pronounced among all compositions, resulting in a peak in the light absorption capabilities curve. Indicating stronger light absorption ability. Therefore, Mo0.5W0.5Te2 is identified as having the most robust light absorption performance in the Mo1−xWxTe2 system.
The density of states (DOS), within the energy range from −3 to 3 eV, for monolayer Mo1−xWxTe2 systems was presented by adjusting the number of states near the Fermi level, in Fig. 4. Electronic states can be systematically categorized into two regions: the region from −3 to 0 eV is formed by a combination of Te-5p and Mo-4d/W-5d orbitals, while the conduction band (0–3 eV) comprises Mo-4d/W-5d and Te-5p states. Around the Fermi level, relatively flat bands may arise due to the d and p characteristics of electronic states. The semiconductor attributes of the Mo1−xWxTe2 monolayer structure are evident from the DOS diagram, with Mo/W and Te orbitals dominating near EF. The transition from semiconductor properties to metallicity remains unaffected by the orbital hybridization changes resulting from varying x in Mo1−xWxTe2. Fig. 4(a) illustrates the DOS of monolayer MoTe2, a direct band gap semiconductor, with electronic states of VBM primarily comprising the hybridization of Te-5p and Mo-4d orbitals, while those of CBM mainly consist of Mo-4d orbitals. Similarly, Fig. 4(e) shows the DOS of monolayer WTe2, which is also a direct band gap semiconductor, with VBM electronic states comprising the hybridization of Te-5p and W-5d orbitals, and CBM electronic states mainly consists of W-5d orbitals. The increasing W content in the system affects the hybridization of Mo-4d/Te-5p orbitals in the original system. The appearance of the lowest band gap at a certain point in the Mo1−xWxTe2 system due to the change in x is attributed to the different valence electron energies of Mo/W. Specifically, when the value of x in the Mo1−xWxTe2 system is not 0, Mo-4d and W-5d orbitals interact with Te-5p orbitals at the Fermi level, breaking the degenerate state of the original MoTe2/WTe2 structure. From Fig. 4(f), it can be found that Mo-4d and W-5d orbital electrons have different energies, and they jointly participate in orbital hybridization to destroy the degenerate state, producing an energy low point, and the band structure is not monotonically changing. Mo0.5W0.5Te2 has the smallest energy low point, which means that it is more prone to exciting transitions, which is very advantageous for optoelectronic devices. Since the semiconductor nature of TMDC materials is primarily influenced by the hybridization of d-p orbitals, it is speculated that band gap variations in the A1−xBxY2 system (where A and B are different transition metal elements and Y is a chalcogen element) also do not change monotonically with x. Opening up new possibilities for fine-tuning the band structure of TMDCs materials.
Optical property
In this section, we calculated the extinction coefficient, refractive index, energy loss function, reflectivity, and the real and imaginary parts of the absorption coefficient of the Mo1−xWxTe2 system at x = 0, 0.25, 0.5, 0.75, 1. The optical properties of matter are described by the transverse dielectric function.| ε(ω) = ε1(ω) + iε2(ω) | (2) |
 | (3) |
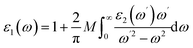 | (4) |
M is the principal value of the integral. Finally, all frequency-related spectra, such as refractive index n(ω), absorption coefficient a(ω), extinction coefficient K(ω), energy loss function index L(ω), and refractive index R(ω), can be directly calculated from the real parts ε1(ω) and imaginary parts ε2(ω).
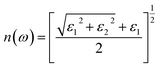 | (5) |
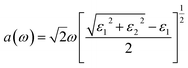 | (6) |
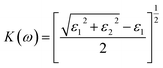 | (7) |
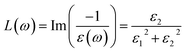 | (8) |
 | (9) |
Fig. 5(a) shows the real part of the dielectric function of the Mo1−xWxTe2 system. The real part reflects the polarization intensity of semiconductor materials under the action of an external electric field as a function of the energy of incident photons. The higher the ε1(ω) value, the stronger the ability of the system to bind charges, therefore increasing its polarizability. When the incident photon energy is 0 eV, the system exhibits a static dielectric constant ε0. It can be seen that when x = 0, 0.25, 0.5, 0.75, and 1, the Mo1−xWxTe2 system exhibits ε0 values of 6.70, 6.61, 6.49, 6.60, and 6.69, respectively. Compared with the values of monolayer MoTe2 or WTe2, ε of Mo1−xWxTe2 all decreases, indicating a decrease in the polarization of the Mo1−xWxTe2 system. In the application of electronic devices, lower polarizability at high frequencies leads to enhanced stability and faster frequency response. It is evident that the alloying system results in a slight reduction in the migration and separation rate of bound electron–hole pairs, as well as lower energy loss. Compared with the original monolayer MoTe2 and WTe2, the alloying system is more suitable for nano-electronic devices. The lowest static dielectric constant is 6.49 at Mo0.5W0.5Te2. The peak value of the Mo1−xWxTe2 system is between monolayer MoTe2 and WTe2. When x = 0.5, it has the lowest polarization, excitation strength, and charge binding ability. Fig. 5(b) shows the imaginary part of the dielectric function of Mo1−xWxTe2. The higher the ε2(ω) value, the greater the probability of photons being absorbed and the stronger the material's photonic absorption energy. ε2(ω) depends on the number of electrons in the excited state, which increases the likelihood of the next transition occurring. The results indicate that monolayer MoTe2 exhibits peaks at 1.749 eV and 2.935 eV, while monolayer WTe2 shows peaks at 2.087 eV and 3.38 eV. These peak values are attributed to the interband transition of the electron Te-5p state to the Mo-4d state and W-5d state. In comparison with monolayer MoTe2 and WTe2, as x = 0.25, 0.5, 0.75, the dielectric peak gradually shifts towards the low energy region.
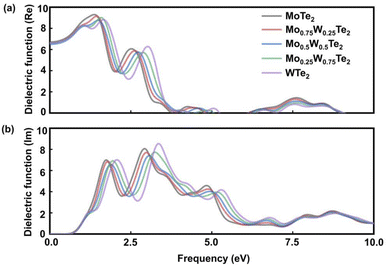 | ||
| Fig. 5 Calculate the (a) real part and (b) imaginary part of the dielectric function of the Mo1−xWxTe2 system when x = 0, 0.25, 0.5, 0.75, 1. | ||
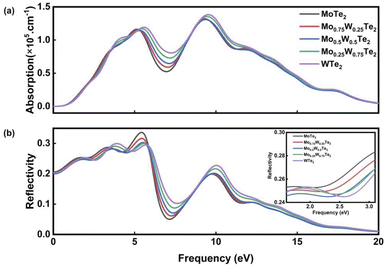
Fig. 6 shows the absorption and reflection coefficients of Mo1−xWxTe2. It can be seen from Fig. 6(a), as x gradually increases, the Mo1−xWxTe2 system exhibits a significant redshift, and its photoreactivity extends to the low-energy region. The alloyed system exhibits a high optical absorption coefficient in the visible region due to its direct band gap structure, enabling optical transitions between overlapping electronic states. The gradually increasing light-absorption capacity can be attributed to the excited state transition of the W-5d state located near the Fermi level in the VBM and CBM. The Mo1−xWxTe2 system maintains the absorbability of ultraviolet light. The enhanced optical absorption for alloyed structure is presumably due to the smaller band gap compared with the corresponding monolayers, which requires less light radiation energy to separate the photo-generated electron–hole pairs.37 As shown in Fig. 6(b), the n(x) of Mo1−xWxTe2 is a function of photon energy. It can be seen that the static reflectance at x = 0, 0.25, 0.5, 0.75, and 1 are 0.207, 0.205, 0.201, 0.203, and 0.204, respectively. As the energy increases, so does the reflectivity. In the energy range above 20 eV, two peaks appear in the alloying system, and the reflectance decreases with increasing energy, gradually approaching 0. It is noteworthy that in the infrared region, Mo0.5W0.5Te2 consistently exhibits the lowest reflectivity within the Mo1−xWxTe2 system, a characteristic that extends to certain visible light regions.
The refractive index R(x) of the Mo1−xWxTe2 system is shown in Fig. 7(a). It can be seen that when x = 0, 0.25, 0.5, 0.75, 1, the static refractive index is 2.581, 2.562, 2.54, 2.563, 2.566, respectively. It is worth noting that the static refractive index of Mo0.5W0.5Te2 is the smallest in the alloy system. The refractive index increases with the increase of energy in the low energy region and reaches a peak value near 1.6 eV. At this time, the peak value mainly comes from the hybridization of Te-5p and W-5d orbits. Then it decreases with the increase of energy. In addition, it can be found that the refraction of high-energy electromagnetic waves is stronger. The extinction coefficient K(x) of the Mo1−xWxTe2 system is shown in Fig. 7(b). The energy range of extinction coefficient variation is 0.9–20 eV, and the extinction coefficient variation is the largest in the energy range of 1.7–9.2 eV. In this interval, the extinction coefficient of alloying systems with different contents has almost the same variation trend. It is worth noting that the peak of extinction coefficient can be effectively reduced when x = 0.5. It can be seen that Mo1−xWxTe2 system can produce strong absorption of light in both visible and ultraviolet regions. This observation is consistent with the loss function image of the Mo1−xWxTe2 system depicted in Fig. 7(c). As illustrated in Fig. 7(c), the two primary loss peaks of the Mo1−xWxTe2 system are situated around 6.1 eV and 12.5 eV, arising from resonance between the Mo-4d and W-5d orbitals and the Te-5p orbitals. In addition, the temperature may affect the photoelectric performance of the Mo1−xWxTe2 system.38
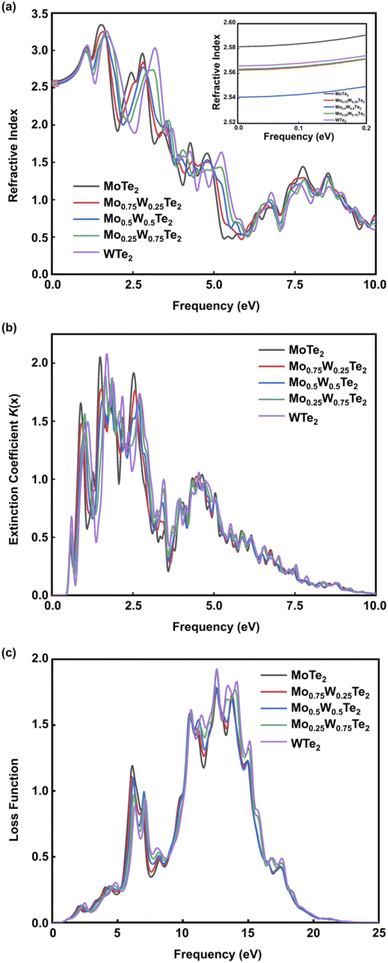 | ||
| Fig. 7 (a) Refractive index of Mo1−xWxTe2 system. (b) Extinction coefficient of Mo1−xWxTe2 system. (c) Loss function of Mo1−xWxTe2 system. | ||
Conclusions
In this work, density functional theory was used to study the Mo1−xWxTe2 system with varying compositions. Through the analysis of phonon spectra, it was found that all modeling systems are thermodynamically stable. The calculated formation energy values reflect that all impurity systems are energetically favorable. These findings provide a theoretical basis for experimental synthesis. Comparing with monolayer MoTe2 and WTe2, Mo1−xWxTe2 shows smaller lattice distortion, which is caused by the valence electron structure and atomic radius outside the Mo–W nucleus. In the analysis of the work function, it is observed that the Mo1−xWxTe2 exhibited lower values than the pure MoTe2 system, which enhanced the transfer of electrons from the bulk to the surface and promoted their participation in photocatalytic reactions. The band gap width of Mo1−xWxTe2 first decreases and then increases with the increase of x. Mo0.5W0.5Te2 bears the narrowest band gap width. The hybridization of Mo-4d orbitals and W-5d with Te-5p orbitals leads to the breaking of the original degeneracy near the Fermi level, resulting in a downward dip in the conduction band. This is visible in the band structures of all studying systems, promoting electron transitions and the generation of photogenerated electron–hole pairs. The static dielectric function value of the monolayer Mo1−xWxTe2 system is higher than that of monolayer MoTe2, indicating that the introduction of dopant generates a polarization electric field, which hinders the recombination of photogenerated electron–hole pairs. According to the analysis of absorption spectra, all alloying systems exhibit a redshift, indicating that the response range to sunlight is expanded after alloying. This extension has been proven to be beneficial for improving photocatalytic ability. Besides, Mo0.5W0.5Te2 exhibits a higher work function and smaller band gap compared to other doped or undoped structures, indicating that alloying in MoTe2 can reduce the Schottky barrier height of WTe2-based transistors and the contact resistance.Data availability
The original crystal structure are downloaded from materials project https://legacy.materialsproject.org/ in cif form. DFT calculations are performed via CASTEP software with certification. The authors will supply the relevant data in response to reasonable requests.Conflicts of interest
There are no conflicts to declare.References
- A. Lherbier, A. R. Botello-Méndez and J.-C. Charlier, Electronic and Transport Properties of Unbalanced Sublattice N-Doping in Graphene, Nano Lett., 2013, 13(4), 1446–1450, DOI:10.1021/nl304351z.
- J. Chen, J. Xi, D. Wang and Z. Shuai, Carrier Mobility in Graphyne Should Be Even Larger than That in Graphene: A Theoretical Prediction, J. Phys. Chem. Lett., 2013, 4(9), 1443–1448, DOI:10.1021/jz4005587.
- N. Ansari, E. Mohebbi and F. Gholami, Nearly Perfect and Broadband Optical Absorption by TMDCs in Cover/TMDC/Spacer/Au/Substrate Multilayers, Appl. Phys. B, 2019, 126(1), 3, DOI:10.1007/s00340-019-7352-3.
- Z. Lin, Y. Liu, Z. Wang, S. Xu, S. Chen, W. Duan and B. Monserrat, Phonon-Limited Valley Polarization in Transition-Metal Dichalcogenides, Phys. Rev. Lett., 2022, 129(2), 027401, DOI:10.1103/PhysRevLett.129.027401.
- M. Rybak, T. Woźniak, M. Birowska, F. Dybała, A. Segura, K. J. Kapcia, P. Scharoch and R. Kudrawiec, Stress-Tuned Optical Transitions in Layered 1T-MX2 (M=Hf, Zr, Sn; X=S, Se) Crystals, Nanomaterials, 2022, 12(19), 3433, DOI:10.3390/nano12193433.
- W. Ai, X. Hu, L. Pan, C. Chen, Y. Wang and X. Shen, Sensing performance of two-dimensional WTe2-based gas sensors, Acta Phys. Sin., 2019, 68(19), 197101, DOI:10.7498/aps.68.20190642.
- Q. Lv, X. Wu, J. Tan, B. Liu, L. Gan, J. Li, Z. Huang, F. Kang and R. Lv, Ultrasensitive Molecular Sensing of Few-Layer Niobium Diselenide, J. Mater. Chem. A, 2021, 9(5), 2725–2733, 10.1039/d0ta09520f.
- C. Wang, M. Jin, D. Liu, F. Liang, C. Luo, P. Li, C. Cai, H. Bi, X. Wu and Z. Di, VSe2 Quantum Dots with High-Density Active Edges for Flexible Efficient Hydrogen Evolution Reaction, J. Phys. D: Appl. Phys., 2021, 54(21), 214006, DOI:10.1088/1361-6463/abe78d.
- S. Wang, C. Ren, H. Tian, J. Yu and M. Sun, MoS2/ZnO van Der Waals Heterostructure as a High-Efficiency Water Splitting Photocatalyst: A First-Principles Study, Phys. Chem. Chem. Phys., 2018, 20(19), 13394–13399, 10.1039/c8cp00808f.
- H. Lin, C. Chang, C. Yu, A. Lee, S. Gu, L. Lu, Y. Zhang, S. Lin, W. Chang, S. Chang and M. Shih, Boost Lasing Performances of 2D Semiconductor in a Hybrid Tungsten Diselenide Monolayer/Cadmium Selenide Quantum Dots Microcavity Laser, Adv. Opt. Mater., 2022, 10(20), 2200799, DOI:10.1002/adom.202200799.
- T. Empante, Y. Zhou, V. Klee, A. Nguyen, I. Lu, M. Valentin, S. Alvillar, E. Preciado, A. Berges, C. Merida, M. Gomez, S. Bobek, M. Isarraraz, E. Reed and L. Bartels, Chemical Vapor Deposition Growth of Few Layer MoTe2 in the 2H, 1T′, and 1T Phases: Tunable Properties of MoTe2 Films, ACS Nano, 2017, 11(1), 900–905, DOI:10.1021/acsnano.6b07499.
- X. Yin, C. Tang, Y. Zheng, J. Gao, J. Wu, H. Zhang, M. Chhowalla, W. Chen and A. Wee, Recent Developments in 2D Transition Metal Dichalcogenides: Phase Transition and Applications of the (Quasi-)Metallic Phases, Chem. Soc. Rev., 2021, 50(18), 10087–10115, 10.1039/d1cs00236h.
- B. Kaur, R. Gupta, S. Dhiman, K. Kaur and C. Bera, Anisotropic Thermoelectric Figure of Merit in MoTe2 Monolayer, Phys. B, 2023, 661, 414898, DOI:10.1016/j.physb.2023.414898.
- H. Weng, X. Dai and Z. Fang, Topological Semimetals Predicted from First-Principles Calculations, J. Phys.: Condens.Matter, 2016, 28(30), 303001, DOI:10.1088/0953-8984/28/30/303001.
- Y. Li, Q. Gu, C. Chen, J. Zhang, Q. Liu, X. Hu, J. Liu, Y. Liu, L. Ling, M. Tian, Y. Wang, N. Samarth, S. Li, T. Zhang, J. Feng and J. Wang, Nontrivial Superconductivity in Topological MoTe2-xSx Crystals, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(38), 9503–9508, DOI:10.1073/pnas.1801650115.
- B. R. Rano, I. M. Syed and S. H. Naqib, Ab Initio Approach to the Elastic, Electronic, and Optical Properties of MoTe2 Topological Weyl Semimetal, J. Alloys Compd., 2020, 829, 154522, DOI:10.1016/j.jallcom.2020.154522.
- J. Xie, F. Xu, T. Wang, Z. Li, G. Fang, H. Dong and X. Guo, Gate Switchable Spin-Orbit Splitting in a MoTe2/WTe2 Heterostructure from First-Principles Calculations, Phys. Rev. B, 2023, 107(16), 165101, DOI:10.1103/PhysRevB.107.165101.
- F. A. Nugera, P. K. Sahoo, Y. Xin, S. Ambardar, D. V. Voronine, U. J. Kim, Y. Han, H. Son and H. R. Gutiérrez, Bandgap Engineering in 2D Lateral Heterostructures of Transition Metal Dichalcogenides via Controlled Alloying, Small, 2022, 18(12), e2106600, DOI:10.1002/smll.202106600.
- S. Susarla, A. Kutana, J. A. Hachtel, V. Kochat, A. Apte, R. Vajtai, J. C. Idrobo, B. I. Yakobson, C. S. Tiwary and P. M. Ajayan, Quaternary 2D Transition Metal Dichalcogenides (TMDs) with Tunable Bandgap, Adv. Mater., 2017, 29(35), 1702457, DOI:10.1002/adma.201702457.
- F. Xiong, X. Zhang, Z. Lin and Y. Chen, Ferroelectric Engineering of Two-Dimensional Group-IV Monochalcogenides: The Effects of Alloying and Strain, J. Materiomics, 2018, 4(2), 139–143, DOI:10.1016/j.jmat.2018.02.005.
- S. M. T.-S. Afrid, S. G. Utsha and A. Zubair, First-principles study on tunable optoelectronic properties of monolayer Mo1−xWxSe2 alloys and defect engineered electronic properties of Mo1−xWxSe2 alloys, Phys. Scr., 2023, 98(10), 104002, DOI:10.1088/1402-4896/acf352.
- H. Yu, H. Yan, H. Li, Z. Li and S. Yin, Spatially graded millimeter sized Mo1−xWxSe2 monolayer alloys: synthesis and memory effect, ACS Appl. Mater. Interfaces, 2021, 13(37), 44693–44702, DOI:10.1021/acsami.1c09176.
- R. Ghosh, Large area chemical vapor deposition growth of monolayer MoSe2 and its controlled sulfurization to MoS2, J. Mater. Res., 2016, 31, 917–922, DOI:10.1557/jmr.2016.7.
- H.-P. Komsa and A. V. Krasheninnikov, Two-Dimensional Transition Metal Dichalcogenide Alloys: Stability and Electronic Properties, J. Phys. Chem. Lett., 2012, 3(23), 3652–3656, DOI:10.1021/jz301673x.
- B. Aslan, I. M. Datye, M. J. Mleczko, K. Sze Cheung, S. Krylyuk, A. Bruma, I. Kalish, A. V. Davydov, E. Pop and T. F. Heinz, Probing the Optical Properties and Strain-Tuning of Ultrathin Mo1–xWxTe2, Nano Lett., 2018, 18(4), 2485–2491, DOI:10.1021/acs.nanolett.8b00049.
- M. D Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-Principles Simulation: Ideas, Illustrations and the CASTEP Code, J. Phys.: Condens.Matter, 2002, 14(11), 2717, DOI:10.1088/0953-8984/14/11/301.
- M. Sun, Q. Ren, Y. Zhao, J.-P. Chou, J. Yu and W. Tang, Electronic and Magnetic Properties of 4d Series Transition Metal Substituted Graphene: A First-Principles Study, Carbon, 2017, 120, 265–273, DOI:10.1016/j.carbon.2017.04.060.
- H. Katsukura, T. Miyata, K. Tomita and T. Mizoguchi, Effect of the van Der Waals Interaction on the Electron Energy-Loss near Edge Structure Theoretical Calculation, Ultramicroscopy, 2017, 178, 88–95, DOI:10.1016/j.ultramic.2016.07.012.
- A. Ohtake, X. Yang and J. Nara, Structure and Morphology of 2H-MoTe2 Monolayer on GaAs (111)B Grown by Molecular-Beam Epitaxy, npj 2D Mater. Appl., 2022, 6(1), 35, DOI:10.1038/s41699-022-00310-y.
- C. Lee, E. Cruz-Silva, L. Calderin, M. Nguyen, M. Hollander, B. Bersch, T. Mallouk and J. Robinson, Tungsten Ditelluride: A Layered Semimetal, Sci. Rep., 2015, 5, 10013, DOI:10.1038/srep10013.
- S. McDonnell, A. Azcatl, R. Addou, C. Gong and R. M. Wallace, Hole Contacts on Transition Metal Dichalcogenides: Interface Chemistry and Band Alignments, ACS Nano, 2014, 8(6), 6265–6272, DOI:10.1021/nn501728w.
- D. Zhang, et al., Solar Cells Based on Two-Dimensional WTe2/PtXY (X, Y = S, Se) Heterostructures with High Photoelectric Conversion Efficiency and Low Power Consumption, ACS Appl. Energy Mater., 2021, 4, 357–364, DOI:10.1021/acsaem.0c0228.
- Tunable Schottky contact in graphene/InP3 van der Waals heterostructures, ScienceDirect, https://www.sciencedirect.com/science/article/abs/pii/S016943322100684X, accessed 2024-08-14.
- D. Zhang, Y. Hu, H. Zhong, S. Yuan and C. Liu, Effects of Out-of-Plane Strains and Electric Fields on the Electronic Structures of Graphene/MTe (M = Al, B) Heterostructures, Nanoscale, 2019, 11(29), 13800–13806, 10.1039/C9NR04287C.
- Z. Chen, W. Guo, J. Ye, K. Zhong, J. Zhang and Z. Huang, Tunable Electronic Structure in Twisted WTe2/WSe2 Heterojunction Bilayer, AIP Adv., 2022, 12(4), 045315, DOI:10.1063/5.0086024.
- Q. Luo, S. Yin, X. Sun, Y. Tang, Z. Feng and X. Dai, Two-Dimensional Type-II XSi2P4/MoTe2 (X = Mo, W) van Der Waals Heterostructures with Tunable Electronic and Optical Properties, New J. Chem., 2022, 46(40), 19407–19418, 10.1039/D2NJ03809A.
- D. Zhang, Q. Gao, Y. Chen, Y. Xia, H. Wang, H. Wang and Y. Ni, Tunable Electronic Properties and Potential Applications of BSe/XS2 (X=Mo, W) van Der Waals Heterostructures, Adv. Theory Simul., 2020, 3(10), 2000144, DOI:10.1002/adts.202000144.
- C. R. Zhu, K. Zhang, M. Glazov, B. Urbaszek, T. Amand and Z. W. Ji, et al., Exciton valley dynamics probed by kerr rotation in WSe2 monolayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 161302, DOI:10.1103/PhysRevB.90.161302.
| This journal is © The Royal Society of Chemistry 2024 |