DOI:
10.1039/D4RA04511D
(Paper)
RSC Adv., 2024,
14, 24240-24249
pH-induced morphological transition of aggregates formed by miktoarm star polymers in dilute solution: a mesoscopic simulation study
Received
20th June 2024
, Accepted 29th July 2024
First published on 2nd August 2024
Abstract
The self-assembly of miktoarm star polymers μ-Ai(B(D))jCk in a neutral solution and the pH-responsive behaviors of vesicles and spherical micelles in an acidic solution have been investigated by DPD simulation. The results show that the self-assembled morphologies can be regulated by the lengths of pH-responsive arm B and hydrophilic arm C, leading to the formation of vesicles, discoidal micelles, and spherical micelles in a neutral solution. The dynamic evolution pathways of vesicles and spherical micelles are categorized into three stages: nucleation, coalescence, and growth. Subsequently, the pH-responsive behaviors of vesicles and spherical micelles have been explored by tuning the protonation degree of pH-responsive arm B. The vesicles evolves from nanodisks to nanosheets, then to nanoribbons, as the protonation degree increases, corresponding to a decrease in pH value, while the spherical micelles undergoes a transition into worm-like micelles, nanosheets, and nanoribbons. Notably, the electrostatic interaction leads the counterions to form a regular hexagonal pattern in nanosheets, while an alternative distribution of charged beads has been observed in nanoribbons. Furthermore, the role of the electrostatic interaction in the morphological transition has been elucidated through the analysis of the distribution of positive and negative charges, as well as the electrostatic potential for associates.
1 Introduction
Miktoarm star polymers have attracted great attention due to their unique self-assembly behavior and potential applications in fields such as drug delivery, nanoreactors for catalysis, and biomaterials.1–7 Compared with linear polymers, the diversity in chemical composition, molecular weight, and functionality of miktoarm star polymers endows them with unique supramolecular assembly capabilities.6 For instance, a variety of nonconcentric multicompartment micelles such as hamburgers, segmented worms, and polygonal bilayer sheets have been observed in aqueous solutions of ABC miktoarm star polymers, which can be tuned by varying the relative length of each block and the interaction between arms.8
Stimuli-responsive miktoarm star polymer can be constructed by arm-first or core-first methods.6,9 A variety of stimuli have been exploited to control the self-assembly behavior by alterations in their chemical or physical properties, such as temperature,10,11 light12 and pH responsive.13,14 For example, miktoarm star polymers containing nitrogen on its constituent monomers usually exhibit specific pH responsiveness due to the protonation. Poly[2-(diethylamino)ethyl methacrylate] (PDEA) has been used as an acidic pH sensitive polymer to synthesize pH-sensitive amphiphilic A2(BC)2 miktoarm star polymers with different block ratios.13 In particular, star-[poly(ethylene glycol)-polystyrene-poly[2-(N,N-diethylamino)ethyl methacrylate]] (μ-PEG-PS-PDEA) with a series of molecular weight (Mn) of PDEA chains were synthesized and their assemblies changed from the large compound vesicles into different nanostructures determined by the Mn of PDEA after CO2 stimulation.15 Besides, poly(L-histidine) (PHIS) have also been used as a pH-responsive polymer due to the presence of nitrogen of imidazole ring on its constituent monomers.16,17 A pH-sensitive polymersomes formed by miktoarm star polymer PEG-PHIS2 can change to cylindrical micelles, spherical micelles, and finally unimers with the decrease of pH value as a result of the gradual protonation of the imidazole groups on PHIS chains.
The mesoscopic theory and simulation become a very suitable way for the research of the self-assembly18–29 and pH-responsive behavior30–32 of star polymers. The dynamic density functional theory has been applied to investigate the equilibrium phase patterns of star block copolymers, and some novel ordering microstructures were observed.18 The self-assembly behavior of symmetric star-like block copolymers (Ax)y(Bx)yC in dilute solution was investigated by Brown dynamics simulation.24,25 It is found that the lamellar worm-like structures can be assembled via the aggregation of soft Janus particles and the morphology can also be influenced by the incompatibility between the two components and solvent conditions. With the increase of solvophobic arms of miktoarm polymers, unique multicompartment aggregates including nanosheets and vesicles composed of lateral patterns were formed by miktoarm star terpolymers21–23 and quaterpolymers,27 respectively. These simulations systematically analyzed the effect of polymer molecular composition, arm length, and interaction strength between arms on the self-assembled nanostructures, which provided a strategy to control the self-assembled structure for experimental research. Furthermore, the complicated kinetics pathway of the multicompartment vesicles formed from miktoarm star terpolymers has been discussed in detail through external potential dynamics (EPD)22 and dissipative particle dynamics(DPD)23 simulations. Meanwhile, the effect of pH on the morphological transition33–35 of polymeric micelles and the drug release36–40 from drug-loaded micelles have been studied by tuning the degree of protonation and ionization of the pH-sensitive polymers in acidic and alkaline environments. For example, Nie et al. found that the degree of swelling of micelles formed by pH-sensitive four-arm star triblock polymers increases as the pH value decrease from 7.4 to 5.37 Another notable example is the study of drug-loaded micelles assembled by A2(BC)2 miktoarm star polymers, where the authors found that the drug release process via a swelling, demicellization, and releasing mechanism.13
The tumor's extracellular pH is lower than those of most normal tissues and blood stream (pH 7.4) ranging of approximately 6–7, while a more pronounced decline in pH can be found in the tumor's intracellular compartments, such as endosomes (pH 5.5) and lysosomes (pH 4.5).41 However, as an excellent targeting drug carrier the phase behaviour of miktoarm star polymers in the aqueous solution at different pH environments is rarely explored through computer simulation. In addition, the endeavor was mostly given to the study of pH-responsive behavior of spherical micelles, while there are few results on vesicle7,14 formed by miktoarm star polymers. Finally, the effect of the electrostatic interaction on the pH-responsive behavior is also a fascinating issue. The pH-responsive mechanism of aggregates self-assembled by miktoarm star polymers still need to be demonstrated in depth. Motivated by the context described above, we have carried out a series of DPD simulation to explore the mechanism of morphological transition. The effect of the length of pH-responsive and hydrophilic arms on the aggregates formed by miktoarm star terpolymers in a neutral aqueous solution has been investigated, as well as their dynamics evolutions. Next we focus on the pH-responsive behavior for vesicle and spherical micelle by tuning the protonation degree of pH-responsive arm. As a result the aggregates formed in a neutral condition can transform to three kinds of associates in an acid environment. The role of electrostatic interaction in morphological transition has been discussed by the distribution of the charged beads and the electrostatic potential for associates.
2 Method and model details
2.1 DPD theory
DPD simulation method42–44 has been extensively applied to investigate the phase behavior of complex fluids, such as polymer solutions, colloidal solutions, liquid crystals, and biological systems. In the method, one DPD bead represents a group of atoms and the motion of all beads obey Newton's equation of motion. The force on a bead i include conservative force![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Cij, dissipative force
Cij, dissipative force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Dij, random force
Dij, random force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Rij. The three forces vanish beyond a certain cutoff radius rc, whose value is usually set to one unit of length in simulations. The conservation force for non-bonded beads is defined by soft repulsion:
Rij. The three forces vanish beyond a certain cutoff radius rc, whose value is usually set to one unit of length in simulations. The conservation force for non-bonded beads is defined by soft repulsion:| |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Cij = aijωC(rij) Cij = aijωC(rij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij = aij(1 − rij/rc) ij = aij(1 − rij/rc)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij ij
| (1) |
where aij is the interaction parameter between beads i and j, which reflects the chemical characteristics of interacting beads; ωC(rij)is the weight function, and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j, rij = |
j, rij = |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij|,
ij|, ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij/rij. The dissipative force corresponding to a frictional force depends on both the position and relative velocities of the beads and the random force is a random interaction between bead i and its neighbor bead j. These two forces act together as the inherent thermostat that determines the system temperature and are expressed by
ij/rij. The dissipative force corresponding to a frictional force depends on both the position and relative velocities of the beads and the random force is a random interaction between bead i and its neighbor bead j. These two forces act together as the inherent thermostat that determines the system temperature and are expressed by| |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Dij = −γωD(rij)( Dij = −γωD(rij)(![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) ij· ij·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij) ij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij = −γ(1 − rij/rc)2( ij = −γ(1 − rij/rc)2(![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) ij· ij·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij) ij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij ij
| (2) |
| |
 | (3) |
where ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) ij =
ij = ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) i −
i − ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) j, γ and σ define the amplitude of the dissipative and the random forces, ωD(rij) and ωR(rij) are the weight functions, ξij is a random number with zero mean and unit variance. To satisfy the equilibrium Gibbs–Boltzmann distribution and the fluctuation-dissipative theorem, the following two relations are required:
j, γ and σ define the amplitude of the dissipative and the random forces, ωD(rij) and ωR(rij) are the weight functions, ξij is a random number with zero mean and unit variance. To satisfy the equilibrium Gibbs–Boltzmann distribution and the fluctuation-dissipative theorem, the following two relations are required:| | |
ωD(rij) = [ωR(rij)]2, σ2 = 2γkBT
| (4) |
The combination with the bead-spring model makes DPD very appropriate for simulations on structure and dynamics of polymer system. The intramolecular interaction between bonding monomers is given by harmonic forces. If beads i and j are connected, the bond force is given by
| |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Sij = −ks(rij − r0) Sij = −ks(rij − r0)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij ij
| (5) |
where
ks is the spring constant and
r0 is the equilibrium bond length.
In order to explore the phenomena of charged system at mesoscopic level, the inclusion of the electrostatic interaction in DPD method is essential. According to González-Melchor,45 the electrostatic force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Eij and electrostatic potential UEij are expressed as
Eij and electrostatic potential UEij are expressed as
| |
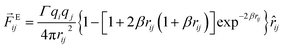 | (6) |
| |
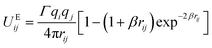 | (7) |
where
Γ =
e2/
kBTε0εrrc,
e is the elementary charge;
ε0is the vacuum permittivity and
εr is the relative permittivity of medium;
q is the bead charge;
β = 5
rc/8
λ,
λ is the decay length of charge in the Slater smearing charge distribution which means that bead charge spread out over a finite volume:
| |
ρ(r) = q![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2r/λ)/πλ3 exp(−2r/λ)/πλ3
| (8) |
In fact, the repulsive interaction parameter aij between different DPD beads is determined by the underlying atomistic interaction when the coarse-grained model of molecule has been established. Groot and Warren44 proposed the linear relationship with Flory–Huggins χij parameter for ρ = 3.0
where
aii is repulsive parameter between the same beads and equals to 25. Flory–Huggins parameter
χij can be obtained from molecular simulation or experimental measurements.
2.2 Model and parameters
The DPD model of miktoarm star polymers with a pH-responsive arm in aqueous solution is described in this section. Considering the application of miktoarm star polymer in drug delivery, poly(caprolactone) (PCL) and poly(ethylene glycol) (PEG) is selected as a hydrophobic and hydrophilic arm owing to good biocompatibility.46 Referring to the coarse-grained method by Lin et al.,11 PCL and PEG are divided into beads A and C, respectively. PDEA is selected as pH-responsive arm and divided into two kinds of beads, B in the main chain and D in the side chain. As shown in Fig. 1, the miktoarm star polymer is named as μ-Ai(B(D))jCk, where i, j, and k are the length of the hydrophobic, pH-responsive, and hydrophilic arm, respectively. In an acidic condition, bead D is protonated and represented by bead DH. A hydrophobic center of miktoarm star terpolymer is represented by a single bead O. One bead W stands for three water molecules. To preserve charge neutrality in the solution, counterions CI are added into solution when the protonation of bead D takes place.
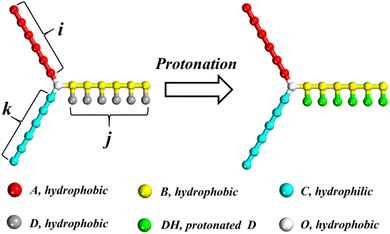 |
| | Fig. 1 Schematic illustration of the miktoarm star polymer μ-Ai(B(D))jCk with a pH-responsive arm. White, red, yellow, cyan, gray and green represent O, A, B, C, D and DH beads, respectively. The meaning of colors in this figure is suitable for all figures in this paper. | |
The choice of the interaction parameters aij in Table 1 in this work is made following the calculation of a previous publication by Lin et al.,13 who carried out molecular dynamics simulation to obtain Flory–Huggins parameters. Using these parameters and combining with experiments, their DPD simulations have been applied to investigate the structure–property relationship of micelles formed by A2(BC)2 miktoarm star polymers. The parameters aij of bead CI with other beads are identical to those with bead W except that bead CI carries one negative unit charge.34,47 The setting of parameters aij of bead DH with other beads are same with bead D except that bead DH carries one positive unit charge. The relationship between pH value and protonation degree of pH-responsive arm is built by the Henderson–Hasselbalch formula:37,48
| |
 | (10) |
where
αH+ is the protonation degree and p
Ka = 6.9. It means that
αH+ depends on the pH value of the solution. At the same pH environment,
αH+ remain unchanged when the system reaches an equilibrium state. At a neutral environment (pH = 7.4), there is no protonated bead D and the protonation degree equals to 0. With the decrease of pH value, more beads D obtain protons and the protonation degree reaches greatest at pH = 5.0.
Table 1 The interaction parameters aij in this work (unit: kBT)
| aij |
A |
B |
C |
D |
DH |
O |
W |
CI |
| A |
25 |
|
|
|
|
|
|
|
| B |
27 |
25 |
|
|
|
|
|
|
| C |
37 |
28 |
25 |
|
|
|
|
|
| D |
26 |
30 |
46 |
25 |
|
|
|
|
| DH |
26 |
30 |
46 |
25 |
25 |
|
|
|
| O |
28 |
35 |
53 |
26 |
26 |
25 |
|
|
| W |
53 |
35 |
26 |
37 |
37 |
82 |
25 |
|
| CI |
53 |
35 |
26 |
37 |
37 |
82 |
25 |
25 |
A simulation box of 40 × 40 × 40 rc3 with periodic boundary condition is sufficient to avoid the finite size effects, containing 1.92 × 105 beads at ρ = 3. The integration of the equation of motion was carried out using the velocity-Verlet algorithm with a time step Δt = 0.05. We select the cutoff radius, the bead mass, and the temperature as the units of the simulation system, i.e., rc = m = kBT = 1.0. The friction coefficient γ and the noise amplitude σ were set to be 4.5 and 3.0, respectively. For the harmonic spring potential, the spring constant ks = 4 and the equilibrium distance r0 = 0.49 The decay length λ = 0.67 and the smearing coefficient β = 0.929 is commonly used, which represents a large part of the smeared charge outside the DPD bead.49 The permittivity coupling constant Γ is set as 13.87, which corresponds to an aqueous environment. In the Ewald sum approach, the electrostatic force was truncated at rcele = 3.0, real-space convergence parameter α = 0.975, and reciprocal vector range nmax = (5, 5, 5),50 which are chosen empirically for computational efficiency.45,51 The choice of the electrostatic parameters in our simulations is based on significant theoretical and simulation results, and the simulation results are not a consequence of this selection. The simulations were performed in a canonical ensemble and carried out with DL_MESO mesoscopic simulation package52 and the images were made with VMD53 software.
3 Results and discussion
In this section, we fix all the interaction parameters in Table 1 and firstly study the effect of the length of pH-responsive and hydrophilic arm (by varying j and k from 5 to 20) on the morphologies and their dynamics evolution of miktoarm star polymer μ-Ai(B(D))jCk in the neutral(αH+ = 0) dilute solution. To simplify the parameter space, the length i of hydrophobic arm A is fixed at 10 and the volume fraction of polymers is set as Φp = 0.1. Secondly, we further discuss the pH-responsive behavior for vesicles and spherical micelles by tuning the protonation degree αH+ from 0 to 100%, corresponding to the decline in pH from 7.4 to 5.0. The role of the electrostatic interaction in the morphology transition has been demonstrated by the radial distribution function of positive and negative charges and the electrostatic potential for associates.
3.1 Morphological phase diagram of miktoarm star polymers in a neutral solution
Huo et al. found that when the length of pH-responsive arm PDEA in amphiphilic star polymers μ-PEG-PS-PDEA changes, polymers self-assembled into vesicles or spherical micelles with different sizes.15 On the other hand, the aggregate geometry of polymers in solution can be regulated by the hydrophilic mass fraction.37 In view of the above two factors, we firstly explore the effect of the length of pH-responsive and hydrophilic arms on the morphologies and their dynamics evolution. Fig. 2 gives the morphological phase diagram of μ-Ai(B(D))jCk in the neutral solution as a function of two lengths j and k. As shown in Fig. 2, vesicle, discoidal and spherical micelles are observed in our simulation and the phase diagram is mainly occupied by spherical micelles. As the length k of the hydrophilic arm C decreases from 20 to 5 at j = 20, the self-assembled structure changes from spherical micelles to discoidal micelles and then to vesicles. However, there is no too much effect of the length j of pH-responsive arm changes on the morphologies in the phase diagram. The distributions of hydrophobic and hydrophilic arms in three kinds of aggregates are shown by the sectional view in Fig. 2(a)–(c). Due to the repulsive interaction between hydrophobic arms is weak (aAB = 26 and aAD = 27), multicompartment structure does not appear in our results and the hydrophobic domains of aggregates are composed by the mixture of arms A, B and D in the three kinds of aggregates.
 |
| | Fig. 2 Left, morphological phase diagram of μ-Ai(B(D))jCk in a neutral solution and corresponding morphologies represented by the symbols. Right, the morphologies and sectional images for three kinds of aggregates. (a)–(c) refer to the vesicle, disk, and sphere structures, respectively. | |
When the length j of the pH-responsive arm increases from 5 to 20 at k = 5 in Fig. 2, only vesicles can be formed by star polymers in solution. In order to understand the influence of the length j on vesicles, the density profiles of four kinds of beads A, B, C and D with the radii around the mass center of vesicle were calculated and shown in Fig. 3(a). According to the density profiles, the inner and outer parts are hydrophilic layers formed by arm C, and the middle part is hydrophobic domain composed by arm A and arm B grafted by D. With the increase of length j, the left peak position in density profile of bead C translocates from 4 to 2, indicating that the cavity size in vesicle decreases obviously. Additionally, there are significant difference in the density profiles of hydrophobic domain when the length j changes. At j = 5 in Fig. 3(a), the center of hydrophobic domain is occupied by bead A and the double peaks in density profiles of beads B and D show that arm B grafted by D is closer to the edge of the hydrophobic domain. Interestingly, the reversal of density profiles in hydrophobic domain of vesicles takes place when the mass fraction of pH-responsive arm increases. At j = 15 and 20 in Fig. 3(b) and (c), the center of hydrophobic domain is occupied by arm B grafted by D, and the double peaks in density profiles of bead A show that arm A is squeezed to the edge of the hydrophobic domain. The vesicle size is characterized by the gyration radius Rg of aggregate:54
| |
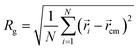 | (11) |
where
N is the total number of beads in the aggregate;
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i
i and
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) cm
cm are the position vector of a bead and the center of mass of the aggregate, respectively. In our simulation, polymer chains are considered as a part of aggregate if the smallest distance between their two hydrophobic beads is less than 1.5.
Fig. 3(d) shows that the
Rg of vesicle decreases from 9.24 to 9.05 with the increase of
j. We notice that as the arm length increases from 5 to 15 there is a sharp decrease in the
Rg value. However, when the arm length increases from 15 to 20, the decrease in
Rg is comparatively much smaller. The physical reason behind this behavior is closely related to the composition ratio
ϕ of hydrophobic beads in miktoarm polymer, which can be calculated by the following formula:
| |
 | (12) |
where
i,
j, and
k are the length of the hydrophobic arm, pH-responsive arm, and hydrophilic arm respectively. According to eqn (12) at
i=10 and
k=5, we plot the curve of
ϕ with the arm length
j in
Fig. 3(d). It can be seen that with the increase of
j,
ϕ changes nonlinearly. From 5 to 15,
ϕ increases rapidly, and the corresponding
Rg decreases rapidly. From 15 to 20,
ϕ increases slowly, corresponding to a slow decrease in
Rg. It follows that the nonlinear increase of the composition ratio
ϕ of hydrophobic beads leads to the nonlinear decrease of
Rg.
 |
| | Fig. 3 The density profiles of four kinds of beads A, B, C and D with the radii around the mass center of vesicle at arm lengths k = 5: (a) j = 5; (b) j = 10; (c) j = 15. (d) The variation of Rg and the composition ratio ϕ of hydrophobic beads in miktoarm polymer with the arm length j. | |
In order to give in-depth understanding on aggregates formed by miktoarm star polymers μ-Ai(B(D))jCk, the dynamic evolutions of vesicles and spherical micelles, have been investigated by calculating mean gyration radius 〈Rg〉 and number of aggregates at different stages. Firstly, Fig. 4(a) gives the variations of 〈Rg〉 and number of aggregates with simulation steps for vesicles formed at arm lengths j = 15 and k = 5. Throughout the dynamic process, 〈Rg〉 increases while number of aggregates decreases in a stepwise way. The nucleation stage takes place in a very short period from the disorder initial state to 2.0 × 104 steps in Fig. 4(a1), and polymers in solution form many small spherical micelles and 〈Rg〉 is about 3. The following stage is from 2.0 × 104 to 1.4 × 105 steps and small spherical micelles begin to coalesce into lamella which can be seen in Fig. 4(a1) and then fold into small vesicle in Fig. 4(a2). Ultimately from 1.4 × 105 to 2.0 × 105 steps, small vesicle grows into the stable vesicle in Fig. 4(a3) by fusing the residual spherical micelles. After 2.0 × 105 steps the value of 〈Rg〉 and the number of aggregates almost keep constants, which clearly shows that the system reaches equilibrium. These results indicate that the formation of vesicles follow three stages, which are of nucleation, coalescence, and growth. Secondly, Fig. 4(b) gives the variations of 〈Rg〉 and number of aggregates with simulation steps for spherical micelles formed at arm lengths j = 20 and k = 15. The dynamic evolution of spherical micelles also undergoes nucleation, coalescence, and growth according to Fig. 4(b1)–(b3). At 2.0 × 104 steps in Fig. 4(b1), it can be seen that small spherical micelles begin to coalesce into worm-like micelle. After the coalescence of small spherical micelles, a longer stable period can be seen from 1.0 × 105 to 3.2 × 105 steps, because a longer hydrophilic arm C can better screen the influence of solvents on hydrophobic domain and make the micelles more stable. At 3.2 × 105 steps, 〈Rg〉 increases from about 5.3 to 6.1 due to the fusion of spherical micelles. In a word, the different evolution stages of vesicle and spherical micelle are accurately divided according to the variations of 〈Rg〉 and number of aggregates with simulation steps and they both obey the same formation mechanism, that is, nucleation, coalescence and growth.
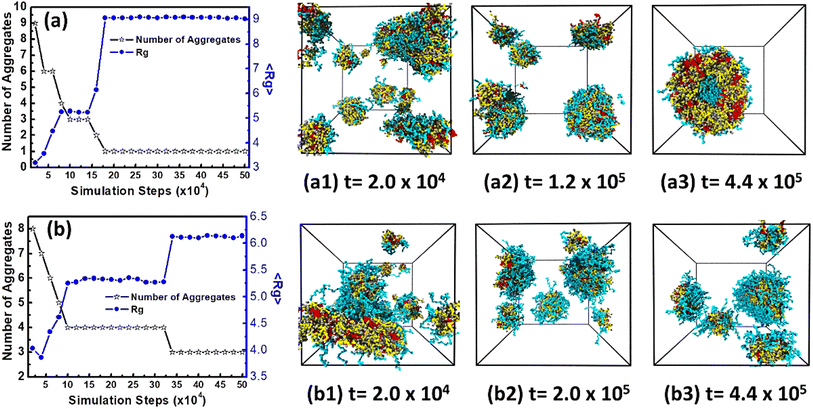 |
| | Fig. 4 The variations of number of aggregates and mean gyration radius 〈Rg〉 with simulation step and the corresponding dynamic evolution: (a) vesicle formed at arm lengths at j = 15 and k = 5; (b) spherical micelle formed at arm lengths at j = 20 and k = 15. Solvents and beads O are omitted for clarity. | |
3.2 Effect of pH values on vesicles and spherical micelles
The vesicles formed at arm lengths j = 15 and k = 5 in Fig. 4(a3) are selected to study the mechanism of morphological transition at different pH values, and five values of αH+ (i.e. 20%, 40%, 60%, 80%, and 100%) are simulated, corresponding to the decline in pH value from 7.4 to 5.0. The initial and equilibrium snapshots for systems with αH+ = 20%, 60%, and 100% are presented in Fig. 5(a)–(c), respectively. When αH+ = 20% in Fig. 5(a1), green protonated beads DH can be seen in the hydrophobic wall of vesicles. The electrostatic interaction makes the counterions CI with negative charge in solution enter the vesicle, resulting in the collapse of vesicles and transforming to a nanodisks as shown in Fig. 5(a2). In order to explicitly show the microstructure of nanodisks, the hydrophobic beads A, B, and D are given in Fig. 5(a3), and the charged beads DH and CI are shown in Fig. 5(a4), respectively. It is worth mentioning that beads CI in nanodisks gather into a few small negative charge domains surrounding by protonated beads DH. With the increase of αH+ to 60% in Fig. 5(b1), the number of beads DH is more than beads D in arm B of polymers and more beads CI exists in solution, which means that the electrostatic interaction becomes stronger in the system. As shown in Fig. 5(b2)–(b4), when αH+ = 60% vesicles changes into nanosheets and the negative charge domains formed by beads CI embedded in nanosheets in a regular hexagonal arrangement. When αH+ = 100% in Fig. 5(c1), a full protonation takes place in the pH-responsive arm B of polymers and the number of beads CI in solution reaches at maximum. Under the strong electrostatic interaction, vesicles transform to the nanoribbons as shown in Fig. 5(c2)–(c4). Meanwhile, some small droplets formed by polymers have also been observed in Fig. 5(c2), which are a part of products of dissociation. According to Fig. 5(c4), beads CI and DH are alternatively distributed in nanoribbons, and the hydrophobic domains are connected by beads CI. Interestingly, a similar morphological transition has been observed in experiments.15 By purging CO2, the PDEA protonation of miktoarm star polymers μ-PEG-PS-PDEA makes vesicles or spherical micelles change into nanosheets, nanoribbons and nanodisks with the increase of Mn of PDEA. The similar results in experiment and simulation originate from the same physical mechanism, i.e. the introduction of the electrostatic interaction. We think that with the increase of αH+, the electrostatic interaction gradually overcomes the hydrophobic interaction to dissociate vesicle, and the ordered arrangement of protonation beads DH and counterions CI builds up a basic frame of the association in equilibrium.
 |
| | Fig. 5 Morphological transition of vesicle at different protonation degrees: (a) αH+ = 20%; (b) αH+ = 60%; (c) αH+ = 100%. Solvents and beads O are omitted for clarity. | |
For further discussion on the associations in an acidic condition in Fig. 5, the radial distribution function g(r) is used to analyze the distribution of polymer beads and charged beads for characterization of the compatibility of different components. The function g(r) gives the probability of finding a pair of beads with a distance r apart. The r corresponding to peak of RDF curve reflects the distance between two kinds of beads. Fig. 6(a) shows the radial distribution function g(r) between hydrophobic beads A and B at different values of αH+. In the systems with αH+ = 20% to 60%, the first pronounced peak at r = 0.95 and the secondary peak at r = 1.75 in RDF curves show that most of beads B appears very close to beads A, which implies that the miscibility between beads A and B is not affected by the electrostatic interaction at the relative weak acid condition. However, in the systems with αH+ = 80% and 100%, the first peak follows by a broad and slowly decaying shoulder in the region from 2 to 8, which means that the microscopic phase separation between beads A and B occurs with the enhancement of the electrostatic interaction. From Fig. 6(a), we also find that the RDF curve for αH+ = 20% decays more sharply compared to other αH+ values. αH+ = 20% represents weak protonation of pH-responsive arm and weak electrostatic interaction, and vesicles transforms into nanodisks. Because the miktoarm polymers of nanodisk still very concentrated in solution, beads A and B distribute in a small space, and the peak value of gAB(r) is high and decreases rapidly with the increase of coordinate r. As the degree of protonation increases, the electrostatic effect becomes stronger, vesicles change into nanosheets or nanoribbons, the distribution range of beads A and B in solution becomes larger, so the peak value of gAB(r) shifts to the right and decays slowly with the increase of coordinate r. From this observation, we think that the weak electrostatic interaction (high pH value) leads to the formation of nanodisks, while the strong electrostatic interaction (low pH value) make vesicles transform into nanosheets or nanoribbons. The g(r) at long distance in Fig. 3(a) does not approaches 1, which reflects that the distribution of the miktoarm polymers of nanodisks, nanosheets, and nanoribbons in solution is nonuniform in the simulation box. The function g(r) between charged beads CI and DH is shown in Fig. 6(b). The shape of RDF curves in Fig. 6(b) present an oscillating pattern and the highest peak appears at about r = 4.0. The oscillating pattern is closely associated with the ordered arrangement of charged beads CI and DH in Fig. 5(a4)–(c4). At αH+ = 20%, the RDF curve is slightly shifted to left side, and the peak at about r = 4 is highest in all curves, which indicates that the charged beads arrange more compactly in nanodisks in Fig. 5(a4). The rest of RDF curves are almost same, demonstrating that the distance between beads CI and DH is same both in nanosheets and in nanoribbons.
 |
| | Fig. 6 Radial distribution functions at different protonation degrees when arm lengths j = 15 and k = 5: (a) gA–B(r), pairs of beads A and B; (b) gCI–DH(r), pairs of beads CI and DH. | |
The morphological transition of spherical micelles depicted in Fig. 4(b3) has been investigated at different αH+ values, as shown in Fig. 7(a)–(c). At αH+ = 20%, spherical micelles transform into a worm-like micelles in Fig. 7(a2), and several spherical negative charge domains are observed in Fig. 7(a4). When αH+ is increased to 60%, spherical micelles turn into nanosheets, as shown in Fig. 7(b2), with a similar arrangement of the negative charge domains as in Fig. 5(b4). Upon further increase in αH+ to 100%, the full protonation of beads D results in the formation of a long nanoribbon alongside small droplets in Fig. 7(c2)–(c4). It can be clearly seen that the long nanoribbon exhibits an alternative arrangement of beads CI and DH. Furthermore, the RDF curves at different values of αH+ are presented in Fig. 8. Comparing to Fig. 6(a), the peak position remains unchanged for all curves in Fig. 8(a), which means the miscibility between beads A and B is not changed after the protonation. However, the gradually decreasing peak height in all curves in Fig. 8(a) implies the association size at equilibrium becomes larger with the increase of αH+. In addition, the distribution of charged beads has been analyzed by the curves gCI–DH(r) in Fig. 8(b). The first peak position is consistently at r = 4 for all curves, suggesting that the distance between beads CI and DH is not related to αH+. However, the secondary peak is clearly seen when αH+ is larger than 60%, corresponding to the ordered arrangement of charged beads, i.e. the hexagonal arrangement in nanosheets and the alternative arrangement in nanoribbons.
 |
| | Fig. 7 Morphological transition of spherical micelle at different protonation degrees: (a) αH+ = 20%; (b) αH+ = 60%; (c) αH+ = 100%. Solvents and beads O are omitted for clarity. | |
 |
| | Fig. 8 Radial distribution functions at different protonation degrees when arm lengths j = 20 and k = 15: (a) gA–B(r), pairs of beads A and B; (b) gCI–DH(r), pairs of beads CI and DH. | |
Finally, the effect of the electrostatic interaction on the morphological transition is analyzed by examining by the electrostatic potential U(r) for associates as a function of distance from their center of mass. The U(r) for associates in Fig. 5 and 7 is calculated based on the electrostatic interaction between two point charges (as described in eqn (7)), and given in Fig. 9. The electrostatic potential curves for αH+ = 20% and 40% in Fig. 9(a) and (b) are depicted above the zero axis, suggesting that a small amount of counterions is not enough to disassemble the aggregate. However, as αH+ exceeds 40%, the oscillation of electrostatic potential curves intensifies, indicating more counterions into the hydrophobic domain driven by electrostatic forces. Consequently, the hydrophobic domains in vesicles or spherical micelles are divided into smaller segments, leading to the formation of nanosheets and nanoribbons. These analyses are helpful to illustrate the significant role of the electrostatic interaction in the dissociation of vesicles and spherical micelles in acidic environments.
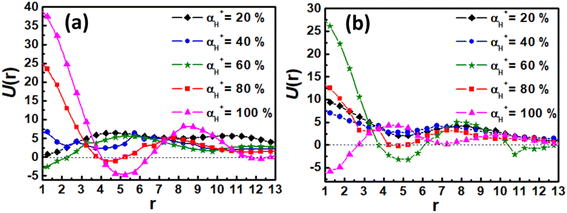 |
| | Fig. 9 The electrostatic potentials as a function of distance from their center of mass for associates at different protonation degrees: (a) the case of vesicle; (b) the case of spherical micelle. | |
4 Conclusions
In summary, the self-assembly of miktoarm star polymers μ-Ai(B(D))jCk in a neutral solution and the pH-responsive behavior of vesicles and spherical micelles in an acidic solution have been investigated by a series of DPD simulations. In a neutral condition, vesicles, discoidal, and spherical micelles have been observed by changing the length of pH-responsive and hydrophilic arms. The length of pH-responsive arm B has a distinct effect on the microstructure of vesicles. With the increase of the length of pH-responsive arm B, the hydrophobic arm A is squeezed from the center to the edge of the wall of vesicles, and the nonlinear increase of the composition ratio of hydrophobic beads leads to the nonlinear decrease of the size of vesicles. Additionally, the dynamic evolution pathways of vesicles and spherical micelles both undergo three stages of nucleation, coalescence, and growth. On the othe hand, the pH-responsive behaviors of vesicles and spherical micelles have been investigated by tuning the protonation degree of pH-responsive arm B in an acidic environment. With the increase in protonation degree corresponding to the decrease in pH value, vesicles transform into nanodisks, nanosheets, and nanoribbons, while spherical micelles turn into worm-like micelles, nanosheets, and nanoribbons. The morphological transitions can be attributed to the enhancement of the electrostatic interaction, which brings more counterions into the hydrophobic domain to dissociate the self-assembled aggregates. Consequently, a regular hexagonal arrangement of counterions appears in nanosheets, while an alternative distribution of charged beads has been observed in nanoribbons. These results are helpful in understanding the mechanism of the morphological transition of aggregates self-assembled by miktoarm star polymers in an acidic environment.
Data availability
The code for DL_MESO package can be found at https://www.ccp5.ac.uk/DL_MESO/. The version of the code employed for this study is version 2.7. The data analysis tools of this article are available at: https://www.scd.stfc.ac.uk/Pages/DL_MESO-useful-links.aspx.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was sponsored by Natural Science Foundation of Chongqing, China (No. CSTB2022NSCQ-MSX0829) and Scientific and Technological Research Program of Chongqing Municipal Education Commission (No. KJQN202101139).
References
- K. Khanna, S. Varshney and A. Kakkar, Polym. Chem., 2010, 1, 1171–1185 RSC.
- L. Yang, X. Hu, W. Wang, S. Liu, T. Sun, Y. Huang, X. Jing and Z. Xie, RSC Adv., 2014, 4, 41588–41596 RSC.
- J. M. Ren, T. G. McKenzie, Q. Fu, E. H. H. Wong, J. Xu, Z. An, S. Shanmugam, T. P. Davis, C. Boyer and G. G. Qiao, Chem. Rev., 2016, 116, 6743–6836 CrossRef CAS PubMed.
- M. Aghajanzadeh, M. Zamani, K. Rostamizadeh, A. Sharafi and H. Danafar, J. Macromol. Sci., Part A: Pure Appl. Chem., 2018, 55, 559–571 CrossRef CAS.
- H. Ding, P. Tan, S. Fu, X. Tian, H. Zhang, X. Ma, Z. Gu and K. Luo, J. Controlled Release, 2022, 348, 206–238 CrossRef CAS PubMed.
- M. Liu, J. R. Blankenship, A. E. Levi, Q. Fu, Z. M. Hudson and C. M. Bates, Chem. Mater., 2022, 34, 6188–6209 CrossRef CAS.
- M. Baghbanbashi and A. Kakkar, Mol. Pharm., 2022, 19, 1687–1703 CrossRef CAS PubMed.
- N. Saito, C. Liu, T. P. Lodge and M. A. Hillmyer, ACS Nano, 2010, 4, 1907–1912 CrossRef CAS PubMed.
- C. Chen, X. Guo, J. Du, B. Choi, H. Tang, A. Feng and S. H. Thang, Polym. Chem., 2019, 10, 228–234 RSC.
- H. Li, D. Yang, Y. Gao, H. Li and J. Xu, RSC Adv., 2015, 5, 96377–96386 RSC.
- G. Pasparakis and C. Tsitsilianis, Polymer, 2020, 211, 123146 CrossRef CAS.
- W. Sun, X. He, C. Gao, X. Liao, M. Xie, S. Lin and D. Yan, Polym. Chem., 2013, 4, 1939–1949 RSC.
- W. J. Lin, S. Y. Nie, Q. Chen, Y. Qian, X. F. Wen and L. J. Zhang, AIChE J., 2014, 60, 3634–3646 CrossRef CAS.
- H. Hu and G. Liu, Macromolecules, 2014, 47, 5096–5103 CrossRef CAS.
- M. Huo, H. Du, M. Zeng, L. Pan, T. Fang, X. Xie, Y. Wei and J. Yuan, Polym. Chem., 2017, 8, 2833–2840 RSC.
- H. Yin, H. C. Kang, K. M. Huh and Y. H. Bae, J. Mater. Chem., 2012, 22, 19168–19178 RSC.
- H. Yin, H. C. Kang, K. M. Huh and Y. H. Bae, Colloids Surf., B, 2014, 116, 128–137 CrossRef CAS PubMed.
- X. He, L. Huang, H. Liang and C. Pan, J. Chem. Phys., 2002, 116, 10508–10513 CrossRef CAS.
- J. Xia and C. Zhong, Macromol. Rapid Commun., 2006, 27, 1110–1114 CrossRef CAS.
- N. Saito, C. Liu, T. P. Lodge and M. A. Hillmyer, Macromolecules, 2008, 41, 8815–8822 CrossRef CAS.
- W. Kong, B. Li, Q. Jin, D. Ding and A.-C. Shi, J. Am. Chem.
Soc., 2009, 131, 8503–8512 CrossRef CAS PubMed.
- L. Wang, R. Xu, Z. Wang and X. He, Soft Matter, 2012, 8, 11462–11470 RSC.
- Y. Guo, Z. Ma, Z. Ding and R. K. Y. Li, Langmuir, 2013, 29, 12811–12817 CrossRef CAS PubMed.
- B. Li, Y.-L. Zhu, H. Liu and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2012, 14, 4964–4970 RSC.
- B. Li, L. Zhao, H.-J. Qian and Z.-Y. Lu, Soft Matter, 2014, 10, 2245–2252 RSC.
- Q. Zhang, J. Lin, L. Wang and Z. Xu, Prog. Polym. Sci., 2017, 75, 1–30 CrossRef CAS.
- J. Wu, Z. Wang, Y. Yin, R. Jiang and B. Li, Macromolecules, 2019, 52, 3680–3688 CrossRef CAS.
- I. D. Rodichkin, R. A. Gumerov and I. I. Potemkin, J. Colloid Interface Sci., 2022, 606, 1966–1973 CrossRef CAS PubMed.
- S. A. Ansary, S. Dwivedi and P. Mishra, J. Mol. Liq., 2023, 380, 121795 CrossRef CAS.
- M. Ramezani and J. Shamsara, J. Mol. Graphics Modell., 2016, 66, 1–8 CrossRef CAS PubMed.
- Y. H. Feng, X. P. Zhang, Z. Q. Zhao and X. D. Guo, Mol. Pharm., 2020, 17, 1778–1799 CrossRef CAS PubMed.
- W. X. Guo, L. F. Hu, Y. H. Feng, B. Z. Chen and X. D. Guo, Colloids Surf., B, 2022, 210, 112202 CrossRef CAS PubMed.
- X. D. Guo, L. J. Zhang, Z. M. Wu and Y. Qian, Macromolecules, 2010, 43, 7839–7844 CrossRef CAS.
- Y. Wang, B. Z. Chen, Y. J. Liu, Z. M. Wu and X. D. Guo, Colloids Surf., B, 2017, 151, 280–286 CrossRef CAS PubMed.
- Y. Wang, D. D. Zhu, J. Zhou, Q. L. Wang, C. Y. Zhang, Y. J. Liu, Z. M. Wu and X. D. Guo, Colloids Surf., B, 2015, 136, 536–544 CrossRef CAS PubMed.
- X. D. Guo, Y. Qian, C. Y. Zhang, S. Y. Nie and L. J. Zhang, Soft Matter, 2012, 8, 9989–9995 RSC.
- S. Y. Nie, Y. Sun, W. J. Lin, W. S. Wu, X. D. Guo, Y. Qian and L. J. Zhang, J. Phys. Chem. B, 2013, 117, 13688–13697 CrossRef CAS PubMed.
- Y. Q. Yang, B. Zhao, Z. D. Li, W. J. Lin, C. Y. Zhang, X. D. Guo, J. F. Wang and L. J. Zhang, Acta Biomater., 2013, 9, 7679–7690 CrossRef CAS PubMed.
- S. Y. Nie, W. J. Lin, N. Yao, X. D. Guo and L. J. Zhang, ACS Appl. Mater. Interfaces, 2014, 6, 17668–17678 CrossRef CAS PubMed.
- Z. Luo, Y. Li, B. Wang and J. Jiang, Macromolecules, 2016, 49, 6084–6094 CrossRef CAS.
- J. Chen, X. Qiu, J. Ouyang, J. Kong, W. Zhong and M. M. Q. Xing, Biomacromolecules, 2011, 12, 3601–3611 CrossRef CAS PubMed.
- P. J. Hoogerbrugge and J. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- M. González-Melchor, E. Mayoral, M. E. Velázquez and J. Alejandre, J. Chem. Phys., 2006, 125, 224107 CrossRef PubMed.
- X. Zhang, Y. Dai, G. Dai and C. Deng, RSC Adv., 2020, 10, 21602–21614 RSC.
- Y. Su, X. Quan, L. Li and J. Zhou, Macromol. Theory Simul., 2018, 27, 1700070 CrossRef.
- W. Min, D. Zhao, X. Quan, D. Sun, L. Li and J. Zhou, Colloids Surf., B, 2017, 152, 260–268 CrossRef CAS PubMed.
- Z. Posel, Z. Limpouchová, K. Šindelka, M. Lísal and K. Procházka, Macromolecules, 2014, 47, 2503–2514 CrossRef CAS.
- J. Mai, D. Sun, L. Li and J. Zhou, J. Chem. Eng. Data, 2016, 61, 3998–4005 CrossRef CAS.
- K. A. Terrón-Mejía, R. López-Rendón and A. G. Goicochea, J. Phys.: Condens. Matter, 2016, 28, 425101 CrossRef PubMed.
- M. A. Seaton, R. L. Anderson, S. Metz and W. Smith, Mol. Simul., 2013, 39, 796–821 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- A. Prhashanna, S. A. Khan and S. B. Chen, Colloids Surf., A, 2016, 506, 457–466 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Gaiqin Liu,
Nan Hu,
Lin Chen and
Jianwei Wei
,
Gaiqin Liu,
Nan Hu,
Lin Chen and
Jianwei Wei *
*
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Cij, dissipative force
Cij, dissipative force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Dij, random force
Dij, random force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Rij. The three forces vanish beyond a certain cutoff radius rc, whose value is usually set to one unit of length in simulations. The conservation force for non-bonded beads is defined by soft repulsion:
Rij. The three forces vanish beyond a certain cutoff radius rc, whose value is usually set to one unit of length in simulations. The conservation force for non-bonded beads is defined by soft repulsion:![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Cij = aijωC(rij)
Cij = aijωC(rij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij = aij(1 − rij/rc)
ij = aij(1 − rij/rc)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij
ij
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j, rij = |
j, rij = |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij|,
ij|, ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij/rij. The dissipative force corresponding to a frictional force depends on both the position and relative velocities of the beads and the random force is a random interaction between bead i and its neighbor bead j. These two forces act together as the inherent thermostat that determines the system temperature and are expressed by
ij/rij. The dissipative force corresponding to a frictional force depends on both the position and relative velocities of the beads and the random force is a random interaction between bead i and its neighbor bead j. These two forces act together as the inherent thermostat that determines the system temperature and are expressed by![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Dij = −γωD(rij)(
Dij = −γωD(rij)(![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) ij·
ij·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij)
ij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij = −γ(1 − rij/rc)2(
ij = −γ(1 − rij/rc)2(![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) ij·
ij·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij)
ij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij
ij

![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) ij =
ij = ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) i −
i − ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) j, γ and σ define the amplitude of the dissipative and the random forces, ωD(rij) and ωR(rij) are the weight functions, ξij is a random number with zero mean and unit variance. To satisfy the equilibrium Gibbs–Boltzmann distribution and the fluctuation-dissipative theorem, the following two relations are required:
j, γ and σ define the amplitude of the dissipative and the random forces, ωD(rij) and ωR(rij) are the weight functions, ξij is a random number with zero mean and unit variance. To satisfy the equilibrium Gibbs–Boltzmann distribution and the fluctuation-dissipative theorem, the following two relations are required:![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Sij = −ks(rij − r0)
Sij = −ks(rij − r0)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij
ij
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Eij and electrostatic potential UEij are expressed as
Eij and electrostatic potential UEij are expressed as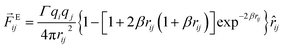
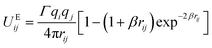
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2r/λ)/πλ3
exp(−2r/λ)/πλ3

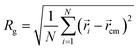
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i and
i and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) cm are the position vector of a bead and the center of mass of the aggregate, respectively. In our simulation, polymer chains are considered as a part of aggregate if the smallest distance between their two hydrophobic beads is less than 1.5. Fig. 3(d) shows that the Rg of vesicle decreases from 9.24 to 9.05 with the increase of j. We notice that as the arm length increases from 5 to 15 there is a sharp decrease in the Rg value. However, when the arm length increases from 15 to 20, the decrease in Rg is comparatively much smaller. The physical reason behind this behavior is closely related to the composition ratio ϕ of hydrophobic beads in miktoarm polymer, which can be calculated by the following formula:
cm are the position vector of a bead and the center of mass of the aggregate, respectively. In our simulation, polymer chains are considered as a part of aggregate if the smallest distance between their two hydrophobic beads is less than 1.5. Fig. 3(d) shows that the Rg of vesicle decreases from 9.24 to 9.05 with the increase of j. We notice that as the arm length increases from 5 to 15 there is a sharp decrease in the Rg value. However, when the arm length increases from 15 to 20, the decrease in Rg is comparatively much smaller. The physical reason behind this behavior is closely related to the composition ratio ϕ of hydrophobic beads in miktoarm polymer, which can be calculated by the following formula:









