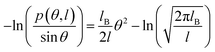Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of temperature on anisotropic bending elasticity of dsRNA: an all-atom molecular dynamics simulation†
Xianghong Wang*a,
Tingting Huanga,
Liyun Li b and
Yanliang Xua
b and
Yanliang Xua
aSchool of Sino-German Engineering, Shanghai Technical Institute of Electronics and Information, Shanghai 201411, China. E-mail: wangxianghong@stiei.edu.cn
bDepartment of Physics, Wenzhou University, Wenzhou 325035, China
First published on 28th May 2024
Abstract
Employing all-atom molecular dynamics simulations, we examined the temperature-dependent behavior of bending elasticity in double-stranded RNA (dsRNA). Specifically, we focused on the bending persistence length and its constituent components, namely, the tilt and roll stiffness. Our results revealed a near-linear decrease in these stiffness components as a function of temperature, thereby highlighting the increased flexibility of dsRNA at elevated temperatures. Furthermore, our data revealed a significant anisotropy in dsRNA bending elasticity, which diminished with increasing temperature, attributable to marked disparities in tilt and roll stiffness components. We delineated the underlying biophysical mechanisms and corroborated our findings with extant literature. These observations offer salient implications for advancing our understanding of nucleic acid elasticity, and are pertinent to potential medical applications.
1 Introduction
RNAs are pivotal in various biological processes, including but not limited to the encapsulation of double-stranded RNA (dsRNA) viral genomes into capsids and structural rearrangements of ribosomes during translation.1–3 Within these biological contexts, RNA undergoes diverse mechanical deformations in response to alterations in physiological conditions such as stretching, bending, and twisting. Concurrently, dsRNA has garnered attention as a promising nanomaterial for biological and nanomedical applications.3 Bend elasticity is a fundamental mechanical property of nucleic acids and is instrumental in shaping their three-dimensional structures under physiological conditions.4 Accordingly, elucidating the impact of environmental variables such as ionic strength and temperature on dsRNA bend elasticity is crucial.Traditionally, bending elasticity is quantified either via the bending persistence length or bending stiffness. For dsDNA, the bending persistence length is approximately 50 nm under standard physiological conditions, as described by the wormlike chain (WLC) model.5,6 Notably, the bending elasticity of dsDNA is sensitive to external conditions, including ionic concentration7–11 and temperature.12–21 Temperature elevations typically manifest as reductions in the bending persistence length of dsDNA, which is attributable to thermal fluctuations within the molecular milieu.22 For examples, the experiments suggested that the bending persistence length decreased as the temperature was increased,17 which have been reproduced in Monte Carlo (MC) and all-atom molecular dynamics (MD) simulations based on various models.19,20,23
For dsRNA, both experimental and computational data suggest a bending persistence length of approximately 60 nm under normal physiological conditions, surpassing that of dsDNA.24–26 For examples, the magnetic tweezer (MT) experiments reported that the dsRNA possesses the bending persistence lengths of lB = 60 ± 1 nm,24 lB = 57 ± 2 nm (ref. 25) and lB = ∼61 nm.26 The all-atom MD data reproduced that the dsRNA have the bending persistence length of lB = 69 ± 4 nm,27 lB = 66.3 nm (ref. 25) and lB = 66.99 ± 1.38 nm.28 The observed disparities between the MT and MD data can be attributed to variations in experimental conditions, such as ionic strength and sequence composition. The influence of sequence composition on elasticity mainly refers to the length and order of base pairs. Generally, the sequence length used in experiments is several thousand bp, while the sequence length used in all-atom simulations is several tens of bp due to the limitations of computational performance. It is noteworthy that the bending persistence length of dsRNA diminishes with an increase in ion concentration.26 Nevertheless, the impact of temperature on the bending persistence length of dsRNA remains an open avenue for investigation.
In the extant Marko and Siggia (MS) elastic model, bending elasticity is partitioned into two orthogonal modes, encapsulated by the tilt and roll angles.29 This partitioning underpins the observed anisotropy in bending rigidities, manifesting as differential flexibility along the major and minor grooves of nucleic acid helices.30 The MS model, extensively employed in dsDNA studies, accounts for the observed bending anisotropies and associated twist–bend couplings.31–35 Previous research cites tilt stiffness values of approximately 100 nm and roll stiffness values of approximately 39 nm for dsDNA at room temperature.31,32,36,37 The inherent asymmetry between these values correlates with the observed molecular geometry of the DNA.36 Such anisotropic behavior has also been observed in dsRNA, albeit with sequence-dependent variations in the extent of anisotropy.38 Recently, Dohnalová et al. used single-molecule MT measurements to determine the temperature-dependence of the dsRNA twist and observed that dsRNA unwinds with increasing temperature, which was correctly predicted by the all-atom MD simulations.39 Dabin et al. investigated the thermal denaturation of dsRNA using the atomistic simulations by varying the temperature in a wide range, in which the sequences and force fields were considered.40
In the present study, we employed all-atom molecular dynamics simulations of a representative dsRNA sequence to scrutinize the temperature-dependent properties of bending elasticity. Our study concentrates on the temperature effects on the bending persistence length, tilt, and roll stiffness, as well as the bending anisotropy, guided by the WLC and MS models. Section 2 outlines the simulation methodology, Section 3 discusses temperature-dependent findings, and Section 4 concludes.
2 Simulation models and method
2.1 All-atom MD simulation
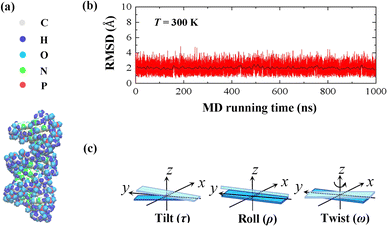
In the current simulations, we selected the initial A-type dsRNA with a 16 bp sequence of 5′-GCGC AAUG GAGU ACGC-3′, which has been used in the previous works.41,42 Our all-atom MD simulations are similar to those in previous studies,21,43,44 and we only briefly describe the content involved in the current simulations. We constructed the initial structure file of the RNA using the UCSF Chimera 1.15 software application,45 as shown in Fig. 1(a), where there are approximately 1026 atoms in the 16 bps sequence. The dsRNA sequence was immersed in an 8 × 8 × 8 nm3 simulation box under periodic boundary conditions. Subsequently, NaCl46 and water molecules were added corresponding to 100 mM salt concentration, where the TIP3P model47 was used to define the water structure. We added Na+ and Cl− ions using by Joung and Cheatham's ion model48 to the environment to maintain a constant concentration. Because nucleic acids are negatively charged, additional 30 Na+ ions are dumped into the solution, which neutralizes the negative charge in the solution environment.Our MD simulations were performed using the Gromacs 4.6 software with the Amber OL3 force fields.49–53 Before the MD simulations, the system needs to be pre-equilibrated to ensure that the MD simulation is performed in an isothermal isobaric environment.54,55 We started with an energy minimization system with a restraining force and subsequently an NVT and NPT simulations. In NVT, the system is warmed up to the desired temperature T by the V-rescale method.54,55 Specifically, this scheme uses the velocity-rescaling method with random terms for temperature coupling to produce the NVT canonical ensemble, retaining the Berendsen thermostat's advantages, which have the first-order decay of the temperature deviation and the absence of oscillations.54,55 After the system was preheated to the desired temperature T, the system pressure was adjusted to 1 atm using the NPT simulation. When these pre-equilibration processes were completed, and a 1000 ns MD simulation was performed at a fixed temperature T without the restraining force. We adjusted the temperature T from 280 K to 320 K, with a step of ΔT = 10 K, where the temperature regulation was similar to those of all-atom MD simulations with Amber force fields.16,20,21,56,57 We checked the validity of the simulation by calculating the root mean square deviation (RMSD) of the system. An example is shown in the RMSD plots for 16 bps dsRNA in Fig. 1(b). The RMSD indicates the extent of structural changes in the dsRNA molecule as follows:
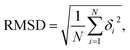 | (1) |
2.2 WLC and MS models
In this study, we focused on the elastic parameters of the MS model and WLC models. In WLC model, the bend elasticity can be described as follows9,58–60
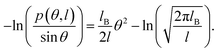 | (2) |
The MS model was originally proposed by Marko and Siggia,29 where three angles Ω1, Ω2 and Ω3 was used to describe the bend and twist elasticities of DNA in recent years.31,34,35,63 These three rotational angles, Ω1, Ω2 and Ω3, are related to the tilt, roll and twist in the rigid base-pair,37 as shown in Fig. 1(c). In the MS model, by considering the symmetry and lowest order of Ω, one can express the energy functional as follows29
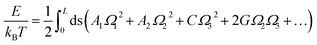 | (3) |
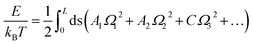 | (4) |
One can further reduce eqn (4) into WLC model by ignoring Ω3.
In the MS model, A1, A2, C and G are related to the elastic moduli Kττ, Kρρ, Kωω and Kρω multiplied by L0 in unit of kBT, where L0 is the contour length of dsRNA. According to the random thermal fluctuation, the elastic modulus K can be expressed as22
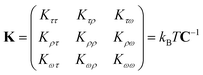 | (5) |
| cov(i,j) = cijσiσj | (6) |
Generally, three angular parameters, tilt, roll and twist, can be used to describe the bending and twisting elasticities of dsRNA, as well as its coupling, in the rigid base-pair (RBP) model, as shown in eqn (5). Here, we try to describe the relationship between MS, TWLC and WLC models, starting from the RBP model. In MS model, only the coupling between the roll and twist, is considered, since the tilt is weakly coupled to roll and twist.29 However, the TWLC model further ignore the coupling between roll and twist angles.32 In WLC model, it only considers the tilt and roll angles by ignoring the twist angle, which can be used to describe the bending elasticities. Such approximation of the WLC model makes the MS model closer to the experiments.
3 Results and discussion
In this study, we focus on the influence of temperature on the bend elasticity of dsRNA, which is characterized by the bending persistence length based on the WLC model and the bending anisotropy based on the MS model. The temperature was adjusted from T = 280 K to T = 320 K with steps of ΔT = 10 K to demonstrate the temperature-dependent bend elasticity of dsRNA. In Subsection 3.1, we discuss the dependence of bending elasticities in Fig. 2 and 3; we analyzed the temperature dependence of tilt and roll stiffnesses, as well as their bending anisotropy, based on the MS model in Fig. 4–7 in Subsection 3.2.3.1 Temperature-dependent bend elasticity
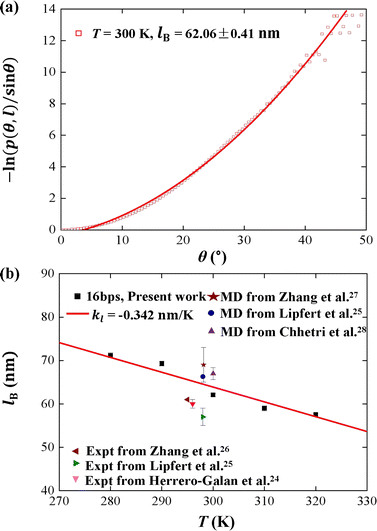
We plotted the bending persistence length lB as a function of temperature T in Fig. 2, according to eqn (1) based on the WLC model. In Fig. 2(a), a typical example is shown, where the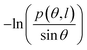 is plotted as a function of the bending angle θ at T = 300 K. We used the quadratic curve to fit the MD data and obtained the bending persistence length lB = 62.06 ± 0.41 nm at T = 300 K. Our MD data are in line with the available all-atom MD simulation data where lB ranges from 66 nm to 69 nm.25,27,28 Previous experiments have suggested that the dsRNA has a persistence length of approximately lB = 57–64 nm under the various salt concentrations.24–26 In particular, Abels et al. used two single-molecule techniques, the MT and AFM, to measure the bending persistence length of dsRNA at room temperature (T = ∼298 K) and obtained lB = 63.8 ± 0.7 nm by MT and lB = 62 ± 2 nm by AFM.64 We listed these data in detail in Table S3 of ESI† where the sequence length and ion concentration were also listed. Actually, the bending persistence length of dsRNA decreases as the concentration of CoHex3+ increases11 and also has a sequence-dependence.38 Thus, the main deviation between the current MD results and experimental data was probably due to the different salt concentrations and sequence lengths used in the current simulation and previous works. For a convenient comparison, we inserted these available data into Fig. 2(b), where the bending persistence lengths were plotted as a function of temperature. Here, we predicted the temperature dependence of bending persistence length lB, as shown in Fig. 2(b), where the temperature T over a range from T = 280 K to T = 320 K. The bending persistence lengths at other temperatures are also obtained by the same fitting methods as those at T = 300 K [see Fig. S2 of ESI†]. We observed a linear relationship between the bending persistence length lB and temperature T, with the slope of kl = −0.342 nm K−1. Previous experiments have reported the linear dependence of temperature on the bending persistence lengths of dsDNA,14,17 and all-atom simulations have also reproduced the linear temperature dependence on the bending persistence lengths of dsDNA where the bending persistence length lB decreases as temperature T increases, with a slope of −0.29 nm K−1.21
is plotted as a function of the bending angle θ at T = 300 K. We used the quadratic curve to fit the MD data and obtained the bending persistence length lB = 62.06 ± 0.41 nm at T = 300 K. Our MD data are in line with the available all-atom MD simulation data where lB ranges from 66 nm to 69 nm.25,27,28 Previous experiments have suggested that the dsRNA has a persistence length of approximately lB = 57–64 nm under the various salt concentrations.24–26 In particular, Abels et al. used two single-molecule techniques, the MT and AFM, to measure the bending persistence length of dsRNA at room temperature (T = ∼298 K) and obtained lB = 63.8 ± 0.7 nm by MT and lB = 62 ± 2 nm by AFM.64 We listed these data in detail in Table S3 of ESI† where the sequence length and ion concentration were also listed. Actually, the bending persistence length of dsRNA decreases as the concentration of CoHex3+ increases11 and also has a sequence-dependence.38 Thus, the main deviation between the current MD results and experimental data was probably due to the different salt concentrations and sequence lengths used in the current simulation and previous works. For a convenient comparison, we inserted these available data into Fig. 2(b), where the bending persistence lengths were plotted as a function of temperature. Here, we predicted the temperature dependence of bending persistence length lB, as shown in Fig. 2(b), where the temperature T over a range from T = 280 K to T = 320 K. The bending persistence lengths at other temperatures are also obtained by the same fitting methods as those at T = 300 K [see Fig. S2 of ESI†]. We observed a linear relationship between the bending persistence length lB and temperature T, with the slope of kl = −0.342 nm K−1. Previous experiments have reported the linear dependence of temperature on the bending persistence lengths of dsDNA,14,17 and all-atom simulations have also reproduced the linear temperature dependence on the bending persistence lengths of dsDNA where the bending persistence length lB decreases as temperature T increases, with a slope of −0.29 nm K−1.21
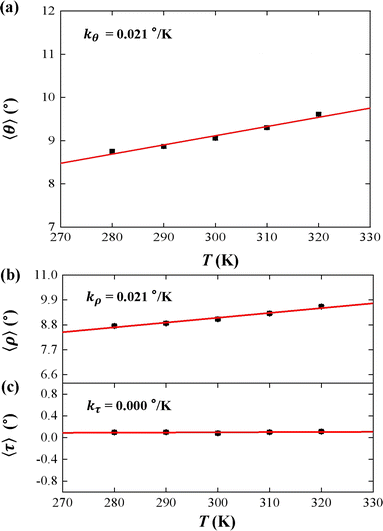
We used the rotational parameters to understand the temperature dependence of lB, as shown in Fig. 3. We plotted the bending angle 〈θ〉 as function of temperature T in Fig. 3(a), where θ is bending angle between two successive bps and 〈⋯〉 denotes assemble average. We obtained the 〈θ〉 from the MD trajectory data, and 〈θ〉 = 9.05° at T = 300 K. We note that the average bending angle 〈θ〉 is much greater than that of dsDNA.21,27,62 Furthermore, we predicted the linear dependence of the average bending angle 〈θ〉 on the temperature T, as shown in Fig. 3(a). The results showed that the bending angle 〈θ〉 increased as the temperature T increased, with a slope of kθ = 0.021° K−1, which is similar to the dsDNA case.21 We are aware that the smaller bending angle reflects the stronger dsDNA rigidity, in which the upward trend illustrated that the dsRNA chain becomes more flexible with the increasing T, supported by the short WLC model about the conformational variations.58,65 In the TWLC model, the bending angle is related to two orthogonal angles, the tilt and roll angles, which hold θ2 = τ2 + ρ2.31,35 To analyze the bending elasticity in more detail, we plotted the 〈τ〉 and 〈ρ〉 as functions of temperature T, as shown in Fig. 3(b) and (c), where τ and ρ are the tilt and roll angles, respectively, between two successive bps. We also listed the more detailed data about the tilt and roll angles at various temperatures in Table S1 of ESI.† We obtained 〈τ〉 = 0.08° and 〈ρ〉 = 9.05° at T = 300 K, which are in line with the available data from the various dsRNA sequences,25,27,28 for example, 〈ρ〉 = 7.5 ± 3.47° and 〈τ〉 = −0.01 ± 4.36° for a 16 bps dsRNA sequence used in the previous MD simulation.28 The results showed that the average roll angle 〈ρ〉 has a linear relationship with temperature T on a slope of kρ = 0.021° K−1. However, the average tilt angle 〈τ〉almost maintain unchanged value, with a slope of kτ = 0.000° K−1, as shown in Fig. 3(b) and (c), which suggests that the bending elasticity is mainly derived from the roll angles.66
3.2 Temperature-dependent tilt and roll stiffnesses
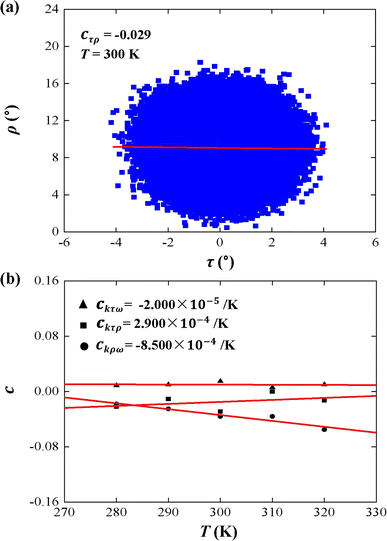
Tilt, roll, and twist are three rotational parameters that play important roles in the bend and twist stiffnesses. In the MS model, the tilt and roll are the two orthogonal components of the bend elasticity. In the current simulations, we concentrated on the bend elasticities involving the tilt and roll angles, as well as the bending anisotropy in Fig. 4 and 5.First, we analyzed the tilt and roll correlations and showed an example at T = 300 K in Fig. 4(a), in which the data between the tilt and roll have negative correlations, with a negative slope of cτρ = −0.029. This weak correlation indicates that the tilt angle was almost independent of the roll angle at T = 300 K. A previous MD simulation also indicated that there was a weak correlation between the tilt and roll angles for dsRNA and dsDNA.25 Correlations between tilt and roll are presented in a manner similar to the previous simulations.43,57 We also provided the tilt and roll correlations at other temperature in Fig. S3 of ESI,† which indicated the correlations between the tilt and roll are also weak. To demonstrate the temperature-dependence of this correlation clearly, we plotted the correlation coefficient as a function of the temperature T, as shown in Fig. 4(b). We then observed a linear relationship between the correlation coefficient cτρ and temperature T with a slope of ckτρ = 2.900 × 10−4 K−1. The very weak upward trend indicates that the correlation between the tilt and roll angles is independent of the temperature T. Actually, the correlations of tilt and roll to the third angle, twist, cannot be neglected in dsRNA, as shown in Fig. 4(b) [see the tilt–twist correlations and roll–twist correlations at various temperatures in Fig. S4 and S5 of ESI†], which differs from the available data for dsDNA.25 This non-correlation between the tilt and roll enables us to analyze the bend elasticity based on the tilt and roll stiffnesses.
We then considered two elastic components, tilt and roll stiffnesses, for the bend elasticity illustrated in the MS model. The MS model has been successfully used in dsDNA to explain the bend and twist elasticities by considering the twist-bending coupling.31–35 This is due to undistortion of dsDNA, where the bending angle is relatively small, which leads to the rotational symmetry of tilt angle. The dsRNA is more bent than dsDNA where the average roll between two successive bps is 〈ρ〉 = 9.05°. This causes the nonzero terms Kτω ≠ 0 [refer to the K elements at various temperatures in Table S2 of ESI†], leading to the deviation of the MS model. However, the Kρω is much larger than Kτω, which enables us to analyze the tilt and roll components for bending elasticities. This is also supported by the fact that the Pearson correlation coefficients between the roll and twist are much larger than those between tilt and twist [refer to Table S2 in ESI† for Kρω and Kτω at various temperatures]. We obtained the tilt and roll modulus, Kττ and Kρρ, according to eqn (5) and (6), and plotted the tilt and roll stiffnesses (tilt and roll persistence lengths), A1 and A2, as function of temperature T, in Fig. 5. Here, the tilt stiffness A1 is determined by31,32
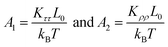 | (7) |
| B = (A1 − A2)/2 | (8) |
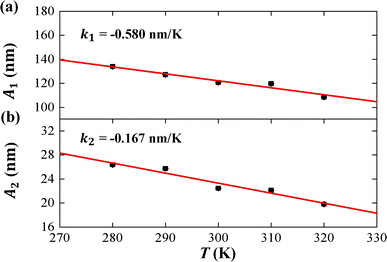
In the current simulations, the dsRNA has an asymmetry parameter of B = 49.17 nm, which indicates a much larger bending anisotropic bending elasticity. This asymmetry parameter was much larger than that in dsDNA where the asymmetry parameter was suggested to be B = 19 nm.30 This anisotropic bending elasticity was also observed in the MD simulations of the dsRNA and dsDNA.38 Importantly, our simulation results predicted that the tilt stiffness A1 and roll stiffness A2 are temperature-dependent, as shown in Fig. 5(a) and (b), respectively. The data fitting indicated a linear relationship between A1 and T with a slope of k1 = −0.580 nm K−1, while the same is true for the roll angle where A2 decreases with T by a slope of k2 = −0.167 nm K−1. Our observations were supported by a theoretical analysis in which there was a linear relationship between the stiffness matrix K and temperature T.16 We also show the effect of temperature on the anisotropic bending elasticity in Fig. S6.† Our simulation results indicate that asymmetry parameter B decreases from 53.85 nm to 44.42 nm when the temperature T increases from 280 K to 320 K, with a slope of k3 = −0.208 nm K−1, indicating that the bending anisotropy become weaker as temperature increases.
3.3 Thermal fluctuations in tilt and roll angles
According to thermal fluctuations, the elasticity can be described by the covariances between the deformation variables.22 Then, we delve into the mechanism governing the temperature dependence of tilt stiffness A1 and roll stiffness A2, as shown in Fig. 6. eqn (5) and (6) suggest that the stiffness matrix K can be described by the Pearson correlation coefficient cov(i, j) and thermal fluctuation σi2. This enables us to estimate that the tilt stiffness A1 and roll stiffness A2 have approximate forms, similar to the stretch–twist elastic matrix,21,22
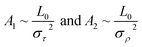 | (9) |
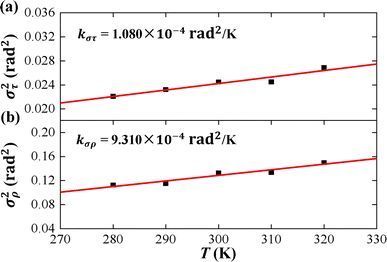
As the contour length L0 remains unchanged values with temperature T, we present the factors στ2 and σρ2 as functions of temperature T to elucidate the decline in tilt stiffness A1 and roll stiffness A2, as shown in Fig. 6. The results indicate that both στ2 and σρ2 increase as the temperature T increases, displaying nearly linear trends, which is similar to the data obtained from MD simulations of dsDNA.21 These findings suggest that the reductions in tilt stiffness A1 and roll stiffness A2 are attributed to the thermal fluctuation components στ2 and σρ2, respectively. However, the fitting results suggest that the decline rates differ between the στ2 and σρ2 as the temperature T increases. Specifically, στ2 increases with a slope of kστ = 1.080 × 10−4 rad2 K−1 while kσρ = 9.310 × 10−4 rad2 K−1 for σρ2. This implies that the thermal fluctuation of the roll angle σρ2 depends more obviously on the temperature T than on the tilt angle, which plays a stronger role in the T-dependent roll stiffness A2.
To understand the thermal fluctuations in more detail, we investigated the thermal fluctuation components σt2 and σr2 for each base pair. An example at T = 300 K was shown in Figs. 7(a) and (b), respectively. The data showed that σr2 is greater than σt2 in each bp, and generally the σt2 and σr2 in U and A bps are greater than those in C and G bps, which is in line with the sequence-dependent data.38,67 The min values of σt2 and σr2 appear in the center of the sequence and the larger values at the two ends, exhibiting the flexibilities of these two ends. These flexibilities are consistent with the flexibility origin of short sequences.62,68 Here, we used the sequence-dependent σt2 and σr2 to clearly illustrate the anisotropic bending elasticities originating from the thermal fluctuations.
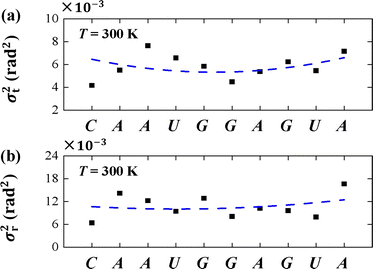 | ||
| Fig. 7 (a) The variance of tilt σt2 for each bp T = 300 K. (b) The variance of roll σr2 for each bp T = 300 K. The dashed curves denote the varying trends along dsRNA sequences. | ||
4 Conclusions
In the present study, we used all-atom MD simulations to investigate the effects of temperature on the bending elasticity of dsRNA. We chose a short dsRNA sequence of 16 bps to analyze the bending persistence length, tilt, and roll stiffness of the dsRNA. We concentrated on the influences of temperature on bending elasticities and bending anisotropy based on WLC and MS models, and analyzed the mechanism of temperature dependence by thermal fluctuations from the rotational deformation variables.In the current simulations, we obtained the bending persistence length lB = 62.06 ± 0.41 nm for dsRNA at T = 300 K, which is in line with the available experimental and MD simulation data. We predicted a linear relationship between the bending persistence length lB and temperature T, with a slope of kl = −0.342 nm K−1. This linear relationship was similar to that observed for dsDNA. To analyze the bending elasticity in more detail, we investigated the 〈τ〉 and 〈ρ〉 as functions of temperature T, and the results showed that the average roll angle 〈ρ〉 has a linear relationship with temperature T at a slope of kρ = 0.021° K−1, while the average tilt angle 〈τ〉 remained almost unchanged, with a slope of kτ = 0.000° K−1, which suggests that the bending elasticity is mainly from the roll angles. We then investigated the tilt and roll stiffness as well as its bending anisotropy. We obtained a tilt stiffness A1 = 120.80 nm and roll stiffness A2 = 22.46 nm at T = 300 K. DsRNA has an asymmetry parameter of B = 49.17 nm, which indicates a much larger bending anisotropic bending elasticity than that of dsDNA, where the asymmetry parameter was suggested to be B = 19 nm. We predicted that the tilt stiffness A1 and roll stiffness A2 decrease linearly with increasing temperature T in linear manners, with a slope of k1 = −0.580 nm K−1 for tilt stiffness, while the same is true for the roll angle, where A2 decreases with T by a slope of k2 = −0.167 nm K−1. Our MD simulation results showed that asymmetry parameter B decreases from 53.85 nm to 44.42 nm when the temperature T increases from 280 K to 320 K, with a slope of k3 = −0.208 nm K−1. This suggests that the bending anisotropy weakened as the temperature increased. Then, we delve into the mechanism governing the temperature dependence of tilt stiffness A1 and roll stiffness A2, which suggests that the thermal fluctuation of the roll angle σρ2 depends more on the temperature T than on the tilt angle. As we know, the bending of RNA plays a key role in the transmission of genetic information and organisms survive, as well as the nucleic acid nanostructures involved in functions related to drug delivery. Our all-atom MD simulations provide a deeper understanding of the bending elasticity of dsRNA, which probably has potential applications in these aspects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank for the financial supports from the Program of National Natural Science Foundation of China (Grant No. 12374215 and 11875205).Notes and references
- F. Tama, M. Valle, J. Frank and C. L. Brooks III, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 9319–9323 Search PubMed.
- B. S. Schuwirth, M. A. Borovinskaya, C. W. Hau, W. Zhang, A. Vila-Sanjurjo, J. M. Holton and J. H. D. Cate, Science, 2005, 310, 827–834 Search PubMed.
- Q. Vicens and J. S. Kieft, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2112677119 CrossRef CAS PubMed.
- A. Basu, D. G. Bobrovnikov and T. Ha, J. Mol. Biol., 2021, 433, 166861 Search PubMed.
- A. Aggarwal, S. Naskar, A. K. Sahoo, S. Mogurampelly, A. Garai and P. K. Maiti, Curr. Opin. Struct. Biol., 2020, 64, 42–50 CrossRef CAS PubMed.
- A. Marin-Gonzalez, J. Vilhena, R. Perez and F. Moreno-Herrero, Q. Rev. Biophys., 2021, 54, e8 Search PubMed.
- A. Garai, S. Saurabh, Y. Lansac and P. K. Maiti, J. Phys. Chem. B, 2015, 119, 11146–11156 CrossRef CAS PubMed.
- A. Brunet, C. Tardin, L. Salomé, P. Rousseau, N. Destainville and M. Manghi, Macromolecules, 2015, 48, 3641–3652 CrossRef CAS.
- A. V. Drozdetski, I. S. Tolokh, L. Pollack, N. Baker and A. V. Onufriev, Phys. Rev. Lett., 2016, 117, 028101 CrossRef PubMed.
- S. Guilbaud, L. Salomé, N. Destainville, M. Manghi and C. Tardin, Phys. Rev. Lett., 2019, 122, 028102 Search PubMed.
- H. Fu, C. Zhang, X.-W. Qiang, Y.-J. Yang, L. Dai, Z.-J. Tan and X.-H. Zhang, Phys. Rev. Lett., 2020, 124, 058101 Search PubMed.
- J.-S. Park, K. J. Lee, S.-C. Hong and J.-Y. Hyon, J. Korean Phys. Soc., 2008, 52, 1927–1931 CrossRef CAS.
- R. A. Forties, R. Bundschuh and M. G. Poirier, Nucleic Acids Res., 2009, 37, 4580–4586 CrossRef CAS PubMed.
- S. Geggier, A. Kotlyar and A. Vologodskii, Nucleic Acids Res., 2011, 39, 1419–1426 Search PubMed.
- N. Theodorakopoulos and M. Peyrard, Phys. Rev. Lett., 2012, 108, 078104 Search PubMed.
- S. Meyer, D. Jost, N. Theodorakopoulos, M. Peyrard, R. Lavery and R. Everaers, Biophys. J., 2013, 105, 1904–1914 Search PubMed.
- R. P. Driessen, G. Sitters, N. Laurens, G. F. Moolenaar, G. J. Wuite, N. Goosen and R. T. Dame, Biochemistry, 2014, 53, 6430–6438 Search PubMed.
- A. Brunet, L. Salomé, P. Rousseau, N. Destainville, M. Manghi and C. Tardin, Nucleic Acids Res., 2018, 46, 2074–2081 CrossRef CAS PubMed.
- J. M. Schurr, Biochemistry, 2019, 251, 106146 Search PubMed.
- H. Dohnalová, T. Drsata, J. Sponer, M. Zacharias, J. Lipfert and F. Lankas, J. Chem. Theory Comput., 2020, 16, 2857–2863 CrossRef PubMed.
- Y. Zhang, L. He and S. Li, J. Chem. Phys., 2023, 158, 094902 Search PubMed.
- F. Lankaš, O. Gonzalez, L. Heffler, G. Stoll, M. Moakher and J. H. Maddocks, Phys. Chem. Chem. Phys., 2009, 11, 10565–10588 Search PubMed.
- J. J. Delrow, P. J. Heath and J. M. Schurr, Biophys. J., 1997, 73, 2688–2701 Search PubMed.
- E. Herrero-Galan, M. E. Fuentes-Perez, C. Carrasco, J. M. Valpuesta, J. L. Carrascosa, F. Moreno-Herrero and J. R. Arias-Gonzalez, J. Am. Chem. Soc., 2013, 135, 122–131 Search PubMed.
- J. Lipfert, G. M. Skinner, J. M. Keegstra, T. Hensgens, T. Jager, D. Dulin, M. Köber, Z. Yu, S. P. Donkers and F.-C. Chou, et al., Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15408–15413 Search PubMed.
- C. Zhang, H. Fu, Y. Yang, E. Zhou, Z. Tan, H. You and X. Zhang, Biophys. J., 2019, 116, 196–204 Search PubMed.
- Y. Zhang, M. Yan, T. Huang and X. Wang, Adv. Theory Simul., 2023, 6, 2200534 Search PubMed.
- K. B. Chhetri, A. Sharma, S. Naskar and P. K. Maiti, Nanoscale, 2022, 14, 6620–6635 RSC.
- J. F. Marko and E. D. Siggia, Macromolecules, 1994, 27, 981–988 CrossRef CAS.
- D. Norouzi, F. Mohammad-Rafiee and R. Golestanian, Phys. Rev. Lett., 2008, 101, 168103 Search PubMed.
- S. K. Nomidis, F. Kriegel, W. Vanderlinden, J. Lipfert and E. Carlon, Phys. Rev. Lett., 2017, 118, 217801 Search PubMed.
- E. Skoruppa, M. Laleman, S. K. Nomidis and E. Carlon, J. Chem. Phys., 2017, 146, 214902 CrossRef PubMed.
- E. Skoruppa, S. K. Nomidis, J. F. Marko and E. Carlon, Phys. Rev. Lett., 2018, 121, 088101 Search PubMed.
- M. Caraglio, E. Skoruppa and E. Carlon, J. Chem. Phys., 2019, 150, 135101 Search PubMed.
- S. K. Nomidis, E. Skoruppa, E. Carlon and J. F. Marko, Phys. Rev. E, 2019, 99, 032414 Search PubMed.
- F. Mohammad-Rafiee and R. Golestanian, Phys. Rev. Lett., 2005, 94, 238102 Search PubMed.
- Y. A. G. Fosado, F. Landuzzi and T. Sakaue, Phys. Rev. Lett., 2023, 130, 058402 Search PubMed.
- I. Faustino, A. Pérez and M. Orozco, Biophys. J., 2010, 99, 1876–1885 CrossRef CAS PubMed.
- H. Dohnalová, M. Seifert, E. Matouskova, M. Klein, F. S. Papini, J. Lipfert, D. Dulin and F. Lankas, J. Phys. Chem. B, 2024, 128, 664–675 Search PubMed.
- A. Dabin and G. Stirnemann, Biochemistry, 2024, 307, 107167 Search PubMed.
- K. Liebl, T. Drsata, F. Lankas, J. Lipfert and M. Zacharias, Nucleic Acids Res., 2015, 43, 10143–10156 Search PubMed.
- A. Marin-Gonzalez, J. Vilhena, R. Perez and F. Moreno-Herrero, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7049–7054 CrossRef CAS PubMed.
- X.-W. Qiang, C. Zhang, H.-L. Dong, F.-J. Tian, H. Fu, Y.-J. Yang, L. Dai, X.-H. Zhang and Z.-J. Tan, Phys. Rev. Lett., 2022, 128, 108103 Search PubMed.
- F.-J. Tian, C. Zhang, E. Zhou, H.-L. Dong, Z.-J. Tan, X.-H. Zhang and L. Dai, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2218425120 Search PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 Search PubMed.
- L. Bao, X. Zhang, Y.-Z. Shi, Y.-Y. Wu and Z.-J. Tan, Biophys. J., 2017, 112, 1094–1104 Search PubMed.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5, 3863–3871 Search PubMed.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041 Search PubMed.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 Search PubMed.
- R. Galindo-Murillo, J. C. Robertson, M. Zgarbova, J. Sponer, M. Otyepka, P. Jurecka and T. E. Cheatham III, J. Chem. Theory Comput., 2016, 12, 4114–4127 Search PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi and A. Balaceanu, et al., Nat. Methods, 2016, 13, 55–58 Search PubMed.
- K. X. Xiong, K. Xi, L. Bao, Z. L. Zhang and Z. J. Tan, Acta Phys. Sin., 2018, 67, 108701 CrossRef.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 Search PubMed.
- Q. Ke, X. Gong, S. Liao, C. Duan and L. Li, J. Mol. Liq., 2022, 365, 120116 CrossRef CAS.
- F. Kriegel, C. Matek, T. Dršata, K. Kulenkampff, S. Tschirpke, M. Zacharias, F. Lankaš and J. Lipfert, Nucleic Acids Res., 2018, 46, 7998–8009 CrossRef CAS PubMed.
- C. Zhang, F. Tian, Y. Lu, B. Yuan, Z.-J. Tan, X.-H. Zhang and L. Dai, Sci. Adv., 2022, 8, eabn1384 CrossRef CAS PubMed.
- A. K. Mazur, Phys. Rev. Lett., 2007, 98, 218102 CrossRef PubMed.
- A. Polley, J. Samuel and S. Sinha, Phys. Rev. E, 2013, 87, 012601 Search PubMed.
- X.-W. Qiang, H.-L. Dong, K.-X. Xiong, W. Zhang and Z.-J. Tan, Commun. Theor. Phys., 2021, 73, 075601 Search PubMed.
- V. Ortiz and J. J. de Pablo, Phys. Rev. Lett., 2011, 106, 238107 Search PubMed.
- Y.-Y. Wu, L. Bao, X. Zhang and Z.-J. Tan, J. Chem. Phys., 2015, 142, 125103 CrossRef PubMed.
- S. Nomidis, M. Caraglio, M. Laleman, K. Phillips, E. Skoruppa and E. Carlon, Phys. Rev. E, 2019, 100, 022402 CrossRef CAS PubMed.
- J. Abels, F. Moreno-Herrero, T. Van der Heijden, C. Dekker and N. H. Dekker, Biophys. J., 2005, 88, 2737–2744 Search PubMed.
- R. Lavery, M. Moakher, J. H. Maddocks, D. Petkeviciute and K. Zakrzewska, Nucleic Acids Res., 2009, 37, 5917–5929 Search PubMed.
- A. Noy and R. Golestanian, Phys. Rev. Lett., 2012, 109, 228101 CrossRef PubMed.
- O. Gonzalez, D. Petkevičiūtė and J. Maddocks, J. Chem. Phys., 2013, 138, 055102 Search PubMed.
- M. Segers, E. Skoruppa, J. A. Stevens, M. Vangilbergen, A. Voorspoels and E. Carlon, J. Chem. Phys., 2021, 155, 027101 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02354d |
| This journal is © The Royal Society of Chemistry 2024 |