Structural, optical and magnetic properties of a new metal–organic Co^II-based complex

Abstract

A mononuclear cobalt(II) complex [C₅H₈N₃]₂[CoCl₄(C₅H₇N₃)₂] (I) was synthesized and structurally characterized. Single crystal X-ray diffraction analysis indicates that monometallic Co(II) ions acted as coordination nodes in a distorted octahedral geometry, giving rise to a supramolecular architecture. The latter is made up of a ½ unit form composed of an anionic element [Co_0.5Cl₂(C₅H₇N₃)]⁻ and one 2-amino-4-methylpyrimidinium cation [C₅H₈N₃]⁺. The crystalline arrangement of this compound adopts the sandwich form where inorganic parts are sandwiched between the organic sheets following the [100] direction. More information regarding the structure hierarchy has been supplied based on Hirshfeld surface analysis; the X⋯H (X = N, Cl) interactions play a crucial role in stabilizing the self-assembly process of I, complemented by the intervention of π⋯π electrostatic interaction created between organic entities. Thermal analyses were carried out to study the thermal behavior process. Static magnetic measurements and ab initio calculations of compound I revealed the easy-axis anisotropy character of the central Co(II) ion. Two-channel field-induced slow-magnetic relaxation was observed; the high-frequency channel is characterized by underbarrier relaxation with U_eff = 16.5 cm⁻¹, and the low-frequency channel involves a direct relaxation process affected by the phonon-bottleneck effect.

---

1 Introduction

Over the past two decades, the field of single-molecule magnets (SMMs) has had a remarkable evolution, and it is now gaining more impetus as the subject is being expanded to include organometallic compounds, lanthanides, and mononuclear transition metal complexes.^1–26 The early research was concentrated on polynuclear transition-metal clusters,^14–16 but recent years have witnessed considerable progress in the exploration of complexes with only one paramagnetic metal ion of high anisotropy, commonly known as single-ion magnets (SIMs).^17,18,26 It should be noted that coordinative unsaturated compounds may be air-sensitive; this could impede their use in practical applications. To solve this issue, research on the more widespread complexes, including six-coordinate Co(II) SIMs, is gaining momentum. The majority of six-coordinate cobalt(II) complexes preferring octahedral architecture display high positive D (axial anisotropy) values.²⁷ The first manifestation of a six-coordinate mononuclear Co(II) complex that exhibits SIMs behavior was discovered in 2012 by Julia Vallejo.¹¹ A few cases of SIMs with 3d metal ions may necessitate a low coordination number to reduce the ligand field concerning the spin–orbit coupling and obtain the intended slow magnetic relaxation effects. The tuning of the local symmetry of the Co(II) center imposed by the ligand field is important for the observation of the slow magnetic relaxation in Co(II)-based SIMs²⁸ and yielded many examples with exceptionally high relaxation barriers for spin flipping, e.g., in ref. 29–31.

It is known that the magnetic anisotropy of metal complexes can be increased by surrounding metal centers with heavier halides (Cl, Br, I) thanks to their greater spin–orbit coupling parameters.^32–36 The kind of halides and the selection of organic ligands have an impact on the structure of the coordinating polyhedron surrounding the central metal ion.

In addition, 2-amino-4-methyl pyrimidine (Ampym) is beneficial to be used as a ligand in this report, owing to its ability to commingle advantageous characteristics and offer various intriguing performances in different fields, such as magnetism,^37,38 optics,^37–39 biology.³⁰

Motivated by the aspects described above, the chemical preparation, the crystallographic description of a new halide Co(II) complex template by Ampym, the spectroscopic characterization, the thermal behavior and magnetic properties, are discussed herein with details to achieve our purposes.

2 Experimental section

2.1. Materials and physical measurements

To be structurally analyzed by X-ray diffraction, a single crystal of about 0.3 × 0.3 × 0.3 mm³ was selected. Details of crystallographic data collection and refinement parameters for I is gathered in Table S1.† An Oxford Gemini S diffractometer with a graphite monochromated Mo–K radiation source (=0.71073 Å) was used to collect the data at 125.8 K. Using direct techniques and SHELXS-13, the molecular structure was solved. SHELXL-13, a full-matrix least-squares method, was then used to improve the solution on F².⁴⁰ Anisotropic displacement parameters were employed for all non-hydrogen atoms. Using an idealized geometry, a riding model, and a fixed isotropic displacement parameter, the hydrogen atoms of the amine were fine-tuned in their positions.

The FT-IR spectrum was recorded at room temperature with a dispersed sample in a KBr pellet using PerkinElmer 1600 FT-IR spectrometer within the range 400–4000 cm⁻¹.

TGA-DSC measurements were performed with a NETZSCH STA 409 PC/PG, using Al₂O₃ crucible. TG/DSC measurements were taken on 27.004 mg in static air, within the 27–900 °C temperature range, with a heating rate of 6 °C min⁻¹.

The solid-state UV-VIS spectroscopy measurements were performed in the reflectance mode on a Specord 250 (AnalyticJena) spectrophotometer in the wavelength range of 190–1100 nm.

Static magnetic measurements were performed in Quantum Design MPMS®3 magnetometer in the temperature range from 1.8 to 300 K in magnetic fields up to 70 kOe. The static susceptibility was estimated as the ratio of the magnetic moment and applied magnetic field of 1 kOe. Alternating-current (AC) susceptibility measurements were performed in Quantum Design MPMS-XL and PPMS (equipped with ACMS option) to cover the frequency range 0.1 Hz to 10 kHz. A nascent polycrystalline (powdered) specimen was fixed in a gelatine capsule with eicosane wax to avoid crystallite reorientation in magnetic fields. The diamagnetic contribution of the capsule, eicosane, and sample was subtracted from the raw data. The electron paramagnetic resonance (EPR) spectra were studied using Bruker ELEXSYS II E500 X-band spectrometer with an operating frequency of 9.4 GHz and ESR910 helium flow-type cryostat on powdered sample mixed with Apiezon N grease attached to the Suprasil sample holder.

2.2. Synthesis

All the employed chemicals were used as received without further purification. Blue single crystals of I (Fig. 1) have been afforded through a slow evaporation process. The preparation protocol consists of preparing two solutions as follows: 0.2 g of 2-amino-4-methylpyrimidine (Ampym) (2 mmol) were dissolved in 50 ml of distilled water (solution 1) and a 0.23 g of CoCl₂·6H₂O (1 mmol) also dissolved in 50 ml of distilled water (solution 2). Then, the solution 2 was added drop by drop in solution 1. The mixture was acidified with hydrochloric acid HCl (pH ≈ 2.5), which was slowly added under magnetic stirring until the homogeneity of the mixture. The final solution was left to evaporate at room temperature, and the obtained crystals were collected after about a week. The purity of the prepared crystals was checked by powder X-ray diffraction (Fig. S2†) and through Elem. Microanal: [Anal./Calc.]: C, 38.16 (37.54); H, 4.88 (4.69); N, 26.17 (26.28); Cl, 22.31 (22.21). The overall yield of the reaction, based on the Co component, was determined to be near 83%. The reaction scheme leading to the formation of the complex I is given below (Scheme 1).

Fig. 1 Recovered blue crystals of compound I.

Scheme 1 Synthesis of complex I.

2.3. Computational details

2.3.1. Periodic density functional theory. Periodic Density Functional Theory (DFT) calculations were performed using the Vienna Ab Initio Simulation Package (VASP) with the projector-augmented wave (PAW) method and Perdew–Burke–Ernzerhof (PBE) functional was used. A cut-off of 500 eV was set to control the number of plane waves.^1–8 The tag K spacing was selected for sampling the Brillouin zone with a value of 0.4.^41–48 That value for (C₅H₈N₃)₂[CoCl₄(C₅H₇N₃)₂] structure was enough to obtain negligible changes in the optimized cell parameters (a = 7.9787 Å, b = 8.8045 Å, c = 11.1457 Å) in good agreement with the experimental values (a = 7.6349 Å, b = 8.9698 Å, c = 11.0037 Å). DFT+U calculations⁴⁹ were performed by applying a U value of 10 eV for d-states of Co. The density and projected density of states (DOS and PDOS, respectively) for the relaxed structures were obtained using the tetrahedron method with Blöchl corrections with 6 6 2 mesh of K points.

2.3.2. Ab initio calculations in magnetic analysis. Ab initio calculations were performed using the ORCA 5.0.4 computational package.⁵⁰ The calculations of single-ion anisotropy parameters were based on the state-averaged complete-active-space self-consistent field (SA-CASSCF) wave functions followed by N-electron valence second-order perturbation theory (NEVPT2).^51–55 The active space of the CASSCF calculations on metal-based d-orbitals was defined at the beginning as CAS(7,5), second d-shell as CAS(7,10) and bonding ligand orbitals as CAS(11,7) were included further. The state-averaged approach was used with all 10 quartets and 40 doublet states equally weighted. The estimate of zero-field splitting parameters was obtained through the quasi-degenerate perturbation theory,⁵⁶ in which an approximation to the Breit–Pauli form of the spin–orbit coupling operator,⁵⁷ and the effective Hamiltonian theory⁵⁸ was utilized. Relativistic effects were taken into account by using the second-order Douglas–Kroll–Hess Hamiltonian (DKH)⁵⁹ together with the corresponding segmented all-electron relativistic contracted (SARC) version of the triple-ζ basis set Def2-TZVP^60,61 for all atoms. All calculations utilized the RI approximation and the chain-of-spheres (RIJCOSX) approximation to exact exchange⁶² with appropriate decontracted auxiliary basis sets SARC/J and Def2-TZVP/C^63,64 and tight SCF convergence criteria.

Vibronic properties were calculated using FREQ keyword as implemented in ORCA from the optimized geometry of the isolated anion in the gas phase obtained by the DFT method using TPSS functional^65,66 with def2-TZVP⁶⁷ and def2/J⁶³ basis sets, including the atom-pairwise dispersion correction with the Becke–Johnson damping scheme (D3BJ).^68,69

3 Results and discussion

3.1. Crystal structure of [C₅H₈N₃]₂[CoCl₄(C₅H₇N₃)₂]

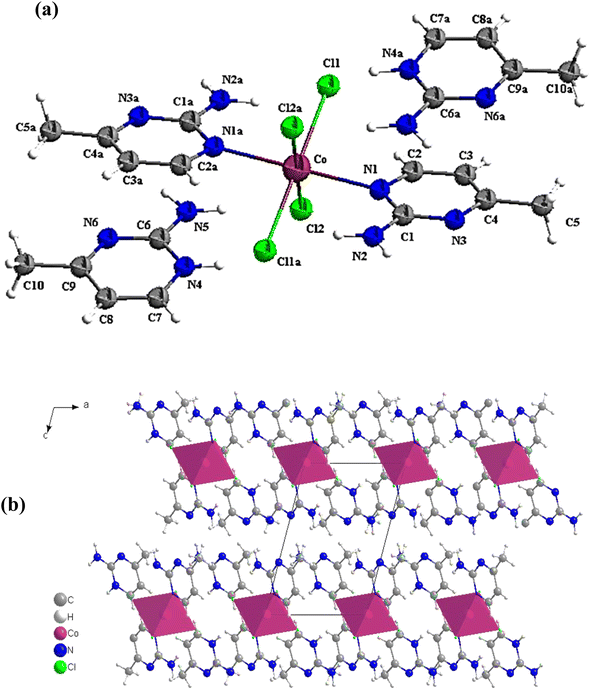
X-ray structure analyses have been performed as explained above. It is demonstrated from them that complex I crystallizes in the triclinic system, space group P1̄, which sets it apart from a similar complex with a comparable geometry, ligands and counter cation but different metal ion reported by Jabeur et al. in 2022. Structural analyses reveal that the CoCl₄N₂ center is best described as a moderately distorted octahedron, ligated through four Cl atoms, originating from the acidified solution and the chloride metal reagent, and the two N atoms from the monodentate amine (Ampym). Co–Cl1/Cl1a, Co–Cl2/Cl2a and Co–N1/N1a bond distances are equal to 2.5088(9) Å, 2.528(9) Å and 2.246(3) Å, respectively. Bond distances are similar to those of the [AmpH]₂[MnCl₄(Amp)₂].⁷⁰

Calculating the octahedron's distortion coefficient, Δ_d can be used to demonstrate how the molecular structure is distorted. The calculation procedure is explained in detail in.³⁰ Using the values mentioned in Table S2,† Δ_d (Co) is equal to 2.2 × 10⁻³ Å, demonstrating that CoCl₄N₂ is moderately deformed (Fig. 2a). The deformation rises from a bending of the CoCl₄ entity out of the pyrimidine entity by 6.42(9)°. As a result of the inversion center at the position of the Co1 atom, both pyrimidine ligands are nevertheless co-planar towards each other, displaced by 0.531(19) Å. The ortho amino groups are positioned anti towards each other.

Fig. 2 (a) Formular unit of I. (b) Projection of the crystal packing of complex I along the b-axis.

In other compounds with similar amine groups, the bond lengths and angles inside the aminopyrimidine cations are near the typical values.^28,29,71 In fact, within the coordinated amine rings, the C–N and C–C bonds are 1.343(3) and 1.396(6) Å, identical to the uncoordinated cation [C₅H₈N₃]⁺ of 1.341(3) and 1.417(6) Å, respectively. Concerning the angle values, the comparison of the C6–N4–C7 angle that is equal to 121.7(4)° with the unprotonated pyrimidine mentioned in ref. 72, that takes the value of 117.94(2)°, we can deduce the rise in this internal angle at the protonated nitrogen atom.

The projection of the crystalline structure along the b-axis is displayed in Fig. 2b. The distorted orthogonal intersection of the CoCl₄ and the Ampym entities of 83.58(9)° results in two individual layer structures intersecting each other. The CoCl₄ fragments stacks along [0 2 3], the planes of the ligands average to [5 4 2].

The cohesiveness of the various components in the crystal is ensured by a complex network of hydrogen bonds and controlled by electrostatic interactions (Fig. 3a and b). The interconnection of free pyrimidines and the other entities is assured via intermolecular hydrogen bands created between N2⋯N6, N5⋯N3, N5⋯Cl2, N4⋯Cl1, N4⋯Cl2. Whereas intramolecular hydrogen bands are manifested between N2⋯Cl1 and C2⋯Cl1 (Table S3†).

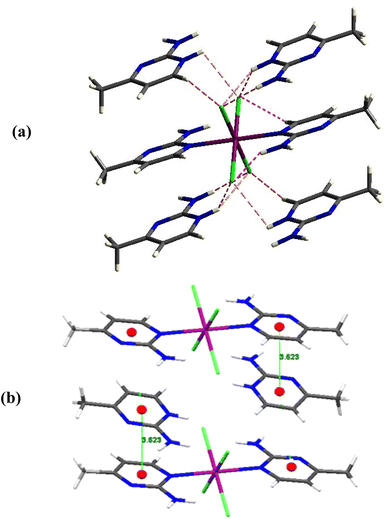Fig. 3 (a) Different types of hydrogen bonding in compound I. (b) Electrostatic interactions between pyrimidines.

3.2. Infrared spectroscopy

With infrared absorption, vibrational characteristics were provided to give further details on the crystal structure (Fig. S3†). The comparison with other compounds linked to the same cation Ampy^28,29 led to the thorough description of all detected bands in the infrared spectra of the cation in complex I. Table S4† summarizes the different values detected at low and high frequencies area. The description of the infrared absorption spectrum was detailed in the ESI.†

3.3. Thermal investigation

Thermal analyses were measured to highlight the phase transitions and the thermal stability of the compounds. The curves obtained during the decomposition of compound I under flowing air with a heating rate of 6 °C min⁻¹ between 25 and 800 °C are reported in Fig. S4.†

3.4. UV-VIS spectroscopy

The optical qualities of our substance were assessed via UV-visible spectroscopy. Due to its magnetic and optical properties, which provide information on the site geometry, Co(II) is often employed as a probe of metal binding sites and this to confirm the octahedral geometry around the cobalt element in this article. The characteristic bands of Co^II hexacoordinated metal and the different transitions are elucidated in the ESI file.†

Periodic DFT calculations have been performed and included in the ESI† to get the band gap of (C₅H₈N₃)₂[CoCl₄(C₅H₇N₃)₂].

3.5. Magnetic properties and theoretical calculations

The behavior of the magnetic properties of I is typical for high-spin Co(II) ions with S = 3/2 (3d⁷ ion) in the center of isolated molecules, as shown by the temperature dependence of the χT product (Fig. 4a) and field dependence of magnetization (plotted against the reduced field in Fig. 4b). The room-temperature value of χT = 3.42 emu K mol⁻¹, corresponding to the effective magnetic moment μ_eff = 5.23 μ_B (μ_B is Bohr magneton) gradually decreases with lowering the temperature with steeper drop at the lowest temperature, which suggests an influence of weak antiferromagnetic intermolecular interactions. The deviation of the room-temperature effective magnetic moment from the spin-only value appears due to the strong influence of the spin–orbit coupling in Co(II) ions. No difference between zero-field cooled (ZFC), and field-cooled (FC) magnetic response was observed as well as no sign of magnetic hysteresis as possible evidence of magnetic ordering or blocking temperature at low temperatures. The deviation between the magnetization curves plotted against the reduced field between 1.8 K and 15 K shows the presence of sizable anisotropy. Our attempts to use the effective spin Hamiltonian to fit the experimental data did not yield satisfactory results. Both positive and negative values of the D-parameter were obtained depending on the starting value in the fitting procedure. Therefore, SA-CASSCF/NEVPT2 calculations were performed on isolated [CoCl₄(C₅H₇N₃)₂]²⁻ anions to predict and be able to apply some constraints on the spin Hamiltonian parameters in the magnetic properties analysis. As shown recently,⁷³ including the second coordination sphere might be beneficial in correctly predicting zero-field splitting parameters. Thus, the calculations were also performed on a molecular unit comprising central [CoCl₄(C₅H₇N₃)₂]²⁻ anion surrounded by four nearest Ampym cations, as shown in Fig. 2. The results of the SA-CASSCF/NEVPT2 calculations using the atom positions estimated from the X-ray diffraction are summarized in Table 1 and Fig. 5. All calculations suggest the presence of the gap energy Δ_1-2 between two lowest doublets in the range approximately 220–250 cm⁻¹ with low-lying excited states, which strongly contribute to the ground state. As one can see, a slight enhancement of the energy gap Δ_1-2 between the two lowest doublets was obtained when the second coordination sphere was included, but the anisotropy of effective g-factors of the ground Kramers doublet was reduced. In addition to the presence of very low-lying excited states, the norm of projected states of the effective Hamiltonian obtained through the 2nd-order spin–orbit coupling contribution to the zero-field splitting is as low as 0.61. In this case, the effective spin Hamiltonian approach for the description of magnetic properties is not applicable.

Fig. 4 (a) Experimental χT product of I measured in the applied field of 1 kOe (open symbols) compared with the simulation obtained directly from CAS(7,5) SA-CASSCF/NEVPT2 results employing single_aniso module on anion unit. (b) Experimental magnetization vs. reduced field at different temperatures.

Table 1 Effective g-factors of the ground Kramers doublet and energy gap Δ_1-2 between two lowest doublets in 1 derived from SA-CASSCF/NEVPT2 calculations done in ORCA

			Δ1-2 (cm^−1)
[CoCl4(C5H7N3)2]^2−
CAS(7,5)	[2.135, 2.774, 7.631]	4.180	241.6
CAS(7,10)	[2.088, 2.879, 7.566]	4.178	223.9
CAS(11,7)	[2.065, 2.812, 7.653]	4.117	233.7
{(C5H8N3)4[CoCl4(C5H7N3)2]}^2+
CAS(7,5)	[2.713, 3.681, 6.638]	4.344	251.9

---

Fig. 5 The energies of six lowest multiplets as obtained from SA-CASSCF/NEVPT2 calculations using isolated [CoCl₄(C₅H₇N₃)₂]²⁻ anion for different CAS including the energies of d-orbitals obtained from AILFT analysis in the case of CAS(7,5).

Ab Initio Ligand Field Theory (AILFT)⁷⁴ analysis yields the energy levels of d-orbitals, which are related to the crystal field parameters and enable the revealing of the type of crystal-field anisotropy. The splitting of the three lowest d-orbital levels by δ_ax and δ_rh, as shown in Fig. 5 for the case of CAS(7,5), gives a reasonable estimate of the axial crystal field parameter Δ_ax and rhombic parameter Δ_rh, as argued in ref. 75. Analysis suggests that orbital doublet state ⁴E_g with negative Δ_ax (easy-axis anisotropy) is the ground state of I with axial parameter Δ_ax ≈ −δ_ax = −870 cm⁻¹ and strong rhombic parameter |Δ_rh| ≈ |δ_rh| = 145 cm⁻¹. The χT vs. T dependence calculated directly by ORCA for [CoCl₄(C₅H₇N₃)₂]²⁻ anion using the obtained set of parameters with CAS(7,5) shown in Fig. 4a suggests the importance of including intermolecular interactions for the correct description of magnetic properties. We have employed the single_aniso⁷⁶ module in ORCA, including six doublet levels and intermolecular interactions zJ to calculate the susceptibility, which agrees well with the experimental data for zJ = 0.4 cm⁻¹.

An X-band EPR experiment was also performed at low temperatures, as shown in Fig. 6. The peak-to-peak signal intensity decreases with increasing temperature, typical for the transitions between the levels of well-isolated ground Kramers doublet. A significant line broadening, most probably due to the presence of unresolved hyperfine splitting, does not allow an accurate determination of effective g-factors of the ground Kramers doublet using an effective S_eff = ½ model. Nevertheless, an attempt to simulate the EPR spectra in the EasySpin simulation package⁷⁷ yielded an estimate of , which appear to be in good agreement with predicted values in Table 1 for increased coordination sphere in {[(C₅H₈N₃)₄] [CoCl₄(C₅H₇N₃)₂]}²⁺ unit.

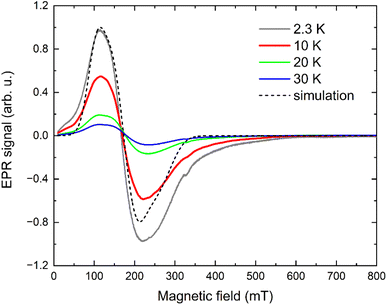Fig. 6 X-band EPR spectra of I measured at 2, 10, 20 and 30 K (solid lines) including a simulation (dashed line) using an effective S_eff = 1/2 model.

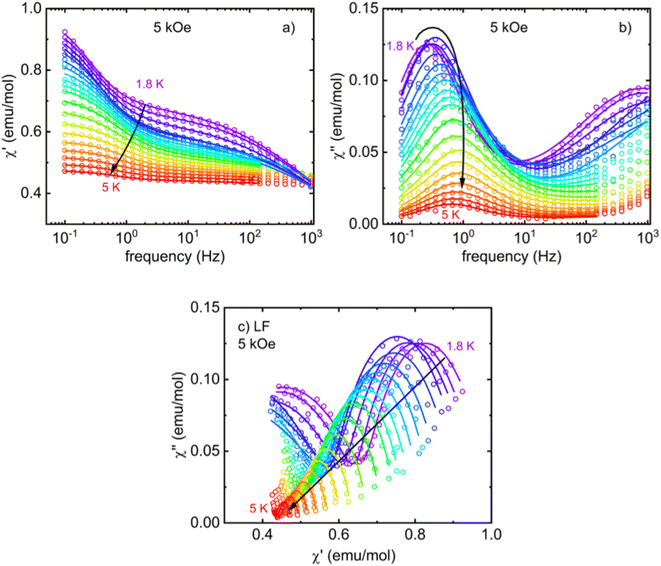
In order to probe the SIM behavior as in other Co(II)-based complexes, the dynamic response of I at low temperatures and in different applied static (DC) magnetic fields was investigated. No signature of relaxation in AC susceptibility was observed in the zero-magnetic field. This seems to be a common consequence of the very fast relaxation of magnetization due to the quantum tunneling of magnetization (QTM) induced by hyperfine interactions with the nuclear spins. Usually, the applied DC field is able to suppress QTM, and slower relaxation pathways can be observed. Indeed, following the application of a small DC magnetic field, two relaxation channels were observed: the high-frequency (HF) relaxation channel close to 1 kHz and the low-frequency (LF) relaxation channel in the region below 1 Hz (Fig. S1† and 8a). The existence of multiple relaxation channels in SIMs has been theoretically predicted^78–80 and observed in many experimental examples. The relaxation times extracted from Fig. S1† and 7a are shown in Fig. 7b. While the LF channel slows down up to the highest experimental field, the HF channel, once it appears at small fields, accelerates above 3 kOe.

Fig. 7 (a) Cole–Cole plots of I in different applied DC fields measured at 2 K including the fits of the modified Debye model with two relaxation channels. (b) Field dependence of relaxation times extracted from Cole–Cole plots.

Next, one DC magnetic field was selected to study the temperature dependence of the relaxation time in the LF and HF regions. The corresponding frequency-dependent AC susceptibility at different temperatures in the applied DC field of 5 kOe is shown in Fig. 8 and 9. Both relaxation channels show a gradual acceleration of the relaxation time upon warming up, but the LF relaxation channel seems to tend to slow again when approaching 5 K. The corresponding Cole–Cole plots for the frequency range 0.1–1 kHz (Fig. 8c) and 20 Hz to 10 kHz (Fig. 9c) were analyzed using the modified Debye model separately (obtained using two separate devices) and yielded the temperature dependence of the relaxation time presented in Fig. 10. In each region, one or two relaxation channels were included in modified Debye model as needed for a proper description of AC susceptibility and extraction of relaxation rates of LF and HF channel. Since there is no saturation of the relaxation time of the HF relaxation channel in the low-temperature region, the QTM was neglected (usually suppressed by the magnetic field). For the easy-axis anisotropy present in I, a contribution of the two-phonon Orbach and Raman relaxation processes govern the spin reversal in Kramers ions with and τ_R⁻¹ = CTⁿ, where U_eff is the energy barrier for thermally activated relaxation within the Orbach process. The exponent n describing the Raman process has a value n = 9 for Kramers ions with an insulated ground doublet,⁸¹ but in SIMs often takes lower values due to the involvement of both acoustic and optical phonons.⁸² The Orbach is more effective at higher temperatures because it requires the exact thermal energy of participating phonons comparable to the energy barrier.

Fig. 8 Frequency dependence of real (a) and imaginary (b) components of AC susceptibility of I measured in an applied DC field 5 kOe in the temperature range 1.8–5 K (c) Cole–Cole plots of LF relaxation channel of I. The fit of the modified Debye model is shown by solid lines of the corresponding color (a second Debye component was included to account for the onset of a high-frequency relaxation channel if necessary).

Fig. 9 Frequency dependence of real (a) and imaginary (b) components of AC susceptibility of I measured in an applied DC field 5 kOe in the temperature range 2–3.25 K in the frequency range 20 Hz to 10 kHz. (c) Cole–Cole plots of HF relaxation channel of I. The fit of the modified Debye model is shown by solid lines of the corresponding color (a second Debye component was included to account for the onset of a low-frequency relaxation channel if necessary).

Fig. 10 Temperature dependence of the relaxation time in reduced coordinates in applied DC field 5 kOe (HF channel, red symbols, LF channel, blue symbols). Models to describe the behavior of the relaxation time are shown by the corresponding lines.

In the Arrhenius-type plot in Fig. 10, one can see a small change in the slope between the low-temperature and high-temperature regimes. The influence of the power law process (Raman, but may contain other influences) to describe the temperature dependence of the relaxation time in the full temperature range was included τ_HF⁻¹ = τ_ORB⁻¹ + τ_R⁻¹ yielding τ₀ = 1.08 × 10⁻⁸ s, U_eff = 16.5 cm⁻¹ (23.8 K), C = 2010.3 K⁻ⁿ, and n = 1.63. The estimated relaxation barrier is much smaller than predicted energy gap Δ_1-2, an effect often observed as underbarrier relaxation in other 3d or 4f SIMs, e.g., in ref. 83–85.

The nature of slow relaxation in SIMs can also be predicted using SA-CASSCF/NEPVT2 energies with the single_aniso module in ORCA, which estimates relaxation transition rates (magnetic moment matrix elements). For Co(II) ions, the two lowest Kramers doublets can be involved in relaxation that were included in the calculation shown in Fig. 11. The transition rate on ground state QTM effect is high (0.817), and QTM will play a significant role in their fast zero-field relaxation unable to detect it by AC susceptibility. Once it is suppressed by the applications of the magnetic field, as in the case of I, the Orbach process may take place (but not only).

Fig. 11 Single_aniso calculations of magnetic moment matrix elements between Kramers doublets for I, based on CAS(7,5) using isolated anion.

The reduction of the observed relaxation barrier in comparison to the prediction may be due to insufficient temperature range to recover the correct barrier (a clear linear region in the Arrhenius plots up to much higher temperatures is needed), and a relatively large τ₀ may suggest the influence of intermolecular interactions. On the other hand, the influence of anharmonic phonons on slow magnetic relaxation was emphasized recently,⁸⁶ stating that the presence of off-resonance phonon modes contributes to much lower U_eff observed experimentally in comparison to expected Δ_1-2 in easy-axis SMMs, so-called underbarrier relaxation. Thus, the study of spin-vibronic coupling with low-energy molecular vibrations, which mediate the spin-phonon-bath energy exchange in SIMs, is of current interest.^87–89 Several reports suggest the presence of low-energy vibrational modes related to the local molecular rotations and torsion with a strong spin-phonon coupling to affect the slow spin-phonon relaxation in some molecular systems.^90–95 Recently, it was shown that the underbarrier relaxation may result from the involvement of such low-energy vibrational modes in the Raman process.^96,97 In addition, an unusual exponential temperature dependence of the relaxation time of the Raman process was predicted, undistinguishable from the Orbach process through the magnetic energy barrier, which could hinder the observation of the actual Orbach process. When the temperature dependence of the relaxation time is analyzed by the standard combination of Orbach and Raman process in such case, a small U_eff and unusually low exponent for the Raman process are obtained as in I. We probed the presence of the low-energy vibrational modes that could be involved in such under barrier relaxation in I using the DFT calculations as implemented in ORCA. The geometry of the isolated [CoCl₄(C₅H₇N₃)₂]²⁻ anion I was optimized using TPSS functional, and vibrational modes were calculated. The lowest calculated energies of vibrational modes below 50 cm⁻¹ are 14.07, 25.10, 26.53, and 46.02 cm⁻¹ and correspond to vibrations involving Ampym ligands. Although, this is a rough approximation since the calculation does not include the Ampym cations surrounding the [CoCl₄(C₅H₇N₃)₂]²⁻ anion, we assume that the energy scale of the low-energy vibrations would not differ significantly in the real crystal.

The LF relaxation channel slows down to very high DC magnetic fields (Fig. 7b) like in other SIMs with more than one relaxation channel, e.g. in ref. 98–103. Such an effect is often observed when the presence of the phonon-bottleneck effect influences the direct relaxation process^104,105 due to weak contact with the thermal reservoir. An anomalous slowing down in the temperature dependence of relaxation time τ_LF was observed above 4 K, which was previously reported in several 3d-ion- or Gd(III)-based magnets,^{100,101,104–109} usually for low-frequency field-induced relaxation channels. Unfortunately, the origin of this behavior remains unclear, and its observation is complicated by the usual intensity decrease of the out-of-phase component of AC susceptibility, which yields higher error bars on the estimated relaxation time in the high-temperature region. The fit of power dependence τ⁻¹ = CTⁿ in the low-temperature region below 3.5 K (Fig. 10) was performed yielding exponent n = 1.98 with C = 0.49 K⁻ⁿ. This seems to be the case of direct relaxation process influenced by the presence of the severe phonon-bottleneck effect¹⁰¹ when the temperature dependence of the relaxation time is indeed renormalized towards τ ∼ T⁻² and the characteristic relaxation time can be is slowed down by several orders of magnitude. The field dependence of the relaxation time for LF channel supports that assumption. In relation to the HF relaxation channel, the presence of phonon-bottleneck effect does not influence the temperature dependence of the Orbach relaxation process, thus, it does not influence the estimation of the relaxation barrier.

In summary, the HF relaxation channel in I is characterized by under barrier relaxation, and the LF relaxation seems to be strongly influenced by the phonon-bottleneck effect in combination with the direct relaxation process.

4 Conclusion

The synthesis, the design, and the structural characterizations of a new mononuclear halide compound with the formula (C₅H₈N₃)₂[CoCl₄(C₅H₇N₃)₂] were discussed in this paper. The whole structure is constructed by infinite chains built up by the hydrogen bonding (N–H⋯Cl, and N–H⋯N) joining the anionic and the cationic components in complementarity with the π–π interactions, which exert an influence over the resulting structure. These latter are proven by Hirshfeld surface analysis. The detailed and rigorous allocation of IR vibration spectra was carried out based on the spectra of homologous compounds, and an assignment of all the bands was given. Optical UV-VIS spectroscopy is an incredibly useful tool in understanding the formation and the conduction type of materials. It confirms the octahedral geometry surrounding the cobalt ion. The optical band gap energy takes a value of 3.4 eV, maybe revealing a semi-conducting behavior of the complex that presents the well-known d–d transitions in the visible region. Band gap value obtained by theoretical calculations is in good agreement with the gap addressed experimentally. These calculations highlight the important role of the Co d-states in the electronic transitions.

Then, it is well established that the geometry around the metal complex plays a decisive role in magnetic features. In fact, the static magnetic measurements supplemented by ab initio calculations report weak antiferromagnetic intermolecular interactions and appreciable easy-axis anisotropy. As a result, compound I behaves as a field-induced SIM with two relaxation channels involved in the slow-magnetic relaxation. Despite the significant energy barrier prediction, the under barrier relaxation, which can be related to low-energy vibronic modes as suggested by recent theoretical predictions, plays an important role in the HF relaxation channel. The importance of the low-energy vibronic modes of the ligands is emphasized by the DFT calculations and related to the recent predictions of unusual exponential temperature dependence of the Raman relaxation. On the other hand, the direct relaxation process, in conjunction with the phonon-bottleneck effect, appears to impact LF relaxation significantly.

Author contributions

Wiem Jabeur: formal analysis, writing – original draft; Marcus Korb: data curation, investigation; Mohamed Hamdi: writing, validation; Mariia Holub: formal analysis, visualization; Dávid Princík: data curation, investigation, Vladimír Zeleňák: data curation, investigation; Antonio Sánchez-Coronilla: formal analysis, investigation; Marwan Shalash: formal analysis, visualization, Erik Čižmár: review & editing, data curation, project administration; Houcine Naïli: project administration, validation, supervision.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FFR-2024-2885-05”. E. Č. and H. N. were supported by the Slovak Research and Development Agency under project No. APVV-18-0197 and APVV-22-0172. Theoretical calculations were performed through CICA - Centro Informático Científico de Andalucía (Spain). ASC thanks funds from Junta de Andalucía (2019/FQM-106; 2021/FQM-106; sol-201800107510-tra FEDER-UCA18-107510) and Ministerio de Ciencia, Innovación y Universidades of the Spanish Government RTI2018-096393-B-I00.

References

1. F. Moro, D. P. Mills, S. T. Liddle and J. Van Slageren, The inherent single-molecule magnet character of trivalent uranium, Angew. Chem., Int. Ed., 2013, 52(12), 3430–3433,  DOI:10.1002/anie.201208015.
2. J. J. Le Roy, M. Jeletic, S. I. Gorelsky, I. Korobkov, L. Ungur, L. F. Chibotaru and M. Murugesu, An organometallic building block approach to produce a multidecker 4f single-molecule magnet, J. Am. Chem. Soc., 2013, 135(9), 3502–3510,  DOI:10.1021/ja310642h.
3. M. R. Saber and K. R. Dunbar, Trigonal bipyramidal 5d–4f molecules with SMM behavior, Chem. Commun., 2014, 50(17), 2177–2179,  10.1039/C3CC49124B.
4. J. M. Zadrozny, J. Telser and J. R. Long, Slow magnetic relaxation in the tetrahedral cobalt(II) complexes [Co(EPh)₄]²⁻ (E=O, S, Se), Polyhedron, 2013, 64, 209–217,  DOI:10.1016/J.POLY.2013.04.008.
5. D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, Slow magnetic relaxation in a high-spin iron(II) complex, J. Am. Chem. Soc., 2010, 132(4), 1224–1225,  DOI:10.1021/JA909560D/SUPPL_FILE/JA909560D_SI_001.PDF.
6. W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, Slow magnetic relaxation in a family of trigonal pyramidal iron(II) pyrrolide complexes, J. Am. Chem. Soc., 2010, 132(51), 18115–18126,  DOI:10.1021/ja105291x.
7. D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, High-Spin Cyclopentadienyl Complexes: A Single-Molecule Magnet Based on the Aryl-Iron(II) Cyclopentadienyl Type, Chem. - Eur. J., 2011, 17(17), 4700–4704,  DOI:10.1002/CHEM.201003288.
8. J. M. Zadrozny and J. R. Long, Slow magnetic relaxation at zero field in the tetrahedral complex [Co(SPh)₄]^2-, J. Am. Chem. Soc., 2011, 133(51), 20732–20734,  DOI:10.1021/JA2100142.
9. A. Buchholz, A. O. Eseola and W. Plass, Slow magnetic relaxation in mononuclear tetrahedral cobalt(II) complexes with 2-(1H-imidazole-2-yl)phenol based ligands, C. R. Chim., 2012, 15(10), 929–936,  DOI:10.1016/J.CRCI.2012.07.005.
10. S. Mossin, B. L. Tran, D. Adhikari, M. Pink, F. W. Heinemann, J. Sutter, R. K. Szilagyi, K. Meyer and D. J. Mindiola, A mononuclear Fe(III) single molecule magnet with a 3/2↔5/2 spin crossover, J. Am. Chem. Soc., 2012, 134(33), 13651–13661,  DOI:10.1021/ja302660k.
11. J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, Field-induced slow magnetic relaxation in a six-coordinate mononuclear cobalt(II) complex with a positive anisotropy, J. Am. Chem. Soc., 2012, 134(38), 15704–15707,  DOI:10.1021/ja3075314.
12. J. M. Zadrozny, J. Liu, N. A. Piro, C. J. Chang, S. Hill and J. R. Long, Slow magnetic relaxation in a pseudotetrahedral cobalt(II) complex with easy-plane anisotropy, Chem. Commun., 2012, 48(33), 3927–3929,  10.1039/C2CC16430B.
13. J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Slow magnetization dynamics in a series of two-coordinate iron(II) complexes, Chem. Sci., 2012, 4(1), 125–138,  10.1039/C2SC20801F.
14. Y. Y. Zhu, C. Cui, Y. Q. Zhang, J. H. Jia, X. Guo, C. Gao, K. Qian, S. D. Jiang, B. W. Wang, Z. M. Wang and S. Gao, Zero-field slow magnetic relaxation from single Co(II) ion: a transition metal single-molecule magnet with high anisotropy barrier, Chem. Sci., 2013, 4(4), 1802–1806,  10.1039/C3SC21893G.
15. T. Jurca, A. Farghal, P. H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, Single-molecule magnet behavior with a single metal center enhanced through peripheral ligand modifications, J. Am. Chem. Soc., 2011, 133(40), 15814–15817,  DOI:10.1021/JA204562M/.
16. S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, Mononuclear single-molecule magnets: Tailoring the magnetic anisotropy of first-row transition-metal complexes, J. Am. Chem. Soc., 2013, 135(18), 7010–7018,  DOI:10.1021/JA4015138.
17. F. Yang, Q. Zhou, Y. Zhang, G. Zeng, G. Li, Z. Shi, B. Wang and S. Feng, Inspiration from old molecules: field-induced slow magnetic relaxation in three air-stable tetrahedral cobalt(II) compounds, Chem. Commun., 2013, 49(46), 5289–5291,  10.1039/C3CC00277B.
18. R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Slow magnetic relaxation in octahedral cobalt(II) field-induced single-ion magnet with positive axial and large rhombic anisotropy, Inorg. Chem., 2014, 53(12), 5896–5898,  DOI:10.1021/IC500916U.
19. A. Eichhöfer, Y. Lan, V. Mereacre, T. Bodenstein and F. Weigend, Slow magnetic relaxation in trigonal-planar mononuclear Fe(II) and Co(II) bis(trimethylsilyl)amido complexes - A comparative study, Inorg. Chem., 2014, 53(4), 1962–1974,  DOI:10.1021/IC401677J.
20. R. Boča, J. Miklovič and J. Titiš, Simple mononuclear cobalt(II) complex: A single-molecule magnet showing two slow relaxation processes, Inorg. Chem., 2014, 53(5), 2367–2369,  DOI:10.1021/IC5000638.
21. R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, High-Spin Molecules: [Mn₁₂O₁₂(O₂CR)₁₆(H₂O)₄], J. Am. Chem. Soc., 1993, 115(5), 1804–1816,  DOI:10.1021/JA00058A027.
22. A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clérac, W. Wernsdorfer, C. E. Anson and A. K. Powell, A Ferromagnetically Coupled Mn₁₉ Aggregate with a Record S=83/2 Ground Spin State, Angew. Chem., 2006, 118(30), 5048–5051,  DOI:10.1002/anie.200601467.
23. C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, A record anisotropy barrier for a single-molecule magnet, J. Am. Chem. Soc., 2007, 129(10), 2754–2755,  DOI:10.1021/JA068961M.
24. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide single-molecule magnets, Chem. Rev., 2013, 113(7), 5110–5148,  DOI:10.1021/CR400018Q.
25. J. M. Frost, K. L. M. Harriman and M. Murugesu, The rise of 3-d single-ion magnets in molecular magnetism: towards materials from molecules?, Chem. Sci., 2016, 7(4), 2470–2491,  10.1039/C5SC03224E.
26. G. A. Craig and M. Murrie, 3d single-ion magnets, Chem. Soc. Rev., 2015, 44(8), 2135–2147,  10.1039/C4CS00439F.
27. C. Rajnák, J. Titiš, J. Moncol’ and R. Boča, Effect of the distant substituent on the slow magnetic relaxation of the mononuclear Co(II) complex with pincer-type ligands, Dalton Trans., 2020, 49(14), 4206–4210,  10.1039/D0DT00096E.
28. S. Ghosh, S. Kamilya, M. Das, S. Mehta, M. E. Boulon, I. Nemec, M. Rouzières, R. Herchel and A. Mondal, Effect of Coordination Geometry on Magnetic Properties in a Series of Cobalt(II) Complexes and Structural Transformation in Mother Liquor, Inorg. Chem., 2020, 59(10), 7067–7081,  DOI:10.1021/ACS.INORGCHEM.0C00538.
29. H. I. Karunadasa, K. D. Arquero, L. A. Berben and J. R. Long, Enhancing the Magnetic Anisotropy of Cyano-Ligated Chromium(II) and Chromium(III) Complexes via Heavy Halide Ligand Effects, Inorg. Chem., 2010, 49(11), 4738–4740,  DOI:10.1021/IC1002995/SUPPL_FILE/IC1002995_SI_002.CIF.
30. W. Jabeur, M. Korb, J. S. Al-Otaibi, E. Čižmár, R. Badraoui, V. Zeleňák and H. Naïli, Physico-chemical characterizations and biological evaluation of a new semiconducting metal–organic compound based on pyrimidine frameworks, Inorg. Chem. Commun., 2022, 139, 109279,  DOI:10.1016/J.INOCHE.2022.109279.
31. W. Jabeur, R. Msalmi, M. Holub, E. Mosconi, E Čižmár, A. Tozri, N. A. Althubiti and H. Naïli, Optical and magnetic characterization of one-dimensional Cu(II)-based perovskite: a high UV–Vis–NIR absorber, J. Mater. Chem. C, 2021, 9(47), 17158–17166,  10.1039/D1TC04336F.
32. X. N. Yao, J. Z. Du, Y. Q. Zhang, X. B. Leng, M. W. Yang, S. D. Jiang, Z. X. Wang, Z. W. Ouyang, L. Deng, B. W. Wang and S. Gao, Two-coordinate Co(II) imido complexes as outstanding single-molecule magnets, J. Am. Chem. Soc., 2017, 139(1), 373–380,  DOI:10.1021/jacs.6b11043.
33. B. Yao, Y. F. Deng, T. Li, J. Xiong, B. W. Wang, Z. Zheng and Y. Z. Zhang, Construction and Magnetic Study of a Trigonal-Prismatic Cobalt(II) Single-Ion Magnet, Inorg. Chem., 2018, 57(22), 14047–14051,  DOI:10.1021/acs.inorgchem.8b02692.
34. M. R. Saber and K. R. Dunbar, Ligands effects on the magnetic anisotropy of tetrahedral cobalt complexes, Chem. Commun., 2014, 50(82), 12266–12269,  10.1039/c4cc05724d.
35. Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sakar and J. van Slageren, A four-coordinate cobalt(II) single-ion magnet with coercivity and a very high energy barrier, Nat. Commun., 2016, 7(Ii), 1–8,  DOI:10.1038/ncomms10467.
36. S. Ye and F. Neese, How do heavier halide ligands affect the signs and magnitudes of the zero-field splittings in halogenonickel(II) Scorpionate Complexes? A Theoretical Investigation Coupled to Ligand-Field Analysis, J. Chem. Theory Comput., 2012, 8(7), 2344–2351,  DOI:10.1021/CT300237F.
37. P. J. Desrochers, J. Telser, S. A. Zvyagin, A. Ozarowski, J. Krzystek and D. A. Vicic, Electronic structure of four-coordinate C_3v nickel(II) scorpionate complexes: Investigation by high-frequency and -field electron paramagnetic resonance and electronic absorption spectroscopies, Inorg. Chem., 2006, 45(22), 8930–8941,  DOI:10.1021/IC060843C.
38. T. Goswami and A. Misra, Ligand effects toward the modulation of magnetic anisotropy and design of magnetic systems with desired anisotropy characteristics, J. Phys. Chem. A, 2012, 116(21), 5207–5215,  DOI:10.1021/JP3006603.
39. J. J. Chen and M. L. Du, Investigation of the zero-field splitting and g-values of d⁸ ions in trigonal compounds CsMgX₃:Ni²⁺ (X = Cl, Br, I), Phys. B, 1996, 228(3–4), 409–413,  DOI:10.1016/S0921-4526(96)00496-6.
40. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 24, 112–122.
41. P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(23), 16223,  DOI:10.1103/PhysRevB.49.16223.
42. G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251,  DOI:10.1103/PhysRevB.49.14251.
43. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558,  DOI:10.1103/PhysRevB.47.558.
44. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169,  DOI:10.1103/PhysRevB.54.11169.
45. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
46. A. D. Becke, Density-functional thermochemistry. I. The effect of the exchange-only gradient correction, J. Chem. Phys., 1992, 96(3), 2155–2160,  DOI:10.1063/1.462066.
47. A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92(9), 5397–5403,  DOI:10.1063/1.458517.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865,  DOI:10.1103/PhysRevLett.77.3865.
49. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(3), 1505,  DOI:10.1103/PhysRevB.57.1505.
50. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327,  DOI:10.1002/wcms.1327.
51. F. Neese, Calculation of the zero-field splitting tensor on the basis of hybrid density functional and Hartree-Fock theory, J. Chem. Phys., 2007, 127(16), 164112,  DOI:10.1063/1.2772857.
52. C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, A quasidegenerate formulation of the second order n-electron valence state perturbation theory approach, J. Chem. Phys., 2004, 121(9), 4043–4049,  DOI:10.1063/1.1778711.
53. C. Angeli, R. Cimiraglia and J. P. Malrieu, n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants, J. Chem. Phys., 2002, 117(20), 9138–9153,  DOI:10.1063/1.1515317.
54. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114(23), 10252,  DOI:10.1063/1.1361246.
55. M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Detailed Ab Initio First-Principles Study of the Magnetic Anisotropy in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes, Inorg. Chem., 2011, 50(16), 7460–7477,  DOI:10.1021/ic200196k.
56. D. Ganyushin and F. Neese, First-principles calculations of zero-field splitting parameters, J. Chem. Phys., 2006, 125(2), 024103,  DOI:10.1063/1.2213976.
57. F. Neese, Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations, J. Chem. Phys., 2005, 122(3), 034107,  DOI:10.1063/1.1829047.
58. R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, Universal theoretical approach to extract anisotropic spin hamiltonians, J. Chem. Theory Comput., 2009, 5(11), 2977–2984,  DOI:10.1021/ct900326e.
59. A. Wolf, M. Reiher and B. A. Hess, The generalized Douglas-Kroll transformation, J. Chem. Phys., 2002, 117(20), 9215–9226,  DOI:10.1063/1.1515314.
60. D. A. Pantazis, X.-Y. Chen, C. R. Landis, and F. Neese, All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms,  DOI:10.1021/ct800047t.
61. A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100(8), 5829–5835,  DOI:10.1063/1.467146.
62. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree-Fock exchange, Chem. Phys., 2009, 356(1–3), 98–109,  DOI:10.1016/j.chemphys.2008.10.036.
63. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065,  10.1039/B515623H.
64. A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn, Theor. Chem. Acc., 2007, 117(4), 587–597,  DOI:10.1007/S00214-007-0250-5/METRICS.
65. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids, Phys. Rev. Lett., 2003, 91(14), 146401,  DOI:10.1103/PHYSREVLETT.91.146401.
66. J. P. Perdew, J. Tao, V. N. Staroverov and G. E. J. Scuseria, Meta-generalized gradient approximation: Explanation of a realistic nonempirical density functional, Chem. Phys., 2004, 120(15), 6898–6911,  DOI:10.1063/1.1665298.
67. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305,  10.1039/B508541A.
68. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344/926936.
69. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465,  DOI:10.1002/JCC.21759.
70. W. Jabeur, R. Msalmi, M. Korb, F. Hassen and A. Guesmi, Excitation dependent white and red-NIR emission, CrystEngComm, 2022, 24, 8467–8476,  10.1039/D2CE01138G.
71. N. Hfidhi, N. Krayem, J. Erwann, T. Bataille and H. Naïli, Lamellar and Supramolecular Feature of New Tutton's Salts Incorporating 2-Amino-4-Methylpyrimidine: Thermal Stability, Optic Study, Antioxidant and Antimicrobial Activities, J. Inorg. Organomet. Polym. Mater., 2021, 31(4), 1549–1564,  DOI:10.1007/S10904-020-01817-X/TABLES/7.
72. T. S. Thakur and G. R. Desiraju, Crystal structure prediction of a co-crystal using a supramolecular synthon approach: 2-Methylbenzoic acid-2-amino-4-methylpyrimidine, Cryst. Growth Des., 2008, 8(11), 4031–4044,  DOI:10.1021/cg800371j.
73. P. Zoufalý, E. Čižmár, J. Kuchár and R. Herchel, The Structural and Magnetic Properties of FeII and CoII Complexes with 2-(furan-2-yl)-5-pyridin-2-yl-1,3,4-oxadiazole, Mol, 2020, 25, 277,  DOI:10.3390/MOLECULES25020277.
74. S. K. Singh, J. Eng, M. Atanasov and F. Neese, Covalency and chemical bonding in transition metal complexes: An ab initio based ligand field perspective, Coord. Chem. Rev., 2017, 344, 2–25,  DOI:10.1016/J.CCR.2017.03.018.
75. D. V. Korchagin, A. V. Palii, E. A. Yureva, A. V. Akimov, E. Y. Misochko, G. V. Shilov, A. D. Talantsev, R. B. Morgunov, A. A. Shakin, S. M. Aldoshin and B. S. Tsukerblat, Evidence of field induced slow magnetic relaxation in cis-[Co(hfac)₂(H₂O)₂] exhibiting tri-axial anisotropy with a negative axial component, Dalton Trans., 2017, 46(23), 7540–7548,  10.1039/C7DT01236E.
76. L. F. Chibotaru and L. Ungur, Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation, J. Chem. Phys., 2012, 137(6), 64112,  DOI:10.1063/1.4739763/72538.
77. S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178(1), 42–55,  DOI:10.1016/j.jmr.2005.08.013.
78. L. T. A. Ho and L. F. Chibotaru, Multiple relaxation times in single-molecule magnets, Phys. Rev. B, 2016, 94(10), 104422,  DOI:10.1103/PHYSREVB.94.104422.
79. L. T. A. Ho and L. F. Chibotaru, Intermolecular mechanism for multiple maxima in molecular dynamic susceptibility, Phys. Rev. B, 2018, 98(17), 174418,  DOI:10.1103/PHYSREVB.98.174418.
80. A. Lunghi and S. Sanvito, Multiple spin-phonon relaxation pathways in a Kramer single-ion magnet, J. Chem. Phys., 2020, 153(17), 174113,  DOI:10.1063/5.0017118.
81. R. L. Carlin, K. Kopinga, O. Kahn and M. Verdaguer, Magnetochemistry of Copper(II): Exchange Interactions in Catenated [Cu(NH₃)₂(CH₃COO)Br], Inorg. Chem., 1986, 25(11), 1786–1789,  DOI:10.1021/ic00231a014.
82. Y. Z. Zhang, S. Gómez-Coca, A. J. Brown, M. R. Saber, X. Zhang and K. R. Dunbar, Trigonal antiprismatic Co(II) single molecule magnets with large uniaxial anisotropies: Importance of Raman and tunneling mechanisms, Chem. Sci., 2016, 7(10), 6519–6527,  10.1039/c6sc02035f.
83. E. Lucaccini, L. Sorace, M. Perfetti, J. P. Costes and R. Sessoli, Beyond the anisotropy barrier: slow relaxation of the magnetization in both easy-axis and easy-plane Ln(trensal) complexes, Chem. Commun., 2014, 50(14), 1648–1651,  10.1039/C3CC48866G.
84. N. Malinová, J. Juráková, B. Brachňáková, J. Dubnická Midlíková, E. Čižmár, V. T. Santana, R. Herchel, M. Orlita, I. Mohelský, J. Moncoľ, P. Neugebauer and I. Šalitroš, Magnetization Slow Dynamics in Mononuclear Co(II) Field-Induced Single-Molecule Magnet, Cryst. Growth Des., 2022, 14, 23,  DOI:10.1021/ACS.CGD.2C01388.
85. J. Juráková, J. Dubnická Midlíková, J. Hrubý, A. Kliuikov, V. T. Santana, J. Pavlík, J. Moncoľ, E. Čižmár, M. Orlita, I. Mohelský, D. Gentili, M. Cavallini and I. Šalitroš, Pentacoordinate cobalt(II) single ion magnets with pendant alkyl chains: shall we go for chloride or bromide?, Inorg. Chem. Front., 2022, 9(6), 1179–1194,  10.1039/D1QI01350E.
86. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets, Nat. Commun., 2017, 8, 1–7,  DOI:10.1038/ncomms14620.
87. L. Escalera-Moreno, N. Suaud, A. Gaita-Ariño and E. Coronado, Determining Key Local Vibrations in the Relaxation of Molecular Spin Qubits and Single-Molecule Magnets, J. Phys. Chem. Lett., 2017, 8(7), 1695–1700,  DOI:10.1021/ACS.JPCLETT.7B00479.
88. A. Sarkar, R. Jose, H. Ghosh and G. Rajaraman, Record High Magnetic Anisotropy in Three-Coordinate MnIIIand CrIIComplexes: A Theoretical Perspective, Inorg. Chem., 2021, 60(13), 9680–9687,  DOI:10.1021/ACS.INORGCHEM.1C00978.
89. L. Tesi, A. Lunghi, M. Atzori, E. Lucaccini, L. Sorace, F. Totti and R. Sessoli, Giant spin–phonon bottleneck effects in evaporable vanadyl-based molecules with long spin coherence, Dalton Trans., 2016, 45(42), 16635–16643,  10.1039/C6DT02559E.
90. M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, Spin Dynamics and Low Energy Vibrations: Insights from Vanadyl-Based Potential Molecular Qubits, J. Am. Chem. Soc., 2017, 139(12), 4338–4341,  DOI:10.1021/JACS.7B01266.
91. A. Lunghi and S. Sanvito, Multiple spin-phonon relaxation pathways in a Kramer single-ion magnet, J. Chem. Phys., 2020, 153(17), 174113,  DOI:10.1063/5.0017118/1062647.
92. A. Albino, S. Benci, M. Atzori, L. Chelazzi, S. Ciattini, A. Taschin, P. Bartolini, A. Lunghi, R. Righini, F. Totti and R. Sessoli, Temperature Dependence of Spin-Phonon Coupling in [VO(acac)₂]: A Computational and Spectroscopic Study, J. Phys. Chem. C, 2021, 125(40), 22100–22110,  DOI:10.1021/ACS.JPCC.1C06916.
93. S. Mondal and A. Lunghi, Unraveling the Contributions to Spin-Lattice Relaxation in Kramers Single-Molecule Magnets, J. Am. Chem. Soc., 2022, 144(50), 22965–22975,  DOI:10.1021/JACS.2C08876.
94. S. Nain, M. Kumar and M. E. Ali, The impact of spin-vibrational coupling on magnetic relaxation of a Co(II) single-molecule magnet, Phys. Chem. Chem. Phys., 2023, 25(21), 14848–14861,  10.1039/D3CP01243C.
95. I. Potočňák, O. Bukrynov, A. Kliuikov, M. Holub, S. Vitushkina, E. Samoľová, E. Čižmár and L. Váhovská, Influence of the phonon-bottleneck effect and low-energy vibrational modes on the slow spin-phonon relaxation in Kramers-ions-based Cu(II) and Co(II) complexes with 4-amino-3,5-bis-(pyridin-2-yl)-1,2,4-triazole and dicyanamide, Dalton Trans., 2024, 53(16), 6950–6964,  10.1039/D4DT00219A.
96. L. Gu and R. Wu, Origins of Slow Magnetic Relaxation in Single-Molecule Magnets, Phys. Rev. Lett., 2020, 125(11), 117203,  DOI:10.1103/PHYSREVLETT.125.117203.
97. L. Gu and R. Wu, Origin of the anomalously low Raman exponents in single molecule magnets, Phys. Rev. B, 2021, 103(1), 014401,  DOI:10.1103/PHYSREVB.103.014401.
98. S. Xue, L. Ungur, Y. N. Guo, J. Tang and L. F. Chibotaru, Field-induced multiple relaxation mechanism of Co^III2Dy^III compound with the dysprosium ion in a low-symmetrical environment, Inorg. Chem., 2014, 53(23), 12658–12663,  DOI:10.1021/ic502443g.
99. F. Habib, I. Korobkov and M. Murugesu, Exposing the intermolecular nature of the second relaxation pathway in a mononuclear cobalt(II) single-molecule magnet with positive anisotropy, Dalton Trans., 2015, 44(14), 6368–6373,  10.1039/C5DT00258C.
100. R. Boča, C. Rajnák, J. Titiš and D. Valigura, Field Supported Slow Magnetic Relaxation in a Mononuclear Cu(II) Complex, Inorg. Chem., 2017, 56(3), 1478–1482,  DOI:10.1021/acs.inorgchem.6b02535.
101. A. Arauzo, E. Bartolomé, A. C. Benniston, S. Melnic, S. Shova, J. Luzón, P. J. Alonso, A. L. Barra and J. Bartolomé, Slow magnetic relaxation in a dimeric Mn₂Ca₂ complex enabled by the large Mn(III) rhombicity, Dalton Trans., 2017, 46(3), 720–732,  10.1039/c6dt02509a.
102. I. Potočňák, K. Ráczová, E. Čižmár, L. Váhovská, O. Bukrynov, S. Vitushkina and L. Findoráková, Low-dimensional compounds containing cyanido groups. Part XXXII. Field-induced multiple slow magnetic relaxation in [Co^II(dcnm)(H₂O)(phen)₂](dcnm) complex with dominant easy-plane anisotropy (dcnm = dicyanonitrosomethanide), Polyhedron, 2017, 137, 112–121,  DOI:10.1016/J.POLY.2017.08.009.
103. P. Konieczny, A. B. Gonzalez-Guillén, K. Luberda-Durnaś, E. Čižmár, R. Pełka, M. Oszajca and W. Łasocha, 1D coordination polymer (OPD)₂Co^IISO₄ showing SMM behaviour and multiple relaxation modes, Dalton Trans., 2019, 48(22), 7560–7570,  10.1039/c9dt00624a.
104. A. Świtlicka, B. Machura, M. Penkala, A. Bieńko, D. C. Bieńko, C. Rajnák, R. Boča and A. Ozarowski, Slow magnetic relaxation in hexacoordinated cobalt(II) field-induced single-ion magnets, Inorg. Chem. Front., 2020, 7(14), 2637–2650,  10.1039/d0qi00257g.
105. M. Orendáč, L. Sedláková, E. Čižmár, A. Orenáčová, A. Feher, S. A. Zvyagin, J. Wosnitza, W. H. Zhu, Z. M. Wang and S. Gao, Spin relaxation and resonant phonon trapping in [Gd₂(fum) ₃(H₂O)₄].3H₂O, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(21), 214410,  DOI:10.1103/PhysRevB.81.214410.
106. C. Rajnák, F. Varga, J. Titiš, J. Moncol and R. Boča, Octahedral-Tetrahedral Systems [Co(dppm O, O)₃]²⁺[CoX₄]^2- Showing Slow Magnetic Relaxation with Two Relaxation Modes, Inorg. Chem., 2018, 57(8), 4352–4358,  DOI:10.1021/acs.inorgchem.7b03193.
107. A. C. Benniston, S. Melnic, C. Turta, A. B. Arauzo, E. Bartolomé, H. W. Harrington and M. R. Probert, Preparation and properties of a calcium(II)-based molecular chain decorated with manganese(II) butterfly-like complexes, Dalton Trans., 2014, 43(35), 13349–13357,  10.1039/C4DT01518E.
108. E. A. Buvaylo, V. N. Kokozay, O. Y. Vassilyeva, B. W. Skelton, A. Ozarowski, J. Titiš, B. Vranovičová and R. Boča, Field-Assisted Slow Magnetic Relaxation in a Six-Coordinate Co(II)-Co(III) Complex with Large Negative Anisotropy, Inorg. Chem., 2017, 56(12), 6999–7009,  DOI:10.1021/ACS.INORGCHEM.7B00605.
109. C. Rajnák, J. Titiš, J. Moncoľ, F. Renz and R. Boča, Slow magnetic relaxation in a high-spin pentacoordinate Fe(II) complex, Chem. Commun., 2019, 55(92), 13868–13871,  10.1039/c9cc06610a.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1897593. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ra02149e

---