Open Access Article
Open Access ArticleSynthesis and characterization of new composite from modified silica-coated MnFe2O4 nanoparticles for removal of tetracycline from aqueous solution
Alireza Banaeia,
Afshin Saadat *b,
Negar Gharibzadeha and
Parinaz Pargol Ghasemi
*b,
Negar Gharibzadeha and
Parinaz Pargol Ghasemi a
a
aDepartment of Chemistry, Payame Noor University, P. O. Box 19395-3697, Tehran, Iran
bDepartment of Chemistry, Germi Branch, Islamic Azad University, Germi, Iran. E-mail: Afshin.Saadat@iau.ac.ir
First published on 30th April 2024
Abstract
In this study, a new composite from silica coated MnFe2O4 nanoparticles, diethylenetriamine, 3-chloropropyl trimethoxysilane and Mg–Al Layered Double Hydroxide (Mg–Al LDH/DETA/CPTMS/SCNPs) composite was synthesized. The Mg–Al LDH/DETA/CPTMS/SCNPs composite was examined by Fourier transform infrared spectrometer (FT-IR), Scanning Electron Microscopy (SEM), Energy Dispersive X-ray (EDS), X-ray diffraction (XRD), Thermogravimetric Analysis (TGA) and Vibrating Sample Magnetometry (VSM). The synthesized composite exhibited magnetic property with a saturation magnetization of 0.40 emu g−1. The Mg–Al LDH/DETA/CPTMS/SCNPs composite was utilized as a successful adsorbent for removal of tetracycline from aqueous solutions. The effect of various operation factors such as initial drug concentration, adsorbent dosage, pH and contact time were investigated. The optimized variable conditions such as adsorbent dose of 60 mg L−1, drug concentration of 100 mg L−1, pH = 7 and contact time 30 min were obtained. For describing the adsorption isotherms, the Langmuir, Freundlich and Temkin adsorption models were utilized. The results indicated that the adsorption isotherm is in good agreement with Langmuir model. According to the Langmuir analysis, the maximum adsorption capacity (qm) of the Mg–Al LDH/DETA/CPTMS/SCNPs composite for tetracycline was obtained to be 40.16 mg g−1. The kinetic studies revealed that the adsorption in all cases to be a pseudo second-order process. The negative value of ΔG° and the positive value of ΔH° showed the adsorption process to be spontaneous and endothermic.
1. Introduction
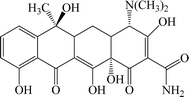
In the current era, the use of organic compounds in various industries such as food and medicine and the release of their effluents into surface and groundwater has become a serious threat to the health of the environment and humans. Wastewaters contain a number of pollutants such as antibiotics, dyes, pesticides, phenols, etc., which are highly toxic and difficult to degrade via chemical, biological, and photolytic processes.1 In this field, antibiotics are one of the most toxic constituents of industrial wastes. Most of the antibiotics in the human and animal body enter the environment without being metabolized as active compounds through urine and feces.2 Other sources of drug pollutants include the discharge of expired drugs, agricultural and veterinary waste, as well as the discharge from laboratory and research activities.3 One of the most widely used antibiotics in the world is tetracycline, which accounts for more than one-third of the total antibiotic production and consumption.4 Tetracycline has high antimicrobial activity against Gram positive and negative bacteria because of its aromatic structure that contains the naphthol chemical group.5,6 The chemical structure of this antibiotic is shown in Fig. 1. In some studies, the amount of tetracycline in surface water and in the wastewater of hospitals and pharmaceutical factories are reported 2–0.38 mg L−1 and 100–500 mg L−1, respectively. The presence of tetracycline in water sources causes impaired fertility, chronic toxicity, allergic reactions, headache and visual disturbances, diarrhea and vomiting.7 Based on this, the need for an efficient system to remove tetracycline from the aqueous environment is felt. Several methods can be used for treating wastewater such as biological treatment, photodegradation, nanofiltration, precipitation, osmosis, coagulation, flocculation, distillation and adsorption.1 However, most of the above mentioned methods are ineffective due to factors such as operational costs, secondary wastes, environmental effects and related problems, efficiency and applications.8 In recent years, the adsorption process has been widely used due to its simple design, being inexpensive, ease of management, high efficiency, ability to regenerate the adsorbent, and compatibility with the environment.9,10 The features of the adsorbate such as ionic charge, hydrophobicity, size and polarity and also physicochemical properties such as morphology, specific surface area and surface polarity determine the effectiveness of the adsorption process.11 Recently, nanocomposites have been widely used in various industries such as water treatment, agriculture and pharmaceuticals industries etc.12–17 In the field of water treatment, various nanocomposites are used for the purification of industrial wastewater via economically efficient adsorption process.18 Ahamad et al. used chitosan based magnetic nanocomposite for removal of tetracycline from aqueous solution.19 Li et al. prepared NiFe2O4–COF–chitosan–terephthalaldehyde nanocomposite and used it for removal of tetracycline.6 In the other work, Shao et al. synthesized MnFe2O4/activated carbon magnetic composites for removal of tetracycline. The result showed this nanocomposite had excellent performance for removal of tetracycline.20 Recent research indicated that LDH hybrids are good multifunctional materials for applying in different applications such as energy storage, photo-catalysis and as nanocomposites in water purification.21 Some important properties of LDH are thermal stability, alkalinity and adjustability resulted from its unique structure which also provides it with an excellent adsorption capacity.22 LDHs, formed from positively charged hydroxide metal sheets and water molecules and internal anions, have been widely studied as favorable tetracycline adsorbents.23–25 In this work, new Mg–Al LDH/DETA/CPTMS/SCNPs composite was prepared (Scheme 1). The synthesized composite was used for the removal of the tetracycline from water solution. Moreover, the effects of various factors such as initial drug concentration, adsorbent dosage, contact time and pH on adsorption behavior were investigated. Adsorption isotherms, kinetics and thermodynamic studies have been reported to account for the nature of adsorption process.2. Materials and methods
2.1. Chemicals and reagents
Ferric chloride hexahydrate (FeCl3·6H2O) and manganese sulfate (MnSO4·H2O) with 98% purity, sodium hydroxide (NaOH) with 98% purity and ammonia (NH3) with 25% purity were purchased from Merck, Germany. Tetraethyl orthosilicate (TEOS), diethylenetriamine and 3-chloropropyl trimethoxysilane with 99% purity were purchased from Merck. Tetracycline hydrochloride were purchased from Sigma-Aldrich.2.2. Instrumentation
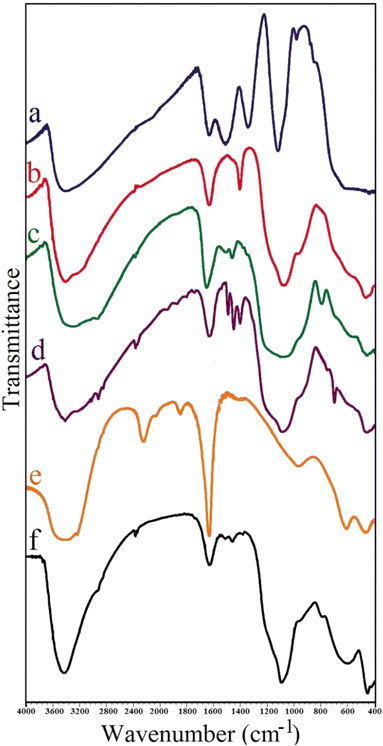
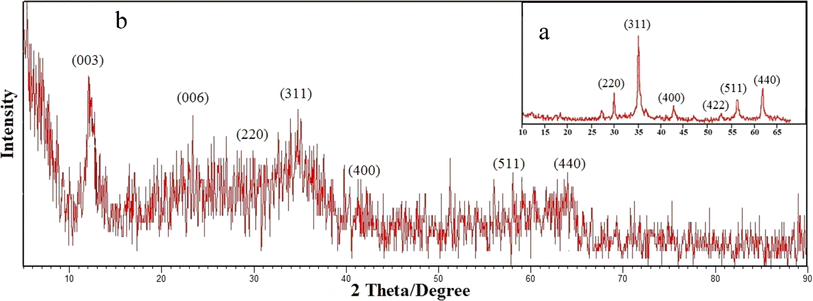
FT-IR spectra (Shimadzu Prestige-21) were applied to record the identity of the as prepared composite. All absorption spectra were recorded in the range of 400–4000 cm−1 using KBr pellets at room temperature. The crystal structure of the synthesized adsorbent was analyzed by performing X-ray diffraction (XRD) on Bruker D8 ADVANCE X-ray diffractometer with Cu Kα radiation (λ = 1.5418 Å) operated at 40 kV and 40 mA. The average size of composite particles is also estimated via Debye–Scherrer (eqn (1)):26
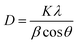 | (1) |
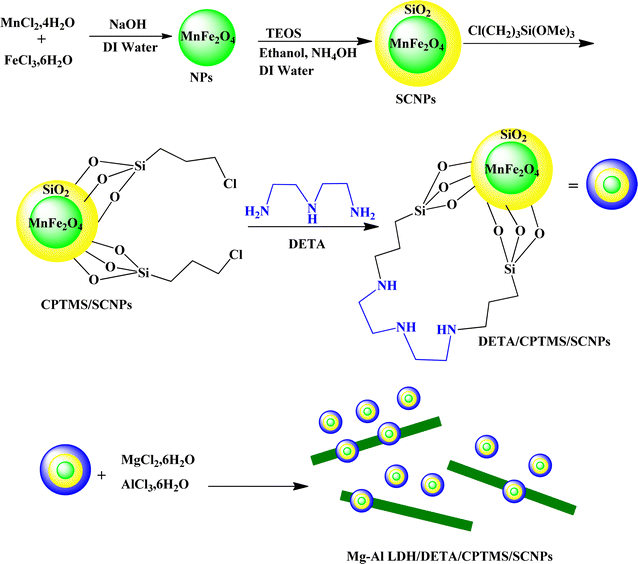
2.3. Preparation of the MnFe2O4@SiO2@CPTMS@DTAM@Mg/Al-LDH composite
2.4. Adsorption experiments
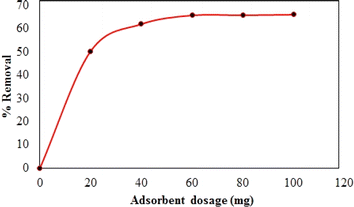
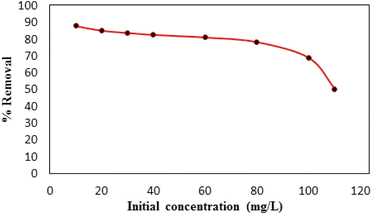
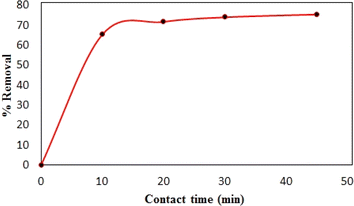
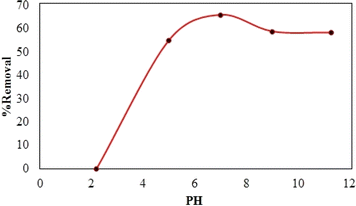
Synthesized composite (Mg–Al LDH/DETA/CPTMS/SCNPs) was used removal of tetracycline from aqueous solutions by batch technique. Experiment parameters such as pH value (2–11), drug concentration (10–120 mg L−1), adsorbent dosage (0–100 mg) and contact time (10–50 min) on the adsorption of tetracycline in aqueous solution were studied in detail. For conducting the experiments, solution of 1000 mg L−1 of tetracycline was prepared in deionized water and diluted to obtain the desired concentrations of drug. All concentrations of tetracycline in water solutions were studied by the ultraviolet visible (UV-Vis) method at 277 nm. The amount of the tetracycline adsorbed onto adsorbent (qe in mg g−1) and the percentage of the tetracycline removed from the solution (R in %) were calculated from the eqn (2) and (3):
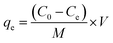 | (2) |
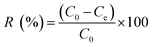 | (3) |
3. Results and discussion
3.1. Preparation of Mg–Al LDH/DETA/CPTMS/SCNPs composite
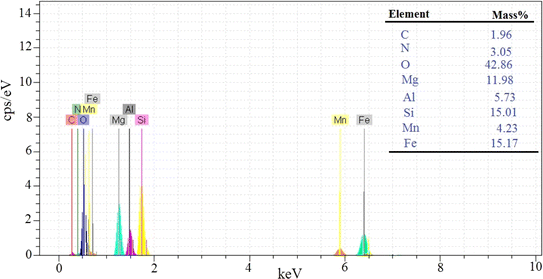
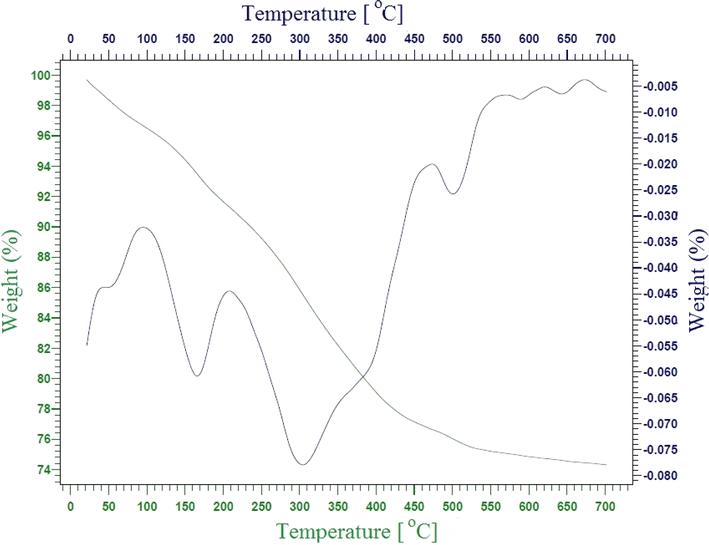
In this study, two-steps method was used for the preparation of Mg–Al LDH/DETA/CPTMS/SCNPs composite. First, the DETA/CPTMS/SCNPs nanoparticles were prepared via reaction of SCNPs nanoparticles, 3-chloropropyl trimethoxysilane and diethylenetriamine. Then, DETA/CPTMS/SCNPs nanoparticles were mixed with Mg–Al LDH. The preparation route of Mg–Al LDH/DETA/CPTMS/SCNPs adsorbent is shown in Scheme 1. The prepared composite was characterized by FI-IR, SEM, EDS, XRD, TGA and VSM. Finally, the composite was applied as an efficient adsorbent for removal of tetracycline from aqueous solutions by batch method.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and −15
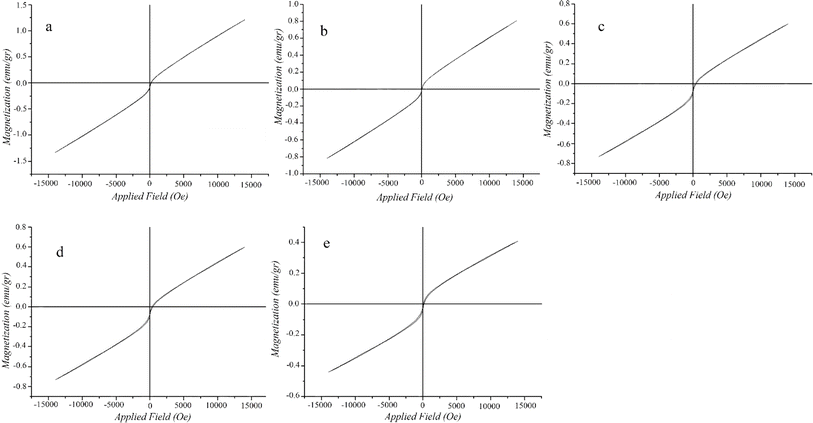
000 and −15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe. As showed in Fig. 7, the magnetization saturation values for NPs, SCNPs, CPTMS/SCNPs, DETA/CPTMS/SCNPs and Mg–Al LDH/DETA/CPTMS/SCNPs composite were gained as 1.21, 0.80, 0.719, 0.60 and 0.40 emu g−1, respectively. The saturation magnetisation value of composite enables to separate the adsorbent from aqueous solution using an external magnet during magnetic solid phase extraction. The magnetic property of composite is strongly affected by the amount of magnetite nanoparticles. The VSM results show coating the surface of the NPs with SiO2, 3-chloropropyl trimethoxysilane, diethylenetriamine and Mg–Al LDH results in a decrease in the saturation magnetization. This is due to the presence of non-magnetic components on the surface of NPs which may produce a layer that is magnetically dead. Therefore, any crystalline disorder within the surface layer leads to a significant decrease in the saturation magnetization of nanoparticles.42,43
000 Oe. As showed in Fig. 7, the magnetization saturation values for NPs, SCNPs, CPTMS/SCNPs, DETA/CPTMS/SCNPs and Mg–Al LDH/DETA/CPTMS/SCNPs composite were gained as 1.21, 0.80, 0.719, 0.60 and 0.40 emu g−1, respectively. The saturation magnetisation value of composite enables to separate the adsorbent from aqueous solution using an external magnet during magnetic solid phase extraction. The magnetic property of composite is strongly affected by the amount of magnetite nanoparticles. The VSM results show coating the surface of the NPs with SiO2, 3-chloropropyl trimethoxysilane, diethylenetriamine and Mg–Al LDH results in a decrease in the saturation magnetization. This is due to the presence of non-magnetic components on the surface of NPs which may produce a layer that is magnetically dead. Therefore, any crystalline disorder within the surface layer leads to a significant decrease in the saturation magnetization of nanoparticles.42,43
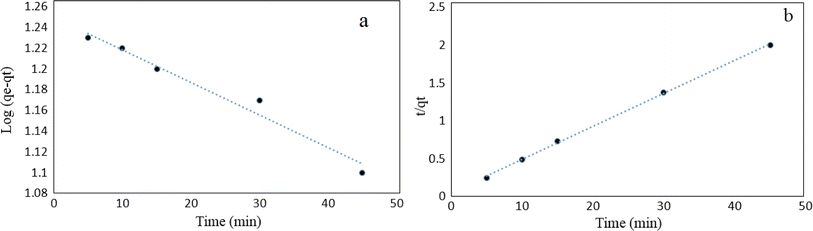
3.2. Sorption studies of tetracycline
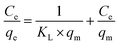 | (4) |
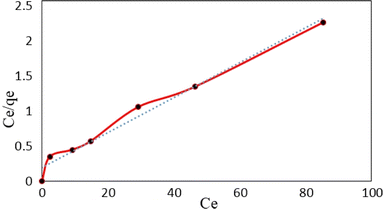
The Freundlich isotherm model demonstrates a heterogeneous adsorption of adsorbate onto the adsorbent surface. Eqn (5) shows the linear form of the Freundlich isotherm model:
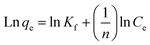 | (5) |
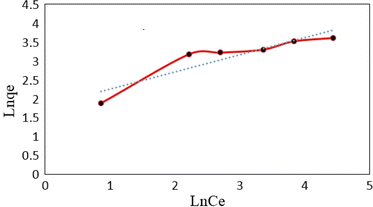
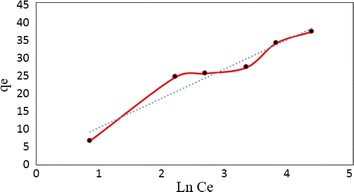
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe versus ln
qe versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce at 25 °C (Fig. 14). Furthermore, the dimensionless separation factor (RL) was calculated by the following eqn (6):
Ce at 25 °C (Fig. 14). Furthermore, the dimensionless separation factor (RL) was calculated by the following eqn (6):
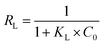 | (6) |
The values of RL can demonstrate the shape of the isotherm to be either unfavorable (RL > 1), linear (RL = 1), favorable (0 < RL < 1) or irreversible (RL = 0).
The Temkin adsorption isotherm directly investigates account of adsorbent–adsorbate interactions. In this model, first, heat of adsorption would decrease linearly rather than logarithmic, then uniform distribution of binding energies up to some maximum binding energy.49 Eqn (7) and (8) show the Temkin isotherm model:
qe = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A + B A + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce Ce
| (7) |
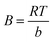 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce (Fig. 15). The Langmuir, Freundlich and Temkin parameters and the regression coefficients R2 of the adsorption of tetracycline onto Mg–Al LDH/DETA/CPTMS/SCNPs composite are given in Table 1. As seen in Table 1, calculated amount of RL was found between 0 and 1, which confirmed a favorable adsorption process for tetracycline removal using Mg–Al LDH/DETA/CPTMS/SCNPs composite. Also according to Table 1, the correlation coefficient (R2) of the Langmuir isotherm was greater than that of the Freundlich and Temkin isotherm models for the adsorption of investigated drug. The applicability of the Langmuir model suggests homogeneous surfaces of the composite and monolayer coverage of tetracycline onto the adsorbent. On the basis of the Langmuir analysis, the maximum adsorption capacity was 40.12 mg g−1 for tetracycline.
Ce (Fig. 15). The Langmuir, Freundlich and Temkin parameters and the regression coefficients R2 of the adsorption of tetracycline onto Mg–Al LDH/DETA/CPTMS/SCNPs composite are given in Table 1. As seen in Table 1, calculated amount of RL was found between 0 and 1, which confirmed a favorable adsorption process for tetracycline removal using Mg–Al LDH/DETA/CPTMS/SCNPs composite. Also according to Table 1, the correlation coefficient (R2) of the Langmuir isotherm was greater than that of the Freundlich and Temkin isotherm models for the adsorption of investigated drug. The applicability of the Langmuir model suggests homogeneous surfaces of the composite and monolayer coverage of tetracycline onto the adsorbent. On the basis of the Langmuir analysis, the maximum adsorption capacity was 40.12 mg g−1 for tetracycline.
| Langmuir isotherm parameters | Freundlich isotherm parameters | Temkin isotherm parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| qm (mg g−1) | KL (L mg−1) | RL | R2 | KF (L mg−1) | n | R2 | A | b (kJ mol−1) | B | R2 |
| 40.12 | 0.125 | 0.13 | 0.982 | 66.06 | 2.23 | 0.841 | 1.86 | 0.301 | 8.23 | 0.9434 |
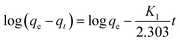 | (9) |
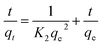 | (10) |
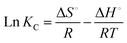 | (11) |
| ΔG° = ΔH° − TΔS° | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KC versus 1/T (Fig. 17). In addition, the values of ΔG° at different temperatures are calculated by eqn (12). Table 2 shows a summary of obtained ΔG°, ΔH° and ΔS°. As it can be observed in Table 2, the obtained positive ΔH° value of enthalpy (38.93) indicate that the adsorption of tetracycline on Mg–Al LDH/DETA/CPTMS/SCNPs composite is an endothermic process.52 The negative values in the change of Gibbs free energy (ΔG°) are showing that the investigated process is spontaneous and feasible.53 The obtained value of ΔS° of 0.168 kJ mol−1 K−1 suggests that the increased randomness at the solid/solution interface during the tetracycline on Mg–Al LDH/DETA/CPTMS/SCNPs composite.
KC versus 1/T (Fig. 17). In addition, the values of ΔG° at different temperatures are calculated by eqn (12). Table 2 shows a summary of obtained ΔG°, ΔH° and ΔS°. As it can be observed in Table 2, the obtained positive ΔH° value of enthalpy (38.93) indicate that the adsorption of tetracycline on Mg–Al LDH/DETA/CPTMS/SCNPs composite is an endothermic process.52 The negative values in the change of Gibbs free energy (ΔG°) are showing that the investigated process is spontaneous and feasible.53 The obtained value of ΔS° of 0.168 kJ mol−1 K−1 suggests that the increased randomness at the solid/solution interface during the tetracycline on Mg–Al LDH/DETA/CPTMS/SCNPs composite.
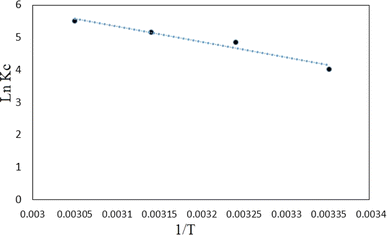 | ||
| Fig. 17 Thermodynamic plot for removal of tetracycline on Mg–Al LDH/DETA/CPTMS/SCNPs composite (200 rpm, 25 °C and pH = 7). | ||
| Drug | Temperature (K) | Parameters | ||
|---|---|---|---|---|
| ΔG° (kJ mol−1) | ΔH° (kJ mol−1) | ΔS° (kJ mol−1 K−1) | ||
| Tetracycline | 297 | −11.13 | 38.93 | 0.168 |
| 308 | −12.81 | |||
| 318 | −14.49 | |||
| 328 | −16.17 | |||
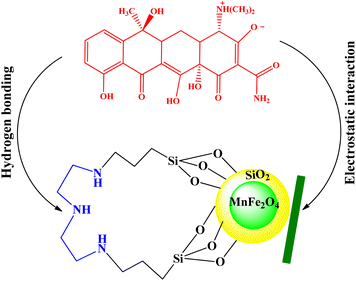
3.3. Adsorption mechanism
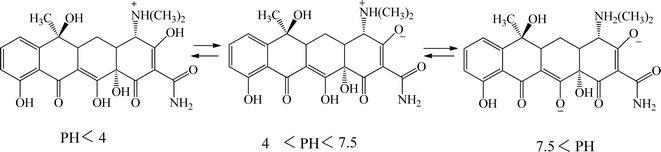
The adsorption mechanism of tetracycline on the absorbent surface depends on factors such as drug nature, adsorbent properties, hydrogen bonding, electrostatic interaction, π–π interaction and van der Waals forces.54 The functional groups on tetracycline and Mg–Al LDH/DETA/CPTMS/SCNPs composite can be protonated or deprotonated through pH changes of the aqueous medium. At low pH (acidic environment), due to the pH effect both compounds have a positive charge and the competition of H+ ions results in less adsorption tendency of tetracycline.55 In the neutral or alkaline environment, the tetracycline is deprotonated. Therefore, the tetracycline molecule was adsorbed by Mg–Al LDH/DETA/CPTMS/SCNPs composite through hydrogen bonding and electrostatic interaction (Fig. 18).3.4. Reusability studies
Reusability is one of the important factors from the cost point of view in studying the adsorption process in water treatment. To examine the regeneration ability of the Mg–Al LDH/DETA/CPTMS/SCNPs composite, four cycle of antibiotic removal were investigated. Fig. 19 present the results of this evaluation. For this aim, 60 mg of adsorbent was added to the solution containing 40 mL of 100 mg per L antibiotic. The sample was stirred for 30 min under 200 rpm at 298 K, then was filtered. The adsorbent was washed with deionized water and ethanol several. The Fig. 19 shows that after four cycles, the drug removal percentage decreased slightly and was still 61%. This suggested that the Mg–Al LDH/DETA/CPTMS/SCNPs composite is efficient for tetracycline.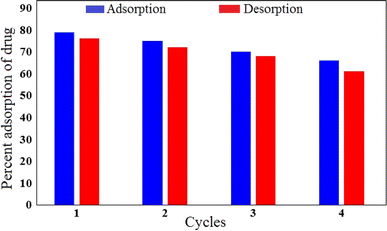 | ||
| Fig. 19 Regeneration studies for the adsorption–desorption of tetracycline onto Mg–Al LDH/DETA/CPTMS/SCNPs composite. | ||
3.5. Comparison with other reported adsorbents
Table 3 demonstrates the result which is gained through comparison of this adsorbent with other established adsorbents. As it is shown in Table 3, the adsorption capacity of Mg–Al LDH/DETA/CPTMS/SCNPs composite is acceptable for removal of tetracycline from aqueous solutions.| Adsorbents | T (K) | pH | qm (mg g−1) | References |
|---|---|---|---|---|
| HAP/ZnO-1 | 298 | 5 | 33.97 | 56 |
| Biochar | 298 | 7 | 4.13 | 57 |
| Silica-composited biochar | 298 | 7 | 22.5 | 58 |
| MnFe2O4/rGO | 298 | 3.3 | 41 | 59 |
| Fe3O4 nanoparticles | 302 | 7 | 19.6 | 60 |
| α-Fe3O4/reduced graphene oxide | 298 | 4 | 18.47 | 61 |
| Halloysite/chitosan nanocomposite | 298 | 8.5 | 15.6 | 62 |
| Rice husk ash | 313 | 5 | 8.37 | 63 |
| Copper/cobalt ferrite@chitosan | 298 | 3.5 | 4.48 | 64 |
| Mg–Al LDH/DETA/CPTMS/SCNPs composite | 298 | 7 | 40.16 | Present study |
4. Conclusion
In the present study, the Mg–Al LDH/DETA/CPTMS/SCNPs composite was prepared via modification of MnFe2O4 by tetraethyl orthosilicate, 3-chloropropyl trimethoxysilane, diethylenetriamine and Mg–Al layered double hydroxide. The synthesized composite was characterized by FT-IR, XRD, SEM, VSM and TGA. The composite exhibited magnetic property with a saturation magnetization of 0.40 emu g−1. The Mg–Al LDH/DETA/CPTMS/SCNPs composite was used successfully as an effective sorbent for the removal of tetracycline from aqueous solutions. The effects of different factors such as adsorbent dosage, initial drug concentration, pH and contact time were studied. The optimized variable conditions such as adsorbent dose of 60 mg L−1, drug concentration of 100 mg L−1, pH = 7 and contact time 30 min were obtained. The better fitted Langmuir isotherm model showed that the adsorption of tetracycline on synthesized composite was mainly monolayer adsorption. According to the Langmuir analysis, the maximum adsorption capacity (qm) of the adsorbent for tetracycline was obtained to be 40.16 mg g−1. The kinetic studies revealed that the adsorption process was more suitable for the pseudo second-order process. The thermodynamic study showed that adsorption of tetracycline on composite was spontaneous and endothermic, which was proceeded via hydrogen bonding and electrostatic interaction.Conflicts of interest
There are no conflicts to declare.References
- N. El Messaoudi, Z. Ciğeroğlu, Z. Mine Şenol, A. Bouich, E. S. Kazan-Kaya, L. Noureen, J. H. Pinê Américo-Pinheiro and C. Fourteen, Green synthesis of nanoparticles for remediation organic pollutants in wastewater by adsorption, Adv. Chem. Pollut., Environ. Manage. Prot., 2024, 10, 305–345, DOI:10.1016/bs.apmp.2023.06.016.
- G. R. Boyd, H. Reemtsma, D. A. Grimm and S. Mitra, Pharmaceuticals and personal care products (PPCPs) in surface and treated waters of Louisiana, Sci. Total Environ., 2003, 311, 135–149, DOI:10.1016/S0048-9697(03)00138-4.
- R. Cao, J. Wang, W. Ben and Z. Qiang, The profile of antibiotic resistance genes in pig manure composting shaped by composting stage: mesophilic-thermophilic and cooling maturation stages, Chemosphere, 2020, 250, 126181, DOI:10.1016/j.chemosphere.2020.126181.
- Q. Qin, X. Wu, L. Chen, Z. Jiang and Y. Xu, Simultaneous removal of tetracycline and Cu(ii) by adsorption and coadsorption using oxidized activated carbon, RSC Adv., 2018, 8, 1744–1752, 10.1039/C7RA12402C.
- H. Sayğılı and F. Güzel, Effective removal of tetracycline from aqueous solution using activated carbon prepared from tomato (Lycopersicon esculentum Mill.) industrial processing waste, Ecotoxicol. Environ. Saf., 2016, 131, 22–29, DOI:10.1016/j.ecoenv.2016.05.001.
- Z. Li, Y. Liu, S. Zou, C. Lu, H. Bai and H. Mu, Removal and adsorption mechanism of tetracycline and cefotaxime contaminants in water by NiFe2O4-COF chitosan-terephthalaldehyde nanocomposites film, Chem. Eng. J., 2020, 382, 123008, DOI:10.1016/j.cej.2019.123008.
- S. Shao and X. Wu, Microbial degradation of tetracycline in the aquatic environment: a review, Crit. Rev. Biotechnol., 2020, 40, 1010–1018, DOI:10.1080/07388551.2020.1805585.
- Z. Mulushewa, W. T. Dinbore and Y. Ayele, Removal of methylene blue from textile waste water using kaolin and zeolite-x synthesized from Ethiopian kaolin, Environ. Anal. Health Toxicol., 2021, 36, e2021007, DOI:10.5620/eaht.2021007.
- S. Wang and H. Wang, Adsorption behavior of antibiotic in soil environment: a critical review, Front. Environ. Sci. Eng., 2015, 9, 565–574, DOI:10.1007/s11783-015-0801-2.
- B. Debnath, M. Majumdar, M. Bhowmik, K. L. Bhowmik, A. Debnath and D. N. Roy, The effective adsorption of tetracycline onto zirconia nanoparticles synthesized by novel microbial green technology, J. Environ. Manage., 2020, 261, 110235, DOI:10.1016/j.jenvman.2020.110235.
- F. Yu, Y. Li, S. Han and J. Ma, Adsorptive removal of antibiotics from aqueous solution using carbon materials, Chemosphere, 2016, 153, 365–385, DOI:10.1016/j.chemosphere.2016.03.083.
- I. Hasana, D. Bhatiaa, S. Waliaa and P. Singha, Removal of Malachite Green by Polyacrylamide-g-Chitosan γ-Fe2O3 Nanocomposite-An Application of Central Composite Design, Groundw. Sustain. Dev., 2020, 11, 100378, DOI:10.1016/j.gsd.2020.100378.
- U. S. Malik, Q. Duan, M. B. K. Niazi, Z. Jahan, U. Liaqat, F. Sher, Y. Gan and H. Hou, Vanillin cross-linked hydrogel membranes interfacial reinforced by carbon nitride nanosheets for enhanced antibacterial activity and mechanical properties, Chin. Chem. Lett., 2023, 34, 108071, DOI:10.1016/j.cclet.2022.108071.
- T. Rasheed, A. A. Hassan, T. Ahmad, S. Khan and F. Sher, Organic Covalent Interaction-based Frameworks as Emerging Catalysts for Environment and Energy Applications: Current Scenario and Opportunities, Chem.–Asian J., 2023, 18, e202300196, DOI:10.1002/asia.202300196.
- M. Kh. Azeem, A. Islam, R. Ullah Khan, A. Rasool, M. A. R. Qureshi, M. Rizwan, F. Sher and T. Rasheed, Eco-friendly three-dimensional hydrogels for sustainable agricultural applications: current and future scenarios, Polym. Adv. Technol., 2023, 34, 3046–3062, DOI:10.1002/pat.6122.
- W. Li, M. Bilal, A. Kumar Singh, F. Sher, S. Salman Ashraf, M. Franco, J. H. Pinê Américo-Pinheiro and H. M. N. Iqbal, Broadening the Scope of Biocatalysis Engineering by Tailoring Enzyme Microenvironment: A Review, Catal. Lett., 2023, 153, 1227–1239, DOI:10.1007/s10562-022-04065-5.
- N. El Messaoudi, Z. Ciğeroğlu, Z. Mine Şenol, E. Sena Kazan-Kaya, Y. Fernine, S. Gubernat and Z. Lopicic, Green synthesis of CuFe2O4 nanoparticles from bioresource extracts and their applications in different areas: a review, Biomass Convers. Biorefin., 2024 DOI:10.1007/s13399-023-05264-9.
- T. Sakshi, An overview on alginate based bio-composite materials for wastewater remedial, Mater. Today: Proc., 2021, 37, 3305–3309, DOI:10.1016/j.matpr.2020.09.120.
- T. Ahamad, M. Naushad, T. Al-Shahrani, N. Al-Hokbany and S. M. Alshehri, Preparation of chitosan based magnetic nanocomposite for tetracycline adsorption: kinetic and thermodynamic studies, Int. J. Biol. Macromol., 2020, 147, 258–267, DOI:10.1016/j.ijbiomac.2020.01.025.
- L. Shao, Z. Ren, G. Zhang and L. Chen, Facile synthesis, characterization of a MnFe2O4/activated carbon magnetic composite and its effectiveness in tetracycline removal, Mater. Chem. Phys., 2012, 135, 16–24, DOI:10.1016/j.matchemphys.2012.03.035.
- M. Zubair, M. Daud, G. McKay, F. Shehzad and M. A. Al-Harthi, Recent progress in layered double hydroxides (LDH)-containing hybrids as adsorbents for water remediation, Appl. Clay Sci., 2017, 143, 279–292, DOI:10.1016/j.clay.2017.04.002.
- X. Yuan, Y. Wang, J. Wang, C. Zhou, Q. Tang and X. Rao, Calcined graphene/MgAl-layered double hydroxides for enhanced Cr (VI) removal, Chem. Eng. J., 2013, 221, 204–213, DOI:10.1016/j.cej.2013.01.090.
- C. Mengbo, L. Xun, W. Wei, G. Ming, L. Yongsheng and Y. Hongbing, Functionalized Zn/Al N-doped carbon nanocomposites with tunable morphology: synergistic ultrafast low-temperature synthesis and tetracycline adsorption, Sep. Purif. Technol., 2021, 278, 119548, DOI:10.1016/j.seppur.2021.119548.
- S. Mufan, Ch. Zhongjing, Y. Yixuan, H. Bingji, H. Guangyu and Ch. Haiqun, A facile solvothermal syntheses of NiFe layered double hydroxide-Bi2MoO6 heterostructure/reduced graphene oxide with efficient photodegradation for tetracycline, Environ. Res., 2022, 204, 112037, DOI:10.1016/j.envres.2021.112037.
- A. Zaher, M. Taha and R. Khaled Mahmoud, Possible adsorption mechanisms of the removal of tetracycline from water by La-doped Zn-Fe-layered double hydroxide, J. Mol. Liq., 2021, 322, 114546, DOI:10.1016/j.molliq.2020.114546.
- A. El Guerraf, S. Ben Jadi, I. Ziani, M. Dalli, F. Sher, M. Bazzaoui and El A. Bazzaoui, Multifunctional Smart Conducting Polymers–Silver Nanocomposites-Modified Biocellulose Fibers for Innovative Food Packaging Applications, Ind. Eng. Chem. Res., 2023, 62, 4540–4553, DOI:10.1021/acs.iecr.2c01327.
- V. Ghobadifar, Gh. Bagheri Marandi, M. Kurdtabar and Gh. Rezanejade Bardajee, Removal of Pb(II) and Cd(II) by MnFe2O4@SiO2@VTMS Nanocomposite Hydrogel from Aqueous Solutions, J. Polym. Environ., 2023, 31, 2686–2704, DOI:10.1007/s10924-022-02670-4.
- Z. Rashid, H. Naeimi and A. H. Zarnani, Fast and highly efficient purification of 6× histidine-tagged recombinant proteins by Ni-decorated MnFe2O4@SiO2@NH2@2AB as novel and efficient affinity adsorbent magnetic nanoparticles, RSC Adv., 2016, 6, 36840–36848, 10.1039/C5RA25949E.
- Z. P. Xu, G. Stevenson, C. Q. Lu, G. Q. Lu, P. F. Bartlett and P. Gray, Stable suspension of layered double hydroxide nanoparticles in aqueous solution, J. Am. Chem. Soc., 2006, 128, 36–37, DOI:10.1021/ja056652a.
- M. Ghobadi, M. Gharabaghi, H. Abdollahi, Z. Boroumand and M. Moradian, MnFe2O4-graphene oxide magnetic nanoparticles as a high-performance adsorbent for rare earth elements: synthesis, isotherms, kinetics, thermodynamics and desorption, J. Hazard. Mater., 2018, 351, 308–316, DOI:10.1016/j.jhazmat.2018.03.011.
- N. U. Yamaguchi, R. Bergamasco and S. Hamoudi, Magnetic MnFe2O4–graphene hybrid composite for efficient removal of glyphosate from water, Chem. Eng. Sci., 2016, 295, 391–402, DOI:10.1016/j.cej.2016.03.051.
- F. Adam, H. Osman and K. M. Hello, The immobilization of 3-(chloropropyl)triethoxysilane onto silica by a simple one-pot synthesis, J. Colloid Interface Sci., 2009, 331, 143–147, DOI:10.1016/j.jcis.2008.11.048.
- A. Kaczmarek, J. Hoffman, J. Morgiel, T. Mościcki, L. Stobiński, Z. Szymański and A. Małolepszy, Luminescent Carbon Dots Synthesized by the Laser Ablation of Graphite in Polyethylenimine and Ethylenediamine, Materials, 2021, 14, 729, DOI:10.3390/ma14040729.
- J. Li, Y. Wang, S. Jiang and H. Zhang, Facile synthesis of magnetic recyclable palladium-gold alloy nanoclusters catalysts PdAur/Fe3O4@LDH and its catalytic applications in Heck reaction, J. Organomet. Chem., 2018, 878, 84–95, DOI:10.1016/j.jorganchem.2018.10.007.
- F. Mi, X. Chen, Y. Ma, S. Yin, F. Yuan and H. Zhang, Facile synthesis of hierarchical core–shell Fe3O4@MgAl-LDH@Au as magnetically recyclable catalysts for catalytic oxidation of alcohols, Chem. Commun., 2011, 47, 12804–12806, 10.1039/C1CC15858A.
- Y. Xiao, J. Zai, L. Tao, B. Li, Q. Han, C. Yu and X. Qian, MnFe2O4–graphene nanocomposites with enhanced performances as anode materials for Li-ion batteries, Phys. Chem. Chem. Phys., 2013, 15, 3939–3945, 10.1039/C3CP50220A.
- Z. Rezvani, F. Arjomandi Rad and F. Khodam, Synthesis and characterization of Mg–Al-layered double hydroxides intercalated with cubane1,4-dicarboxylate anions, Dalton Trans., 2015, 44, 988–996, 10.1039/C4DT03152K.
- Li. Tianxiang, Sh. Zhengren, He. Xianru, J. Ping, Lu. Xiaobin, R. Zhang and X. Wang, Aging-resistant functionalized ldh–sas/nitrile-butadiene rubber composites: preparation and study of aging kinetics/anti-aging mechanism, Materials, 2018, 11, 836, DOI:10.3390/ma11050836.
- S. N. Golovin, M. N. Yapryntsev, I. G. Ryl'tsova, S. V. Savilov, K. I. Maslakov and O. E. Lebedeva, Synthesis and thermal behavior of Co/AlCe layered double hydroxide, Solid State Sci., 2021, 111, 106498, DOI:10.1016/j.solidstatesciences.2020.106498.
- Y. Zhang, Li. Lijuan, Sh. Dong and F. Song, Synthesis and application of low-cost layered double hydroxides intercalated by gluconic acid anion for flame retardancy and tensile strength conservation of high filling epoxy resin, J. Colloid Interface Sci., 2021, 594, 791–801, DOI:10.1016/j.jcis.2021.03.088.
- A. A. Ali Ahmed, Z. A. Talib and M. Z. Hussein, Thermal, optical and dielectric properties of Zn–Al layered double hydroxide, Appl. Clay Sci., 2012, 56, 68–76, DOI:10.1016/j.clay.2011.11.024.
- L. Gui-yin, J. Jiang Yu-ren, K. Huang, P. Ding and J. Chen, Preparation and properties of magnetic Fe3O4–chitosan nanoparticles, J. Alloys Compd., 2008, 466, 451–456, DOI:10.1016/j.jallcom.2007.11.100.
- R. Hosseinzadeh, M. Mavvaji and I. Moradi, Synthesis and Characterization of Fe3O4@SiO2@MgAl-LDH@Au.Pd as an Efficient and Magnetically Recyclable Catalyst for Reduction of 4-Nitrophenol and Suzuki Coupling Reactions, Arabian J. Sci. Eng., 2023, 48, 7525–7541, DOI:10.1007/s13369-022-07543-5.
- W. Honghai, X. Hanrui, H. Guangping, Y. Guan and Y. Zhang, Effects of the pH and anions on the adsorption of tetracycline on iron-montmorillonite, Appl. Clay Sci., 2016, 119, 161–169, DOI:10.1016/j.clay.2015.08.001.
- Zh. Yanping, G. Xueyuan, G. Shixiang, J. Geng and X. Wang, Adsorption of tetracycline (TC) onto montmorillonite: cations and humic acid effects, Geoderma, 2012, 183, 12–18, DOI:10.1016/j.geoderma.2012.03.004.
- A. Saadat, A. Banaei, M. Sattarifar and P. Pargolghasemi, Preparation 2-hydroxy-1-naphthaldehyde cross-linked Fe3O4@chitosan-polyacrylamide nanocomposite for removal of everzol black from aqueous solutions, Sci. Rep., 2023, 13, 10618, DOI:10.1038/s41598-023-37243-5.
- A. Tabak, E. Eren, B. Afsin and B. Caglar, Determination of adsorptive properties of a Turkish Sepiolite for removal of Reactive Blue 15 anionic dye from aqueous solutions, J. Hazard. Mater., 2009, 161, 1087–1094, DOI:10.1016/j.jhazmat.2008.04.062.
- R. Satheesh, K. Vignesh, M. Rajarajan, A. Suganthi, S. Sreekantan, M. Kang and B. Sub Kwak, Removal of congo red from water using quercetin modified α-Fe2O3 nanoparticles as effective nanoadsorbent, Mater. Chem. Phys., 2016, 180, 53–65, DOI:10.1016/j.matchemphys.2016.05.029.
- N. Wang, J. Chen, J. Wang, J. Feng and W. Yan, Removal of Methylene Blue by Polyaniline/TiO2 Hydrate: Adsorption Kinetic, Isotherm and Mechanism Studies, Powder Technol., 2019, 347, 93–102, DOI:10.1016/j.powtec.2019.02.049.
- S. X. Chen, J. Wang, Z. L. Wu, Q. Deng, W. F. Tu, G. P. Dai, Z. L. Zeng and S. G. Deng, Enhanced Cr(VI) removal by polyethylenimine and phosphorus codoped hierarchical porous carbons, J. Colloid Interface Sci., 2018, 523, 110–120, DOI:10.1016/j.jcis.2018.03.057.
- A. A. Alqadami, M. Naushad, M. A. Abdalla, M. R. Khan and Z. A. Alothman, Adsorptive removal of toxic dye using Fe3O4–TSC nanocomposite: equilibrium, kinetic and thermodynamic studies, J. Chem. Eng. Data, 2016, 61, 3806–3813, DOI:10.1021/acs.jced.6b00446.
- R. Shan, L. Yan, K. Yang, S. Yu, Y. Hao, H. Yu and B. Du, Magnetic Fe3O4/MgAl-LDH composite for effective removal of three red dyes from aqueous solution, J. Chem. Eng., 2014, 252, 38–46, DOI:10.1016/j.cej.2014.04.105.
- Y. Jiang, B. Liu, J. Xu, K. Pan, H. Hou, J. Hu and J. Yang, Cross-linked chitosan/β-cyclodextrin composite for selective removal of methyl orange: adsorption performance and mechanism, Carbohydr. Polym., 2018, 182, 106–114, DOI:10.1016/j.carbpol.2017.10.097.
- R. Natarajan, K. Saikia, S. K. Ponnusamy, A. K. Rathankumar, D. S. Rajendran, S. Venkataraman, D. B. Tannani, V. Arvind, T. Somanna, K. Banerjee, N. Mohideen and V. K. Vaidyanathan, Understanding the factors affecting adsorption of pharmaceuticals on different adsorbents- a critical literature update, Chemosphere, 2022, 287, 131958, DOI:10.1016/j.chemosphere.2021.131958.
- H. Zhu, T. Chen, J. Liu and D. Li, Adsorption of tetracycline antibiotics from an aqueous solution onto graphene oxide/calcium alginate composite fibers, RSC Adv., 2018, 8, 2616–2621, 10.1039/C7RA11964J.
- C. Oliveira, A. L. M. de Oliveira, L. Chantelle, R. Landers, S. Medina-Carrasco, M. Del Mar Orta, E. C. Silva Filho and M. G. Fonseca, Zinc(II) modified hydroxyapatites for tetracycline removal: Zn(II) doping or ZnO deposition and their influence in the adsorption, Polyhedron, 2021, 194, 114879, DOI:10.1016/j.poly.2020.114879.
- Y. Dai, J. Li and D. Shan, Adsorption of tetracycline in aqueous solution by biochar derived from waste Auricularia auricula dregs, Chemosphere, 2020, 238, 124432, DOI:10.1016/j.chemosphere.2019.124432.
- Z. Zhao, T. Nie and W. Zhou, Enhanced biochar stabilities and adsorption properties for tetracycline by synthesizing silica-composited biochar, Environ. Pollut., 2019, 254, 113015, DOI:10.1016/j.envpol.2019.113015.
- W. A. Khanday and B. H. Hameed, Zeolite-hydroxyapatite-activated oil palm ash composite for antibiotic tetracycline adsorption, Fuel, 2018, 215, 499–505, DOI:10.1016/j.fuel.2017.11.068.
- W. Zhai, J. He, P. Han, M. Zeng, X. Gao and Q. He, Adsorption mechanism for tetracycline onto magnetic Fe3O4 nanoparticles: adsorption isotherm and dynamic behavior, location of adsorption sites and interaction bonds, Vacuum, 2022, 195, 110634, DOI:10.1016/j.vacuum.2021.110634.
- A. M. Huízar-Félix, C. Aguilar-Flores, A. Martínez-de-la Cruz, J. M. Barandiarán, S. Sepúlveda-Guzmán and R. Cruz-Silva, Removal of tetracycline pollutants by adsorption and magnetic separation using reduced graphene oxide decorated with α-Fe2O3 nanoparticles, Nanomaterials, 2019, 9, 313, DOI:10.3390/nano9030313.
- S. Erdem, M. Öztekin and Y. S. Açıkel, Investigation of tetracycline removal from aqueous solutions using halloysite/chitosan nanocomposites and halloysite nanotubes/alginate hydrogel beads, Environ. Nanotechnol., Monit. Manage., 2021, 16, 100576, DOI:10.1016/j.enmm.2021.100576.
- Y. Chen, F. Wang, L. Duan, H. Yang and J. Gao, Tetracycline adsorption onto rice husk ash, an agricultural waste: its kinetic and thermodynamic studies, J. Mol. Liq., 2016, 222, 487–494, DOI:10.1016/j.molliq.2016.07.090.
- A. Nasiri, S. Rajabi, A. Amiri, M. Fattahizade, O. Hasani, A. Lalehzari and M. Hashemi, Adsorption of tetracycline using CuCoFe2O4@chitosan as a new and green magnetic nanohybrid adsorbent from aqueous solutions: isotherm, kinetic and thermodynamic study, Arabian J. Chem., 2022, 15, 104014, DOI:10.1016/j.arabjc.2022.104014.
| This journal is © The Royal Society of Chemistry 2024 |