DOI:
10.1039/D3RA08750F
(Paper)
RSC Adv., 2024,
14, 12303-12312
Kinetic and reactivity of gas-phase reaction of acyclic dienes with hydroxyl radical in the 273–318 K temperature range†
Received
22nd December 2023
, Accepted 23rd March 2024
First published on 16th April 2024
Abstract
As dienes contain two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, theoretically, they are much more chemically reactive with hydroxyl radical (˙OH) than alkenes and alkanes, and the reaction with ˙OH is one of the main atmospheric degradation routes of dienes during the daytime. In our work, rate coefficients of three types of acyclic dienes: conjugated as 3-methyl-1,3-pentadiene (3M13PD), isolated as 1,4-hexadiene (14HD), and cumulated as 1,2-pentadiene (12PD) reaction with ˙OH were measured in the temperature range of 273–318 K and 1 atm using the relative rate method. At 298 ± 3 K, the rate coefficients for those reactions were determined to be k3M13PD+OH = (15.09 ± 0.72) × 10−11, k14HD+OH = (9.13 ± 0.62) × 10−11, k12PD+OH = (3.34 ± 0.40) × 10−11 (as units of cm3 per molecule per s), in the excellent agreement with values of previously reported. The first measured temperature dependence for 3M13PD, 14HD and 12PD reaction with ˙OH can be expressed by the following Arrhenius expressions in units of cm3 per molecule per s: k3M13PD+OH = (8.10 ± 2.23) × 10−11
C bonds, theoretically, they are much more chemically reactive with hydroxyl radical (˙OH) than alkenes and alkanes, and the reaction with ˙OH is one of the main atmospheric degradation routes of dienes during the daytime. In our work, rate coefficients of three types of acyclic dienes: conjugated as 3-methyl-1,3-pentadiene (3M13PD), isolated as 1,4-hexadiene (14HD), and cumulated as 1,2-pentadiene (12PD) reaction with ˙OH were measured in the temperature range of 273–318 K and 1 atm using the relative rate method. At 298 ± 3 K, the rate coefficients for those reactions were determined to be k3M13PD+OH = (15.09 ± 0.72) × 10−11, k14HD+OH = (9.13 ± 0.62) × 10−11, k12PD+OH = (3.34 ± 0.40) × 10−11 (as units of cm3 per molecule per s), in the excellent agreement with values of previously reported. The first measured temperature dependence for 3M13PD, 14HD and 12PD reaction with ˙OH can be expressed by the following Arrhenius expressions in units of cm3 per molecule per s: k3M13PD+OH = (8.10 ± 2.23) × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(173 ± 71)/T]; k14HD+OH = (9.82 ± 5.10) × 10−12
exp[(173 ± 71)/T]; k14HD+OH = (9.82 ± 5.10) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(666 ± 123)/T]; k12PD+OH = (1.13 ± 0.87) × 10−12
exp[(666 ± 123)/T]; k12PD+OH = (1.13 ± 0.87) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(1038 ± 167)/T] (as units of cm3 per molecule per s). The kinetic discussion revealed that the relative position between these two C
exp[(1038 ± 167)/T] (as units of cm3 per molecule per s). The kinetic discussion revealed that the relative position between these two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C could significantly affect the reactivity of acyclic dienes toward ˙OH. A simple structure–activity relationship (SAR) method was proposed to estimate the reaction rate coefficients of acyclic dienes with ˙OH.
C could significantly affect the reactivity of acyclic dienes toward ˙OH. A simple structure–activity relationship (SAR) method was proposed to estimate the reaction rate coefficients of acyclic dienes with ˙OH.
1 Introduction
Dienes are unsaturated hydrocarbons containing two carbon–carbon double bonds in the molecule. The general formula for the acyclic ones is CnH(2n−2). Depending on whether the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are adjacent to each other, separated by one single bond or by more than one, the acyclic dienes are named and classified by IUPAC to be cumulated dienes, conjugated dienes, and isolated dienes.1,2 Isoprene is one of the most important representatives of conjugated diene found in the atmosphere. It counts for about half of the total amount of biogenic volatile organic compounds (BVOCs) released from vegetation, around 600 teragrams of carbon per year (Tg C per year).3–5 1,3-Butadiene is another important acyclic diene in the atmosphere, and it is listed as a critical hazardous air pollutant due to its carcinogenic and mutagenic properties. Its concentration can reach up to 1 ppbv measured in urban areas.6,7 Acyclic dienes are also essential raw materials for organic synthesis,8,9 e.g., 1,3-butadiene, 1,2-pentadiene, 1,4-hexadiene, and 3-methyl-1,3-pentadiene are used in the synthesis of rubbers,10 polymers,11 coatings,12 and biodiesel.13,14 Hence, large amounts of acyclic dienes could be released into the atmosphere during production, transportation, and usage.15–18 The main removal pathway of acyclic dienes in the atmosphere could be their reaction with ˙OH.19–21 The rate coefficients for the reactions of ˙OH and the subsequent degradation mechanism with isoprene22–25 and 1,3-butadiene26–28 have been widely studied. Several previous investigations have shown that the reaction of acyclic dienes with ˙OH in the presence of NOx could produce critical atmospheric pollutants such as peroxyacetyl nitrate (PAN), organic nitrates and carbonyl compounds.29–34 However, the reactivity of most of the acyclic dienes towards ˙OH still not well investigated.35–38 It is, indeed, of interest to conduct comprehensive studies on a more extensive set of acyclic dienes with various chemical structures in order to improve the knowledge of their atmospheric fate and impacts.
C bonds are adjacent to each other, separated by one single bond or by more than one, the acyclic dienes are named and classified by IUPAC to be cumulated dienes, conjugated dienes, and isolated dienes.1,2 Isoprene is one of the most important representatives of conjugated diene found in the atmosphere. It counts for about half of the total amount of biogenic volatile organic compounds (BVOCs) released from vegetation, around 600 teragrams of carbon per year (Tg C per year).3–5 1,3-Butadiene is another important acyclic diene in the atmosphere, and it is listed as a critical hazardous air pollutant due to its carcinogenic and mutagenic properties. Its concentration can reach up to 1 ppbv measured in urban areas.6,7 Acyclic dienes are also essential raw materials for organic synthesis,8,9 e.g., 1,3-butadiene, 1,2-pentadiene, 1,4-hexadiene, and 3-methyl-1,3-pentadiene are used in the synthesis of rubbers,10 polymers,11 coatings,12 and biodiesel.13,14 Hence, large amounts of acyclic dienes could be released into the atmosphere during production, transportation, and usage.15–18 The main removal pathway of acyclic dienes in the atmosphere could be their reaction with ˙OH.19–21 The rate coefficients for the reactions of ˙OH and the subsequent degradation mechanism with isoprene22–25 and 1,3-butadiene26–28 have been widely studied. Several previous investigations have shown that the reaction of acyclic dienes with ˙OH in the presence of NOx could produce critical atmospheric pollutants such as peroxyacetyl nitrate (PAN), organic nitrates and carbonyl compounds.29–34 However, the reactivity of most of the acyclic dienes towards ˙OH still not well investigated.35–38 It is, indeed, of interest to conduct comprehensive studies on a more extensive set of acyclic dienes with various chemical structures in order to improve the knowledge of their atmospheric fate and impacts.
3-Methyl-1,3-pentadiene (3M13PD), 1,4-hexadiene (14HD), and 1,2-pentadiene (12PD) are three critical acyclic dienes, which are widely used in industry,13,14 as shown in Scheme 1. Based on the molecular structure, 3M13PD, 14HD, and 12PD are categorized as conjugated, isolated, and cumulated diene, respectively. However, only one study conducted by Ohta in 1983![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 reported the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH at 297 ± 2 K. Ohta 1983
39 reported the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH at 297 ± 2 K. Ohta 1983![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 also proposed one structure–activity relationship (SAR) method to estimate the rate coefficients of conjugated diene and isolated diene, but not cumulated diene. To the best of our knowledge, no available temperature-dependence data on the reaction of ˙OH with 3M13PD, 14HD, or 12PD has been reported so far.
39 also proposed one structure–activity relationship (SAR) method to estimate the rate coefficients of conjugated diene and isolated diene, but not cumulated diene. To the best of our knowledge, no available temperature-dependence data on the reaction of ˙OH with 3M13PD, 14HD, or 12PD has been reported so far.
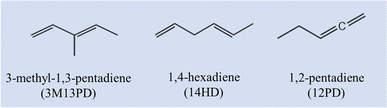 |
| | Scheme 1 Structures and abbreviations for the three dienes. | |
In this work, we conducted a comprehensive investigation into the rate coefficients of the reaction of ˙OH with 3M13PD, 14HD, and 12PD over a wide temperature range of 273–318 K. Our research yielded crucial insights into the underlying mechanisms of these reactions and a deeper understanding of the factors that influence their rate coefficients. Furthermore, this work enables us to recommend a novel and simple SAR approach to estimate the rate coefficients of dienes with ˙OH, which can be used effectively in atmospheric models to advance our understanding of these reactions.
2 Materials and methods
2.1 Atmospheric simulation chamber
A Teflon chamber with a volume of 300 liters is suspended in the middle of the climatic incubator, which was designed to maintain a constant temperature (±1 K) and relative humidity (±2%). Two 254 nm UV lamps were used to initiate photo-oxidation in the chamber, and the reflective internal stainless-steel material ensured that the UV light was homogeneously spread. In this work, the temperature range was set to 273–318 K. Zero air to fill and purge the Teflon chamber was made by mixing pure nitrogen and oxygen in the ratio of N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 = 4
O2 = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Known concentrations of the gas-phase chemicals were injected into the chamber through a mass flow controller (MFC). The chemicals in the liquid phase were introduced into the chamber by injecting a known volume into a three-way bubbler and then flushed with zero air. The inlet line was purged with 5 L of zero air after each chemical introduction to ensure the sample was completely introduced into the chamber. The Teflon chamber was also well-cleaned by inflating, shaking, and pumping three times. The time profiles of the concentration of the species of interest were monitored using an on-line gas chromatography-photoionization detector (GC-PID) (GC-4400, East & West Analytical Instruments, Inc., China). The packed column was operated at 45 °C, and N2 was used as the carrier gas.
1. Known concentrations of the gas-phase chemicals were injected into the chamber through a mass flow controller (MFC). The chemicals in the liquid phase were introduced into the chamber by injecting a known volume into a three-way bubbler and then flushed with zero air. The inlet line was purged with 5 L of zero air after each chemical introduction to ensure the sample was completely introduced into the chamber. The Teflon chamber was also well-cleaned by inflating, shaking, and pumping three times. The time profiles of the concentration of the species of interest were monitored using an on-line gas chromatography-photoionization detector (GC-PID) (GC-4400, East & West Analytical Instruments, Inc., China). The packed column was operated at 45 °C, and N2 was used as the carrier gas.
2.2 Kinetic study method
During the experiments, the diene (3M13PD or 14HD or 12PD) and references (propene and 1,3-butadiene) were introduced into the 300 L Teflon chamber and kept for 1 hour to estimate their wall loss rates. Then H2O2 was injected into the chamber and photolyzed at 254 nm to initiate ˙OH. The photolysis rate of H2O2 can be calculated from the precursor cross section, quantum yield and the actinic flux at 254 nm, in this work, the H2O2 photolysis rate was calculated to be ∼10−4 s−1, ensure a fast decay of the dienes and references.| | |
H2O2 + hν(254 nm) → 2˙OH
| (R1) |
The loss of the studied dienes and references, including wall loss and reaction with ˙OH, can be represented by the following reactions:
| |
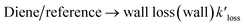 | (R2) |
| | |
Diene + ˙OH → products kdiene
| (R3) |
| | |
Reference + OH → products kref
| (R4) |
The following equation can express the changes in the concentrations of the studies dienes and references:
| |
 | (1) |
where [diene]
0 and [ref]
0 represent the initial concentration of diene and reference compounds, while [diene]
t, and [ref]
t are the concentrations at reaction time. The
kref and
kdiene are the rate coefficients of the ˙OH reactions with reference and diene, respectively. The ratio
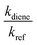
, can be derived from the linear least regression of
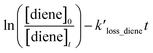 vs.
vs. 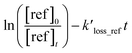
.
2.3 Materials
The acyclic dienes used in this work and their stated purities are 3-methyl-1,3-pentadiene (99%, from Macklin), 1,4-hexadiene (99%, from Rhawn), 1,2-pentadiene (95%, from Aladdin), and H2O2 (30%, from SCR Co., Ltd). Propene (1%) and 1,3-butadiene (1%), both used as references, were supplied by Air Liquide. N2 (99.999%) and O2 (99.999%) were provided by Beijing Haike Co.
3 Results
3.1 Rate coefficient determination at 298 ± 3 K
Table 1 provides a summary of the experimental conditions and the obtained rate coefficients at the temperature of 298 ± 3 K. The concentrations of the studied dienes and references were in the range of (5–11) × 1012 molecule per cm3. As shown in Fig. S1,† both acyclic dienes and references began to decrease after ˙OH formed from the photolysis of H2O2. Fig. 1 presents the plots of 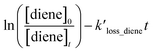 as the function of
as the function of 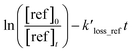 for all the experiments from which the ratios of
for all the experiments from which the ratios of 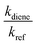 were obtained (Table 1). We repeated the experiments for each reference at least three times to ensure reproducibility. The uncertainties of
were obtained (Table 1). We repeated the experiments for each reference at least three times to ensure reproducibility. The uncertainties of 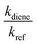 were taken as 2σ of the linear fitting of Fig. 1 when plotting all the experimental results together. The rate coefficients of reference compounds reacting with ˙OH are: kpropene+OH = 4.85 × 10−12
were taken as 2σ of the linear fitting of Fig. 1 when plotting all the experimental results together. The rate coefficients of reference compounds reacting with ˙OH are: kpropene+OH = 4.85 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[504/T],40 k1,3-butadiene+OH = 1.48 × 10−11
exp[504/T],40 k1,3-butadiene+OH = 1.48 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[448/T],40 in units of cm3 per molecule per s. Hence, the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH were calculated through eqn (1), as shown in Table 1. The obtained rate coefficients using propene and 1,3-butadiene agreed well with each other (differences < 15%). The error of kdiene was calculated using the equation of
exp[448/T],40 in units of cm3 per molecule per s. Hence, the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH were calculated through eqn (1), as shown in Table 1. The obtained rate coefficients using propene and 1,3-butadiene agreed well with each other (differences < 15%). The error of kdiene was calculated using the equation of 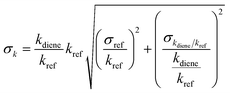 . Finally, the derived rate coefficients of studied dienes reaction ˙OH were weighted average of kdiene_ref (Table 1) and calculated as follows: kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5, as units of cm3 per molecule per s.
. Finally, the derived rate coefficients of studied dienes reaction ˙OH were weighted average of kdiene_ref (Table 1) and calculated as follows: kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5, as units of cm3 per molecule per s.
Table 1 Summary of the experimental conditions and results in the relative rate method at 298 K and 1 atm
| Diene |
[Diene] × 1012 molecule per cm3 |
Ref |
No. of exps |
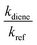
a |
kdiene_refb × 10−11 cm3 per molecule per s |
kavc × 10−11 cm3 per molecule per s |
kref extracted from Calvert, Jack G. et al. “The Mechanisms of Atmospheric Oxidation of the Alkenes.” (2000).40 The error was calculated as follows: 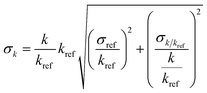 .48 Weighted average49 kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5. .48 Weighted average49 kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5. |
| 3M13PD |
5.13–7.69 |
1,3-Butadiene |
4 |
2.15 ± 0.07 |
14.41 ± 0.85 |
15.09 ± 0.72 |
| Propene |
3 |
6.51 ± 0.17 |
16.66 ± 1.29 |
| 14HD |
6.69–11.15 |
1,3-Butadiene |
3 |
1.27 ± 0.04 |
8.44 ± 0.75 |
9.13 ± 0.62 |
| Propene |
3 |
3.79 ± 0.07 |
9.94 ± 0.81 |
| 12PD |
5.48–9.13 |
1,3-Butadiene |
7 |
0.46 ± 0.02 |
3.07 ± 0.30 |
3.34 ± 0.40 |
| Propene |
6 |
1.42 ± 0.05 |
3.72 ± 0.35 |
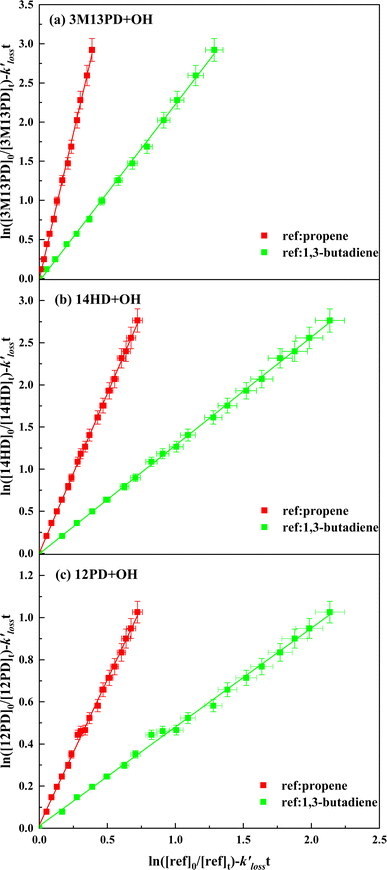 |
| | Fig. 1 Plots of relative kinetic data obtained from the reaction of (a) 3M13PD, (b) 14HD, and (c) 12PD with ˙OH using 1,3-butadiene (green square) and propene (red square) as the reference compounds. | |
The rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH were measured at 297 K and 1 atm by Ohta (1983).39 The reported rate coefficients were (13.9 ± 0.8) × 10−11, (9.25 ± 0.55) × 10−11, and (3.63 ± 0.13) × 10−11, respectively, where the experiments were conducted using propene, 1,3-butadiene and 1,3-pentadiene as the references compounds in a ∼200 L cylindrical reaction cell. The values obtained in this work are consistent with those of Ohta (1983)39 within a bias of less than 7%. As a result, the reaction rates of 3M13PD, 14HD, and 12PD with ˙OH follow the order of k3M13PD+OH > k14HD+OH > k12PD+OH. It is widely accepted that ˙OH addition to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is the primary mechanism for ˙OH reaction with alkenes.20,41 An explanation of alkene reactivity has been studied and reported is that the more specific-addition sites an alkene can provide, the more reactive the alkene is for its reaction with ˙OH.35,42 Cumulated diene, 12PD contains a propadiene group (C
C bond is the primary mechanism for ˙OH reaction with alkenes.20,41 An explanation of alkene reactivity has been studied and reported is that the more specific-addition sites an alkene can provide, the more reactive the alkene is for its reaction with ˙OH.35,42 Cumulated diene, 12PD contains a propadiene group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–), and the intermolecular addition of ˙OH to 12PD takes place at three potential sites due to the two tightly linked double bonds forming a unique π-bond structure.43,44 In contrast, conjugated diene 3M13PD and isolated diene 14HD can provide four addition sites, which explains why 12PD is less reactive toward ˙OH than 3M13PD, 14HD, where k12PD+OH is 3–5 times lower than k3M13PD+OH and k14HD+OH. It has been reported in related experiments that the substitution of alkyl groups on the C
C–), and the intermolecular addition of ˙OH to 12PD takes place at three potential sites due to the two tightly linked double bonds forming a unique π-bond structure.43,44 In contrast, conjugated diene 3M13PD and isolated diene 14HD can provide four addition sites, which explains why 12PD is less reactive toward ˙OH than 3M13PD, 14HD, where k12PD+OH is 3–5 times lower than k3M13PD+OH and k14HD+OH. It has been reported in related experiments that the substitution of alkyl groups on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond increases the reactivity of alkene toward ˙OH because –CH3 groups are supposed to increase the electron density in the neighbor C
C bond increases the reactivity of alkene toward ˙OH because –CH3 groups are supposed to increase the electron density in the neighbor C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond as well as decrease the ionization energy and, therefore increase the reactivity.40,45–47 Hence, although both 3M13PD and 14HD contain four addition sites for ˙OH, more alkyl groups on 3M13PD than on 14HD could be an important reason why k3M13PD+OH is 1.6 times greater than k14HD+OH. The reactivity of conjugated diene, isolated diene, and cumulated diene will be further discussed in the following sections.
C bond as well as decrease the ionization energy and, therefore increase the reactivity.40,45–47 Hence, although both 3M13PD and 14HD contain four addition sites for ˙OH, more alkyl groups on 3M13PD than on 14HD could be an important reason why k3M13PD+OH is 1.6 times greater than k14HD+OH. The reactivity of conjugated diene, isolated diene, and cumulated diene will be further discussed in the following sections.
3.2 Temperature dependence
The rate coefficients for the reactions of 3M13PD, 14HD, and 12PD with ˙OH were studied at temperatures ranging from 273 K to 318 K. The experimental conditions and results are presented in Table S1.† Fig. 2 shows the rate coefficients for each reaction as a function of 1/T. Using the results from this study and a previous one by Ohta (1983),39 we derived an Arrhenius expression, k = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−Ea/RT, for the temperature range of 273–318 K. The units for the rate coefficients are cm3 per molecule per s and are listed in Table 2.
e−Ea/RT, for the temperature range of 273–318 K. The units for the rate coefficients are cm3 per molecule per s and are listed in Table 2.
k3M13PD+OH = (8.10 ± 2.23) × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(173 ± 71)/T] exp[(173 ± 71)/T] |
k14HD+OH = (9.82 ± 5.10) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(666 ± 123)/T] exp[(666 ± 123)/T] |
k12PD+OH = (1.13 ± 0.87) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(1038 ± 167)/T] exp[(1038 ± 167)/T] |
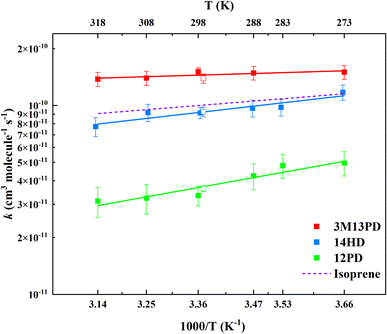 |
| | Fig. 2 Arrhenius plots of data from Table 2 as well as the data from Ohta (1983).39 The solid lines represent the Arrhenius parameter least-squares fits to the individual data points for each diene. The error bars of the individual points are calculated as above σav. The dashed line expresses the Arrhenius expression for isoprene at temperatures of 273–318 K with data from IUPAC.50 | |
Table 2 Rate coefficients and Arrhenius parameters of 3M13PD, 14HD, and 12PD reaction with OH at temperatures of 273–318 K
| Diene |
T (K) |
k × 10−11 cm3 per molecule per s |
A × 10−12 cm3 per molecule per s |
−Ea/R (K) |
R2 |
| Cite from Ohta, T. (1983).39 |
| 3M13PD |
273 |
15.01 ± 1.25 |
80.98 ± 22.30 |
173 ± 71 |
0.82 |
| 288 |
14.86 ± 1.22 |
| 297a |
13.90 ± 0.80 |
| 298 |
15.09 ± 0.72 |
| 308 |
13.96 ± 1.19 |
| 318 |
13.78 ± 1.18 |
| 14HD |
273 |
11.74 ± 1.09 |
9.82 ± 5.1 |
666 ± 123 |
0.88 |
| 283 |
9.78 ± 0.99 |
| 288 |
9.67 ± 0.99 |
| 297a |
9.25 ± 0.55 |
| 298 |
9.13 ± 0.62 |
| 308 |
9.17 ± 0.96 |
| 318 |
7.73 ± 0.88 |
| 12PD |
273 |
4.96 ± 0.73 |
1.13 ± 0.87 |
1038 ± 167 |
0.90 |
| 283 |
4.81 ± 0.70 |
| 288 |
4.24 ± 0.66 |
| 297a |
3.63 ± 0.13 |
| 298 |
3.34 ± 0.40 |
| 308 |
3.23 ± 0.57 |
| 318 |
3.12 ± 0.56 |
This work provides the first temperature dependence data for k3M13PD+OH, k14HD+OH, and k12PD+OH. We have determined the activation energy of −1.44, −5.54, and −8.64 for 3M13PD, 14HD, and 12PD reactions with ˙OH, respectively, in units of kJ mol−1. As Fig. 2 shows, the temperature dependence of k14HD+OH and k12PD+OH are significantly negative compared to that of k3M13PD+OH, which is slightly negative to near zero. The strong negative temperature dependence of k14HD+OH and k12PD+OH is consistent with the kisoprene (rate coefficient of isoprene reaction with ˙OH), as shown by the dashed line in Fig. 2, with data from IUPAC.50 The negative temperature dependence of the rate coefficient for the reaction of ˙OH with alkenes has been extensively discussed.41,51–53 Arguably, the most studied and reported example of an explanation for the negative temperature dependence is a pre-reaction complex reaction mechanism.47,54–56 The OH-addition reaction is not a simple process and it involves the formation of a pre-reactive complex, which can either reverse back to the reactants or evolve irreversibly to an addition adduct known as R5 or β-hydroxyalkyl radical.45,57,58 Hence, the overall rate coefficient (kobs) depends on the rates of three competitive reactions, i.e., kobs = kR5akR5c/(kR5b + kR5c). Atkinson et al., 1985 (ref. 58) noted that the negative temperature dependence would arise when kR5b > kR5c for ER5b > ER5c (activation energy).
| |
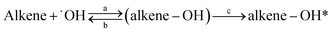 | (R5) |
where (alkene–OH) is the pre-reactive complex and alkene–OH* is the addition adduct. According to Singleton and Cvetanovic's hypothesis,
57 there is no bond breaking in the process of the formation of the pre-reaction complex, so the
ER5a is considered to be zero or near-zero. Then, the net activation energy for the overall reaction is
Ea =
ER5c −
ER5b. Because of the special molecular structure of 12PD, it may be unstable in its pre-reaction complex, which means that
ER5b is lower. And R5b is more favored by an increase in temperature than R5c, which ultimately leads to a larger
Ea. This may explain why a stronger negative temperature dependence was observed for
k12PD+OH than for
k14HD+OH and
k3M13PD+OH (
Fig. 2). Also, if
kR5b is greater than
kR5c for
ER5b >
ER5c, the overall rate coefficient of the diene reaction with ˙OH (
kobs) will be smaller. This is consistent with the reaction order observed in this study at 298 K, which is
k12PD+OH <
k14HD+OH <
k3M13PD+OH.
Similar to the Arrhenius equation, the Eyring equation, based on transition state theory, also describes the rate of reaction as a function of temperature.59,60 The Eyring equation gives an idea of how the reaction progresses at the molecular level,46 and the linear form equation is as follows: 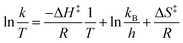 . Where, k is the rate constant, kB is the Boltzmann's constant (1.381 × 10−23 J K−1), T is the absolute temperature in Kelvin (K), h is plank's constant (6.626 × 10−34 J s), R is the gas constant (8.314 J mol−1 K−1), ΔH‡ is the enthalpy of activation and ΔS‡ is the entropy of activation.
. Where, k is the rate constant, kB is the Boltzmann's constant (1.381 × 10−23 J K−1), T is the absolute temperature in Kelvin (K), h is plank's constant (6.626 × 10−34 J s), R is the gas constant (8.314 J mol−1 K−1), ΔH‡ is the enthalpy of activation and ΔS‡ is the entropy of activation.
As shown in Fig. S2 and Table S2,† the values for ΔH‡ and ΔS‡ can be determined from kinetic data obtained from a ln(k/T) vs. 1/T plot. We find that the activation enthalpies of the reaction of 3M13PD, 14HD, and 12PD with OH are all negative, −3.91, −7.99, and −11.09, respectively, in kJ mol−1. Negative activation enthalpies prove that the reaction is exothermic, which makes it easy to understand that the rate of the reaction slows down as the temperature increases. Similar to the standard enthalpy, negative values represent a more stable energy structure.61,62 Thus, this again illustrates the rules of reactivity of dienes with ˙OH: 3M13PD > 14HD > 12PD.
4 Discussion
As discussed above, the reaction order of three different types of dienes, namely conjugated diene, isolated diene, and cumulated diene, was determined. The results showed that the reactivity of conjugated diene (k3M13PD+OH) towards ˙OH was higher than that of isolated diene (k14HD+OH), which in turn was higher than that of cumulated diene (k12PD+OH). To further explore the relationship between diene structure and its reactivity towards ˙OH, as shown in Table S3,† we compiled data from a database63 and this work and plotted the rate coefficients against the number of carbon atoms for a series of straight-chain dienes in Fig. 3. The data in Fig. 3 including conjugated dienes: 1,3-butadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC
CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (Z)-1,3-pentadiene (C/C
C), (Z)-1,3-pentadiene (C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C\C
C\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (3E)-penta-1,3-diene (C/C
C), (3E)-penta-1,3-diene (C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C
C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (3E)-hexa-1,3-diene (CC/C
C), (3E)-hexa-1,3-diene (CC/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C
C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (Z/E)-2,4-hexadiene (CC
C), (Z/E)-2,4-hexadiene (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC
CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC), isolated dienes: 1,4-pentadiene (C
CC), isolated dienes: 1,4-pentadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCC
CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 1,4-hexadiene (C
C), 1,4-hexadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC/C
CC/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C), 1,5-hexadiene (C
C/C), 1,5-hexadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCCC
CCCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), and cumulated dienes: propadiene (C
C), and cumulated dienes: propadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), methylallene (CC
C), methylallene (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 1,2-pentadiene (CCC
C), 1,2-pentadiene (CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). The results again showed that the reactivity of conjugated dienes toward ˙OH is higher than expected for an isolated C
C). The results again showed that the reactivity of conjugated dienes toward ˙OH is higher than expected for an isolated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond and then cumulated C
C bond and then cumulated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. This phenomenon could be explained by the relative position of the two C
C bond. This phenomenon could be explained by the relative position of the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds on the acyclic diene.
C bonds on the acyclic diene.
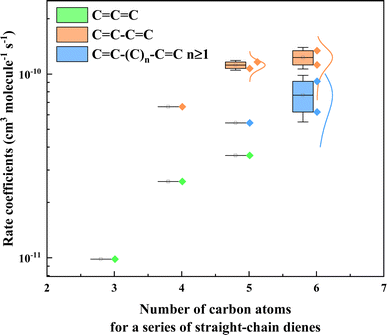 |
| | Fig. 3 Plots the rate coefficients versus the number of carbon atoms for a series of straight-chain dienes, including cumulated diene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), conjugated diene (C C), conjugated diene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), and isolated diene (C C), and isolated diene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–(C)n–C C–(C)n–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, n ≥ 1). The rate coefficient values for dienes' reaction with OH radicals are from McGillen et al. (2020)63 and are shown in Table S3.† C, n ≥ 1). The rate coefficient values for dienes' reaction with OH radicals are from McGillen et al. (2020)63 and are shown in Table S3.† | |
According to the classical transition state theory, a certain energy barrier must be overcome for adding ˙OH to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond to occur.28,64,65 Hence, the relative position of two C
C bond to occur.28,64,65 Hence, the relative position of two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds on an acyclic diene likely affects its energy barrier and then reactivity. To explain this further, we take the example of 1,3-, 1,4- and 1,2-pentadiene. The energy barriers for the reaction of the three dienes with ˙OH have been calculated by utilizing the m062x/6-31+G(d,p) and m062x/6-311+G(3df,3pd) level of theory (see details in Fig. S3†). The stability of the initial OH adduct will ultimately affect the overall reactivity of the alkene with ˙OH.42 For example, in 1,3-pentadiene, the four pathways are grouped two by two, as IM1 and IM4 have similar potential heights and are lower than IM2 and IM3. For conjugated dienes, the pi-electron density overlap allows the electrons to “delocalise” over a larger area,1,66 explaining why IM2 and IM3 are so similar. Likewise, the conjugated stabilized structure reduces the overall energy (−40.16 kcal mol−1) of this isomer, which accounts for the reactivity enhancement of conjugated dienes towards ˙OH. Accordingly, the overall rate coefficient of 1,3-pentadiene is higher than the sum of two corresponding mono-alkene, e.g. k1,3-pentadiene of 11.60 × 10−11 cm3 per molecule per s is higher than the sum of the rate coefficients of 1-pentene (k1-pentene) and 2-pentene (k2-pentene) reaction with ˙OH as 9.72 × 10−11 cm3 per molecule per s, where k1-pentene and k2-pentene are 3.22 ± 0.48 and 6.50 ± 2.00 × 10−11 cm3 per molecule per s,63 respectively. This phenomenon could also be applied to other conjugated dienes (Table S3†).
C bonds on an acyclic diene likely affects its energy barrier and then reactivity. To explain this further, we take the example of 1,3-, 1,4- and 1,2-pentadiene. The energy barriers for the reaction of the three dienes with ˙OH have been calculated by utilizing the m062x/6-31+G(d,p) and m062x/6-311+G(3df,3pd) level of theory (see details in Fig. S3†). The stability of the initial OH adduct will ultimately affect the overall reactivity of the alkene with ˙OH.42 For example, in 1,3-pentadiene, the four pathways are grouped two by two, as IM1 and IM4 have similar potential heights and are lower than IM2 and IM3. For conjugated dienes, the pi-electron density overlap allows the electrons to “delocalise” over a larger area,1,66 explaining why IM2 and IM3 are so similar. Likewise, the conjugated stabilized structure reduces the overall energy (−40.16 kcal mol−1) of this isomer, which accounts for the reactivity enhancement of conjugated dienes towards ˙OH. Accordingly, the overall rate coefficient of 1,3-pentadiene is higher than the sum of two corresponding mono-alkene, e.g. k1,3-pentadiene of 11.60 × 10−11 cm3 per molecule per s is higher than the sum of the rate coefficients of 1-pentene (k1-pentene) and 2-pentene (k2-pentene) reaction with ˙OH as 9.72 × 10−11 cm3 per molecule per s, where k1-pentene and k2-pentene are 3.22 ± 0.48 and 6.50 ± 2.00 × 10−11 cm3 per molecule per s,63 respectively. This phenomenon could also be applied to other conjugated dienes (Table S3†).
In contrast, in 1,4-pentadiene of an isolated diene, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are separated by one (or more for other isolated dienes) sp3-hybridized carbon atom. As such, each C
C bonds are separated by one (or more for other isolated dienes) sp3-hybridized carbon atom. As such, each C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond behaves independently of the other, and the electron density cannot spread out as well or evenly. This also resulted in very similar potential barriers for all four channels (IM1 = IM4 = −30.33 kcal mol−1, IM2 = IM3 = −31.25 kcal mol−1), as shown in Fig. S3c.† Compared to 1,4-pentadiene, the conjugation effect makes IM1 and IM4 lower for 1,3-pentadiene. The adduct of 1,4-pentadiene with OH lacks resonance stabilization, which may affect the exothermic nature of the reaction and the height of the potential barriers for the formation of the internal transition states of the adduct. It will ultimately affect the overall reactivity of 1,4-pentadiene with ˙OH.42,66 Generally, the overall rate coefficients of 1,4-pentadiene are expected to be equal to the sum of two corresponding mono-alkenes, but in fact, they are lower than the sum of rate coefficients of mono-alkenes, e.g., k1,4-pentadiene of 5.41 × 10−11 cm3 per molecule per s is lower than k1-pentene + k1-pentene as 6.44 × 10−11 cm3 per molecule per s, and it is same for other isolated dienes (Table S3†). This finding indicates that the interaction also exists between these two isolated C
C bond behaves independently of the other, and the electron density cannot spread out as well or evenly. This also resulted in very similar potential barriers for all four channels (IM1 = IM4 = −30.33 kcal mol−1, IM2 = IM3 = −31.25 kcal mol−1), as shown in Fig. S3c.† Compared to 1,4-pentadiene, the conjugation effect makes IM1 and IM4 lower for 1,3-pentadiene. The adduct of 1,4-pentadiene with OH lacks resonance stabilization, which may affect the exothermic nature of the reaction and the height of the potential barriers for the formation of the internal transition states of the adduct. It will ultimately affect the overall reactivity of 1,4-pentadiene with ˙OH.42,66 Generally, the overall rate coefficients of 1,4-pentadiene are expected to be equal to the sum of two corresponding mono-alkenes, but in fact, they are lower than the sum of rate coefficients of mono-alkenes, e.g., k1,4-pentadiene of 5.41 × 10−11 cm3 per molecule per s is lower than k1-pentene + k1-pentene as 6.44 × 10−11 cm3 per molecule per s, and it is same for other isolated dienes (Table S3†). This finding indicates that the interaction also exists between these two isolated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, which was not expected before.
C bonds, which was not expected before.
Cumulated dienes are a class of dienes with adjacent double bonds, where these two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are shorter than those in typical alkene according to a high level of bond energy.43,67 These bonds form a special pi bond that leads to a possible stronger reactivity at the C2 position, but less reactive for C1 and C3. This seems surprising considering that the energy of IM2 is −56.69 kcal mol−1 (Fig. S3c†). However, laboratory results suggest that this bonding may reduce the reactivity of cumene to ˙OH. Meanwhile, the fact that there are only three specific addition sites may be another reason why the reaction rate coefficient of 1,2-pentadiene is lower than that of 1,3- and 1,4-pentadiene. For example, the k12PD of 3.34 × 10−11 cm3 per molecule per s (this work) is almost three times lower than the sum of rate coefficients of the according mono-alkenes 1-pentene and 2-pentene reaction with ˙OH k1-pentene + k2-pentene = 9.72 × 10−11 cm3 per molecule per s. Calvert et al., (2000) noted that the rate coefficient values for cumulated dienes reaction with ˙OH are very similar to those of the corresponding mono-alkene by replacing the C
C bonds are shorter than those in typical alkene according to a high level of bond energy.43,67 These bonds form a special pi bond that leads to a possible stronger reactivity at the C2 position, but less reactive for C1 and C3. This seems surprising considering that the energy of IM2 is −56.69 kcal mol−1 (Fig. S3c†). However, laboratory results suggest that this bonding may reduce the reactivity of cumene to ˙OH. Meanwhile, the fact that there are only three specific addition sites may be another reason why the reaction rate coefficient of 1,2-pentadiene is lower than that of 1,3- and 1,4-pentadiene. For example, the k12PD of 3.34 × 10−11 cm3 per molecule per s (this work) is almost three times lower than the sum of rate coefficients of the according mono-alkenes 1-pentene and 2-pentene reaction with ˙OH k1-pentene + k2-pentene = 9.72 × 10−11 cm3 per molecule per s. Calvert et al., (2000) noted that the rate coefficient values for cumulated dienes reaction with ˙OH are very similar to those of the corresponding mono-alkene by replacing the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C with a single C
C with a single C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C.40 Therefore, the second adjacent C
C.40 Therefore, the second adjacent C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond probably has a strong interaction on the “tradition” C
C bond probably has a strong interaction on the “tradition” C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, which needs further research.
C bond, which needs further research.
It is, however, of interest to ascertain other factors to affect the reactivity of acyclic dienes toward ˙OH. The number of available sites for ˙OH addition directly relates to the alkene's reactivity. For instance, 1-hexene has two reaction sites, while 14HD has four sites, making 14HD more than twice as reactive as 1-hexene.37 Although cumulated dienes have two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, they can only provide up to three addition sites, which may be why 12PD has a lower rate coefficient than 1,3-PD and 1,4-PD for reacting with ˙OH. Additionally, studies have shown that more alkyl substitutions on the C
C bonds, they can only provide up to three addition sites, which may be why 12PD has a lower rate coefficient than 1,3-PD and 1,4-PD for reacting with ˙OH. Additionally, studies have shown that more alkyl substitutions on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond would increase the ˙OH addition reactivity of alkene.40,46 For example, k3M13PD+OH > k1,3-pentadiene+OH > k1,3-butadiene+OH, with increasing numbers of –CH3 group from 1,3-butadiene (C
C bond would increase the ˙OH addition reactivity of alkene.40,46 For example, k3M13PD+OH > k1,3-pentadiene+OH > k1,3-butadiene+OH, with increasing numbers of –CH3 group from 1,3-butadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 1,3-pentadiene (C
C), 1,3-pentadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C), to 3M13PD (C
C–C), to 3M13PD (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C–C(C)
C–C–C(C)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C). We categorized the rate coefficient values for acyclic dienes into three base structures: C
C–C). We categorized the rate coefficient values for acyclic dienes into three base structures: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–(C)n–C
C–(C)n–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C. Fig. 4 illustrates the relationship between the rate coefficients of acyclic dienes' reaction with ˙OH and the number of alkyl groups on the acyclic diene (see detail in Table S4†). It shows that the more alkyl groups attached to the C
C. Fig. 4 illustrates the relationship between the rate coefficients of acyclic dienes' reaction with ˙OH and the number of alkyl groups on the acyclic diene (see detail in Table S4†). It shows that the more alkyl groups attached to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, the higher the ˙OH addition reactivity of the acyclic diene, with the –CH3 group having a stronger effect than –CH2CH3. The effect of alkyl groups is to increase the electron density in the adjacent double bond, lowering the ionization energy and thus increasing the reactivity with ˙OH.46
C bond, the higher the ˙OH addition reactivity of the acyclic diene, with the –CH3 group having a stronger effect than –CH2CH3. The effect of alkyl groups is to increase the electron density in the adjacent double bond, lowering the ionization energy and thus increasing the reactivity with ˙OH.46
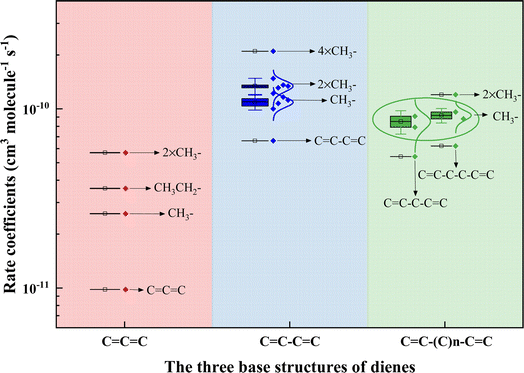 |
| | Fig. 4 Plot of the relationship between the rate coefficients of dienes reacting with the OH radical and the number of alkyl groups on the acyclic diene. The rate coefficient values for acyclic dienes have been categorized into three base structures: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–(C)n–C C–(C)n–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, based on information from this study and existing literature.39,63 C, based on information from this study and existing literature.39,63 | |
Applying the relations found here, we could predict the rate coefficients (kpred) of conjugated diene and isolated diene reaction with ˙OH by summing up the rate coefficients (kcal) of corresponding mono-alkene that we derived by converting one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond to a C–C bond, e.g., 1,4-hexadiene → 1-hexene + 2-hexene (see detail in Table S3†). We plotted the rate coefficients of the dienes reaction with ˙OH (kexp) as a function of the sum of corresponding mono-alkenes (kcal) in Fig. 5. The plot clearly shows that the slopes of conjugated dienes and isolated dienes are 0.89 and 1.11, respectively. Therefore, we believe that a factor should be multiplied to the sum to obtain an accurate rate coefficient estimate. The factor for conjugated diene and isolated diene is the slope obtained from Fig. 5. The effect of the relative positions of the two C
C bond to a C–C bond, e.g., 1,4-hexadiene → 1-hexene + 2-hexene (see detail in Table S3†). We plotted the rate coefficients of the dienes reaction with ˙OH (kexp) as a function of the sum of corresponding mono-alkenes (kcal) in Fig. 5. The plot clearly shows that the slopes of conjugated dienes and isolated dienes are 0.89 and 1.11, respectively. Therefore, we believe that a factor should be multiplied to the sum to obtain an accurate rate coefficient estimate. The factor for conjugated diene and isolated diene is the slope obtained from Fig. 5. The effect of the relative positions of the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds of a diene on its energy barrier and reactivity can also be demonstrated intuitively by the factor. For example, the factor for conjugated diene is 0.89 (<1), meaning kexp > kcal, which indicates a possible positive effect between the two C
C bonds of a diene on its energy barrier and reactivity can also be demonstrated intuitively by the factor. For example, the factor for conjugated diene is 0.89 (<1), meaning kexp > kcal, which indicates a possible positive effect between the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds of the conjugated diene. On the contrary, the effect may be negative. This result is also in agreement with our earlier discussion of the reactivity of the three species of dienes.
C bonds of the conjugated diene. On the contrary, the effect may be negative. This result is also in agreement with our earlier discussion of the reactivity of the three species of dienes.
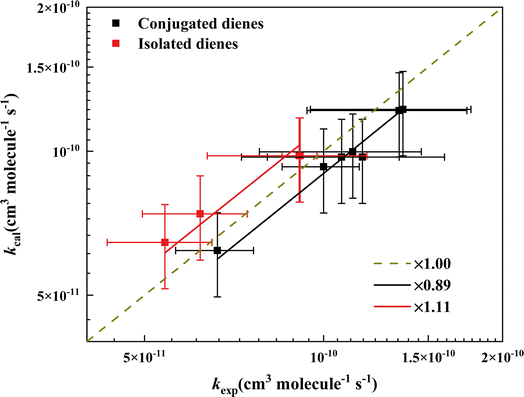 |
| | Fig. 5 Comparison of the calculated and experimental rate coefficients for reaction of ˙OH with acyclic dienes. The black and red squares represent conjugated and isolated dienes. The brown dashed line shows the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line. The black and red solid lines indicate the correction factors of 0.89 and 1.11 for predicting the rate coefficients of conjugated and isolated dienes reaction with ˙OH. 1 line. The black and red solid lines indicate the correction factors of 0.89 and 1.11 for predicting the rate coefficients of conjugated and isolated dienes reaction with ˙OH. | |
For cumulated dienes estimate, their reaction rate coefficients are in excellent agreement with those of the corresponding mono-alkene (within 1.2 times difference) by treating C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C as a single “traditional” C
C as a single “traditional” C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, as suggested by Calvert in 2000.40 In summary, the agreement between the SAR predictions and the experimental value is very excellent, with an average deviation of less than 8%.
C bond, as suggested by Calvert in 2000.40 In summary, the agreement between the SAR predictions and the experimental value is very excellent, with an average deviation of less than 8%.
5 Conclusions
Studies of ˙OH attack on diverse dienes are still rare, with most interest centering on the isoprene, 1,3-butadiene. In this work, rate coefficients for three kinds of acyclic dienes including conjugated, isolated, and cumulated, accordingly, 3M13PD, 14HD, and 12PD reaction of ˙OH were measured in the temperature range of 273–318 K and 1 atm using the relative rate method. At 298 ± 3 K, we discovered that the rate coefficients for those reactions were k3M13PD+OH = (15.09 ± 0.72) × 10−11, k14HD+OH = (9.13 ± 0.62) × 10−11, k12PD+OH = (3.34 ± 0.40) × 10−11 (units of cm3 per molecule per s). These values are in excellent agreement with the only previously reported value. Based on these rates, we calculated the lifetime of 3M13PD, 14HD, and 12PD to be 1.84 h, 3.04 h, and 8.32 h, respectively, due to their reaction with ˙OH. This study also provides the first temperature dependence of the reaction of ˙OH with 3M13PD, 14HD, and 12PD. The temperature dependence can be expressed by the following Arrhenius expressions in units of cm3 per molecule per s:
k3M13PD+OH = (8.10 ± 2.23) × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(173 ± 71)/T] exp[(173 ± 71)/T] |
k14HD+OH = (9.82 ± 5.10) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(666 ± 123)/T] exp[(666 ± 123)/T] |
k12PD+OH = (1.13 ± 0.87) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(1038 ± 167)/T] exp[(1038 ± 167)/T] |
This kinetic measurement over an extended temperature range of 298 K provides new insights into the reactivity of the acyclic dienes functional group. The OH addition reactivity order of conjugated diene > isolated diene > cumulated diene is observed, which suggests that the relative position of two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C on the acyclic dienes could determine its reactivity. The number and type of alkyl group and the number of addition sites on diene could also strongly affect its reactivity. The more alkyl substituents on the C
C on the acyclic dienes could determine its reactivity. The number and type of alkyl group and the number of addition sites on diene could also strongly affect its reactivity. The more alkyl substituents on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, the faster the reaction rate coefficient is. Following the reactivity discussion, we proposed that the rate coefficients of conjugated diene and isolated diene reaction with ˙OH could be calculated from a simple SAR method by summing up the rate coefficients of corresponding mono-alkenes and multiplying a correction factor. The present SAR method has the advantage of being easy to compute without the need for complex parameters. Our work provides a simple idea to estimate the reaction coefficients of dienes or poly-alkenes with ˙OH. We must state that the SAR proposed in this paper are reasonably reliable (within <8% of the experimental values) when used within the database used in its derivation, but the reliability of the method may not be guaranteed when extrapolated to dienes outside of this database. Therefore, we will continue to validate this estimation technique in future studies.
C bond, the faster the reaction rate coefficient is. Following the reactivity discussion, we proposed that the rate coefficients of conjugated diene and isolated diene reaction with ˙OH could be calculated from a simple SAR method by summing up the rate coefficients of corresponding mono-alkenes and multiplying a correction factor. The present SAR method has the advantage of being easy to compute without the need for complex parameters. Our work provides a simple idea to estimate the reaction coefficients of dienes or poly-alkenes with ˙OH. We must state that the SAR proposed in this paper are reasonably reliable (within <8% of the experimental values) when used within the database used in its derivation, but the reliability of the method may not be guaranteed when extrapolated to dienes outside of this database. Therefore, we will continue to validate this estimation technique in future studies.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This research was supported by the National Key R&D Program of China (No. 2022YFC3701100), National Natural Science Foundation of China (No. 21976106), funding of youth scientist from Research Center for Eco-Environmental Sciences – Chinese Academy of Sciences (RCEES-CAS), One Hundred Person Project of the Chinese Academy of Sciences and Science Fund Program for Distinguished Young Scholars of the National Natural Science Foundation of China (Overseas).
References
- R. J. Ouellette and J. D. Rawn, in Organic Chemistry, ed. R. J. Ouellette and J. D. Rawn, Academic Press, 2nd edn, 2018, pp. 321–351 Search PubMed.
- G. P. Moss, P. A. S. Smith and D. Tavernier, Pure Appl. Chem., 1995, 67, 1307–1375 Search PubMed.
- X. Yuan, Y. Xu, V. Calatayud, Z. Li, Z. Feng and F. Loreto, Atmos. Environ., 2023, 314, 120096 CrossRef CAS.
- J. Kesselmeier and M. Staudt, J. Atmos. Chem., 1999, 33, 23–88 CrossRef CAS.
- S. Liu, J. Xing, H. Zhang, D. Ding, F. Zhang, B. Zhao, S. K. Sahu and S. Wang, Atmos. Environ., 2019, 218, 117020 CrossRef CAS.
- E. Grosjean, D. Grosjean and R. A. Rasmussen, Environ. Sci. Technol., 1998, 32, 2061–2069 CrossRef CAS.
- F. Faulhammer, in Encyclopedia of Toxicology, ed. P. J. Wexler, Academic Press, Oxford, 4th edn, 2024, pp. 317–324 Search PubMed.
- P.-Z. Wang, W.-J. Xiao and J.-R. Chen, Chin. J. Catal., 2022, 43, 548–557 CrossRef CAS.
- T. Sato, T. Suto, Y. Nagashima, S. Mukai and N. Chida, Asian J. Org. Chem., 2021, 10, 2486–2502 CrossRef CAS.
- F. A. Soares and A. Steinbüchel, Macromol. Biosci., 2021, 21, 2100261 CrossRef CAS PubMed.
- S. Liu, J. Yan, Q. Zhang and Y. Yan, J. Inorg. Organomet. Polym. Mater., 2022, 32, 3368–3394 CrossRef CAS.
- A. Shoji, K. Nakamura, S. Nishiyama, D. S. Kumar, K. Murato, Y. Nakagawa, H. Noguchi, K. Kashiwagi, Y. Yoshida and S. Ishii, J. Photopolym. Sci. Technol., 2007, 20, 817–822 CrossRef CAS.
- Y. Bai, Y. Wang and X. Wang, Renewable Energy, 2021, 171, 266–274 CrossRef CAS.
- A. Li, L. Zhu, Y. Mao, J. Zhai, D. Han, X. Lu and Z. Huang, Combust. Flame, 2019, 199, 152–167 CrossRef CAS.
- R. T. Pavlovic, D. T. Allen and E. C. McDonald-Buller, Ind. Eng. Chem. Res., 2012, 51, 12653–12662 CrossRef CAS.
- M. Leuchner and B. Rappenglück, Atmos. Environ., 2010, 44, 4056–4067 CrossRef CAS.
- J. Zheng, M. Shao, W. Che, L. Zhang, L. Zhong, Y. Zhang and D. Streets, Environ. Sci. Technol., 2009, 43, 8580–8586 CrossRef CAS PubMed.
- C.-H. Chen, Y.-C. Chuang, C.-C. Hsieh and C.-S. Lee, Atmos. Pollut. Res., 2019, 10, 1060–1074 CrossRef CAS.
- B. H. Czader and B. Rappenglück, Atmos. Environ., 2015, 102, 30–42 CrossRef CAS.
- R. Atkinson, J. Phys. Chem. Ref. Data, 1997, 26, 215–290 CrossRef CAS.
- R. Atkinson, Atmos. Environ., 2000, 34, 2063–2101 CrossRef CAS.
- J. Fan and R. Zhang, Environ. Chem., 2004, 1, 140–149 CrossRef CAS.
- X. Chen, D. Hulbert and P. B. Shepson, J. Geophys. Res.: Atmos., 1998, 103, 25563–25568 CrossRef CAS.
- B. Chuong and P. S. Stevens, J. Geophys. Res.: Atmos., 2002, 107, ACH 2-1 CrossRef.
- M. Karl, H.-P. Dorn, F. Holland, R. Koppmann, D. Poppe, L. Rupp, A. Schaub and A. Wahner, J. Atmos. Chem., 2006, 55, 167–187 CrossRef CAS.
- E. C. Tuazon, A. Alvarado, S. M. Aschmann, R. Atkinson and J. Arey, Environ. Sci. Technol., 1999, 33, 3586–3595 CrossRef CAS.
- J. Baker, J. Arey and R. Atkinson, Environ. Sci. Technol., 2005, 39, 4091–4099 CrossRef CAS PubMed.
- Z. Li, P. Nguyen, M. Fatima de Leon, J. H. Wang, K. Han and G. Z. He, J. Phys. Chem. A, 2006, 110, 2698–2708 CrossRef CAS PubMed.
- A. P. Teng, J. D. Crounse, L. Lee, J. M. St. Clair, R. C. Cohen and P. O. Wennberg, Atmos. Chem. Phys., 2015, 15, 4297–4316 CrossRef CAS.
- Y. Sakamoto, N. Kohno, S. Ramasamy, K. Sato, Y. Morino and Y. Kajii, Atmos. Environ., 2022, 271, 118916 CrossRef CAS.
- D. J. Barket Jr, J. W. Grossenbacher, J. M. Hurst, P. B. Shepson, K. Olszyna, T. Thornberry, M. A. Carroll, J. Roberts, C. Stroud, J. Bottenheim and T. Biesenthal, J. Geophys. Res.: Atmos., 2004, 109, D11310 CrossRef.
- J. W. Grossenbacher, D. J. Barket Jr, P. B. Shepson, M. A. Carroll, K. Olszyna and E. Apel, J. Geophys. Res.: Atmos., 2004, 109, D11311 CrossRef.
- Y. Cao, Q. Ma, B. Chu and H. He, Front. Environ. Sci. Eng., 2022, 17, 48 CrossRef.
- Y. Yang, X. Zheng, W. Ren, J. Liu, X. Fu, S. Meng, S. Chen and C. Cai, Front. Environ. Sci. Eng., 2022, 16, 137 CrossRef CAS.
- J. Peeters, W. Boullart, V. Pultau, S. Vandenberk and L. Vereecken, J. Phys. Chem. A, 2007, 111, 1618–1631 CrossRef CAS PubMed.
- S. Singh and Z. Li, J. Phys. Chem. A, 2007, 111, 11843–11851 CrossRef CAS PubMed.
- F. Khaled, B. R. Giri, D. Liu, E. Assaf, C. Fittschen and A. Farooq, J. Phys. Chem. A, 2019, 123, 2261–2271 CrossRef CAS PubMed.
- R. Atkinson, Int. J. Chem. Kinet., 1987, 19, 799–828 CrossRef CAS.
- T. Ohta, J. Phys. Chem., 1983, 87, 1209–1213 CrossRef CAS.
- J. G. Calvert, R. Atkinson, J. A. Kerr, S. Madronich, G. K. Moortgat, T. J. Wallington and G. Yarwood, The Mechanisms of Atmospheric Oxidation of the Alkenes, Oxford University Press, 2000 Search PubMed.
- T. Spangenberg, S. P. K. Köhler, B. Hansmann, U. Wachsmuth, B. Abel and M. A. Smith, J. Phys. Chem. A, 2004, 108, 7527–7534 CrossRef CAS.
- B. R. Giri, T. V.-T. Mai, T. T.-D. Nguyen, M. Szőri, L. K. Huynh and A. Farooq, Combust. Flame, 2022, 241, 112153 CrossRef CAS.
- L. Liu, R. M. Ward and J. M. Schomaker, Chem. Rev., 2019, 119, 12422–12490 CrossRef CAS PubMed.
- E. Es-sebbar, F. Khaled, A. Elwardany and A. Farooq, J. Phys. Chem. A, 2016, 120, 7998–8005 CrossRef CAS PubMed.
- R. Atkinson, J. Phys. Chem. Ref. Data, 1989, Monograph No. 1, 1–246 Search PubMed.
- R. Castañeda-Arriaga and J. R. Alvarez-Idaboy, Int. J. Quantum Chem., 2012, 112, 3479–3483 CrossRef.
- J. R. Alvarez-Idaboy, N. Mora-Diez and A. Vivier-Bunge, J. Am. Chem. Soc., 2000, 122, 3715–3720 CrossRef CAS.
- H. El Othmani, Y. Ren, Y. Bedjanian, S. El Hajjaji, C. Tovar, P. Wiesen, A. Mellouki, M. R. McGillen and V. Daële, ACS Earth Space Chem., 2021, 5, 960–968 CrossRef CAS.
- Y. Ren, M. Cai, V. Daële and A. Mellouki, Atmos. Environ., 2019, 200, 243–253 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi, J. Troe and I. Subcommittee, Atmos. Chem. Phys., 2006, 6, 3625–4055 CrossRef CAS.
- A. B. Vakhtin, J. E. Murphy and S. R. Leone, J. Phys. Chem. A, 2003, 107, 10055–10062 CrossRef CAS.
- C. K. Westbrook, W. J. Pitz, M. Mehl, P.-A. Glaude, O. Herbinet, S. Bax, F. Battin-Leclerc, O. Mathieu, E. L. Petersen, J. Bugler and H. J. Curran, J. Phys. Chem. A, 2015, 119, 7462–7480 CrossRef CAS PubMed.
- M. R. McGillen, C. J. Percival, D. E. Shallcross and J. N. Harvey, Phys. Chem. Chem. Phys., 2007, 9, 4349–4356 RSC.
- S. Sekušak, K. R. Liedl and A. Sabljić, J. Phys. Chem. A, 1998, 102, 1583–1594 CrossRef.
- I. Díaz-Acosta, J. R. Alvarez-Idaboy and A. Vivier-Bunge, Int. J. Chem. Kinet., 1999, 31, 29–36 CrossRef.
- R. J. Cvetanović, J. Phys. Chem. Ref. Data, 1987, 16, 261–326 CrossRef.
- D. L. Singleton and R. J. Cvetanovic, J. Am. Chem. Soc., 1976, 98, 6812–6819 CrossRef CAS.
- R. Atkinson, Chem. Rev., 1986, 86, 69–201 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- V. H. Carvalho-Silva, N. D. Coutinho and V. Aquilanti, Front. Chem., 2019, 7, 380 CrossRef CAS PubMed.
- P. Saha and S. Chowdhury, in Thermodynamics, ed. M. Tadashi, IntechOpen, Rijeka, 2011 Search PubMed.
- P. Ptáček, F. Šoukal and T. Opravil, in Introducing the Effective Mass of Activated Complex and the Discussion on the Wave Function of this Instanton, ed. P. Ptáček, T. Opravil and F. Šoukal, IntechOpen, Rijeka, 2018 Search PubMed.
- M. R. McGillen, W. P. L. Carter, A. Mellouki, J. J. Orlando, B. Picquet-Varrault and T. J. Wallington, Earth Syst. Sci. Data, 2020, 12, 1203–1216 CrossRef.
- R. Izsák, M. Szőri, P. J. Knowles and B. Viskolcz, J. Chem. Theory Comput., 2009, 5, 2313–2321 CrossRef PubMed.
- J. R. Alvarez-Idaboy, I. Díaz-Acosta and A. Vivier-Bunge, J. Comput. Chem., 1998, 19, 811–819 CrossRef CAS.
- R. J. Ouellette and J. D. Rawn, in Organic Chemistry, ed. R. J. Ouellette and J. D. Rawn, Academic Press, 2nd edn, 2018, pp. 135–165 Search PubMed.
- D. R. Taylor, Chem. Rev., 1967, 67, 317–359 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Time profile of reactants during the reaction time; experimental conditions at temperatures of 273–318 K; rate coefficients for the reaction of OH radicals with dienes and corresponding mono-alkenes; rate coefficients for the reaction with OH of a series of straight-chain dienes; rate coefficients of dienes reaction with OH radical vs. the alkyl groups on the diene. See DOI: https://doi.org/10.1039/d3ra08750f |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Xinmiao Xubc,
Han Lyu
ab,
Xinmiao Xubc,
Han Lyu d,
Yunfeng Lie,
Yangang Ren
d,
Yunfeng Lie,
Yangang Ren *bc,
Jinhe Wangd,
Yujing Mubc,
Abdelwahid Mellouki
*bc,
Jinhe Wangd,
Yujing Mubc,
Abdelwahid Mellouki fg and
Zongzheng Yang*a
fg and
Zongzheng Yang*a
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, theoretically, they are much more chemically reactive with hydroxyl radical (˙OH) than alkenes and alkanes, and the reaction with ˙OH is one of the main atmospheric degradation routes of dienes during the daytime. In our work, rate coefficients of three types of acyclic dienes: conjugated as 3-methyl-1,3-pentadiene (3M13PD), isolated as 1,4-hexadiene (14HD), and cumulated as 1,2-pentadiene (12PD) reaction with ˙OH were measured in the temperature range of 273–318 K and 1 atm using the relative rate method. At 298 ± 3 K, the rate coefficients for those reactions were determined to be k3M13PD+OH = (15.09 ± 0.72) × 10−11, k14HD+OH = (9.13 ± 0.62) × 10−11, k12PD+OH = (3.34 ± 0.40) × 10−11 (as units of cm3 per molecule per s), in the excellent agreement with values of previously reported. The first measured temperature dependence for 3M13PD, 14HD and 12PD reaction with ˙OH can be expressed by the following Arrhenius expressions in units of cm3 per molecule per s: k3M13PD+OH = (8.10 ± 2.23) × 10−11
C bonds, theoretically, they are much more chemically reactive with hydroxyl radical (˙OH) than alkenes and alkanes, and the reaction with ˙OH is one of the main atmospheric degradation routes of dienes during the daytime. In our work, rate coefficients of three types of acyclic dienes: conjugated as 3-methyl-1,3-pentadiene (3M13PD), isolated as 1,4-hexadiene (14HD), and cumulated as 1,2-pentadiene (12PD) reaction with ˙OH were measured in the temperature range of 273–318 K and 1 atm using the relative rate method. At 298 ± 3 K, the rate coefficients for those reactions were determined to be k3M13PD+OH = (15.09 ± 0.72) × 10−11, k14HD+OH = (9.13 ± 0.62) × 10−11, k12PD+OH = (3.34 ± 0.40) × 10−11 (as units of cm3 per molecule per s), in the excellent agreement with values of previously reported. The first measured temperature dependence for 3M13PD, 14HD and 12PD reaction with ˙OH can be expressed by the following Arrhenius expressions in units of cm3 per molecule per s: k3M13PD+OH = (8.10 ± 2.23) × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(173 ± 71)/T]; k14HD+OH = (9.82 ± 5.10) × 10−12
exp[(173 ± 71)/T]; k14HD+OH = (9.82 ± 5.10) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(666 ± 123)/T]; k12PD+OH = (1.13 ± 0.87) × 10−12
exp[(666 ± 123)/T]; k12PD+OH = (1.13 ± 0.87) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(1038 ± 167)/T] (as units of cm3 per molecule per s). The kinetic discussion revealed that the relative position between these two C
exp[(1038 ± 167)/T] (as units of cm3 per molecule per s). The kinetic discussion revealed that the relative position between these two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C could significantly affect the reactivity of acyclic dienes toward ˙OH. A simple structure–activity relationship (SAR) method was proposed to estimate the reaction rate coefficients of acyclic dienes with ˙OH.
C could significantly affect the reactivity of acyclic dienes toward ˙OH. A simple structure–activity relationship (SAR) method was proposed to estimate the reaction rate coefficients of acyclic dienes with ˙OH.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are adjacent to each other, separated by one single bond or by more than one, the acyclic dienes are named and classified by IUPAC to be cumulated dienes, conjugated dienes, and isolated dienes.1,2 Isoprene is one of the most important representatives of conjugated diene found in the atmosphere. It counts for about half of the total amount of biogenic volatile organic compounds (BVOCs) released from vegetation, around 600 teragrams of carbon per year (Tg C per year).3–5 1,3-Butadiene is another important acyclic diene in the atmosphere, and it is listed as a critical hazardous air pollutant due to its carcinogenic and mutagenic properties. Its concentration can reach up to 1 ppbv measured in urban areas.6,7 Acyclic dienes are also essential raw materials for organic synthesis,8,9 e.g., 1,3-butadiene, 1,2-pentadiene, 1,4-hexadiene, and 3-methyl-1,3-pentadiene are used in the synthesis of rubbers,10 polymers,11 coatings,12 and biodiesel.13,14 Hence, large amounts of acyclic dienes could be released into the atmosphere during production, transportation, and usage.15–18 The main removal pathway of acyclic dienes in the atmosphere could be their reaction with ˙OH.19–21 The rate coefficients for the reactions of ˙OH and the subsequent degradation mechanism with isoprene22–25 and 1,3-butadiene26–28 have been widely studied. Several previous investigations have shown that the reaction of acyclic dienes with ˙OH in the presence of NOx could produce critical atmospheric pollutants such as peroxyacetyl nitrate (PAN), organic nitrates and carbonyl compounds.29–34 However, the reactivity of most of the acyclic dienes towards ˙OH still not well investigated.35–38 It is, indeed, of interest to conduct comprehensive studies on a more extensive set of acyclic dienes with various chemical structures in order to improve the knowledge of their atmospheric fate and impacts.
C bonds are adjacent to each other, separated by one single bond or by more than one, the acyclic dienes are named and classified by IUPAC to be cumulated dienes, conjugated dienes, and isolated dienes.1,2 Isoprene is one of the most important representatives of conjugated diene found in the atmosphere. It counts for about half of the total amount of biogenic volatile organic compounds (BVOCs) released from vegetation, around 600 teragrams of carbon per year (Tg C per year).3–5 1,3-Butadiene is another important acyclic diene in the atmosphere, and it is listed as a critical hazardous air pollutant due to its carcinogenic and mutagenic properties. Its concentration can reach up to 1 ppbv measured in urban areas.6,7 Acyclic dienes are also essential raw materials for organic synthesis,8,9 e.g., 1,3-butadiene, 1,2-pentadiene, 1,4-hexadiene, and 3-methyl-1,3-pentadiene are used in the synthesis of rubbers,10 polymers,11 coatings,12 and biodiesel.13,14 Hence, large amounts of acyclic dienes could be released into the atmosphere during production, transportation, and usage.15–18 The main removal pathway of acyclic dienes in the atmosphere could be their reaction with ˙OH.19–21 The rate coefficients for the reactions of ˙OH and the subsequent degradation mechanism with isoprene22–25 and 1,3-butadiene26–28 have been widely studied. Several previous investigations have shown that the reaction of acyclic dienes with ˙OH in the presence of NOx could produce critical atmospheric pollutants such as peroxyacetyl nitrate (PAN), organic nitrates and carbonyl compounds.29–34 However, the reactivity of most of the acyclic dienes towards ˙OH still not well investigated.35–38 It is, indeed, of interest to conduct comprehensive studies on a more extensive set of acyclic dienes with various chemical structures in order to improve the knowledge of their atmospheric fate and impacts.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 reported the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH at 297 ± 2 K. Ohta 1983
39 reported the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH at 297 ± 2 K. Ohta 1983![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 also proposed one structure–activity relationship (SAR) method to estimate the rate coefficients of conjugated diene and isolated diene, but not cumulated diene. To the best of our knowledge, no available temperature-dependence data on the reaction of ˙OH with 3M13PD, 14HD, or 12PD has been reported so far.
39 also proposed one structure–activity relationship (SAR) method to estimate the rate coefficients of conjugated diene and isolated diene, but not cumulated diene. To the best of our knowledge, no available temperature-dependence data on the reaction of ˙OH with 3M13PD, 14HD, or 12PD has been reported so far.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 = 4
O2 = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Known concentrations of the gas-phase chemicals were injected into the chamber through a mass flow controller (MFC). The chemicals in the liquid phase were introduced into the chamber by injecting a known volume into a three-way bubbler and then flushed with zero air. The inlet line was purged with 5 L of zero air after each chemical introduction to ensure the sample was completely introduced into the chamber. The Teflon chamber was also well-cleaned by inflating, shaking, and pumping three times. The time profiles of the concentration of the species of interest were monitored using an on-line gas chromatography-photoionization detector (GC-PID) (GC-4400, East & West Analytical Instruments, Inc., China). The packed column was operated at 45 °C, and N2 was used as the carrier gas.
1. Known concentrations of the gas-phase chemicals were injected into the chamber through a mass flow controller (MFC). The chemicals in the liquid phase were introduced into the chamber by injecting a known volume into a three-way bubbler and then flushed with zero air. The inlet line was purged with 5 L of zero air after each chemical introduction to ensure the sample was completely introduced into the chamber. The Teflon chamber was also well-cleaned by inflating, shaking, and pumping three times. The time profiles of the concentration of the species of interest were monitored using an on-line gas chromatography-photoionization detector (GC-PID) (GC-4400, East & West Analytical Instruments, Inc., China). The packed column was operated at 45 °C, and N2 was used as the carrier gas.
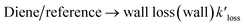

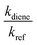 , can be derived from the linear least regression of
, can be derived from the linear least regression of 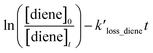 vs.
vs. 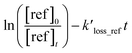 .
.
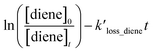 as the function of
as the function of 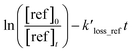 for all the experiments from which the ratios of
for all the experiments from which the ratios of 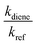 were obtained (Table 1). We repeated the experiments for each reference at least three times to ensure reproducibility. The uncertainties of
were obtained (Table 1). We repeated the experiments for each reference at least three times to ensure reproducibility. The uncertainties of 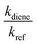 were taken as 2σ of the linear fitting of Fig. 1 when plotting all the experimental results together. The rate coefficients of reference compounds reacting with ˙OH are: kpropene+OH = 4.85 × 10−12
were taken as 2σ of the linear fitting of Fig. 1 when plotting all the experimental results together. The rate coefficients of reference compounds reacting with ˙OH are: kpropene+OH = 4.85 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[504/T],40 k1,3-butadiene+OH = 1.48 × 10−11
exp[504/T],40 k1,3-butadiene+OH = 1.48 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[448/T],40 in units of cm3 per molecule per s. Hence, the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH were calculated through eqn (1), as shown in Table 1. The obtained rate coefficients using propene and 1,3-butadiene agreed well with each other (differences < 15%). The error of kdiene was calculated using the equation of
exp[448/T],40 in units of cm3 per molecule per s. Hence, the rate coefficients of 3M13PD, 14HD, and 12PD reaction with ˙OH were calculated through eqn (1), as shown in Table 1. The obtained rate coefficients using propene and 1,3-butadiene agreed well with each other (differences < 15%). The error of kdiene was calculated using the equation of  . Finally, the derived rate coefficients of studied dienes reaction ˙OH were weighted average of kdiene_ref (Table 1) and calculated as follows: kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5, as units of cm3 per molecule per s.
. Finally, the derived rate coefficients of studied dienes reaction ˙OH were weighted average of kdiene_ref (Table 1) and calculated as follows: kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5, as units of cm3 per molecule per s.
 .48c Weighted average49 kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5.
.48c Weighted average49 kav = (wdiene_ref1kdiene_ref1 + wdiene_ref2kdiene_ref2 + …)/(wdiene_ref1 + wdiene_ref2 + …), where wdiene_ref1 = 1/σdiene_ref12, etc. The error, σav, was given by: σav = (1/σdiene_ref1 + 1/σdiene_ref2 + …)−0.5.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is the primary mechanism for ˙OH reaction with alkenes.20,41 An explanation of alkene reactivity has been studied and reported is that the more specific-addition sites an alkene can provide, the more reactive the alkene is for its reaction with ˙OH.35,42 Cumulated diene, 12PD contains a propadiene group (C
C bond is the primary mechanism for ˙OH reaction with alkenes.20,41 An explanation of alkene reactivity has been studied and reported is that the more specific-addition sites an alkene can provide, the more reactive the alkene is for its reaction with ˙OH.35,42 Cumulated diene, 12PD contains a propadiene group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–), and the intermolecular addition of ˙OH to 12PD takes place at three potential sites due to the two tightly linked double bonds forming a unique π-bond structure.43,44 In contrast, conjugated diene 3M13PD and isolated diene 14HD can provide four addition sites, which explains why 12PD is less reactive toward ˙OH than 3M13PD, 14HD, where k12PD+OH is 3–5 times lower than k3M13PD+OH and k14HD+OH. It has been reported in related experiments that the substitution of alkyl groups on the C
C–), and the intermolecular addition of ˙OH to 12PD takes place at three potential sites due to the two tightly linked double bonds forming a unique π-bond structure.43,44 In contrast, conjugated diene 3M13PD and isolated diene 14HD can provide four addition sites, which explains why 12PD is less reactive toward ˙OH than 3M13PD, 14HD, where k12PD+OH is 3–5 times lower than k3M13PD+OH and k14HD+OH. It has been reported in related experiments that the substitution of alkyl groups on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond increases the reactivity of alkene toward ˙OH because –CH3 groups are supposed to increase the electron density in the neighbor C
C bond increases the reactivity of alkene toward ˙OH because –CH3 groups are supposed to increase the electron density in the neighbor C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond as well as decrease the ionization energy and, therefore increase the reactivity.40,45–47 Hence, although both 3M13PD and 14HD contain four addition sites for ˙OH, more alkyl groups on 3M13PD than on 14HD could be an important reason why k3M13PD+OH is 1.6 times greater than k14HD+OH. The reactivity of conjugated diene, isolated diene, and cumulated diene will be further discussed in the following sections.
C bond as well as decrease the ionization energy and, therefore increase the reactivity.40,45–47 Hence, although both 3M13PD and 14HD contain four addition sites for ˙OH, more alkyl groups on 3M13PD than on 14HD could be an important reason why k3M13PD+OH is 1.6 times greater than k14HD+OH. The reactivity of conjugated diene, isolated diene, and cumulated diene will be further discussed in the following sections.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−Ea/RT, for the temperature range of 273–318 K. The units for the rate coefficients are cm3 per molecule per s and are listed in Table 2.
e−Ea/RT, for the temperature range of 273–318 K. The units for the rate coefficients are cm3 per molecule per s and are listed in Table 2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(173 ± 71)/T]
exp[(173 ± 71)/T]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(666 ± 123)/T]
exp[(666 ± 123)/T]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(1038 ± 167)/T]
exp[(1038 ± 167)/T]
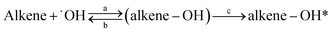
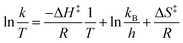 . Where, k is the rate constant, kB is the Boltzmann's constant (1.381 × 10−23 J K−1), T is the absolute temperature in Kelvin (K), h is plank's constant (6.626 × 10−34 J s), R is the gas constant (8.314 J mol−1 K−1), ΔH‡ is the enthalpy of activation and ΔS‡ is the entropy of activation.
. Where, k is the rate constant, kB is the Boltzmann's constant (1.381 × 10−23 J K−1), T is the absolute temperature in Kelvin (K), h is plank's constant (6.626 × 10−34 J s), R is the gas constant (8.314 J mol−1 K−1), ΔH‡ is the enthalpy of activation and ΔS‡ is the entropy of activation.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC
CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (Z)-1,3-pentadiene (C/C
C), (Z)-1,3-pentadiene (C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C\C
C\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (3E)-penta-1,3-diene (C/C
C), (3E)-penta-1,3-diene (C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C
C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (3E)-hexa-1,3-diene (CC/C
C), (3E)-hexa-1,3-diene (CC/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C
C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), (Z/E)-2,4-hexadiene (CC
C), (Z/E)-2,4-hexadiene (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC
CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC), isolated dienes: 1,4-pentadiene (C
CC), isolated dienes: 1,4-pentadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCC
CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 1,4-hexadiene (C
C), 1,4-hexadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CC/C
CC/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C), 1,5-hexadiene (C
C/C), 1,5-hexadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCCC
CCCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), and cumulated dienes: propadiene (C
C), and cumulated dienes: propadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), methylallene (CC
C), methylallene (CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 1,2-pentadiene (CCC
C), 1,2-pentadiene (CCC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). The results again showed that the reactivity of conjugated dienes toward ˙OH is higher than expected for an isolated C
C). The results again showed that the reactivity of conjugated dienes toward ˙OH is higher than expected for an isolated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond and then cumulated C
C bond and then cumulated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. This phenomenon could be explained by the relative position of the two C
C bond. This phenomenon could be explained by the relative position of the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds on the acyclic diene.
C bonds on the acyclic diene.

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), conjugated diene (C
C), conjugated diene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), and isolated diene (C
C), and isolated diene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–(C)n–C
C–(C)n–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, n ≥ 1). The rate coefficient values for dienes' reaction with OH radicals are from McGillen et al. (2020)63 and are shown in Table S3.†
C, n ≥ 1). The rate coefficient values for dienes' reaction with OH radicals are from McGillen et al. (2020)63 and are shown in Table S3.†![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond to occur.28,64,65 Hence, the relative position of two C
C bond to occur.28,64,65 Hence, the relative position of two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds on an acyclic diene likely affects its energy barrier and then reactivity. To explain this further, we take the example of 1,3-, 1,4- and 1,2-pentadiene. The energy barriers for the reaction of the three dienes with ˙OH have been calculated by utilizing the m062x/6-31+G(d,p) and m062x/6-311+G(3df,3pd) level of theory (see details in Fig. S3†). The stability of the initial OH adduct will ultimately affect the overall reactivity of the alkene with ˙OH.42 For example, in 1,3-pentadiene, the four pathways are grouped two by two, as IM1 and IM4 have similar potential heights and are lower than IM2 and IM3. For conjugated dienes, the pi-electron density overlap allows the electrons to “delocalise” over a larger area,1,66 explaining why IM2 and IM3 are so similar. Likewise, the conjugated stabilized structure reduces the overall energy (−40.16 kcal mol−1) of this isomer, which accounts for the reactivity enhancement of conjugated dienes towards ˙OH. Accordingly, the overall rate coefficient of 1,3-pentadiene is higher than the sum of two corresponding mono-alkene, e.g. k1,3-pentadiene of 11.60 × 10−11 cm3 per molecule per s is higher than the sum of the rate coefficients of 1-pentene (k1-pentene) and 2-pentene (k2-pentene) reaction with ˙OH as 9.72 × 10−11 cm3 per molecule per s, where k1-pentene and k2-pentene are 3.22 ± 0.48 and 6.50 ± 2.00 × 10−11 cm3 per molecule per s,63 respectively. This phenomenon could also be applied to other conjugated dienes (Table S3†).
C bonds on an acyclic diene likely affects its energy barrier and then reactivity. To explain this further, we take the example of 1,3-, 1,4- and 1,2-pentadiene. The energy barriers for the reaction of the three dienes with ˙OH have been calculated by utilizing the m062x/6-31+G(d,p) and m062x/6-311+G(3df,3pd) level of theory (see details in Fig. S3†). The stability of the initial OH adduct will ultimately affect the overall reactivity of the alkene with ˙OH.42 For example, in 1,3-pentadiene, the four pathways are grouped two by two, as IM1 and IM4 have similar potential heights and are lower than IM2 and IM3. For conjugated dienes, the pi-electron density overlap allows the electrons to “delocalise” over a larger area,1,66 explaining why IM2 and IM3 are so similar. Likewise, the conjugated stabilized structure reduces the overall energy (−40.16 kcal mol−1) of this isomer, which accounts for the reactivity enhancement of conjugated dienes towards ˙OH. Accordingly, the overall rate coefficient of 1,3-pentadiene is higher than the sum of two corresponding mono-alkene, e.g. k1,3-pentadiene of 11.60 × 10−11 cm3 per molecule per s is higher than the sum of the rate coefficients of 1-pentene (k1-pentene) and 2-pentene (k2-pentene) reaction with ˙OH as 9.72 × 10−11 cm3 per molecule per s, where k1-pentene and k2-pentene are 3.22 ± 0.48 and 6.50 ± 2.00 × 10−11 cm3 per molecule per s,63 respectively. This phenomenon could also be applied to other conjugated dienes (Table S3†).![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are separated by one (or more for other isolated dienes) sp3-hybridized carbon atom. As such, each C
C bonds are separated by one (or more for other isolated dienes) sp3-hybridized carbon atom. As such, each C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond behaves independently of the other, and the electron density cannot spread out as well or evenly. This also resulted in very similar potential barriers for all four channels (IM1 = IM4 = −30.33 kcal mol−1, IM2 = IM3 = −31.25 kcal mol−1), as shown in Fig. S3c.† Compared to 1,4-pentadiene, the conjugation effect makes IM1 and IM4 lower for 1,3-pentadiene. The adduct of 1,4-pentadiene with OH lacks resonance stabilization, which may affect the exothermic nature of the reaction and the height of the potential barriers for the formation of the internal transition states of the adduct. It will ultimately affect the overall reactivity of 1,4-pentadiene with ˙OH.42,66 Generally, the overall rate coefficients of 1,4-pentadiene are expected to be equal to the sum of two corresponding mono-alkenes, but in fact, they are lower than the sum of rate coefficients of mono-alkenes, e.g., k1,4-pentadiene of 5.41 × 10−11 cm3 per molecule per s is lower than k1-pentene + k1-pentene as 6.44 × 10−11 cm3 per molecule per s, and it is same for other isolated dienes (Table S3†). This finding indicates that the interaction also exists between these two isolated C
C bond behaves independently of the other, and the electron density cannot spread out as well or evenly. This also resulted in very similar potential barriers for all four channels (IM1 = IM4 = −30.33 kcal mol−1, IM2 = IM3 = −31.25 kcal mol−1), as shown in Fig. S3c.† Compared to 1,4-pentadiene, the conjugation effect makes IM1 and IM4 lower for 1,3-pentadiene. The adduct of 1,4-pentadiene with OH lacks resonance stabilization, which may affect the exothermic nature of the reaction and the height of the potential barriers for the formation of the internal transition states of the adduct. It will ultimately affect the overall reactivity of 1,4-pentadiene with ˙OH.42,66 Generally, the overall rate coefficients of 1,4-pentadiene are expected to be equal to the sum of two corresponding mono-alkenes, but in fact, they are lower than the sum of rate coefficients of mono-alkenes, e.g., k1,4-pentadiene of 5.41 × 10−11 cm3 per molecule per s is lower than k1-pentene + k1-pentene as 6.44 × 10−11 cm3 per molecule per s, and it is same for other isolated dienes (Table S3†). This finding indicates that the interaction also exists between these two isolated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, which was not expected before.
C bonds, which was not expected before.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are shorter than those in typical alkene according to a high level of bond energy.43,67 These bonds form a special pi bond that leads to a possible stronger reactivity at the C2 position, but less reactive for C1 and C3. This seems surprising considering that the energy of IM2 is −56.69 kcal mol−1 (Fig. S3c†). However, laboratory results suggest that this bonding may reduce the reactivity of cumene to ˙OH. Meanwhile, the fact that there are only three specific addition sites may be another reason why the reaction rate coefficient of 1,2-pentadiene is lower than that of 1,3- and 1,4-pentadiene. For example, the k12PD of 3.34 × 10−11 cm3 per molecule per s (this work) is almost three times lower than the sum of rate coefficients of the according mono-alkenes 1-pentene and 2-pentene reaction with ˙OH k1-pentene + k2-pentene = 9.72 × 10−11 cm3 per molecule per s. Calvert et al., (2000) noted that the rate coefficient values for cumulated dienes reaction with ˙OH are very similar to those of the corresponding mono-alkene by replacing the C
C bonds are shorter than those in typical alkene according to a high level of bond energy.43,67 These bonds form a special pi bond that leads to a possible stronger reactivity at the C2 position, but less reactive for C1 and C3. This seems surprising considering that the energy of IM2 is −56.69 kcal mol−1 (Fig. S3c†). However, laboratory results suggest that this bonding may reduce the reactivity of cumene to ˙OH. Meanwhile, the fact that there are only three specific addition sites may be another reason why the reaction rate coefficient of 1,2-pentadiene is lower than that of 1,3- and 1,4-pentadiene. For example, the k12PD of 3.34 × 10−11 cm3 per molecule per s (this work) is almost three times lower than the sum of rate coefficients of the according mono-alkenes 1-pentene and 2-pentene reaction with ˙OH k1-pentene + k2-pentene = 9.72 × 10−11 cm3 per molecule per s. Calvert et al., (2000) noted that the rate coefficient values for cumulated dienes reaction with ˙OH are very similar to those of the corresponding mono-alkene by replacing the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C with a single C
C with a single C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C.40 Therefore, the second adjacent C
C.40 Therefore, the second adjacent C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond probably has a strong interaction on the “tradition” C
C bond probably has a strong interaction on the “tradition” C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, which needs further research.
C bond, which needs further research.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, they can only provide up to three addition sites, which may be why 12PD has a lower rate coefficient than 1,3-PD and 1,4-PD for reacting with ˙OH. Additionally, studies have shown that more alkyl substitutions on the C
C bonds, they can only provide up to three addition sites, which may be why 12PD has a lower rate coefficient than 1,3-PD and 1,4-PD for reacting with ˙OH. Additionally, studies have shown that more alkyl substitutions on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond would increase the ˙OH addition reactivity of alkene.40,46 For example, k3M13PD+OH > k1,3-pentadiene+OH > k1,3-butadiene+OH, with increasing numbers of –CH3 group from 1,3-butadiene (C
C bond would increase the ˙OH addition reactivity of alkene.40,46 For example, k3M13PD+OH > k1,3-pentadiene+OH > k1,3-butadiene+OH, with increasing numbers of –CH3 group from 1,3-butadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 1,3-pentadiene (C
C), 1,3-pentadiene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C), to 3M13PD (C
C–C), to 3M13PD (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C–C(C)
C–C–C(C)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C). We categorized the rate coefficient values for acyclic dienes into three base structures: C
C–C). We categorized the rate coefficient values for acyclic dienes into three base structures: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–(C)n–C
C–(C)n–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C. Fig. 4 illustrates the relationship between the rate coefficients of acyclic dienes' reaction with ˙OH and the number of alkyl groups on the acyclic diene (see detail in Table S4†). It shows that the more alkyl groups attached to the C
C. Fig. 4 illustrates the relationship between the rate coefficients of acyclic dienes' reaction with ˙OH and the number of alkyl groups on the acyclic diene (see detail in Table S4†). It shows that the more alkyl groups attached to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, the higher the ˙OH addition reactivity of the acyclic diene, with the –CH3 group having a stronger effect than –CH2CH3. The effect of alkyl groups is to increase the electron density in the adjacent double bond, lowering the ionization energy and thus increasing the reactivity with ˙OH.46
C bond, the higher the ˙OH addition reactivity of the acyclic diene, with the –CH3 group having a stronger effect than –CH2CH3. The effect of alkyl groups is to increase the electron density in the adjacent double bond, lowering the ionization energy and thus increasing the reactivity with ˙OH.46
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–(C)n–C
C–(C)n–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, based on information from this study and existing literature.39,63
C, based on information from this study and existing literature.39,63![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond to a C–C bond, e.g., 1,4-hexadiene → 1-hexene + 2-hexene (see detail in Table S3†). We plotted the rate coefficients of the dienes reaction with ˙OH (kexp) as a function of the sum of corresponding mono-alkenes (kcal) in Fig. 5. The plot clearly shows that the slopes of conjugated dienes and isolated dienes are 0.89 and 1.11, respectively. Therefore, we believe that a factor should be multiplied to the sum to obtain an accurate rate coefficient estimate. The factor for conjugated diene and isolated diene is the slope obtained from Fig. 5. The effect of the relative positions of the two C
C bond to a C–C bond, e.g., 1,4-hexadiene → 1-hexene + 2-hexene (see detail in Table S3†). We plotted the rate coefficients of the dienes reaction with ˙OH (kexp) as a function of the sum of corresponding mono-alkenes (kcal) in Fig. 5. The plot clearly shows that the slopes of conjugated dienes and isolated dienes are 0.89 and 1.11, respectively. Therefore, we believe that a factor should be multiplied to the sum to obtain an accurate rate coefficient estimate. The factor for conjugated diene and isolated diene is the slope obtained from Fig. 5. The effect of the relative positions of the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds of a diene on its energy barrier and reactivity can also be demonstrated intuitively by the factor. For example, the factor for conjugated diene is 0.89 (<1), meaning kexp > kcal, which indicates a possible positive effect between the two C
C bonds of a diene on its energy barrier and reactivity can also be demonstrated intuitively by the factor. For example, the factor for conjugated diene is 0.89 (<1), meaning kexp > kcal, which indicates a possible positive effect between the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds of the conjugated diene. On the contrary, the effect may be negative. This result is also in agreement with our earlier discussion of the reactivity of the three species of dienes.
C bonds of the conjugated diene. On the contrary, the effect may be negative. This result is also in agreement with our earlier discussion of the reactivity of the three species of dienes.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C as a single “traditional” C
C as a single “traditional” C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, as suggested by Calvert in 2000.40 In summary, the agreement between the SAR predictions and the experimental value is very excellent, with an average deviation of less than 8%.
C bond, as suggested by Calvert in 2000.40 In summary, the agreement between the SAR predictions and the experimental value is very excellent, with an average deviation of less than 8%.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(173 ± 71)/T]
exp[(173 ± 71)/T]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(666 ± 123)/T]
exp[(666 ± 123)/T]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(1038 ± 167)/T]
exp[(1038 ± 167)/T]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C on the acyclic dienes could determine its reactivity. The number and type of alkyl group and the number of addition sites on diene could also strongly affect its reactivity. The more alkyl substituents on the C
C on the acyclic dienes could determine its reactivity. The number and type of alkyl group and the number of addition sites on diene could also strongly affect its reactivity. The more alkyl substituents on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, the faster the reaction rate coefficient is. Following the reactivity discussion, we proposed that the rate coefficients of conjugated diene and isolated diene reaction with ˙OH could be calculated from a simple SAR method by summing up the rate coefficients of corresponding mono-alkenes and multiplying a correction factor. The present SAR method has the advantage of being easy to compute without the need for complex parameters. Our work provides a simple idea to estimate the reaction coefficients of dienes or poly-alkenes with ˙OH. We must state that the SAR proposed in this paper are reasonably reliable (within <8% of the experimental values) when used within the database used in its derivation, but the reliability of the method may not be guaranteed when extrapolated to dienes outside of this database. Therefore, we will continue to validate this estimation technique in future studies.
C bond, the faster the reaction rate coefficient is. Following the reactivity discussion, we proposed that the rate coefficients of conjugated diene and isolated diene reaction with ˙OH could be calculated from a simple SAR method by summing up the rate coefficients of corresponding mono-alkenes and multiplying a correction factor. The present SAR method has the advantage of being easy to compute without the need for complex parameters. Our work provides a simple idea to estimate the reaction coefficients of dienes or poly-alkenes with ˙OH. We must state that the SAR proposed in this paper are reasonably reliable (within <8% of the experimental values) when used within the database used in its derivation, but the reliability of the method may not be guaranteed when extrapolated to dienes outside of this database. Therefore, we will continue to validate this estimation technique in future studies.