Open Access Article
Open Access ArticleNi-doping effects on formation and migration of oxygen vacancies in SrFe1−xNixO3−δ oxygen carriers
Ting
Jia
 *a,
Yinuo
Hao
a,
Hua
Hao
*a,
Yinuo
Hao
a,
Hua
Hao
 a and
Zhi
Zeng
bc
a and
Zhi
Zeng
bc
aSchool of Physics, Hangzhou Normal University, Hangzhou, Zhejiang 311121, China. E-mail: tjia@hznu.edu.cn
bKey Laboratory of Materials Physics, Institute of Solid State Physics, HFIPS, Chinese Academy of Sciences, Hefei, 230031, China
cScience Island Branch of Graduate School, University of Science and Technology of China, Hefei, 230026, China
First published on 20th February 2024
Abstract
Ni is a promising B-site doping element capable of improving the oxygen carrier performance of SrFeO3 perovskite. In this work, the effect of Ni doping on the formation and migration of oxygen vacancies in SrFe1−xNixO3−δ (x = 0, 0.0625, 0.125, 0.1875, and 0.25) is investigated using density functional theory calculations. Our results show that the oxygen vacancies formed from Ni–O–Fe chains exhibit lower formation energy (Ef) compared to those from Fe–O–Fe chains in each doping system. Additionally, Ef generally decreases with an increase of Ni content. This Ni-promoted formation of VO is attributed to three factors: weakened Ni–O bonding, the closure of O-2p states to the Fermi level by Ni–O hybridization, and Ni3+ decreasing the positive charges to be compensated by VO formation. Due to these multiple advantages, a modest Ni doping of x = 0.25 can induce a higher PO2 and a lower T comparted to the relatively larger Co doping of x = 0.5, thermodynamically. Kinetically, Ni-doping appears to be a disadvantage as it hinders oxygen migration, due to a higher oxygen migration barrier through SrSrNi compared to the SrSrFe pathway. However, the overall oxygen ion conduction would not be significantly influenced by hopping through a nearby pathway of SrSrFe with a low migration barrier in a system doped with a small amount of Ni. In a word, a small amount of Ni doping has an advantage over Co doping in terms of enhancing the oxygen carrier performance of the parent SrFeO3 system.
1. Introduction
Metal-oxide perovskites ABO3−δ are a type of oxygen-carrier material, which can reversibly store and release oxygen by changing their oxygen content and structure under different partial oxygen pressures of the surrounding atmosphere and/or temperature. They have potential applications in energy storage, catalysis, gas sensing, and chemical looping.1–4 Oxygen vacancy formation and migration are essential properties of oxygen carriers. Among a large number of possible non-stoichiometric perovskites, SrFeO3−δ with a large fluctuation of oxygen non-stoichiometric values over a wide temperature range (δ = 0 to ∼0.5 from 0 to 1400 °C)5–7 has been identified as a promising oxygen carrier for air separation.8–11 However, it is noted that a pure SrFeO3−δ system has some issues in limited oxygen carrying capacity, releasing oxygen at a very low oxygen partial pressure and poor stability under a pure CO or CO2 atmosphere, etc.Therefore, many efforts have been made to enhance its chemical stability and improve its performance by A/B-site substitution.2,12–20 In particular, 3d transition metals are good candidates for B-site dopants, since these ions have similar ionic radii to that of Fe and may take part in redox reactions. Demizu et al. have reported that SrFe1−xTixO3−δ has a more stable perovskite structure under reducing conditions and exhibits faster oxygen storage/release rates compared to the unsubstituted SrFeO3−δ.21 Mn and Co are neighboring atoms of Fe in the periodic table and thus are considered as the preferred dopants for the Fe site. It has been found that the crystal structure of SrFe1−xMnxO3−δ is stable during oxygen desorption and Fe ions are more easily reduced.22 Our previous work on the optimal Co-doping of SrFe1−xCoxO3−δ showed that Co-doping can promote oxygen release and revealed the optimal Co-doping value and the promotion mechanism.23
It has been reported that oxygen vacancy formation becomes easier as the radius of the B-site cation decreases.24–26 Since Ni is the next nearest neighbor of Fe and has a smaller ionic radius, using Ni as a B-site dopant is very likely to improve the oxygen-carrier performance of SrFeO3−δ. In particular, our recent work has shown that low Ni doping in Sr1−xCaxFeO3 can promote oxygen vacancy formation.14 Therefore, in this work, we will systematically study the effect of Ni doping on the formation and migration of oxygen vacancies in SrFe1−xNixO3−δ and reveal relevant mechanisms.
2. Methods
All calculations were performed within the Vienna ab initio simulation package (VASP)27–29 and projector-augmented wave (PAW) method30 based on density functional theory (DFT). The spin-polarized Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA)31 was used for the exchange-correlation potential. The plane-wave basis set was converged at a cutoff energy of 450 eV. To account for the strong electron correlations of Fe and Ni ions, we employed the generalized gradient approximation plus Hubbard U (GGA + U) method32 with U = 4 eV (6 eV) for Fe (Ni) 3d electrons. The parent structure of SrFeO3 (SFO) with a cubic lattice constant of 3.857 Å was selected from the experimental results.33 A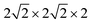 supercell with 80 atoms was used to build the Ni doping systems. We substitute 1, 2, 3, or 4 Fe by Ni in the 80 atom supercell symmetrically, corresponding to SrFe0.9375Ni0.0625O3 (SFN0.0625), SrFe0.875Ni0.125O3 (SFN0.125), SrFe0.8125Ni0.1875O3 (SFN0.1875), and SrFe0.75Ni0.25O3 (SFN0.25) in Fig. 1. The substitution Ni atoms are located at the coordinate (0, 0.75, 0.75) in SFN0.0625, coordinates (0.75, 0.5, 0.25) and (0.25, 0, 0.25) in SFN0.125, coordinates (0.25, 0.5, 0.25), (0.25, 0, 0.75), and (0.75, 0.5, 0.75) in SFN0.1875, and coordinates (0.25, 0.5, 0.25), (0.25, 0, 0.75), (0.75, 0.5, 0.75) and (0.75, 0, 0.25) in SFN0.25. A k-point mesh of 3 × 3 × 5 generated by the Monkhorst–Pack scheme34 was used for the
supercell with 80 atoms was used to build the Ni doping systems. We substitute 1, 2, 3, or 4 Fe by Ni in the 80 atom supercell symmetrically, corresponding to SrFe0.9375Ni0.0625O3 (SFN0.0625), SrFe0.875Ni0.125O3 (SFN0.125), SrFe0.8125Ni0.1875O3 (SFN0.1875), and SrFe0.75Ni0.25O3 (SFN0.25) in Fig. 1. The substitution Ni atoms are located at the coordinate (0, 0.75, 0.75) in SFN0.0625, coordinates (0.75, 0.5, 0.25) and (0.25, 0, 0.25) in SFN0.125, coordinates (0.25, 0.5, 0.25), (0.25, 0, 0.75), and (0.75, 0.5, 0.75) in SFN0.1875, and coordinates (0.25, 0.5, 0.25), (0.25, 0, 0.75), (0.75, 0.5, 0.75) and (0.75, 0, 0.25) in SFN0.25. A k-point mesh of 3 × 3 × 5 generated by the Monkhorst–Pack scheme34 was used for the 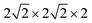 supercell. To maintain a cubic shape cell but restore FeO6 octahedron distortion, the structural optimization was performed iteratively between the atomic positions relaxation and volume relaxation,35,36 where we used a Methfessel–Paxton Fermi-level smearing with a width of 0.2 eV. The total energy was converged within 10−4 eV per atom and the Hellmann–Feynman force on each atomic site was converged to within 0.01 eV Å−1. Oxygen migration paths and barriers were determined using the climbing image-nudged elastic band (CI-NEB) method,37 where three intermediate images with the distance about 0.68 Å and a force tolerance of 0.03 eV Å−1 were used to determine the minimum energy pathway.
supercell. To maintain a cubic shape cell but restore FeO6 octahedron distortion, the structural optimization was performed iteratively between the atomic positions relaxation and volume relaxation,35,36 where we used a Methfessel–Paxton Fermi-level smearing with a width of 0.2 eV. The total energy was converged within 10−4 eV per atom and the Hellmann–Feynman force on each atomic site was converged to within 0.01 eV Å−1. Oxygen migration paths and barriers were determined using the climbing image-nudged elastic band (CI-NEB) method,37 where three intermediate images with the distance about 0.68 Å and a force tolerance of 0.03 eV Å−1 were used to determine the minimum energy pathway.
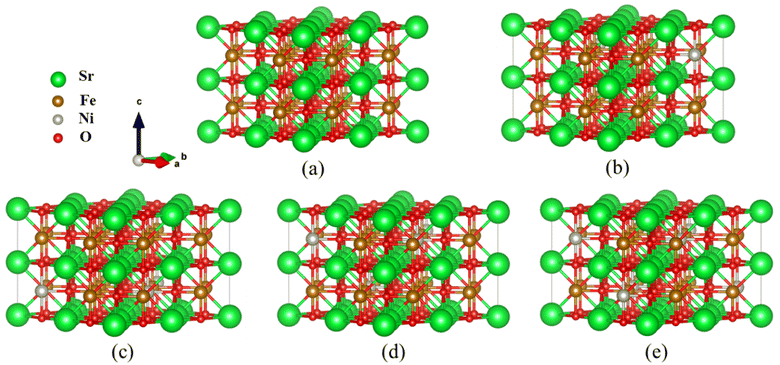 | ||
Fig. 1 Optimized 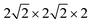 supercell for (a) SFO, (b) SFN0.0625, (c) SFN0.125, (d) SFN0.1875, and (e) SFN0.25. supercell for (a) SFO, (b) SFN0.0625, (c) SFN0.125, (d) SFN0.1875, and (e) SFN0.25. | ||
Based on the fully relaxed 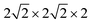 (80 atoms, 16 formula unit) supercell in Fig. 1, structures with an oxygen vacancy (VO) was created by removing one neutral oxygen atom, corresponding to an oxygen nonstoichiometry of δ = 0.0625. Since structures with relatively low VO concentrations have similar lattice parameters to that without VO, the lattice parameters of the oxygen nonstoichiometry cell were fixed at the value of stoichiometric supercell, whereas all atomic positions were fully relaxed. The formation energy Ef of VO was calculated according to
(80 atoms, 16 formula unit) supercell in Fig. 1, structures with an oxygen vacancy (VO) was created by removing one neutral oxygen atom, corresponding to an oxygen nonstoichiometry of δ = 0.0625. Since structures with relatively low VO concentrations have similar lattice parameters to that without VO, the lattice parameters of the oxygen nonstoichiometry cell were fixed at the value of stoichiometric supercell, whereas all atomic positions were fully relaxed. The formation energy Ef of VO was calculated according to
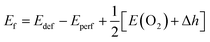 | (1) |
To further consider the thermal and vibrational effects, the feasibility of oxygen removal from the perovskites is considered by the temperature and pressure dependent Ef or the free energy of VO formation:
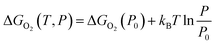 | (2) |
| ΔGO2(P0) = 2Ef + ΔGO2(P0,T) = 2Ef + [ΔHO2(P0,T) − TSO2(P0,T)] | (3) |
The enthalpy ΔHO2(P0,T) and entropy SO2(P0,T) of O2 at P0 (0.1 MPa) are obtained from the JANAF thermochemical tables.39 Here, the thermal and vibrational contributions from solid SrFe1−xNixO3 and SrFe1−xNixO3−δ were neglected because they are mostly canceled and negligible compared with O2 gas. The variation of ΔGO2(P0) on temperature is depicted by an Ellingham diagram.40
3. Results and discussion
3.1 Oxygen vacancy formation
A crucial factor that governs the redox performance of oxygen carriers is the extent of oxygen vacancies. Oxygen vacancy formation energy provides insights into the ease of oxygen removal and refilling. Thus, we calculated the oxygen vacancy formation energy for the Ni doping systems SrFe1−xNixO3 (x = 0, 0.0625, 0.125, 0.1875, and 0.25), as shown in Table 1. Firstly, we noticed that the lattice constants of SrFe1−xNixO3 decreased very little (or showed nearly no change) with the increase of Ni doping. Normally, the lattice constants should decrease more significantly with Ni doping than with Co doping, due to the tetravalent ionic radius of Ni4+ (0.480 Å) < Co4+ (0.530 Å) < Fe4+ (0.585 Å). Therefore, the doping Ni ions may not be tetravalent here.| x | a (Å) | Fe-VO (Ni-VO), VO-Fe (Å) | E f (eV) | E bond (eV) | E relax (eV) |
|---|---|---|---|---|---|
| 0 | 3.841 | 1.920, 1.920 | 2.102 (2.155) | 3.162 | −1.060 |
| 0.0625 | 3.840 | (1.955), 1.871 | 1.760 | 2.674 | −0.914 |
| (1.972), 1.868 | 1.531 (2.174) | 2.605 | −1.074 | ||
| 1.936, 1.903 | 1.860 | 2.960 | −1.100 | ||
| 1.926, 1.913 | 1.901 | 2.997 | −1.096 | ||
| 1.925, 1.929 | 1.965 | 2.979 | −1.014 | ||
| 0.125 | 3.839 | (1.966), 1.873 | 1.705 (1.774) | 2.677 | −0.972 |
| 1.933, 1.906 | 1.779 | 2.897 | −1.118 | ||
| 1.924, 1.915 | 1.809 | 2.929 | −1.120 | ||
| 0.1875 | 3.839 | (1.963), 1.876 | 1.606 | 2.594 | −0.988 |
| (1.951), 1.871 | 1.578 (1.824) | 2.516 | −0.938 | ||
| 1.926, 1.913 | 1.716 | 2.817 | −1.101 | ||
| 1.941, 1.900 | 1.725 | 2.808 | −1.083 | ||
| 1.935, 1.922 | 1.665 | 2.788 | −1.123 | ||
| 0.25 | 3.838 | (1.956), 1.881 | 1.293 (1.817) | 2.381 | −1.088 |
| 1.918, 1.920 | 1.554 | 2.926 | −1.372 |
To calculate the formation energy Ef of VO for SrFe1−xNixO3−δ (x = 0, 0.0625, 0.125, 0.1875, and 0.25, δ = 0.0625), a single O atom should be removed from all the studied systems. Due to both B-site substitution and structural distortion, the lowered symmetry results in nonequivalent O sites along Fe–O–Fe or Ni–O–Fe chains. Therefore, we exhaustivity sampled VO from all nonequivalent O sites, defined as the distances of Fe–O (Ni–O) and O–Fe above 0.01 Å. The nonequivalent O sites for each doping system and the corresponding Ef values are shown in Table 1. In the same Ni doping content, the Ef of VO from the Ni–O–Fe chains is obviously smaller than that from Fe–O–Fe chains. Besides, the Ef generally decreased as the Ni content changed from x = 0 to x = 0.25. These trends suggest that Ni doping promotes VO formation and even has an advantage over Co doping.23
Then, we explored the origin of the Ni doping effect on VO formation and the reason that Ni doping shows a better performance than Co doping. As we know, there are several mechanisms for the promotion of VO formation.16 Firstly, we noticed that the Ef of VO from Ni–O–Fe chains is lower than that from Fe–O–Fe chains (Table 1). We divided Ef into two terms of the Fe (Ni)–O bonding and relaxation contributions Ef = Ebond + Erelax, where Ebond is the energy needed to remove an O from the stoichiometric structure, Erelax is the energy obtained from further structural relaxation in the presence of VO. As shown in Table 1, Ebond shows the same trend with Ef that Ebond of VO from Ni–O–Fe chains is lower than that from Fe–O–Fe chains, while the Erelax is comparable for VO from either Ni–O–Fe or Fe–O–Fe chains. Therefore, the weakened Ni–O–Fe bond strength upon Ni doping is one of the key factors to promote VO formation. Comparatively, Co doping has little influence on the Co–O–Fe or Fe–O–Fe bond strength.23
To further understand the mechanism of the Ni-doping induced Ef decrease, we analyzed the density of states (DOS) projected on the Sr, Fe, Ni, and O ions for SrFe1−xNixO3 (x = 0, 0.0625, 0.125, 0.1875, and 0.25) shown in Fig. 2(a). For the parent SrFeO3 system, the hybridized Fe–O orbitals form a broad conduction band crossing the Fermi level, conforming to the metallic nature of this compound. The majority of the spin states of Fe are mostly occupied while the minority spin states are nearly unoccupied, reflecting a high spin (t32ge1g, S = 2) Fe4+. The orbitals induced by Ni doping are also hybridized with O-2p bands and are located near the Fermi level with Fe–O hybridization states. With the increase of the Ni doping value, the hybridization or O-2p states near the Fermi level are increased. This change is similar to Co doping23 which can decrease Ef of VO and thus promote the VO formation, since the increased O-2p states near the Fermi level can reduce the spatial and energetic redistribution energy needed at VO formation.
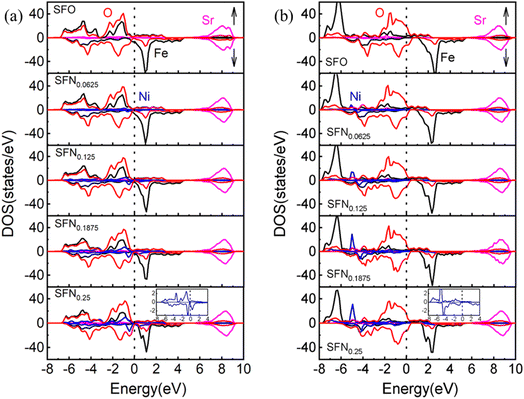 | ||
| Fig. 2 The partial DOS of SrFe1−xNixO3−δ (x = 0, 0.0625, 0.125, 0.1875, and 0.25) by (a) GGA and (b) GGA + U. The Fermi level (dotted line) is set at 0 eV. Bottom inset: the enlarged DOS for Ni ion. | ||
If we take a closer look at the DOS of Ni ion (shown in the bottom inset of Fig. 2(a)), its majority spin states are fully occupied and minority spin states are partially occupied, indicating a more possible high-spin Ni3+ (t52ge2g, S = 3/2) than low spin Ni4+ (t62ge0g, S = 0).41 The exchange splitting of Fe4+ is larger than the high-spin Ni3+, corresponding to the aforementioned DOS change upon Ni doping that the hybridization states of Ni–O are closer to the Fermi level than that of Fe–O. In addition, the ionic radius of high-spin Ni3+ is 0.60 Å, which is comparable with the ionic size of Fe4+ (0.585 Å). Again, this provides a reasonable explanation for the little decrease of the lattice constants upon Ni doping. Besides, from the relaxed distances of Ni–O–Fe in Table 1, the Fe–O bond lengths are always shorter than the Ni–O bond lengths in all the Ni doping systems. These results also indicate that the Fe ions have a higher charge state, a smaller ionic radius, and a stronger p–d covalency than the Ni ions. Therefore, our results have consistently suggested a high-spin Ni3+ in SrFe1−xNixO3. However, due to the small Ni doping here, the orbital characteristics of Fe4+ ions show little change and thus Fe4+ in SrFe1−xNixO3 are not changed to Fe5+ along with Ni3+ as found in SrFe0.5Ni0.5O3.41 Whereas, the holes introduced by Ni3+ substitution would cause a change in cation stoichiometry and hence an imbalance in the net charge. The tendency of compensation to maintain the overall electrical neutrality would withdraw charge from the oxygen sublattice and thus promote the generation of VO. Thus far, we have identified three factors causing the Ni-doping induced Ef decrease: (1) the weakened Ni–O bonding, (2) moving the O-2p states to the Fermi level by Ni–O hybridization, (3) Ni3+ decreasing the positive charges to be compensated by VO formation. For these reasons, Ni doping has an advantage over Co doping in terms of enhancing the oxygen carrier performance of SrFeO3−δ.
To explore the effects of the onsite Coulomb interactions on the electronic structures, the DOS calculated by GGA + U is shown in Fig. 2(b). The bonding–antibonding splitting of the Fe/Ni 3d bands is significantly enhanced such that the bonding states of Fe (Ni) ions are pushed downwards to about −6 (−5) eV. In the minority spin, the 3d bands of Fe/Ni move upwards slightly. The antibonding states near the Fermi level are mainly composed of O-2p states. Consequently, the Ni–O hybridization induced O-2p states closing to the Fermi level is weakened in GGA + U. Due to the lack of this factor, the Ef of Ni doping phases calculated by GGA + U is generally larger than that calculated by GGA. As shown in Table 1, the VO configuration with the lowest Ef for each Ni doping value is calculated by GGA + U. Unlike the gradual decreases of Ef upon Ni doping in GGA, the Ef by GGA + U shows an abrupt decrease when the Ni content increases to x = 0.125. Nevertheless, the conclusion of Ni doping promoting VO formation from GGA and GGA + U is consistent.
3.2 Thermodynamic properties of oxygen storage/release
In experiments, it is impossible to measure the oxygen vacancy formation energy. Instead, oxygen partial pressures and temperatures are used to quantitatively determine the experimental conditions. Therefore, the dependence of free energy for the oxygen release reaction SrFe1−xNixO3 → SrFe1−xNixO3−δ + O2 on the oxygen partial pressure (PO2) and temperature (T) is portrayed in Fig. 3. The variation of Gibbs free energy (ΔG) versus T can be obtained by using the thermodynamic eqn (3), where Ef for each Ni doping system is an averaged Ef value of SrFe1−xNixO3−δ (δ = 0.0625) calculated by GGA from Table 1. As shown in Fig. 3(a), this so-called Ellingham diagram at an oxygen partial pressure of 0.1 MPa is commonly applied to compare the free energies of oxygen formation as a function of T. The generally decreasing trend of Ef in Table 1 is well expressed in that the oxygen release temperature is decreased with increased Ni doping. However, the SrFe1−xNixO3 systems are still thermodynamically stable (ΔG > 0) when the temperature is higher than 1200 K, which means that the oxygen release will not occur spontaneously at T < 1200 K. Then, based on eqn (2), the dependence of ΔG on PO2 and T is shown in Fig. 3(b), where only the equilibrium curve (ΔG = 0) is explicitly plotted. The equilibrium curves separate the diagram into two parts: below the line, oxygen will be released from SrFe1−xNixO3 (ΔG < 0, reduction); above the line, oxygen will be captured by SrFe1−xNixO3−δ (ΔG > 0, oxidation). Therefore, the oxygen release will occur at low O2 pressure and high temperature. The capability of oxygen release is still increased upon Ni doping. Compared with the Co-doping effect on the oxygen release from SrFe1−xCoxO3−δ (Fig. 4 in ref. 23), a little Ni doping x = 0.25 can induce a higher PO2 and a lower T than a relatively large Co doping x = 0.5.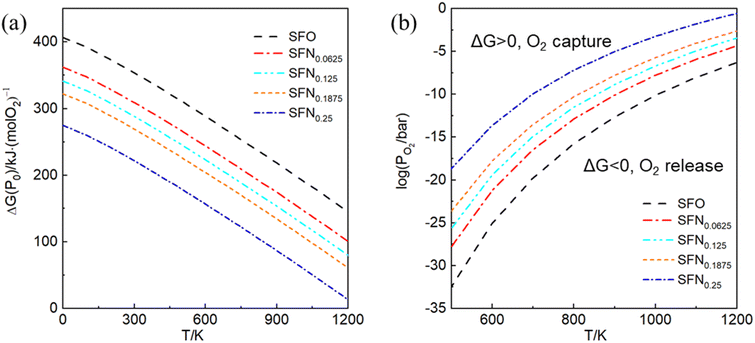 | ||
| Fig. 3 (a) The Ellingham diagram, (b) counterplotting of ΔG vs. the O2 pressure and temperature of SrFe1−xNixO3−δ (x = 0, 0.0625, 0.125, 0.1875, and 0.25). | ||
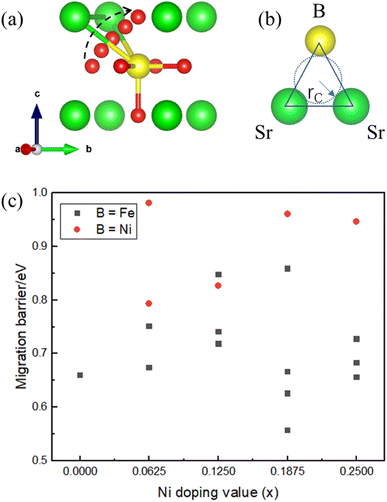
3.3 Oxygen ion migration
The energy barrier of oxygen migration is another important factor in oxygen carrier performance. In ABO3−δ perovskites, oxygen migration occurs by hopping to the nearby VO site, which should pass through a “critical triangle” formed by one B-site cation and two A-site cations (as shown in Fig. 4). For SrFe1−xNixO3−δ, Sr is the only A site element, while B-site cation could be Fe or Ni. Thus, there are at least two pathways for SrSrFe and SrSrNi (Fig. 4(b)). However, the possible diffusion pathways of oxygen are not only distinguished by the variation of the surrounding B-site cation configuration but also by the nonequivalent Fe–O or Ni–O bond length in the structural distortion. Considering these two factors, we calculated oxygen migration barriers for all possible pathways in SrFe1−xNixO3−δ. As shown in Fig. 4(c), the migration barriers generally have a higher value with the B site of Ni than Fe in each doping configuration. The one exception is a slightly higher value with a B site of Fe than Ni in x = 0.125 doping configuration, so the difference of detailed barrier energies for each Ni doping value is also related to their own local distortion. In general, Ni doping increases the migration barrier and thus hinders oxygen migration.Then, we related the trend of the migration barrier with the migration bottleneck, which is the “critical triangle” formed by SrSrFe or SrSrNi (Fig. 4(b)). The bottleneck radius rC is determined by the lattice constant and the ionic radii of A-site and B-site cations.42 The migration bottleneck is a rough method used to understand the tendency of migration barriers, since the lattice constant is an averaged reflection of bond properties and the specific barrier values also rely on the local distortion. Usually, a larger rC value gives rise to a smaller migration barrier. Since the lattice constants of SrFe1−xNixO3 are nearly the same from Table 1 and A-site is only Sr, rC would be distinguished by the ionic radii of B-site cations Fe/Ni. If we use the tetravalent ionic radius of Fe4+ (0.585 Å) and Ni4+ (0.480 Å), the corresponding rC values would be 1.032 and 1.067. It means that the bottleneck of SrSrNi is larger than SrSrFe and thus the migration barriers should have a lower value with the B site of Ni than Fe, which is inconsistent with our barrier results in Fig. 4(c). Whereas, if the ionic radius of Ni is the aforementioned high-spin Ni3+ (0.60 Å), the rC value of SrSrNi is 1.027, which is smaller than that of SrSrFe. The tendency of migration barriers is reasonable. Therefore, the conclusion of a high-spin Ni3+ in SrFe1−xNixO3 is reversely verified by the migration barrier results.
Here, we used a small amount of Ni-doped Fe, in which Ni is surrounded by Fe even in the x = 0.25 doping system, thus the oxygen hopping can always find a nearby pathway of SrSrFe with a low migration barrier. Therefore, although the pathway of SrSrNi induced by Ni doping is averse to oxygen migration, there would be little impact on the overall oxygen ion conduction for the little Ni doping systems.
4. Conclusions
In conclusion, we have studied the formation and migration of oxygen vacancies in SrFe1−xNixO3−δ (x = 0, 0.0625, 0.125, 0.1875, and 0.25) perovskites. The Ef calculation results show that VO forms more easily from Ni–O–Fe chains than Fe–O–Fe chains and Ef generally decreases as Ni content increases, reflecting that Ni doping can promote VO formation. This Ni-promoted formation of VO results from three factors: weakened Ni–O bonding, the closing O-2p states to the Fermi level by Ni–O hybridization, and the Ni3+ decreasing the positive charges to be compensated by VO formation. Due to the influence of these multiple factors, Ni doping has an advantage over Co doping in the promotion of VO formation. Thermodynamically, the Ellingham diagram shows that a little Ni doping x = 0.25 can induce a higher PO2 and a lower T than relatively large Co doping x = 0.5. Kinetically, the oxygen migration pathway of SrSrNi has a higher energy barrier than that of SrSrFe. Considering that the oxygen hopping can always find a nearby pathway of SrSrFe with a low migration barrier in a system with a small amount of Ni doping, the overall oxygen ion conduction would be little influenced. Therefore, a small amount of Ni doing can significantly improve the oxygen carrier performance of the parent SrFeO3 system and promote its application in energy storage, catalysis, gas sensing, chemical looping, etc.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (grant no. 11774349) and the startup project from Hangzhou Normal University.References
- J. Dou, E. Krzystowczyk, X. Wang, T. Robbins, L. Ma, X. Liu and F. Li, ChemSusChem, 2020, 13, 385–393 CrossRef CAS.
- E. Krzystowczyk, X. Wang, J. Dou, V. Haribal and F. Li, Phys. Chem. Chem. Phys., 2020, 22, 8924–8932 RSC.
- Y. Yoshiyama, S. Hosokawa, M. Haneda, M. Morishita, H. Asakura, K. Teramura and T. Tanaka, ACS Appl. Mater. Interfaces, 2023, 15, 5293–5300 CrossRef CAS.
- D. Yu, L. Wang, C. Zhang, C. Peng, X. Yu, X. Fan, B. Liu, K. Li, Z. Li and Y. Wei, ACS Catal., 2022, 12, 15056–15075 CrossRef CAS.
- J. Hombo, Y. Matsumoto and T. Kawano, J. Solid State Chem., 1990, 84, 138–143 CrossRef CAS.
- J. Mizusaki, M. Okayasu, S. Yamauchi and K. Fueki, J. Solid State Chem., 1992, 99, 166–172 CrossRef CAS.
- Y. Takeda, K. Kanno, T. Takada, O. Yamamoto, M. Takano, N. Nakayama and Y. Bando, J. Solid State Chem., 1986, 63, 237–249 CrossRef CAS.
- C. Y. Lau, M. T. Dunstan, W. Hu, C. P. Grey and S. A. Scott, Energy Environ. Sci., 2017, 10, 818–831 RSC.
- J. Vieten, B. Bulfin, D. E. Starr, A. Hariki, F. M. F. de Groot, A. Azarpira, C. Zachäus, M. Hävecker, K. Skorupska, N. Knoblauch, M. Schmücker, M. Roeb and C. Sattler, Energy Technol., 2019, 7, 131–139 CrossRef CAS.
- E. Marek, W. Hu, M. Gaultois, C. P. Grey and S. A. Scott, Appl. Energy, 2018, 223, 369–382 CrossRef CAS.
- S. Brendelberger, J. Vieten, M. J. Vidyasagar, M. Roeb and C. Sattler, Sol. Energy, 2018, 170, 273–279 CrossRef CAS.
- J. Dou, E. Krzystowczyk, X. Wang, T. Robbins, L. Ma, X. Liu and F. Li, ChemSusChem, 2020, 13, 385–393 CrossRef CAS.
- G. Luongo, F. Donat and C. R. Müller, Phys. Chem. Chem. Phys., 2020, 22, 9272–9282 RSC.
- E. J. Popczun, T. Jia, S. Natesakhawat, W. Xu, C. M. Marin, Y. Duan and J. W. Lekse, J. Alloys Compd., 2022, 896, 162783 CrossRef CAS.
- J. Vieten, B. Bulfin, P. Huck, M. Horton, D. Guban, L. Zhu, Y. Lu, K. A. Persson, M. Roeb and C. Sattler, Energy Environ. Sci., 2019, 12, 1369–1384 RSC.
- T. Jia, E. J. Popczun, J. W. Lekse and Y. Duan, Appl. Energy, 2021, 281, 116040 CrossRef CAS.
- N. Miura, H. Ikeda and A. Tsuchida, Ind. Eng. Chem. Res., 2016, 55, 3091–3096 CrossRef CAS.
- S. Chen, H. Cheng, Y. Liu, X. Xiong, Q. Sun, X. Lu and S. Li, Phys. Chem. Chem. Phys., 2021, 23, 27266–27272 RSC.
- Y. Han, J. Yi and X. Guo, Solid State Ionics, 2014, 267, 44–48 CrossRef CAS.
- J. Zhu, S. Guo, Z. Chu and W. Jin, J. Mater. Chem. A, 2015, 3, 22564–22573 RSC.
- A. Demizu, K. Beppu, S. Hosokawa, K. Kato, H. Asakura, K. Teramura and T. Tanaka, J. Phys. Chem. C, 2017, 121, 19358–19364 CrossRef CAS.
- F. Fujishiro, N. Oshima, N. Kamioka, T. Sakuragi and M. Oishi, J. Solid State Chem., 2020, 283, 121152 CrossRef CAS.
- T. Jia, E. J. Popczun, J. W. Lekse and Y. Duan, Phys. Chem. Chem. Phys., 2020, 22, 16721–16726 RSC.
- H.-Y. Su and K. Sun, J. Mater. Sci., 2015, 50, 1701–1709 CrossRef CAS.
- M. T. Curnan and J. R. Kitchin, J. Phys. Chem. C, 2014, 118, 28776–28790 CrossRef CAS.
- A. A. Emery and C. Wolverton, Sci. Data, 2017, 4, 170153 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- P. Manimuthu and C. Venkateswaran, J. Phys. D: Appl. Phys., 2011, 45, 015303 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- Y.-L. Lee, Y. Duan, D. Morgan, D. C. Sorescu, H. Abernathy and G. Hackett, Phys. Rev. Appl., 2017, 8, 044001 CrossRef.
- Y.-L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- M. W. Chase Jr, J. Phys. Chem. Ref. Data, Monogr., 1998, 9, 1–1951 Search PubMed.
- H. J. T. Ellingham, J. Soc. Chem. Ind., 1944, 63, 125–133 CrossRef CAS.
- F. Fan, Z. Li, Z. Zhao, K. Yang and H. Wu, Phys. Rev. B, 2016, 94, 214401 CrossRef.
- J. A. Kilner and R. J. Brook, Solid State Ion., 1982, 6, 237–252 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |