 Open Access Article
Open Access ArticleTuning lithium–yttrium chloride local structure through coordination control and mixing during synthesis†
Teerth
Brahmbhatt
ab,
Cheng
Li
c,
Mounesha N.
Garaga
 d,
Wan-Yu
Tsai
d,
Wan-Yu
Tsai
 a,
Steve G.
Greenbaum
a,
Steve G.
Greenbaum
 d,
Jagjit
Nanda
ef and
Robert L.
Sacci
d,
Jagjit
Nanda
ef and
Robert L.
Sacci
 *a
*a
aChemical Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN 37830, USA. E-mail: saccirl@ornl.gov
bBredesen Center for Interdisciplinary Research and Education, University of Tennessee, Knoxville, TN 37996, USA
cNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37830, USA
dDepartment of Physics and Astronomy, Hunter College, City University of New York, New York, NY 10065, USA
eApplied Energy Division, SLAC National Laboratory, Menlo Park, CA 94025, USA
fMaterials Science and Engineering, Stanford University, Stanford, CA 94035, USA
First published on 17th April 2024
Abstract
Lithium halide-based solid electrolytes have high Li+ conductivity and can be synthesized through low-temperature aqueous solution routes. While Li3InCl6 can be readily synthesized through dehydration, other analogous materials, such as Li3YCl6, cannot. This difference may be due to differences in H2O coordination strength, which leads to partial hydrolysis to form YOCl. In this work, we followed and compared Li3YCl6 synthesis using three different methods using in situ neutron diffraction. The data revealed that forming an ammonium halide complex intermediate is essential in synthesizing Li3YCl6 from an aqueous solution. In carefully examining the Li3YCl6 products, we found that changes in local structure follow on to drive significant differences in ionic transport and Li+ diffusivity as determined through diffusion NMR measurements. These changes were ascribed to the change in the correlative transport of Li+. This work provides insight into the reaction mechanisms involved in synthesizing halide solid electrolytes and highlights the importance of considering their synthetic and processing conditions to optimize their performance in all-solid-state batteries.
1. Introduction
The demand for denser, safer, and more portable energy storage has led to significant interest in all-solid-state batteries (ASSBs) and solid electrolytes.1 Solid Electrolytes enable the replacement of conventional flammable organic liquid electrolytes2 and span many material classes including polymers,3 oxides,4 sulfides,5 hydrides,6 and more recently, halides.7 Halide solid electrolytes have shown promise due to their high ionic conductivity, high voltage cathode compatibility, and adaptability in synthesis and processing routes.8 Compositions such as Li3InCl6 have garnered interest due to their compatibility with aqueous and organic solvent-based synthesis.9,10 Direct synthesis of other A3MX6 (A = Li, M = Sc, Y, Ho, Yb, Er, etc., X = F, Cl, Br, I) compositions in water or other solvents is limited due to the hydrolysis of MCl3·nH2O intermediates upon heating. This decomposition route leads to the formation of MOCl and LiCl impurities. However, recent reports have shown that it is possible to synthesize these other compositions in water using ammonium halide coordination reagents.11,12This report provides a detailed examination of the formation pathway for Li3YCl6 and establishes synthesis-structure property correlations to guide the optimization of halide solid electrolyte-based ASSBs. Large-scale synthesis and optimization of battery materials is not trivial13,14 and often requires process monitoring. A key enabler of large-scale chemical production is an intimate understanding of the reaction mechanism during synthesis.15 In addition, many solid electrolyte properties are greatly influenced by the chosen synthesis route.16 The formation mechanism of halide solid electrolytes through these novel solvent-based routes is poorly understood. Previous work suggested that the addition of ammonium halides resulted in the formation of a complex halide intermediate of the form (NH4)3MX6, eqn (1).17,18 This intermediate, shown in Fig. 1, is suspected to provide an alternative reaction route away from the oxyhalide formation side reaction (eqn (2)) during the dehydration and the subsequent annealing steps at 350–550 °C.
 | (1) |
 | (2) |
 | ||
| Fig. 1 Representative crystal structures of the (NH4)3YCl6 and anhydrous Li3YCl6 phases. Octahedrals represent YCl63− polyanions. | ||
We utilized in situ neutron powder diffraction (NPD) to track the formation of Li3YCl6 (LYC) across multiple synthesis routes. NPD is well suited for probing reactions at relevant mass scales due to its high penetrative power and sensitivity to Li.19,20 In addition, neutrons are far more sensitive to protons and deuterons groups within NH4Cl and complex halide intermediates than X-ray diffraction. Deuterated precursors (D2O and ND4Cl) were used for NPD experiments to minimize the incoherent scattering background of protons. We confirmed the formation of (ND4)3YCl6 during the aqueous synthesis of LYC and its decomposition. We show that dehydration of the complex before reaching high temperatures is critical even in the wet chemical synthesis route to avoid the formation of LiCl and YOCl impurities. We observe in multiple reaction mechanisms that the LYC formation and then melting at higher temperatures is crucial to driving proper mixing of precursors and intermediates, agreeing with a previous report by Asano et al. where LYC was thermally stable up to 450 °C.21 To our knowledge, this is the first instance of providing structural characterization after melting the solid electrolyte phase using in situ diffraction techniques.22 Melting of the LYC phase could play an essential role in separator fabrication through melt infiltration or casting methods.23 We characterize the influence of the LYC synthesis route on the ionic and electronic conductivity and observe the significant role of grain boundaries in the total ionic conductivity of LYC solid electrolytes that undergo annealing.
2. Experimental
2.1 Synthesis
The aqueous ammonium coordinated (AC) and ammonium free (AF) synthesis of LYC was prepared by weighing out 34 mol% excess of anhydrous YCl3 (Sigma Aldrich 99.99%, 451363), stoichiometric amounts of LiCl (Sigma Aldrich 99%, 793620) and NH4Cl (Sigma Aldrich 99.5%, A4514) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 molar ratio in a glovebox (1
3 molar ratio in a glovebox (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for AF synthesis). The mixture was then transferred to a round bottom flask and dissolved in DI water, sonicated for 15 minutes, and excess water was evaporated via rotovap. The sample was then dried overnight at 150 °C under vacuum to remove excess water. The white powder was ground in an agate mortar and pestle, pelletized, placed in an alumina combustion boat, and annealed at 500 °C (heating rate 5 °C min−1) for 5 h under argon flow (30 mL min−1) in a glovebox.
0 for AF synthesis). The mixture was then transferred to a round bottom flask and dissolved in DI water, sonicated for 15 minutes, and excess water was evaporated via rotovap. The sample was then dried overnight at 150 °C under vacuum to remove excess water. The white powder was ground in an agate mortar and pestle, pelletized, placed in an alumina combustion boat, and annealed at 500 °C (heating rate 5 °C min−1) for 5 h under argon flow (30 mL min−1) in a glovebox.
The mechanochemical (MC) synthesis of Li3YCl6 was conducted in a Fritsch Pulvirisette 7 planetary ball mill. Here, the LiCl and anhydrous YCl3 were loaded into zirconia milling jars (45 mL volume) with Y-stabilized zirconia milling media (5 mm diameter) inside a glovebox. The media-to-powder ratio was 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The mixture was milled at 510 rpm for 48 cycles with 15 min of milling and a 15 min pausing step to allow the sample to cool; after the initial 48 cycles, the jar was taken into a glovebox, and the sample was scraped off the walls of the jar to prevent the formation of hot zones during milling, this was followed by another 48 cycles under the same conditions. The milled powder was pelletized and annealed at equivalent conditions to the AC and AF samples. For clarity, this sample is referred to as the mechanochemical annealed (MCA) sample, and the unannealed sample is referred to as the MC sample.
1. The mixture was milled at 510 rpm for 48 cycles with 15 min of milling and a 15 min pausing step to allow the sample to cool; after the initial 48 cycles, the jar was taken into a glovebox, and the sample was scraped off the walls of the jar to prevent the formation of hot zones during milling, this was followed by another 48 cycles under the same conditions. The milled powder was pelletized and annealed at equivalent conditions to the AC and AF samples. For clarity, this sample is referred to as the mechanochemical annealed (MCA) sample, and the unannealed sample is referred to as the MC sample.
2.2 Characterization
Ex situ NPD patterns were collected on POWGEN (BL-11A) at 1.5 Å wavelength. The samples were loaded into vanadium cans under an argon atmosphere in a glovebox and sealed with copper gaskets and aluminum lids. The patterns were measured at 300 K. The samples were absorption corrected after data collection. Rietveld refinements against the neutron diffraction data were performed using GSAS II.24 The following parameters were refined: (1) background using a Chebyshev polynomial with 10 coefficients, (2) scale factor, (3) sample-induced peak broadening, (4) lattice parameters, (5) atomic positions, (6) isotropic thermal displacement parameters, and (7) occupancies.The loss of ammonium salt was confirmed using infrared spectroscopy using an Agilent Cary 650 spectrometer equipped with an attenuated total reflection accessory (Specac Ltd). Before measurement, the samples were protected from moisture by sealing them in the diamond crystal holder in a glovebox.
3. Results and discussion
3.1 Synthesis and phase evolution
Summary plots of in situ neutron diffraction measurements are presented in Fig. 2, along with phase evolution and thermal analyses. We compared three reaction routes for LYC production at relatively large scales (3–5 grams): ammonium coordinated (AC), ammonium free (AF), and dry mechanochemical (MC). This sample size aligns with a typical laboratory-scale synthesis procedure. For the two aqueous routes, the precursors (LiCl and YCl3, with and without ammonium chloride) were dissolved in water and dried in a vacuum at 80 °C before measurement. Note that the deuteron will contribute to coherent scattering, making it possible to observe the formation of complex intermediates during the phase evolution. The reactions were conducted by heating the dried precursors under flowing Ar with a temperature ramp rate set to 5 °C min−1 and 1 hour holds at 100, 200, 300, 400, and 500 °C before cooling to room temperature (∼30 °C). | ||
| Fig. 2 Visualization of the synthesis pathways using in situ neutron diffraction of the AC (a), AF (c), and MC (e), along with their respective phase evolutions with thermal analysis spectra from TGA and DSC (b, d, and f). The contour plots are during heating from 47 to 500 °C only. The initial NPD pattern is the precursors after dissolution and vacuum drying (or mixing) prior to ramping, and the final NPD pattern is the RT product obtained after cooling. Endothermic peaks are numbered for textual clarity (see Fig. S1–3† for high-resolution images). | ||
After comparing the three ND contour plots, the first observation reveals that the AC route (Fig. 2a) is more complex than the others. At 50 °C, YCl3 and ND4Cl precursors are present (identified by peaks at 2.76 and 1.58 Å, respectively), and the diffraction intensities begin to fade at 100 °C (Fig. 2a). We also initially observe both YCl3 and YCl3·6H2O (peaks at 2.74 and 3.91 Å respectively), as well as small amounts of ND4Cl and LiCl (1.93 and 2.96 Å respectively). Rietveld refinement of the patterns within the contour plot quantifies the phase evolution (Fig. 2b). As the guidelines point out, these precursors are consumed and form the (ND4)3YCl6 complex intermediate, AYC, at 100 °C (identified by the peak at 3.83 Å). The AYC complex assumes a C2/c structure of the form Cs3BiCl6, where YCl63− octahedrals are indeed formed and stabilized.29 Unlike the final product, trigonal LYC (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1), the cations are not well ordered into rows, as shown in Fig. 1. This reaction is accompanied by an intermediate phase(s), which we call LYC-I. We note here that this intermediate is only seen during the AC route. The formation of AYC is seen in the thermal analysis (Fig. 2b), which displays an endothermic peak at 100 °C (Peak 1) and significant weight loss corresponding to D2O loss. The AYC complex is not long-lived, being consumed at 200 °C and giving way to more intense LYC-I peaks and YCl3 formation (Fig. 2a). DSC shows an endothermic process at 175 °C (Peak 2) that appears to be a convolution of the AYC decomposition and LYC-I formation. Between 200 and 500 °C, the phase fraction of LYC-I increases and YCl3 decreases, ending with LYC-I melting, also congruent with an endothermic feature at 475 °C (Peak 4). Within this range, we also observed an endothermic process with significant mass loss between 330 and 375 °C (Peak 3), which correlates with ND4Cl decomposition.30 Given that LYC has known polymorphs and no additional phase was observed in the reaction, we believe LYC-I to be a metastable polymorph.
m1), the cations are not well ordered into rows, as shown in Fig. 1. This reaction is accompanied by an intermediate phase(s), which we call LYC-I. We note here that this intermediate is only seen during the AC route. The formation of AYC is seen in the thermal analysis (Fig. 2b), which displays an endothermic peak at 100 °C (Peak 1) and significant weight loss corresponding to D2O loss. The AYC complex is not long-lived, being consumed at 200 °C and giving way to more intense LYC-I peaks and YCl3 formation (Fig. 2a). DSC shows an endothermic process at 175 °C (Peak 2) that appears to be a convolution of the AYC decomposition and LYC-I formation. Between 200 and 500 °C, the phase fraction of LYC-I increases and YCl3 decreases, ending with LYC-I melting, also congruent with an endothermic feature at 475 °C (Peak 4). Within this range, we also observed an endothermic process with significant mass loss between 330 and 375 °C (Peak 3), which correlates with ND4Cl decomposition.30 Given that LYC has known polymorphs and no additional phase was observed in the reaction, we believe LYC-I to be a metastable polymorph.
Ex situ infrared spectroscopy in Fig. S4† confirms the presence of H2O with NH4+ cations with strong vibrations at 3100–3200 cm−1 (N–H stretching) and 1420 cm−1 (N–H scissoring). These bands are absent after annealing at 350 °C and the O–H bands are absent after annealing at 500 °C. The resulting LYC phase that crystallized from all in situ melts was the target trigonal LYC phase (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1). We note that while the YCl3 impurity appears significant in the AC sample, it is likely the result of the LYC melt dripping through the quartz basket's porous bottom. The ex situ samples do not show this impurity in similarly large phase fractions, as discussed later.
m1). We note that while the YCl3 impurity appears significant in the AC sample, it is likely the result of the LYC melt dripping through the quartz basket's porous bottom. The ex situ samples do not show this impurity in similarly large phase fractions, as discussed later.
The AF sample contour plot (Fig. 2c) begins with LiCl and YCl3·6D2O phases being present with no anhydrous YCl3 phase detected (Fig. 2d). The DSC shows no feature at 100 °C associated with intermediate complexes (Fig. 2d); however, during heating to 175 °C the DSC curve shows a large endothermic process alongside substantial mass loss (Peak 1). These results correlate with YCl3 hydrate consumption and LYC formation in Fig. 2d. The LYC formed here is the targeted trigonal phase and is associated with the second more minor endothermic process in the DSC (230 °C, Peak 2 in DSC). The consumption of the YCl3 hydrate also results in the formation of the YOCl impurity phase that is formed around 350 °C (Peak 3).31 This fact demonstrates that the synthesis routes result in differing intermediate phases and reaction kinetics and may allow for trapping novel metastable phases. LYC continues to increase until 500 °C when it melts, leaving insoluble YOCl and LiCl behind. DSC shows LYC melting as a smaller endothermic peak at 475 °C (Peak 4) commensurate with this route's less efficient LYC formation. After cooling, LYC reforms while YOCl and LiCl impurities remain, allowing us to conclude that ammonium chloride is required to protect the YCl3 precursor from hydrolysis during heating.
Fig. 2e and f show MC reaction route evolution starting with planetary milled LiCl and YCl3 for 24 h. This reaction proceeds through the most direct route, with LYC being already formed with unreacted LiCl at 68 and 32 wt%, respectively (Fig. 2f). While YCl3 was not initially detected, we suspect it was present as an amorphous phase, given its immediate appearance with heating. During the temperature ramp, the LiCl phase decreases, and after 175 °C, an endothermic process (Peak 1) is observed and the YCl3 phase decreases. The latter effect correlated to the small exothermic peak ∼275 °C (Peak 2) in Fig. 2f. Again, LYC melts at 475 °C (Peak 3 in the DSC) with residual YCl3 being present (9 wt%) after cooldown. The LYC phase observed throughout this route was trigonal; however, it started from a nanocrystalline subproduct that has a significant amount of Y2–Y3 site disorder in line with previous reports.32,33
We followed the formation of (ND4)3YCl6 (AYC) by mixing ND4Cl and YCl3 in D2O using in situ NPD (Fig. 3). While solving the crystal structure is outside the scope of this report, we highlight a few findings. The temperature-dependent stack plot in Fig. 3a shows the initial sample containing anhydrous YCl3 and ND4Cl (peaks at 2.76 and 3.94 Å, respectively). As the temperature reaches 100 °C, the ND4Cl peaks vanish, and the AYC peaks form, which are stable up to 250 °C. The thermal analysis shows residual dehydration and AYC formation are likely convoluted between Peaks 1 and 2 in the DSC. During the AC reaction, AYC was observed during the dehydration, and the peaks vanished as the temperature reached 175 °C (Fig. 2b). This suggests that the reaction to form LYC from AYC through the replacement of ammonia with Li+ is thermodynamically and kinetically favorable.
This conclusion is reinforced by the fact that Meyer et al. proposed a decomposition of (ND4)3[YCl6] back into YCl3 and NH4Cl at around 425 °C, which we do not see evidence for in the AC route.34 We also do not observe the presence of large amounts of LiCl during the AC phase evolution prior to forming Li3YCl6, which could signal the existence of a distinct (NH4)3[YCl6]·3LiCl composite structure.11 We note that when comparing the thermal analysis of all the aqueous processes (Fig. 2b, d and f), an approximate weight loss of 30% from room temperature to 200 °C is seen, corresponding to D2O being removed from the structure. Ammonium chloride allows water to be removed from YCl3·6H2O without hydrolysis to YOCl at lower temperatures, presumably by shifting the structure from coordination with water to a hexahedral coordination with Cl−. The last two endothermic peaks (3 and 4) in Fig. 3b do not seem to directly correlate to any observed changes in the in situ NPD data. Some possible explanations for this can be gleaned from a similar process observed in the other samples. For the MCA sample, we observe a similar small endothermic peak coinciding with the crystallization of YCl3 (Peak 1), which could coincide with the YCl3 observed in the 150 and 250 °C NPD data. Previous work observed a phase transition of NH4Cl from an α to a β high-temperature phase at 180 °C; however, we do not see the characteristic strong reflection for this phase in the NPD data (the expected peak at 3.298 Å is absent).34 The final small endothermic process at ∼250 °C (Peak 4 in Fig. 3b) could be the consumption of residual YCl3 as observed in the AF reaction route. Lastly, YOCl formation is not observed in the NPD because the sample stayed below the crystallization temperature (∼330 °C).
3.2 Synthesis–structure–property correlation
Recent literature reviews have established the significant relationship between the synthesis route and solid electrolyte properties ranging from the room temperature ionic conductivity to the electrochemical stability window.16,35 Here, we summarize observations related to atomic structure from ND (lattice parameters), particle morphology, and bulk and grain boundary conductivity. In Fig. 4 we display the Rietveld refinement results for NPD data collected on each of the three products within sealed vanadium cans at room temperature. We note here that the samples always have approximately 5% chloride impurity, whether it was YCl3 or LiCl. In this study, the impurity was stochastic; however, we didn't apply significant effort in resolving the causal relationship other than annealing drives YCl3 impurity formation. When comparing the lattice parameters of the MC and MCA samples obtained from NPD, we find that upon annealing, the lattice volume contracts from 662.13 to 659.02 ± 0.02 Å3, and the lattice parameters a and c contract from 11.235 to 11.220 ± 0.001 Å and 6.0573 to 6.0493 ± 0.0006 Å, respectively. The AC product has a similar lattice volume to the MCA sample, 660 Å3. It is possible for the differences in lattice parameters to be driven by Y2–Y3 site disorder, where zero site disorder would correspond to 100% occupation of the Y2 site.21,33 Upon milling, the MC sample starts with 39% site disorder, and after annealing, this is reduced to 22% site disorder for the MCA sample. This trend of decreasing site disorder as a function of annealing agrees with previous reports.33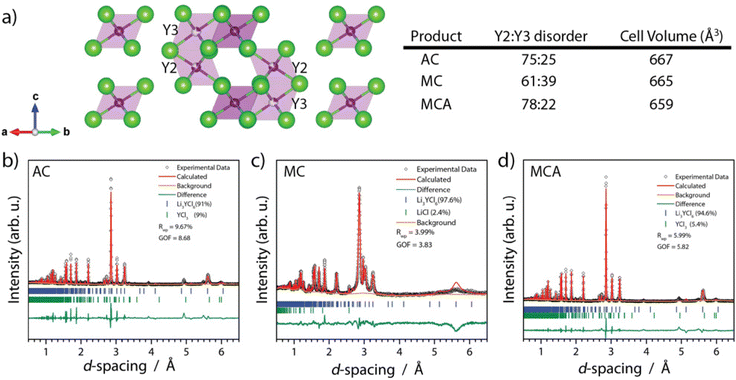 | ||
| Fig. 4 (a) Refined crystal structure of tetragonal LYC product highlighting the Y2 and Y3 site disorder along with Rietveld refinement of the (b) LYC-AC (c) LYC-MC (d) LYC-MCA products’ measured ND data. See Fig. S5–7† for high-resolution images. | ||
The degree of disorder can be qualitatively evaluated through 7Li static NMR. As shown in Fig. 6, the MC sample exhibits two distinct features: a narrow and a broad 7Li peak. The narrow Gaussian peak itself is a superposition of a quadrupole central transition and a partially narrowed response, which is attributed to Li+ ions undergoing rapid hopping. At the same time, the latter broad satellite quadrupolar feature corresponds to those occupying crystallographic inequivalent sites.36 The disorder in the latter is featured by distribution in quadrupolar parameters, resulting in a rounded line shape without well-defined divergences. These narrow and broad peaks converge at elevated temperatures due to rapid Li+ motion (see Fig. S8†).
In the annealed MCA sample, two distinct 7Li features have been identified. The peak associated with Li+ ions situated in inequivalent crystallographic sites exhibits a well-defined quadrupole powder pattern, consistent with the diffraction result that annealing induces ordering in the Li+ sublattice. On the contrary, the static spectrum of the solution-synthesized AC product reveals three distinct 7Li features. A single narrow peak is ascribed to the fast-moving Li+ ions, while two well-defined quadrupolar features are associated with Li+ ions sited in different inequivalent crystallographic sites. This highlights the more heterogeneous structure of sample AC compared to the MCA sample. In both samples, the quadrupolar features narrow with temperature, which can be attributed to increased Li+ motion. The representative deconvolution of static spectra is shown in ESI Fig. S9.†
We used electrochemical impedance spectroscopy (EIS) to investigate the impact of the synthesis route on the ionic conductivity and activation energy. The activation energy was obtained by the Arrhenius relationship for solid-state ionic transport in eqn (3),
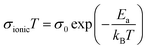 | (3) |
PFG NMR was utilized to measure Li+ diffusivity, DLi+, as functions of temperature and diffusion time (i.e., gradient pulse separation), as displayed in Fig. 7. It is worth noting that, firstly, Li+ diffusion in MCA is slower compared to AC and MC, which is consistent with conductivity results. Secondly, The DLi+ of AC and MC are found to be comparable. All DLi+ exhibit increase with temperature, demonstrating Arrhenius behavior; Ea = 0.43 eV for AC and MC, and 0.33 eV for MCA. The dependence of DLi+ on Δ shows a decreasing trend for all samples (Fig. 7b). In free isotropic diffusion, D is independent of Δ. The results here indicate that free diffusion is restricted roughly to the length scale of the PFG experiment, given by ∼(Dt)1/2, which is on the order of 1 μm and is similar to the average particle size of 800 nm as determined by electron micrographs.
We estimated the correlated migration of the Li+ ions using the inverse Haven ratio (HR−1), which is the ratio of the measured conductivity and the theoretically derived value obtained by a tracer diffusion coefficient and the Nernst–Einstein relationship.
 | (4) |
| Product | H R −1 at 25 °C | H R −1 at 70 °C |
|---|---|---|
| AC | 2.69 | 2.55 |
| MC | 1.80 | 1.47 |
| MCA | 0.35 | 0.62 |
4. Conclusions
Our work compares the reaction mechanism across multiple synthetic routes, showing that LYC formation differs in terms of intermediate phases and kinetics. Aqueous ammonium coordinated routes are a promising strategy for optimizing not only the performance of halide solid electrolytes but also the processing and, eventually, large-scale production. We show the importance of forming complex halide intermediates necessary to synthesize Li3YCl6 through aqueous routes. Control of this intermediate is the key to enabling process control for large batch reactor reaction engineering for halide solid electrolytes. The LYC products were also found to differ significantly in their ionic transport. These differences are shown to be driven by changes in local microstructure, which affected the correlated Li+ transport or the concentration of mobile Li+. We find annealing of LYC induces grain boundary formation regardless of the synthesis route. For the LYC properties to be optimized for use in either halide-based or bilayer-based ASSBs, careful consideration must be made as to the ideal synthesis route to use for both processing and optimization performance. Potential future directions include optimizing processing parameters to enable microstructures with smaller grain boundary resistance and favorable particle size distributions, as well as exploring novel liquid-phase techniques compatible with higher and lower valence transition metal chlorides such as ZrCl2 and HfCl2.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by the Vehicle Technologies Office (VTO) under the Office of Energy Efficiency and Renewable Energy (EERE) as part of the Battery Materials Research (BMR) program. The NPD experiments were conducted at the Spallation Neutron Source, and the SEM was conducted at the Center for Nanophase Materials Sciences; both are DOE Office of Science User Facilities operated by the Oak Ridge National Laboratory.This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan).
References
- J. Janek and W. G. Zeier, A Solid Future for Battery Development, Nat. Energy, 2016, 1(9), 16141, DOI:10.1038/nenergy.2016.141.
- J. Wang, R. Chen, L. Yang, M. Zan, P. Chen, Y. Li, W. Li, H. Yu, X. Yu, X. Huang, L. Chen and H. Li, Raising the Intrinsic Safety of Layered Oxide Cathodes by Surface Re–Lithiation with LLZTO Garnet–Type Solid Electrolytes, Adv. Mater., 2022, 34(19), 2200655, DOI:10.1002/adma.202200655.
- L. Yue, J. Ma, J. Zhang, J. Zhao, S. Dong, Z. Liu, G. Cui and L. Chen, All Solid-State Polymer Electrolytes for High-Performance Lithium Ion Batteries, Energy Storage Mater., 2016, 5, 139–164, DOI:10.1016/j.ensm.2016.07.003.
- M. Jia, N. Zhao, H. Huo and X. Guo, Comprehensive Investigation into Garnet Electrolytes Toward Application-Oriented Solid Lithium Batteries, Electrochem. Energy Rev., 2020, 3(4), 656–689, DOI:10.1007/s41918-020-00076-1.
- X. Bai, T. Yu, Z. Ren, S. Gong, R. Yang and C. Zhao, Key Issues and Emerging Trends in Sulfide All Solid State Lithium Battery, Energy Storage Mater., 2022, 51, 527–549, DOI:10.1016/j.ensm.2022.07.006.
- Y. Pang, Y. Liu, J. Yang, S. Zheng and C. Wang, Hydrides for Solid-State Batteries: A Review, Mater. Today Nano, 2022, 18, 100194, DOI:10.1016/j.mtnano.2022.100194.
- H. Kwak, S. Wang, J. Park, Y. Liu, K. T. Kim, Y. Choi, Y. Mo and Y. S. Jung, Emerging Halide Superionic Conductors for All-Solid-State Batteries: Design, Synthesis, and Practical Applications, ACS Energy Lett., 2022, 7(5), 1776–1805, DOI:10.1021/acsenergylett.2c00438.
- C. Wang, J. Liang, J. T. Kim and X. Sun, Prospects of Halide-Based All-Solid-State Batteries: From Material Design to Practical Application, Sci. Adv., 2022, 8(36), eadc9516, DOI:10.1126/sciadv.adc9516.
- X. Li, J. Liang, N. Chen, J. Luo, K. R. Adair, C. Wang, M. N. Banis, T. Sham, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li and X. Sun, Water–Mediated Synthesis of a Superionic Halide Solid Electrolyte, Angew. Chem., Int. Ed., 2019, 58(46), 16427–16432, DOI:10.1002/anie.201909805.
- X. Luo, D. Cai, X. Wang, X. Xia, C. Gu and J. Tu, A Novel Ethanol-Mediated Synthesis of Superionic Halide Electrolytes for High-Voltage All-Solid-State Lithium–Metal Batteries, ACS Appl. Mater. Interfaces, 2022, 14(26), 29844–29855, DOI:10.1021/acsami.2c06216.
- C. Wang, J. Liang, J. Luo, J. Liu, X. Li, F. Zhao, R. Li, H. Huang, S. Zhao, L. Zhang, J. Wang and X. Sun, A Universal Wet-Chemistry Synthesis of Solid-State Halide Electrolytes for All-Solid-State Lithium-Metal Batteries, Sci. Adv., 2021, 7(37), eabh1896, DOI:10.1126/sciadv.abh1896.
- X. Shi, Z. Zeng, H. Zhang, B. Huang, M. Sun, H. H. Wong, Q. Lu, W. Luo, Y. Huang, Y. Du and C. Yan, Gram–Scale Synthesis of Nanosized Li 3 HoBr 6 Solid Electrolyte for All–Solid–State Li–Se Battery, Small Methods, 2021, 5(11), 2101002, DOI:10.1002/smtd.202101002.
- M. R. Palacin, Battery Materials Design Essentials, Acc. Mater. Res., 2021, 2(5), 319–326, DOI:10.1021/accountsmr.1c00026.
- R. Jain, A. S. Lakhnot, K. Bhimani, S. Sharma, V. Mahajani, R. A. Panchal, M. Kamble, F. Han, C. Wang and N. Koratkar, Nanostructuring versus Microstructuring in Battery Electrodes, Nat. Rev. Mater., 2022, 7(9), 736–746, DOI:10.1038/s41578-022-00454-9.
- V. Sebastian, M. Arruebo and J. Santamaria, Reaction Engineering Strategies for the Production of Inorganic Nanomaterials, Small, 2014, 10(5), 835–853, DOI:10.1002/smll.201301641.
- A. Banik, T. Famprikis, M. Ghidiu, S. Ohno, M. A. Kraft and W. G. Zeier, On the Underestimated Influence of Synthetic Conditions in Solid Ionic Conductors, Chem. Sci., 2021, 12(18), 6238–6263, 10.1039/D0SC06553F.
- M. Simon and G. Meyer, The Oxidation of Tantalum with Ammonium Chloride as an Example of a Novel Route to Early Transitional Metal–Nitrogen Cluster Compounds. Synthesis and Crystal Structure of (NH 4) 6 [Ta 5 (NH) 4 Cl 17 ], J. Chem. Soc., Chem. Commun., 1993,(5), 460–461, 10.1039/C39930000460.
- G. Meyer, E. Garcia and J. D. Corbett, The Ammonium Chloride Route to Anhydrous Rare Earth Chlorides-The Example of Ycl3, in Inorganic Syntheses, ed. H. R. Allcock, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2007, pp. 146–150. DOI:10.1002/9780470132562.ch35.
- R. L. Sacci, T. H. Bennett, A. R. Drews, V. Anandan, M. J. Kirkham, L. L. Daemen and J. Nanda, Phase Evolution during Lithium–Indium Halide Superionic Conductor Dehydration, J. Mater. Chem. A, 2021, 9(2), 990–996, 10.1039/D0TA10012A.
- R. L. Sacci, R. D. McAuliffe, T. F. Malkowski, N. Kidder, X. C. Chen, A. Huq, M. Kirkham, B. L. Armstrong, L. L. Daemen and G. M. Veith, La 2 Zr 2 O 7 Nanoparticle-Mediated Synthesis of Porous Al-Doped Li 7 La 3 Zr 2 O 12 Garnet, Inorg. Chem., 2021, 60(13), 10012–10021, DOI:10.1021/acs.inorgchem.1c01300.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Solid Halide Electrolytes with High Lithium-Ion Conductivity for Application in 4 V Class Bulk-Type All-Solid-State Batteries, Adv. Mater., 2018, 30(44), 1803075, DOI:10.1002/adma.201803075.
- Y. Wu, S. Wang, H. Li, L. Chen and F. Wu, Progress in Thermal Stability of all–solid–state–Li–ion–batteries, InfoMat, 2021, 3(8), 827–853, DOI:10.1002/inf2.12224.
- Y. Xiao, K. Turcheniuk, A. Narla, A.-Y. Song, X. Ren, A. Magasinski, A. Jain, S. Huang, H. Lee and G. Yushin, Electrolyte Melt Infiltration for Scalable Manufacturing of Inorganic All-Solid-State Lithium-Ion Batteries, Nat. Mater., 2021, 20(7), 984–990, DOI:10.1038/s41563-021-00943-2.
- B. H. Toby and R. B. Von Dreele, GSAS-II: The Genesis of a Modern Open-Source All Purpose Crystallography Software Package, J. Appl. Crystallogr., 2013, 46(2), 544–549, DOI:10.1107/S0021889813003531.
- M. Kirkham, L. Heroux, M. Ruiz-Rodriguez and A. Huq, AGES: Automated Gas Environment System for in Situ Neutron Powder Diffraction, Rev. Sci. Instrum., 2018, 89(9), 092904, DOI:10.1063/1.5031432.
- A. Huq, M. Kirkham, P. F. Peterson, J. P. Hodges, P. S. Whitfield, K. Page, T. Hűgle, E. B. Iverson, A. Parizzi and G. Rennich, POWGEN: Rebuild of a Third-Generation Powder Diffractometer at the Spallation Neutron Source, J. Appl. Crystallogr., 2019, 52(5), 1189–1201, DOI:10.1107/S160057671901121X.
- E. O. Stejskal and J. E. Tanner, Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient, J. Chem. Phys., 1965, 42(1), 288–292 CrossRef CAS.
- D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, Z. Gan and G. Hoatson, Modelling One- and Two-Dimensional Solid-State NMR Spectra, Magn. Reson. Chem., 2002, 40, 70–76, DOI:10.1002/mrc.984.
- H. Mattfeld and G. Meyer, Ternäre Halogenide Vom Typ A3MX6. I A3YCl6 (A = K, NH4, Rb, Cs): Synthese, Strukturen, Thermisches Verhalten. Über Einige Analoge Chloride Der Lanthanide, Z. Anorg. Allg. Chem., 1992, 618(12), 13–17, DOI:10.1002/zaac.19926180103.
- G. Yudoyono, N. Ichzan, V. Zharvan, R. Daniyati, H. Santoso, B. Indarto, Y. H. Pramono and M. Zainuri, Darminto. Effect of Calcination Temperature on the Photocatalytic Activity of TiO2 Powders Prepared by Co-Precipitation of TiCl3; Semarang, Indonesia, 2016, p. 020099. DOI:10.1063/1.4945553.
- P. K. Todd, M. J. McDermott, C. L. Rom, A. A. Corrao, J. J. Denney, S. S. Dwaraknath, P. G. Khalifah, K. A. Persson and J. R. Neilson, Selectivity in Yttrium Manganese Oxide Synthesis via Local Chemical Potentials in Hyperdimensional Phase Space, J. Am. Chem. Soc., 2021, 143(37), 15185–15194, DOI:10.1021/jacs.1c06229.
- M. Gombotz and H. M. R. Wilkening, Fast Li Ion Dynamics in the Mechanosynthesized Nanostructured Form of the Solid Electrolyte Li3YBr6, ACS Sustainable Chem. Eng., 2021, 9(2), 743–755, DOI:10.1021/acssuschemeng.0c06694.
- R. Schlem, S. Muy, N. Prinz, A. Banik, Y. Shao-Horn, M. Zobel and W. G. Zeier, Mechanochemical Synthesis: A Tool to Tune Cation Site Disorder and Ionic Transport Properties of Li3MCl6 (M = Y, Er) Superionic Conductors, Adv. Energy Mater., 2020, 10(6), 1903719, DOI:10.1002/aenm.201903719.
- G. Meyer and P. Ax, An Analysis of the Ammonium Chloride Route to Anhydrous Rare-Earth Metal Chlorides, Mater. Res. Bull., 1982, 17(11), 1447–1455, DOI:10.1016/0025-5408(82)90231-8.
- Y. W. Choi, C. M. Araujo and R. Lizárraga, Amorphisation-Induced Electrochemical Stability of Solid-Electrolytes in Li-Metal Batteries: The Case of Li 3 ClO, J. Power Sources, 2022, 521, 230916, DOI:10.1016/j.jpowsour.2021.230916.
- V. Epp, Ö. Gün, H.-J. Deiseroth and M. Wilkening, Long-Range Li+ Dynamics in the Lithium Argyrodite Li7PSe6 as Probed by Rotating-Frame Spin–Lattice Relaxation NMR, Phys. Chem. Chem. Phys., 2013, 15, 7123–7132, 10.1039/C3CP44379E.
- V. Jagannadham, How Do We Introduce the Arrhenius Pre-Exponential Factor (A) to Graduate Students?, Creat. Educ., 2010, 01(02), 128–129, DOI:10.4236/ce.2010.12019.
- Y. Gao, N. Li, Y. Wu, W. Yang and S. Bo, Rethinking the Design of Ionic Conductors Using Meyer–Neldel–Conductivity Plot, Adv. Energy Mater., 2021, 11(13), 2100325, DOI:10.1002/aenm.202100325.
- R. Li, P. Lu, X. Liang, L. Liu, M. Avdeev, Z. Deng, S. Li, K. Xu, J. Feng, R. Si, F. Wu, Z. Zhang and Y.-S. Hu, Superionic Conductivity Invoked by Enhanced Correlation Migration in Lithium Halides Solid Electrolytes, ACS Energy Lett., 2024, 9, 1043–1052, DOI:10.1021/acsenergylett.3c02496.
Footnote |
| † Electronic supplementary information (ESI) available: Showing powder diffraction of phase transitions and refinements in more detail. See DOI: https://doi.org/10.1039/d4qi00559g |
| This journal is © the Partner Organisations 2024 |




