Ultrahigh-speed absolute temperature sensing using ferroelectric HfO₂ enabled by transient negative differential capacitance

Abstract

Conventional ferroelectric polarization-driven temperature sensors, like pyroelectric sensors, often face challenges such as slow response times, limited compatibility with conventional nanoelectronics, and inability to operate under constant temperature conditions. These shortcomings hinder their adaptability to a broad range of applications, especially when compared to thermal and optical sensors. To address these challenges, we introduce a proof-of-concept methodology that enables ferroelectric-based pyroelectric sensors to measure absolute temperatures with high accuracy and speed. Specifically, we demonstrate that a perturbation pulse (+0.8 V, duration = 180 ns) can serve as an effective probe for quantifying both absolute and dynamic temperatures across ferroelectric hafnium zirconium oxide (HZO) nanolaminates. The device demonstrates an ultrafast response time of ∼50 nanoseconds, offering one million readings per second and a temperature sensing accuracy comparable to the state-of-the-art temperature sensing accuracy of 1.0 K. The observed performance is attributed to the temperature-dependent change of transient negative differential capacitance and effective ferroelectric polarization of HZO. For potential applications, we successfully integrated the sensor with a commercially available universal serial bus interface, thereby demonstrating real-time temperature monitoring during data transfer and environmental heating activities. Our research significantly broadens the range of applications for pyroelectric sensors for both steady-state and rapid dynamic temperature measurements.

---

1. Introduction

The pyroelectric effect, an intrinsic feature of ferroelectric materials, stimulates the generation of transient electric potential in response to temperature changes.^1–3 For instance, a temperature change, ΔT, in a time period, Δt, generates a pyroelectric response current, I_p, which is mathematically expressed as: , where p represents the pyroelectric coefficient of the material, A is the effective area of the device, and dT/dt signifies the rate of temperature change.^1,2,4 This feature reveals vast potential across a multitude of applications, including energy harvesting, augmented night vision technologies, and sophisticated environmental monitoring.⁴ While pyroelectric sensors exhibit notable sensitivity to temperature variations, they fall short when it comes to determining their absolute temperature values – a deficiency rooted in their fundamental operating principles that depends on the rate of charge (i.e., dT/dt). Consequently, the potential of the ferroelectric-based pyroelectric effect, despite its transformative prospects, has been somewhat underutilized, especially in comparison with traditional temperature and optical sensors.^5,6 Indeed, the inability to measure absolute temperature remains a substantial roadblock hampering the large-scale adoption of pyroelectric sensors in diverse temperature-dependent applications.

Moreover, conceptually new pyroelectric sensors, with absolute temperature-sensing capabilities and simply integrated into existing complementary metal–oxide–semiconductor (CMOS) frameworks, hold promise as a platform for high-performance, real-time temperature monitoring and warning alarm system design. Such advancements could signal a transformative change in reliability in the field of modern nanoelectronics by allowing rapid validation of operational integrity and immediate mitigation of temperature-related issues, thereby improving the overall efficiency and performance.^7,8 One significant challenge in nanoelectronics is the issue of excessive heat, especially Joule heating, which can cause unwanted failures when operating at high frequencies.^9,10 Traditional temperature sensors and alarms are less effective in this scenario due to their high latency and significant energy consumption. Likewise, pyroelectric sensors typically have slow response times that often exceed the millisecond range and enable us to measure absolute temperature values, especially when integrated into nanoelectronics.^1,4 As a result, the formidable challenge of developing temperature sensors compatible with CMOS technology that are also capable of performing ultra-high-speed operation persists. To effectively manage thermal challenges, it is essential to develop more robust warning alarm systems capable of detecting a small temperature increase in real-time and triggering safety measures instantly.

To address the limitations inherent to conventional pyroelectric-based temperature sensors—such as slow response times, restricted compatibility with nanoelectronics, and the inability to operate reliably under constant temperature conditions—our study introduces a proof-of-concept methodology. This approach enables ferroelectric-based pyroelectric sensors to measure absolute temperatures with both high accuracy and ultrafast speed. Particularly, utilizing a perturbation signal in the form of a short electric pulse (+0.8 V with a duration of 180 ns), we have effectively quantified both absolute and dynamic temperatures across devices fabricated from ferroelectric hafnium zirconium oxide (HZO) nanolaminates. Remarkably, these devices exhibited an ultrafast response time of approximately 50 nanoseconds, thereby offering a measurement rate of one million readings per second and achieving a state-of-the-art temperature sensing accuracy of 1.0 K. The superior performance of these sensors is attributed to their transient negative differential capacitance due to the HZO material, a finding corroborated through both transient response analysis and piezoresponse force microscopy. To evaluate the sensor's real-world applicability and versatility, we successfully integrated it with a commercially available universal serial bus (USB) interface, demonstrating real-time temperature monitoring capabilities during data transfer and environmental heating activities. Thus, our research significantly broadens the range of applications for pyroelectric sensors, positioning them as highly versatile and accurate tools for scenarios requiring both steady-state and rapid dynamic temperature measurements.

2. Experimental section

2.1 Device growth

A ferroelectric layer was prepared by growing HfO₂ (∼2 nm) and ZrO₂ (∼2 nm) nanolaminates on SiO₂ (∼2 nm)/Si substrates using plasma-enhanced atomic layer deposition, as shown in Fig. S1.† We used TDMAH as a source material for HfO₂ layer formation. The entire operation was performed at an ambient temperature of 250 °C using a precursor canister maintained at 60 °C. Additionally, both argon and oxygen lines were temperature-stabilized at 80 °C. The experiment was conducted under a steady working pressure of 0.5 Torr. Initially, the lines for argon and oxygen were cleaned and preheated for 200 seconds. The argon flow rates were set at 300 sccm towards the source material and 100 sccm to maintain vapor pressure, while the oxygen flow rate was adjusted to 300 sccm. After this, TDMAH was introduced for a period of 2 seconds and then cleared from the lines for 15 seconds, which was immediately followed by a 4-second oxygen input. Subsequently, an oxygen plasma treatment was applied for 2 seconds at either 50 W or 100 W of RF energy, and then the system was cleared of oxygen for an additional 10 seconds. This cycle continued until the required film depth was reached. For the development of ZrO₂ layers, the process conditions included a substrate heat setting of 200 °C and utilized TEMAZ as the precursor. This involved a quick 2-second TEMAZ injection, followed by a 15-second clearing phase. Oxygen was then fed into the system for 4 seconds and cleared out for 10 seconds. The gold (Au) and chromium (Cr) layers, which serve as electrodes, were deposited on top of HZO and Si, respectively.

2.2 Measurement techniques

Piezoresponse force microscopy (PFM) evaluations were carried out using an AC240 TM conductive atomic force microscope (AFM) tip. PFM was performed at a resonant frequency of 365 kHz, with the AFM probe subjected to an alternating voltage of +1 V. To mitigate the risk of unintentional mechanical modifications during data collection, a uniform applied force of 68 nN was maintained in all AFM-based analyses. For detailed structural and elemental analyses, we employed a JEOL JEM-2100 F transmission electron microscope (TEM) along with electron energy-loss spectroscopy (EELS) and energy-dispersive X-ray spectroscopy (EDS) mapping.

2.3 Electrical measurements

A proportional integral derivative (PID) controller was employed to adjust and track the temperature. Short electrical pulses were delivered to the top Au/Cr electrode using a Keithley 4200A-SCS parameter measurement unit featuring RPM modules. Simultaneously, the voltage difference across the device was captured using a Tektronix MDO32 oscilloscope. The corresponding negative pulses and the current were graphically represented as functions of time. A pulse duration of 180 nanoseconds was carefully selected to minimize hysteresis effects. External heat sources were used to alter the temperature, while an oscilloscope was used to record the voltage fluctuations across the device.

3. Results and discussion

Fundamentally, ferroelectric-based temperature sensors, like pyroelectric sensors, operate based on the principle of temperature variation. In fact, when the device is subjected to heating or cooling through infrared light or thermal energy, the degree of polarization undergoes a corresponding change.^1,2,4,11 This alteration subsequently triggers an electrical response by altering the density of free carriers, as illustrated in Fig. 1a. However, unfortunately, the sensor remains in a passive state and maintains charge neutrality, offering no response under constant temperature conditions even though the magnitude of polarization may differ, as shown by green backgrounds in the output of Fig. 1a.^1,4,11

Fig. 1 Working concept and device geometry. (a) Cartoon diagram illustrating the principle of pyroelectric sensing. The device remains electrically neutral at both low and high temperatures. Free carriers move in response to temperature changes (i.e., dT/dt), generating pyroelectric current peaks as depicted by the bottom red curve. The device remains passive at a constant temperature, as indicated by the green background. (b) Schematic representation of the pulse response of a ferroelectric device. The response is distinguishable at low, high, and varying temperatures, as indicated by the active parts. (c) Circuit diagram of the measurement system, showing the voltage pulse, V_a, and voltage across the device, V_HZO. The device's temperature is externally varied through heating. (d) Cross-section TEM image of HfO₂/ZrO₂/HfO₂/ZrO₂/HfO₂ on SiO₂/Si, showing a clear contrast change. (e) EDS maps of oxygen (left), Zr (middle), and Hf (right), respectively. (f) High-resolution TEM image, showing uniform layers on native oxide-covered Si. The scale bars for (d), (e), and (f) are 10, 10, and 4 nm, respectively. (g) Inverse FFT image converted from the FFT image, as shown in the inset, of HfO₂/ZrO₂.

Since the magnitude of polarization depends on the absolute value of temperature, we propose that a small perturbation signal, such as a nanosecond duration electric pulse V_a, could enable us to examine the magnitude of polarization, as depicted schematically in Fig. 1b. Indeed, this perturbation signal will serve as a probe to measure the response of a ferroelectric device, which is directly correlated with the effective polarization—or the magnitude of absolute temperature. This concept introduces a new type of sensor that is responsive to both temperature changes and absolute temperature values, in contrast to the typical pyroelectric sensor. It is important to note that the magnitude and duration of the perturbation signal must remain sufficiently small to avoid causing any significant shift in the direction of polarization.

We depicted a schematic diagram of the measurement setup in Fig. 1c, where a small perturbation electric pulse (V_a, duration in the range of nanoseconds) was applied to a ferroelectric device, and the resulting current (I_D) was measured. Detailed information about the measurement process is provided in the Experimental section. Cross-sectional scanning transmission electron microscopy (STEM) confirms the uniformity of the HfO₂ and ZrO₂ layers parallel to the Si substrate, as shown in Fig. 1d and Fig. S1.† Additionally, TEM images allow us to distinguish the HfO₂ and ZrO₂ layers, with an aggregate thickness of around 10 nm (Fig. 1d). The contrasts between the HfO₂ and ZrO₂ layers result from differences in atomic numbers between Hf and Zr. EDS elemental mapping reveals a uniform distribution of oxygen (green), zirconium (blue), and hafnium (pink), which are desirable for a high-performance device.

Furthermore, in Fig. 1f, a high-resolution TEM image shows the bottom Si along with native oxide, SiO₂. This image also highlights well-defined interfaces between HfO₂ and ZrO₂. A fast Fourier transform (FFT) image and the corresponding generated inverse FFT image of the HfO₂/ZrO₂ layer are depicted in the inset of Fig. 1g and Fig. 1g, respectively. The appearance of two bright spots, as marked by the black circles in the inset of Fig. 1g, indicates the existence of an orthorhombic phase, namely Pca2₁ (polar phase), oriented along the [111] direction, confirming the presence of the ferroelectric HfO₂ phase (see Fig. S1†).^12–15 Additionally, the inverse FFT image shows the well-defined planes from HfO₂ to ZrO₂, which are in alignment with a planar orientation of approximately 0.309 nm, corresponding to the (111) plane in the orthorhombic crystalline structure of HfO₂.^14,16,17 Overall, the TEM imaging confirms the growth of a crystalline HfO₂/ZrO₂ nanolaminate over Si. At this stage, the ferroelectric nature of the device was also tested by recording its polarization (P)–voltage (V) curves and performing related positive up and negative down (PUND) measurements, as depicted in Fig. S2.†

Following this, we measured the transient response (I_D-time, t) of the device in response to a single +0.8 V pulse with a duration (d) of approximately 180 ns (i.e., perturbation), while incrementally increasing the temperature from room temperature (RT, approximately 300 K) to 465 K. Upon application of the pulse, the I_D rapidly increases to reach its peak value before decaying towards the negative peak and returning to its initial level (approximately 0 μA), as shown in Fig. 2a. Indeed, a single pulse generates both positive and negative current peaks during the ‘on’ and ‘off’ phases of the pulse. Importantly, similar sharp current peaks resulting from the impact of a single pulse have frequently been observed in ferroelectric materials and are generally attributed to the dynamic response of ferroelectric polarization.^13,18–20 Additionally, when the device underwent a controlled, gradual temperature change, a corresponding temperature-dependent shift in I_D was observed. For instance, the peak value of I_D increased from 29 μA to 310 μA as the temperature increased from RT to 465 K, as indicated by the blue dotted arrow in Fig. 2a. This shift in I_D is likely due to changes in the effective polarization as the temperature changes.^13,18–21 This significant trend underscores the strong temperature-dependent characteristics of I_D, thereby offering a potential platform for sensing temperature variations.

Fig. 2 Dynamic and constant temperature sensing. (a) Transient response upon increasing the temperature from room temperature (RT) to 465 K, as indicated by a blue dotted arrow. The color scale bar represents the temperature range. The top inset displays the applied voltage pulse, V_a. (b) Variation in the peak value of I_D as a function of absolute temperature. S denotes the sensitivity value. A background color highlights the warning range specifically relevant to nanoelectronics. Variation in the peak value of I_D as a function of absolute temperature. A linear relationship is observed up to 420 K, with a sensitivity (S) of 124 μA K⁻¹. Beyond 420 K, the sensitivity increases to 258 μA K⁻¹. The linear fit equation offers a method for converting current outputs into specific temperature values. (c) Transient response over 200 cycles at two distinct but constant temperatures of 360 K and 450 K. σ represents the standard deviation. (d) Stability of I_D across multiple measurements at different temperatures. The temperature range was ±1 K. (e) I_D variation upon increasing the temperature from 305 to 310 K with an interval of 0.5 K. For this measurement, the device was maintained in thermal equilibrium for sufficient time. (f) Humidity-dependent response at three varying temperatures.

For a better understanding, Fig. 2b illustrates the peak value of I_D as a function of temperature, ranging from RT to 465 K. The plot reveals two distinct behaviors: initially, the current shows a linear increase with a shallow slope up to 420 K, and then beyond this temperature, the I_D rises more steeply. These results could be attributed to the temperature-dependent degradation of the ferroelectric properties of HZO.^22–24 Linear behavior is particularly important for the practical applications of this device, while the rapid increase in current could be leveraged to design a warning system. To quantitatively understand these trends, we calculated the sensitivity, defined as . This metric, closely related to the slope of the linear region, was found to be 124% μA K⁻¹ from RT to 420 K. Beyond 420 K, the sensitivity increased to 258% μA K⁻¹. This enhanced sensitivity, more than twice the initial value, could serve as a valuable indicator for setting warning alarms in nanoelectronics by integrating this device, thereby helping to prevent heat-induced damage. Indeed, the device is capable of sensing temperature changes, much like pyroelectric sensors.^1,4

It is also noteworthy that, as shown in Fig. 2a, the I_D exhibits a linear increase with temperature up to 420 K, after which the relationship becomes more complex due to the temperature-dependent degradation of the ferroelectric properties of HZO. To perform a quantitative analysis, we plotted the peak value of I_D as a function of temperature, as illustrated in Fig. 2b. This plot demonstrates a linear relationship with an S of approximately 124 μA K⁻¹ up to 420 K. Beyond this temperature, the sensitivity increases to 258 μA K⁻¹, reflecting a steeper slope. This initial linearity allows for accurate temperature determination based on the current signal. Additionally, we have included more data points and a fitted linear regression line in Fig. 2b to highlight the predictability of temperature based on current measurements. The equation derived from this linear fit can be utilized to directly convert current outputs to temperature, thus enhancing the sensor's usability for real-time temperature monitoring.

Further investigations were conducted to measure the transient response of the device (V_a = 0.8 V, d = 180 ns) at two constant temperatures: 360 ± 1 K and 450 ± 1 K, across multiple measurement cycles. As depicted in Fig. 2c, the device exhibits temperature-dependent, highly stable, and sharply defined distinguishable current peaks, offering constant temperature sensing. In fact, remarkable consistency was observed, characterized by a low standard deviation (σ) of less than 2.7% at 360 K and 4.7% at 450 K, respectively, over numerous cycles (refer to Fig. 2c). This emphasizes the device's robustness in constant-temperature sensing, contrasting it with typical pyroelectric sensors.^1,2,4 Indeed, these results indicate that different temperature surroundings cause corresponding device responses when subjected to nanosecond pulses. This could potentially pave the way for the development of ultrafast, highly precise absolute thermal sensors. Moreover, our quantitative analysis reveals modest energy consumption (E), calculated as E = V × I_D × d = 43 picowatts, making the device even more efficient than current state-of-the-art temperature sensors.

As further evidence for the ability to measure temperature consistently, we found that the peak value of I_D was stable over 200 cycles at various but constant temperatures. The current level showed a notable dependency on temperature but displayed remarkable stability (σ < 2%) when the temperature was held constant. This enables more accurate and reliable temperature sensing, as shown in Fig. 2d. Indeed, when the thermal environment is fixed, the I_D level appears to stabilize, consistently supporting the hypothesis that temperature is a primary factor affecting current levels.

To probe into the details of accurate temperature sensing, we examined the mean value and standard deviation of maximum I_D over forty pulses (with d = 180 ns and a separation of 1 μs) in the temperature range of 305–310 K, coinciding with an incremental temperature change of 0.5 K, as depicted in Fig. 2e and Fig. S3.† This reveals clearly separable mean values that gradually increase with temperature, offering accuracy close to 1.0 K (∼1.0 °C). Indeed, the mean value is dependent on the absolute temperature, leading to a sensitivity close to 1.0 K. This distinctive feature substantiates its potential for delivering high-precision temperature readings with high stability over time, even under conditions that necessitate monitoring subtle temperature changes.

We further investigated the stability of current responses under varying humidity conditions—specifically at levels of 20%, 40%, and 60%—across three distinct temperatures. The current showed high stability across these different humidity levels at each temperature setting, as illustrated in Fig. 2f. This remarkable stability under fluctuating environmental conditions confirms the device's robustness, making it a highly dependable sensor in scenarios where variations in humidity are expected, such as in nanoelectronics. It is worth mentioning that the versatility of our approach is not limited to ferroelectric HfO₂-based devices; it can also be generalized to other systems, including those requiring higher temperature sensing, by selecting appropriate ferroelectric materials.

To rigorously assess the response to applied short pulses, the cumulative charge Q(t), defined by the equation , where I(t) represents the current flowing through the device,¹⁹ was calculated in response to nanosecond pulses (d = 180 ns) at various voltage magnitudes ranging from 0.1 to 3.5 V. Fig. 3a illustrates the transient charge behavior, displaying the maximum charge (Q_max, i.e., peak value) supplied to the device, as indicated by the blue dotted vertical arrow. Additionally, a residual charge, Q_res, persists even after the removal of the voltage pulses (noticeable at 800 ns), as shown by the black dotted arrow in Fig. 3a. It is important to note that this Q_res accounts for leakage current.^18–21 Furthermore, the difference between Q_max and Q_res, labeled as Q_total, represents the actual charge that is reversibly stored and released from the device.^18–20 Notably, both Q_max and Q_res are dependent on the magnitude of the applied voltage, indicating the dynamic behavior of the device. It is worth noting that the device may not be fully charged during these short pulses (i.e., 180 ns); however, this does not compromise the device's effective performance, as shown in Fig. S4.† Importantly, Q_max, Q_res, and consequently Q_total are all dependent on the applied voltage, as demonstrated in Fig. 3b. For instance, when the voltage is relatively low (<0.9 V), Q_res is negligible (close to zero), making Q_max and Q_total essentially equivalent and thus indicating nominal leakage current. This contrasts with higher voltages, where a significant Q_res was measured (see the blue curve in Fig. 3b). This discrepancy could be attributed to the higher electric field, which might allow for leakage current to flow. A critical observation is that the Q_total–V curve reveals a capacitance enhancement (i.e., the slope of the curve, , especially in low voltage ranges greater than 0.9 V). This enhancement is significant and can be attributed to the negative differential capacitance of the device.^18–20

Fig. 3 Working mechanism. (a) Charge versus time curves for varying applied electric fields showing saturation charge (Q_max) and residual charge (Q_res). (b) Charge versus voltage curves depicting Q_max, Q_res, and the total charge (Q_total). (c) Curves for Q_deviceversus E_device (blue curve) and Q_totalversus E_HZO (pink curve), respectively. (d) PFM phase hysteresis loops as a function of tip voltage (V_tip), with the red arrows indicating the direction of polarization. (e) PFM phase image at −3 V (upper half) and −6 V (lower half), illustrating the domain structure. The mapped area is 500 × 500 nm². (f) Distribution of the phase from the PFM image. (g) Temperature dependence of Q_max and Q_res. (h) Polarization versus voltage curves at various temperatures, measured at 1 kHz frequency. (i) Polarization decay with increasing temperature, indicating phase transition behavior.

To understand the charge boosted behavior of the device, the average electric field (E_HZO) within the HZO layer was calculated using the equation as: , where C_d is the capacitance per unit area of SiO₂ considered to be a constant value of 1.38.^13,20 As clearly shown by the pink curve in Fig. 3c, the Q_d–E_HZO relationship closely resembles an ‘S’ shape, indicating that the device exhibits negative differential capacitance, as evidenced by , within the range of −0.1 to 0.1 MV cm⁻¹. This behavior is in contrast to traditional capacitors, which generally show a linear variation with voltage. In contrast, the typical P–V loop does not exhibit the NDC, as shown by the blue curve in Fig. 3c with Q_device–E_device, where Q_device and E_device are charge and electric field across the device. This observation aligns well with the reported literature and highlights the essential ferroelectric characteristics of HZO films, including a coercive field of 1.5 MV cm⁻¹ and a remanent polarization (P_r) of ∼26 μC cm⁻². It is typically regarded that generating relatively higher voltages (or fields) is required to realize the NDC. However, the observed NDC at relatively lower voltages could arise from a combination of ferroelectric (FF-HfO₂) and antiferroelectric (AFE-ZrO₂) layers and in the range of recently reported values.¹⁹ This arrangement is like a ferroelectric–dielectric (polar–nonpolar) multi-layered structure, which could induce depolarization fields in the ferroelectric layer.^17,19,25,26 These depolarization fields locally stabilize the ferroelectric material in an energy state higher than its inherent ground state, resulting in an energy landscape characterized by a negative curve and thus leading to a negative capacitance effect.^17,27

Various approaches, including both single-domain and multi-domain theories, have been proposed to explain the negative differential capacitance (NDC).¹³ To gain microscopic evidence, piezoresponse force microscopy (PFM) measurements were performed. To investigate polarization flipping, the phase change as a function of the applied tip voltage, V_tip, was measured over twenty cycles. As illustrated in Fig. 3d, the phase—which is related to polarization—changes gradually, rather than abruptly, from −90 to +90 degrees as V_tip increases from −6.0 to +6.0 V. The phase remains high at a V_tip of 0 V during the reverse voltage scan (i.e., from +6.0 to −6.0 V), leading to a clear and highly stable hysteresis loop. This gradual change in polarization is crucial for achieving a hysteresis-free NDC in the ferroelectric/dielectric structure.

In addition, PFM maps displaying the phase (which is related to the direction of polarization) were taken over the same 500 × 500 nm² area at different switching stages (see Fig. 3e). Initially, the device was uniformly pre-polled at +6.0 V, resulting in a uniform positive polarization in the ferroelectric material, as shown in Fig. S5.† Subsequently, a mixed state was induced by applying a voltage of −3.0 V, which is close to the negative coercive field observed in P–V measurements. As expected, some domains changed their polarization, while others remained fixed; this is evident in the top panel of Fig. 3e. Moreover, to induce the opposite state, the maximum voltage allowable by the setup, i.e., −6.0 V, was applied. It should be noted that even with an applied voltage of −6.0 V, localized domain flipping was observed, indicating the presence of multi-domains in the device. Therefore, the presence of nanodomains in the nanolaminate structure could enable the low energy operative thermal sensor. At this point, the distribution of the phase is also plotted in Fig. 3f, which shows two clear peaks separated by 180°.

Indeed, it is noted that both transient NDC and leakage current contribute to the increase in the I_D value. To demonstrate this, the values of Q_max and Q_res are plotted as functions of temperature, as shown in Fig. 3g. It is important to note that Q_res, which is related to the increase in leakage current, gradually increases with temperature. This indicates a degradation of the ferroelectric nature of HZO and matches well with previous literature reports.^28,29 Therefore, the increase in I_D can be attributed to changes in the ferroelectric polarization of HZO. To confirm the role of temperature, P–V hysteresis loops were obtained at different temperatures, as depicted in Fig. 3h, showing a clear temperature-dependent shift of the P–V loops. For clarity, the values of 2P_r at 0 V are plotted as a function of temperature, as shown in Fig. 3i. Fig. 3i shows a significant change in polarization from 26 to 17 μC cm⁻² when the temperature is increased from RT to 460 K. Hence, based on the observations in Q_res (Fig. 3g) and the change in effective polarization (Fig. 3i) with increasing temperature, the ferroelectric nature of HZO diminishes. This leads to an increase in transient current, as observed in Fig. 2a. The response of the device to the applied short pulses is primarily driven by the NDC effect, associated with the effective polarization of HZO.^18–20 Since the effective polarization of HZO depends on the absolute temperature, the transient response of the device is consequently influenced by the NDC effect.

Leveraging the device's ultrafast and accurate temperature-sensing capabilities, we tested its compatibility with nanoelectronics through integration with a commercially available universal serial bus (USB) drive. Subsequently, we monitored real-time temperature variation caused by both laptop data transfers and external heat sources. Fig. 4a provides a comprehensive illustration of the seamless integration of the device with USB ports, as well as a schematic outlining the data transfer process from the laptop. Initially, the device was stabilized at RT and transferred a large data set (12 GB) from the computer to the USB drive. During this process, we monitored the transient response by applying perturbing pulses (0.8 V, d = 180 ns) at two-minute intervals, noting that the entire data transfer was completed within 20 minutes. Fig. 4b depicts the collected responses, which display dynamic behavior, as marked by the blue dotted arrow. For instance, the peak value of I_D gradually increased as the monitoring time extended from 2 to 14 minutes, signifying a rising temperature in the USB drive. This rise equated to an approximately 8 K increase above RT, aligning well with the specifications in the standard data sheet. Indeed, to further validate these findings, we utilized a K-type temperature sensor and measured the temperature change, which was found to be 7.9 K, confirming that the measured temperature changes with our device are accurate. This confirms the device's robustness in both integration and temperature sensing.

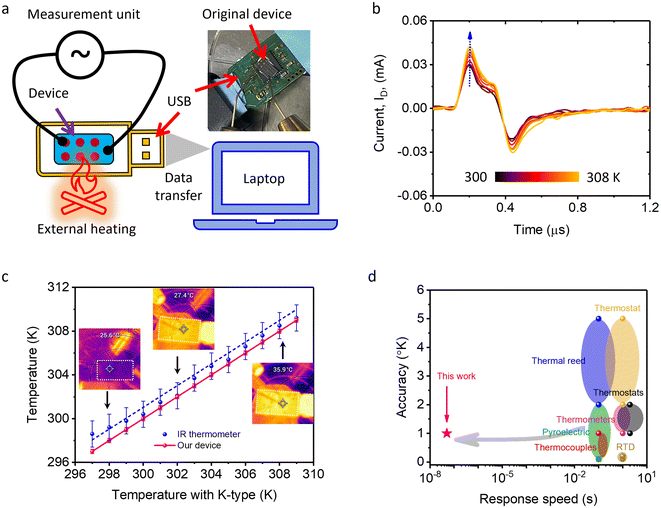Fig. 4 Real-time temperature monitoring. (a) Schematic diagram of data transfer from a laptop to a USB and temperature measurement using the device. The top inset shows an original photograph of the integrated device. Heating was also performed using external sources. (b) Measurement of I_D values for various time intervals during data transfer. A shift in the I_D peak value is indicated by a blue dotted arrow. The scale bar represents the change in temperature. (c) Temperature measured using a K-type thermocouple (x-axis) compared with temperature measurements from our device and thermal mapping. The insets display original photographs captured using a thermal imaging tool. (d) Response speed versus accuracy of temperature mapping, offering a clear comparison between state-of-the-art thermal sensors and our device. Response speed versus accuracy of temperature mapping, offering a clear comparison between state-of-the-art thermal sensors and our device. Table 1 provides a detailed comparison of our HfO₂-based sensor with other related pyroelectric sensors, highlighting its superior performance in terms of response time and accuracy. The minimal detectable change in absolute temperature using our sensor is approximately 1 K.

To emulate real-world conditions that could potentially damage nanoelectronics, we subjected the integrated device to external heating using hot air, which gradually increased the temperature from 297 to 309 K. This can generate a similar scenario to that generated due to overheating resulting from the excess use of nanoelectronics. The primary aim of this test was to measure the temperature using three different tools: a K-type sensor, thermal imaging, and our device. The temperature measurements from our device and thermal imaging, plotted as a function of temperature measured using the K-type sensor, are shown in Fig. 4c. The insets depicted in Fig. 4c provide a detailed temperature map, facilitating a rough comparison with established thermal monitors. Impressively, our device exhibited a one-to-one correspondence with existing thermal image sensors, thereby affirming its high performance and reliability in comparison with commercially available K-type sensors. This comprehensive analysis not only demonstrates the sensor's superior accuracy and responsiveness, but also its resilience under environmental stresses, positioning it as a potential industry leader in thermal monitoring applications.

With an ultrafast response time of just 50 nanoseconds—measured from 10% to 90% of the peak value of the output I_D—our device outperforms conventional temperature sensors by several orders of magnitude. Specifically, it operates up to one million times faster than its state-of-the-art commercial counterparts, as depicted in Fig. 4d. This ultrahigh speed translates to a theoretical capacity to support as many as million readings per second, in stark contrast to the limited 100 readings per second achievable with standard sensors. This leap in speed is facilitated by the unique utilization of ferroelectric polarization as the operative mechanism. Unlike conventional sensors that rely on thermocouples, RTDs, or thermistors, often made from ceramics or polymers, our innovative approach harnesses the negative differential capacitance effect of ferroelectric materials. This allows for almost instantaneous responsiveness to temperature variations. In terms of measurement accuracy, the device has a margin of error less than 1.0 K, comfortably falling within the industry-standard accuracy ranges of ±1–±2 K. The unique combination of ultrafast response time and exceptional accuracy offers groundbreaking opportunities for scenarios demanding real-time monitoring and instant decision-making processes. In addition to highlighting the advantages of our HfO₂-based sensor in terms of response time and accuracy, we have compared its performance with other related pyroelectric sensors. Table 1 provides a comprehensive comparison of the sensing properties, including response time, accuracy, sensitivity, and the operational temperature range. This comparison illustrates the superior performance of our sensor in key aspects. Our developed method for pyroelectric measurements of absolute temperature achieves an accuracy of approximately 1 K, a notable result for Si-compatible ferroelectric HfO₂. It is important to highlight that dynamic methods can measure temperature changes as small as 0.001 Kelvin or even less, as discussed by Sidney B. Lang.³⁰ To evaluate the sensitivity of our sensor further, we analyzed the data from Fig. 4d and found that it can detect minimal changes in absolute temperature as small as 1 K. This high sensitivity, combined with an ultrafast response time of 50 ns, underscores the potential of our sensor for precise, real-time temperature monitoring. Considering its ultrafast response characteristics and high accuracy, the device has the potential to revolutionize applications that hinge on nanosecond-level fluctuations, such as high-frequency trading systems. Likewise, it has promising applications in advanced scientific endeavours. Industries like nanoelectronics, automotive, and aerospace can also benefit from integrating such high-speed and reliable sensors to boost performance and safety measures.

Table 1 Comparison of the sensing properties among related pyroelectric sensors

S. no.	Sensor type	Response time	Accuracy	Sensitivity	Operational temperature range	Ref.
1	PZT-based	∼1 ms	±2.0 K	21.4 mV nm^−1	263–300 K	1
2	ZnO/ZnTe-based	62 μs	…	…	19.9–22.8 °C	31
3	Cu(In,Ga)Se2	6.8/7.9 μs	…	235.4 mV mm^−1	…	32
4	P(VDF–TrFE)	0.5 s	…	0.82 V K^−1	…	33
5	P(VDF–TrFE)	1.7 s	…	6.4 V K^−1	0.05–10 K	34
6	HfO2-based (this Work)	∼50 ns	±1.0 K	124 μA K^−1	RT to 465 K	This work

---

4. Conclusion

In conclusion, our research has addressed the significant limitations that have historically plagued conventional pyroelectric sensors, such as slow response times, limited compatibility with nanoelectronics, and operational difficulties under constant temperature conditions. Through the introduction of a pioneering proof-of-concept methodology, we have enabled pyroelectric sensors to measure absolute temperatures with unparalleled accuracy and rapidity. A key innovation of our approach is the use of a perturbation signal, specifically a short electric pulse (+0.8 V with a duration of 180 ns), serving as an effective probe for temperature measurement. This technique has been successfully implemented in devices fabricated from ferroelectric hafnium zirconium oxide (HZO) nanolaminates. These optimized sensors exhibited an impressive response time of approximately 50 nanoseconds and a temperature sensing accuracy comparable to state-of-the-art sensors, measuring up to 1.0 K with a throughput of one million readings per second. This enhanced performance can be attributed to the negative differential capacitance characteristics of the HZO material, a fact substantiated through transient response analysis and piezoresponse force microscopy. Further extending the practical applicability of our sensor, we demonstrated its seamless integration with a commercially available universal serial bus interface, enabling real-time temperature monitoring in various applications including data transfer and environmental heating. Overall, our findings significantly expand the utility and adaptability of pyroelectric sensors, making them highly suitable for applications demanding both steady-state and rapid dynamic temperature measurements.

Author contributions

Mohit Kumar: conceptualization, data curation, formal analysis, funding acquisition, and writing – original draft. Hayoung Park: data curation and formal analysis. Hyungtak Seo: funding acquisition, project administration, resources, and writing – review & editing.

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This study was supported by the National Research Foundation of Korea [NRF-2023R1A2C2003242 and NRF-2022M3I7A3037878] of the Ministry of Science and ICT, Republic of Korea. This work is also supported by Korea Evaluation Institute of Industrial Technology (Project no: 20022717) funded by Ministry of Trade, Industry and Energy, Republic of Korea.

References

1. M.-M. Yang, Z.-D. Luo, Z. Mi, J. Zhao, S. Pei E and M. Alexe, Nature, 2020, 584, 377–381.
2. D. You, C. Xu, W. Zhang, J. Zhao, F. Qin and Z. Shi, Nano Energy, 2019, 62, 310–318.
3. J. Lee, K. Yang, J. Y. Kwon, J. E. Kim, D. I. Han, D. H. Lee, J. H. Yoon and M. H. Park, Nano Convergence, 2023, 10, 55.
4. D. Zhang, H. Wu, C. R. Bowen and Y. Yang, Small, 2021, 17, 2103960.
5. H. Chen, K. Liu, L. Hu, A. A. Al-Ghamdi and X. Fang, Mater. Today, 2015, 18, 493–502.
6. Y. Chen, Y. Wang, Z. Wang, Y. Gu, Y. Ye, X. Chai, J. Ye, Y. Chen, R. Xie, Y. Zhou, Z. Hu, Q. Li, L. Zhang, F. Wang, P. Wang, J. Miao, J. Wang, X. Chen, W. Lu, P. Zhou and W. Hu, Nat. Electron., 2021, 4, 357–363.
7. V. K. Sangwan and M. C. Hersam, Nat. Nanotechnol., 2020, 15, 517–528.
8. C. Kaspar, B. J. Ravoo, W. G. van der Wiel, S. V. Wegner and W. H. P. Pernice, Nature, 2021, 594, 345–355.
9. M. Li, D. W. Kim, S. Gu, D. Y. Parkinson, H. Barnard and K. N. Tu, J. Appl. Phys., 2016, 120, 075105.
10. Y. Liu, M. Li, D. W. Kim, S. Gu and K. N. Tu, J. Appl. Phys., 2015, 118, 135304.
11. M. Kumar and H. Seo, Adv. Mater., 2022, 34, 2106881.
12. S. Kang, W.-S. Jang, A. N. Morozovska, O. Kwon, Y. Jin, Y.-H. Kim, H. Bae, C. Wang, S.-H. Yang, A. Belianinov, S Randolph, E. A. Eliseev, L. Collins, Y. Park, S. Jo, M.-H. Jung, K.-J. Go, H. W. Cho, S.-Y. Choi, J. H. Jang, S. Kim, H. Y. Jeong, J. Lee, O. S. Ovchinnikova, J. Heo, S. V. Kalinin, Y.-M. Kim and Y. Kim, Science, 2022, 376, 731–738.
13. M. Hoffmann, M. Gui, S. Slesazeck, R. Fontanini, M. Segatto, D. Esseni and T. Mikolajick, Adv. Funct. Mater., 2022, 32, 2108494.
14. X. Xu, F. T. Huang, Y. Qi, S. Singh, K. M. Rabe, D. Obeysekera, J. Yang, M. W. Chu and S. W. Cheong, Nat. Mater., 2021, 20, 826–832.
15. H. Kwak, N. Kim, S. Jeon, S. Kim and J. Woo, Nano Convergence, 2024, 11, 9.
16. M. H. Park, Y. H. Lee, H. J. Kim, Y. J. Kim, T. Moon, K. D. Kim, J. Müller, A. Kersch, U. Schroeder, T. Mikolajick and C. S. Hwang, Adv. Mater., 2015, 27, 1811–1831.
17. S. S. Cheema, N. Shanker, L. C. Wang, C. H. Hsu, S. L. Hsu, Y. H. Liao, M. S. Jose, J. Gomez, W. Chakraborty, W. Li, J. H. Bae, S. K. Volkman, D. Kwon, Y. Rho, G. Pinelli, R. Rastogi, D. Pipitone, C. Stull, M. Cook, B. Tyrrell, V. A. Stoica, Z. Zhang, J. W. Freeland, C. J. Tassone, A. Mehta, G. Saheli, D. Thompson, D. I. Suh, W. T. Koo, K. J. Nam, D. J. Jung, W. B. Song, C. H. Lin, S. Nam, J. Heo, N. Parihar, C. P. Grigoropoulos, P. Shafer, P. Fay, R. Ramesh, S. Mahapatra, J. Ciston, S. Datta, M. Mohamed, C. Hu and S. Salahuddin, Nature, 2022, 604, 65–71.
18. A. I. Khan, K. Chatterjee, B. Wang, S. Drapcho, L. You, C. Serrao, S. R. Bakaul, R. Ramesh and S. Salahuddin, Nat. Mater., 2015, 14, 182–186.
19. S. Jo, H. Lee, D. H. Choe, J. H. Kim, Y. S. Lee, O. Kwon, S. Nam, Y. Park, K. Kim, B. G. Chae, S. Kim, S. Kang, T. Moon, H. Bae, J. Y. Won, D. J. Yun, M. Jeong, H. H. Lee, Y. Cho, K. H. Lee, H. J. Lee, S. Lee, K. J. Nam, D. Jung, B. J. Kuh, D. Ha, Y. Kim, S. Park, Y. Kim, E. Lee and J. Heo, Nat. Electron., 2023, 6, 390–397.
20. M. Hoffmann, M. Pešić, K. Chatterjee, A. I. Khan, S. Salahuddin, S. Slesazeck, U. Schroeder and T. Mikolajick, Adv. Funct. Mater., 2016, 26, 8643–8649.
21. S. C. Chang, U. E. Avci, D. E. Nikonov, S. Manipatruni and I. A. Young, Phys. Rev. Appl., 2018, 9, 014010.
22. J. Liu, S. Liu, L. H. Liu, B. Hanrahan and S. T. Pantelides, Phys. Rev. Appl., 2019, 12, 034032.
23. P. D. Lomenzo, S. Jachalke, H. Stoecker, E. Mehner, C. Richter, T. Mikolajick and U. Schroeder, Nano Energy, 2020, 74, 104733.
24. C. Mart, T. Kämpfe, S. Zybell and W. Weinreich, Appl. Phys. Lett., 2018, 112, 052905.
25. M. Pešić, M. Hoffmann, C. Richter, T. Mikolajick and U. Schroeder, Adv. Funct. Mater., 2016, 26, 7486–7494.
26. M. Hoffmann, Z. Wang, N. Tasneem, A. Zubair, P. V. Ravindran, M. Tian, A. A. Gaskell, D. Triyoso, S. Consiglio, K. Tapily, R. Clark, J. Hur, S. S. K. Pentapati, S. K. Lim, M. Dopita, S. Yu, W. Chern, J. Kacher, S. E. Reyes-Lillo, D. Antoniadis, J. Ravichandran, S. Slesazeck, T. Mikolajick and A. I. Khan, Nat. Commun., 2022, 13, 1228.
27. M. Hoffmann, F. P. G. Fengler, M. Herzig, T. Mittmann, B. Max, U. Schroeder, R. Negrea, L. Pintilie, S. Slesazeck and T. Mikolajick, Nature, 2019, 565, 464–467.
28. S. Li, D. Zhou, Z. Shi, M. Hoffmann, T. Mikolajick and U. Schroeder, ACS Appl. Electron. Mater., 2021, 3, 2415–2422.
29. H. Chen, L. Tang, L. Liu, Y. Chen, H. Luo, X. Yuan and D. Zhang, Materialia, 2020, 14, 100919.
30. S. B. Lang, Phys. Today, 2005, 58, 31–36.
31. D. You, C. Xu, W. Zhang, J. Zhao, F. Qin and Z. Shi, Nano Energy, 2019, 62, 310–318.
32. J. Liu, J. Chen, Z. Zhang, S. Wang and S. Qiao, Nano Energy, 2023, 109, 108254.
33. C. Cai, H. Zhang, B. Li, Z. Han, F. Wang, P. Hou and W. Liu, Adv. Electron. Mater., 2023, 9, 2201084.
34. B. Li, C. Cai, Y. Liu, F. Wang, B. Yang, Q. Li, P. Zhang, B. Deng, P. Hou and W. Liu, Nat. Commun., 2023, 14, 4000.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02776k

---