Harnessing machine learning for efficient large-scale interatomic potential for sildenafil and pharmaceuticals containing H, C, N, O, and S

Abstract

In this study a cutting-edge approach to producing accurate and computationally efficient interatomic potentials using machine learning algorithms is presented. Specifically, the study focuses on the application of Allegro, a novel machine learning algorithm, running on high-performance GPUs for training potentials. The choice of training parameters plays a pivotal role in the quality of the potential functions. To enable this methodology, the “Solvated Protein Fragments” dataset, containing nearly 2.7 million Density Functional Theory (DFT) calculations for many-body intermolecular interactions involving protein fragments and water molecules, encompassing H, C, N, O, and S elements, is considered as the training dataset. The project optimizes computational efficiency by reducing the initial dataset size according to the intended application. To assess the efficacy of the approach, the sildenafil citrate, iso-sildenafil, aspirin, ibuprofen, mebendazole and urea, representing all five relevant elements, serve as the test bed. The results of the Allegro-trained potentials demonstrate outstanding performance, benefiting from the combination of an appropriate training dataset and parameter selection. This notably enhanced computational efficiency when compared to the computationally intensive DFT method aided by GPU acceleration. Validation of the produced interatomic potentials is achieved through Allegro's own evaluation mechanism, yielding exceptional accuracy. Further verification is carried out through LAMMPS molecular dynamics simulations. Structural optimization by energy minimization and NPT Molecular Dynamics simulations are performed for each potential, assessing relaxation processes and energy reduction. Additional structures, including urea, ammonia, uracil, oxalic acid, and acetic acid, are tested, highlighting the potential's versatility in describing systems containing the aforementioned elements. Visualization of the results confirms the scientific accuracy of each structure's relaxation. The findings of this study demonstrate strong scaling and the potential for applications in pharmaceutical research, allowing the exploration of larger molecular structures not previously amenable to computational analysis at this level of accuracy The success of the machine learning approach underscores its potential to revolutionize computational solid-state physics.

---

Introduction

Molecular dynamics (MD) are integral to computational research across fields such as energy storage and manipulation, nanostructure devices and pharmaceutical industries. These simulations rely on accurate predictions of the potential energy and atomic forces to describe the behavior of complex systems over time scales extending to several nanoseconds. It's a technique for simulating the behavior of molecular or crystalline systems and it is crucial for understanding the underlying structure and dynamics.¹ It allows for the derivation of kinetic and thermodynamic properties, particularly in the study of biologically important macromolecules.^2,3 The technique provides microscopic information, such as atomic positions and velocities, which can be converted to macroscopic observables like pressure and temperature.⁴ Despite the challenge of dealing with systems involving many bodies, molecular dynamics calculations have been instrumental in advancing our understanding of various scientific fields.^5,6

In the realm of contemporary scientific investigation, molecular dynamics (MD) simulations have advanced to encompass a diverse array of length scales, spanning from the microcosmic world of individual atoms to the macroscopic realm of nanometers. The ability to navigate these extensive spatial and temporal dimensions is handled by the utilization of conventional interatomic potentials, frequently denoted as force fields. These established force fields play a pivotal role in predicting both the energy and classical forces governing atomic behavior within a given atomic arrangement. Notably, computations using these established potentials provide computational efficiency, demonstrating linear scaling with the number of atoms involved. This computational edge establishes conventional potentials as an essential element in conducting expansive atomistic simulations. Interatomic potentials play a crucial role in molecular dynamics simulations, influencing the accuracy and applicability of the results. Interatomic potentials are crucial for molecular dynamics and kinetic Monte Carlo⁷ simulations, but their accuracy is often limited by the constraints of pairwise force-fields. Empirical potentials, particularly within the shell model, have shown success in predicting defect properties and solid properties.^8,9 These potentials can be designed to reproduce various properties, such as elastic properties and defect energies.^10,11 The critical role of interatomic potentials in molecular dynamics simulations, particularly in accurately representing the behavior of different materials and molecules from simulating radiation damage effects in metals,¹² to developing a ‘magnetic’ interatomic potential for simulating magnetic α-iron.¹³ Mahadevan et al.¹⁴ contributes to this discussion by introducing a dissociative water potential for molecular dynamics simulations, demonstrating its ability to accurately reproduce the properties of water.

An additional approach is methods like density functional theory (DFT), that have high accuracy but only work for small amount of atoms and short simulations. Classical force fields, can handle larger systems and longer simulations, without the previous acuracy of the DFT. Classical force fields, have limitations in accurately simulating complex molecules due to their crude approximations. Recent advancements have shown improving their accuracy and general applicability.¹⁵ Optimization strategies have been proposed to improve the description of ion pairing in classical force fields, particularly for complex polyatomic ions.¹⁶

Recent research has made significant strides in addressing the challenges of accuracy and efficiency in traditional interatomic potentials. A dynamic multiscale molecular dynamics simulation method that combines classical and machine learning potentials was implemented,¹⁷ achieving both high accuracy and efficiency. Additionaly Kocabaş et al.¹⁸ developed Gaussian approximation potentials for two-dimensional materials, demonstrating their accuracy and computational efficiency. After 2016, the emergence of machine learning algorithms,^19–21 particularly artificial neural networks, offers a promising solution to the everlasting problem of accuracy versus computational time. By constructing flexible models for interatomic potential energy calculation through machine learning, researchers aim to bridge the gap between high fidelity and computational efficiency, enabling the study of large numbers of atoms over extended time scales, while maintaining accurate dynamics. This advancement represents a pivotal development in the realm of computational chemistry, materials science, and biology, promising to overcome the historical trade-off between efficiency and fidelity in simulations.

Machine learning interatomic potentials, often referred to as MLIPs or ML interatomic potentials, are a class of models used in computational chemistry to describe the interactions between atoms in a material. These potentials are developed using machine learning techniques, particularly neural networks, to approximate the potential energy surface of a system. Machine learning interatomic potentials (MLIPs) offer a more flexible and data-driven approach to modeling these interactions. These potentials possess a set of defining characteristics that have become pivotal in contemporary scientific research. Firstly, they embrace a data-driven approach, meticulously trained on extensive datasets derived from precise quantum mechanical calculations, like density functional theory (DFT), allowing the model to comprehend the intricate relationship between atomic positions and potential energy. Zuo et al.²² and Deringer et al.²³ both highlight the superior performance of machine learning-based interatomic potentials in predicting energies and forces, as well as properties such as elastic constants and phonon dispersion curves. These models, which are based on local environment descriptors, have been shown to outperform classical interatomic potentials. These studies collectively underscore the transformative potential of machine learning in molecular dynamics and its applications in pharmaceuticals.^24,25

MLIPs often leverage neural networks, a subset of machine learning models, to represent potential energy functions, capturing complex non-linear relationships in the data. Their notable flexibility enables the encapsulation of a broad spectrum of interatomic interactions, accommodating short-range and long-range forces and adapting to complex chemical environments. Thanks to their foundation on high-fidelity reference data, MLIPs have the potential to offer accurate descriptions of interatomic forces and potential energy surfaces, elevating their accuracy beyond traditional force fields. Furthermore, once trained, MLIPs significantly reduce computational costs compared to quantum mechanical calculations, expediting evaluations and enabling longer molecular dynamics simulations. Recent advancements in the field of interatomic potentials have seen the development of E(3)-equivariant graph neural networks, which have shown promise in achieving both data efficiency and accuracy. Batzner et al.⁴³ introduced Neural Equivariant Interatomic Potentials (NequIP), a E(3)-equivariant neural network approach that outperforms existing models with significantly fewer training data. This was further explored²⁶ and proposed a unified mathematical framework that encompasses both NequIP and the Atomic Cluster Expansion (ACE), shedding light on critical design choices for achieving high accuracy. Musaelian et al.⁴² introduced Allegro, a strictly local equivariant deep learning interatomic potential that achieves excellent accuracy and scalability of parallel computation, outperforming existing deep message passing neural networks and transformers. These studies collectively highlight the potential of E(3)-equivariant graph neural networks in the development of data-efficient and accurate interatomic potentials.

The Allegro (or NequIP) machine learning algorithm, outperforms some other state-of-the-art models in terms of accuracy, scalability, and computational efficiency for various compounds. The target compound for this work was sildenafil and the test molecules (ethanol, malonaldehyde, naphthalene, paracetamol, salicylic acid, toluene, uracil) addressed in the publication provided⁴³ by Materials Intelligence Group at Harvard University, that developed NequIP/Allegro were a good indication that this model could adequately describe the atomic interactions needed.

Allegro uses a combination of neural networks and linear scaling functions to accurately predict molecular energies and forces, which are crucial for understanding chemical reactions. For interatomic forces, Allegro shows better performance than most other methods tested across a range of molecules, outperforming machine learning models like FCHL19, UNiTE, GAP, ACE.⁴² Allegro demonstrates its ability to handle large molecular systems effectively, achieving good accuracy for large molecules while other models struggle with similar accuracy for such large systems. Also, the potential exported from this tool is compatible in a comprehensive format from LAMMPS which by design makes massively parallel thus scalable. The training process is performed using the PyTorch library which utilizes a python class called torch. Tensor, that enables the model to be operatable on CUDA-enabled NVidia GPUs. This and the huge boom of resources spent on AI-HPC infrastructure by the academic community make it also scalable. Although the studies do not provide explicit benchmarks for computational efficiency, Allegro's ability to achieve good accuracy and scalability implies that it can perform calculations more efficiently than some other methods tested.

Their increasing prominence results from their ability to bridge the divide between the precision of quantum mechanical methods and the computational efficiency of classical force fields, making them invaluable for researching complex materials, chemical reactions, and biological systems where accurate modeling of atomic interactions is paramount. As we explore the realms of cutting-edge scientific inquiry, the synergy between machine learning interatomic potentials (MLIPs) and pharmaceutical nanotechnological strategies becomes increasingly evident. MLIPs, fueled by the power of neural networks and E(3)-equivariant graph structures, not only revolutionize our understanding of atomic interactions but also bridge the gap between quantum precision and classical computational efficiency.

Concurrently, pharmaceutical research struggles with the nuances of drug behavior. Sildenafil for instance, which is a phosphodiesterase type 5 (PDE5) inhibitor, has been successful in treating conditions such as erectile dysfunction and pulmonary arterial hypertension.⁵⁴ However, its pharmacokinetics (how the body absorbs, distributes, metabolizes, and excretes the drug) and pharmacodynamics (how the drug affects the body) are complex, leading to challenges in formulating and administering it.⁵⁴ To address these challenges, nanotechnological strategies have been proposed. Nanotechnology involves manipulating materials at the nanoscale to enhance the bioavailability of silymarin, a compound with potential therapeutic benefits for liver and neurodegenerative diseases.

Researchers have proposed nanotechnological strategies to improve the bioavailability of silymarin, and the suggestion is that similar strategies could potentially be applied to enhance the bioavailability of sildenafil as well.^27,28 Bioavailability refers to the proportion of a drug that enters the bloodstream when introduced into the body and is made available for use or storage. Enhancing bioavailability is important for improving the effectiveness of a drug. The existing knowledge on the synthesis of sildenafil and its analogues provides a foundation for further research in this area, indicating that there is potential for the development of new compounds or improved methods related to sildenafil and its derivatives.

In the context of sildenafil and its pharmacokinetic and pharmacodynamic complexities, and hopefully for a broader spectrum of compounds, a good interatomic potential might be essential. Sildenafil and most pharmaceutical compounds are complex molecules with various functional groups. The complexities in sildenafil's pharmacokinetics mentioned involve how the drug is absorbed, distributed, metabolized, and excreted in the body. Sildenafil's therapeutic effects are related to its interaction with specific molecular targets. A reliable interatomic potential can assist in simulating all the aforementioned processes.

This convergence of computational precision in MLIPs and the drive to enhance drug efficacy through nanotechnology sets the stage for a collaborative frontier. The capability of MLIPs to accurately model atomic interactions find resonance in the pursuit of improving drug bioavailability and effectiveness. As we navigate this interdisciplinary terrain, the exchange of insights between these scientific disciplines holds the promise of breakthroughs that transcend traditional boundaries, shaping a future where advancements in one field catalyze innovation in another.

Of course, MILPs still have their limitations and the drug industry has special needs. Machine Learning Interatomic Potentials (MLIPs) may not be stable enough for long simulations, which can be a problem when applying these potentials for pharmaceuticals. Molecular dynamics Simulations that are performed in increased temperature or for a prolonged time are not as robust as they should be.²⁹ Also, in general MLIPs provide decent accuracy at force field computational cost,³⁰ though achieving the “holy grail” of accuracy of DFT is still challenging. Additionally, variation in equivariant geometric representations influences the extrapolation behavior of most MLIPs. The transferability of these neural networks has been developed with protein dynamics sampling in mind³¹ but still for all the reasons above the solution to longer MD simulation is not found yet. Extra challenges can be attributed relating to data quality, model interpretability, and regulatory considerations³² also their stability and applicability in capturing nonlocal charge transfer.³³ The final goal of this scientific field is of course to produce a universal neural network potential for material research and has been proposed³⁴ but its stability and accuracy, even promising remains to be thoroughly investigated.

In conclusion, the primary reasons machine learning interatomic potentials pose a problem in longer molecular simulations are their instability and accuracy limitations over extended timescales. Despite these challenges, ML techniques have been refined and applied to various stages of drug discovery, with a growing focus on clinical trial design and analysis.³⁵ These concerns underscore the need for further research and development to address the challenges and ensure reliability and effectiveness.

Using the developed machine learning, interatomic potential has been shown to accurately calculate elastic constants and melting temperature for various key molecules beyond sildenafil. Since the potential is validated from the standpoint of physics it could enable researchers to predict how subtle modifications in molecular structure influence the pharmacokinetic and pharmacodynamic properties of drugs. By understanding interaction strength and stability, new analogues with greater effectiveness and reduced side effects can be designed. One example of pharmaceutical compound design application could be the treatment of pulmonary hypertension in infants.³⁶ It's really challenging to create a sildenafil dosing plan for infants or children. The reason for this is that newborns have a different pharmacokinetic profile compared to adults and we already established potentials like the one developed could help predict subtle structural modification of molecules used in drugs.

Nanotechnological strategies, such as nanoparticle-based³⁷ delivery systems, can greatly benefit from our model's predictions. Optimizing the surface of nanoparticles in order to enhance loading capacity and release profile of sildenafil can be achieved with molecular dynamics interactions studies or stability tests.³⁸ Possible nanotechnological strategies could be biodegradable nano-in-micro dry powder sildenafil formulations³⁹ or the use of nano encapsulated sildenafil⁴⁰ for pulmonary hypertension treatment. The development of biodegradable nanoparticle platforms can be advanced by utilizing interatomic potentials in molecular dynamics simulations to analyze the interactions between sildenafil molecules and other formulation components.

The general map of this project consists of various following three stages:

1. Creation of a Machine Learning Interatomic Potential.

 a. Infrastructure and software requirement

 b. Finding the appropriate DFT dataset

 c. Fine tuning the dataset

 d. Developing molecular dynamics tests for various molecules

 e. Comparing physical properties, elastic constants and melting temperature.

2. Validation of the model in silico.

3. Validation of the model in vitro.

The first stage has been completed, and we have successfully developed the potential and conducted preliminary tests from a physics standpoint. To further validate our model's accuracy, there are plans to simulate the binding of sildenafil analogues to PDE5 inhibitors and compare these predictions with experimental binding affinity data. This future work will enable a direct comparison between in vitro and in silico results, which will be presented as a standalone publication.

Methods-computational details

The primary objective of this project is to develop an interatomic potential for organic compounds commonly employed in the pharmaceutical industry. The goal is to achieve accuracy comparable to density functional theory (DFT) while maintaining a reasonable simulation time frame. Our choice of molecular dynamics software is LAMMPS⁴¹ due to its versatility, scalability, active community support, and open-source nature. To train a compatible interatomic potential in LAMMPS, we utilize the Neural Equivariant Interatomic Potential (NequIP). This framework, originally introduced by Musaelian A. et al. in their recent publication,⁴² implements a subcategory of MLIPs based on atom-centered message-passing neural networks (MPNNs) with a strong track record of promising results.^43,44 MPNNs are specialized neural networks designed for graph-structured data, where atoms and their connections form a graph. They facilitate the exchange of information between neighboring atoms, allowing the network to capture complex relationships and structural properties within the material.

NequIP's equivariance ensures that it respects the inherent symmetries and transformations within the physical system it models. In the context of E(3)-equivariant MLIP, this means that the model's predictions align with the symmetries and transformations present in three-dimensional space. Simply put, equivariance signifies that when a molecule undergoes rotational changes, the corresponding force vectors rotate accordingly, a key feature enabled by NequIP's E(3)-equivariant convolutions. An outstanding characteristic of NequIP is its exceptional performance, outperforming existing methods while requiring significantly less training data. This underscores the ability of deep neural networks to operate effectively without the need for extensive training datasets. NequIP utilizes relative position vectors combined with higher-order geometric tensors as features and descriptors, ensuring the model's consistency even under rotational transformations. Convolutional operations are performed within a defined cutoff distance, enhancing the precision of the analysis.

This novel approach excels in terms of accuracy across diverse systems, especially when compared to traditional ML-IP methods. Importantly, NequIP's data efficiency allows for effective utilization of limited datasets with minimal reference calculations, simultaneously competing with kernel-based methods. The E(3)-equivariant architecture underpinning NequIP substantially enhances its performance by accurately representing tensor properties and symmetry operations, maintaining transformational consistency even as coordinates change.

The “Solvated Protein Fragments” dataset⁴⁵ probes many-body intermolecular interactions between “protein fragments” and water molecules, which are important for the description of many biologically relevant condensed phase systems. According to creators⁴⁶ the dataset encompasses interactions between “protein fragments” and water molecules, a key aspect when simulating protein-ligand complexes in computational chemistry. The term ‘protein fragments’ here typically refers to portions of proteins or peptides that can be artificially generated from the full amino acid sequence. This approach is commonly used for studying interactions involving smaller segments of biomolecules, which would include both protein parts and potential ligands such as sildenafil in drug-target studies which actually was the main target molecule of this study. Finally, by considering all possible charge states due to protonation and deprotonation (especially for carboxylic acids and amines), the dataset ensures that it captures different ionic forms of molecules which are essential when simulating pharmacologically active compounds, as these can significantly impact their interaction with proteins.

In total, the dataset provides reference energies, forces, and dipole moments for 2 731 180 structures. The goal from the beginning was to be competitive in accuracy with more computationally heavy methods the choice of using the whole protein fragment dataset was out of the question. There were three different sub-datasets extracted from this original one. The first one only containing structures with all the C, N, H, O, S elements with approximate size 260 mb. This would allow for a preliminary exploration of the protein fragments and their interactions. This initial training set was used only as a way of validating the feasibility of the project producing accurate results but not adequate enough for the scope of this work. The second sub-dataset improved accuracy by adding to the database the two extra types of “building blocks” for molecules, hydroxyl (OH) and methylidyne moieties (CH), increasing the size to 627mb containing 364 935 different molecules. This data set produced a potential sufficiently accurate in lattice constant calculation but insufficient of describing the elastic constants of iso-sildenafil. Finally, the last modification on the dataset is implemented by adding the carbonyl (CO) related structures that can be included in available molecules reaching 1gb in size and 721 662 different molecules. These additions likely expanded the range of chemical environments and interactions that the dataset could represent. These groups are common in organic molecules and would be important for modeling a wide range of molecular interactions.

Eventually the best model was trained with a total amount of 721 662 structures, split into 300 000 for training and 10 000 for validation. The dataset was re-shuffled after each training epoch. We use three layers, 128 features for both even and odd irreps and a 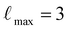. The 2-body latent MLP consists of four hidden layers of dimensions [128, 256, 512, 1024], using SiLU nonlinearities on the outputs of the hidden layers. All four MLPs were initialized according to a uniform distribution of unit variance. A radial cutoff of 4.5 Å was used on the training process of the potential.

Each modification seems to be a step towards creating a more comprehensive and accurate dataset for the project's needs, particularly for modeling the behavior of complex molecules like iso-sildenafil and sildenafil. The other compounds (ibuprofen, c – mebendazole, aspirin and urea) were used as extra validation compounds, in an effort to broaden the spectrum of possible interactions the potential can capture and validate whether the previous modifications were actually impactful. The model has been tested on a diverse set of compounds, including sildenafil, iso-sildenafil, aspirin, ibuprofen, mebendazole, and urea. It was able to accurately predict their properties, suggesting that our dataset and model cover a significant portion of the conformational space and diversity of molecular interactions. Furthermore, our validation process, which included Allegro's own evaluation mechanism and LAMMPS molecular dynamics simulations, demonstrated the reliability and applicability of the developed interatomic potentials. This further supports the conclusion that our dataset and model cover, not completely but a significant portion of the conformational space and diversity of molecular interactions for sildenafil and related molecules. Although no different spatial arrangements of the molecules have been tested, there is a strong indication that our dataset and model cover a significant portion of the conformational space for these molecules. It should be acknowledged that further research could be done to ensure even broader coverage.

The flowchart in Fig. 1 illustrates in a detailed way the iterative process of training and testing machine learning interatomic potential. Initially, an original dataset is selected, and sub-datasets are created based on specific atoms or molecules. These sub-datasets undergo training, and the resulting models are deployed as potentials. The subsequent steps involve evaluating the stability of the system through potential energy calculations for the basic diatomic pairs (H₂, S₂, N₂, O₂), followed by relaxation, specifically iso-sildenafil crystal relaxation and check for stability. This is where the first checking step happens. If the system is deemed stable exhibiting sufficient accuracy on the calculation of the lattice constants, the potential is further tested for elastic constants for all the previously mentioned test pharmaceutical compounds. This is where the second checking step takes place. If the obtained values are realistic, the process proceeds to calculate the melting temperature using iso-sildenafil as a model crystal. If the system calculated a melting temperature with realistic value, a functional interatomic potential is achieved.

Fig. 1 Flowchart describing the process followed to train and evaluate the potential.

All training process was performed with the Allegro code available from Materials Intelligence Group, Harvard University on the projects GitHub repository https://github.com/mir-group/allegro at the time available under release v.0.2.0. (currently unavailable). Allegro is not a standalone software but a an extension package for the NequIP code available at https://github.com/mir-group/nequip, the used version is a user forked version https://github.com/Hongyu-yu/nequip of the original code, on the para_stress branch, with v.0.6.0., under the git commit 6ca00ac. Also, for the training PyTorch was used with version 1.11.0+cu113 (cuda enabled), and Python with v.3.9.18.

The crystal lattice relaxations and elastic constant calculations and melting temperature calculation were run with the LAMMPS code available at https://github.com/lammps/lammps.git under the git commit 6a8ca34 modified pre compilation with the user forked pair_allegro stress branch code available at https://github.com/Hongyu-yu/pair_allegro, git commit b20f966.

The elastic constant calculation was performed using one of the example scripts in LAMMPS repository available at https://github.com/lammps/lammps/blob/develop/examples/ELASTIC/in.elastic in the development branch, under the git commit ae2a7e2.

The Density Functional Theory (DFT) calculations we perform for the test compound (iso)sildenafil were done using VASP 6.1.1^47,48 and the PBE GGA (PAW_PBE S 06Sep2000) approximation for the exchange-correlation energy. The standard PAW VASP pseudopotentials were used. The process required three different steps. The first relaxation of the sample with ISIF = 3. With ISIF = 3 there is calculation of the forces and stress tensor. Also, all the possible degrees of freedom that are allowed to change during the relaxation process (ionic positions, cell volume, cell shape) are activated and used. The second relaxation of the sample with ISIF = 1. Relaxation using forces and only the trace of the stress tensor and the degrees of freedom that change are only the positions of the ions. Finally, the stress calculation with ISIF = 3 and IBRION = 6. The cutoff energy of the plane-wave basis was 500 eV. The partial occupancies were treated using the Gaussian smearing (ISMEAR = 0) with a width of 0.05 eV. One k point was used at gamma and the elastic constants were determined with 0.1 Å deformation.

Finally, Ovito basic 3.8.5 was used to visualize the molecules.

Results and discussion

Checking the performance of the interatomic potential produced is relaxing for only a single timestep the basic diatomic molecules of the atoms that take part in the most usual pharmaceutical compounds. These molecules are H₂, S₂, N₂, O₂ and on Fig. 2 its visible the expected graph of the “stereotypical” potential with the minimum energy dip. The naturally occurring bond length is that with minimum energy and appears for all four molecules, approximately at the minimum. These diatomic bonds lengths reported in the bibliography are O₂ = 1.208 Å, N₂ = 1.098 Å, S₂ = 1.889 Å, H₂ = 0.741 Å⁴⁹ and compared to the minimum values of the plot (O₂ = 1.069 Å, N₂ = 1.129 Å, S₂ = 2.159 Å, H₂ = 0.759 Å) seem comparable.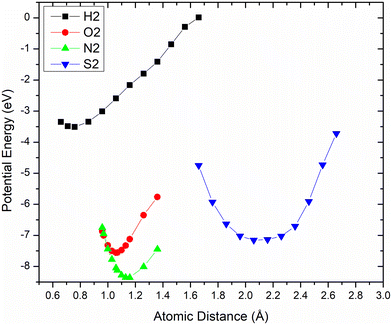

Fig. 2 Potential Energy scatter plots for diatomic hydrogen (black), nitrogen (green), oxygen (red), sulfur (blue).

The potential is evaluated through a series of tests, compared with results from DFT calculation and experimental determination of certain values like melting temperature, elastic constants, and potential energy. A series of test molecules have been selected to assess the accuracy and performance of our methodology, in line with the training dataset derived from the “Solvated Protein Fragments” dataset. These test molecules, namely aspirin, (iso)sildenafil, mebendazole, urea, and ibuprofen, are given in Fig. 3 and represent a diverse set of chemical compounds with a range of properties and intermolecular interactions encompassing H, C, N, O, and S elements. Our objective is to thoroughly evaluate the capabilities of our interatomic potential for chemical compounds containing these specific molecules. The first step before proceeding with calculating anything is always to minimize the potential energy of all molecules.

Fig. 3 (a) The unit cell of aspirin, (b) of ibuprofen, (c) of iso-sildenafil, (d) of c – mebendazole (e) of sildenafil citrate and (f) of urea. The atoms are colored as follows: brown = carbon, red = oxygen, hydrogen = white, yellow = sulfur, blue = nitrogen.

However, if the elastic constants are not realistic, indicating a potential instability, the system goes through a refinement process. It returns to the original dataset and selects a new sub-dataset with different criteria, initiating a cycle of improvement. This iterative approach ensures that the machine learning model is exposed to diverse molecular configurations and properties, enhancing its adaptability and performance.

The inclusion of multiple sub-datasets with varying sizes and molecular compositions underscores the refinement aspect, demonstrating a systematic strategy for addressing potential limitations and inaccuracies in earlier stages. Overall, the flowchart represents a comprehensive and dynamic methodology for developing accurate and versatile machine learning interatomic potentials.

The first pharmaceutical substance used is acetylsalicylic acid (ASA) known as Aspirin, a nonsteroidal anti-inflammatory drug used to reduce pain, fever, and/or inflammation, and as an anticoagulant. Its chemical formula is C₉H₈O₄. Acetylsalicylic acid is a member of the class of benzoic acid derivatives that is salicylic acid in which the hydrogen that is attached to the phenolic hydroxyl group has been replaced by an acetoxy group. At room temperature, aspirin crystallizes in a monoclinic crystal structure (space group P21/c) with four formula units per unit cell [a = 1.1416 nm, b = 0.6598 nm, c = 1.1483 nm, and β = 95.60°].⁵⁰ The crystal structure used⁵¹ initially had [a = 1.1233 nm, b = 0.6544 nm, c = 1.231 nm, and β = 95.89°] and after potential energy minimization [a = 1.116 nm, b = 0.734 nm, c = 1.128 nm, and β = 95.89°].

The second substance used is (iso)sildenafil and its chemical formula is C₂₂H₃₀N₆O₄S. Sildenafil was the first API structure rationally developed utilizing computational drug-design protocols.

The crystal of sildenafil citrate adopts the orthorhombic system, space group Pbca (61) with unit cell parameters being [a = 24.002 Å, b = 10.9833 Å, c = 24.363 Å, α = β = γ = 90°, V = 6422.9 ų and Z = 8]⁵² and after potential energy minimization [a = 24.936 Å, b = 11.562 Å, c = 24.688 Å, α = β = γ = 90°, V = 7118.2 ų and Z = 8]. Iso-sildenafil is monoclinic, space group P21/n (14) with [a = 9.7550 Å, b = 7.6070 Å, c = 32.568 Å, β = 94.741°, V = 2408.5 ų and Z = 4]⁵³ and after potential energy minimization [a = 9.7550 Å, b = 7.6070 Å, c = 32.568 Å, β = 94.741°, V = 2408.5 ų and Z = 4]. Sildenafil is a common and effective treatment for erectile dysfunction, and since its formal approval for medical use in the public in 1998, continues to see millions of prescriptions written for it internationally. Sildenafil Molecular Weight is 474.6 g mol⁻¹.

The third substance we use is Ibuprofen is a monocarboxylic acid, that is propionic acid in which one of the hydrogens at position 2 is substituted by a 4-(2-methylpropyl) phenyl group. Its chemical formula is C₁₃H₁₈O₂. It has a role as a non-steroidal anti-inflammatory drug, a non-narcotic analgesic, a cyclooxygenase 2 inhibitor, a cyclooxygenase 1 inhibitor, an antipyretic, a xenobiotic, an environmental contaminant, a radical scavenger, a drug allergen and a geroprotector. Ibuprofen crystallizes in monoclinic crystal structure, space group P21/c with cell dimensions being [a = 14.668 Å, b = 7.888 Å, c = 10.727 Å, and β = 99.437°]⁵⁴ and after potential energy minimization being [a = 14.979 Å, b = 8.220 Å, c = 10.54 Å, and β = 99.439°].

Furthermore, we used Urea and its formula is H₂NCONH₂. Urea has important uses as a fertilizer and feed supplement, as well as a starting material for the manufacture of plastics and drugs. Urea crystallizes in the tetragonal crystal group, P4̄2₁m (113) with cell dimensions being [a = 5.589 Å, b = 5.589 Å, c = 4.694 Å, α = β = γ = 90°]⁵⁵ and after potential energy minimization being [a = 5.968 Å, b = 5.968 Å, c = 4.973 Å, α = β = γ = 90°].

The final substance is Mebendazole C₁₆H₁₃N₃O₃ that is a broad-spectrum anthelmintic. Mebendazole (MBZ) presents three different polymorphs: A, B and C. Form C is more appropriate for handling drugs. Regarding the crystal structure of mebendazole form C, it crystallizes in a triclinic (P1̄) space group (2), with unit-cell parameters being [a = 5.1480 Å, b = 7.8779 Å, c = 17.907 Å, α = 82.425°, β = 82.743°, γ = 71.091°]⁵⁶ and after potential energy minimization being [a = 4.997 Å, b = 8.122 Å, c = 18.757 Å, α = 82.716°, β = 82.906°, γ = 71.549°].

There is a list of elastic constants that can be calculated to benchmark the performance using the algorithm provided by Sandia National Laboratories, Dr Aidan Thompson published in the official project GitHub repository and are displayed on Table 1. The elastic constants are calculated by our Allegro-trained potential, Dreiding force field⁵⁷ and by DFT calculations.

Table 1 Table containing the elastic constants and moduli

Constant	Sildenafil (DFT)	Sildenafil (Allegro)	Sildenafil (Dreiding)	Aspirin (DFT)	Aspirin (RUS)	Aspirin (Allegro)	Aspirin (Dreiding)	Ibuprofen (Allegro)	Mebendazole (Allegro)	Iso sildenafil (Allegro)	Iso sildenafil (DFT)	Urea (Allegro)
C11all	16.14	19.18	113.54	11.14	11.29	11.14	61.23	7.70	21.51	19.01	37.09	38.79
C22all	21.98	16.56	116.99	12.72	12.10	12.72	103.58	11.30	36.91	28.33	18.64	39.15
C33all	31.96	15.16	−72.15	9.36	10.67	9.36	87.14	8.00	37.56	31.09	38.68	46.69
C12all	27.38	16.58	66.41	9.94	7.65	9.94	54.43	5.15	6.40	8.24	17.42	31.69
C13all	27.87	16.11	68.03	5.77	4.57	5.77	67.88	5.70	17.30	10.29	20.72	10.75
C23all	11.30	−1.06	16.72	5.73	5.67	5.73	42.19	3.63	12.30	6.87	16.42	11.04
C44all	−0.90	8.98	25.16	0.37	3.38	0.37	13.66	2.33	11.54	10.72	6.2	7.63
C55all	−7.01	7.55	3.57	2.84	2.74	2.84	20.27	1.55	13.38	11.85	6.57	7.61
C66all	7.63	0.66	30.90	7.69	4.52	7.69	23.37	0.37	8.30	11.45	9.69	28.52
C14all	0.00	−0.17	1.68	0.00	−	0.00	16.90	0.01	4.82	0.01	0	0.07
C15all	0.00	−0.17	7.32	4.77	−0.17	4.77	−3.97	−3.11	−5.34	8.18	0	0.02
C16all	0.00	0.06	−7.24	0.00	—	0.00	−28.41	0.11	−3.93	−0.01	4.74	0.02
C24all	0.00	−1.67	6.87	0.00	—	0.00	16.76	0.01	−0.69	−0.01	0	0.06
C25all	0.00	−0.16	9.74	2.60	0.60	2.60	−3.07	−1.54	−2.70	4.46	0	0.01
C26all	0.00	0.16	−2.45	0.00	—	0.00	−35.54	0.05	−6.04	−0.01	5.65	0.02
C34all	0.00	−1.02	6.81	0.01	—	0.01	2.42	−0.02	2.36	−0.02	0	−0.07
C35all	0.00	−0.08	12.98	4.10	−0.25	4.10	−22.89	0.14	−11.25	7.72	0	−0.10
C36all	0.00	0.02	8.57	0.00	—	0.00	−24.78	−0.05	0.59	−0.02	5.6	0.06
C45all	0.00	0.20	4.47	0.00	—	0.00	−5.78	0.03	−4.39	0.00	1.68	0.00
C46all	0.00	0.04	2.96	0.18	0.32	0.18	−11.12	−2.30	−3.33	3.65	0	0.00
C56all	0.00	0.00	−5.66	0.00	—	0.00	9.14	0.13	−0.27	0.01	0	−0.06
Bulk modulus	—	12.68	51.19	8.46	—	8.46	64.54	6.22	18.67	14.36	—	25.73
Shear modulus 1	—	5.73	19.88	3.63	—	3.63	19.10	1.41	11.07	11.34	—	14.59
Shear modulus 2	—	3.21	1.20	1.96	—	1.96	14.58	2.09	10.00	8.84	—	11.86
Poisson ratio	—	0.38	0.49	0.39	—	0.39	0.395	0.35	0.27	0.24	—	0.30

---

Shear modulus is extracted using the elasticity matrix D, defined in terms of bulk modulus K and shear modulus G.

The provided LAMMPS algorithm for elastic constants calculation calculates shear modulus with two different formulas. One using the average value:

And the second one extracting it from more complex terms on top left corner of the matrix:

Johannes D. Bauer et al.⁵⁸ determined elastic properties of acetylsalicylic acid crystals(aspirin) by Resonant Ultrasound Spectroscopy (RUS), using a home-built device with sample fixed between two ultrasound transducers with one of the transducers acting as an ultrasound generator, and the other one as an ultra-sound detector. Comparison of only the elastic constant provided by them, can be seen on the graph below Fig. 4(a) and found in acceptable agreement. In Fig. 4(b) and (c) the comparison of the calculated elastic constants by MD using our MLIP for iso sildenafil and sildenafil citrate respectively versus the calculated elastic constant with DFT(current study by VASP) is presented. It should be noticed that the elastic constants are in agreement with DFT, especially for the case of iso sildenafil.

Fig. 4 (a) Comparison of the calculated elastic constants for aspirin with MD using the 1gb trained potential vs. the experimentally calculated using RUS. (b) Comparison of the calculated elastic constants for iso-sildenafil with MD using the 1gb trained potential vs. the calculated elastic constant with DFT. (c) Comparison of the calculated elastic constants for sildenafil citrate with MD using the 1gb trained potential vs. the calculated elastic constant with DFT.

In J. F. Nye book Physical Properties of Crystals: Their Representation by Tensors and Matrices⁵⁹ there is a reference table for all the crystal systems. For the monoclinic (aspirin) it is indeed that the constants C14, C16, C24, C26, C34, C36, C45, C56 are zero, the same zero values that are reported in the experimental Resonant Ultrasound Spectroscopy and the MD values in Table 1.

Based on the provided data, comparison with DFT and experimental data for Aspirin, Allegro appears to be the superior model for predicting the mechanical properties of both sildenafil and aspirin. An extra validation for the adequate behavior of the trained potential are the cell parameters after the potential energy minimization that are given in Table 2.

Table 2 Table containing cell parameters for sildenafil and aspirin

	a	b	c
Sildenafil
Bibliographic	24.002	10.983	24.363
Allegro	24.936	11.562	24.688
Dreiding	26.097	11.942	26.492
Aspirin
Bibliographic	11.416	6.598	11.483
Allegro	11.162	7.340	11.284
Dreiding	11.784	6.865	11.844

---

The melting temperature can be approximated from the scatter plot graph Potential energy/temperature. As long as the increase of potential energy in respect to temperature is linear this is an indication of crystalline structure. The temperature at which this linear behavior deviates significantly, showing a sharp energy jump towards higher energy, is an indication that the crystalline material has melted, which is also confirmed by the visualization of the atomic model. Four distinct melting simulations were performed and the graphs of the potential energy versus the temperature are presented in Fig. 5 According to Petr Melnikov et al.⁶⁰ the sildenafil citrate melting point is 462.55 K (189.4 °C) and the sildenafil base 525.05 K (251.9 °C). The results of the analysis of the simulations are given in Table 3 and average melting temperature is 500.75 ± 30 K (227.6 °C).

Fig. 5 Melting molecular dynamics simulations for iso sildenafil using the Allegro trained potential.

Table 3 Melting point of iso-sildenafil calculated by MD simulations

Case	Melting temp
Melting sim 1	516
Melting sim 2	480
Melting sim 3	497
Melting sim 4	510
Average	500.75 ± 30 K

---

Conclusions

This article presents the development of functional interatomic potentials through the successful application of the Allegro machine learning algorithm. The study leverages the power of high-performance GPUs and a carefully chosen training dataset, the “Solvated Protein Fragments”, containing nearly 2.7 million Density Functional Theory calculations. The results showcase the exceptional performance of the Allegro-trained potentials, demonstrating a significant leap in computational efficiency compared to the computationally intensive DFT method.

The methodology employed in this study, using the Neural Equivariant Interatomic Potential (NequIP) framework based on atom-centered message-passing neural networks, proves to be effective in achieving accuracy comparable to density functional theory while maintaining a feasible simulation time frame. NequIP's E(3)-equivariant architecture ensures a consistent representation of tensor properties and symmetry operations, contributing to its outstanding performance with minimal training data. The systematic approach to dataset selection and refinement, illustrated in the flowchart, emphasizes the adaptability and performance enhancement of the machine learning model. The inclusion of multiple sub-datasets with varying sizes and molecular compositions addresses potential limitations and inaccuracies, resulting in a comprehensive and dynamic methodology for developing accurate and versatile machine learning interatomic potentials. The extensive validation process, including comparisons with DFT calculations, experimental measurements of melting temperature, elastic constants, and potential energy, demonstrates the reliability and applicability of the developed interatomic potentials. The tested pharmaceutical molecules, sildenafil citrate, iso-sildenafil, aspirin, mebendazole, urea, and ibuprofen, represent a diverse set of compounds, and the results showcase the model's capability to accurately describe their properties and interactions even in complex molecules. The success of this machine learning approach underscores its potential to revolutionize computational condensed matter physics, particularly in the field of pharmaceutical research. The ability to explore larger molecular structures with increased efficiency opens new possibilities for studying complex materials, chemical reactions, and biological systems. Overall, this research marks a significant step towards overcoming the historical trade-off between simulation time and accuracy, paving the way for future advancements in the application of machine learning interatomic potentials in various scientific domains.

Data availability

The DFT sub-datasets utilized in this study, comprising different atom types, have been thoughtfully compiled to support the rigorous training and testing of our machine learning interatomic potential. In the interest of transparency and collaboration, we have deposited our datasets in a dedicated repository. Researchers interested in exploring the nuances of interatomic potentials, can freely access our datasets for further investigation. The modified dataset is openly available⁶¹ providing a straightforward resource for advancing the understanding and application of machine learning interatomic potentials across various molecular systems used by the pharmaceutics industry. Also, the final deployed interatomic potential is also openly available.⁶² The final potential is available for download through zenodo and the link to download is https://doi.org/10.5281/ZENODO.10465906.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been co-financed by the European Union and Greek National Funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call RESEARCH—CREATE—INNOVATE (project code: T2EΔK-00540). This article is based upon work from COST action CA22154 – Data-Driven Applications towards the Engineering of Functional Materials: an Open Network (DAEMON), supported by COST (European Cooperation in Science and Technology). The machine learning process and the molecular dynamics simulations were executed in the in-house HPC owned by Center for Computation and Technology in Louisiana State University using the latest Nvidia A100 GPU. Furthermore, this work was supported by computational time granted from the Greek Research & Technology Network (GRNET) in the “ARIS” National HPC infrastructure under the project NOUS (pr015006) and the Aristotle University of Thessaloniki (AUTh) HPC Infrastructure and Resources. The authors are grateful to Dr G. Nikoulis for valuable discussions and support.

References

1. K. H. Nam, Int. J. Mater. Sci., 2021, 22, 3761.
2. R. Petrenko and J. Meller, Encyclopedia of Life Sciences, 2010.
3. J. Šponer, G. Bussi, M. Krepl, P. Banáš, S. Bottaro, R. A. Cunha, A. Gil-Ley, G. Pinamonti, S. Poblete, P. Jurečka, N. G. Walter and M. Otyepka, Chem. Rev., 2018, 118, 4177–4338.
4. M. P. Allen and D. J. Tildesley, Computer simulation of liquids, 2017.
5. H. Tian, D. Xie, Y. Yang, T.-L. Ren, G. Zhang, Y.-F. Wang, C.-J. Zhou, P.-G. Peng, L.-G. Wang and L.-T. Liu, Sci. Rep., 2012, 2 DOI:10.1038/srep00523.
6. M. S. Bødker, S. S. Sørensen, J. C. Mauro and M. M. Smedskjaer, Front. Mater., 2019, 6 DOI:10.3389/fmats.2019.00175.
7. G. J. Ackland, Compr. Nucl. Mater., 2012, 267–291.
8. A. M. Stoneham and J. H. Harding, Annu. Rev. Phys. Chem., 1986, 37, 53–80.
9. R. D. Levine, Molecular reaction Dynamics, 2005.
10. J. Behler, J. Chem. Phys., 2016, 145, 170901.
11. L. Pastewka, M. Mrovec, M. Moseler and P. Gumbsch, MRS Bull., 2012, 37, 493–503.
12. K. Nordlund and S. L. Dudarev, C. R. Phys., 2008, 9, 343–352.
13. S. L. Dudarev and P. M. Derlet, J. Phys.: Condens. Matter, 2007, 19, 239001.
14. T. S. Mahadevan and S. H. Garofalini, J. Phys. Chem. B, 2007, 111, 8919–8927.
15. C. Liu, J.-P. Piquemal and P. Ren, J. Chem. Theory Comput., 2019, 15, 4122–4139.
16. J. Kahlen, L. Salimi, M. Sulpizi, C. Peter and D. Donadio, J. Phys. Chem. B, 2014, 118, 3960–3972.
17. P. Wang, Y. Shao, H. Wang and W. Yang, Extreme Mech. Lett., 2018, 24, 1–5.
18. T. Kocabaş, M. Keçeli, Á. Vázquez-Mayagoitia and C. Sevik, Nanoscale, 2023, 15, 8772–8780.
19. M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, M. Kudlur, J. Levenberg, R. Monga, S. Moore, D. G. Murray, B. Steiner, P. Tucker, V. Vasudevan, P. Warden, M. Wicke, Y. Yu and X. Zheng, arxiv, 2016, arXiv:1605.08695 [cs.DC],  DOI:10.48550/arXiv.1605.08695.
20. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
21. A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, J. Comput. Phys., 2015, 285, 316–330.
22. Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, J. Phys. Chem. A, 2020, 124, 731–745.
23. V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765.
24. T. Mueller, A. Hernandez and C. Wang, J. Chem. Phys., 2020, 152, 050902.
25. K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326–2331.
26. I. Batatia, S. Batzner, D. P. Kovács, A. Musaelian, G. N. C. Simm, R. Drautz, C. Ortner, B. Kozinsky and G. Csányi, arXiv, 2022, preprint, arXiv:2205.06643,  DOI:10.48550/arXiv.2205.06643.
27. A. Di Costanzo and R. Angelico, Molecules, 2019, 24, 2155.
28. S. S. Kesharwani, V. Jain, S. Dey, S. Sharma, P. Mallya and V. A. Kumar, J. Drug Delivery Sci. Technol., 2020, 60, 102021.
29. S. Stocker, J. Gasteiger, F. Becker, S. Günnemann and J. T. Margraf, Mach. Learn.: Sci. Technol., 2022, 3, 045010.
30. J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203.
31. M. M. Sultan, H. K. Wayment-Steele and V. S. Pande, J. Chem. Theory Comput., 2018, 14, 1887–1894.
32. F. C. Udegbe, O. R. Ebulue, C. C. Ebulue and C. S. Ekesiobi, Comput. Sci. IT Res. J., 2024, 5, 892–902.
33. T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Acc. Chem. Res., 2021, 54, 808–817.
34. S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, T. Watanabe, Y. Yayama, H. Iriguchi, Y. Asano, T. Onodera, T. Ishii, T. Kudo, H. Ono, R. Sawada, R. Ishitani, M. Ong, T. Yamaguchi, T. Kataoka, A. Hayashi, N. Charoenphakdee and T. Ibuka, Nat. Commun., 2022, 13, 2991.
35. W. Khalid, M. Y. Khalid, M. Hena, A. Sarwar and S. Iqbal, Pharm. Commun., 2023, 2, 63–69.
36. L. Simonca and R. Tulloh, Children, 2017, 4, 60.
37. S. A. A. Rizvi and A. M. Saleh, Saudi Pharm. J., 2018, 26, 64–70.
38. A. Kowalczuk, R. Trzcinska, B. Trzebicka, A. H. E. Müller, A. Dworak and C. B. Tsvetanov, Prog. Polym. Sci., 2014, 39, 43–86.
39. R. B. Restani, R. F. Pires, P. V. Baptista, A. R. Fernandes, T. Casimiro, V. D. B. Bonifácio and A. Aguiar-Ricardo, Part. Part. Syst. Charact., 2020, 37, 1900447.
40. M. Beck-Broichsitter, T. Schmehl, T. Gessler, W. Seeger and T. Kissel, J. Controlled Release, 2012, 157, 469–477.
41. S. Plimpton, A. Kohlmeyer, A. Thompson, S. Moore and R. Berger, LAMMPS Stable release 29 September 2021, Zenodo, 2021.
42. A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14, 579.
43. S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453.
44. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001.
45. U. O. Thorsten and M. MarkusSolvated protein fragments, https://zenodo.org/records/2605372, (accessed August 29, 2024).
46. O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693.
47. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
48. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
49. NIST Computational Chemistry Comparison and Benchmark Database , NIST Standard Reference Database Number 101, Release 22, May 2022, ed. R. D. Johnson III.
50. C. Hauf, A.-A. Hernandez Salvador, M. Holtz, M. Woerner and T. Elsaesser, Struct. Dyn., 2019, 6, 014503.
51. National Center for Biotechnology Information , PubChem Compound Summary for CID 2244, Aspirin, 2024, https://pubchem.ncbi.nlm.nih.gov/compound/Aspirin (accessed August 29, 2024).
52. A. Ouranidis, A. Tsiaxerli, E. Vardaka, C. K. Markopoulou, C. K. Zacharis, I. Nicolaou, D. Hatzichristou, A.-B. Haidich, N. Kostomitsopoulos and K. Kachrimanis, Pharmaceuticals, 2021, 14, 365.
53. M. M. El-Abadelah, S. S. Sabri, M. A. Khanfar, W. Voelter and C. Maichle-Moessmer, 2000, CCDC 135041: Experimental Crystal Structure Determination, 2000,  DOI:10.5517/cc4jj5b.
54. K. H. Stone, S. H. Lapidus and P. W. Stephens, J. Appl. Crystallogr., 2009, 42, 385–391.
55. V. Zavodnik, A. Stash, V. Tsirelson, R. de Vries and D. Feil, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 45–54.
56. F. T. Martins, P. P. Neves, J. Ellena, G. E. Camí, E. V. Brusau and G. E. Narda, J. Pharm. Sci., 2009, 98, 2336–2344.
57. C. Patiño, L. Alzate-Vargas, C. Li, B. Haley and A. Strachan, LAMMPS Data-File Generator, nanoHUB, 2021.
58. J. D. Bauer, E. Haussühl, B. Winkler, D. Arbeck, V. Milman and S. Robertson, Cryst. Growth Des., 2010, 10, 3132–3140.
59. J. F. Nye, Physical properties of crystals: Their Representation by Tensors and Matrices, Oxford University Press, 1985.
60. P. Melnikov, P. P. Corbi, A. Cuin, M. Cavicchioli and W. R. Guimarães, J. Pharm. Sci., 2003, 92, 2140–2143.
61. E. Nikidis, N. Kyriakopoulos, R. Tohid, K. Kachrimanis and J. Kioseoglou, Modified Solvated Protein Fragments Dataset, https://zenodo.org/records/10465952, (accessed August 29, 2024).
62. E. Nikidis, N. Kyriakopoulos, R. Tohid, K. Kachrimanis and J. Kioseoglou, Large-Scale Interatomic Potentials (Allegro-LAMMPS Compatible), https://zenodo.org/records/10465907, (accessed August 29, 2024).

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr00929k

---