How substituents tune quantum interference in meta-OPE3 molecular junctions to control thermoelectric transport

Abstract

Quantum interference (QI) can strongly affect electric and thermoelectric properties of molecular junctions (MJs). So far, however, a limited number of experimental studies have explored the influence of QI on thermoelectric transport in MJs. To address this open point, we synthesized derivatives of meta-OPE3 with an electron-withdrawing nitro (–NO₂) substituent or an electron-donating N,N-dimethyl amine (–NMe₂) substituent, attached at two different positions of the central phenylene ring, and systematically studied the electrical conductance and thermopower of the corresponding gold–molecule–gold junctions. We show that (i) the electrical conductance of MJs depends weakly on the polarity of the substituents but strongly on the substitution position and (ii) MJs with the N,N-dimethyl amine group feature a higher thermopower than MJs with the nitro group. We also present calculations based on first principles, which explain these trends and show that the transport properties are highly sensitive to microscopic details in junctions, exhibiting destructive QI features.

---

Introduction

The ability to manipulate charge and energy transport through a single molecule is key to the development of novel molecular materials and devices for highly efficient energy conversion and molecule-based electronics and sensors.^1–3 Towards this goal, researchers have developed various experimental tools and employed them to probe electric,^4–6 thermoelectric^7–9 and thermal^10,11 transport properties of single-molecule junctions (SMJs). In the last decade, quantum interference (QI) has emerged as a promising route to control electron flow through SMJs. In general, QI arises when the de Broglie waves of electrons propagate across a molecule through multiple pathways instead of one pathway, leading to either constructive or destructive electron transmission patterns.^12,13 For example, destructive QI, i.e. reduced transmission through a molecular junction (MJ), has been experimentally observed in both π-conjugated and σ-bonded molecular systems, and such materials show suppressed electrical conductance and increased thermopower.^14–19

To gain deeper insight into QI phenomena, recent studies have explored the impact of intramolecular structural variations on the destructive or constructive interference in SMJs which includes geometrical isomerism,^20,21 heteroatom substitution within the molecular backbones,^{17,18,22–25} different anchoring groups to the contacted electrodes instead of traditional sulfur containing ones,^21,26 addition of different repeating molecular units into the backbone²⁷ such as oligo(phenyleneethynylene)s,²⁸ distinct molecular bridging schemes,²⁹ as well as design of organic radial molecules.³⁰ In addition, it has been theoretically predicted that introducing different substituents to a current-carrying molecular backbone could tune the destructive QI.^31,32 In this context it is interesting to note that meta-OPE3 molecules (see Fig. 1a) can transport electrons due to the fully π-conjugated rigid rod-like structures and the small energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of ∼3 eV,^33,34 and they are promising candidates for achieving destructive QI in SMJs.^35,36 In fact, recently Miao et al.¹⁶ showed that when compared with para-OPE3 junctions (Fig. 1a), meta-OPE3 junctions feature a lower conductance yet higher thermopower, which was attributed to strong destructive QI effects. Furthermore, Jiang et al.³⁷ demonstrated that meta-OPE3 with a methoxide (–OMe) group attached to the central phenylene ring at different positions resulted in a dramatic change in the degree of destructive QI, suggesting that the attachment of electron-donating (ED) substituents at different positions of the central core is an effective way to tune destructive QI at room temperature. Zotti et al.³⁸ employed the concepts of bond-resonance and induction to explain how substituents in meta-OPE3 derivatives influence QI and charge transport. However, a key question – “How can the thermoelectric properties of SMJs be controlled by tuning QI effects via the electronic properties and the position of the substituents?” – has not yet been fully explored experimentally.

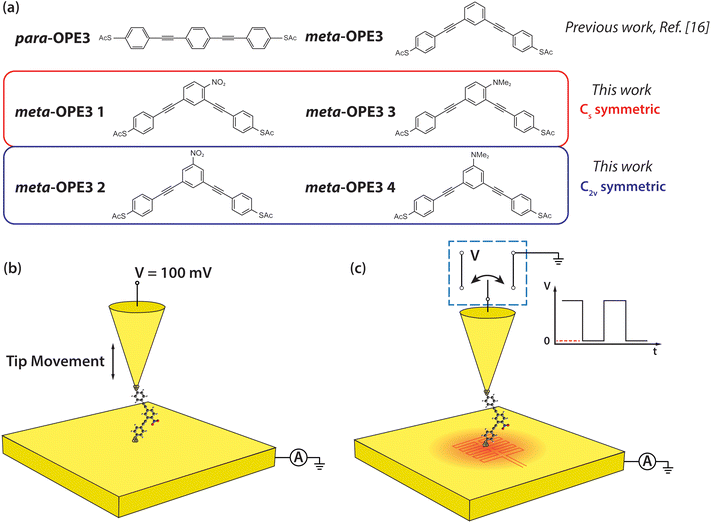Fig. 1 Schematic of the molecules and of the experimental setup. (a) Structures of para-OPE3 and meta-OPE3 reference molecules, investigated in previous work,¹⁶ and meta-OPE3 derivatives, studied newly in this work. (b) Schematic of the experimental approach for probing the electrical conductance of SMJs. A 100 mV DC bias is applied to the Au tip, while the Au substrate is grounded during the measurements. (c) Schematic of the experimental approach employed for probing thermoelectric properties of SMJs. The Au substrate was heated to the desired temperature (∼5.7 K, ∼9 K, ∼11.4 K) using an attached thin film resistive heater. While recording the current flowing between tip and substrate, the voltage applied to the Au tip was modulated as a square wave, periodically switching between 100 mV and 0 V.

In this study, we aim to provide insight into the important question stated above by investigating both experimentally and theoretically the electrical conductance and thermopower of a series of meta-OPE3 based molecules (see Fig. 1a). Specifically, we employ two functional groups with opposite polarities, the electron-withdrawing (EW) nitro (–NO₂) substituent and the ED N,N-dimethyl amine (–NMe₂) substituent, attached on the central phenylene ring at two different positions (see the C_2v and C_s symmetric configurations shown in Fig. 1a). All four molecules were terminated by the thioacetate (–SAc) protecting group to enable the formation of Au–S covalent linkages through in situ deprotection of the sulfur atom when preparing the monolayer of these molecules on a clean template-stripped Au substrate.^3,29,39

Experimental

Chemical synthesis

To elucidate the influence of both the position of a substituent at the central phenylene unit and its electronic nature on the electrical conductance and the thermopower, four different derivatives of meta-OPE3 were synthesized (Fig. 1a): meta-OPE3 1 is C_s symmetric and contains a EW NO₂ substituent, meta-OPE3 2 is C_2v symmetric and contains a EW NO₂ substituent, meta-OPE3 3 is C_s symmetric and contains a ED NMe₂ substituent, meta-OPE3 4 is C_2v symmetric and contains a ED NMe₂ substituent. The two-step synthesis of meta-OPE3 1–4 from readily available starting materials is shown in Fig. 2a. New and optimized reaction steps are discussed in the ESI† together with the full characterization of the target molecules and the corresponding intermediates.

Fig. 2 (a) Synthetic scheme for the four meta-OPE3 1–4 compounds used in this study. Molecular structure of (b) meta-OPE3 1 and (c) meta-OPE3 4, as determined by SC-XRD analysis, shown with anisotropic displacement ellipsoids at the 30% and 50% probability level, respectively. Color code: H, white; C, black; N, blue; O, red; S, yellow.

The first step is a Sonogashira coupling^40,41 between tert-butyl-S protected thiophenylacetylene (1) and respective substituted meta-diiodobenzene (2 to 5), yielding the corresponding t-butyl-S protected precursors 6 to 9. The tert-butyl group was chosen since in our hands the S-acetyl group, typically used in the attachment of the S-part of meta-OPE3 1–4 to the gold surface, did not survive the conditions of the Sonogashira coupling. After the coupling reaction, the tert-butyl group was exchanged for an acetyl group in one step, using an acylating reagent and TiCl₄ as Lewis acid promoter,⁴² giving meta-OPE3 1–4 in good to very good yields. The identity of all compounds was established by ¹H NMR, ¹³C NMR, and HRMS. The purity was proven by E.A.

X-diffraction (XRD) analysis

A single crystal of meta-OPE3 1 was obtained by diffusion of dichloromethane into a heptane solution of meta-OPE3 1, and the structure was solved in the space group P2(1)/c by XRD analysis (Fig. 2b). A single crystal of meta-OPE3 4 was obtained by the slow evaporation of meta-OPE3 4 in chloroform, and the crystal was solved in the triclinic space group P1̄ (Fig. 2c). Interestingly, the terminal phenyl group in one end of meta-OPE3 1 is almost coplanar to the terminal phenyl group in the other end, while being orthogonal in meta-OPE3 4 (Fig. S10†). We attribute this to differences in the crystal packing of meta-OPE3 1 compared to meta-OPE3 4 (Fig. S11†). More details about the X-ray structures can be found in Tables S1–S3.†

Conductance measurements

To probe the electrical conductance of the MJs, we first prepared a layer of the respective meta-OPE3 derivative, i.e. using each of the molecules shown in Fig. 1a, by the drop-casting method.⁴³ The electrical conductance of the meta-OPE3 derivatives was measured by using the scanning tunneling microscopy break junction (STM-BJ) method.^6,43 As shown in Fig. 1b, a DC bias voltage of 100 mV was applied to the Au tip, created by electrochemical etching, while the freshly prepared template-stripped Au substrate was grounded. Next, we displaced the STM tip towards the substrate at a constant speed of ∼0.2–0.4 nm s⁻¹, while monitoring the current flowing between the tip and the substrate using a current amplifier (model DDPCA 300 at a suitably chosen gain of 10⁻⁹ A V⁻¹). This process is continued until the signal from the current amplifier saturates (the current saturates at 10 nA, which corresponds to an electrical conductance of ∼1.29 × 10⁻³G₀), after which the tip is further displaced towards the substrate by ∼1 nm to ensure that an Au–Au contact is created (i.e., the electrical conductance is typically above 10G₀). Subsequently, the tip was withdrawn from the Au substrate at ∼0.2–0.4 nm s⁻¹, while recording the current. During this process, molecules were stochastically trapped between the tip and the substrate. Further details on sample fabrication and measurements are presented in the ESI.†

The results obtained from these experiments are displayed in Fig. 3. Specifically, conductance histograms for meta-OPE3 1–4 molecules are shown in Fig. 3a–d, respectively. The insets in each of the panels show representative conductance vs. time traces, where the plateaus in the electrical conductance evolution indicate the formation and subsequent rupture of these MJs. We note that each histogram, plotted in Fig. 3a–d, was constructed from ∼1000 such independent experimental conductance traces (more details of the data analysis can be found in the ESI†). From the Gaussian-fitted peaks in the conductance histograms we identify the most probable conductance of the given MJ. We list all the measured conductances in Table 1, along with those previously determined by Miao et al.¹⁶ for para-OPE3 and meta-OPE3.

Fig. 3 Conductance histograms of SMJs studied in this work. The conductance histograms of (a) meta-OPE3 1, (b) meta-OPE3 2, (c) meta-OPE3 3, and (d) meta-OPE3 4 SMJs were each constructed from ∼1000 independently measured conductance traces at a voltage bias of 100 mV without any data selection. A Gaussian fit to the data is also shown, and the peak of the Gaussian fit represents the most probable electrical conductance of the corresponding meta-OPE3 SMJ. Representative conductance–time traces are plotted in the insets.

Table 1 Experimentally determined single-molecule conductances and thermopowers of para-OPE3,¹⁶meta-OPE3¹⁶ and meta-OPE3 1–4

Molecule	Exp. G (G0)	Exp. S (μV K^−1)
para-OPE3 ^16	(1.2 ± 0.6) × 10^−4	10.8 ± 9.5
meta-OPE3 ^16	(1.1 ± 0.4) × 10^−5	20.9 ± 15.4
meta-OPE3 1	(1.11 ± 0.01) × 10^−5	13.55 ± 1.91
meta-OPE3 2	(2.86 ± 0.05) × 10^−6	16.50 ± 3.10
meta-OPE3 3	(1.01 ± 0.04) × 10^−5	18.17 ± 2.90
meta-OPE3 4	(2.14 ± 0.01) × 10^−6	28.59 ± 4.53

---

In Table 1 we observe that the electrical conductances of the C_s symmetrical meta-OPE3 1 and 3 junctions are both very close to each other. In contrast, C_2v symmetrical meta-OPE3 2 and meta-OPE3 4, which are substituted with pendant groups at the symmetric position of the central phenylene ring, yield significantly smaller conductances of ∼2.86 × 10⁻⁶G₀ and ∼2.14 × 10⁻⁶G₀, respectively. They are almost five times smaller than the electrical conductances of meta-OPE3 1 and meta-OPE3 3 MJs, where the pendant group is in an unsymmetric position of the central phenylene ring. Since EW or ED groups make little difference to the conductance of meta-OPE3 2 compared to meta-OPE3 4 and for meta-OPE3 1 compared to meta-OPE3 3, we conclude that the conductance in the meta-OPE3 series is generally only weakly dependent on the polarity of the pendant groups, i.e. EW (–NO₂) or ED (–NMe₂), when they are attached to the central phenylene ring, but importantly depends strongly on the position of the pendant group on the central phenylene ring. Our results are in line with those of Jiang et al. in a SMJ study using meta-OPE3 derivatives, containing an ED methoxy group in the symmetrical and unsymmetrical position of the central phenylene. Those authors reported that the symmetrical substitution showed lower conductance than the unsymmetrical one.³⁷ Hence, our experimental results as well as those reported by Jiang et al. show that the effect of destructive QI on the electrical conductance of meta-OPE3 junctions, observed in past work,¹⁶ can be reduced by adding functional substituents (ED or EW) in the unsymmetrical position, simultaneously increasing the conductance.

Thermopower measurements

Next, we measured the thermoelectric properties of SMJs. In these experiments, a thin film resistive heater was attached to the bottom substrate to establish a desired temperature differential (ΔT) across the tip and the substrate. When a MJ, with a conductance (G) that is within ±50% of the most probable conductance – the peak value obtained from the linear-scale conductance histogram – was formed,^16,44 the tip was held static, and we switched the bias applied to the tip periodically between 0 V to 100 mV (see Fig. 1c), while the electric current flowing through the junction was recorded (see ESI† and our recent work⁴⁴ for more details). In each switching cycle the electric current flowing at 100 mV bias was used to confirm the intactness of the SMJs, and the thermoelectric current (I_th) was monitored at 0 V for obtaining the thermopower. This switching process was continued until the MJ broke, as detected by a drop in the current at an applied bias of 100 mV. Afterwards, the tip was withdrawn until the conductance reached negligible levels, and the entire process of forming a metallic contact, trapping a molecule and measuring the thermoelectric current was repeated.

Data obtained from such measurements was converted into a thermoelectric voltage (ΔV_TE) via

here, ΔV_TE is defined to be positive when the thermoelectric current I_th at 0 V flows from the tip to the substrate and negative when current flows in the opposite direction. The thermoelectric voltages obtained from ∼5000 independent measurements for each kind of MJ at the respective temperature differential were combined to construct thermoelectric voltage histograms. The thermoelectric voltage histograms for meta-OPE3 1–4, obtained at temperature differentials of 0 K, 5.7 K, 9 K and 11.4 K (estimated as described in past work⁴⁴), are shown in Fig. 4. The peak position of the thermoelectric voltage histogram is fitted using a Gaussian function to obtain the most probable thermoelectric voltage at each temperature differential. The inset of each panel shows the linear fitting of this most probable ΔV_TEvs. ΔT for meta-OPE3 1–4 from which one can readily evaluate ΔV_TE/ΔT for each junction.

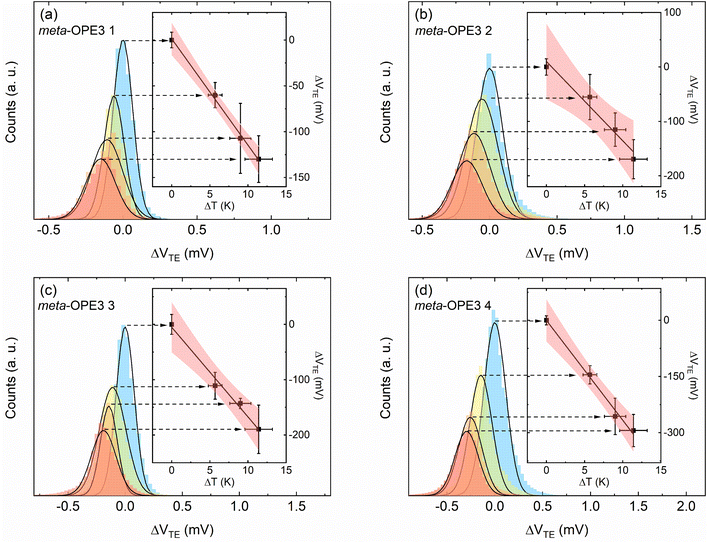Fig. 4 Temperature-dependent thermovoltage histograms and the corresponding linear fitting for SMJs studied in this work. The thermovoltage histograms of (a) meta-OPE3 1, (b) meta-OPE3 2, (c) meta-OPE3 3, and (d) meta-OPE3 4 were constructed using the flowing current measured at 0 V bias for four different temperature differentials across the SMJ (ΔT = 0 K, 5.7 K, 9 K and 11.4 K). Each histogram was constructed from data, obtained from ∼5000 bias-switching cycles without any data selection using multiple samples (2 to 4 samples), as described in the manuscript and in the ESI.† The insets present the peak values of the histograms (obtained from Gaussian fits) as a function of the applied temperature differential. The slope ΔV_TE/ΔT of the linear fit to the data enables the estimation of the thermopower of the SMJ viaeqn (2).

Subsequently, the thermopower of the SMJ (S_junction) was obtained using the expression (see ESI† for more details):

here, the thermopower of the copper wire (S_Cu) enters, as we employ a copper wire to provide electrical access to the sample substrate. It equals 1.94 μV K⁻¹ at 300 K. The SMJ thermopowers obtained using this approach are in the range of 10 to 30 μV K⁻¹ (see Table 1). The positive values indicate that charge transport in all four types of MJs is hole-dominated. In addition, the measured thermopowers are similar in magnitude to that of the parent meta-OPE3.¹⁶

Theoretical modelling

In the simplest picture of off-resonant hole transport in a Lorentzian HOMO model, we would expect the conductance and thermopower to increase for the ED substituent and to decrease for the EW substituent, if the HOMO level is shifted up or down in energy, respectively. In agreement with this simple model the thermopower of meta-OPE3 1 and 2 is indeed less than that of meta-OPE3 3 and 4 SMJs, respectively. The previously discussed trends in the conductance and the fact that the measured thermopower of meta-OPE3 3 is below the thermopower of the unsubstituted meta-OPE3 show, however, that the situation is more complicated, as can be anticipated from the QI effects reported in previous work.¹⁶ Let us therefore elucidate the experimental observations by detailed first principles modelling.

Quantum transport calculations

To further explore the effect of the position and the character of the substituent group, we perform ab initio electronic structure calculations and compute quantum transport properties based on linear response theory and the Landauer–Büttiker formalism.⁴⁵ The conductance G and thermopower S of the MJs are obtained fromwheree is the elementary charge, T the absolute temperature of the junction, E the energy, f(E) the Fermi–Dirac distribution and τ(E) the transmission function. In eqn (4), we approximate the chemical potential μ by the Fermi energy E_F and set the temperature to T = 300 K. To compute the transmission τ(E), we use the non-equilibrium Green's functions formalism,⁴⁵ as implemented in a custom code.⁴⁶ The underlying information on the electronic structure is obtained from density functional theory (DFT) in the TURBOMOLE⁴⁷ quantum chemistry software package. Since we find the DFT quantum transport properties directly derived from the PBE exchange–correlation functional⁴⁸ to be inaccurate (see ESI†), we report transport results below for the DFT+Σ correction scheme.^49,50 It consists of two parts, namely a molecular term, correcting energies of the isolated molecule, and an image-charge term, accounting for the effect of electrode polarizations. We refer to the ESI† for more detailed information on computational procedures.

For each of the four meta-OPE3 derivatives and the parent meta-OPE3 molecule, we study two different junction geometries. In the first one, called the top–top (TT) geometry, the sulfur atom on each side binds to a single gold atom at the top of a gold tip. For the second one, called hollow–hollow (HH) geometry, the gold atom at the top is removed and each sulfur binds to the three gold atoms of the next layer, making it a blunt electrode tip. To obtain comparable contact geometries, we optimize the structure of the reference meta-OPE3 SMJ in HH and TT configurations with DFT, add the relevant side groups for meta-OPE3 1–4 and reoptimize these SMJs. The resulting structures are shown in Fig. 5a and b (see ESI† for further details).

Fig. 5 (a) HH and (b) TT junction geometries of meta-OPE3 and meta-OPE3 1–4 from top to bottom. Transmission curves based on the DFT+Σ approach for the meta-OPE3 molecule and its derivatives meta-OPE3 1–4 in the (c) HH and (d) TT junction configurations.

Transmission curves, computed with the DFT+Σ approach, are plotted in Fig. 5c and d. If we compare the transmission of the meta-OPE3 derivatives with the parent meta-OPE3, we find additional peak and dip features inside the original HOMO–LUMO gap. They arise from electronic states newly introduced by the attached side groups. In the rather symmetric HH geometry, the transmission inside the HOMO–LUMO gap is almost mirror symmetric for meta-OPE3 1 and 3 as well as meta-OPE3 2 and 4, which originates from the EW character of the nitro group and the ED character of the N,N-dimethylamine group. They add new states in the LUMO region for meta-OPE3 1 and 2 and in the HOMO region for meta-OPE3 3 and 4, respectively. The side groups also change the position of the main destructive QI dip of meta-OPE3 inside the gap. It moves to a lower energy for meta-OPE3 1 and 2 but to a higher one for meta-OPE3 3 and 4. For meta-OPE3 1 the main destructive QI is shifted substantially more to lower energies into the HOMO region (by nearly 2 eV) than for meta-OPE3 2. At the same time, we find a regular transmission peak for meta-OPE3 1 in the LUMO area (around 2.5 eV above the Fermi energy) but an energetically very narrow Fano-like antiresonance^45,51 for meta-OPE3 2 (around 3 eV above E_F). These differences are clearly caused by the position of the nitro group. Analogous effects are visible for meta-OPE3 3 compared to meta-OPE3 4, where the main destructive QI dip is strongly shifted into the LUMO region for meta-OPE3 3 (around 3 eV above E_F) but only very weakly for meta-OPE3 4 (see 1.5 eV above E_F), and an antiresonance in the HOMO appears only for meta-OPE3 4 (around 1 eV below E_F). The antiresonances at around 3 eV above and 1 eV below the Fermi energy for meta-OPE3 2 and meta-OPE3 4, respectively, are so narrow that they have little influence on the transmission at the Fermi energy. Overall, we see that the transmissions of meta-OPE3 1 and 3 are larger at the Fermi energy than for meta-OPE3 2 and 4. The transmissions for the TT configuration show similar features as those of the HH geometry just discussed in detail. The biggest differences are that minima from the main destructive QI feature are shifted to around 1 eV lower energies for meta-OPE3 2–4, which changes the minimum at around 2 eV above E_F for meta-OPE3 3 to a rather broad dip, as compared to the narrow destructive QI minimum for the HH SMJ at 3 eV above E_F. To summarize, the transmission curves show characteristic changes, reflecting both the electronic character as well as the attachment point of the substituents on the molecule.

Calculated conductance and thermopower values are presented in Table 2. As a result of the characteristic changes in the energy-dependent transmission, the conductance of meta-OPE3 1 and 3 SMJs is larger than those of meta-OPE3 2 and 4 both for HH and TT geometries. This trend agrees perfectly with the experimental observations. But quantitatively, although the experimental conductance values of meta-OPE3 2 and meta-OPE3 4 are bracketed by the theoretical calculations, those of meta-OPE3 1 and meta-OPE3 3 tend to be overestimated. When we add meta-OPE3 to the comparison, we see that theory systematically predicts the symmetric molecules meta-OPE3, meta-OPE3 2 and 4 to yield a lower conductance, and the unsymmetric SMJs formed by meta-OPE3 1 and meta-OPE3 3 to yield a higher one. This trend is broken by meta-OPE3 in the experiments, and our quantum transport calculations underestimate the conductance of meta-OPE3 SMJs by a factor of up to 40. Thus, whereas the conductance of meta-OPE3 is experimentally on par with those of meta-OPE3 1 and meta-OPE3 3, theory predicts it to be so with meta-OPE3 2 and meta-OPE3 4. These differences between theory and experiment are somewhat ameliorated, if one considers the larger standard deviations of the older measurements¹⁶ for meta-OPE3 (see Table 1). Similar to the conductance, computed thermopower values sensitively depend on the junction geometry. For instance, the thermopower is negative for the meta-OPE3 1 junction in the HH configuration but positive for TT, and vice versa for meta-OPE3 2. Apart from the meta-OPE3 2 SMJ in the HH geometry, we find a tendency of smaller thermopower values for meta-OPE3 1 and 2, containing the EW (–NO₂) substituent, compared to meta-OPE3 3 and 4, containing the ED (–NMe₂) substituent. Hence the trend in the thermopower agrees with the electronic character of the added side group and the resulting energies of the additional molecular levels. The calculations predict the reference molecule meta-OPE3 to have a similar thermopower as meta-OPE3 3 and 4, each containing one ED group, which is consistent with the observations.

Table 2 Calculated single-molecule conductances and thermopowers of meta-OPE3 1–4 based on the DFT+Σ approach for HH and TT junction geometries^a

Molecule	G (G0) [HH]	G (G0) [TT]	S (μV K^−1) [HH]	S (μV K^−1) [TT]
a HH = hollow–hollow geometry (see Fig. 5a); TT = top–top (TT) geometry (see Fig. 5b).
meta-OPE3	3.84 × 10^−6	2.69 × 10^−7	21.5	27.4
meta-OPE3 1	1.18 × 10^−5	6.98 × 10^−5	−1.4	7.0
meta-OPE3 2	1.85 × 10^−7	4.58 × 10^−6	46.6	−3.7
meta-OPE3 3	6.65 × 10^−5	6.62 × 10^−5	20.4	23.6
meta-OPE3 4	4.43 × 10^−6	2.39 × 10^−7	19.9	22.3

---

Conclusions

We have synthesized four meta-OPE3 derivatives and studied – both experimentally and computationally – the electric and thermoelectric transport of the corresponding SMJs with respect to the variation of the position and electronic character of an attached substituent on the central phenylene unit. The parent unsubstituted meta-OPE3 served as a reference. Our experiments show that the charge transport properties of meta-OPE3 based SMJs, which are known to feature destructive QI effects, can indeed be tailored by the substituents. We demonstrated that when substituents are attached, the electrical conductance of C_s low-symmetry meta-OPE3 SMJs is higher than those of C_2v high-symmetry ones. The attachment point possesses a more important influence on conductance than the electronic EW (–NO₂) or ED (–NMe₂) character of the side groups. Compared to the parent meta-OPE3 SMJ the conductance tends to be similar or suppressed by the substituents, but no strong conductance increase was found. Using the same side group, the thermopower in C_s symmetric meta-OPE3 SMJs (meta-OPE3 1 and meta-OPE3 3) is lower than in C_2v symmetric ones (meta-OPE3 2 and meta-OPE3 4), and C_2v symmetric molecules possess a thermopower of similar magnitude as the C_2v symmetric parent meta-OPE3 molecule. Furthermore, the thermopowers of meta-OPE3 derivatives with an EW side group (meta-OPE3 1 and meta-OPE3 2) are smaller than those with an ED side group (meta-OPE3 3 and meta-OPE3 4).

Our computational results rationalize the main experimental observations and reveal the characteristic changes in charge transport properties that arise from different attachment points, leading to different molecular symmetries, as well as from electronic characters of the side groups. In particular, the conductance is predicted to be ordered rather by molecular symmetry than by the electronic properties of the substituents, i.e., meta-OPE3 1 and 3 as well as meta-OPE3 2 and 4 form pairs of similar conductance. Thermopower values are found to be very sensitive to the junction geometry and show relatively large variations. Within the series of meta-OPE3 derivatives, thermopower values are better ordered by the electronic character of the side group than by molecular symmetry. Quantitative discrepancies between the experimental and computational results for the complex molecular junctions involving destructive quantum interferences highlight the need for further studies to bridge the gap.

In summary, our results reveal that substituents at the central phenylene of the meta-OPE3 framework offer a promising way to separately optimize conductance and thermopower of SMJs, since the former is mainly sensitive to the position of the pendant group attached and the latter to its electronic (EW vs. ED) character. Interestingly meta-OPE3 4 SMJs yield the lowest conductance but highest thermopower. Overall, our study provides important insights into how thermoelectric properties can be tuned via substituents in MJs featuring destructive QI. Further investigations addressing the challenge of measuring thermoelectric transport properties of low-conducting molecular junctions are needed.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

The project was conceived by K. W., P. R., E. M., F. P., and H. L. H. X. and K. W. designed the compounds and their synthesis. Chemical synthesis and characterization were performed by H. X. and H. F. under the guidance of K. W. S. Y. and Y. L. performed the measurements of electrical conductance and thermopower of single molecule junctions and processed the experimental data under the guidance of E. M. and P. R. A. K. G. collected and analyzed the X-ray diffraction data. DFT and quantum transport calculations were carried out by L. M. under the guidance of F. P. The manuscript was written by S. Y., Y. L., L. M., F. P., P. R., E. M., and K. W. with comments and inputs from all authors.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

H. L. acknowledges support from the Knut and Alice Wallenberg foundation (project 2016.0089) and from NanoLund. P. R. and E. M. acknowledge funding from the Department of Energy (DE-SC0004871, scanning probe microscopy), the Office of Naval Research (N00014-20-1-2476, instrumentation) and the National Science Foundation (1803983, analysis). F. P. is supported by the Collaborative Research Center 1585, Project C02 of the German Research Foundation (grant number 492723217). H. X. acknowledges financial support from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7-People-2013-ITN) under REA grant agreement no. 608153 (PhD4Energy), the Royal Physiographic Society in Lund, and NanoLund. K. W. thanks the Carl Trygger foundation for a post-doc fellowship to H. F. and NanoLund for support.

References

1. D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440.
2. K. Wang, E. Meyhofer and P. Reddy, Adv. Funct. Mater., 2020, 30, 1904534.
3. T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002.
4. R. Smit, Y. Noat, C. Untiedt, N. Lang, M. C. van Hemert and J. M. van Ruitenbeek, Nature, 2002, 419, 906–909.
5. L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907.
6. B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223.
7. C. Evangeli, K. Gillemot, E. Leary, M. T. Gonzalez, G. Rubio-Bollinger, C. J. Lambert and N. Agraït, Nano Lett., 2013, 13, 2141–2145.
8. Y. Kim, W. Jeong, K. Kim, W. Lee and P. Reddy, Nat. Nanotechnol., 2014, 9, 881–885.
9. P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568–1571.
10. L. Cui, S. Hur, Z. A. Akbar, J. C. Klöckner, W. Jeong, F. Pauly, S.-Y. Jang, P. Reddy and E. Meyhofer, Nature, 2019, 572, 628–633.
11. N. Mosso, H. Sadeghi, A. Gemma, S. Sangtarash, U. Drechsler, C. Lambert and B. Gotsmann, Nano Lett., 2019, 19, 7614–7622.
12. H. Chen, H. Zheng, C. Hu, K. Cai, Y. Jiao, L. Zhang, F. Jiang, I. Roy, Y. Qiu, D. Shen, Y. Feng, F. M. Alsubaie, H. Guo, W. Hong and J. F. Stoddart, Matter, 2020, 2, 378–389.
13. H. Chen, S. Hou, Q. Wu, F. Jiang, P. Zhou, L. Zhang, Y. Jiao, B. Song, Q.-H. Guo, X.-Y. Chen, W. Hong, C. J. Lambert and J. F. Stoddart, Matter, 2021, 4, 3662–3676.
14. J. Liu, X. Huang, F. Wang and W. Hong, Acc. Chem. Res., 2018, 52, 151–160.
15. M. H. Garner, H. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. Liu, F. Ng, H. Li, S. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419.
16. R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. Pedersen, M. Leijnse, F. Pauly, K. Wärnmark, E. Meyhofer, P. Reddy and H. Linke, Nano Lett., 2018, 18, 5666–5672.
17. D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur and T. Wandlowski, Nat. Commun., 2015, 6, 6389.
18. I. M. Grace, G. Olsen, J. Hurtado-Gallego, L. Rincón-García, G. Rubio-Bollinger, M. R. Bryce, N. Agraït and C. J. Lambert, Nanoscale, 2020, 12, 14682–14688.
19. J. Hurtado-Gallego, S. van der Poel, M. Blaschke, A. Gallego, C. Hsu, R. López-Nebreda, M. Mayor, F. Pauly, N. Agraït and H. S. van der Zant, Nanoscale, 2024, 16, 10751–10759.
20. K. Reznikova, C. W. Hsu, W. M. Schosser, A. Gallego, K. Beltako, F. Pauly, H. S. J. van der Zant and M. Mayor, J. Am. Chem. Soc., 2021, 143, 13944–13951.
21. C. A. Martin, D. Ding, J. K. Sørensen, T. Bjørnholm, J. M. van Ruitenbeek and H. S. J. van der Zant, J. Am. Chem. Soc., 2008, 130, 13198–13199.
22. G. Yzambart, L. Rincón-García, A. A. Al-Jobory, A. K. Ismael, G. Rubio-Bollinger, C. J. Lambert, N. Agraït and M. R. Bryce, J. Phys. Chem. C, 2018, 122, 27198–27204.
23. H. Chen, Y. Chen, H. Zhang, W. Cao, C. Fang, Y. Zhou, Z. Xiao, J. Shi, W. Chen and J. Liu, Chin. Chem. Lett., 2022, 33, 523–526.
24. R. J. Salthouse, J. Hurtado-Gallego, I. M. Grace, R. Davidson, O. Alshammari, N. Agraït, C. J. Lambert and M. R. Bryce, J. Phys. Chem. C, 2023, 127, 13751–13758.
25. A. Daaoub, L. Ornago, D. Vogel, P. Bastante, S. Sangtarash, M. Parmeggiani, J. Kamer, N. Agraït, M. Mayor and H. van der Zant, J. Phys. Chem. Lett., 2022, 13, 9156–9164.
26. A. Mishchenko, L. A. Zotti, D. Vonlanthen, M. Bürkle, F. Pauly, J. C. Cuevas, M. Mayor and T. Wandlowski, J. Am. Chem. Soc., 2011, 133, 184–187.
27. J. E. Greenwald, J. Cameron, N. J. Findlay, T. Fu, S. Gunasekaran, P. J. Skabara and L. Venkataraman, Nat. Nanotechnol., 2021, 16, 313–317.
28. H. Dekkiche, A. Gemma, F. Tabatabaei, A. S. Batsanov, T. Niehaus, B. Gotsmann and M. R. Bryce, Nanoscale, 2020, 12, 18908–18917.
29. L. Xiang, J. L. Palma, Y. Li, V. Mujica, M. A. Ratner and N. Tao, Nat. Commun., 2017, 8, 14471.
30. J. Hurtado-Gallego, S. Sangtarash, R. Davidson, L. Rincón-García, A. Daaoub, G. Rubio-Bollinger, C. J. Lambert, V. S. Oganesyan, M. R. Bryce and N. Agraït, Nano Lett., 2022, 22, 948–953.
31. C. Lambert, Chem. Soc. Rev., 2015, 44, 875–888.
32. L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 10668–10711.
33. S. Wu, M. T. González, R. Huber, S. Grunder, M. Mayor, C. Schönenberger and M. Calame, Nat. Nanotechnol., 2008, 3, 569–574.
34. V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. Garcia-Suarez, P. Buiter, J. L. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262–5275.
35. L. Ornago, P. Zwick, S. van der Poel, T. Brandl, M. El Abbassi, M. L. Perrin, D. Dulić, H. S. van der Zant and M. Mayor, J. Phys. Chem. C, 2024, 128, 1413–1422.
36. B. Alanazi, A. Alajmi, A. Aljobory, C. Lambert and A. Ismael, J. Mater. Chem. C, 2024, 12, 6905–6910.
37. F. Jiang, D. I. Trupp, N. Algethami, H. Zheng, W. He, A. Alqorashi, C. Zhu, C. Tang, R. Li, J. Liu, H. Sadeghi, J. Shi, R. Davidson, M. Korb, A. N. Sobolev, M. Naher, S. Sangtarash, P. J. Low, W. Hong and C. J. Lambert, Angew. Chem., 2019, 131, 18987–18993.
38. L. A. Zotti and E. Leary, Phys. Chem. Chem. Phys., 2020, 22, 5638–5646.
39. N. Stuhr-Hansen, J. B. Christensen, N. Harrit and T. Bjørnholm, J. Org. Chem., 2003, 68, 1275–1282.
40. K. V. Arundhathi, P. Vaishnavi, T. Aneeja and G. Anilkumar, RSC Adv., 2023, 13, 4823–4834.
41. K. Sonogashira, Y. Tohda and N. Hagihara, Tetrahedron Lett., 1975, 16, 4467–4470.
42. T. C. Pijper, J. Robertus, W. R. Browne and B. L. Feringa, Org. Biomol. Chem., 2015, 13, 265–268.
43. J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1170.
44. H. Xu, H. Fan, Y. Luan, S. Yan, L. Martin, R. Miao, F. Pauly, E. Meyhofer, P. Reddy, H. Linke and K. Wärnmark, J. Am. Chem. Soc., 2023, 145, 23541–23555.
45. J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific, 2nd edn, 2017.
46. F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019.
47. Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. D. Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 . Erratum: Phys. Rev. Lett., 1997, 78, 1396.
49. L. A. Zotti, M. Bürkle, F. Pauly, W. Lee, K. Kim, W. Jeong, Y. Asai, P. Reddy and J. C. Cuevas, New J. Phys., 2014, 16, 015004.
50. S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Nano Lett., 2007, 7, 3477–3482.
51. U. Fano, Phys. Rev., 1961, 124, 1866.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2300114 and 2300115. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4nr02188f

‡ These authors contributed equally to this work.

---