Anomalous size dependence of the coercivity of nanopatterned CrGeTe₃

Abstract

The coercivity of single-domain magnetic nanoparticles typically decreases with the nanoparticle size and reaches zero when thermal fluctuations overcome the magnetic anisotropy. Here, we used SQUID-on-tip microscopy to investigate the coercivity of square-shaped CrGeTe₃ nanoislands with a wide range of sizes and width-to-thickness aspect ratios. The results reveal an anomalous size-dependent coercivity, with smaller islands exhibiting higher coercivity. The nonconventional scaling of the coercivity in CrGeTe₃ nanoislands was found to be inversely proportional to the island width and thickness (1/wd). This scaling implies that the nanoisland magnetic anisotropy is proportional to the perimeter rather than the volume, suggesting a magnetic edge state. In addition, we observe that 1600 nm wide islands display multi-domain structures with zero net remnant field, corresponding to the magnetic properties of pristine CrGeTe₃ flakes. Our findings highlight the significant influence of edge states on the magnetic properties of CrGeTe₃ and deepen our understanding of low-dimensional magnetic systems.

---

Introduction

The physics of magnetic nanoparticles has been studied thoroughly in the last few decades.^1–3 In particular, numerous studies have focused on measuring the size-dependence of the coercive field.^4–7 It is well understood that a nanoparticle smaller than some characteristic size D_s, becomes a single domain. The absence of domain walls typically increases the nucleation energy for a magnetic domain, thereby raising the magnetic coercivity with respect to a multi-domain particle with D > D_s ^4–8 (Fig. 1a, blue curve). The magnetization of single-domain particles with uniaxial anisotropy is modeled as a macrospin, which is a two-level system where the energy barrier is determined by the magnetic anisotropy, which is proportional to the volume.^4–8 Due to finite-temperature fluctuations, a lower anisotropy barrier results in a lower coercivity. For sufficiently small nanoparticles, the anisotropy barrier becomes comparable to the thermal fluctuations, and the particle is in the superparamagnetic state⁹ (SP, Fig. 1a, left-most regime, where H_c = 0).

Fig. 1 SOT images of the island arrays patterned in CrGeTe₃via FIB. (a) (Blue curve) A schematic representation of the typical coercive field H_c dependence on the nanoparticle characteristic size D. (Red solid curve) Same as blue curve but based on the experimental results for CrGeTe₃. (Red dashed curve) Extrapolation based on our results. Insets: (i) schematic illustration of the SQUID-on-tip (SOT) measurement. (ii–v) Typical B_z(x, y) images of CGT island with distinct dimensions. (ii and iii) Single magnetic domain array with characteristic size smaller than D_s. (iv) B_z(x, y) images of four multi-domain CGT islands with width w = 1600 nm > D_s. (v) Unpatterned CGT flake with w ∼ 10 μm and d = 50 nm. The image size is 5 × 5 ii–iii, 4.2 × 4.2 iv and 3 × 3 μm² v. (b–d) B_z(x, y) images acquired near the coercive field of the corresponding array. The island dimensions are d = 60 nm for all arrays, with widths, w = 150 nm b, 600 nm c, and 1600 nm d. Imaging parameters: (b) μ₀H_z = 70 mT, area scan 4.1 × 4.1 μm², pixel size 32 nm, (c) μ₀H_z = 20 mT, area scan 11 × 11 μm², pixel size 115 nm, and (d) μ₀H_z = 100 mT, area scan 4.2 × 4.2 μm², pixel size 30 nm. The scale bar is 1000 nm in b, c, d. The black to white color scale represents lower and higher magnetic fields, respectively.

The discovery of two-dimensional (2D) van der Waals (vdW) materials with long-range magnetic order has opened a fascinating new area of magnetic materials.^10–13 The magnetic properties of these materials often differ from those of their bulk counterparts, and are thickness-dependent, thereby affording unprecedented control over their magnetism.^14–17 Experimental evidence indicates that confinement causes a transition from soft to hard ferromagnetism in Fe₃GeTe₂,¹⁸ CrSiTe₃,¹⁹ CrGeTe₃,²⁰ and CrI.²¹ Specifically, CrGeTe₃ (CGT) films with a thickness d < 10 nm exhibit a net magnetization at zero applied magnetic field.^20,22 In contrast, the interior of thicker flakes (d > 10 nm) has zero net magnetization at zero applied field, with hard ferromagnetism appearing only at the sample edge.²⁰ More recently, artificial edges fabricated by Ga⁺ focused ion beam (FIB) etching have been shown to exhibit hard ferromagnetic (FM) properties like those of cleaved flakes, which enables direct writing of magnetic nanowires.²³ The presence of edges in narrow quasi-1D structures defined with a FIB can transform the interior region into a hard magnet. These findings raise the question of the potential influence of edges on the coercivity of CGT nanoparticles.

Here, we employed SQUID-on-tip (SOT) microscopy^24,25 at 4.2 K to measure the coercivity of FIB-patterned square-shaped CGT nanoislands with a range of island dimensions and width-to-thickness aspect ratios. Our results reveal an anomalous size dependence of the coercive field of the islands. The smallest nanoislands, with w × w × d = 150 × 150 × 60 nm³ (w being the width), exhibit larger coercivity than the larger single-domain nanoislands with size w × w × d = 600 × 600 × 60 nm³ (illustrated schematically by the red curve in Fig. 1a). This outcome is unexpected because coercivity usually diminishes with decreasing particle volume.^4–8 Finally, we demonstrate that islands with dimensions 1600 × 1600 × 60 nm³ stabilize multi-domain structures at zero applied field and exhibit magnetic properties similar to a large pristine exfoliated CGT flake with the same thickness.

Results

CGT flakes were exfoliated on top of a SiO₂-coated Si wafer. We etched vertical and horizontal lines using a 30 keV Ga⁺ FIB, resulting in an array of square-shaped magnetic islands. The synthesis and fabrication details are presented in ESI Note 1.† The effect of island geometry was examined by varying the effective crystal thickness from d = 25 to 70 nm and the width from w = 150 to 1600 nm. The island dimensions was measured by cross-sectional STEM, see ESI Note 2† for details. The number of islands in each array varied between 81 and 121 for islands with w < 1600 nm (see ESI Table 1† for details). Probing the properties of a large number of island allow us to reduce the statistical uncertainty (see ESI Note 3†). The out-of-plane component of the magnetic field, B_z(x, y), emanating from the array, was imaged at 4.2 K using a scanning SOT microscope,^24,25 as presented schematically in Fig. 1a (see also ESI Note 4†). Fig. 1b–d represent magnetic images of islands acquired near the coercive field of the respective array, where the black/white color-coded area indicates a magnetic moment pointing downwards/upwards. The array parameters of the islands are: thickness, d = 60 nm for all, and widths, w = 150, 600, and 1600 nm in Fig. 1b–d, respectively. The results indicate that small islands (w ≤ 600 nm, Fig. 1b and c), are single-domain, while larger islands with w = 1600 nm, exhibit fragmentation into multiple magnetic domains (Fig. 1d).

We characterize the magnetic response of the arrays to an applied out-of-plane magnetic field H_z, by counting the number of islands pointing in a given direction. Fig. 2a plots the resulting normalized magnetization curves, M(H_z)/M_tot, where M_tot = N|m_i|; N is the number of islands, and m_i is the magnetic moment per island. m_i is estimated by using the volumetric spin density (≈3μ_B/Cr) that was found to be constant down to a few layers.²⁶ This value is consistent with our bulk magnetic measurements (ESI Note 2†).

Fig. 2 Field evolution of island arrays in CrGeTe₃. (a) Hysteresis curves drawn from B_z(x, y) measured on arrays with volumes V ranging between 1.35 × 10⁶ and 30 × 10⁶ nm³. The array's coercive field H^a_c is marked with black dots. The hysteresis curves were measured by ramping the field in one direction and were symmetrized to obtain the second branch of the M(H_z)/M_tot curve (see ESI Note 3†). Curves were shifted vertically for clarity. (b) The median island coercive field, Hⁱ_c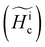, as a function of the parameter w/V = 1/wd. Several SOT images are shown in ESI Fig. 2.†

The hysteretic curves of all the arrays display a smooth magnetization reversal. The range of fields over which magnetization reversal occurs, the transition width, ΔH_z, was found to be similar for all measured arrays ΔH_z = H_l − H_f = 73 ± 7 mT, where H_f (H_l) is the field at which the first (last) island reverses its magnetization. The microscopic mechanism responsible for the island variability remains unknown. Here, the island variability is treated as an additional uncertainty on the individual island coercive field (see ESI Note 3†).

The coercive field of the array H^a_c is reached when M(H^a_c) = 0, or when the magnetization of half of the islands point in a given direction. Therefore, H^a_c is the median value of the field at which a single-island reverses its magnetization, defined as 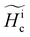. Notably, varies significantly with the island geometry, and ranges from 15 to 100 mT (black dots in Fig. 2a). In the absence of a stable magnetic domain wall, the magnetic saturation field is Hⁱ_c = 2K/m_i, where K is the island magnetic anisotropy. Therefore, measuring H^a_c allows us to determine the median single-island magnetic anisotropy K. For larger particles, K ≫ k_bT, Hⁱ_c is expected to be constant given that K and m_i are proportional to the island volume. However, for smaller particles, Hⁱ_c is expected to decrease and reach zero when K ∼ k_bT. In striking contrast, we observe the opposite trend, and the results indicate that islands with smaller volumes tend to exhibit larger values of (Fig. 2a).

Notably, is not fully determined by the island's volume, given that islands with comparable volumes, V₁ = 1.4 ± 0.1 × 10⁶ nm³ and V₃ = 1.4 ± 0.1 × 10⁶ nm³, but different aspect ratios, have significantly different values, with , respectively (Fig. 2a and Table 1). Distinct values of are measured in arrays with the same thickness but different widths. Arrays V₃ and V₇, with d = 60 ± 2 nm and widths w = 150 ± 5 and 600 ± 5 nm, have values of 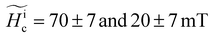, respectively. Finally, arrays V₆ and V₇, with comparable widths, w = 550 ± 5 and 600 ± 5 nm, not only differ in values of , respectively, but also undergo a transition from ideal hard FM (|M(H_z = 0)/M_tot| = 1) to a softer FM (|M(H_z = 0)/M_tot| < 1). Taking the influence of the demagnetizing factor into account, ESI Fig. 1† presents a plot of Hⁱ_cvs. the shape anisotropy of each island,²⁷ and lacks evidence of any trend in the observed data (see values in Table 1).

Table 1 A summary of the islands’ parameters and results presented in Fig. 2. The uncertainty on the dimension is ±5 nm for the width w and ±2 nm for the thickness d

Array #	Effective size w × w × d (nm^3)	Volume (10^6 nm^3)	Width-to-volume ratio (10^−4 nm^−2)	Shape anisotropy (10^−6 eV nm^−3)	Island magnetization (eV T^−1)	Median island Coercivity (mT)	Transition width ΔHz = Hl − Hf (mT)	Median island anisotropy (eV)
1	200 × 200 × 35	1.4 ± 0.1	1.43 ± 0.09	5.0 ± 0.4	290 ± 20	99 ± 4	76 ± 6	14 ± 2
2	220 × 220 × 35	1.7 ± 0.1	1.30 ± 0.08	5.3 ± 0.4	360 ± 30	89 ± 4	72 ± 6	15 ± 2
3	150 × 150 × 60	1.4 ± 0.1	1.11 ± 0.05	2.8 ± 0.3	280 ± 20	70 ± 5	82 ± 7	10 ± 2
4	240 × 240 × 35	2.0 ± 0.1	1.19 ± 0.07	5.5 ± 0.4	420 ± 30	67 ± 4	80 ± 7	14 ± 2
5	230 × 230 × 45	2.4 ± 0.1	0.96 ± 0.05	4.8 ± 0.3	500 ± 30	60 ± 4	75 ± 6	15 ± 2
6	550 × 550 × 25	7.5 ± 0.6	0.73 ± 0.06	7.3 ± 0.2	1600 ± 100	60 ± 4	77 ± 6	47 ± 8
7	600 × 600 × 60	21.6 ± 0.8	0.28 ± 0.01	6.2 ± 0.1	4500 ± 200	20 ± 4	65 ± 6	50 ± 20
8	650 × 650 × 70	30 ± 1	0.220 ± 0.007	6.1 ± 0.1	6200 ± 200	17 ± 4	61 ± 6	50 ± 20

---

Examining arrays with the same thickness, d = 35 nm, and varying widths, w = 200, 220, and 240 nm (V₁, V₂ and V₄), revealed a monotonic trend in H_c (see Table 1 and Fig. 2a). Previous results revealed that the magnetism at the edge of thick flakes with d > 10 nm, has finite coercivity in contrast to the sample interior, which has no net remnant field.³ Assuming that the anisotropy barrier is governed by a one-dimensional magnetic edge state, we find that K is proportional to w (the island perimeter) and not to the volume, as is commonly observed.^4–8 As a result, we find that , where V = w²d. Fig. 2b reveals the linear relation between the measured and 1/wd. This experimental evidence thus demonstrates that the magnetic properties of the island are governed by a one-dimensional magnetic edge state.

For larger islands with w = 1600 nm and d = 60 nm, a multi-domain state is observed during the magnetization reversal (Fig. 1d). Fig. 3 presents a sequence of B_z(x, y) SOT images of four islands between negative to positive saturation. After excursion of μ₀H_z = −200 mT, all islands hold their magnetization up to μ₀H_z = −70 mT (Fig. 3a uniform black color code). In contrast to smaller islands, here the islands’ magnetization breaks into a multi-domain state at demagnetization fields in the range μ₀H_d = −65 to −20 mT. Fig. 3b acquired at μ₀H_z = −40 mT depicts two islands at saturation magnetization (black) and two islands in the multi-domain state (gray). The magnetic domains are smaller than the tip diameter (∼150 nm), resulting in a magnetic contrast of 1 mT. At μ₀H_z = 0 mT, all the islands are in the multi-domain states where hard ferromagnetism is observed on the edges, resulting in a negative stray magnetic field as reported previously for patterned CGT²³ (ESI Fig. 3†). Increasing the out-of-plane field caused the magnetic domains with a magnetic moment parallel to the field to grow at the expense of domains with antiparallel magnetic moments. Fig. 3d and e demonstrate that the last domains to reverse their magnetization are long and thin, and tend to touch the edge of the island. At the saturation field of μ₀H_z = 130 mT, the islands’ magnetization is saturated in the positive direction and parallel with the external magnetic field (Fig. 3f).

Fig. 3 Magnetic field response of the CrGeTe₃ with w × w × d = 1600 × 1600 × 60 nm³ islands. (a–f) Sequence of SQUID-on-tip B_z(x, y) images at distinct values of an applied out-of-plane field μ₀H_z. (g) Illustrated hysteresis curves drawn from B_z(x, y) measured on array that comprise 16 islands of volume V = 1600 × 1600 × 60 nm³. The red/blue curve correspond to the island with largest/smallest demagnetization field H_d. The green dots represent H_d and saturation field H_s measured for pristine 60 nm thick CrGeTe₃ flake, extracted from ref. 20. The dashed lines represent the fields at which the islands are in the multi-domain state. Imaging parameters: μ₀H_z = −70 a, −40 b, 0 c, 100 d, 120 e, and 130 f mT. Area scan 4.2 × 4.2 μm², pixel size 30 nm. The black to white color scale represents lower and higher magnetic field, respectively. The color scale is 16, 24, 3, 3, 9, and 18 mT for a–f, respectively.

Fig. 3g illustrated two sketched magnetization curves of distinct individual island drawn from SOT images of sixteen islands. Each individual island exhibit slightly different properties. In particular, H_d varied from H_d = −65 to −20 mT and the corresponding two extreme cases are plotted in red and blue curves, respectively (see images taken at such field in ESI Fig. 4†). The dashed lines represent the fields at which the islands are in the multi-domain state up to a saturation field H_s = 130 mT, which shows significantly less variability than H_d. The reason for the better reproducibility of H_s over H_d is not understood and will require more investigation. In the multi-domain state, previous measurements showed no magnetic hysteresis.²⁰ We compare the illustrated hysteresis loops of individual islands with the data measured previously on a pristine (exfoliated) CGT flake.²⁰ Notably, the saturation field H_s = 130 mT, and a demagnetization field H_d of −66 mT (represented by the green dots), are close to the values seen in the red curve. We conclude that for this array, the islands hysteresis loops are comparable to that of the pristine CGT flake (same value of H_s and H_d values being in the same range). This contrasts with arrays with smaller island volumes that exhibit hard ferromagnetism.

Discussion

This study was designed to investigate the magnetic properties of CGT nanoislands as a function of size and aspect ratio. The results reveal a transition from hard ferromagnetic single-domain islands to multi-domain and zero remnant field islands. For d = 60 nm, the transition occurs between w = 650 and 1600 nm. A similar transition was previously observed in FIB-patterned CGT stripes with a length of 10 μm and d = 50 nm.²³ In the case of the stripe geometry, the transition occurred between w = 270 and 400 nm, which is significantly smaller than the currently observed values for islands. The larger w length scale range over which CGT remains a hard ferromagnet in the present study is consistent with the larger (factor two) perimeter-to-volume ratio in an island compared to a stripe of length much larger than width.

Another manifestation of the island edge is the unique dependence of the island saturation field on the island geometry, namely, Hⁱ_c ∝ 1/wd. This unusual dependence can be explained by assuming the magnetic anisotropy, K, scales with the island perimeter rather than the volume. The microscopic mechanism causing this edge state is currently unknown. Several mechanisms were considered in the past.^20,23 One of them is related to the in-plane dangling bonds. If such a mechanism would be dominant, one should find magnetism also at step-edges between two terraces. Previous work showed the absence of magnetism at such step-edges (see Fig. S9 in ref. 20) and suggests that this scenario is less probable. Moreover, magnetic edges were found at the edges of cleaved samples exposed to air, encapsulated²⁰ and amorphized,²³ reinforcing the idea that the effect of in-plane dangling bound is negligible. Gallium contamination was also considered as a potential mechanism. However, magnetic edges were found in samples that were never exposed to the Ga beam. Moreover, we did not observe any sign of higher gallium concentration at the edge of the crystalline part of the island (see ESI Fig. 6†), ruling out the potential role of gallium contamination. It is plausible that some strain appears at low temperatures at the interface between the amorphous and crystalline CGT regions. However, given that such magnetic edge state was found in cleaved samples, where such interface does not exist, tends to rule out this scenario. Another plausible mechanism is the presence of strain at the sample edges.^28,29 Recently, similar edge state in another material is thought to be caused by the Stoner mechanism.³⁰ Notably, applying this model to CGT is not straightforward since CGT is insulating and further investigation will be necessary to confirm the presence of such a state in CGT.

Another consequence of the finding that the magnetic anisotropy is proportional to w is that Hⁱ_c will not grow indefinitely with reducing size; it is rather expected to reach zero at the blocking temperature T_B = K/25k_b.⁸ In the range of sizes investigated here, we find K = 0.078 × 10⁻⁹w. By setting T_B = 4 K, we can estimate that the smallest w that would result in a finite Hⁱ_c is w ∼ 0.1 nm. This is a non-physical dimension given that it is smaller than the lattice constant. We can therefore conclude that our model (K ∝ w) must break down at a length larger than 0.1 nm. Previous results indicated that the magnetism of two-dimensional flakes becomes undetectable below ∼7 layers.²⁶ Although the out-of-plane coupling is usually weaker in magnetic van der Waals materials, we expect that the nanoislands could be scaled down to such dimensions. In the current study we were not able to reach this regime, since the smallest island achievable with Ga⁺ based FIB is of width w ∼ 100 nm. Other techniques, such as He based FIB, have a higher resolution that could allow us to investigate smaller sizes.

To conclude, our results demonstrate that we can adjust the local magnetic properties of CGT by controlling the dimensions, here achieved by using Ga⁺ FIB fabrication of square-shaped nanoislands. We report an anomalous size-dependence of island coercivity, which is inversely proportional to the width and thickness. In addition, we observe the transition between single and multi-domain above a critical width. Notably, controlling ferromagnetic order in vdW heterostructures may play a substantial role in spintronic devices^31–34 and in the study of proximity-induced phenomena.^35,36

Author contributions

Y. A. and A. N. conceived the experiment. E. H. and H. S. synthesized the CGT crystals. J. M. characterized the CGT crystals. A. N., Y. Z., and N. F. carried out the scanning SOT measurements. Y. A., M. K., H. Steinberg, and A. N. fabricated the CGT devices. A. N. characterized the CGT devices. A. N. analyzed the data. Y. A. and A. N. constructed the scanning SOT microscope. M. E. H. developed the SOT readout system. A. N., O. M., and Y. A. wrote the paper with contributions from all authors.

Data availability

All the raw data shown in this article is available upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank O. Agam, M. Kläui, and A. Capua for fruitful discussions. We thank A. Vakahi and S. Remennik for technical support and J. L. Martínez for his support in performing the bulk magnetic characterization. This work was supported by the European Research Council (ERC) Foundation grant no. 802952 and the Israel Science Foundation (ISF) grant no. 645/23. The international collaboration on this work was fostered by the EU-COST Action CA21144 (Superqmap). H. Steinberg acknowledges funding provided by the DFG Priority program grant 443404566 and Israel Science Foundation (ISF) grant 164/23. O. Millo is grateful for support from ISF grant no. 576/21 and the Harry de Jur Chair in Applied Science. H. Suderow and E. Herrera acknowledge the Spanish Research State Agency (PID2020-114071RB-I00, CEX2023001316-M, TED2021-130546B-I00), by the Comunidad de Madrid through program NANOMAGCOST-CM (program no. S2018/NMT-4321).

References

1. J. Ge, Y. Hu, M. Biasini, W. P. Beyermann and Y. Yin, Superparamagnetic Magnetite Colloidal Nanocrystal Clusters, Angew. Chem., Int. Ed., 2007, 46, 4342–4345.
2. M. Duan, J. G. Shapter, W. Qi, S. Yang and G. Gao, Recent progress in magnetic nanoparticles: synthesis, properties, and applications, Nanotechnology, 2018, 29, 452001.
3. Z. Ma, J. Mohapatra, K. Wei, J. P. Liu and S. Sun, Magnetic Nanoparticles: Synthesis, Anisotropy, and Applications, Chem. Rev., 2023, 123, 3904–3943.
4. J. Sung Lee, J. Myung Cha, H. Young Yoon, J.-K. Lee and Y. Keun Kim, Magnetic multi-granule nanoclusters: A model system that exhibits universal size effect of magnetic coercivity, Sci. Rep., 2015, 5, 12135.
5. E. F. Kneller and F. E. Luborsky, Particle Size Dependence of Coercivity and Remanence of Single-Domain Particles, J. Appl. Phys., 1963, 34, 656–658.
6. M. P. Sharrock, Time-dependent magnetic phenomena and particle-size effects in recording media, IEEE Trans. Magn., 1990, 26, 193–197.
7. D. Lisjak and A. Mertelj, Anisotropic magnetic nanoparticles: A review of their properties, syntheses and potential applications, Prog. Mater. Sci., 2018, 95, 286–328.
8. B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, Wiley, 2008,  DOI:10.1002/9780470386323.
9. C. P. Bean and J. D. Livingston, Superparamagnetism, J. Appl. Phys., 1959, 30, S120–S129.
10. S. Yang, T. Zhang and C. Jiang, van der Waals Magnets: Material Family, Detection and Modulation of Magnetism, and Perspective in Spintronics, Adv. Sci., 2021, 8, 2002488.
11. Y. Deng, et al., Layer-Number-Dependent Magnetism and Anomalous Hall Effect in van der Waals Ferromagnet Fe₅GeTe₂, Nano Lett., 2022, 22, 9839–9846.
12. W. Zhang, P. K. J. Wong, R. Zhu and A. T. S. Wee, van der Waals magnets: Wonder building blocks for two–dimensional spintronics?, InfoMat, 2019, 1, 479–495.
13. C. Jin and L. Kou, Two-dimensional non-van der Waals magnetic layers: functional materials for potential device applications, J. Phys. D: Appl. Phys., 2021, 54, 413001.
14. L. Thiel, et al., Probing magnetism in 2D materials at the nanoscale with single-spin microscopy, Science, 2019, 364, 973–976.
15. Q. H. Wang, et al., The Magnetic Genome of Two-Dimensional van der Waals Materials, ACS Nano, 2022, 16, 6960–7079.
16. T. Song, et al., Direct visualization of magnetic domains and moiré magnetism in twisted 2D magnets, Science, 2021, 374, 1140–1144.
17. B. Niu, et al., Coexistence of Magnetic Orders in Two-Dimensional Magnet CrI3, Nano Lett., 2020, 20, 553–558.
18. C. Tan, et al., Hard magnetic properties in nanoflake van der Waals Fe3GeTe2, Nat. Commun., 2018, 9, 1554.
19. C. Zhang, et al., Hard ferromagnetic behavior in atomically thin CrSiTe3 flakes, Nanoscale, 2022, 14, 5851–5858.
20. A. Noah, et al., Interior and Edge Magnetization in Thin Exfoliated CrGeTe3 Films, Nano Lett., 2022, 22, 3165–3172.
21. B. Huang, et al., Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270–273.
22. C. Gong, et al., Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature, 2017, 546, 265–269.
23. A. Noah, et al., Nano-Patterned Magnetic Edges in CrGeTe3 for Quasi 1-D Spintronic Devices, ACS Appl. Nano Mater., 2023, 6, 8627–8634.
24. Y. Anahory, et al., SQUID-on-tip with single-electron spin sensitivity for high-field and ultra-low temperature nanomagnetic imaging, Nanoscale, 2020, 12, 3174–3182.
25. D. Vasyukov, et al., A scanning superconducting quantum interference device with single electron spin sensitivity, Nat. Nanotechnol., 2013, 8, 639–644.
26. A. Vervelaki, et al., Visualizing thickness-dependent magnetic textures in few-layer Cr2Ge2Te6, Commun. Mater., 2024, 5, 40.
27. A. Aharoni, Demagnetizing factors for rectangular ferromagnetic prisms, J. Appl. Phys., 1998, 83, 3432–3434.
28. M. Šiškins, et al., Nanomechanical probing and strain tuning of the Curie temperature in suspended Cr2Ge2Te6-based heterostructures, npj 2D Mater. Appl., 2022, 6, 41.
29. A. O'Neill, et al., Enhanced Room Temperature Ferromagnetism in Highly Strained 2D Semiconductor Cr2Ge2Te6, ACS Nano, 2023, 17, 735–742.
30. S. Liu, et al., Surface-induced ferromagnetism and anomalous Hall transport at Zr2S (001), Phys. Rev. Mater., 2023, 7, 024409.
31. T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Antiferromagnetic spintronics, Nat. Nanotechnol., 2016, 11, 231–241.
32. A. Hirohata, et al., Review on spintronics: Principles and device applications, J. Magn. Magn. Mater., 2020, 509, 166711.
33. E. J. Telford, et al., Coupling between magnetic order and charge transport in a two-dimensional magnetic semiconductor, Nat. Mater., 2022, 21, 754–760.
34. H. Kurebayashi, J. H. Garcia, S. Khan, J. Sinova and S. Roche, Magnetism, symmetry and spin transport in van der Waals layered systems, Nat. Rev. Phys., 2022, 4, 150–166.
35. W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Graphene spintronics, Nat. Nanotechnol., 2014, 9, 794–807.
36. J. Linder and J. W. A. Robinson, Superconducting spintronics, Nat. Phys., 2015, 11, 307–315.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02106a

---