Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Composition-dependent morphologies of CeO2 nanoparticles in the presence of Co-adsorbed H2O and CO2: a density functional theory study
Samuel
Moxon
 a,
Adam R.
Symington
b,
Joshua S.
Tse
a,
Adam R.
Symington
b,
Joshua S.
Tse
 a,
Joseph M.
Flitcroft
a,
Joseph M.
Flitcroft
 c,
Jonathan M.
Skelton
c,
Jonathan M.
Skelton
 c,
Lisa J.
Gillie
a,
David J.
Cooke
a,
Stephen C.
Parker
c,
Lisa J.
Gillie
a,
David J.
Cooke
a,
Stephen C.
Parker
 b and
Marco
Molinari
b and
Marco
Molinari
 *a
*a
aDepartment of Physical and Life Sciences, University of Huddersfield, Queensgate, Huddersfield, HD1 3DH, UK. E-mail: m.molinari@hud.ac.uk
bDepartment of Chemistry, University of Bath, Claverton Down, Bath, BA2 7AY, UK
cDepartment of Chemistry, University of Manchester, Manchester, M13 9PL, UK
First published on 16th May 2024
Abstract
Catalytic activity is affected by surface morphology, and specific surfaces display greater activity than others. A key challenge is to define synthetic strategies to enhance the expression of more active surfaces and to maintain their stability during the lifespan of the catalyst. In this work, we outline an ab initio approach, based on density functional theory, to predict surface composition and particle morphology as a function of environmental conditions, and we apply this to CeO2 nanoparticles in the presence of co-adsorbed H2O and CO2 as an industrially relevant test case. We find that dissociative adsorption of both molecules is generally the most favourable, and that the presence of H2O can stabilise co-adsorbed CO2. We show that changes in adsorption strength with temperature and adsorbate partial pressure lead to significant changes in surface stability, and in particular that co-adsorption of H2O and CO2 stabilizes the {100} and {110} surfaces over the {111} surface. Based on the changes in surface free energy induced by the adsorbed species, we predict that cuboidal nanoparticles are favoured in the presence of co-adsorbed H2O and CO2, suggesting that cuboidal particles should experience a lower thermodynamic driving force to reconstruct and thus be more stable as catalysts for processes involving these species.
Introduction
Cerium dioxide (CeO2) is a widely-employed catalyst for a number of important chemical processes including those in three-way catalytic converters, solid-oxide electrolyzer cells and the water–gas shift reaction.1–5 CeO2 nanoparticles have also shown activity mimicking biological enzymes and have hence been termed “nanozymes”.6–8,115 The catalytic activity of CeO2 nanoparticles (CeNPs) is determined by their surface composition and reactivity. CeNPs can exhibit many shapes, but most frequently form octahedra (dominant {111} surface), cubes ({100}), and rods ({110}9 and a mixture of {100} and {111}10–13 surfaces). The structure and stability of these surfaces is well characterised in the literature.9–11,14–22 Octahedral CeNPs are the most stable,13,23–26 and rods and cubes may therefore experience a thermodynamic driving force to reconstruct under certain operating conditions21,27 (e.g. {111} facets appear in rods above 500 K).28,29 As different particle shapes exhibit different reactivities,17,30–33 it is essential to control the morphology to ensure the optimum performance of CeO2-based catalysts and nanozymes.34It has been shown that small-molecule adsorbates such as CO2 and H2O can stabilise the {100} facet over the {111} facet and therefore inhibit the formation of more stable octahedral nanoparticles.25,26,35 The interaction of individual molecules such as H2O26,36–40 and CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25,41–43 with CeO2 surfaces has thus drawn considerable interest. The behaviour in the presence of CO2 is critical in automotive three-way catalytic converters, as the reactions progress through surface-bound CO2.43–46 H2O is a ubiquitous surface adsorbate and is also a reactant in the water-splitting reaction in solid-oxide electrolyzer cells, where the reaction pathway has been shown to depend sensitively on the surfaces exposed by the catalyst.35 CeNPs show enhanced oxidative catalysis in the presence of water molecules,47 implying that the catalytic performance of CeNPs can be improved in the presence of H2O. The water-gas shift reaction, which converts CO and H2O to CO2 and H2, relies on the presence of surface-bound H2O but can be deactivated (“poisoned”) by CO2.44,48 Given that the {100} surface has a higher affinity for both H2O49 and CO2,25 control of the dominant facets of the catalyst can have a substantial impact on performance.
25,41–43 with CeO2 surfaces has thus drawn considerable interest. The behaviour in the presence of CO2 is critical in automotive three-way catalytic converters, as the reactions progress through surface-bound CO2.43–46 H2O is a ubiquitous surface adsorbate and is also a reactant in the water-splitting reaction in solid-oxide electrolyzer cells, where the reaction pathway has been shown to depend sensitively on the surfaces exposed by the catalyst.35 CeNPs show enhanced oxidative catalysis in the presence of water molecules,47 implying that the catalytic performance of CeNPs can be improved in the presence of H2O. The water-gas shift reaction, which converts CO and H2O to CO2 and H2, relies on the presence of surface-bound H2O but can be deactivated (“poisoned”) by CO2.44,48 Given that the {100} surface has a higher affinity for both H2O49 and CO2,25 control of the dominant facets of the catalyst can have a substantial impact on performance.
While the adsorption of individual molecules on CeO2 surfaces has been widely studied, despite the importance in catalytic processes the co-adsorption of CO2 and H2O has not. To give just one example, the co-adsorption of H2O and CO2 is important in the production of syngas, which involves the reduction of stoichiometric CeO2 followed by re-oxidation using H2O and CO2 to produce H2 and CO.50–54
In this work, we outline an approach to predict the surface composition and morphology of CeO2 nanoparticles as a function of temperature, and H2O and CO2 partial pressure based on density functional theory (DFT) calculations. We first compute the adsorption energies of singly- and co-adsorbed CO2 and H2O on the stoichiometric and oxygen deficient surfaces of CeO2 typically expressed by CeNPs. We then proceed to predict the surface compositions, in the form of thermodynamic surface phase diagrams, and the desorption temperatures of the adsorbates, as a function of environmental conditions. Finally, we combine both sets of calculations to predict the thermodynamically stable particle morphologies and surface compositions, and we discuss the implications of our predictions for the design and optimisation of CeO2-based catalysts.
Computational methodology
DFT calculations were performed using the Vienna ab initio simulation package (VASP) code.55 A plane-wave basis with a cut-off energy of 500 eV was used together with projected augmented-wave (PAW) pseudopotentials56,57 with frozen cores of [He] for C and O, and [Xe] for Ce. Electron exchange and correlation were treated with the Perdew–Burke–Ernzerhof (PBE) generalised gradient approximation (GGA) functional58 with the Liechtenstein Hubbard U correction (i.e., PBE+U).59 In the Lichtenstein model, the coulombic (U) and exchange (J) parameters are treated as independent variables. We chose U = 5 eV and J = 0 eV, which makes the Liechtenstein model equivalent to the Dudarev60 model with Ueff = U − J = 5 eV. The use of DFT+U for calculations on CeO2 is well established in the literature, and our chosen U = 5 eV has been shown to correctly describe the localised Ce3+ states in reduced systems.36,46,61–63 There are other approximations available to study CeO2, including hybrid functionals and the inclusion of van der Waals interactions,64–66 but they have been shown to gain similar results to GGA+U for the adsorption of different molecules on CeO2 surfaces.41,67Bulk CeO2 and Ce2O3
The conventional unit cell of bulk CeO2 contains four CeO2 units and has the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (no. 225). We obtained an optimised lattice constant of 5.498 Å, which compares well to experimental measurements of 5.412–5.418 Å,68,69 and computational studies.116 The Brillouin zone was sampled using a Γ-centred 5 × 5 × 5 k-point grid. The unit cell of bulk Ce2O3 includes 16 Ce2O3 units and has the Ia
m space group (no. 225). We obtained an optimised lattice constant of 5.498 Å, which compares well to experimental measurements of 5.412–5.418 Å,68,69 and computational studies.116 The Brillouin zone was sampled using a Γ-centred 5 × 5 × 5 k-point grid. The unit cell of bulk Ce2O3 includes 16 Ce2O3 units and has the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group (no. 206) with an optimised lattice constant of 11.374 Å, which also compares well to the experimental value of 11.126 Å.70 We have used the cubic bixbyite structure as more representative of the volume expansion associated with the reduction of fluorite CeO2.71 The Brillouin zone was sampled using a Γ-centred 4 × 4 × 4 k-point grid. Both structures were minimised using the conjugate gradient method with electronic total energy and ionic force convergence thresholds of 10−5 eV and 10−3 eV Å−1 respectively.
space group (no. 206) with an optimised lattice constant of 11.374 Å, which also compares well to the experimental value of 11.126 Å.70 We have used the cubic bixbyite structure as more representative of the volume expansion associated with the reduction of fluorite CeO2.71 The Brillouin zone was sampled using a Γ-centred 4 × 4 × 4 k-point grid. Both structures were minimised using the conjugate gradient method with electronic total energy and ionic force convergence thresholds of 10−5 eV and 10−3 eV Å−1 respectively.
CeO2 surfaces
CeO2 surfaces were modelled using the slab method,72 using models with two identical surfaces separated by a vacuum gap of 15 Å in the direction perpendicular to the surface to avoid interactions between periodic images. The METADISE code73 was used to generate these model structures, by reorientating bulk CeO2 so that the surface termination of choice lies perpendicular to the direction of the vacuum gap. The {100}, {110} and {111} surface models are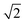 ×
× 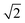 , 2 ×
, 2 × 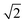 and 1 × 1 expansions of the CeO2 surface repeat unit, respectively, and the {100} and {110} models are 7 layers thick (28 CeO2 units) while the {111} model is 5-layers thick (20 CeO2 units). To quench the dipole on the {100} surface, half the oxygen atoms were transposed from the top to the bottom surface. The size of the slabs used are in line with previous studies,25,26 and as the slab models do not reconstruct during simulation, they should be sufficient to simulate nanoparticles that remain crystalline and of nanometre scale. However, the effect of the slab thickness on the morphology of nanoparticles should be the focus of future work. The Brillouin zones of all three surface models were sampled using Γ-centred 2 × 2 × 1 k-point grids. The geometries were minimised using the conjugate gradient method with total energy and force thresholds of 10−5 eV and 10−2 eV Å−1. These parameters have previously been used for similar calculations of CeO2.26,36
and 1 × 1 expansions of the CeO2 surface repeat unit, respectively, and the {100} and {110} models are 7 layers thick (28 CeO2 units) while the {111} model is 5-layers thick (20 CeO2 units). To quench the dipole on the {100} surface, half the oxygen atoms were transposed from the top to the bottom surface. The size of the slabs used are in line with previous studies,25,26 and as the slab models do not reconstruct during simulation, they should be sufficient to simulate nanoparticles that remain crystalline and of nanometre scale. However, the effect of the slab thickness on the morphology of nanoparticles should be the focus of future work. The Brillouin zones of all three surface models were sampled using Γ-centred 2 × 2 × 1 k-point grids. The geometries were minimised using the conjugate gradient method with total energy and force thresholds of 10−5 eV and 10−2 eV Å−1. These parameters have previously been used for similar calculations of CeO2.26,36
To generate the O-deficient (reduced) surfaces, an oxygen vacancy was introduced on both sides of the corresponding stoichiometric slab models. Each oxygen vacancy introduces two excess electrons, which localise on surface Ce atoms to create two surface Ce3+. While there is no constraint placed on the position of the Ce3+, our setup ensures that both sides of the slab remain equivalent.
CeO2 surfaces with adsorbates
The (co-)adsorption of H2O and/or CO2 molecules were modelled with different starting configurations to sample adsorption modes. Due to the complex adsorption energy landscape, we only considered those configurations that maximize the hydrogen bond network and the interactions between the adsorbates and surfaces. A complete list of the surfaces we examined is presented in Table 1 together with the labelling scheme used in the discussion. In each entry {hkl} are the Miller indices of the surface (i.e., {100}, {110} or {111}), X = S or R denotes a stoichiometric or reduced surface, the molecular formulae indicate the adsorbed species (single adsorption of H2O and CO2 or co-adsorption of H2O–CO2), and the final letters indicate associative (A), dissociative (D) and/or molecular (M) adsorption of each adsorbate. For example, the associative adsorption of CO2 on the stoichiometric {111} surface is labelled {111}S-CO2-A, and the co-adsorption of dissociatively adsorbed H2O and molecularly adsorbed CO2 on the {100} O-deficient surface is {100}R-H2O-CO2-DM. In the Results and discussion, we only present the adsorption energies of the most stable configurations (i.e. those with the most negative energy of adsorption Eads).| Surface | Adsorption description |
|---|---|
| Bare surface | {hkl}X |
| Single adsorption of CO2 | {hkl}X-CO2-A |
| {hkl}X-CO2-M | |
| Single adsorption of H2O | {hkl}X-H2O-D |
| {hkl}X-H2O-M | |
| Co-adsorption of H2O and CO2 | {hkl}X-H2O-CO2-DA |
| {hkl}X-H2O-CO2-DM | |
| {hkl}X-H2O-CO2-MA | |
| {hkl}X-H2O-CO2-MM |
Small molecules
Isolated CO2, H2O, and O2 were modelled in cubic cells with side length 10 Å. These calculations used the same convergence criteria as the surface calculations, with the Brillouin zones sampled at the Γ-point as appropriate for an aperiodic system.Analysis and imaging
VESTA75 was used to visualise the models. Data analysis was performed using the Surfinpy code74,76,77 and the Wulff construction routines in Pymatgen.78Results and discussion
Structure and energetics of bare surfaces
We first examine the bare {100}, {110} and {111} surfaces without adsorbates. The surface energies γ of the bare stoichiometric and O-deficient surfaces were calculated as: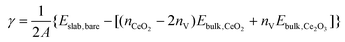 | (1) |
For the O-deficient surfaces, the heat of reduction Ered is given by:
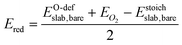 | (2) |
Adsorption of H2O and CO2
The strength with which molecules adsorb at a surface is captured by the adsorption energies Eads defined as: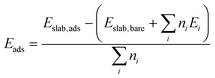 | (3) |
Fig. 1 compares the calculated Eads for the configurations listed in Table 1 for the stoichiometric and O-deficient {100}, {110} and {111} surfaces. In general, associative or dissociative adsorption is stronger than molecular adsorption, with the exception that the {111}S-H2O-M and {111}S-H2O-D configurations have similar energies, as highlighted in previous literature.36 The adsorption energies of the stoichiometric surfaces follow the order {100} < {110} < {111} (i.e., adsorption at the {100} surface is most favourable), as do the Eads for {hkl}R-CO2-A. On the other hand, the Eads for molecular CO2 adsorption at the O-deficient surfaces follow the order {100} < {111} < {110} (i.e., adsorption on {111} is more favourable than on {110}). The latter trend has been observed in previous computational studies of H2O adsorption on ceria.26 The Eads for {hkl}R-H2O-M follow a different trend with {111} < {100} < {110} (i.e., adsorption is most favourable at the {111} surface).
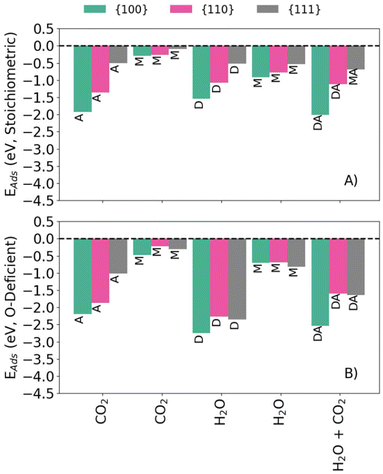 | ||
| Fig. 1 (Co-)Adsorption energies of H2O and CO2 onto stoichiometric (A) and O-deficient (B) {100} (green) {110} (pink) and {111} (grey) CeO2 surfaces. The labels correspond to those in Table 1. | ||
The co-adsorption energies on the stoichiometric surfaces follow the same general trend of {100} < {110} < {111} as for single adsorption, whereas for the O-deficient surfaces we predict a trend of {100} < {111} ≈ {110}. This might be due to H2O adsorbing molecularly to the stoichiometric {111} surface but dissociatively to the corresponding O-deficient surface.
Structure and energetics of CO2 adsorption
The geometries of associatively and molecularly adsorbed CO2 at the stoichiometric and reduced {100}, {110} and {111} surfaces are compared in Fig. 2. On all six surfaces, associatively adsorbed CO2 bonds to a surface oxygen to form a CO32− (carbonate) ion, and on the O-deficient surfaces the carbonate ions tend to reside close to oxygen vacancies.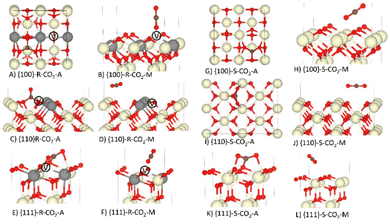 | ||
| Fig. 2 Associative (A) and molecular (M) adsorption of CO2 on the O-deficient (R) and stoichiometric (S) {100}, {110} and {111} surfaces of CeO2. The Ce, O and C atoms are shown in cream, red and brown. In the reduced models, the grey atoms show the positions of the Ce3+ and the white atoms marked V show the positions of the oxygen vacancies. Please refer to Table 1 and related text for description of the configurations A-L. | ||
The calculated energies of our {hkl}S-CO2-A models are generally in good agreement with the literature,25 but we obtain a less stable {100}R-CO2-A configuration (−2.20 eV vs. −2.36 eV25) and more stable {110}R-CO2-A and {111}R-CO2-A configurations (−1.87/−1.02 eV vs. −1.56/−0.68 eV25). We tentatively attribute these discrepancies to different positions of the oxygen vacancies with respect to the localised Ce3+ in our and previous models, but despite multiple attempts, we were unable to reproduce the previous results.
The {100}S-CO2-A (Fig. 2G) and {100}R-CO2-A (Fig. 2A) configurations with the most negative Eads comprise flat tridentate carbonate ions.25,43 The geometry of the {100}S-CO2-A configuration has been confirmed experimentally using near-edge X-ray absorption fine structure (NEXAFS) measurements, and a previous Eads of −1.93 eV obtained with PBE+U agrees very well with our predicted −1.92 eV.43 Albrecht et al.43 do not provide geometries for the {100}R-CO2-M or {100}S-CO2-M configurations, but they quoted Eads of −0.2 to −0.3 eV that again agree well with our predicted −0.22 and −0.27 eV.
Our {100}R-CO2-M structure (Fig. 2B) is in good agreement with the similar GGA+U calculations of Zhou et al.79 However, we predict a different {100}R-CO2-A configuration, which we attribute to a different configuration of the {100} flexible surface oxygen layer.2,80,81
XPS measurements by Yang et al.82 indicated that CO2 adsorbs to the {110} surface as {110}S-CO2-A, {110}R-CO2-A, {110}S-CO2-M or {110}R-CO2-M, but were unable to determine geometries. We can therefore only compare our {110} configurations to other DFT studies. Our {110}S-CO2-A model is consistent with that obtained by Symington et al.25 (Fig. 2I) and has a quantitatively similar Eads (−1.35 vs −1.32 eV). We also predict a similar {110}R-CO2-A geometry (Fig. 2C).25 Other studies have predicted monodentate carbonate species, where one of the O atoms lies in an oxygen vacancy and the other two adopt a “bent” configuration above the surface,24,42,83 but according to our calculations this configuration is less stable than the bidentate one in Fig. 2C.
Adsorption of CO2 at the {111} surface has received considerable interest in the context of CO adsorption.41,45,84,85 We predict a similar {111}S-CO2-A geometry to Hahn et al.41 and Symington et al.25 (Fig. 2K) and a similar {111}S-CO2-M configuration to Hahn et al.41 (Fig. 2L). The predicted Eads of our {111}S-CO2-A model compares well to the value obtained by Symington et al. (−0.51 vs. −0.52 eV),25 but we find a more favourable {111}R-CO2-A configuration with Eads = −1.02 eV compared to −0.68 eV.25
Structure and energetics of H2O adsorption
The geometries of dissociatively and molecularly adsorbed H2O on the stoichiometric and O-deficient {100}, {110} and {111} surfaces are shown in Fig. 3. In the {hkl}S-H2O-M and {hkl}R-H2O-M configurations molecular H2O adsorbs above the surface. On the other hand, in the {hkl}S-H2O-D models the hydroxyl OH bonds to the surface Ce and in the {hkl}R-H2O-D models the OH “heals” the oxygen vacancy. In both models the dissociated H forms a bond with a nearby surface O.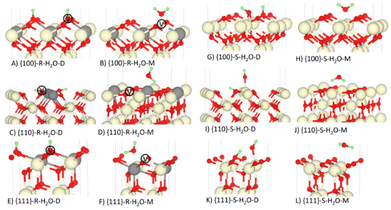 | ||
| Fig. 3 Dissociative (D) and molecular (M) adsorption of H2O on the stoichiometric (S) and O-deficient (R) {100}, {110} and {111} surfaces of CeO2. The Ce, O and H atoms are shown in cream, red and green. In the reduced models, the grey atoms show the positions of the Ce3+ and the white atoms marked V show the positions of the oxygen vacancies. Please refer to Table 1 and related text for description of the configurations A-L. | ||
Most experimental and computational studies of H2O adsorption on CeO2 surfaces focus on the {111} and {100} surfaces. There is some debate over whether the {111}S-H2O-A or {111}S-H2O-M configuration is more stable, with a number of experimental86,87 and computational26,36,88 studies finding very similar Eads while other experimental89,90 and theoretical37,38,87,88 studies indicate molecular adsorption to be more stable.
The most stable configuration of {111}S-H2O-M has also been the subject of considerable debate in the computational literature. Some studies predict the most favourable configuration to be the H2O molecules lying flat on the surface and forming the two H-bonds to surface O atoms, whereas others predict a tilted configuration where the molecule forms only one H-bond to be more stable. Molinari et al.36 calculated the Eads for both configurations and found the tilted configuration, equivalent to our {111}S-H2O-M model (Fig. 3L), had the lowest adsorption energy, albeit with a minimal difference of 0.02 eV.
On the other hand, there is unanimous agreement that the {111}R-H2O-D is more stable than {111}R-H2O-M.26,36,38,87,88,90,91 The temperature-programmed desorption (TPD) and X-ray photoelectron spectroscopy (XPS) experiments performed by Henderson et al.90 found that dissociative adsorption of H2O at the reduced {111} surface does not result in Ce3+ being oxidised, in agreement with our predictions (Fig. 3E). We obtain a more stable {110}R-H2O-D than in previous studies by Molinari et al.36 and Symington et al. (Fig. 3C),26 which we attribute to a stronger H-bond network in our predicted geometry.
According to O 1s soft XPS (sXPS) measurements by Mullins et al.,86 in an aqueous environment {100}S-H2O-D dominates over {100}S-H2O-M, which is consistent with the more favourable predicted Eads for the former (−2.35 vs. −0.82 eV). Our predicted geometries and Eads for {100}S-H2O-D, {100}R-H2O-D, {100}S-H2O-M and {100}R-H2O-M are in good agreement with Molinari et al.,36 and our geometries and Eads for {100}S-H2O-D and {100}R-H2O-D similarly agree well with Symington et al.26
Structure and energetics of the co-adsorption of CO2 and H2O
Having demonstrated that our calculations reproduce previous experimental and theoretical results for the single adsorption of CO2 and H2O on ceria surfaces, we next considered the co-adsorption of both species (Table 1 and Fig. 4). Co-adsorption is highly likely under experimental conditions, but literature investigating this is much sparser.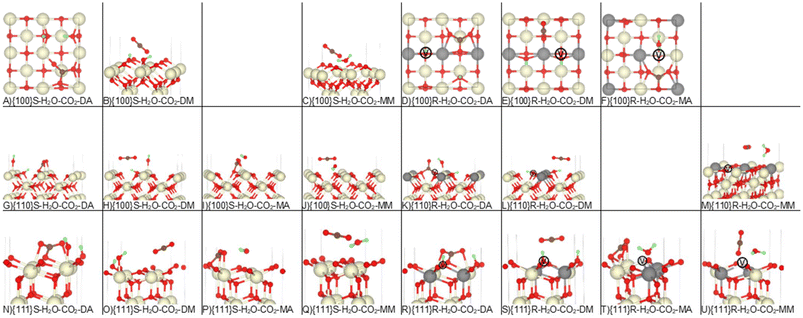 | ||
| Fig. 4 Co-adsorption of H2O and CO2 on the stoichiometric and reduced CeO2 surfaces. The Ce, O, H and C atoms are shown in cream, red, green and brown. In the reduced models, the grey atoms show the positions of the Ce3+ and the white atoms marked V show the positions of the oxygen vacancies. Please refer to Table 1 and related text for description of the configurations A-U. | ||
In all configurations, the adsorbates were placed to maximise the hydrogen bond network, the interactions between adsorbates, and the interactions between the adsorbates and the surfaces. While we attempted to optimise all possible combinations of dissociative, associative and molecular adsorption of the two molecules, the initial binding configurations were not always retained.
The co-adsorption of CO2 and H2O generally appears to have little impact on the local geometries of either species (cf. Fig. 2–4). We compute per-adsorbate Eads for co-adsorption (cf.eqn (3)), which allows us to compare with the adsorption energies of the individually adsorbed species. If the Eads for a co-adsorbed configuration is lower (more negative) than for an individually adsorbed species, then the adsorption is synergistic and co-adsorption favours the adsorption. On the other hand, if the Eads is higher (more positive) than for an individual adsorption, the adsorption is antagonistic and co-adsorption disfavours the adsorption.
Despite the minimal structural changes, the dissociative adsorption of H2O at O-deficient surfaces appears to be destabilised by the presence of CO2, whereas molecularly adsorbed CO2 appears to be stabilised by H2O (Fig. 1). The {100}S-H2O-CO2-DA and {110}S-H2O-CO2-DA configurations are notable exceptions, with dissociatively adsorbed H2O stabilising associatively-bound CO2, and vice versa.
In general, the Eads for co-adsorption at different surfaces follow similar trends to single adsorption, viz.: (1) adsorption is more favourable at the O-deficient surfaces compared to the stoichiometric surfaces; (2) associative and dissociative adsorption are more favourable than molecular adsorption; and (3) the Eads for the stoichiometric and O-deficient surfaces follow the trend {100} > {110} > {111} and {100} < {111} < {110}, respectively.
Prediction of surface compositions
We now use the calculated surface energies to predict the lowest-energy surface composition, i.e., stoichiometric or O-deficient and with or without adsorbates, as a function of temperature and O2, H2O and CO2 partial pressure. To account for the partial pressures of the adsorbates, eqn (1) is modified to: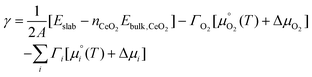 | (4) |
Γ O2 is the surface coverage related to the oxygen surface composition in terms of O2, and given by:
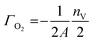 | (5) |
This quantity is negative for O-deficient surfaces and nil for stoichiometric surfaces. Γi are similarly the surface coverages of the small molecules i:
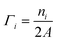 | (6) |
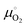 is the standard chemical potential of O2 calculated as:
is the standard chemical potential of O2 calculated as:
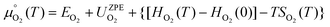 | (7) |
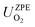 are the total energy and vibrational zero-point energy, respectively, evaluated using DFT, and the term in braces is a temperature correction to the Gibbs free energy using experimental data from the NIST database.92
are the total energy and vibrational zero-point energy, respectively, evaluated using DFT, and the term in braces is a temperature correction to the Gibbs free energy using experimental data from the NIST database.92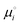 are the standard chemical potentials of the adsorbates calculated as:
are the standard chemical potentials of the adsorbates calculated as: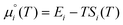 | (8) |
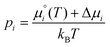 | (9) |
We note here two key differences between eqn (1) and (4). First, we consider the formation of O-deficient surfaces via loss of surface O as gaseous O2 rather than formation from a mixture of bulk CeO2 and Ce2O3. This is necessary to account for the effects of temperature and variable O2 partial pressure in our modelling and is also more realistic, since under most experimental conditions CeO2 will be in contact with a reservoir of O2 and not Ce2O3. Secondly, we use the chemical potentials of the gaseous adsorbates rather than the DFT energies, which allows us to account for the effects of temperature and variable partial pressures.
Surface composition as a function of ΔμO2 and ΔμCO2 or ΔμH2O
We first map the most stable configurations of the {100}, {110} and {111} surfaces as a function of the chemical potential of O2 and CO2 or H2O (Fig. 5). As expected, high ΔμO2 (high pO2, oxidising conditions), favours the stoichiometric surfaces, while low ΔμO2 (low pO2, reducing conditions) favours the O-deficient surfaces. Similarly, high ΔμCO2/ΔμH2O favour adsorption of the molecules, as there is an excess of the adsorbates, whereas low ΔμCO2 or ΔμH2O favour bare surfaces.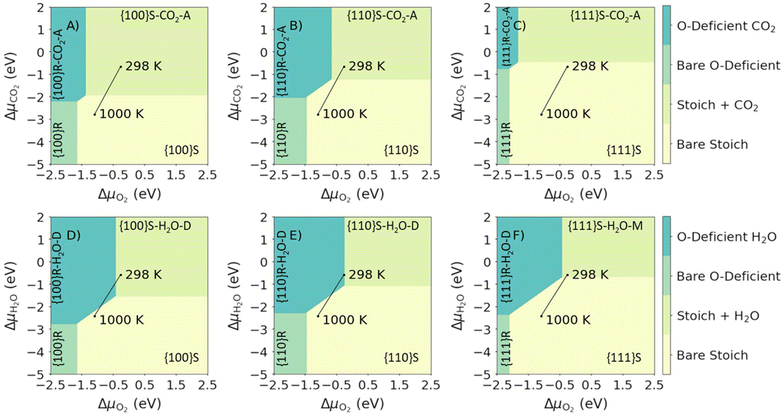 | ||
| Fig. 5 Surface phase diagrams for the adsorption of single molecules on CeO2 surfaces. Plots in the top and bottom rows show the most favourable surface compositions as a function of ΔμO2 and ΔμCO2 (top row, A–C) or ΔμH2O (bottom row D–F). The three columns show the compositions of the {100} (left column, A and D), {110} (centre column, B and E) and {111} surfaces (right column, C and F). The most stable compositions under each set of conditions are indicated using the notation in Table 1. The two points mark the most stable phases with the gases (O2 and CO2/H2O) present at a fixed p = 1 bar, obtained by adjusting the corresponding Δμ, at T = 298 and 1000 K, and the connecting line shows the change in composition with temperature. | ||
We can also use this approach to predict changes to the surface composition with temperature. To do so, we consider temperatures of 298 to 1000 K with the pressures of the gases (i.e. pO2 and pCO2/pH2O) maintained at a constant 1 bar by varying the corresponding Δμi. In the presence of CO2, the most stable surface composition of all the surfaces changes from stoichiometric with associatively adsorbed CO2 at 298 K to bare stoichiometric surfaces at 1000 K (Fig. 5A–C). In the presence of H2O the most stable compositions of the {100} and {110} surfaces are predicted to change from stoichiometric with dissociatively-adsorbed H2O at 298 K to bare stoichiometric at 1000 K (Fig. 5D/E). The {111} behaves similarly but with molecular rather than dissociative adsorption favoured at low temperature (Fig. 5F).
Surface composition as a function of ΔμCO2 and ΔμH2O at fixed ΔμO2
To consider the co-adsorption of CO2 and H2O, we fix the oxygen stoichiometry and predict the most favourable compositions of the stoichiometric and O-deficient surfaces as a function of the chemical potentials of CO2 and H2O. To do so, the expression for the surface energies is modified as: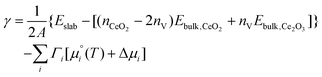 | (10) |
This differs from eqn (4) in that we consider the formation of the surfaces from bulk CeO2 and Ce2O3, as we need to fix one of the chemical potentials and we chose to fix ΔμO2.
Fig. 6 shows the most stable surface compositions of the stoichiometric and O-deficient {100}, {110} and {111} surfaces as a function of ΔμCO2 and ΔμH2O. Our calculations lead to three observations: (1) at low ΔμCO2 and ΔμH2O (i.e., low partial pressures of both adsorbates) the bare surfaces are the most stable; (2) at high ΔμCO2 or ΔμH2O the surfaces with the corresponding adsorbates are the most stable; and (3) at high ΔμCO2 and ΔμH2O, the most stable surfaces are those with both molecules co-adsorbed. At 1 bar pCO2 and pH2O, we predict that both H2O and CO2 are co-adsorbed at 298 K, with molecular or dissociative H2O and associative CO2 adsorption. For the O-deficient {100} surface, we predict desorption of CO2 on heating to 1000 K, while for all other surfaces we predict the desorption of both species on heating.
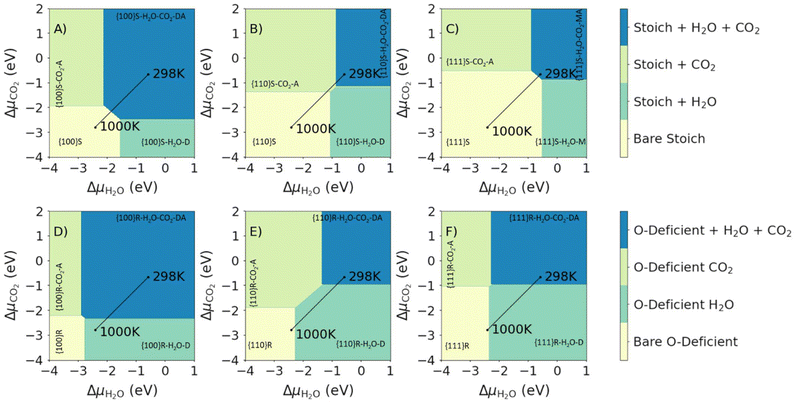 | ||
| Fig. 6 Surface phase diagrams for the co-adsorption of H2O and CO2 on CeO2 surfaces. Each plot shows the most favourable surface compositions as a function of ΔμH2O and ΔμCO2. Plots in the top and bottom rows show the most favourable compositions of the stoichiometric (top row, A–C, high ΔμO2) and O-deficient ceria surfaces (bottom row, D–F, low ΔμO2). The three columns show the compositions of the {100} (left column, A and D), {110} (centre column, B and E) and {111} surfaces (right column, C and F). The most stable compositions under each set of conditions are indicated using the notation in Table 1. The two points mark the most stable phases with H2O and CO2 present at a fixed p = 1 bar, obtained by adjusting the corresponding Δμ, at T = 298 and 1000 K, and the connecting line shows the change in composition with temperature. | ||
Prediction of desorption temperatures
In addition to predicting the most favourable surface composition as a function of the chemical potentials (partial pressures) of the adsorbates, it is also useful to predict the desorption temperatures TD, defined as the highest temperature required to desorb an adsorbate from the surface at a given adsorbate partial pressure.To do so, we implement a thermodynamic strategy employed successfully in the literature.25,26,36,93 The energies of the surfaces with adsorbates γads can be rewritten as:
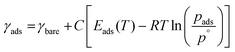 | (11) |
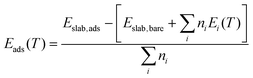 | (12) |
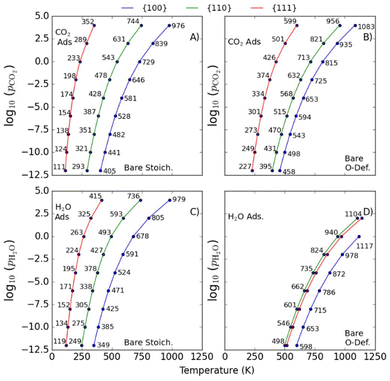
Here, the Ei(T) are equivalent to the 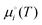 in eqn (8). We then determine the most stable surface (i.e., bare or with (an) adsorbate(s)) as a function of T and pads. The phase boundary between the bare surfaces and surfaces with adsorbate then determines the TD at a given pads. Fig. 7 shows calculations for individually adsorbed H2O and CO2 on the three stoichiometric and O-deficient ceria surfaces.
in eqn (8). We then determine the most stable surface (i.e., bare or with (an) adsorbate(s)) as a function of T and pads. The phase boundary between the bare surfaces and surfaces with adsorbate then determines the TD at a given pads. Fig. 7 shows calculations for individually adsorbed H2O and CO2 on the three stoichiometric and O-deficient ceria surfaces.
Higher TD are indicative of stronger adsorption to the surface. In general, we predict higher TD for the {100} and {110} surfaces compared to the {111} surface, with the notable exception of a higher predicted TD,H2O for the O-deficient {111} surface than the O-deficient {110} surface (Fig. 7D).
We also predict lower TD for species adsorbed to the stoichiometric surfaces, in line with previous studies (cf.Fig. 7A/B and 7C/D).2,12,25,26,36,43 The TD of singly-adsorbed H2O and CO2 (TD,H2O/TD,CO2) have been investigated both computationally25,26,36,38 and experimentally,2,43,82,90,91,94–98 but we are not aware of any measurements or predictions for the co-adsorption of the two species.
T D of CO2 (TD,CO2)
Table 2 compare our calculated TD for associatively-adsorbed CO2 to previous studies. The TD,CO2 for stoichiometric and O-deficient {100} surfaces were measured as 700 and 765 K in ultra-high vacuum (UHV) based on C 1s and O 1s photoemission and C k-edge NEXAFS.43 The exact pressure is not given, but assuming a “ballpark” pCO2 ≈10−10 bar for UHV measurements, we predict values of 441 and 498 K. The higher values measured experimentally may be due to a higher level of oxygen deficiency in the experimental samples (CeO1.7vs. CeO1.93 in our O-deficient {100} model). The TD,CO2 for the stoichiometric and O-deficient {110} surfaces were measured UHV to be 400 and 500 K at pCO2 = 10−12 bar,82 and our predicted values are approximately 100 K lower at 293 and 395 K. For the {111} surface we predict TD,CO2 = 146 and 287 K for the stoichiometric and O-deficient surfaces at pCO2 = 10−7 bar, which compare relatively well to the TD < 200 K measured by Senanayake et al. under similar conditions.95 We note however that the experimental TD of the O-deficient surface may be lower due to the presence of surface oxygen vacancy clusters. Finally, we predict higher TD,CO2 for our {110}R-CO2-A and {111}R-CO2-A models but a lower TD,CO2 for our {100}R-CO2-A configuration compared to a previous study using PBEsol+U,25 which can be explained by our configurations being lower and higher in energy, respectively.| Model | Type of study | log10(pCO2) | ||||
|---|---|---|---|---|---|---|
| −12 | −10 | −7 | 0 | 2 | ||
a ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ref. 82 quotes a typical pressure of 2 × 10−10 mbar, which we have approximated as log10(pCO2) = −12. Ref. 82 quotes a typical pressure of 2 × 10−10 mbar, which we have approximated as log10(pCO2) = −12.
|
||||||
| {111}S-CO2-A | Comp. (this study) | 111 | 124 | 146 | 233 | 289 |
| Comp.25 | 121 | 133 | — | 246 | 292 | |
| Expt.95 | — | — | <200 | — | — | |
| {111}R-CO2-A | Comp. (this study) | 227 | 249 | 287 | 426 | 501 |
| Comp.25 | 154 | 169 | — | 308 | 363 | |
| Expt.95 | — | — | <200 | — | — | |
| {110}S-CO2-A | Comp. (this study) | 293 | 321 | 369 | 543 | 631 |
| Comp.25 | 289 | 314 | — | 535 | 615 | |
| Expt.82 | 400a | — | — | — | — | |
| {110}R-CO2-A | Comp. (this study) | 395 | 431 | 493 | 713 | 821 |
| Comp.25 | 338 | 366 | — | 615 | 705 | |
| Expt.82 | 500 | — | — | — | ||
| {100}S-CO2-A | Comp. (this study) | 405 | 441 | 504 | 729 | 839 |
| Comp.25 | 395 | 427 | — | 708 | 808 | |
| Expt.43 | — | 700 | — | — | — | |
| {100}R-CO2-A | Comp. (this study) | 458 | 498 | 568 | 815 | 935 |
| Comp.25 | 510 | 551 | — | 894 | 1017 | |
| Expt.43 | — | 765 | — | — | — | |
T D of H2O (TD,H2O)
Experimental measurements of TD,H2O are limited to the {100}2,98 and {111}2,90,91,94,96 surfaces. Table 3 compares our predictions to previous computational and experimental studies. Due to the similarity in the adsorption energies of dissociative and molecular H2O at the {111} surface it is impossible for experiments to study either in isolation, and we instead list the most prevalent configurations. Our predicted TD,H2O on the stoichiometric and O-deficient {111} surfaces compare well with other literature. We note that Fronzi et al.38 predict higher TD,H2O for molecularly adsorbed H2O on the stoichiometric {111} surface than other studies, which we attribute to them considering the chemical potentials of Ce, O and H. Our predictions agree well with other calculations of the TD,H2O for dissociatively adsorbed H2O on the stoichiometric {110} surface,26,36 but we predict higher TD,H2O for the O-deficient {110} surface due to the more favourable configuration found in the present study. The TD,H2O for our {100}S-H2O-D configuration again compares well with the literature.36 We predict lower TD,H2O for dissociatively-adsorbed H2O at the stoichiometric and O-deficient {100} surfaces than Mullins et al.2,86 which we tentatively attribute to the flexibility of the {100} oxygen sublattice.| Model | Type of study | Pressure log10(pH2O) | ||||
|---|---|---|---|---|---|---|
| −12 | −10 | 0 | 1 | |||
| a Due to the energetic similarity of the {111}S-H2O-D and {111}S-H2O-M configurations it is impractical for experiments to study either in isolation and we therefore list the most prevalent configurations. b Exact pressure during the measurements not specified. | ||||||
| {111}S-H2O-M | Comp. (this study) | 119 | 134 | 263 | 291 | — |
| {111}S-H2O-D | Comp.26 | 154 | 134 | 270 | — | — |
| {111}S-H2O-M | Comp.36 | 150–175 | 175–200 | — | 325–350 | — |
| {111}S-H2O-M | Comp.38 | 330 | 370 | 700 | — | — |
| {111}S-H2O-Da | Expt.2 | — | 200–300 | — | — | — |
| {111}S-H2O-Ma | Expt.91 | — | <200 | — | — | — |
| {111}S-H2O-M | Expt.90 | — | — | — | 320–420 | |
| {111}S-H2O-Da | Expt.94 | — | — | — | 300 | |
| {111}S-H2O-Ma | Expt.96 | — | — | — | 300 | |
| {111}R-H2O-D | Comp. (this study) | 516 | 566 | 972 | 1048 | — |
| Comp.26 | 521 | 571 | 837 | — | — | |
| Comp.36 | 500–525 | 550–575 | — | >1000 | — | |
| Expt.2 | — | >500 | — | — | — | |
| Expt.91 | — | >500 | — | — | — | |
| Expt.94 | — | — | — | — | 550 | |
| Expt.96 | — | — | — | — | 600 | |
| {110}S-H2O-D | Comp. (this study) | 249 | 275 | 493 | 538 | — |
| Comp.26 | 275 | 304 | 462 | — | — | |
| Comp.36 | 275–300 | 300–325 | — | 575–600 | — | |
| {110}R-H2O-D | Comp. (this study) | 498 | 546 | 940 | 1015 | — |
| Comp.26 | 349 | 384 | 575 | — | — | |
| Comp.36 | 350–375 | 400–425 | — | 725–750 | — | |
| {100}S-H2O-D | Comp. (this study) | 349 | 385 | 678 | 735 | — |
| Comp.26 | 382 | 420 | 613 | — | — | |
| Comp.36 | 400–425 | 475–500 | — | 825–850 | — | |
| Expt.2,86 | — | <600 | — | — | ||
| Expt.98 | — | — | — | 275 | ||
| {100}R-H2O-D | Comp. (this study) | 598 | 653 | 1117 | 1204 | — |
| Comp.26 | 610 | 667 | 975 | — | — | |
| Comp.36 | 575–600 | 400–425 | — | >1000 | — | |
| Expt.2,86 | — | <750 | — | — | — | |
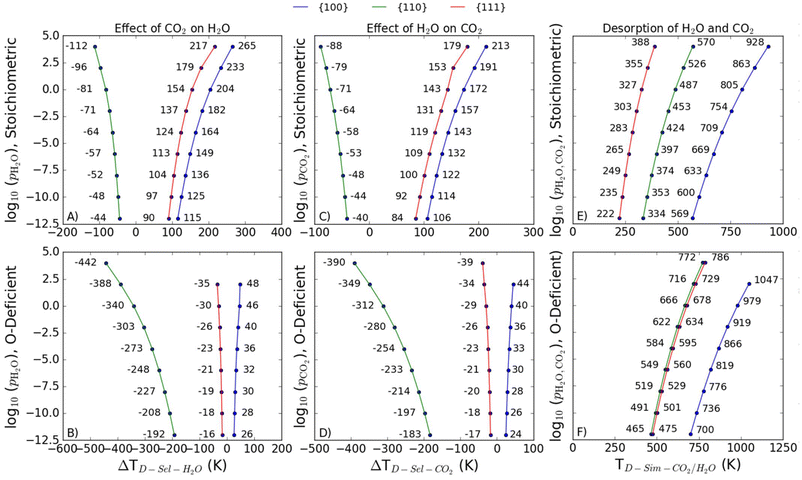
T D of co-adsorbed H2O and CO2
To consider desorption of co-adsorbed species we consider two scenarios, viz.: (1) selective desorption, where one molecule desorbs and the other remains adsorbed; and (2) simultaneous desorption, where both molecules desorb from the surface. These are illustrated in the reaction schemes shown below: | (13) |
 | (14) |
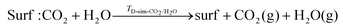 | (15) |
Selective desorption of CO2 or H2O
It is also useful to define a shift in desorption temperature, ΔTD, as the difference between the TD for selective desorption when two co-adsorbed and the TD of the singly adsorbed species:| ΔTD-sel-i = TD-sel-i − TD,i | (16) |
We find that the presence of both adsorbates has a destabilising effect on both the stoichiometric and O-deficient {110} surface (i.e., ΔTD-sel-CO2 and ΔTD-sel-H2O > 0) but a stabilising effect on both stoichiometric and O-deficient {100} surfaces (ΔTD-sel-CO2 < 0 and ΔTD-sel-H2O < 0; Fig. 8A–D). On the other hand, we see a synergistic stabilising effect on the stoichiometric {111} surface (Fig. 8A/C) but an antagonistic effect on the O-deficient {111} surface (Fig. 8B/D).
Simultaneous desorption of CO2 and H2O
As for single adsorption, the TD for simultaneous desorption represents the highest temperature at a given set of adsorbate partial pressures required for both co-adsorbed molecules to desorb together, and thus define a phase boundary between a bare surface and a surface with both species co-adsorbed.The predicted TD-sim-CO2/H2O for the O-deficient surfaces is larger than for the stoichiometric surfaces, indicating that it is easier to simultaneously desorb H2O and CO2 from the stoichiometric surfaces than the O-deficient surfaces (Fig. 8E/F). The predictive TD-sim-CO2/H2O for the stoichiometric surfaces fall in the order of {100} > {110} > {111} (Fig. 8E), while the TD from the O-deficient {110} and {111} surfaces are reversed to give an order of {100} > {111} > {110} (Fig. 8F).
Comparison of selective and simultaneous desorption
It is of interest to compare the desorption temperatures for selective and simultaneous desorption, as in catalytic processes involving both species the temperature and partial pressure of the gases should be optimised to ensure the required species are present on the surface. As a reference point, Table 4 summarises the calculated TD for the singly-adsorbed and co-adsorbed molecules for each of the stoichiometric and O-deficient surfaces at a reference pCO2/pH2O = 1 bar.| Reference | Partial pressure | Stoichiometric | O-deficient | ||||
|---|---|---|---|---|---|---|---|
| {111} | {110} | {100} | {111} | {110} | {100} | ||
| T D,CO2 | p CO2 = 1 bar | 234 | 543 | 730 | 713 | 427 | 730 |
| T D,H2O | p H2O = 1 bar | 264 | 494 | 678 | 972 | 941 | 1118 |
| T D-sim-CO2/H2O | p CO2 = pH2O = 1 bar | 328 | 487 | 806 | 679 | 666 | 980 |
| T D-sel-CO2 | p CO2 = 1 bar | 377 | 472 | 902 | 397 | 401 | 856 |
| T D-sim-H2O | p H2O = 1 bar | 418 | 412 | 883 | 941 | 600 | 1164 |
For both the stoichiometric and O-deficient {110} surfaces, the predicted TD-sim-CO2/H2O are higher than the TD for selective desorption, indicating the molecules will desorb selectively rather than simultaneously. The reverse is true for the stoichiometric {111} and {100} surfaces, for which the calculations predict it is more favourable for both molecules to desorb simultaneously. On all three O-deficient surfaces, the TD-sel-CO2 are the lowest, suggesting CO2 would likely desorb first, whereas on the stoichiometric {110} surface the TD-sel-H2O is the lowest, suggesting H2O would desorb first.
Surface area and morphology
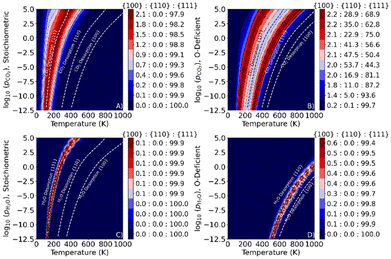
We now utilise our predicted surface free energies and desorption temperatures to predict the equilibrium surface composition and, hence, the morphology of CeNPs as a function of temperature and adsorbate partial pressure. We begin by predicting the relative areas of the {111}, {110} and {100} surfaces taking into consideration the TD of the adsorbates and the impact of the molecules on the surface energies. The effect of different conditions on the relative areas can be most conveniently visualised in the form of “surface area” phase diagrams showing the proportions of the different surfaces, and whether bare or with adsorbed species, as a function of temperature and/or adsorbate partial pressure(s).Relative surface areas in the presence of CO2
Fig. 9A shows the predicted area ratio of the {100}, {110} and {111} surfaces in stoichiometric CeNPs as a function of temperature and pCO2. We also show on these plots the predicted TD,CO2 of the three surfaces, which provides an indication of whether CO2 would be adsorbed under a given set of conditions. Under most conditions, we predict that the CeNPs are dominated by the {111} surface, corresponding to an octahedral morphology. However, over a narrow range of temperatures around the TD,CO2 for the {111} surface, we predict a small proportion of the {100} surface, which would produce the truncated octahedral shape predicted by Symington et al.25 The dominant {111} composition, together with TD,CO2 being lowest at this surface, additionally indicates that at high T the CeNPs are predicted to present bare surfaces.Fig. 9B shows our predictions for O-deficient CeNPs. At the extremes of temperature (i.e., low and high T), we again predict the {111} surface to be dominant. However, around TD,CO2 for the {111} surface, the area of the {110} is predicted to increase to just over half of the total ratio, yielding an octahedron with flat edges. These differences in surface composition result in CO2 being adsorbed over a wider range of temperatures than for stoichiometric NPs. We predict a greater dominance of the {110} surface than Symington et al.,25 which we attribute to our lower-energy {110}R-CO2-A configuration. Symington et al. also predict a higher proportion of the {100} surface than in this study, which we put down to them considering higher CO2 coverage and finding a lower-energy configuration with two CO2 molecules adsorbed to the surface.
Barroso Bogeat et al. found that ceria nanocubes interact strongly with CO2,99 and that the redox properties of the nanocubes can be improved by forming {111} dominated pyramids.13 Hashimoto et al.100 reported that catalytic behaviour to CO2 methanation falls in the order of {110} > {100} > {111} for cubic, rod-like and octahedral NiOx-decorated CeO2 nanostructures, which they attributed to the enhanced reactivity of oxygen atoms on the {110} surface compared to the {100} and {111} surfaces. This is corroborated by DFT calculations indicating a lower reduction energy at the {110} surface26,36,101,102 and classical molecular dynamics simulations indicating easier reconstruction and faceting of the {110} compared to the {100} and {111} surface.17 Therefore, when designing a catalyst for CO2 activation, an oxygen deficient material with large {100} facets and wide {110} edge surfaces is likely to be optimal. This is supported by the IR measurements by Wu et al.,45 which demonstrated that carbonates are less strongly adsorbed to the less reactive octahedral nanoparticles (dominant {111}) than to the more active rods and cubes (dominant {100} and {110}).
Relative surface areas in the presence of H2O
Fig. 9C and D show the predicted area ratios of the {100}, {110} and {111} surface areas as a function of temperature and pH2O for stoichiometric and O-deficient CeNPs. As for CO2 adsorption, we predict that {111} surface is dominant, suggesting octahedral particles, with a small proportion of the {100} surface present close to the predicted TD,H2O for the {111} surface. Unlike with CO2 adsorption, however, we predict similar behaviour for both the stoichiometric and O-deficient surfaces, with the main difference being the higher TD,H2O from the latter. As a consequence, the stoichiometric CeNPs are predicted to express bare surfaces above the (relatively low) TD,H2O for the {111} surface, while the O-deficient CeNPs are predicted to have adsorbed H2O under a much wider range of conditions.Ziemba et al.103,104 showed that polycrystalline Au/CeO2 catalysts with dominant {111} surfaces had higher catalytic activity for the low-temperature water-gas shift reaction than octahedral, cubic and rod-like CeNPs, with the activity falling in the order of octahedral > cubic > rod-like. Since we predict the octahedral CeNPs to be the most stable, we would not expect a catalyst to lose performance over time due to surface reconstruction. Symington et al. predicted that O-deficient CeNPs should form truncated octahedra at low temperature.26 Under conditions of T = 300 K and pH2O = 1 bar, they predicted a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 ratio of the {111}, {110} and {100}, with H2O adsorbed to all surfaces, whereas we predict 100% {111} with adsorbed H2O. The difference may be because the 16.7% coverage modelled in the previous study is lower than the 25% in the present study, and the coverage would impact the relative energies of the three surfaces. This indicates that catalyst design should also consider the surface coverage, as this may influence the stability of a particular morphology.
30 ratio of the {111}, {110} and {100}, with H2O adsorbed to all surfaces, whereas we predict 100% {111} with adsorbed H2O. The difference may be because the 16.7% coverage modelled in the previous study is lower than the 25% in the present study, and the coverage would impact the relative energies of the three surfaces. This indicates that catalyst design should also consider the surface coverage, as this may influence the stability of a particular morphology.
Relative surface areas in the presence of CO2 and H2O
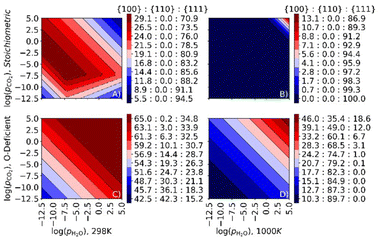
To examine the impact of co-adsorption on the surface area ratio, we plot surface phase diagrams as a function of pCO2 and pH2O at fixed T = 298 and 1000 K (Fig. 10). In this analysis, comparing the temperature to the selective and simultaneous desorption temperatures at a given set of pressures indicates whether the surface is bare or has CO2, H2O or both molecules co-adsorbed.For the stoichiometric surfaces, under most conditions, we predict a truncated octahedral shape at 298 K and an octahedral shape at 1000 K (Fig. 10A/B). At 298 K and pCO2 = pH2O = 1 bar, we predict that both H2O and CO2 are co-adsorbed to the nanoparticle surface, and that CO2 desorbs from the stoichiometric {110} and {111} surfaces at pCO2 < 10−9 and 10−4 bar, respectively, while H2O desorbs from both surfaces at pH2O < 10−5 bar. At 298 K, we predict a higher proportion of the {100} surface than with individual adsorption of CO2 or H2O (cf.Fig. 9A/C), indicating that the co-adsorption stabilises this surface and hence favours truncated octahedral over octahedral particles. At 1000 K and pCO2 = pH2O = 1 bar, we predict bare surfaces and a dominant {111} surface under all conditions except for high adsorbate partial pressures, indicating that the co-adsorption has relatively little effect on the surface area ratios at higher temperature.
Surface phase diagrams for the O-deficient surfaces are shown in Fig. 10C/D. At 298 K and pCO2 = pH2O = 1 bar, the area ratio of the {100}, {110} and {111} surfaces is 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2
0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34.8, which corresponds to a truncated octahedron (Fig. 10C). Under these conditions, CO2 and H2O are predicted to be co-adsorbed to all surfaces. At a lower partial pressure of 10−10 bar of both adsorbates, the surface area ratio is 51.6
34.8, which corresponds to a truncated octahedron (Fig. 10C). Under these conditions, CO2 and H2O are predicted to be co-adsorbed to all surfaces. At a lower partial pressure of 10−10 bar of both adsorbates, the surface area ratio is 51.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24.7
24.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23.8, i.e., including a higher proportion of the {110} surface, which implies a complex NP shape with significant proportions of all three surfaces exposed. We predict that both H2O and CO2 are adsorbed at the {100} surface, with H2O but not CO2 adsorbed at the {110} and {111} surfaces.
23.8, i.e., including a higher proportion of the {110} surface, which implies a complex NP shape with significant proportions of all three surfaces exposed. We predict that both H2O and CO2 are adsorbed at the {100} surface, with H2O but not CO2 adsorbed at the {110} and {111} surfaces.
At a higher temperature of 1000 K (Fig. 10D) the calculations predict a lower proportion of the {111} surface, and at pCO2 = pH2O = 1 bar the surface area ratio is 24.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74.8
74.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 for the {100}
1.0 for the {100}![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) {110}
{110}![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) {111} surfaces, indicating a rod-like morphology. Under these conditions H2O remains adsorbed to the {100} surface but the other two surfaces are bare. The adsorption of H2O may therefore stabilise the {100} surface.
{111} surfaces, indicating a rod-like morphology. Under these conditions H2O remains adsorbed to the {100} surface but the other two surfaces are bare. The adsorption of H2O may therefore stabilise the {100} surface.
Predicted particle morphologies
The surface area ratios from the surface phase diagrams provides an indication of the nanoparticle morphologies, but more accurate shapes can be predicted using the Wulff construction.105 To aid the reader in conceptualising these, Fig. 11A shows an idealised three-component phase diagram of the particle shapes obtained for different relative areas of the {100}, {110} and {111} surfaces, under the assumption that it is possible to obtain all ratios. However, in reality, it is likely that certain area ratios are not thermodynamically stable and would either be difficult to access synthetically and/or unstable to ageing,25,26,106 resulting in so-called “morphology gaps” analogous to the “solubility gaps” in phase diagrams of three-component alloys.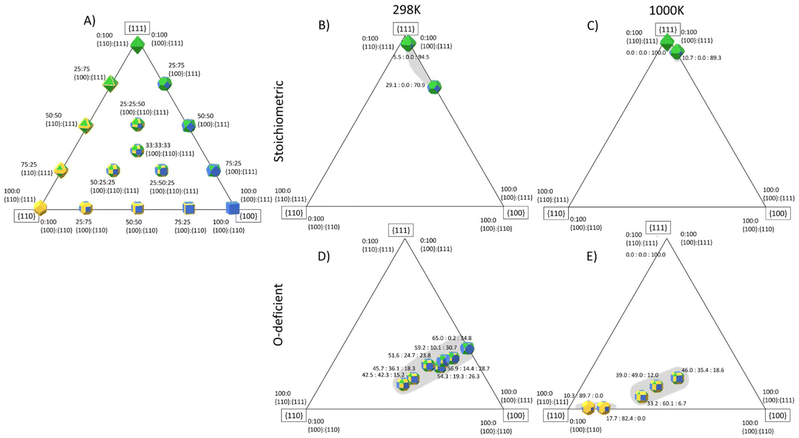 | ||
| Fig. 11 Predicted particle morphology of ceria nanoparticles (CeNPs) as a function of the relative areas of the {111} (green), {110} (yellow) and {100} surfaces (blue) surfaces. The three corners of the triangle show the shapes of particles formed from single surfaces, the three sides show the shapes obtained with different ratios of two surfaces areas, and points within the triangle show the shapes obtained with different proportions of all three surfaces. (A) Particle morphologies assuming all surface area ratios are accessible. (B)/(C) Stoichiometric CeNP shapes based on the area ratios predicted to be accessible at 298 K (B) and 1000 K (C). (D)/(E) O-deficient CeNP shapes based on the area ratios predicted to be accessible at 298 K (D) and 1000 K (E). In (B)–(E) the grey areas show regions of accessible surface area ratios where the corresponding CeNP shapes are thermodynamically stable. The Wulff constructions were generated using the WulffPack Python package.110 | ||
Based on our calculations, we predict the range of shapes accessible to stoichiometric and O-deficient CeNPs at 298 and 1000 K (Fig. 11B/C and D/E). As for the analysis in Fig. 10, the surface speciation can also be inferred from the calculated desorption temperatures. To aid discussion, we also list in Table 5, which CeNP shapes are predicted to be thermodynamically accessible at both 298 and 1000 K and pCO2/pH2O corresponding to low, high and intermediate adsorbate pressures.
At both 298 and 1000 K, we predict that stoichiometric CeNPs will adopt shapes based around truncated octahedra. At 1000 K and pCO2 = pH2O = 1 bar, the {100} surface is bare and therefore destabilised, resulting in a more octahedral shape, whereas at 298 K the adsorption of both molecules and consequent stabilisation results in stronger expression of this surface. On the other hand, for both high pCO2 = pH2O = 105 bar and low pCO2 = pH2O = 10−12 bar, we predict a more octahedral morphology with dominant {111} facets.
O-deficient CeNPs are predicted to form truncated octahedra at 298 K and pCO2 = pH2O = 1 bar. Under these conditions, CO2 and H2O are adsorbed to all three surfaces. Low adsorbate pressures increase the areas of {110} and {100} surfaces and result in a rhombicuboctahedral shape expressing all three surfaces but with a smaller proportion of the {111} surface. Under these conditions, we predict that H2O is adsorbed to all three surfaces while CO2 selectively desorbs from the {110} and {111} surfaces. At 1000 K and pCO2 = pH2O = 1 bar, we predict bare octahedra, whereas at high adsorbate pressures both CO2 and H2O are present on the {100} surface, resulting in a larger expression of the {111} and {100} surfaces and a cuboidal-like morphology. This is due to the adsorbates stabilising the {100} surface and is consistent with literature studies showing that the presence of H2O and CO2 can stabilise the {100} surface at the expense of the {111} surface.25,26,35
Previous work by Aneggi et al.27 predicted a significant effect of temperature on the shapes of CeNPs, and at temperatures above 773 K they predicted similar shapes to those our calculations identify as accessible in Fig. 11B and E.
Predicting particle morphologies is a powerful technique for linking the atomistic surface calculations to experiments. Morphological control is also key to exploiting facet-dependant properties, and studies have shown that the morphology is strongly linked to the catalytic activity.14,16,17,19,21,27,107
It has been shown that the particle shape can be controlled through the synthesis, and that it is possible to access shapes that may not be the most thermodynamically preferred.9–11,14–22 However, over time and under catalytic cycling the nanoparticles will experience a thermodynamic driving force to reconstruct to the most stable structures under their operating conditions. Our predicted morphologies can therefore be used to aid in the design of catalysts and to provide an indication of how ageing might affect long-term performance. For example, Caddeo et al.18 found that nanocubes show the highest redox catalytic ability, due to the greatest expression of reactive {100} surfaces,108 and our study predicts that such shapes should be accessible under controlled conditions.
Discussion
Finally, we combine our predictions with experimental evidence for which particle shapes/surfaces are best for certain applications to develop some more general guidelines for the design and optimisation of ceria-based catalysts.The water-gas shift reaction, which converts CO and H2O to CO2 and H2, depends on the presence of surface-bound H2O but can be deactivated or “poisoned” by the presence of CO2.44,48 Nanocubes are expected to promote this reaction as the {100} surface has a higher affinity for H2O.49 It has also been demonstrated that CO2 and H2O can stabilise {100} over {111} facets and therefore inhibit the formation of more stable octahedral nanoparticles with reduced expression of the desired {100} surface.26,35 We predict that the proportion of the {100} surface could be enhanced and/or maintained on ageing under O-deficient conditions, suggesting that a reducing environment may be optimal. The selective stabilisation of the {100} surface can be related to the ease with which water can dissociate on this surface, evident from the much lower energy for dissociative compared to molecular adsorption (−2.75 vs. −0.7 eV; this energy difference is largest for the {100} surface).
It is also well known that the {100} surface can be “capped” by capping agents that can influence the resulting morphology,109 and it has been suggested that H2O could act as such a species. In this scenario, adsorption of H2O would block mass transport to the {100} surface and preserve the desired cuboidal morphology.26
Our calculations support this by showing that H2O binds strongly to, and therefore difficult to remove from, the {100} surface, and that it can stabilise the {100} surface over the {111} facet. Our calculations further highlight the impact of temperature and adsorbate partial pressure in maintaining this desirable particle morphology. At room temperature and pressure, H2O is adsorbed to the {100} surface, but under typical high-temperature operation, and assuming some degree of O-deficiency in the surfaces, the operating temperature would need to be kept below 1117 K to maintain the blocking effect. If higher operating temperatures were required, then the partial pressure of H2O could be increased to compensate.
A second example of where our work may have implications in catalyst design is when using supercritical fluids (SCFs) during synthesis.111,112 Symington et al.25 predicted that that CeNPs treated in supercritical CO2 will become nanocubes but did not consider the presence of H2O. It has been shown that in the presence of supercritical H2O ceria forms nanocubes. This morphology is desirable because nanocubes have been shown to exhibit high catalytic activity toward the deNOx reaction.111,113 However, our results suggest that under supercritical H2O (646 K and pH2O = 221 bar) an octahedral morphology is preferred. This in turn implies that the formation of nanocubes in the experimental studies with supercritical H2O may be a kinetic effect and that the catalysts may experience a thermodynamic driving force for transformation to an octahedral morphology over time.
Conclusions
In summary, we have outlined a comprehensive theoretical framework for analysing surface speciation and predicting the thermodynamically stable particle morphologies accessible under a given set of environmental conditions. Advances in the synthesis of nanoparticles allow specific morphologies to be targeted, and our methodology complements these efforts by providing a means to determine whether a target shape is thermodynamically stable under the environmental conditions of a given target application. This is critical for catalysis, particularly in higher-temperature processes, where it is essential that the catalysts can undergo multiple catalytic cycles without loss of activity, and, since activity is generally morphology dependent, nanoparticulate catalysts must maintain their shapes over their lifetime.In this work we have investigated CeO2 as an industrially important catalyst. Our methodology allows us to map the thermodynamically stable shapes of CeO2 nanoparticles as a function of temperature, CO2 and H2O adsorbate pressure, and surface composition, which in turn enables thermodynamically-driven evolution to the particle morphology under operating conditions to be anticipated and understood. In particular, we have predicted that co-adsorbed CO2 and H2O stabilize the {100} and {110} surfaces, and particularly the O-deficient surfaces, producing cuboidal morphologies. If this morphology is desirable, our modelling therefore suggests conditions to obtain it. Alternatively, our modelling predicts that nanoparticles prepared in other, kinetically trapped morphologies will experience a drive toward reconstruction to this shape during thermal ageing, which could have a detrimental impact on performance if not anticipated.
Finally, we note that the modelling procedure we adopt in this work is general and could be applied to other systems and/or adsorbates, thus providing insight into the nanoparticulate forms of other fluorite materials with similar industrially important applications.
Future studies should focus on increasing the complexity of the DFT calculations by including adsorbates of different nature and their concentration, as well as the complex morphology of nanoparticles surfaces including edges, kinks, and steps. Furthermore, ceria can still maintain its structure and be reduced with very high concentrations of Ce3+,114 and while our protocol will be able to account for all range of oxygen partial pressure, of course this would need to be developed in further research.
Data access statement
Raw data related to this research are available at https://doi.org/10.17632/9hd54s429tAuthor contributions
Conceptualization: S. M., S. C. P., M. M.; data curation: S. M., M. M.; formal analysis: S. M., J. S. T., J. M. F., J. M. S., M. M.; funding acquisition: L. J. G., D. J. C., M. M.; investigation: S. M., L. J. G., D. J. C., M. M.; methodology: S. M., J. S. T., A. R. S., J. M. S., M. M.; project administration: M. M.; resources: L. J. G., D. J. C., M. M.; supervision: L. J. G., D. J. C., M. M.; validation: S. M., J. M. S., M. M.; visualization: S. M., J. M. S., L. J. G., D. J. C., S. C. P., M. M.; writing – original draft: S. M., J. M. S., M. M.; writing – review & editing: S. M., A. R. S., J. S. T., J. M. F., J. M. S., L. J. G., D. J. C., S. C. P., M. M.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the University of Huddersfield (UoH) EPSRC-DTP competition 2018–19 (EP/R513234/1) for funding SM. JMS is grateful to UK Research and Innovation (UKRI) for the award of a Future Leaders Fellowship (MR/T043121/1), and to the University of Manchester (UoM) for the previous support of a UoM Presidential Fellowship. Calculations were run on the ARCHER and ARCHER2 UK National Supercomputing Services via our membership of the UK HEC Materials Chemistry Consortium (MCC; EPSRC EP/L000202/1, EP/R029431/1, EP/X035859/1). Analysis was performed on the Orion and Violeta computing facilities at UoH.References
- J. J. Delgado, E. del Río, X. Chen, G. Blanco, J. M. Pintado, S. Bernal and J. J. Calvino, Catalysis by Ceria and Related Materials, 2013, 47–138 CrossRef.
- D. R. Mullins, Surf. Sci. Rep., 2015, 70, 42–85 CrossRef CAS.
- L. Vivier and D. Duprez, ChemSusChem, 2010, 3, 654–678 CrossRef CAS PubMed.
- A. S. Karakoti, N. A. Monteiro-Riviere, R. Aggarwal, J. P. Davis, R. J. Narayan, W. T. Seif, J. McGinnis and S. Seal, JOM, 2008, 60, 33–37 CrossRef CAS PubMed.
- T. Montini, M. Melchionna, M. Monai and P. Fornasiero, Chem. Rev., 2016, 116, 5987–6041 CrossRef CAS PubMed.
- J. Wu, X. Wang, Q. Wang, Z. Lou, S. Li, Y. Zhu, L. Qin and H. Wei, Chem. Soc. Rev., 2019, 48, 1004–1076 RSC.
- Y. Huang, J. Ren and X. Qu, Chem. Rev., 2019, 119, 4357–4412 CrossRef CAS PubMed.
- F. Wei, C. J. Neal, T. S. Sakthivel, Y. Fu, M. Omer, A. Adhikary, S. Ward, K. M. Ta, S. Moxon, M. Molinari, J. Asiatico, M. Kinzel, S. N. Yarmolenko, V. San Cheong, N. Orlovskaya, R. Ghosh, S. Seal and M. Coathup, Bioact. Mater., 2023, 21, 547–565 CAS.
- Z. Tan, G. Li, H. L. Chou, Y. Li, X. Yi, A. H. Mahadi, A. Zheng, S. C. Edman Tsang and Y. K. Peng, ACS Catal., 2020, 10, 4003–4011 CrossRef CAS.
- T. Sakthivel, S. Das, A. Kumar, D. L. Reid, A. Gupta, D. C. Sayle and S. Seal, ChemPlusChem, 2013, 78, 1446–1455 CrossRef CAS PubMed.
- M. J. Manto, P. Xie and C. Wang, ACS Catal., 2017, 7, 1931–1938 CrossRef CAS.
- C. Yang, X. Yu, S. Heißler, A. Nefedov, S. Colussi, J. Llorca, A. Trovarelli, Y. Wang and C. Wöll, Angew. Chem., Int. Ed., 2017, 56, 375–379 CrossRef CAS PubMed.
- C. Yang, M. Capdevila-Cortada, C. Dong, Y. Zhou, J. Wang, X. Yu, A. Nefedov, S. Heißler, N. López, W. Shen, C. Wöll and Y. Wang, J. Phys. Chem. Lett., 2020, 11, 7925–7931 CrossRef CAS PubMed.
- T. X. T. Sayle, M. Molinari, S. Das, U. M. Bhatta, G. Möbus, S. C. Parker, S. Seal and D. C. Sayle, Nanoscale, 2013, 5, 6063–6073 RSC.
- L. M. Morgan, M. Molinari, A. Corrias and D. C. Sayle, ACS Appl. Mater. Interfaces, 2018, 10, 32510–32515 CrossRef CAS PubMed.
- T. X. T. Sayle, M. Cantoni, U. M. Bhatta, S. C. Parker, S. R. Hall, G. Möbus, M. Molinari, D. Reid, S. Seal and D. C. Sayle, Chem. Mater., 2012, 24, 1811–1821 CrossRef CAS.
- U. Castanet, C. Feral-Martin, A. Demourgues, R. L. Neale, D. C. Sayle, F. Caddeo, J. M. Flitcroft, R. Caygill, B. J. Pointon, M. Molinari and J. Majimel, ACS Appl. Mater. Interfaces, 2019, 11, 11384–11390 CrossRef CAS PubMed.
- F. Caddeo, A. Casu, D. Loche, L. M. Morgan, G. Mountjoy, C. O'Regan, M. F. Casula, S. Hayama, A. Corrias and A. Falqui, J. Colloid Interface Sci., 2021, 583, 376–384 CrossRef CAS PubMed.
- F. Polo-Garzon, Z. Bao, X. Zhang, W. Huang and Z. Wu, ACS Catal., 2019, 9, 5692–5707 CrossRef CAS.
- Z. L. Wang and X. Feng, J. Phys. Chem. B, 2003, 107, 13563–13566 CrossRef CAS.
- A. Trovarelli and J. Llorca, ACS Catal., 2017, 7, 4716–4735 CrossRef CAS.
- Y. Lin, Z. Wu, J. Wen, K. R. Poeppelmeier and L. D. Marks, Nano Lett., 2014, 14, 191–196 CrossRef CAS PubMed.
- G. Möbus, Z. Saghi, D. C. Sayle, U. M. Bhatta, A. Stringfellow and T. X. T. Sayle, Adv. Funct. Mater., 2011, 21, 1971–1976 CrossRef.
- J. V. Kildgaard, H. A. Hansen and T. Vegge, Mater. Today Adv., 2020, 8, 100111 CrossRef.
- A. R. Symington, R. M. Harker, M. T. Storr, M. Molinari and S. C. Parker, J. Phys. Chem. C, 2020, 124, 23210–23220 CrossRef CAS.
- A. R. Symington, M. Molinari, S. Moxon, J. M. Flitcroft, D. C. Sayle and S. C. Parker, J. Phys. Chem. C, 2020, 124, 3577–3588 CrossRef CAS.
- E. Aneggi, D. Wiater, C. De Leitenburg, J. Llorca and A. Trovarelli, ACS Catal., 2014, 4, 172–181 CrossRef CAS.
- S. Chen, T. Cao, Y. Gao, D. Li, F. Xiong and W. Huang, J. Phys. Chem. C, 2016, 120, 21472–21485 CrossRef CAS.
- N. Ta, J. Liu, S. Chenna, P. A. Crozier, Y. Li, A. Chen and W. Shen, J. Am. Chem. Soc., 2012, 134, 20585–20588 CrossRef CAS PubMed.
- K. Zhou and Y. Li, Angew. Chem., Int. Ed., 2012, 51, 602–613 CrossRef CAS PubMed.
- L. Litti, J. Reguera, F. J. Garciá De Abajo, M. Meneghetti and L. M. Liz-Marzán, Nanoscale Horiz., 2020, 5, 102–108 RSC.
- P. Zhao, Z. Cao, X. Liu, P. Ren, D. B. Cao, H. Xiang, H. Jiao, Y. Yang, Y. W. Li and X. D. Wen, ACS Catal., 2019, 9, 2768–2776 CrossRef CAS.
- P. Stelmachowski, K. Ciura and G. Grzybek, Catal. Sci. Technol., 2016, 6, 5554–5560 RSC.
- Y. Fu, C. J. Neal, E. Kolanthai, S. Munir, K. M. Ta, M. Molinari and S. Seal, Colloids Surf., A, 2023, 679, 132616 CrossRef CAS.
- T. Wu, N. López, T. Vegge and H. A. Hansen, J. Catal., 2020, 388, 1–10 CrossRef CAS.
- M. Molinari, S. C. Parker, D. C. Sayle and M. S. Islam, J. Phys. Chem. C, 2012, 116, 7073–7082 CrossRef CAS.
- S. Kumar and P. K. Schelling, J. Chem. Phys., 2006, 125, 204704 CrossRef PubMed.
- M. Fronzi, S. Piccinin, B. Delley, E. Traversa and C. Stampfl, Phys. Chem. Chem. Phys., 2009, 11, 9188–9199 RSC.
- A. Röckert, J. Kullgren and K. Hermansson, J. Chem. Theory Comput., 2022, 18, 7683–7694 CrossRef PubMed.
- X. Sun, E. Vøllestad, P. M. Rørvik, S. Prodinger, G. N. Kalantzopoulos, A. Chatzitakis and T. Norby, Appl. Surf. Sci., 2023, 611, 155590 CrossRef CAS.
- K. R. Hahn, M. Iannuzzi, A. P. Seitsonen and J. Hutter, J. Phys. Chem. C, 2013, 117, 1701–1711 CrossRef CAS.
- Z. Cheng, B. J. Sherman and C. S. Lo, J. Chem. Phys., 2013, 138, 014702 CrossRef PubMed.
- P. M. Albrecht, D. E. Jiang and D. R. Mullins, J. Phys. Chem. C, 2014, 118, 9042–9050 CrossRef CAS.
- X. Liu, W. Ruettinger, X. Xu and R. Farrauto, Appl. Catal., B, 2005, 56, 69–75 CrossRef CAS.
- Z. Wu, M. Li and S. H. Overbury, J. Catal., 2012, 285, 61–73 CrossRef CAS.
- M. Nolan and G. W. Watson, J. Phys. Chem. B, 2006, 110, 16600–16606 CrossRef CAS PubMed.
- A. Kumar, S. Das, P. Munusamy, W. Self, D. R. Baer, D. C. Sayle and S. Seal, Environ. Sci. Nano, 2014, 1, 516–532 RSC.
- C. H. Kim and L. T. Thompson, J. Catal., 2005, 230, 66–74 CrossRef CAS.
- Z. Tan, Y. Chen, J. Zhang, J. Chou, A. Hu and Y. Peng, Chem. – Eur. J., 2020, 26, 10598–10606 CrossRef CAS PubMed.
- T. Montini, M. Melchionna, M. Monai and P. Fornasiero, Chem. Rev., 2016, 116, 5987–6041 CrossRef CAS PubMed.
- J. R. Scheffe, M. Welte and A. Steinfeld, Ind. Eng. Chem. Res., 2014, 53, 2175–2182 CrossRef CAS.
- P. Furler, J. R. Scheffe and A. Steinfeld, Energy Environ. Sci., 2012, 5, 6098–6103 RSC.
- M. Tou, J. Jin, Y. Hao, A. Steinfeld and R. Michalsky, React. Chem. Eng., 2019, 4, 1431–1438 RSC.
- A. Haeussler, S. Abanades, J. Jouannaux, M. Drobek, A. Ayral and A. Julbe, AIMS Mater. Sci., 2019, 6, 657–684 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- M. Nolan, S. Grigoleit, D. C. Sayle, S. C. Parker and G. W. Watson, Surf. Sci., 2005, 576, 217–229 CrossRef CAS.
- M. Nolan, S. C. Parker and G. W. Watson, Surf. Sci., 2005, 595, 223–232 CrossRef CAS.
- D. O. Scanlon, N. M. Galea, B. J. Morgan and G. W. Watson, J. Phys. Chem. C, 2009, 113, 11095–11103 CrossRef CAS.
- J. Paier, C. Penschke and J. Sauer, Chem. Rev., 2013, 113, 3949–3985 CrossRef CAS PubMed.
- X. Zhang, L. Zhu, Q. Hou, J. Guan, Y. Lu, T. W. Keal, J. Buckeridge, C. R. A. Catlow and A. A. Sokol, Chem. Mater., 2023, 35, 207–227 CrossRef CAS PubMed.
- X. Zhang, T. Liu, L. Zhu, J. Guan, Y. Lu, T. W. Keal, J. Buckeridge, C. R. A. Catlow and A. A. Sokol, Angew. Chem., Int. Ed., 2023, 62, e202308411 CrossRef CAS PubMed.
- D. Fernández-Torre, K. Kośmider, J. Carrasco, M. V. Ganduglia-Pirovano and R. Pérez, J. Phys. Chem. C, 2012, 116, 13584–13593 CrossRef.
- C. Artini, M. Pani, M. M. Carnasciali, J. R. Plaisier and G. A. Costa, Inorg. Chem., 2016, 55, 10567–10579 CrossRef CAS PubMed.
- Y. Ma, Y. Ma, G. Giuli, H. Euchner, A. Groß, G. O. Lepore, F. d'Acapito, D. Geiger, J. Biskupek, U. Kaiser, H. M. Schütz, A. Carlsson, T. Diemant, R. J. Behm, M. Kuenzel, S. Passerini and D. Bresser, Adv. Energy Mater., 2020, 10, 2000783 CrossRef CAS.
- D. J. M. Bevan, J. Inorg. Nucl. Chem., 1955, 1, 49–59 CrossRef CAS.
- J. L. F. Da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 193108 CrossRef.
- P. M. Oliver, S. C. Parker and W. C. Mackrodt, Modell. Simul. Mater. Sci. Eng., 1993, 1, 755 CrossRef CAS.
- G. W. Watson, E. T. Kelsey, N. H. de Leeuw, D. J. Harris and S. C. Parker, J. Chem. Soc., Faraday Trans., 1996, 92, 433–438 RSC.
- A. Symington, J. Tse, M. Molinari, A. Marmier and S. Parker, J. Open Source Softw., 2019, 4, 1210–1211 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. S. Tse, M. Molinari, S. C. Parker and A. R. Symington, J. Open Source Softw., 2022, 7, 4014 CrossRef.
- J. S. Tse, J. Grant, J. M. Skelton, L. J. Gillie, R. Zhu, G. L. Pesce, R. J. Ball, S. C. Parker and M. Molinari, Phys. Chem. Chem. Phys., 2023, 25, 18011–18022 RSC.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080 CrossRef CAS PubMed.
- C.-Y. Zhou, D. Wang and X.-Q. Gong, Phys. Chem. Chem. Phys., 2019, 21, 19987–19994 RSC.
- K. M. Ta, D. J. Cooke, L. J. Gillie, S. C. Parker, S. Seal, P. B. Wilson, R. M. Phillips, J. M. Skelton and M. Molinari, J. Phys. Chem. C, 2023, 127, 20183–20193 CrossRef CAS PubMed.
- M. Molinari, A. R. Symington, D. C. Sayle, T. S. Sakthivel, S. Seal and S. C. Parker, ACS Appl. Bio Mater., 2019, 2, 1098–1106 CrossRef CAS PubMed.
- C. Yang, F. Bebensee, J. Chen, X. Yu, A. Nefedov and C. Wöll, ChemPhysChem, 2017, 18, 1874–1880 CrossRef CAS PubMed.
- J. Zhang, X.-Q. Gong and G. Lu, Surf. Sci., 2015, 632, 164–173 CrossRef CAS.
- T. X. T. Sayle, S. C. Parker and C. R. A. Catlow, Surf. Sci., 1994, 316, 329–336 CrossRef CAS.
- R. Farra, S. Wrabetz, M. E. Schuster, E. Stotz, N. G. Hamilton, A. P. Amrute, J. Pérez-Ramírez, N. López and D. Teschner, Phys. Chem. Chem. Phys., 2013, 15, 3454–3465 RSC.
- D. R. Mullins, P. M. Albrecht, T.-L. Chen, F. C. Calaza, M. D. Biegalski, H. M. Christen and S. H. Overbury, J. Phys. Chem. C, 2012, 116, 19419–19428 CrossRef CAS.
- B. Chen, Y. Ma, L. Ding, L. Xu, Z. Wu, Q. Yuan and W. Huang, J. Phys. Chem. C, 2013, 117, 5800–5810 CrossRef CAS.
- M. B. Watkins, A. S. Foster and A. L. Shluger, J. Phys. Chem. C, 2007, 111, 15337–15341 CrossRef CAS.
- S. Gritschneder and M. Reichling, Nanotechnology, 2007, 18, 044024 CrossRef.
- M. A. Henderson, C. L. Perkins, M. H. Engelhard, S. Thevuthasan and C. H. F. Peden, Surf. Sci., 2003, 526, 1–18 CrossRef CAS.
- V. Matolín, I. Matolínová, F. Dvořák, V. Johánek, J. Mysliveček, K. C. Prince, T. Skála, O. Stetsovych, N. Tsud, M. Václavů and B. Šmíd, Catal. Today, 2012, 181, 124–132 CrossRef.
- M. W. Chase, NIST-JANAF Thermochemical Tables, NIST, American Institute of Physics, 4th edn, 1998 Search PubMed.
- S. Moxon, A. R. Symington, J. S. Tse, J. Dawson, J. M. Flitcroft, S. C. Parker, D. J. Cooke, R. M. Harker and M. Molinari, Phys. Chem. Chem. Phys., 2020, 22, 7728–7737 RSC.
- S. D. Senanayake and D. R. Mullins, J. Phys. Chem. C, 2008, 112, 9744–9752 CrossRef CAS.
- S. D. Senanayake, D. Stacchiola, J. Evans, M. Estrella, L. Barrio, M. Pérez, J. Hrbek and J. A. Rodriguez, J. Catal., 2010, 271, 392–400 CrossRef CAS.
- L. Kundakovic, D. R. Mullins and S. H. Overbury, Surf. Sci., 2000, 457, 51–62 CrossRef CAS.
- T. Staudt, Y. Lykhach, N. Tsud, T. Skála, K. C. Prince, V. Matolín and J. Libuda, J. Catal., 2010, 275, 181–185 CrossRef CAS.
- G. S. Herman, Y. J. Kim, S. A. Chambers and C. H. F. Peden, Langmuir, 1999, 15, 3993–3997 CrossRef CAS.
- A. Barroso Bogeat, G. Blanco, J. M. Pintado, D. Goma and J. J. Calvino Gámez, Surf. Interfaces, 2021, 26, 101353 CrossRef CAS.
- N. Hashimoto, K. Mori, K. Asahara, S. Shibata, H. Jida, Y. Kuwahara and H. Yamashita, Langmuir, 2021, 37, 5376–5384 CrossRef CAS PubMed.
- M. Nolan, S. C. Parker and G. W. Watson, J. Phys. Chem. B, 2006, 110, 2256–2262 CrossRef CAS PubMed.
- P. R. L. Keating, D. O. Scanlon and G. W. Watson, J. Phys.: Condens. Matter, 2009, 21, 405502 CrossRef CAS PubMed.
- M. Ziemba, M. V. Ganduglia-Pirovano and C. Hess, Faraday Discuss., 2021, 229, 232–250 RSC.
- M. Ziemba, C. Schilling, M. V. Ganduglia-Pirovano and C. Hess, Acc. Chem. Res., 2021, 54, 2884–2893 CrossRef CAS PubMed.
- G. Wulff, Z. Kristallogr. – Cryst. Mater., 1901, 34, 449–530 CrossRef CAS.
- D. C. Sayle, F. Caddeo, L. M. Morgan, R. L. Neale, T. X. T. Sayle, C. Brambila, J. Nutter, U. Bhatta, K. M. Ta, J. M. Flitcroft, T. S. Sakthivel, S. Seal, G. Möbus and M. Molinari, Nano Today, 2023, 51, 101916 CrossRef CAS.
- K. Zhou, X. Wang, X. Sun, Q. Peng and Y. Li, J. Catal., 2005, 229, 206–212 CrossRef CAS.
- H. X. Mai, L. D. Sun, Y. W. Zhang, R. Si, W. Feng, H. P. Zhang, H. C. Liu and C. H. Yan, J. Phys. Chem. B, 2005, 109, 24380–24385 CrossRef CAS PubMed.
- M. J. Davies, P. R. Kenway, P. J. Lawrence, S. C. Parker, W. C. Mackrodt and P. W. Tasker, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 555–563 RSC.
- M. J. Rahm and P. Erhart, J. Open Source Softw., 2020, 5, 1944 CrossRef.
- T. Adschiri, Y.-W. Lee, M. Goto and S. Takami, Green Chem., 2011, 13, 1380–1390 RSC.
- M. K. M. Lane and J. B. Zimmerman, Green Chem., 2019, 21, 3769–3781 RSC.
- J. Zhang, H. Kumagai, K. Yamamura, S. Ohara, S. Takami, A. Morikawa, H. Shinjoh, K. Kaneko, T. Adschiri and A. Suda, Nano Lett., 2011, 11, 361–364 CrossRef CAS PubMed.
- X. Hao, A. Yoko, C. Chen, K. Inoue, M. Saito, G. Seong, S. Takami, T. Adschiri and Y. Ikuhara, Small, 2018, 14, 1802915 CrossRef PubMed.
- A. S. Pugazhendhi, C. J. Neal, K. M. Ta, M. Molinari, U. Kumar, F. Wei, E. Kolanthai, A. Ady, C. Drake, M. Hughes, S. Yooseph, S. Seal and M. J. Coathup, Biomater., 2024, 307, 122527 CrossRef CAS PubMed.
- N. Anwar, R. M. Harker, M. T. Storr, M. Molinari and C. K. Skylaris, Comput. Mater. Sci., 2023, 229, 112396 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |