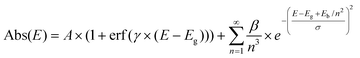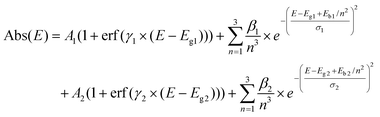Quantum-confined bismuth iodide perovskite nanocrystals in mesoporous matrices

Abstract

Bismuth iodide perovskite nanocrystals are considered a viable alternative to the Pb halide ones due to their reduced toxicity and increased stability. However, it is still challenging to fabricate nanocrystals with a small and controlled size, and their electronic properties are not well understood. Here, we propose the growth of Bi iodide perovskite nanocrystals using different mesoporous silica with ordered pores of controlled diameter as templates. We obtain a series of confined Cs₃Bi₂I₉ and MA₃Bi₂I₉ perovskites with diameters of 2.3, 3.7, 7.4, and 9.2 nm, and precise size control. The complex absorption spectra of the encapsulated perovskites cannot be properly fitted using classical Tauc or Elliott formalisms. By fitting the spectra with a modified Elliott formula, the bandgap values and exciton binding energies (70–400 meV) could be extracted. The calculated bandgaps scale with the pore sizes. Using a combined experimental and theoretical approach, we demonstrate for the first time quantum confinement in 0D Bi-iodide perovskite nanocrystals.

---

Introduction

Lead halide perovskites (LHPs) with general formula APbX₃ (A = Cs⁺, methylammonium, MA; B = Pb²⁺; X = I⁻, Br⁻ or Cl⁻) have recently emerged spectacularly as a promising class of materials for optoelectronics. Due to their excellent optical and electronic properties (high absorption coefficients, suitable bandgaps, spontaneous dissociation of excitons), low cost and ease of processing, very efficient and record-breaking LHP-based optoelectronic devices, such as solar cells and light-emitting diodes, have been fabricated.^1,2 However, the widespread applications of LHPs are currently limited by the toxicity of lead. Some of the most promising alternative, less toxic materials are bismuth halide perovskites (BiHPs), A₃Bi₂X₉.³ They are attractive due to their bandgaps in the visible range (1.8–2.7 eV), defect tolerance, and the much lower toxicity of bismuth as compared to lead.⁴ BiHPs have a peculiar structure: in contrast to LHPs, a 3D perovskite network of corner-sharing PbX₆ octahedra, the BiHPs form vacancy-ordered networks of bismuth halide Bi₂X₉³⁻ dioctahedral clusters, separated by organic (MA) or inorganic (Cs) cations. In the case of A₃Bi₂I₉, the dioctahedra are isolated without the direct formation of electronic bands, resulting in a 0D perovskite structure with intriguing properties in between crystalline semiconductors and molecular crystals. As a result, the electronic coupling between the dioctahedra is considered to be rather weak. In contrast to the narrow bands of 3D LHPs, the emission of BiHP is generally characterized by large bands stemming from different local environments of free and self-trapped excitons.⁵ The charge transport properties in low-dimensional perovskites are less adapted for optoelectronic devices with strongly anisotropic transport and low charge mobility compared to the 3D ones. At the same time, the localized excitons with high binding energy can undergo efficient radiative recombination, which is beneficial for light-emitting devices.⁶

The properties of halogenated perovskite crystals can be tuned and enhanced by reducing their size and controlling their surface chemistry. For instance, the synthesis of colloidal LHP nanocrystals (NCs) has recently been strongly developed.⁷ BiHPs NCs that are Pb-free, have high photoluminescence (PL) quantum yields, and relatively low polydispersity have also been actively synthesized, mainly by hot-injection or ligand-assisted reprecipitation approaches.^3,8 Colloidal NCs are typically synthesized in solution using surface ligands for stabilization. Meanwhile, the presence of ligands on the surface of nanoparticles can hinder charge transfer in photocatalytic systems. However, removing these ligands may induce degradation and introduce surface defects.⁹ To address this issue, nanoporous matrices with ordered porosity can be used as hosts for the encapsulation of nanoparticles. This allows for fine control of the size and shape of the NCs, while also protecting their surface. Additionally, the use of nanoporous matrices eliminates the need for surface ligands and provides easy access to small-sized nanoparticles. Furthermore, mesoporous silica matrices with ordered nanometer-sized channels can serve as ideal platforms for studying the optical and electronic properties of the encapsulated materials.^10,11

The encapsulation of metal halide perovskites was first demonstrated only recently. For instance, mesoporous silica or alumina have been used to confine LHP NCs in pores ranging from 3–12 nm. Some studies have shown strong quantum confinement effects depending on the pore size.^12–14 Furthermore, encapsulating LHP systems in this way can significantly enhance their environmental stability by preventing the diffusion of degrading gases, such as water vapor and O₂.¹⁵ Most studies focus on encapsulating LHPs in mesoporous matrices. However, only a few works have extended this approach to lead-free perovskites, such as Cs₂AgBiBr₆,¹⁶ Cs₂SnX₆,¹⁷ and Cs₃Bi₂Br₉.^18,19 Existing reports on the latter focus on the photocatalytic applications of the obtained materials, with no study on their fundamental optical properties. Little is known about the properties of BiHP NCs in the quantum confinement regime. Synthesizing small-sized perovskite NCs in a controlled manner is generally challenging due to the fast reaction kinetics observed in classical syntheses.

Excitonic quantum confinement can be achieved in LHP NCs chemically, through control of the thermodynamic equilibrium of the halides, resulting in small 0D NCs in solution;²⁰ structurally, by synthesizing 1D- or 2D-confined nanoparticles such as nanoplatelets;²¹ or spatially, by confining the perovskites in the pores of nanoporous materials, as previously mentioned. Quantum confinement in lead-free halide perovskites has been studied to a lesser extent. In the case of BiHPs, only a few works report the reliable synthesis of sufficiently small 0D NCs^22,23 or nanoplatelets.^21,24,25 Furthermore, there is a large controversy surrounding the presence of quantum confinement in such structures due to several factors. Firstly, there is confusion around the absorption and emission properties of BiHPs, which are often used as an indicator of quantum confinement. For instance, if chemically synthesized cesium bismuth bromide NCs are not properly purified, the optical signatures of several reaction products can be observed: Cs₃Bi₂Br₉, Cs₃BiBr₆ NCs, but also oleic acid, oleylamine, and BiBr₃ salt used for the synthesis. These products can be luminescent with peaks in the same region (300–450 nm) and could be mistakenly assigned to the confined structure signatures.^24,26,27 Secondly, unlike LHPs, there is limited information available on the fundamental physical properties of BiHPs, such as electron/hole effective masses, Bohr exciton radius, and exciton binding energy. It is important to note that this lack of information poses a challenge for the development of BiHP-based devices. The possibility of quantum confinement in 0D perovskite nanostructures is currently under debate. While excitons are already confined within the [Bi₂X₉]³⁻ dioctahedra with high effective masses of the charge carriers and thus high exciton binding strength, the wavefunctions of isolated dioctahedra can still extend spatially enough to overlap, albeit with less interaction than in 3D LHPs.

In this work, we encapsulated several bismuth iodide perovskites in mesoporous silica matrices with ordered pores. The pore sizes were controlled within a range of 2 to 9 nm to precisely tune the size of the perovskite nanocrystals within the pores. These mesoporous matrices provide an ideal platform to study the fundamental influence of the perovskite crystallite sizes on their optical and electronic properties. A modified Elliott's model was used to fit the absorption spectra and extract the bandgap values and exciton binding energies of Cs₃Bi₂I₉ and MA₃Bi₂I₉ perovskites in the pores. As the main result, we demonstrate, for the first time, that the bandgap of the confined 0D BiHP perovskite NCs is dependent on the size of the pores, strongly indicating quantum confinement effects. DFT calculations were used to model the electronic structure of bismuth halide perovskite clusters of different sizes, confirming this hypothesis.

Results and discussion

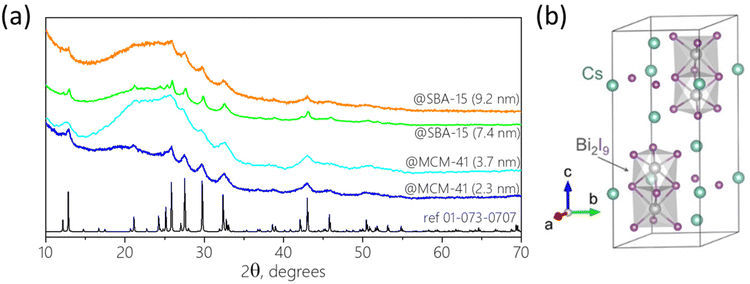
Bismuth iodide perovskites A₃Bi₂I₉ (A = MA, Cs) were grown in the pores of various mesoporous silica matrices with well-ordered pores, such as SBA-15 (7.4 and 9.2 nm pore size) and MCM-41 (2.3 and 3.7 nm pore size) by solution impregnation followed by drying and crystallization at 100 °C. First, BiHP-based nanomaterials were studied with the initial loading of 14.5% mass (perovskite vs. silica). For MA₃Bi₂I₉, electron microscopy images show efficient growth of the perovskite nanocrystals within the pore channels of SBA-15 with 7.4 nm pore diameter (Fig. 1 and S1, S2†). The NCs are located within the pores, and are well isolated with homogeneous sizes of 6.5–7 nm corresponding well to the pore diameter. The images obtained for confined Cs₃Bi₂I₉ were less clear likely due to the material's sensitivity to electron beam damage, as previously observed in similar systems (Fig. S3†).^12,16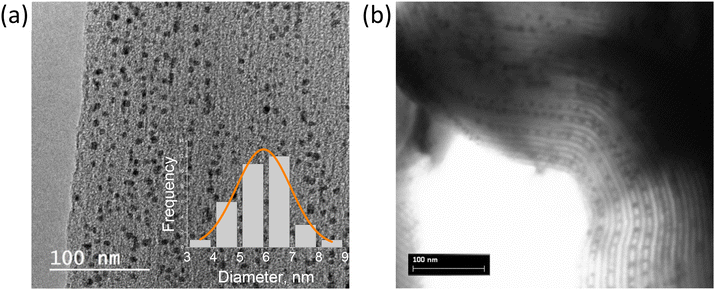

Fig. 1 TEM (a) and STEM (b) images of MA₃Bi₂I₉@SBA-15 (7.4 nm pore size, 14.5 mass%), inset shows the size histogram of the NCs in the pores.

Textural properties of the samples were studied by N₂ physisorption. Upon perovskite addition, the total (micro- and meso-sized) pore volume decreases from 0.90 cm³ g⁻¹ for pure SBA-15 matrix with 7.4 nm pore size to 0.67 cm³ g⁻¹ for 14.5 mass% loading of MA₃Bi₂I₉ (Tables S1, S2 and Fig. S4, S5†), while the specific surface area decreases from 828 to 500 m² g⁻¹. This demonstrates that the MA₃Bi₂I₉ perovskite indeed grows inside the pores of SBA-15 reducing their volume.

Powder X-ray diffractograms (XRD) of the nanocomposites exhibit significant background peaks from the amorphous SBA-15 and MCM-41 silica matrices, along with well-defined peaks corresponding to the confined perovskites for all compositions studied (Fig. 2a and S6†). The perovskite phase peaks are significantly broadened compared to the bulk material due to the small crystallite sizes. Refinement of the diffractograms allowed assigning the perovskite peaks to the pure phase hexagonal Cs₃Bi₂I₉ structure with P6₃/mmc space group (a = b = 8.46 Å, c = 21.62 Å) corresponding to the expected 0D dimer unit cell (Fig. 2b) and to the monoclinic MA₃Bi₂I₉ with C2/c one (a = 8.70 Å, b = 14.80 Å, c = 21.51 Å, β = 91.43°), respectively. Careful analysis of the relative intensity of the diffraction peaks did not reveal any preferential crystalline orientation for any of the perovskites in various matrices. The goodness-of-fit (GoF) values of 2–3 obtained from the refinement studies also signify high-resolution data, further confirming the pure phase perovskite. Estimating peak width using the Scherrer formula was challenging due to the low intensity of the perovskite signals and strong background. However, for certain materials it was possible to calculate the crystallite size that corresponded well with the pore diameter of the matrices using manual precision profile fitting. Thus, for Cs₃Bi₂I₉@MCM-41 with a pore size of 2.3 nm, the coherent length in perovskite crystals was found to be 3.0 nm. This confirms that at low loading the perovskite crystallization occurs mainly within the pores, which naturally limits the size of the BiHP NCs.

Fig. 2 (a) XRD pattern of Cs₃Bi₂I₉ encapsulated in various mesoporous matrices (14.5 mass%). Reference (black line): ICDD 01-073-0707; (b) schematic illustration of a unit cell of Cs₃Bi₂I₉ with a 0D dimer structure.

We then performed a detailed XPS analysis of the nanohybrids to study the chemical structure of the confined perovskites. While the survey spectra show the presence of all expected elements, it is challenging to interpret the high-resolution ones taking into account the domination of the Si peaks from the silica matrix and an unfortunate overlapping of the Si 2s, Bi 4f_7/2 and Cs 4p_3/2 peaks. Nevertheless, we have deconvoluted the ensemble peaks in the regions of all elements of interest for Cs₃Bi₂I₉ and MA₃Bi₂I₉ confined in SBA-15 (Fig. S7†). Interestingly, for both materials the Bi 4f pattern shows the presence of a Bi³⁺ 4f_7/2 peak in the region typically corresponding to the perovskite (ca. 159.0 eV) accompanied by a peak at around 157.3 eV, which corresponds to Bi⁰ normally not expected in such materials. Previously, similar Pb⁰ metallic peaks have been observed in the case of some LHPs, and after some debate have been explained by the in situ radiolysis formation mechanism induced by the X-rays during the measurement, ruling out the initial presence of metallic lead in the perovskite.²⁸ In the case of Bi-containing materials, the Bi³⁺ reduction to Bi⁰ during the XPS measurement has also been reported and similarly was explained by the degradation during X-ray radiation.²⁹ We hypothesize that in our case, most of the bismuth in confined perovskites exists in the Bi³⁺ form bound to I, while the signature of the metallic Bi is induced by the measurement conditions. Both Cs₃Bi₂I₉ and MA₃Bi₂I₉@SBA-15 materials have pronounced peaks at 619.2 and 630.6 eV corresponding to I 3d_5/2 and 3d_3/2 electrons of the iodide, respectively. In addition, a characteristic peak of Cs 3d is present for Cs₃Bi₂I₉, while N 1s is observable for MA₃Bi₂I₉, confirming the expected composition of the encapsulated perovskites. The EDX mapping images of the Cs₃Bi₂I₉ and MA₃Bi₂I₉ encapsulated in SBA-15 (7.3 nm) and MCM-41 (2.3 nm) silica show that the elements of the perovskites (Cs, Bi, I) are uniformly distributed in mesoporous materials confirming the absence of visible large perovskite crystals outside of the pores regardless of the pore size and perovskite material (Fig. S8–S10†).

To determine the chemical composition and effective loading of the perovskites in the mesoporous matrices we have performed several analyses. One of the indicators of the loading and localization of the perovskites within the silica matrix is the [Bi] : [Si] atomic concentration ratio. Thus, for Cs₃Bi₂I₉@SBA-15 (9.2 nm pores, 14.5 mass%) there is a considerable discrepancy between the [Bi] : [Si] values obtained by different techniques: XPS (0.049), EDX (0.010), and ICP-OES (0.014). This can be explained by the difference in the probing depths of these techniques: XPS can probe ca. 3 nm from the surface, EDX gets the signal up to microns-deep below the surface, while the ICP-OES gets the information from the total amount of the matter dissolved. The seemingly lower [Bi] : [Si] ratio obtained by the XPS compared to the other techniques indicates that Bi is less visible by this surface-specific technique and thus most of the perovskite is not located on the surface but is confined deeper in the matrix.

To get more insight into the optical properties of the confined BiHP perovskites, UV-vis absorption spectroscopy was performed on the nanohybrids (Fig. 3).

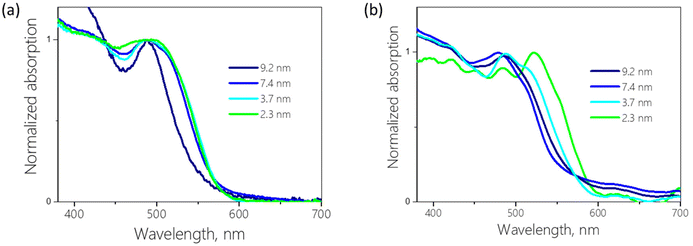Fig. 3 Absorption spectra of 14.5 (a) and 7.3 (b) mass% Cs₃Bi₂I₉ encapsulated in various mesoporous matrices.

The spectra of the powders show multi-feature patterns with several overlapping peaks. The absorption spectra of Cs₃Bi₂I₉ are mostly dominated by a peak at around 500 nm, which is generally assigned to the excitonic transition in the A₃Bi₂I₉ perovskites.⁴ In addition to the main peak, complex feature structure is visible at higher energies with several distinct peaks in the case of Cs₃Bi₂I₉ confined in SBA-15 with low loading (Fig. 3b). As a function of the silica pore size, the main peak exhibits significant changes in its shape and shifts in position. If solely quantum-confinement were at the origin of this behavior, a spectral shift to higher energy (lower wavelength) would be expected with decreasing pore size because of the increasing bandgap. However, several spectra in Fig. 3 show the reverse trend, i.e., an apparent red-shift of the main absorption peak for smaller pores.

To better understand this phenomenon, the absorption spectra need to be treated to deconvolute possible contributions to the multiple peaks and to potentially determine the bandgaps. Tauc plots are often used to extract the bandgap values from the UV-vis absorption spectra, however, while simple to process, they cannot be by default applied to any system. For example, due to the large energy difference between the excitonic peak and continuum of the conduction band, Tauc plots are not adapted to study semiconductors with a strong exciton binding energy.⁶ Bismuth halide perovskites fall in this category and in their case the use of the Tauc plot methodology can lead to the underestimation of the bandgap values and large discrepancy in the reported results.³⁰ The Elliott fit is an alternative, less commonly applied approach, which aims at simulating the specific contributions of the excitonic transitions and the continuous band above the bandgap and reconstruction of the absorption spectra using the following formula:

where E_g and E_b are the bandgap and exciton binding energies; A, β, γ, σ are various fitting parameters, and n is the exciton transition number.³¹ The first term describes the transitions to continuum states in the conduction band, while the second one – the contribution from the discrete excitonic states below the E_g bandgap. Often, in the absorption spectrum, the continuum component mixes with the excitonic one due to thermal effects, however, at cryogenic temperatures or for the materials with highly bound excitons a characteristic Gaussian peak below the bulk continuum onset can arise. In our case, the following assumptions were applied: the excitonic states are fitted using Gaussians, and the transitions above n = 3 were neglected in the fit, in coherence with common practice.³² In addition to the more reliable estimation of the bandgap, by using this approach it is possible to extract the excitonic binding energy.³³ This formula can be used in various forms and has been previously successfully applied to several systems including some lead-free perovskites.^34–36

However, for most of the nanohybrids studied in this work the Elliott fit failed to provide a satisfactory fit (Fig. S11†). To adapt this method to the BiHPs studied, we have modified the Elliott's formula by introducing a second independent term (A₂…) as follows:

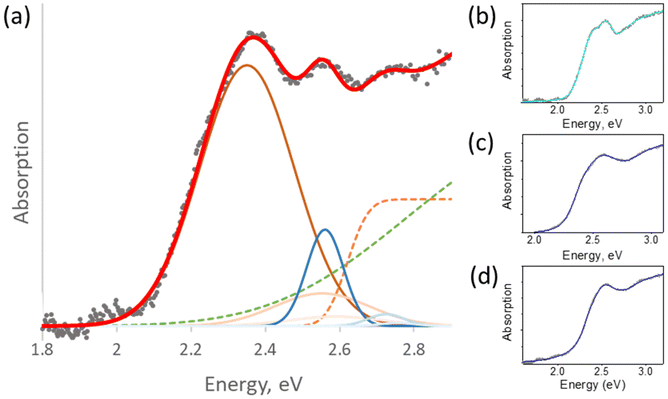
Using this modification, we managed to successfully fit the absorption spectra of all confined BiHP nanohybrids studied in this work (with different mesoporous silica pore diameters, BiHP loading, and chemical composition) and extract the key parameters (Fig. 4). The overall quality of fit is very satisfactory for the different materials with χ² of 10⁻⁴–10⁻⁵.

Fig. 4 (a) Absorption spectrum of Cs₃Bi₂I₉@MCM-41 (2.3 nm, 7.3 mass%) (grey dots) fitted with a double Elliott curve (red). The constituents of the fit are highlighted: the continuum curve (dotted green), as well as two series of excitonic peaks (shades of orange and shades of blue); absorption spectra with Elliott fit of: Cs₃Bi₂I₉ encapsulated in MCM-41 (3.7 nm, 7.3 mass%) (b), SBA-15 (7.4 nm, 7.3 mass%) (c), and SBA-15 (9.2 nm, 7.3 mass%) (d).

Thus, using the modified Elliott's formula, two bandgap values were extracted due to two formula terms for every material studied. To interpret the occurrence of the two bandgaps observed, several hypotheses can be proposed: for example, they could originate from two chemically different materials, such as Cs₃BiI₆ or BiI₃ in addition to the Cs₃Bi₂I₉. This hypothesis is however highly unlikely based on the XRD analyses highlighting the presence of only one single crystalline Cs₃Bi₂I₉ material in the nanohybrids (vide supra). Alternatively, the two different absorption signatures could come from a material in a single chemical composition but present in two different forms.

To better understand the origin of two distinct bandgap values, we first studied their dependence on the diameters of the silica pores (Fig. 3 and Table 1).

Table 1 Bandgap values of Cs₃Bi₂I₉ confined in mesoporous matrices with different pore sizes extracted from the absorption spectra using Elliott's formula (E_g = bandgap energy, E_b = exciton binding energy)

Pore diameter, nm	E g1, eV	E b1, meV	E g2, eV	E b2, meV
9.2	2.55	80	2.63	400
7.4	2.61	100	2.65	260
3.7	2.66	110	2.76	370
2.3	2.62	270	2.78	220

---

As mentioned above, due to the large variability of the Cs₃Bi₂I₉ BiHPs bandgap values reported in the literature (from 1.9 to 2.9 eV), it is hard to compare the obtained results to reference values. However, the average bandgaps found in our work (2.6–2.8 eV) are in line with reliable sources.^36,37 Noteworthy, while the 1^st (lower) bandgap remains mostly unchanged (around 2.6 eV) with decreasing pore diameter, the second, larger one is increasing from 2.63 to 2.78 eV. This interesting phenomenon could be due to the existence of the perovskite material in two forms, a non-confined one (1^st bandgap, smaller, constant values) and a quantum-confined one (2^nd bandgap, scaling with the pore diameter). The exciton binding energies calculated from the Elliott's fit (80–400 meV) are expectedly large compared to those of LHPs (<10 meV) due to the low 0D dimensionality of the BiHPs. Overall, they are in line with the values typically found for Cs₃Bi₂I₉ perovskites synthesized using different methods (70–300 meV).^22,36–38 The calculated exciton binding energies show higher values for the “confined” Cs₃Bi₂I₉ perovskite (E_b2, Table 1). This trend is typically observed for materials in the quantum confinement regime, such as quantum dots, due to the reduced dielectric constant and lower screening of e–h interactions compared to the bulk material. Therefore, this behavior supports our hypothesis that the BiHP NCs obtained in small pores exhibit quantum confinement effects. Our current understanding is that the different properties originate from two distinct materials: perovskite NCs confined inside the pores and (larger) particles grown outside of them. The first one has its dimensions limited below the Bohr radius and thus is quantum-confined, while the second displays bulk-like properties. This bulk-like perovskite can be locally visible on some electron microscopy images (Fig. S2†). Previously, such a coexistence of materials has been demonstrated in the case of LHPs confined in mesoporous matrices.¹²

MA₃Bi₂I₉ NCs confined in the silica matrix with ordered pores give rise to absorption spectra showing a similar behavior as a function of the pore diameter, which could be equally fitted using Elliott's formula (see Fig. S12†). The calculated bandgap and exciton binding energy values are close to those found for the Cs₃Bi₂I₉ showing as expected only moderate influence of the cations on the optical properties of such 0D materials. MA₃Bi₂I₉ NCs confined in the pores follow the same trend as the Cs₃Bi₂I₉ NCs, with the presence of two transitions, one with lower energy corresponding to the bulk material (ca. 2.55 eV), and another to the confined one (2.67–2.75 eV), albeit with a smaller dependence on the pore size compared to the Cs₃Bi₂I₉ case (Table S3†). As the Bohr radius value for the MA₃Bi₂I₉ perovskite is not available in the literature, it is not possible to explain unambiguously the origin of this difference. Meanwhile, we can expect that it should be lower compared to that of Cs₃Bi₂I₉ (2 and 6 nm as a function of the direction),³⁶ leading to a weaker confinement regime observed for this material in the pore size range studied. The bulk bandgap values found are slightly higher than those typically reported in the literature,³⁰ however most of the studies rely on the bandgap determination using Tauc plots, which as mentioned above could be irrelevant in the case of materials with high E_b such as MA₃Bi₂I₉. The exciton binding energies we found for this material (80–340 meV) are in the range of reported values (70–400 meV).^38–40

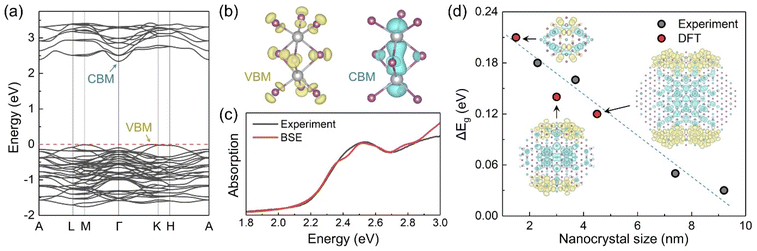
The experimental observations were further complemented with DFT calculations. Fig. 5a displays the calculated band structure of Cs₃Bi₂I₉, indicating the presence of an indirect bandgap.²⁴ Thus, phonon-mediated carrier recombination from the conduction band minimum (CBM) to the valence band maximum (VBM) is expected to be delayed, the PL yield should be low.^36,41Fig. 5b shows the charge density distributions of the VBM and CBM states within an individual Bi₂I₉ dioctahedron as the dioctahedra are fully separated by the Cs atoms. The VBM and CBM states are mainly contributed by the I and Bi atoms, respectively, which is consistent with the element-projected band structure results (Fig. S14†).⁴¹ Compared with the corner-sharing octahedra in most perovskites,⁴² the face-sharing configuration of Bi₂I₉ in Cs₃Bi₂I₉ reduces the Bi–Bi distance and removes intermediate halide atoms, enabling Bi–Bi orbital hybridization and making the CBM state more localized. Such localized distribution of the VBM and CBM states is anticipated to produce a large exciton binding energy, as confirmed experimentally. We simulated the optical absorption spectrum of Cs₃Bi₂I₉ with the excitonic effect by solving the Bethe–Salpeter equation (BSE), as shown in Fig. 5c. The simulated absorption curve is averaged over all directions and shifted along the energy axis to match the experimental excitonic peak. The raw data can be found in Fig. S15.† The shape of the simulated curve agrees with the experimental curve well (Cs₃Bi₂I₉@SBA-15, 9.2 nm, 7.3 mass% was chosen for comparison having the smallest contribution of the quantum-confined component), indicating that the strong exciton binding energy is an intrinsic property of Cs₃Bi₂I₉. To study the quantum confinement effect, we constructed Cs₃Bi₂I₉ quantum dot models of different sizes. The periodic models are separated by the vacuum region in the x and y directions and are maintained extended in the z direction, mimicking the experimental samples confined in pores (see Fig. S16†). Because the interactions between the Cs₃Bi₂I₉ quantum dots and the outer silica matrices are missing in the computational models, some localized surface states are manually eliminated to get reasonable band-edge states (Fig. S17–S19†). Fig. 5d shows changes in the bandgap due to the quantum confinement effect from both experimental and computational results, and the absolute values are given in Fig. S20.† The bandgap is systematically underestimated in the DFT calculations due to the limitations of the PBE functional. Employing more accurate hybrid functionals and considering spin–orbital coupling (SOC) can hardly improve the accuracy as shown in Fig. S13.† Below, we focus on the relative changes of the bandgap. The bandgap change exhibits a linear relationship with the nanocrystal size, and the quantum confinement effect is expected to disappear when the system size is larger than 10 nm. Note that the charge density distributions of the VBM (yellow) and CBM (blue) states drawn in the figure for the large nanocrystal are still different from a uniform distribution in the bulk Cs₃Bi₂I₉. The VBM and the CBM tend to distribute at the edge and the center of the quantum dots, respectively. This spatial separation can reduce the exciton binding energy, which is in line with the experimentally observed negative correlation between the exciton binding energy of the confined Cs₃Bi₂I₉ and the pore size. Furthermore, some defects can be produced at the interface between the quantum dots and the silica matrices.⁴³ These defects may trap the photo-generated carriers and promote their nonradiative recombination, reducing the PL activity.

Fig. 5 (a) Band structure of Cs₃Bi₂I₉. (b) Charge density distributions of VBM and CBM within a single Bi₂X₉ dioctahedron. Color code: grey for Bi and purple for I. (c) Optical absorption spectrum of Cs₃Bi₂I₉ from experiment (Cs₃Bi₂I₉@SBA-15, 9.2 nm, 7.3 mass%) and calculation (bulk model). The computational curve is shifted to match the excitonic peak. (d) Bandgap changes between the confined systems with different sizes and the bulk Cs₃Bi₂I₉ (E^confined_g − E^bulk_g). The top view of the computational models and the relevant charge density distributions of VBM (yellow) and CBM (blue) are plotted.

Typically, for the materials such as BiHP, the confinement effects are more rarely observed due to the lower structural dimensionality with excitons mostly localized in the dioctahedra, and consequent higher effective masses with low bands dispersion. However, the wavefunctions of the dioctahedra do interact and the effect of the confinement should become visible below the exciton Bohr radius. In contrast to the LHPs, the Bohr radii for BiHPs are much less studied with the values calculated only for Cs₃Bi₂I₉ of 0.9,²² 2 and 6 nm (as a function of the crystalline orientation).³⁶ In the literature, there are no examples of purely quantum-confined Cs₃Bi₂I₉ nanostructures: in most reported cases it is not occurring because of the relatively large size of the synthesized nanocrystals and/or poor control over the size distribution.^22,36,41 In one work the quantum confinement is demonstrated for alloyed Cs₃Bi₂(Cl_xI_1−x)₉ structures;⁴⁴ whereas in another one, the reported shift of the photoluminescence claimed to be due to the size change of the 20 nm Mn²⁺-doped NCs most likely originated from the lattice contraction or related crystalline effects rather than the size-dependent bandgap change.⁴⁵ To the contrary, our system provides a versatile and powerful tool to unambiguously demonstrate and study the quantum confinement effects by precisely controlling the NCs size using silica matrices with accurately defined pore sizes.

The effect of the perovskite loading was studied by varying the precursor volume added to the constant mass amount of the mesoporous silica. For example, when the MA₃Bi₂I₉ loading in the 7.4 nm SBA-15 matrix increases from 7.3 to 14.5, the N₂ adsorption–desorption isotherms show the total pore volume firstly remains stable (0.67 cm³ g⁻¹) and significantly lower than the one of initial SBA-15 (0.90 cm³ g⁻¹). When the loading increases further to 29.0 mass%, the pore volume decreases to 0.57 cm³ g⁻¹, and the surface area decreases from 500 and 406 m² g⁻¹, respectively (Table S1†), indicating that the perovskite occupies more cavities in the matrices. Noteworthy, the different perovskite loading does not affect the bandgap values calculated from the absorption spectra using Elliott's formula (Fig. S21 and Table S4†). We can still distinguish two distinct bandgaps for all loadings, however, their deconvoluted values do not change with increasing amount of perovskite, only their corresponding contribution to the spectra is affected as expressed by the β₁/β₂ coefficient ratio taken from Elliott's calculations. This demonstrates that the bandgap of the perovskite is defined mostly by the pore size of the matrix and not by the total amount of the material. This finding corroborates the hypothesis given above: the two bandgaps found for the nanohybrids studied can be ascribed to the confined perovskite (with higher bandgap) and to perovskite crystallized outside of the pores: with higher loading of the perovskite and constant pores’ availability, more material remains outside in the non-confined bulk regime (Fig. S2†).

BiHPs confined in mesoporous matrices showed no photoluminescence at room temperature when excited with visible light. We assume that the silica matrix provides some passivation for the perovskites even in the absence of the ligands typically used to passivate their surface in the case of colloidal nanocrystals, but some other external or internal factors may come into play to hinder the radiative decay of the excited electrons. One of the possible reasons is the excitonic coupling of the perovskites with the silica framework in direct contact with their surface.⁴⁶ Furthermore, BiHPs can have deep-level defects that significantly impact their performance in photovoltaic applications by trapping excited electrons.⁴⁷ Cs₃Bi₂I₉ in different forms (nanocrystals, thin films) typically exhibits low PL quantum yield of <1% ²² and even single crystals of this material are only weakly luminescent at room temperature⁴⁸ due to the indirect bandgap, above-mentioned potential intragap defects, and self-trapping caused by strong exciton–phonon coupling.

Conclusions

In summary, we synthesized bismuth iodide perovskites confined in mesoporous silica matrices with ordered pores of controlled diameters. These matrices are an appropriate means to control the size of the confined perovskite nanocrystals precisely and access small sizes in the quantum confinement regime. The composition (A₃Bi₂I₉) and crystal structure of the BiHP NCs encapsulated in the pores were confirmed, and the effect of size on their optical properties was systematically studied. The absorption spectra were accurately fitted using a modified Elliott's equation, which revealed the presence of two independent bandgaps in the materials. One bandgap scales with the pore sizes arising from the encapsulated NCs, while the other is invariant and originates from perovskite grown outside the pores. The study shows that the calculated exciton binding energies are high, ranging from 70 to 400 meV, and they scale with the pore size. It is demonstrated for the first time that the 0D BiHPs exhibit the quantum confinement effect, which is more pronounced in Cs₃Bi₂I₉ than in MA₃Bi₂I₉. This conclusion is supported by DFT calculations on BiHP clusters with varying dimensions.

The proposed approach can be extended to study other types of halide perovskite nanocrystals in mesoporous materials’ pores to understand their physical properties. These nanohybrids can be used as photocatalysts, and with an efficient surface passivation strategy, as light emitters.

Author contributions

S. D., A. G., M. V., A. R., and D. A. conducted experimental work on synthesis and characterization of encapsulated perovskites. D. L. conducted DFT simulations under the guidance of A. V. and O. V. P., S. P. and S. S. guided the XRD analysis. W. L. L. conducted TEM microscopy. B. L. and P. R. helped in designing and discussing the research. The funding was obtained by D. A., A. R., A. V., and O. V. P. All authors contributed to the writing, editing and commenting of the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This project has received financial support from the CNRS through the MITI interdisciplinary program and from the French National Research Agency (grant ANR EncaPer ANR-23-CE09-0013-01). A. G. acknowledges the financial support from FOCUS ECC CEA program for his doctoral fellowship. W. L. L. acknowledges the support of Dr G. Schoehn. This work used the platforms of the Grenoble Instruct-ERIC center (ISBG; UAR 3518 CNRS-CEA-UGA-EMBL) within the Grenoble Partnership for Structural Biology (PSB), supported by FRISBI (ANR-10-INBS-0005-02) and GRAL, financed within the University Grenoble Alpes graduate school (Ecoles Universitaires de Recherche) CBH-EUR-GS (ANR-17-EURE-0003). The IBS Electron Microscope facility is supported by the Auvergne Rhône-Alpes Region, the Fonds Feder, the Fondation pour la Recherche Médicale and GIS-IBiSA. O. V. P. acknowledges support of the US National Science Foundation (grant CHE2154367). The authors thank Céline Rivaux for helping in ICP-OES measurements, and Loïc Vidal for transmission electronic microscopy analysis.

References

1. A. Fakharuddin, M. K. Gangishetty, M. Abdi-Jalebi, S.-H. Chin, A. R. bin Mohd Yusoff, D. N. Congreve, W. Tress, F. Deschler, M. Vasilopoulou and H. J. Bolink, Nat. Electron., 2022, 5, 203–216.
2. H. J. Snaith, Nat. Mater., 2018, 17, 372–376.
3. D. Aldakov and P. Reiss, J. Phys. Chem. C, 2019, 123, 12527–12541.
4. S. Attique, N. Ali, S. Ali, R. Khatoon, N. Li, A. Khesro, S. Rauf, S. Yang and H. Wu, Adv. Sci., 2020, 7, 1903143.
5. S. Sun, M. Lu, X. Gao, Z. Shi, X. Bai, W. W. Yu and Y. Zhang, Adv. Sci., 2021, 8, 2102689.
6. R. L. Z. Hoye, J. Hidalgo, R. A. Jagt, J. P. Correa-Baena, T. Fix and J. L. MacManus-Driscoll, Adv. Energy Mater., 2022, 12, 2100499.
7. J. Shamsi, A. S. Urban, M. Imran, L. De Trizio and L. Manna, Chem. Rev., 2019, 119, 3296–3348.
8. T. A. de Souza Carvalho, L. F. Magalhaes, C. I. do Livramento Santos, T. A. Z. de Freitas, B. R. Carvalho Vale, A. F. Vale da Fonseca and M. A. Schiavon, Chem. – Eur. J., 2023, 29, e202202518.
9. J. Wang, Y. Shi, Y. Wang and Z. Li, ACS Energy Lett., 2022, 7, 2043–2059.
10. A. Rubino, L. Caliò, A. García-Bennett, M. E. Calvo and H. Míguez, Adv. Opt. Mater., 2020, 8, 1901868.
11. D. O. Tiede, A. Rubino, M. E. Calvo, J. F. Galisteo-López and H. Míguez, J. Phys. Chem. C, 2020, 124, 8041–8046.
12. D. N. Dirin, L. Protesescu, D. Trummer, I. V. Kochetygov, S. Yakunin, F. Krumeich, N. P. Stadie and M. V. Kovalenko, Nano Lett., 2016, 16, 5866–5874.
13. M. Anaya, A. Rubino, T. C. Rojas, J. F. Galisteo-López, M. E. Calvo and H. Míguez, Adv. Opt. Mater., 2017, 5, 1601087.
14. V. Malgras, S. Tominaka, J. W. Ryan, J. Henzie, T. Takei, K. Ohara and Y. Yamauchi, J. Am. Chem. Soc., 2016, 138, 13874–13881.
15. H.-C. Wang, S.-Y. Lin, A.-C. Tang, B. P. Singh, H.-C. Tong, C.-Y. Chen, Y.-C. Lee, T.-L. Tsai and R.-S. Liu, Angew. Chem., Int. Ed., 2016, 55, 7924–7929.
16. Y.-Q. Hu, L.-J. Fan, H.-Y. Hui, H.-Q. Wen, D.-S. Yang and G.-D. Feng, Inorg. Chem., 2019, 58, 8500–8505.
17. Z. Pan, B. Liu, B. Wang, Y. Liu, T. Si, W. Yi, Y. Wu, J. Li and B. Cao, Chem. Phys. Lett., 2021, 782, 139023.
18. Y. Dai, C. Poidevin, C. Ochoa-Hernández, A. A. Auer and H. Tüysüz, Angew. Chem., Int. Ed., 2020, 59, 5788–5796.
19. Z. Cui, P. Wang, Y. Wu, X. Liu, G. Chen, P. Gao, Q. Zhang, Z. Wang, Z. Zheng, H. Cheng, Y. Liu, Y. Dai and B. Huang, Appl. Catal., B, 2022, 310, 121375.
20. T. Qiao and D. H. Son, Acc. Chem. Res., 2021, 54, 1399–1408.
21. C. Otero-Martínez, J. Ye, J. Sung, I. Pastoriza-Santos, J. Pérez-Juste, Z. Xia, A. Rao, R. L. Z. Z. Hoye, L. Polavarapu, C. Otero-Martínez, J. Ye, J. Sung, I. Pastoriza-Santos, J. Pérez-Juste, Z. Xia, A. Rao, R. L. Z. Z. Hoye and L. Polavarapu, Adv. Mater., 2022, 34, 2107105.
22. J. Pal, A. Bhunia, S. Chakraborty, S. Manna, S. Das, A. Dewan, S. Datta and A. Nag, J. Phys. Chem. C, 2018, 122, 10643–10649.
23. S. S. Bhosale, A. K. Kharade, E. Jokar, A. Fathi, S. Chang and E. W.-G. Diau, J. Am. Chem. Soc., 2019, 141, 20434–20442.
24. S. E. Creutz, H. Liu, M. E. Kaiser, X. Li and D. R. Gamelin, Chem. Mater., 2019, 31, 4685–4697.
25. L. Lian, G. Zhai, F. Cheng, Y. Xia, M. Zheng, J. Ke, M. Gao, H. Liu, D. Zhang, L. Li, J. Gao, J. Tang and J. Zhang, CrystEngComm, 2018, 20, 7473–7478.
26. J. Kim, J. Park, S.-W. Nam, M. Shin, S. Jun, Y.-H. Cho and B. Shin, ACS Appl. Energy Mater., 2020, 3, 4650–4657.
27. M. N. Tran, I. J. Cleveland, G. A. Pustorino and E. S. Aydil, J. Mater. Chem. A, 2021, 9, 13026–13035.
28. S. Béchu, M. Ralaiarisoa, A. Etcheberry and P. Schulz, Adv. Energy Mater., 2020, 10, 1904007.
29. D. M. Fabian and S. Ardo, J. Mater. Chem. A, 2016, 4, 6837–6841.
30. C. Wu, Q. Zhang, G. Liu, Z. Zhang, D. Wang, B. Qu, Z. Chen and L. Xiao, Adv. Energy Mater., 2020, 10, 1–30.
31. R. J. Elliott, Phys. Rev., 1957, 108, 1384–1389.
32. D. M. Niedzwiedzki, H. Zhou and P. Biswas, J. Phys. Chem. C, 2022, 126, 1046–1054.
33. M. Baranowski and P. Plochocka, Adv. Energy Mater., 2020, 10, 1903659.
34. M. Pantaler, V. Diez-Cabanes, V. I. E. E. Queloz, A. Sutanto, P. A. Schouwink, M. Pastore, I. García-Benito, M. K. Nazeeruddin, D. Beljonne, D. C. Lupascu, C. Quarti and G. Grancini, JACS Au, 2022, 2, 136–149.
35. R.-I. Biega, M. R. Filip, L. Leppert and J. B. Neaton, J. Phys. Chem. Lett., 2021, 12, 2057–2063.
36. S. Rieger, B. J. Bohn, M. Döblinger, A. F. Richter, Y. Tong, K. Wang, P. Müller-Buschbaum, L. Polavarapu, L. Leppert, J. K. Stolarczyk and J. Feldmann, Phys. Rev. B, 2019, 100, 201404.
37. V. F. Machulin, F. V. Motsnyi, O. M. Smolanka, G. S. Svechnikov and E. Y. Peresh, Low Temp. Phys., 2004, 30, 964–967.
38. B.-W. Park, B. Philippe, X. Zhang, H. Rensmo, G. Boschloo and E. M. J. Johansson, Adv. Mater., 2015, 27, 6806–6813.
39. S. Öz, J. C. Hebig, E. Jung, T. Singh, A. Lepcha, S. Olthof, F. Jan, Y. Gao, R. German, P. H. M. van Loosdrecht, K. Meerholz, T. Kirchartz and S. Mathur, Sol. Energy Mater. Sol. Cells, 2016, 158, 195–201.
40. B. Yoo, A. Aziz, D. Ghosh, H. Park, G. Min, M. S. Islam and S. A. Haque, J. Phys. Chem. C, 2021, 125, 8938–8946.
41. S. Ghimire, C. Rehhagen, S. Fiedler, U. Parekh, R. Lesyuk, S. Lochbrunner and C. Klinke, Nanoscale, 2022, 15, 2096–2105.
42. Y. Xie, B. Peng, I. Bravić, Y. Yu, Y. Dong, R. Liang, Q. Ou, B. Monserrat and S. Zhang, Adv. Sci., 2020, 7, 2001698.
43. B. Ghosh, S. Chakraborty, H. Wei, C. Guet, S. Li, S. Mhaisalkar and N. Mathews, J. Phys. Chem. C, 2017, 121, 17062–17067.
44. K. Kundu, P. Acharyya, K. Maji, R. Sasmal, S. S. Agasti and K. Biswas, Angew. Chem., Int. Ed., 2020, 59, 13093–13100.
45. M. Liu, H. Ali-Löytty, A. Hiltunen, E. Sarlin, S. Qudsia, J. Smått, M. Valden and P. Vivo, Small, 2021, 17, 2100101.
46. N. Alarcos, B. Cohen, M. Ziółek and A. Douhal, Chem. Rev., 2017, 117, 13639–13720.
47. D. Liu, C. M. Perez, A. S. Vasenko and O. V. Prezhdo, J. Phys. Chem. Lett., 2022, 13, 3645–3651.
48. K. M. McCall, C. C. Stoumpos, S. S. Kostina, M. G. Kanatzidis and B. W. Wessels, Chem. Mater., 2017, 29, 4129–4145.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental part, as well as additional microscopy images, XRD diffractograms, absorption spectra, N₂ adsorption–desorption isotherms, XPS spectra, EDX cartography images, and supplementary DFT data. See DOI: https://doi.org/10.1039/d4nr00430b

---