Variability in HfO₂-based memristors described with a new bidimensional statistical technique

Abstract

A new statistical analysis is presented to assess cycle-to-cycle variability in resistive memories. This method employs two-dimensional (2D) distributions of parameters to analyse both set and reset voltages and currents, coupled with a 2D coefficient of variation (CV). This 2D methodology significantly enhances the analysis, providing a more thorough and comprehensive understanding of the data compared to conventional one-dimensional methods. Resistive switching (RS) data from two different technologies based on hafnium oxide are used in the variability study. The 2D CV allows a more compact assessment of technology suitability for applications such as non-volatile memories, neuromorphic computing and random number generation circuits.

---

5. Introduction

Memristors are being scrutinized by the scientific community to optimize their fabrication in terms of the materials employed and their growth processes. The industrial applications of these devices are unquestionable nowadays in the realm of non-volatile memory circuits, random number generation, high frequency switches and neuromorphic engineering.¹ Resistive Random Access Memories (RRAM) are an important subgroup of memristors, also known as resistive memories. They can be built by means of metal–insulator–metal (MIM) and metal–insulator–semiconductor (MIS) stacks, with the insulator as the key layer since it is where resistive switching takes place.^2,3 Different transition metal oxides have been studied in recent years from the device operational viewpoint and outstanding results have been obtained, for instance, great endurance data (above >10¹⁰ cycles),⁴ short writing/reading times (<10 ns),⁵ good scalability (down to ∼2 nm),⁶ large HRS (High Resistance State)/LRS (Low Resistance State) resistance ratios (>100),⁷ very low write switching energies (∼0.1 pJ) and CMOS fabrication technology compatibility.⁸

Considering these features, various developments have been performed in the field of non-volatile memory. For instance, the integration of these devices in the 22 nm technology node has been demonstrated by TSMC⁹ and INTEL.¹⁰ Additionally, significant advancements have been observed in the neuromorphic computing landscape^11–16 where RS devices demonstrate the capability to mimic biological synapses, as their switching mechanisms closely resemble the dynamics of neuronal behavior.^17–19

Nevertheless, there are some hurdles to overcome to further improve the technologies based on resistive memories. Among the issues to tackle, one is linked to the need for accurate simulation tools and compact models, and the other is related to the variability exhibited by these devices. Variability has two components: cycle-to-cycle variability due to the inherent stochastic mechanisms behind the RS operation along consecutive series of set and reset cycles^20,21 and device-to-device variability,²² the usual variability addressed in conventional nanoelectronic integrated circuits. Variability has been analyzed from different perspectives: characterization and parameter extraction²³ and modeling.²⁴ In addition, from a statistical viewpoint, cycle-to-cycle variability has been studied using time series;^25,26 a new approach based on phase-type distribution functions (advanced distribution functions that can fit any other classical distribution function by changing their internal parameters) has also been successfully employed.^27,28 Finally, state-of-the-art functional data analysis has been employed to deepen our understanding of the memristor experimental data structure.^29,30 In the present work, a new methodology is proposed to statistically analyze experimental cycle-to-cycle variability in resistive memories, in line with previous results on this issue.³¹

The conventional analysis of cycle-to-cycle variability is performed by extracting RS parameters: the set and reset voltages (V_set, V_reset) and the corresponding set and reset currents (I_set, I_reset) and the low voltage device resistances (R_LRS and R_HRS). The statistical study includes the calculation of cumulative distribution functions (CDFs), coefficients of variation (CV) (standard deviation to mean ratio, σ/μ) and fitting different distribution functions to evaluate the data structure.²⁸ However, these studies traditionally assume one-dimensional distributions. For instance, in an RS series of 500 cycles, V_set and V_reset are obtained, and CDFs and CVs are computed. Each I–V curve, corresponding to either a set or a reset process, yields a 1D dataset. Nevertheless, from the statistical perspective, a better representation is obtained by using a 2D dataset, and therefore a better variability evaluation can be performed. In this work, the proposed and developed methodology is presented.

The details of the device fabrication and measurement setups are given in section 2. Section 3 is devoted to the new variability analysis and section 4 to the main results and the corresponding discussion. The conclusions are drawn in section 5.

2. Device fabrication, measurement setup and parameter extraction

For the sake of clarity, in our statistical study, we have employed two different RRAM technologies based on MIS and MIM structures. The MIS devices are based on the unipolar Ni/HfO₂/Si stack (Fig. 1a) fabricated on (100) n-type CZ silicon wafers with resistivity (0.007–0.013) Ω cm. The insulator is a 20 nm-thick hafnium oxide layer grown by atomic layer deposition (ALD), using tetrakis (dimethylamido)-hafnium (TDMAH) and H₂O as precursors, at 225 °C with N₂ as a carrier and purge gas.³² The current–voltage curves were measured using an HP-4155B semiconductor parameter analyser (connected to the computer via GPIB and controlled using MATLAB) applying a voltage ramp to the device. The voltage was applied to the top Ni electrode, while the Si substrate was grounded. More than 2500 curves were obtained in an RS series with consecutive set and reset cycles after a forming process with a compliance current of 0.1 mA (see Fig. 1b).

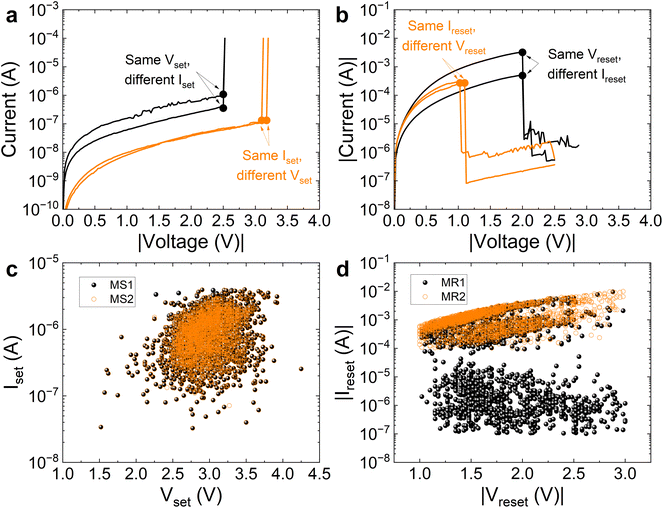
Fig. 1 (a) Cross-section scheme of the MIS device with a dielectric thickness (HfO₂) of 20 nm. (b) Current versus voltage absolute value for consecutive set and reset processes (more than 2500 cycles). (c) Set and reset curves with the set and reset parameters indicated. Two different numerical techniques have been employed for each extraction procedure (set voltage: MS1, based on the localization of the current derivative maximum,³³ and MS2, consisting of the determination of the set I–V curve knee;³³ reset voltage: MR1, based on the current derivative minimum calculation,³³ and MR2, where the current maximum is obtained³³). (d) Absolute value of set and reset voltages versus cycle number, (e) absolute value of set and reset currents versus cycle number.

The MIM devices studied were fabricated with the TiN/Ti/HfO₂/W stack³⁴ on highly-doped N-type silicon wafers (ρ = 4 mΩ cm). The electrodes were grown as follows: the top electrode consists of a 200 nm TiN/10 nm Ti bi-layer, and the bottom one is a 50 nm-thick W layer deposited on a 20 nm-thick Ti adherence layer on a silicon substrate. The insulator consists of a 10 nm-thick HfO₂ grown by ALD using TDMAH and H₂O as precursors, at 225 °C with N₂ as a carrier and purge gas (see Fig. 2a). Deposition of a 500 nm Al layer on the back of the wafer allows for electrically contacting the W bottom electrode through the Si–n⁺ substrate.³⁵ The 1000 RS I–V curves were measured applying a voltage ramp to the device (see Fig. 2b) with a voltage limitation of 1 V for the set process and −1.3 V for the reset process. For these devices, the I–V curves were programmed with a MATLAB software tool that controls a Keysight B1500A SPA via GPIB.

Fig. 2 (a) Cross-section scheme of the active area of the MIM device with a dielectric thickness (HfO₂) of 10 nm. (b) Current versus voltage for consecutive set and reset processes. (c) Set and reset curves with the set and reset parameters indicated. Two different numerical techniques have been employed for each extraction procedure (set voltage: MS1, based on the localization of the current derivative maximum,³³ and MS2, consisting of the determination of the set I–V curve knee;³³ reset voltage: MR1, based on the current derivative minimum calculation,³³ and MR2, where the current maximum is obtained³³). (d) Absolute value of set and reset voltages versus cycle number, (e) absolute value of set and reset currents versus cycle number.

The RS parameter extraction was performed following two numerical methodologies previously introduced in ref. 33. For the set voltage (V_set) extraction, the MS1 technique is based on the current derivative maximum localization and the MS2 procedure consists of the determination of the set I–V curve knee (Fig. 1c and 2c). In the case of the reset voltage (V_reset), the MR1 procedure is based on the current derivative minimum calculation and MR2 is linked to the current maximum (Fig. 1c and 2c). The set and reset voltages extracted using these procedures are shown in Fig. 1d and 2d for the MIS and MIM devices, respectively. The corresponding set (I_set) and reset (I_reset) currents are also shown in Fig. 1e and 2eversus cycle number.

3. Two-dimensional statistical analysis of variability

The motivation for a new technique for the analysis of variability is illustrated in Fig. 3a, b and 4a, b for the MIS and MIM devices, respectively. In Fig. 3a and 4a, the I–V curves show the same V_set but have different I_set, and other curves with the same I_set have different V_set. Similar issues are highlighted in Fig. 3b and 4b for reset processes.

Fig. 3 (a) Set I–V curves for the MIS devices. The curves in black have the same set voltage, although different set current; the curves in orange have the same set current although different set voltage. (b) Reset I–V curves for the MIS devices. The curves in black have the same reset voltage, although different reset current; the curves in orange have the same reset current although different reset voltage. (c) I_setversus V_set for two different extraction procedures in the MIS devices, (d) absolute value of I_resetversus absolute value of V_reset for two different extraction procedures in the MIS devices.

Fig. 4 (a) Set I–V curves for the MIM devices. The curves in black have the same set voltage, although different set current; the curves in blue have the same set current although different set voltage. (b) Reset I–V curves for the MIM devices. The curves in black have the same reset voltage, although different reset current; the curves in blue have the same reset current although different reset voltage. (c) I_setversus V_set for two different extraction procedures in the MIM devices, (d) absolute value of I_resetversus absolute value of V_reset for two different extraction procedures in the MIM devices.

In view of these results, it is clear that a 1D analysis of variability, in our cycle-to-cycle variability case, is not appropriate, or at least it is not complete. However, most of the reported studies utilize just one of the variables considered previously, i.e., the set or reset voltages, or the corresponding currents; in all of the cases, it is a 1D approach. In this respect, a different statistical approach should be addressed using the variable pairs (V_set, I_set) and (V_reset, I_reset), that is, the point clouds shown in Fig. 3c, d (MIS devices) and 4c, d (MIM devices). Consequently, the coefficient of variation (CV) should be evaluated in a multivariate manner.

As highlighted above, CV is commonly used to estimate the variability of statistical populations. Even though the statistical populations are characterized by multiple variables, as is the case in our study, conventional 1D CVs are typically employed for each single variable. By doing so, the correlation between the variables is ignored and the analysis does not summarize the variability of multivariate data into a single index. The introduction of a 2D CV calculation (with the potential to handle higher dimensions) addresses this limitation. The extension of univariate CVs to the multivariate scenario is not trivial; there are several proposals in the literature.^36–39 This issue is described in the Appendix.

4. Results and discussion

As explained in the Appendix, the multivariate coefficient of variation (the 2D CV) suggested in ref. 40, MCV_VN, is employed in our calculations. The values of the variables used to calculate the coefficients depend on their units. From a statistical viewpoint, if the value of a variable is considerably greater compared to others, its mean will also be greater than the other variables. Consequently, this variable will likely have a more important effect on coefficients such as the ones introduced in our study. This influence should be carefully considered to ensure an accurate interpretation of the statistical results. This well-known issue affects many statistical models; regressions are an obvious example, but others are impacted as well. For this reason, a transformation over the original extracted RS data is needed (these modifications of variables are usual in advanced statistical techniques). The most common transformation is the standardization. A variable is standardized by subtracting from it its sample mean and then dividing the result by the variable standard deviation. However, the new variable would have a standard deviation that equals one and a mean equal to zero, which implies an undefined CV. To address this issue, an effective alternative is scaling using the root mean square.⁴¹ Denoting the set/reset voltage or current as variable X, the transformation proposed is (where n is the number of cycles). The univariate (1D) CVs for X* and X are the same, but the 2D CV is not affected by the issue highlighted above anymore. See the results in Fig. 5 (the data are given in Table 1).

Fig. 5 1D and 2D coefficients of variation for the transformed data of the set/reset voltages and currents shown in Fig. 3 and 4, for the two different technologies we are considering, (a) MIS devices and (b) MIM devices.

Table 1 1D and 2D coefficients of variation for the transformed data of the set/reset voltages and currents shown in Fig. 3 and 4

Device type	Variable	Univariate (1D CV)	MCVVN (2D CV)
MIS	V reset (MR1)	0.23	0.67
	I reset (MR1)	1.16
	V reset (MR2)	0.24	0.55
	I reset (MR2)	0.83
	V set (MS1)	0.10	0.44
	I set (MS1)	0.69
	V set (MS2)	0.10	0.44
	I set (MS2)	0.68
MIM	V reset (MR1)	0.01	0.05
	I reset (MR1)	0.08
	V reset (MR2)	0.01	0.02
	I reset (MR2)	0.02
	V set (MS1)	0.18	0.35
	I set (MS1)	0.49
	V set (MS2)	0.12	0.30
	I set (MS2)	0.42

---

It is important to interpret the coefficients in Fig. 5, taking into consideration Fig. 3 and 4. The 1D CV(V_reset) for the MIS devices is 0.23 for MR1. This value is reasonable for a certain technology for neuromorphic computing and hardware cryptography applications; however, the 2D CV equals 0.67, a much worse number that is influenced, obviously, by the high 1D CV(I_reset) that equals 1.16. The spread of the black point cloud in Fig. 3d visually represents this variability. Similar results (although the 2D CV is lower) are obtained for the MR2, MS1 and MS2 techniques in the MIS technology. In all of the cases, the variability of the set and reset currents, higher than the set and reset voltages, is reflected in the much more informative 2D CVs (green bars in Fig. 5).

In the comparison of different technologies (for the MS2 numerical technique), notice that 1D CV(V_set) = 0.10 for MS2(MIS) and 0.12 for MS2(MIM). An analysis based on these numbers would lead to an almost similar variability; however, the role played by the variability on I_set leads to a 2D CV(MIS) > 2D CV(MIM). Graphically, we can observe that the point cloud dispersion for the MIS technology (Fig. 3c) is higher than in the MIM case (Fig. 4c). This indicates a more complex relationship between these variables than what is indicated by the 1D CV alone. For MS1, we have a similar issue, although the 2D CV difference between MIS and MIM is lower. The point cloud in Fig. 4c is more spread out than in the MS2 case. It is noteworthy that the reset 2D CVs for the MIM technology show outstanding results in terms of variability, both for MR1 and MR2; therefore, if we take into consideration the high R_HRL/R_LRS that is achieved, this technology would successfully respond for non-volatile memory applications.

5. Conclusions

A statistical study is performed on the variability of two different resistive memory technologies based on HfO₂ dielectrics. A new 2D coefficient of variation is introduced to account for the joint variation of set or reset voltages and currents at once. The data employed in the study allow us to prove that the new coefficient performs a more comprehensive description of variability than its one-dimensional counterparts for the voltage and current in both technologies. The implementation of this new 2D coefficient of variation is a significant advancement, offering enhanced insights that are crucial for evaluating the suitability of specific technologies in applications such as non-volatile memories, neuromorphic computing, hardware cryptography, etc.

Conflicts of interest

The authors declare no competing interest.

Appendix

Let X = (X₁, …, X_p)’ be a p-dimensional random vector distributed according to a given distribution F with mean vector μ ≠ 0 and covariance matrix Σ. For the case we are considering here, p = 2, our vectors are X = (V_set, I_set)' and X = (V_reset, I_reset)' with different values for each RS cycle. Hereinafter, we consider the X = (V_set, I_set)' vector, but it would be the same for the reset scenario. The mean vector for the set process is obtained as μ = (mean(V_set), mean(I_set)) and μ′ stands for the transposed matrix of the mean vector. The covariance matrix (also known as the auto-covariance matrix or variance–covariance matrix) is calculated as shown in eqn (1):where cov stands for the statistical covariance and var for the statistical variance. Different definitions of the multivariate coefficient of variation (MCV) have been introduced in the literature: in ref. 36 (MCV_R), ref. 38 (MCV_VV), ref. 37 (MCV_VN) and ref. 39 (MCV_AZ).where det stands for the determinant and tr for the trace of a matrix. All these MCVs are reduced to the univariate CV when p = 1; however, they are not equal to each other for the multivariate setting. The main properties and differences between them are described in depth both theoretically and via simulations in ref. 39 and 40. The MCV_AZ coefficient is more explicit and closer in its definition to the univariate CV. Therefore, it has already been generalized for the case where observations are functions instead of vectors⁴² and it has been applied previously to the analysis of variability in RRAMs in the context of functional data analysis.³⁰ In this case, we considered the whole measured I–V curve as the basic element to use in our statistical study.³⁰ However, in the approach we are presenting here, ref. 40 suggests the use of MCV_VN because of its intuitive definition and interesting invariance and robustness. For that reason, MCV_VN is the one employed in our work. It is interesting to highlight that MCV_VN requires non-singularity of the covariance matrix, i.e., a non-zero determinant. Then, MCV_VN could not be used in these scenarios. The solution would be to consider the MCV_AZ coefficient instead, which was proposed to solve this practical problem.^39,40

For the sake of simplicity, we also name the univariate CV as 1D CV and the multivariate CV as 2D CV, since in our work p = 2.

Finally, it is important to highlight that in case we had more information for the set and reset points (i.e. different input voltage ramps, compliance currents, etc.), we could use variance matrices and mean vectors with higher dimensions, although the mathematical formalism would not change.

Acknowledgements

Research supported by the projects PID2022-139586NB-C44, PID2022-139586NB-C42 and PID2020-113961GB-I00 funded by MCIN/AEI/10.13039/501100011033 and FEDER, EU, and the “María de Maeztu” Excellence Unit IMAG reference CEX2020-001105-M, funded by MCIN/AEI/10.13039/501100011033. IMB authors thank the CSIC funding through project 20225AT012, the Generalitat de Catalunya-AGAUR through project 2021 SGR 00497 and the support provided by the project CR32023-040125, funded by MICIU/AEI/10.13039/501100011033, and by the European Union through the NextGenerationEU/PRTR program. M. B. G. acknowledges the grant RYC2020-030150-I funded by MCIN/AEI/ 10.13039/501100011033 and by “ESF Investing in your future”.

References

1. M. Lanza, A. Sebastian, W. D. Lu, M. Le Gallo, M.-F. Chang, D. Akinwande, F. M. Puglisi, H. N. Alshareef, M. Liu and J. B. Roldan, Science, 2022, 376(6597), 1–13.
2. F. Pan, S. Gao, C. Chen, C. Song and F. Zeng, Mater. Sci. Eng., R, 2014, 83, 1–59.
3. J. S. Lee, S. Lee and T. W. Noh, Appl. Phys. Rev., 2015, 2, 031303.
4. J. J. Yang, M.-X. Zhang, J. P. Strachan, F. Miao, M. D. Pickett, R. D. Kelley, G. Medeiros-Ribeiro and R. S. Williams, Appl. Phys. Lett., 2010, 97, 232102.
5. A. C. Torrezan, J. P. Strachan, G. Medeiros-Ribeiro and R. S. Williams, Nanotechnology, 2011, 22, 485203.
6. S. Pi, C. Li, H. Jiang, W. W. Xia, H. L. Xin, J. J. Yang and Q. F. Xia, Nat. Nanotechnol., 2019, 14, 35–39.
7. C. Yoshida, K. Tsunoda, H. Noshiro and Y. Sugiyama, Appl. Phys. Lett., 2007, 91, 223510.
8. S. Spiga, A. Sebastian, D. Querlioz and B. Rajendran, Memristive devices for brain-inspired computing, Elsevier, 2020.
9. C.-C. Chou , et al., 2020 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, pp. 1–2.
10. P. Jain , et al., 2019 IEEE International Solid-State Circuits Conference - (ISSCC), San Francisco, CA, USA, pp. 212–214.
11. S. Ambrogio, et al., Nature, 2018, 558, 60–67.
12. V. Milo, G. Pedretti, R. Carboni, A. Calderoni, N. Ramaswamy, S. Ambrogio, D. Ielmini, 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, pp. 16.8.1–16.8.4.
13. M. Prezioso, F. Merrikh-Bayat, B. D. Hoskins, G. C. Adam, K. K. Likharev and D. B. Strukov, Nature, 2015, 521, 61–64.
14. J. B. Roldan, D. Maldonado, C. Aguilera-Pedregosa, E. Moreno, F. Aguirre, R. Romero-Zaliz, A. García-Vico, Y. Shen, M. Lanza, Y. Yuan and M. Lanza, npj 2D Mater. Appl., 2022, 6, 63.
15. A. Sebastian, M. Le Gallo and R. Khaddam-Aljameh, et al., Nat. Nanotechnol., 2020, 15, 529–544.
16. F. Aguirre, et al., Nat. Commun., 2024, 15(1), 1974.
17. J. Tang, et al., Adv. Mater., 2019, 31, 1902761.
18. M. Ismail, C. Mahata, O. Kwon and S. Kim, ACS Appl. Electron. Mater., 2022, 4(3), 1288–1300.
19. M. Maestro-Izquierdo, M. B. González and F. Campabadal, Microelectron. Eng., 2019, 215, 111014.
20. M. B. Gonzalez, J. M. Rafí, O. Beldarrain, M. Zabala and F. Campabadal, IEEE Trans. Device Mater. Reliab., 2014, 14(2), 769–771.
21. A. Grossi , et al., 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, pp. 4.7.1–4.7.4.
22. E. Pérez, D. Maldonado, C. Acal, J. E. Ruiz-Castro, F. J. Alonso, A. M. Aguilera, F. Jiménez-Molinos, Ch. Wenger and J. B. Roldán, Microelectron. Eng., 2019, 214, 104–109.
23. D. Maldonado, S. Aldana, M. B. González, F. Jiménez-Molinos, M. J. Ibáñez, D. Barrera, F. Campabadal and J. B. Roldán, Microelectron. Eng., 2022, 257, 111736.
24. V. Agudov, A. V. Safonov, A. V. Krichigin, A. A. Kharcheva, A. A. Dubkov, D. Valenti, D. V. Guseinov, A. I. Belov, A. N. Mikhaylov, A. Carollo and B. Spagnolo, J. Stat. Mech.: Theory Exp., 2020, 024003.
25. F. J. Alonso, D. Maldonado, A. M. Aguilera and J. B. Roldan, Chaos, Solitons Fractals, 2021, 143, 110461.
26. M. R. Hossain, P. S. Paul, M. Sadia, A. Dhungel, J. S. Najem and M. S. Hasan, 2022 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Maldives, pp. 1–6.
27. C. Acal, J. E. Ruiz-Castro, A. M. Aguilera, F. Jiménez-Molinos and J. B. Roldán, J. Comput. Appl. Mater., 2019, 345, 23–32.
28. J. E. Ruiz-Castro, C. Acal, A. M. Aguilera, M. C. Aguilera-Morillo and J. B. Roldán, Mater. Comput. Simul., 2021, 186, 71–79.
29. C. Acal, A. M. Aguilera, M. C. Aguilera-Morillo, F. Jiménez-Molinos and J. B. Roldán, Mater. Comput. Simul., 2021, 186, 41–51.
30. C. Acal, D. Maldonado, A. M. Aguilera, K. Zhu, M. Lanza and J. B. Roldán, ACS Appl. Mater. Interfaces, 2023, 15(15), 19102–19110.
31. J. B. Roldán, E. Miranda, D. Maldonado, A. N. Mikhaylov, N. V. Agudov, A. A. Dubkov, M. N. Koryazhkina, M. B. González, M. A. Villena, S. Poblador, M. Saludes-Tapia, R. Picos, F. Jiménez-Molinos, S. G. Stavrinides, E. Salvador, F. J. Alonso, F. Campabadal, B. Spagnolo, M. Lanza and L. O. Chua, Adv. Intell. Syst., 2023, 2200338.
32. M. B. Gonzalez, J. Martin-Martinez, R. Rodriguez, M. C. Acero, M. Nafria, F. Campabadal and X. Aymerich, Microelectron. Eng., 2015, 147, 59–62.
33. D. Maldonado, S. Aldana, M. B. González, F. Jiménez-Molinos, F. Campabadal and J. B. Roldán, Microelectron. Eng., 2022, 265, 111876.
34. S. Poblador, M. B. González and F. Campabadal, Microelectron. Eng., 2018, 187–188, 148.
35. S. Poblador, M. Maestro-Izquierdo, M. Zabala, M. B. González and F. Campabadal, Microelectron. Eng., 2020, 223, 111232.
36. R. A. Reyment, Studies on Nigerian Upper Cretaceous and Lower Tertiary Ostracoda. P. 1, Senonian and Maestrichtian Ostracoda, Almqvist & Wiksell, 1960.
37. V. Voinov and M. Nikulin, Unbiased Estimators and their Applications, Multivariate Case, 1997, vol. 2.
38. L. Van Valen, J. Theor. Biol., 1974, 45(1), 235–247.
39. A. Albert and L. Zhang, Biol. J., 2010, 52(5), 667–675.
40. S. Aerts, G. Haesbroeck and C. Ruwet, J. Multivar. Anal., 2015, 142, 183–198.
41. R. A. Becker, J. M. Chambers and A. R. Wilks, The new S Language, Wandswort & Brooks/Cole, 1988.
42. M. Krzysko and L. Smaga, Stat. Interface, 2019, 12(4), 647–658.

---