The use of collective variables and enhanced sampling in the simulations of existing and emerging microporous materials

Abstract

Microporous materials, including zeolites, metal–organic frameworks, and cage compounds, offer diverse functionalities due to their unique dynamics and guest confinement properties. These materials play a significant role in separation, catalysis, and sensing, but their complexity hinders exploration using traditional atomistic simulations. This review explores collective variables (CVs) paired with enhanced sampling as a powerful approach to enable efficient investigation of key features in microporous materials. We highlight successful applications of CVs in studying adsorption, diffusion, phase transitions, and mechanical properties, demonstrating their crucial role in guiding material design and optimisation. The future of CVs lies in integration with techniques like machine learning, allowing for enhanced efficiency and accuracy. By tailoring CVs to specific materials and developing multi-scale approaches we can further unlock the intricacies of these fascinating materials. Simulations are a cornerstone in unravelling the complexities of microporous materials and are crucial for our future understanding.

---

1 Introduction

The fundamental goal of computational chemistry is to predict experiments or to investigate phenomena that are not accessible by experiments. To achieve this, a model is created to represent the key characteristics of the experiment or system. In the field of computational chemistry two major methods for the simulation of the model persist. Firstly, the Monte Carlo method (MC), which uses repeated random sampling to mimic the experiment. Secondly, molecular dynamics (MD), in which the system is propagated not stochastically but deterministically by following Newton's equations of motion. Both approaches attempt to uncover the potential energy surface upon which the system of interest exists. For chemical applications the sampling of the free energy or the Gibbs free energy is of highest interest as it is a very comprehensive energy expression. Under the right conditions (i.a. from equilibrium) the free energy difference amounts to the work performed by the system, including chemical processes.¹ Yet many chemical systems, including microporous materials as we will see, are too complex for plain MC or MD to capture the desired section of the free energy surface within realistic calculation times. The need of interacting with the system and exploring the free energy surface in a more target-oriented manner is evident and these kind of simulations are called ‘enhanced’.²

Porosity is a sought after property to target exciting new applications.³ Many scientists aspire to control the size and shape of the porous space, as well as the scaffolds that define it. Microporous materials (pore diameter <2 nm) are of particular interest as these pore sizes are within molecular or atomistic resolution. There are many examples of established and emerging microporous materials including zeolites, metal–organic frameworks (MOFs) and also non-periodic, molecular systems, such as cage compounds (Fig. 1).^4–6 Each of these different classes have their respective advantages and allow for a wide range of accessible internal volumes and pore structures leading to confinement effects used for separation and catalysis.^7–9 There are many other classes of porous materials that show promise in the same applications, not discussed in detail here, including covalent organic frameworks (COFs), hydrogen bonded frameworks (HOFs) and polymers such as conjugated microporous polymers (CMPs).

Fig. 1 Atomistic representations of the materials discussed in this review. The zeolite structure of SOD as an assembly of tetrahedra (A). MOFs with an example of MOF-5 is shown, which combines a zinc-oxo cluster with a terephthalate ligand (B). A metallosupramolecular cage formed by palladium and organic ligand (C).¹⁰

In understanding the promising application of these materials it is noted that some exhibit novel properties by themselves, but also the encapsulation of a guest can lead to new and unexpected properties of both guest and host. For example, a change in density of adsorbed water results from interactions with the interface, the constraints of geometry causes water reorientation in zeolites to be hindered.^11,12 This confinement effects the phase diagram, it is lowering the freezing point, thereby making supercooled liquids and glasses accessible.¹³ It is not only the adsorbate that is affected by adsorption, also the adsorbent material can exhibit significant changes. Adsorbents can exhibit structural changes¹⁴ or undergo phase transitions in flexible solids.¹⁵ This is also observed in biomolecules where the effects of water filling the binding pocket of a protein can decisively impact the behavior of proteins.¹⁶ Simulations have played a vital role in understanding this behaviour by following these processes atomistically and describing the energy cost of these processes.

Zeolites are natural occurring aluminosilicate minerals where the substructure consists of tetrahedral SiO₄ and AlO₄ elementary building blocks connected by common oxygen atoms.⁴ Zeolites, often referred to as molecular sieves, are widely recognized and used for their separation properties, whether on a laboratory scale for drying solvents or on a industrial scale for drying gas streams, e.g. for LNG.¹⁷ There has long been a large discrepancy between hypothetical possible zeolite frameworks and those synthetically realised, the zeolite conundrum.¹⁸ There are more than two million predicted structures,^18,19 but only 256 listed in the International Zeolite Association database (as of 14/02/2024).²⁰ Molecular simulations are imperative in the study of zeolites to not only analyse the individual frameworks, but also screen the feasibility of all the hypothetical frameworks.

Metal-organic frameworks (MOFs) are a class of material that has attracted greatly increasing attention in recent years. In the last 10 years, there have been more than 20 000 MOF structures registered in the Cambridge Structural Database (CSD).²¹ These materials consist of metal clusters as nodes and organic linkers connecting the nodes extending in two or three dimensions as frameworks. Again, the porosity, the amazingly high surface area²² combined with a high degree of functionalisation²³ is making these materials promising for a variety of applications. Particularly noteworthy is the, in contrast to zeolites, exceptional property of flexibility, which was predicted²⁴ and discovered.²⁵ This third-generation of flexible MOFs are often referred to as “soft porous crystals” (SPCs), which show drastic structural transformations within the solid phase. A prominent example are MOFs that show a change in unit cell volume upon external stimuli.²⁶ This behaviour is often referred to as ‘breathing’, where the MOF switches between a closed or narrow pore phase (cp or np) to an open pore phase (op). Despite the attention and great number of registered MOF structures, only ∼100 structures exhibit breathing behaviour.²⁷ The dynamic behaviour of MOFs and their exciting applications calls for the study with advanced approaches such as enhanced sampling of molecular dynamics simulations.

Zeolites and MOFs are framework structures, connected in two or three dimensions, but there are also macromolecular cage architectures which are discrete entities and still display the sought after property of porosity.⁶ One famous representative is the C₆₀-fullerene, or buckyball,²⁸ but the inside of the fullerene is not readily accessible by guests (Li⁺ is a notable exception).²⁹ Akin to the Zeolites and MOFs, many cages also demonstrate a high degree of functionalisation of their internal accessible volume. An abundance of these open cages³⁰ have been developed, either purely organic³¹or including metal ions as coordination cages.³² In contrast to extended materials, their discrete nature leads to the solubility of these cages that can even produce a porous liquid, i.e. a liquid with permanent porosity.³³ Further, these discrete entities can be packed, solidified, in many different ways. These solids, which can be disordered and amorphous, have also been investigated for their bulk porosity.³⁴ This porosity can arise from the cage pores itself (intrinsic porosity) or from the voids in between the cages that results from inefficient packing (extrinsic porosity), or a combination of both.³⁵ Since amorphous solids cannot be analysed via common experimental characterisation methods (e.g. X-ray diffraction), simulations of these amorphous cage packings are of crucial importance to understand their properties.^36,37

Research into zeolites, MOFs and cages requires the collaboration of many scientists from a wide variety of fields, including a significant contribution from computational chemists using atomistic simulation to both understand existing observations and predict new avenues of investigation.³⁸ In this review, we describe simulations combining enhanced sampling and collective variables, a combination of different structural features, to understand the complex dynamic behaviour of these exciting materials and showcase illustrative examples. It is this ability for atomistic simulations to describe the powerful effects of dynamics and confinement leading researchers to new materials and new applications.

2 Background

Any simulation can be broken down into its component parts, variables (x) connected by mathematical relations. In a broad definition collective variables (CVs) are only that, a collection of variables contracted into one:

CV = A{x_i}, (1)

with A a transformation matrix. The goal of a collective variable is the reduction of many variables to a lower-dimensional set of variables, that still describe the crucial characteristics of the system. In molecular simulation, CVs have also been called ‘order parameters’, ‘(surrogate) reaction coordinates’, and many other terms. In this review, they will be defined as follows: the individual variables x_i are projected or transformed onto the CVs (A{x_i}) and then span a reaction coordinate

ξ(t) = ξ(CV_i(t),…) = ξ(x_j(t),…) for i, j ∈ N (2)

CVs are chosen to describe a reaction coordinate such that the reaction coordinate consists out of a set of discrete CVs (ξ({CV_i})). The idea is to find CVs as a target to drive the enhanced simulation. As a practical example is the distance CV, here the CV is the distance between two groups of atoms (e.g. 3 Å) while the reaction coordinate ξ spans the whole path between association and dissociation (e.g. from 1 Å–10 Å), here the positions of the atoms are the individual variables x_i. Many techniques and methods exist to find suitable ways to transform the variables into CVs (addressing rescaling errors), namely principal component analysis,³⁹ or for a more direct application the dihedral principle component analysis (dPCA)⁴⁰ for protein folding. Important to keep in mind is that a loss of information is inevitable, for example errors in rescaling the reduced quantities as well as errors in the projection of them are the core issues when handling CVs.⁴¹ Projection errors result from the projection of higher dimensional data onto a set of lower dimensions (see Fig. 2A), while rescaling errors occur from the transformation of the data. Whereas unitary transformations such as PCA conserve the metric of the space, others, such as dPCA, do not. A change in the metric of the space can cause distortions of the rep- resented data (see Fig. 2B). Although projection and rescaling errors can be checked and carefully handled, it is always possible to completely overlook a governing characteristic, which is why the process under investigation must be carefully assessed with respect to all influencing effects. Another intricacy posed by some enhanced simulation methods is the ‘sufficient’ sampling for energy calculation, new protocols are systematizing and quantifying this concept.⁴²

Fig. 2 Schematic depiction of projection errors for a model energy surface (A) and rescaling errors with respect to the geometry distortions of methane (B).

In this review CVs are clustered into three groups: state variables, structural variables and other types and we will also outline approaches that enhance the sampling of these variables (see Fig. 3).

Fig. 3 Selection of the Collective Variables (CVs) discussed in this work. The state variables are in the top row and structural and other types in the bottom row.

3 Applications of collective variables with enhanced sampling

3.1 State collective variables

In thermodynamics, a state variable is an independent variable of a state function: it describes a thermodynamic state independently of the system's path. Examples are the number of particles (N), volume (V), temperature (T), pressure (P) and Gibbs free energy (G). State variables are already collective variables, for example the instantaneous temperature is given bywith N the number of particles, m_i the mass, v_i the velocity, k_b the Boltzmann factor and N_f the number of degrees of freedom (usually N_f = 3N − 3). The work performed by a system, at equilibrium, from state A to B is equal to the free energy difference. To maintain equilibrium, a simulation is carried out with certain state variables held constant, leading to the definition of ensembles. Common ensembles are the canonical ensemble (NVT), isothermal–isobaric ensemble (NPT) and microcanonical ensemble (NVE), where the letters in the brackets always indicate which state variable is kept constant.

Firstly, in the chemical context the state variable N is often referred to as the number of atoms or molecules and it is sampled in the grand canonical ensemble (μVT), with μ the chemical potential.⁴³ The change in the number of atoms of the porous scaffold itself is interesting for crystal growth⁴⁴ but in the case for porous materials, an investigation of their adsorption properties, i.e. a change in the number of guests, is often of greater interest. For simulating equilibrium processes such as adsorption, MC simulations are inherently better suited, because their dynamics have no hysteresis (due to the stochastic processes) and one can more easily insert or delete a molecule without affecting the system. These MC simulations can exchange molecules between the inside of a pore and the external reservoir which captures external gas pressure and there are several reviews on simulating adsorption in MOFs.^45,46 Research has been active and newer methods like GCMC-MD hybrid simulations^47,48 have been developed. The GCMC-MD method includes a MD simulation as a trial move within the MC simulation, thus combining the advantages of both methods in a comprehensive way. This leads to the investigation of dynamic properties of the scaffold with respect to the adsorption of guests. The guest-induced breathing of MIL-53 with CO₂ was investigated by Vanduyfhuys et al.⁴⁸ and Ghoufi et al.⁴⁷ Another example of the combination of MC and MD is the dual control volume grand canonical MD (MC)^49,50 where the simulation box is divided into control volumes and transport regions. The MC step keeps the chemical potential in the control volumes constant, whereby the concentration differs in both control volumes (dual volume) thus creating a concentration gradient in the transport regions, unlike in the GCMC-MD scheme the MC move is initialised at a pre-set ratio to the MD steps. This approach has been particularly effective in studying the transport properties of zeolite membranes, the membrane would be placed in the transport regions.⁵¹

The volume V is easily represented by the size of the simulation cell, as the standard approach is to use a finite simulation cell with a fixed volume and approximate the environment with infinite repetitions of the cell (periodic boundary conditions). For directly interacting with the volume a bias force (pressure) has to be applied to the volume of the simulation cell, the CV, and than the system can be driven along the reaction coordinate sampling the different volumes. The bias forces can be applied in different ways leading to various enhanced sampled techniques. Two of these enhanced simulation techniques are metadynamics (2002 by Laio and Parrinello^52,53) and umbrella sampling (by Torrie and Valleau in 1977 ⁵⁴). These different approaches for sampling the free energy surface are schematically depicted in Fig. 4.

Fig. 4 Schematic depiction of the sampling scheme in MD plain (A), metadynamics plain (B), metadynamics tempered (C) and umbrella sampling plain (D).

In Fig. 4A it can be seen that plain molecular dynamics fail to sample outside of the minimum. Therefore in the approach of metadynamics, a potential (Gaussian function) is added to the free energy surface (defined by a chosen CV). This potential is added on top of any previous potential after a pre-set time and is always added to the point, or configuration, the system is currently at. These added potentials discourage the system to visit the previous points in the future again and over time this leads to the exploration above energy barriers and outside of the minimum. The approach of metadynamics is often referred to as “filling the free energy wells with computational sand”⁵⁵ (see Fig. 4B). If the height and width (or the resulting forces on the system) are adaptively tempered during the simulation the free energy surface can be more accurately sampled – avoiding excess computational time (see Fig. 4C). A somewhat opposite approach is chosen in umbrella sampling, where a potential is added to the free energy surface in order to constrain the system at a certain point and, after a pre-set time, the applied potential moves along a pre-defined reaction coordinate in discrete steps (windows), see Fig. 4D. The added potential is usually a harmonic potential, hence the name umbrella sampling. Especially for SPCs, the exploration of the volume and thus the discovery of multiple solid phases has attracted much attention. Among other enhanced simulation techniques, umbrella sampling and metadynamics have been employed to construct the free energy profile as a function of the unit cell volume for MIL-53 to great success (see Fig. 5).^56–58

Fig. 5 The free energy profiles of MIL53(Al) with respect to the unit cell volume. The two wells of free energy represent the two solid phases. The switching between the closed pore (cp) and large pore (lp) is considered as the breathing of the MOF. Calculated with a variety of enhanced simulation techniques and free energy calculation methods. Reprinted with permission from ref. 56.

Multiple simulations carried out at different, but constant, temperatures T_i can be used to create a temperature profile with discrete temperature steps. The interplay of linker functionality in MOFs was analyzed in terms of CO₂ capture with respect to temperature.⁵⁹ Investigating a defined temperature profile in combination with a discrete volume profile was applied to describe the phenomenon of negative thermal expansion for a variety of MOFs (also with phonon analysis).^60–62 Many MOFs shrink upon heating and switchable thermal expansion, both negative and positive thermal expansion, could be shown.⁶³ Additionally the correlation of thermal expansion with pore size was also shown.⁵ Some properties, phenomena or processes occur so rarely that they are not plausible to occur in the time span feasible for simulations. The simulation time would not be enough to wait for these events to happen so these rare events of minima on the free energy surface are not easily accessible. To access these regions on the free energy surface (configurations in phase space) that would have been separated by to high energy barriers, one approach is to exchange simulations at high temperatures for simulations at low temperatures and vice versa. The sampling of rare events becomes more likely if the temperature is higher and more kinetic energy is present in the system to overcome energetic barriers. The enhanced methods that use this strategy are called parallel tempering or replica exchange (see Fig. 6). Parallel tempering or replica exchange can be employed with any state variable, including any variable within the probability function or the partition function.⁶⁴ For example the Hamiltonian⁶⁵ or force field parameters or the more apparent ones temperature, pressure and volume, can be chosen. Other methods utilising temperature in enhanced simulations are simulated annealing.⁶⁶ An artifical temperature is introduced to initially heat up the system and then gradually cool it down again. The temperature introduces stochasticity into the system and, hopefully, frees the system to find the global minimum, this is inspired by the annealing technique in metallurgy. Addressing the Zeolite conundrum, many hypothetical zeolites were discovered by simulated annealing.¹⁹ Even more zeolite frameworks were constructed, with the scheme of replica exchange, but with replicas of the equilibrium constants for condensation/hydrolysis (see Fig. 7).⁶⁷ For some of these hypothetical zeolites, the temperature replica exchange Monte Carlo method was utilised for screening their thermodynamic feasibility, thereby reducing the number of possible hypothetical zeolites again.⁶⁸ The replica exchange method can also be combined with other enhanced simulation techniques, for example, in the search for the relevant structural CVs in MOF phase transitions, the temperature replica exchange method was used to identify them and then umbrella sampling was utilised to sample these CVs.⁶⁹

Fig. 6 Schematic depiction of the temperature replica exchange scheme.

Fig. 7 Replica exchange reactive Monte Carlo simulations for constructing zeolites. The structure shown in (a) (unit cell), (b) and (c) results from a single replica as well as those from (d) (unit cell), (e) and (f) stem from a second single replica. Color code: Si (yellow), bridging oxygen (red). Reprinted (adapted) with permission from ref. 67. Copyright 2015 American Chemical Society.

Similar to the temperature, the pressure P is also often held constant during the simulation (NPT ensemble) and an excellent comparison of barostats in MOFs was reported by Rogge et al.⁷⁰ To demonstrate the complete picture of adsorption properties, many adsorption simulations are carried out at a range of discrete pressures,^48,71 where the goal is often to create the temperature-pressure-gas phase diagram of the studied material.⁷² Due to the large degree of flexibility possessed by many MOFs, mechanical stress and shear forces are fundamental properties for their characterisation.⁷³ One of the first calculation of the bulk modulus for a MOF was by Fuentes-Cabrera et al. for MOF-5 (ab initio).⁷⁴ Later, the bulk modulus was also calculated by means of classical MD simulations.^75,76 The definition of temperature as undirected kinetic energy leads to a purely isotropic phenomenon, while pressure, in contrast, can be anisotropic and the reduction to a single CV therefore entails an additional loss of information. It was shown that the existence of high anisotropy in elastic properties together with small shear moduli (sub-GPa), is a signature of the flexibility of soft porous crystals and leads to their ability to undergo large phase transitions.^26,77 The internal pressure was sampled by Rogge et al. and used in thermodynamic integration to create the free energy profile. This was carried out for a discrete range of volumes, thus studying the breathing phases of MOFs.^48,70 The procedure or concept behind thermodynamic integration⁷⁸ resembles that of umbrella sampling, with an infinitely strong potential.⁷⁹

3.2 Structural collective variables

In the field of chemistry, especially within classical simulations, changes to the free energy surface are often results of structural changes to the molecule or molecules. The structural definitions can come in many forms—from bending angles over out-of-plane angles to torsion angles—the ways of defining structural CVs is limitless.

Distance (d) as a CV is most commonly used as follows: the center of mass of two groups of molecules are defined and enhanced simulation techniques, e.g. umbrella sampling, are used to sample along the distance coordinate between both groups. Notable examples of using the distance CV within umbrella sampling are the guest-host encapsulation mechanisms for cage compounds.⁸⁰ A different approach to sampling is steered MD, where the same type of bias potential (e.g. harmonic) can be used as in umbrella sampling but instead of constraining the motion of a group a continuous net displacement (defined by a distance) along one direction is enforced (see Fig. 8). Steered MD simulations are often focused on transport properties, for example, the transport of ions, or small molecules, through zeolite membranes was simulated with steered MD.^81,82 A more complex implementation of the steered MD scheme is the concentration gradient driven molecular dynamics. Depending on the composition of a liquid mixture, a steered MD is triggered to equilibrate between two reservoirs, through e.g. a zeolite membrane.⁸³

Fig. 8 Schematic depiction of sampling with steered MD.

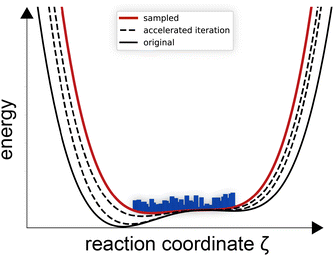
In contrast to umbrella sampling and steered MD, accelerated MD⁸⁴ changes the surface itself, see Fig. 9. The system is not forced above barriers, but the barriers itself are lowered. Accelerated MD has been used to study the encapsulation or de-capsulation of fullerenes in supramolecular cages, where the advantage of accelerated MD over applied force based methods has been showcased.⁸⁵ The host, as with protein-ligand analogues, exhibits self-folding and general dynamic adaptive capabilities that might have been hindered in a simulation with added strain.⁸⁵ Importantly, metadynamics does not need to know the exact reaction coordinate, while accelerated MD does not even need to know the CVs and only umbrella sampling needs previous understanding of the reaction coordinate and CVs.

Fig. 9 Schematic depiction of sampling with accelerated MD.

For the framework atoms in three-dimensional materials there are few applications for the distance CV. The distance CV was used to model the adsorption of water into MOF-5 (via the nudged elastic band model and thermodynamic integration).⁸⁶ Not for adsorption, but for the self assembly of MOFs (MOF-5) the distance CV was utilised successfully.⁸⁷ In some instances the distance CV is also implemented more indirectly, e.g. for imitating pressure on the MOF.⁸⁸

Angles (Θ_i) are essential for the characterisation of materials and molecules, hence they are a key metric for the screening of new materials such as zeolites.⁸⁹ In particular, the flexibility of soft porous crystals, MOFs, raises many geometrical questions such as which angle measurement would be the angle of rotation for the organic linker? To solve this groups have quantified rotational barriers by a large variety of ab initio computational studies^90–92 and combined MD/DFT protocols.⁹³ Interestingly, these soft materials exhibit surprisingly low energy barriers that lead to extremely fast rotations.⁹⁴ While enhanced simulation techniques can allow for the exploration of higher energy regimes in these cases due to the low energy regimes present alternative approaches are needed.⁹⁵ Regardless, some interesting observations have been made considering angles to study rotations. For example, the rotations were not only studied independently, but as coupled motions with the breathing behaviour of MOFs,⁹⁶ or as synchronized rotation for fluid transport.⁹⁷ Elsaidi et al. describe the impact of ring rotation upon gas adsorption.⁹⁸ Other types of linker dynamics, namely out of plane swinging, were studied by Coudert and co-workers.⁹⁹

Beyond dynamics of the MOF framework itself the dynamics of guests were also investigated. A rotational and translational analysis of encapsulated guests within MOFs including CO₂ ¹⁰⁰ and larger organic molecules¹⁰¹ were reported. Another example of enhanced simulation techniques in the field of MOFs, utilising angles, would be the usage of the unit cell vector angle to study the asymmetrical structure transformations for gas adsorption.¹⁰² For cage compounds, similar to MOFs, the tracing of the bending and twisting of the linker is of interest, especially with respect to guest encapsulation.^103,104 A different, interesting, approach is restraining the intermolecular angle between guest and host, the guest is kept with a specified orientation to the host cage during the encapsulation.⁸⁰

The above summarises a few and widely studied structural CVs but there are many more such as root mean square deviation (RMSD)¹⁰⁵, hydrogen bond between two atoms, gyration, coordination number (between groups, atoms or both)¹⁰⁶ and intermolecular angles (e.g. contact angles¹⁰⁷). There truly is an endless way to combine angles between reference points and the best choice may not be obvious.

3.3 Other collective variables

Simulations can also be driven to explore different phases or conditions in other ways than structural manipulation or changes to the state variables. One way is to stimulate the molecules/atoms using an external electric field. Electronic and optical properties and their corresponding variables are ubiquitous and often indirectly represented with other observables or CVs. Especially in applications and experiments they are the go-to ansatz for interaction with a system.

The responses of MOFs to light have been extensively studied, but mostly experimentally.¹⁰⁸ Reports from a theoretical or computational perspective have been comparatively spare and are still very much in development.¹⁰⁹ For example, most light absorption/emission analysis is based on band structure calculations.¹¹⁰ The influence of metal exchange^74,111 and ligand exchange¹¹² was analyzed, with respect to these electronic properties. Piezochromism (change in electric and optical properties due to pressure) of MOFs was investigated.¹¹³ Furthermore, the electronic changes upon gas adsorption were also investigated.¹¹⁴

The effect of an electric field as an external stimuli is of great interest in the community. Notably, the enhanced separation of gas molecules as response to an electrostatic-field was reported.¹¹⁵ This enhancement effect was argued by the dihedral angle of dipolar linkers.¹¹⁶ By using dipolar linkers within the MOF framework, the rotation of the linker as response to an electric field was shown.¹¹⁷ Also the typical breathing behaviour of MOFs could be induced by an electric field.¹¹⁸ Beyond that, an interesting field of research is the luminescence of MOFs, but they require computational intensive methods (like time-dependent density functional theory) and this has only been achieved for few MOFs.^119–121

In another approach CVs can be created from non-physical intermediate states in order to bridge two physical states by a reaction coordinate. These simulations are referred to as alchemical calculations/simulations. Upon the definition of the reaction coordinate along intermediate alchemical states the free energy is calculated by free energy perturbation or thermodynamic integration. For cage compounds, alchemical calculations can be employed to calculate binding energies of guest-host interactions.¹²² Another example of the use of alchemical calculations is the systematic substitution of carbon units (C,C) in fullerene by their isoelectronic pairs of Boron and Nitrogen (B,N). This allowed the exploration of the chemical space for numerous possible alchemical cage derivatives.¹²³

4 Limitations and future directions

Collective variables (CVs) offer a powerful tool for simulating complex microporous materials but they are not without limitations. One key challenge lies in the careful selection of CVs where choosing inappropriate CVs that fail to capture the essential features of the system can lead to misleading results. This highlights the importance of a deep understanding of the system to guide the selection of relevant CVs. Additionally, the use of CVs inherently involves a trade-off between dimensionality and information. By focusing on a reduced set of CVs, some atomistic details and potentially relevant information might be lost.⁴¹ This necessitates careful consideration of the balance between computational efficiency and the level of detail required for the specific investigation.

There are several advanced approaches (beyond statistical methods like PCA) that exist to identify and extract the dominant CVs of a simulation. The combination of graph theory for the topology of molecules together with metadynamics enabled the discovery of isomers, nanoclusters, association, and dissociation reactions.¹²⁴ In another approach by Demuynck et al., time-structure based independent component analysis (tICA)¹²⁵ was used to extract the dominant/accurate CVs of structural transformations to further employ enhanced simulation techniques upon these CVs.⁶⁹ They included a whole range of structural transformations for the analysis of the flexibility of the studied MOFs, based on Kitagawa and coworkers definitions of the different modes of flexibility.¹²⁶ Using a set of parameters including volume, linker bend angles, interlinker distances and the dihedral angle associated with the so-called knee-cap motion (metal to linker) the different phases of CAU-13 were successfully described. Given the sheer quantity and possibilities of CVs, it is not surprising that discovering the crucial CVs to describe the respective system is a hurdle.

Employing only volume as a CV cannot describe the different possible forms a given volume can take. Therefore, studies were performed with special focus on the flexibility of the cell shaping.¹²⁷ A different perspective on the volume is to consider the internal volume. This can be done by investigation of the pore size distributions and the accessible pore volume can be calculated by adsorption simulations.^128,129 Recently, theoretical approaches to generate isotherms corresponding to the individual pores were reported.^130,131 Pore volume may also be deployed as a CV but this is not entirely straightforward. For example, non-periodic MOF nanocrystallites, i.e. finite systems, lack the cell volume as a variable, therefore individual pore volumes defined by their tetrahedral tessellation can be used as a CV to drive phase transitions though the crystal.¹³²

Integrating machine learning techniques offers possibilities such as active learning for dynamic CV selection and dimensionality reduction.¹³³ Machine learning has been showen to be a very powerful and flexible tool for extracting the mechanistically important CVs,^134,105 and also in providing good low-dimensional system projections, energy surfaces, that can be used for sampling.^135,136 Alternatively, or in addition, machine learned potentials¹³⁷ enables efficient screening and has been demonstrated, for example, in zeolites.¹³⁸ As another example, the common form of transportation of H₂ is under extreme high pressures, therefore the investigation of hydrogen storage in MOFs under lower pressures is of great importance and interest (via fluid mechanics and artificial neural networks).¹³⁹

One more way CVs could be used more in the future is by combining both state variables and structural variables in a variety of ways. For example, this may be realised by joining methods together like the GCMC-MD scheme⁴⁸ or by successive employment such as the dual control control GCMD(MC). Another approach could also be temperature replica exchange followed by umbrella sampling. Recent advances demonstrate an increased use and development of novel enhanced simulation approaches.¹⁴⁰

Bridging the gap between atomistic and continuum simulations through multiscale modeling and hybrid approaches holds immense potential for efficient exploration of large-scale phenomena while retaining crucial atomistic details.¹⁴¹ These advancements will solidify CVs as a powerful tool for unlocking the complexities of microporous materials and driving innovation in material design and discovery.

5 Conclusion

Microporous materials, encompassing zeolites, MOFs, and cage compounds, have emerged as a class of versatile materials with diverse applications. Their unique properties, including dynamics and confinement effects have propelled them to the forefront of research in separation, catalysis, and sensing. However, traditional atomistic simulations can struggle to capture the complexities of these materials due to their inherent limitations in describing rare events.

Collective variables (CVs) and enhanced sampling are powerful tools, enabling efficient exploration of the essential features of microporous materials. This review has highlighted the successful application of CVs in studying various aspects of these materials, including adsorption, diffusion, phase transitions, and mechanical properties. By providing valuable insights into their dynamic behavior, these advanced simulations play a crucial role in guiding the design and optimization of microporous materials for specific applications.

Author contributions

K. S. and J. D. E. conceived and drafted this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. D. E. is the recipient of an Australian Research Council Discovery Early Career Award (project number DE220100163) funded by the Australian Government. Phoenix HPC service at the University of Adelaide are thanked for providing high-performance computing resources. This research was supported by the Australian Government's National Collaborative Research Infrastructure Strategy (NCRIS), with access to computational resources provided by Pawsey Supercomputing Research Centre through the National Computational Merit Allocation Scheme.

References

1. C. Jarzynski, Nonequilibrium equality for free energy differences, Phys. Rev. Lett., 1997, 78(14), 2690.
2. J. Hénin, T. Lelièvre, M.R. Shirts, O. Valsson and L. Delemotte, Enhanced Sampling Methods for Molecular Dynamics Simulations [Article v1.0], Living Journal of Computational Molecular Science, 2022, 4(1), 1583.
3. M. E. Davis, Nature, 2002, 417, 813–821.
4. J. Weitkamp, Solid State Ionics, 2000, 131, 175–188.
5. J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450–1459.
6. D. Zhang, T. K. Ronson, Y.-Q. Zou and J. R. Nitschke, Nat. Rev. Chem., 2021, 5, 168–182.
7. S. Kulprathipanja, Zeolites in industrial separation and catalysis, John Wiley & Sons, 2010.
8. R. Freund, O. Zaremba, G. Arnauts, R. Ameloot, G. Skorupskii, M. Dincă, A. Bavykina, J. Gascon, A. Ejsmont and J. Goscianska, et al. , Angew. Chem., Int. Ed., 2021, 60, 23975–24001.
9. Y. Fang, J. A. Powell, E. Li, Q. Wang, Z. Perry, A. Kirchon, X. Yang, Z. Xiao, C. Zhu and L. Zhang, et al. , Chem. Soc. Rev., 2019, 48, 4707–4730.
10. B. Chen, J. J. Holstein, S. Horiuchi, W. G. Hiller and G. H. Clever, J. Am. Chem. Soc., 2019, 141, 8907–8913.
11. G. Liu, Y. Li and J. Jonas, J. Chem. Phys., 1991, 95, 6892–6901.
12. A. C. Fogarty, F.-X. Coudert, A. Boutin and D. Laage, ChemPhysChem, 2014, 15, 521–529.
13. F. He, L.-M. Wang and R. Richert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 144205.
14. A. Walther, I. Regeni, J. J. Holstein and G. H. Clever, J. Am. Chem. Soc., 2023, 145, 25365–25371.
15. C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526.
16. R. Baron, P. Setny and J. A. McCammon, J. Am. Chem. Soc., 2010, 132, 12091–12097.
17. Y. Sun, J. Tang, G. Li, Y. Hua, Y. Sun, S. Hu and X. Wen, Microporous Mesoporous Mater., 2022, 340, 112032.
18. V. A. Blatov, G. D. Ilyushin and D. M. Proserpio, Chem. Mater., 2013, 25, 412–424.
19. M. W. Deem, R. Pophale, P. A. Cheeseman and D. J. Earl, J. Phys. Chem. C, 2009, 113, 21353–21360.
20. C. Baerlocher and L. McCusker, Database of Zeolite Structures, 1996, https://www.iza-structure.org/databases/.
21. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
22. Z. Chen, K. O. Kirlikovali, P. Li and O. K. Farha, Acc. Chem. Res., 2022, 55, 579–591.
23. T. Islamoglu, S. Goswami, Z. Li, A. J. Howarth, O. K. Farha and J. T. Hupp, Acc. Chem. Res., 2017, 50, 805–813.
24. S. Kitagawa and M. Kondo, Bull. Chem. Soc. Jpn., 1998, 71, 1739–1753.
25. S. Kitagawa, R. Kitaura and S.-i. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375.
26. S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695–704.
27. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096.
28. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
29. E. Kwon, T. Matsukawa, A. Hoshikawa, T. Ishigaki, S. Aoyagi, K. Kawachi and Y. Kasama, Chem. Phys. Lett., 2022, 801, 139678.
30. M. Fujita, Molecular self-assembly: organic versus inorganic approaches, Springer, 2003, vol. 96.
31. X. Yang, Z. Ullah, J. F. Stoddart and C. T. Yavuz, Chem. Rev., 2023, 123, 4602–4634.
32. E. G. Percástegui, T. K. Ronson and J. R. Nitschke, Chem. Rev., 2020, 120, 13480–13544.
33. N. O'Reilly, N. Giri and S. L. James, Chem. – Eur. J., 2007, 13, 3020–3025.
34. A. I. Cooper, Angew. Chem., Int. Ed., 2011, 5, 996–998.
35. T. Tozawa, J. T. Jones, S. I. Swamy, S. Jiang, D. J. Adams, S. Shakespeare, R. Clowes, D. Bradshaw, T. Hasell and S. Y. Chong, et al. , Nat. Mater., 2009, 8, 973–978.
36. J. D. Evans, D. M. Huang, M. R. Hill, C. J. Sumby, D. S. Sholl, A. W. Thornton and C. J. Doonan, J. Phys. Chem. C, 2015, 119, 7746–7754.
37. S. Jiang, K. E. Jelfs, D. Holden, T. Hasell, S. Y. Chong, M. Haranczyk, A. Trewin and A. I. Cooper, J. Am. Chem. Soc., 2013, 135, 17818–17830.
38. J. D. Evans, G. Fraux, R. Gaillac, D. Kohen, F. Trousselet, J.-M. Vanson and F.-X. Coudert, Chem. Mater., 2016, 29, 199–212.
39. I. T. Jolliffe, Principal component analysis for special types of data, Springer, 2002.
40. Y. Mu, P. H. Nguyen and G. Stock, Proteins: Struct., Funct., Bioinf., 2005, 58, 45–52.
41. A. Altis, M. Otten, P. H. Nguyen, R. Hegger and G. Stock, J. Chem. Phys., 2008, 128, 245102.
42. S. Borgmans, S. M. J. Rogge, L. Vanduyfhuys and V. Van Speybroeck, OGRe: Optimal Grid Refinement Protocol for Accurate Free Energy Surfaces and Its Application in Proton Hopping in Zeolites and 2D COF Stacking, J. Chem. Theory Comput., 2023, 19(24), 9032–9048.
43. C. Perego, M. Salvalaglio and M. Parrinello, Molecular dynamics simulations of solutions at constant chemical potential, J. Chem. Phys., 2015, 142, 14.
44. A. V. Dighe, R. Y. Nemade and M. R. Singh, Processes, 2019, 7, 527.
45. T. Düren, Y.-S. Bae and R. Q. Snurr, Chem. Soc. Rev., 2009, 38, 1237–1247.
46. R. Krishna and J. M. van Baten, Phys. Chem. Chem. Phys., 2011, 13, 10593–10616.
47. A. Ghoufi and G. Maurin, J. Phys. Chem. C, 2010, 114, 6496–6502.
48. S. M. Rogge, R. Goeminne, R. Demuynck, J. J. Gutiérrez-Sevillano, S. Vandenbrande, L. Vanduyfhuys, M. Waroquier, T. Verstraelen and V. Van Speybroeck, Adv. Theory Simul., 2019, 2, 1800177.
49. H. Takaba, R. Koshita, K. Mizukami, Y. Oumi, N. Ito, M. Kubo, A. Fahmi and A. Miyamoto, J. Membr. Sci., 1997, 134, 127–139.
50. E. J. Maginn, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1993, 97, 4173–4181.
51. D. A. Newsome and D. S. Sholl, J. Phys. Chem. B, 2005, 109, 7237–7244.
52. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
53. A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843.
54. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
55. E. Darve and A. Pohorille, J. Chem. Phys., 2001, 115, 9169–9183.
56. R. Demuynck, S. M. Rogge, L. Vanduyfhuys, J. Wieme, M. Waroquier and V. Van Speybroeck, J. Chem. Theory Comput., 2017, 13, 5861–5873.
57. J. Wieme, L. Vanduyfhuys, S. Rogge, M. Waroquier and V. Van Speybroeck, J. Phys. Chem. C, 2016, 120, 14934–14947.
58. E. Cockayne, J. Phys. Chem. C, 2017, 121, 4312–4317.
59. W. Zhang, H. Huang, C. Zhong and D. Liu, Phys. Chem. Chem. Phys., 2012, 14, 2317–2325.
60. J. D. Evans, J. P. Dürholt, S. Kaskel and R. Schmid, J. Mater. Chem. A, 2019, 7, 24019–24026.
61. W. Zhou, H. Wu, T. Yildirim, J. R. Simpson and A. H. Walker, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054114.
62. J. K. Bristow, D. Tiana and A. Walsh, J. Chem. Theory Comput., 2014, 10, 4644–4652.
63. B. Garai, V. Bon, A. Efimova, M. Gerlach, I. Senkovska and S. Kaskel, J. Mater. Chem. A, 2020, 8, 20420–20428.
64. M. D. Rintoul, S. J. Plimpton and M. P. Sears, Parallel tempering Monte Carlo in LAMMPS., Sandia national laboratories (snl), albuquerque, nm, and livermore, ca⋯technical report, 2003.
65. H. Fukunishi, O. Watanabe and S. Takada, J. Chem. Phys., 2002, 116, 9058–9067.
66. C. Tsallis and D. A. Stariolo, Phys. A, 1996, 233, 395–406.
67. S.-C. Chien, S. M. Auerbach and P. A. Monson, J. Phys. Chem. C, 2015, 119, 26628–26635.
68. C. Bores, S. M. Auerbach and P. A. Monson, Mol. Simul., 2018, 44, 453–462.
69. R. Demuynck, J. Wieme, S. M. Rogge, K. D. Dedecker, L. Vanduyfhuys, M. Waroquier and V. Van Speybroeck, J. Chem. Theory Comput., 2018, 14, 5511–5526.
70. S. Rogge, L. Vanduyfhuys, A. Ghysels, M. Waroquier, T. Verstraelen, G. Maurin and V. Van Speybroeck, J. Chem. Theory Comput., 2015, 11, 5583–5597.
71. J. D. Evans, L. Bocquet and F.-X. Coudert, Chem, 2016, 1, 873–886.
72. F.-X. Coudert, M. Jeffroy, A. H. Fuchs, A. Boutin and C. Mellot-Draznieks, J. Am. Chem. Soc., 2008, 130, 14294–14302.
73. P. Z. Moghadam, S. M. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron and V. Van Speybroeck, et al. , Matter, 2019, 1, 219–234.
74. M. Fuentes-Cabrera, D. M. Nicholson, B. G. Sumpter and M. Widom, J. Chem. Phys., 2005, 123, 124713.
75. S. S. Han and W. A. Goddard, J. Phys. Chem. C, 2007, 111, 15185–15191.
76. M. Tafipolsky, S. Amirjalayer and R. Schmid, J. Phys. Chem. C, 2010, 114, 14402–14409.
77. A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502.
78. J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313.
79. J. Kästner, H. M. Senn, S. Thiel, N. Otte and W. Thiel, J. Chem. Theory Comput., 2006, 2, 452–461.
80. S. Juber, S. Wingbermühle, P. Nuernberger, G. H. Clever and L. V. Schäfer, Phys. Chem. Chem. Phys., 2021, 23, 7321–7332.
81. K. R. Hinkle, C. J. Jameson and S. Murad, J. Phys. Chem. C, 2014, 118, 23803–23810.
82. S. S. M. Khadem, A. H. Mashhadzadeh, F. Yousefi, S. M. Sajadi, S. Habibzadeh, M. T. Munir, N. Rabiee, R. S. Varma, M. Badawi and E. C. Lima, et al. , J. Mol. Liq., 2022, 359, 119250.
83. A. Ozcan, C. Perego, M. Salvalaglio, M. Parrinello and O. Yazaydin, Chem. Sci., 2017, 8, 3858–3865.
84. D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929.
85. C. García-Simón, C. Colomban, Y. A. Çetin, A. Gimeno, M. Pujals, E. Ubasart, C. Fuertes-Espinosa, K. Asad, N. Chronakis and M. Costas, et al. , J. Am. Chem. Soc., 2020, 142, 16051–16063.
86. Y. Ming, N. Kumar and D. J. Siegel, ACS Omega, 2017, 2, 4921–4928.
87. Y. J. Colón, A. Z. Guo, L. W. Antony, K. Q. Hoffmann and J. J. de Pablo, J. Chem. Phys., 2019, 150, 104502.
88. J. Keupp and R. Schmid, Adv. Theory Simul., 2019, 2, 1900117.
89. D. J. Earl and M. W. Deem, Ind. Eng. Chem. Res., 2006, 45, 5449–5454.
90. N. Sinha, I. Deshpande and S. Pakhira, ChemistrySelect, 2019, 4, 8584–8592.
91. S. Pakhira, RSC Adv., 2019, 9, 38137–38147.
92. E. B. Winston, P. J. Lowell, J. Vacek, J. Chocholoušová, J. Michl and J. C. Price, Phys. Chem. Chem. Phys., 2008, 10, 5188–5191.
93. J. Schnabel, A. Schulz, P. Lunkenheimer and D. Volkmer, Commun. Chem., 2023, 6, 161.
94. J. Perego, S. Bracco, M. Negroni, C. X. Bezuidenhout, G. Prando, P. Carretta, A. Comotti and P. Sozzani, Nat. Chem., 2020, 12, 845–851.
95. A. Gonzalez-Nelson, F.-X. Coudert and M. A. van Der Veen, Nanomaterials, 2019, 9, 330.
96. A. Gonzalez-Nelson, S. Mula, M. Šimėnas, S. Balčiūnas, A. R. Altenhof, C. S. Vojvodin, S. Canossa, J. Banys, R. W. Schurko, F.-X. Coudert and M. A. van der Veen, J. Am. Chem. Soc., 2021, 143, 12053–12062.
97. J. D. Evans, S. Krause and B. L. Feringa, Faraday Discuss., 2021, 225, 286–300.
98. S. K. Elsaidi, M. H. Mohamed, C. M. Simon, E. Braun, T. Pham, K. A. Forrest, W. Xu, D. Banerjee, B. Space and M. J. Zaworotko, et al. , Chem. Sci., 2017, 8, 2373–2380.
99. F.-X. Coudert, ChemPhysChem, 2017, 18, 2732–2738.
100. M. Peksa, S. Burrekaew, R. Schmid, J. Lang and F. Stallmach, Microporous Mesoporous Mater., 2015, 216, 75–81.
101. V. J. Witherspoon, L. M. Yu, S. Jawahery, E. Braun, S. M. Moosavi, S. K. Schnell, B. Smit and J. A. Reimer, J. Phys. Chem. C, 2017, 121, 15456–15462.
102. A. Ghysels, L. Vanduyfhuys, M. Vandichel, M. Waroquier, V. Van Speybroeck and B. Smit, J. Phys. Chem. C, 2013, 117, 11540–11554.
103. T. A. Young, V. Martí-Centelles, J. Wang, P. J. Lusby and F. Duarte, J. Am. Chem. Soc., 2019, 142, 1300–1310.
104. R. L. Martin, B. Smit and M. Haranczyk, J. Chem. Inf. Model., 2012, 52, 308–318.
105. S. Bhakat, Collective variable discovery in the age of machine learning: reality, hype and everything in between, RSC Adv., 2022, 12(38), 25010–25024.
106. V. Van Speybroeck, M. Bocus, P. Cnudde and L. Vanduyfhuys, ACS Catal., 2023, 13, 11455–11493.
107. H. Jiang and A. J. Patel, Curr. Opin. Chem. Eng., 2019, 23, 130–137.
108. F.-X. Coudert, Chem. Mater., 2015, 27, 1905–1916.
109. F.-X. Coudert and A. H. Fuchs, Coord. Chem. Rev., 2016, 307, 211–236.
110. M. Mattesini, J. Soler and F. Yndurain, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094111.
111. L.-M. Yang, G.-Y. Fang, J. Ma, E. Ganz and S. S. Han, Cryst. Growth Des., 2014, 14, 2532–2541.
112. E. Flage-Larsen, A. Røyset, J. H. Cavka and K. Thorshaug, J. Phys. Chem. C, 2013, 117, 20610–20616.
113. K. T. Butler, C. H. Hendon and A. Walsh, ACS Appl. Mater. Interfaces, 2014, 6, 22044–22050.
114. S. Ling and B. Slater, J. Phys. Chem. C, 2015, 119, 16667–16677.
115. Q. Yang and C. Zhong, ChemPhysChem, 2006, 7, 1417–1421.
116. S. Namsani and A. O. Yazaydin, Mol. Syst. Des. Eng., 2018, 3, 951–958.
117. J. P. Dürholt, B. F. Jahromi and R. Schmid, ACS Cent. Sci., 2019, 5, 1440–1448.
118. R. Schmid, An electric field induced breath for metal–organic frameworks, 2017.
119. H. Zhang, L. Zhou, J. Wei, Z. Li, P. Lin and S. Du, J. Mater. Chem., 2012, 22, 21210–21217.
120. M. Ji, X. Lan, Z. Han, C. Hao and J. Qiu, Inorg. Chem., 2012, 51, 12389–12394.
121. M. Ji, C. Hao, D. Wang, H. Li and J. Qiu, Dalton Trans., 2013, 42, 3464–3470.
122. G. Norjmaa, P. Vidossich, J.-D. Maréchal and G. Ujaque, J. Chem. Inf. Model., 2021, 61, 4370–4381.
123. R. Balawender, M. Lesiuk, F. De Proft and P. Geerlings, J. Chem. Theory Comput., 2018, 14, 1154–1168.
124. F. Pietrucci and W. Andreoni, Phys. Rev. Lett., 2011, 107, 085504.
125. L. Molgedey and H. G. Schuster, Phys. Rev. Lett., 1994, 72, 3634.
126. S. Kitagawa and K. Uemura, Chem. Soc. Rev., 2005, 34, 109–119.
127. S. M. Rogge, S. Caroes, R. Demuynck, M. Waroquier, V. Van Speybroeck and A. Ghysels, J. Chem. Theory Comput., 2018, 14, 1186–1197.
128. S. Krause, J. D. Evans, V. Bon, I. Senkovska, P. Iacomi, F. Kolbe, S. Ehrling, E. Troschke, J. Getzschmann and D. M. Többens, et al. , Nat. Commun., 2019, 10, 3632.
129. J. Getzschmann, I. Senkovska, D. Wallacher, M. Tovar, D. Fairen-Jimenez, T. Düren, J. M. Van Baten, R. Krishna and S. Kaskel, Microporous Mesoporous Mater., 2010, 136, 50–58.
130. S. Parashar, Q. Zhu, S. Dantas and A. V. Neimark, ACS Appl. Nano Mater., 2021, 4, 5531–5540.
131. J. D. Evans, CrystEngComm, 2022, 24, 7326–7334.
132. L. Schaper and R. Schmid, Commun. Chem., 2023, 6, 233.
133. C. Wehmeyer and F. Noé, J. Chem. Phys., 2018, 148, 241703.
134. H. Sidky, W. Chen and A.L. Ferguson, Machine learning for collective variable discovery and enhanced sampling in biomolecular simulation, Mol. Phys., 2020, 118(5), e1737742.
135. J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98(14), 17501293.
136. G. Mishne, U. Shaham, A. Cloninger and I. Cohen, Diffusion nets, Applied and Computational Harmonic Analysis, 2019, 47(2), 259–285.
137. S. Vandenhaute, M. Cools-Ceuppens, S. DeKeyser, T. Verstraelen and V. Van Speybroeck, npj Comput. Mater., 2023, 9, 1–8.
138. A. Erlebach, P. Nachtigall and L. Grajciar, npj Comput. Mater., 2022, 8, 174.
139. H. Pourrahmani, M. H. Mohammadi, B. Pourhasani, A. Gharehghani, M. Moghimi and J. Van Herle, Sci. Rep., 2023, 13, 18032.
140. M. Bertazzo, D. Gobbo, S. Decherchi and A. Cavalli, J. Chem. Theory Comput., 2021, 17, 5287–5300.
141. N. Hansen and F. J. Keil, Soft Mater., 2012, 10, 179–201.

---