Open Access Article
Open Access ArticleAnisotropic thermo-mechanical response of layered hexagonal boron nitride and black phosphorus: application as a simultaneous pressure and temperature sensor
Hermann
Muhammad
a,
Mohamed
Mezouar
 *a,
Gaston
Garbarino
a,
Tomasz
Poręba
*a,
Gaston
Garbarino
a,
Tomasz
Poręba
 a,
Giorgia
Confalonieri
a,
Giorgia
Confalonieri
 a,
Matteo
Ceppatelli
a,
Matteo
Ceppatelli
 bc,
Manuel
Serrano-Ruiz
bc,
Manuel
Serrano-Ruiz
 c,
Maurizio
Peruzzini
c,
Maurizio
Peruzzini
 c and
Frédéric
Datchi
c and
Frédéric
Datchi
 d
d
aEuropean Synchrotron Radiation Facility (ESRF), 71 Avenue des Martyrs, Grenoble, France. E-mail: mezouar@esrf.fr
bLENS, European Laboratory for Non-linear Spectroscopy, Via N. Carrara 1, I-50019 Sesto Fiorentino, Firenze, Italy
cICCOM-CNR, Institute of Chemistry of Organo Metallic Compounds, National Research Council of Italy Via Madonna del Piano 10, I-50019 Sesto Fiorentino, Firenze, Italy
dInstitut de Minéralogie, de Physique des Matériaux et de Cosmochimie (IMPMC), Sorbonne Universit, é and CNRS UMR 7590, MNHN, 4 place Jussieu, F-75005 Paris, France
First published on 4th April 2024
Abstract
Hexagonal boron nitride (hBN) and black phosphorus (bP) are crystalline materials that can be seen as ordered stackings of two-dimensional layers, which lead to outstanding anisotropic physical properties. Knowledge of the thermal equations of state of hBN and bP is of great interest in the field of 2D materials for a better understanding of their anisotropic thermo-mechanical properties and exfoliation mechanism towards the preparation of important single-layer materials like hexagonal boron nitride nanosheets and phosphorene. Despite several theoretical and experimental studies, important uncertainties remain in the determination of the thermoelastic parameters of hBN and bP. Here, we report accurate thermal expansion and compressibility measurements along the individual crystallographic axes, using in situ high-temperature and high-pressure high-resolution synchrotron X-ray diffraction. In particular, we have quantitatively determined the subtle variations of the in-plane and volumetric thermal expansion coefficients and compressibility parameters by subjecting these materials to hydrostatic conditions and by collecting a large number of data points in small pressure and temperature increments. In addition, based on the anisotropic behavior of bP, we propose the use of this material as a sensor for the simultaneous determination of pressure and temperature in the range of 0–5 GPa and 298–1700 K, respectively.
Introduction
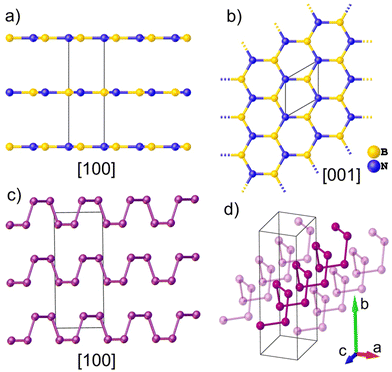
Thermal equations of state (EOS) are fundamental properties of condensed matter3 that are of great significance in a variety of research fields including solid-state physics, materials science and chemistry. They are intimately linked to the materials’ atomic arrangement and provide invaluable information about the nature and amplitude of the microscopic interactions that are particularly relevant for understanding the behavior of layered materials at the nanoscale level. In addition, thermal EOS can be directly related to first-principles calculations based on density functional theory (DFT).4,5 With the advent of the determination of interatomic potentials by machine learning, this type of numerical simulation has proven particularly well suited to predicting the thermo-mechanical properties of 2D materials.6 Materials with strong spatial anisotropy are of particular interest because they often exhibit exceptional directional physicochemical properties.7 Among them, hexagonal boron nitride (hBN)1 and black phosphorus (bP)2 have attracted great attention from chemists, physicists and materials scientists since their discovery. hBN is a layered crystalline solid isostructural to graphite. It is formed of single-atom thick layers of alternating boron and nitrogen arranged in the same hexagonal lattice (Fig. 1a and b), while graphite is made of single-atom thick layers of carbon that give rise to graphene.8 As such, these materials exhibit similar anisotropic properties along the in-plane and out-of-plane directions. The hBN sheets present an AA′ stacking pattern along the crystallographic c-axis, resulting in a crystalline structure with the space group P63/mmc.9 Despite being an electrical insulator with a ∼5.9 eV band gap, hBN is a good thermal conductor,10 which makes it one of the rare materials combining these two generally antagonistic physical properties. As hBN is commonly depicted as the insulating isostructure of graphene, it constitutes a material of choice in industrial applications such as coating11 and a dielectric material,12 and in important device applications.13 hBN is also known for its chemical inertness,14,15 and tribological properties16–18 that make it interesting as a solid lubricant19,20 and high-temperature ceramic material.21Black phosphorus (bP) is the most stable allotrope of phosphorus under ambient conditions of pressure and temperature.22,23 It was first synthesized by subjecting white phosphorus to moderate pressure and temperature conditions (P > 1.2 GPa and T > 500 K)24 and since 2014, it has acquired increasing importance as the bulk material for the preparation of phosphorene by exfoliation techniques.25,26 Indeed, bP exhibits a crystalline layered structure (with A17 orthorhombic structure and the space group Cmce) made by the ordered stacks of 2D puckered layers of P atoms, called phosphorene by analogy to graphene (Fig. 1c and d). As hBN, and due to its puckered structure, few layered phosphorene exhibits an outstanding anisotropic mechanical behavior along the in-plane zigzag [100] and armchair [001] directions, such as a negative Poisson's ratio27,28 and very contrasting directional Young's modulus.29 In contrast to graphene,30 which needs doping to become a semiconductor, and similar to transition metal dichalcogenide (TMD) monolayers,31 such as MoS2, phosphorene is a 2D semiconductor with a direct band gap value of about 2 eV significantly larger than bP (0.3 eV).25,32,33 In addition, it presents a high carrier mobility (∼1000 cm2 V−1 s−1), a good current on/off ratio (∼104–105) and anisotropic in-plane properties, which make phosphorene and phosphorene-based heterostructures very promising for future applications in nanophotonics, nanoelectronics,25,34,35 energy storage,36 sensing37,38 and catalysis.39
hBN and bP exhibit strong covalent intralayer bonds with sp2 (hBN) and sp3 (bP) hybridization and relatively weak van der Waals interlayer forces which lead to very contrasting directional thermal equations of state (EOS). The precise determination of the EOS parameters of these materials is made very difficult due to the weak pressure and temperature variations of the intra-plane inter-atomic distances. Indeed, for both materials, the intra-plane compressibility is 1 to 2 orders of magnitude lower than the inter-plane ones.40–46 Additionally, nonlinear pressure and temperature effects have also been reported,40–58 although not yet precisely quantified.
Here, we report accurate directional thermal EOS of hBN and bP using in situ high-resolution synchrotron X-ray diffraction (XRD) performed under perfect hydrostatic conditions using liquid He as the pressure transmitting medium. Besides providing an accurate description of the effects of pressure and temperature on the lattice parameters and volume of these two materials, our findings allowed us to highlight a new pressure–temperature metrology based on the exceptional anisotropic properties of bP, which can be simultaneously used as a pressure and temperature sensor during XRD experiments in an extended P–T domain.
Experimental methods
High purity powders of hexagonal boron nitride (hBN) purchased from the company Goodfellow (product code: B-60-RD-000105), and black phosphorus (bP, 99.999+% purity) synthesized at ICCOM-CNR (Florence, Italy) from red phosphorus as described in ref. 59 have been used as starting materials.Three independent experimental runs (run 1–3) were carried out to determine precisely the thermal equations of state (EOS) of hBN and bP using in situ monochromatic X-ray diffraction. Runs 1 and 2 were devoted to the determination of the ambient pressure thermal expansion coefficients of hBN and bP, while run 3 was focused on the low pressure (P < 10 GPa) room temperature EOS of these materials. All the experimental work has been conducted at the European Synchrotron Radiation Facility (ESRF, Grenoble, France). Runs 1 and 3 were performed at the high-pressure XRD beamline ID2760 while run 2 was carried out at the high-resolution powder XRD beamline ID22.61,62 In the following, more details about the different runs are provided.
Run 1
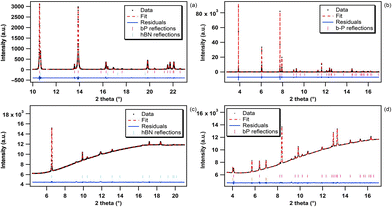
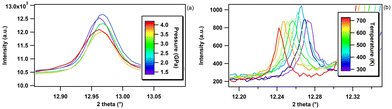
This high-temperature run was carried out by increasing the temperature by small increments at ambient pressure using the resistive heating device of a Paris–Edinburgh (PE) press.63,64 This system can generate stable and homogeneous temperatures (T) over a wide T range from 298 to 2500 K. A standard PE sample geometry as detailed in ref. 65 and 66 was employed. bP was confined inside a cylindrical diamond capsule of 1 mm height and 1 and 1.5 mm inner and outer diameter, respectively, to ensure good thermal conductivity and minimize the temperature gradients. This diamond capsule was inserted into a chemically inert hBN cylinder and closed using two hBN caps. No evidence of the chemical reactivity of bP was observed in any of the collected X-ray diffraction patterns. The sample container was placed inside a cylindrical graphite heater of 1.9 mm inner diameter, 2.4 mm outer diameter and 3.1 mm height that was sealed using two graphite caps in contact with 2 copper electrodes. To thermally insulate the graphite heater, it was contained in an X-ray transparent boron–epoxy gasket.64 Temperature was measured with a precision of ±1 K using a chromel–alumel thermocouple in contact with the diamond capsule. Monochromatic X-ray diffraction measurements were performed at the beamline ID27. The incident X-ray beam energy was fixed to 20 keV (λ = 0.6199 Å), covering a large scattering angle from 3 to 25°. Two-dimensional XRD patterns were collected in transmission geometry using a MAR165 CCD detector. A high-efficiency multichannel collimator67 was used to remove most of the parasitic elastic and inelastic X-ray signals emitted by the sample assembly (the graphite heater and boron–epoxy gasket). The sample to detector distance, detector tilt angles and beam center were accurately determined using a LaB6 powder standard. The two-dimensional XRD images were integrated using the PyFAI software68 as implemented in the DIOPTAS69 suite. The resulting one-dimensional XRD patterns have been analyzed using the GSAS software.70 The unit-cell parameters and volume of hBN and bP have been obtained by Le Bail71 extraction of d-spacings using a pseudo-Voigt peak shape function. As hBN and bP were contained in the same sample assembly, the XRD patterns contain contributions from both samples. A typical XRD pattern of hBN and bP obtained under ambient pressure and at 300 K and the corresponding Le Bail adjustment are presented in Fig. 2a. The temperature was increased from room T to 760 K by small T increments of 10 K up to 470 K and slightly larger ones (15 K) at higher T.Run 2
In order to cross-check the results obtained in run 1 for bP, run 2 has been performed using a different experimental set up. This high-T run 2 has been carried out at the high-resolution powder diffraction beamline ID22 (ESRF) using a heating device consisting of a hot gas blower from the company Cyberstar positioned at an optimum distance (∼5 mm) from the sample. This device generates a smooth laminar flow of hot air that results in a homogeneous temperature distribution over a large volume of more than 10 mm3. This homogeneously heated volume is much larger than the sample (∼1 mm3) ensuring very small temperature gradients. bP was contained in a 0.5 mm inner diameter quartz capillary. The incident energy was set to 35 keV (λ = 0.3543 Å). The temperature interval covered in this run was from 298 to 715 K as it has been previously reported that bP starts to decompose at higher T.53 As this run was intended to validate run 1, data were obtained at wider temperature intervals of the order of 60 K (±1 K). High resolution XRD patterns were collected over the 2θ range of 1°–62° using a multi-analyzer stage of 13 silicon (111) crystals coupled to a Dectris Eiger2 CdTe pixel detector. As for run 1, the structural parameters were derived by Le Bail71 extraction of the d-spacings using a pseudo-Voigt peak shape function using the GSAS software.70 A typical XRD pattern obtained at 300 K and ambient pressure and the corresponding Le Bail fitting are shown in Fig. 2b.Run 3
Run 3 was dedicated to the accurate determination of the room T equation of state (EOS) of bP and hBN. As for run 1, the X-ray diffraction measurements were conducted at the ID27 high-pressure XRD beamline. Fine powder samples of bP and hBN were loaded together in a Le Toulec type membrane diamond anvil cell.72 The high-pressure cavity consisted of a 300 μm hole drilled in a 50 μm thick rhenium foil. Helium, which remains liquid below 11 GPa and thus provides perfect hydrostatic conditions over the whole investigated pressure range, was used as the pressure transmitting medium. The pressure was determined from the shift of the R1 luminescence peak of a ruby chip placed in the pressure cavity using the Ruby2020 pressure scale.73 The pressure (P) was determined as the average of the pressures measured before and after XRD data collection with a maximum P difference of 0.1 GPa. P was increased in fine steps (0.15 GPa steps in the 0–4 GPa pressure range and 0.4 GPa steps in the 4–10.5 GPa pressure range) up to 10.5 GPa. This has been essential to accurately determine the very small in-plane cell parameter variation of hBN and bP. The incident X-ray beam energy was fixed at 33.169 keV (λ = 0.3738 Å) using a silicon (111) double-crystal monochromator. The two-dimensional diffraction images were collected in transmission geometry using a Dectris Eiger2 9M CdTe pixel detector. The sample to detector distance, detector tilt angles and beam center were accurately determined using a CeO2 powder standard. The data were analyzed in a similar way as for run 1 and 2 (Le Bail fitting). Typical diffraction patterns of bP and hBN acquired during run 3 at room temperature and ambient pressure, respectively, and the corresponding Le Bail refinements are shown in Fig. 2c and d, respectively.In high-pressure (P) high-temperature (T) experiments, the main sources of errors come from the presence of pressure and temperature gradients inside the sample, and P–T variations during the measurement. In the present case, a perfectly hydrostatic pressure medium (liquid helium) and a homogeneous heating device were employed, the errors due to the P and T gradients were thus negligible and below the absolute accuracy of the pressure and temperature sensors (typically 1% in the present P–T range). As noted above, the pressure measured before and after the XRD patterns were collected differed by at most 0.1 GPa. The pressure uncertainty was thus taken as the difference between the average and the measured ones. Another source of error in the present experiments comes from the instrumental resolution of the beamline ID27, which is about 3 × 10−3 Å in d-spacing and affects the determination of the lattice parameters. To minimize this, we collected a large set of data (60 and 40 points for the temperature and pressure runs, respectively) on a finely spaced grid of P and T. The error bars for every fitted parameter on these data sets were taken as the estimated standard deviations provided by the least squares refinements.
Thermal expansion of hBN and bP under ambient pressure
Hexagonal boron nitride
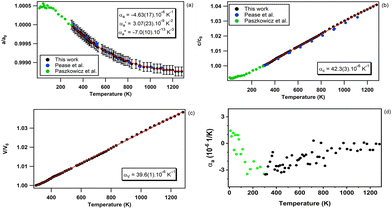
The temperature dependence of the unit-cell parameters and volume of hBN obtained in run 1 is presented in Fig. 3. The resulting directional and volumetric thermal expansion coefficients are listed in Table 1.| Exp | T range (K) | α a (10−6 K−1) | α ′a (10−9 K−2) | α ′′a (10−13 K−3) | α c (10−6 K−1) | α V (10−6 K−1) | Technique |
|---|---|---|---|---|---|---|---|
| This work | 298–1280 | −4.63(17) | 3.07(23) | −7.0(10) | 42.3(1) | 39.6(1) | Powder XRD |
| Pease48 | 273–1073 | −2.9 | 1.9 | — | 40.5 | — | Powder XRD |
| Zhao et al.42 | 300–1280 | −0.0098 | 0.0102 | — | 51.6 | 49.1(19) | Powder XRD |
| Paszkowicz et al.49 | 128–297.5 | −2.72 | 0 | — | 3.2 | — | Powder XRD |
| Solozhenko et al.41 | 300–1800 | — | — | — | — | 40.9(8) | Powder XRD |
| Yates et al.51 | 80–780 | −2.76 | — | — | 38.0 | — | Interferometric measurements |
The c lattice parameter presents, within experimental error, a standard linear and positive temperature evolution up to 1280 K – the maximum temperature reached in this run (see Fig. 3b). A linear regression of the data gives:
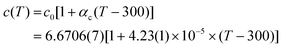 | (1) |
As previously reported,48,49 along the a crystallographic axis, we observed an unusual negative variation of the thermal expansion (Fig. 3a). Indeed, along this axis the network contracts in a non-linear way, at least up to 1280 K. It is worth noting, that the absolute temperature variation of the a lattice parameter is 2 orders of magnitude weaker than that of c. Its temperature dependence can be expressed as a third order polynomial expression:
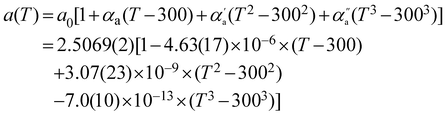 | (2) |
Due to the weak effect along the a-axis, the evolution of the unit-cell volume of hBN is dominated by the temperature effect on the c lattice parameter and evolves linearly with T over the probed temperature range as expressed by:
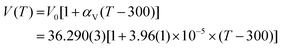 | (3) |
The large contrast between the directional thermal expansion coefficients corresponding to the a and c lattice parameters is explained by the anisotropic structure of hBN, particularly by the striking difference in nature between the covalent chemical bonds in the ab plane and the van der Waals interactions along the c axis of the hexagonal lattice. As shown in Fig. 3a and Table 1, the negative thermal expansion along the a-axis has already been reported48,49 for bulk hBN although never precisely quantified in a wide temperature domain. This is explained by the low number of collected data points and narrower temperature interval probed in these former studies. As suggested by Pease,48 this unusual variation may be due to the fact that the strong in-plane chemical bonds oppose standard thermal expansion by layer puckering effects related to out-of-plane thermal motion. In-plane negative thermal expansion has also been reported for single-layer hBN, both experimentally using in situ electron microscopy,74 temperature-dependent Raman spectroscopy10,75 and, theoretically using ab initio molecular dynamic simulations.76 The much larger and positive thermal expansion along the c axis results from the weak van der Waals forces that are acting along this crystallographic direction.
Black phosphorus
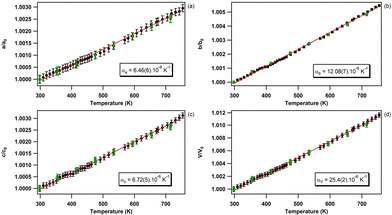
The relative temperature dependence of the unit-cell parameters and volume of bP obtained from Le Bail fitting71 is presented in Fig. 4. The evolution of the directional and volumetric thermal expansions from runs 1 and 2, obtained using two different experimental methods, are in excellent agreement. A linear regression is employed to determine the directional and volumetric thermal expansions in the 298–750 K temperature range. As reported in previous studies,53 the sudden reduction of the Bragg reflection intensities (not shown here), followed by their complete disappearance, attests for the decomposition of bP at higher temperature. The obtained linear and volumetric thermal expansion coefficients are listed and compared with the literature data in Table 2.| Exp | T range (K) | α a (10−6 K−1) | α b (10−6 K−1) | α c (10−6 K−1) | α V (10−6 K−1) | Technique |
|---|---|---|---|---|---|---|
| This work | 298–750 | 6.46(6) | 12.08(7) | 6.72(5) | 25.4(2) | Powder XRD |
| Henry et al.53 | 300–706 | 6.4(1) | 11.8(1) | 6.5(2) | 24.8(2) | Powder XRD |
| Faber et al.54 | 300–575 | 8(5) | 11(2) | 5(5) | 22(12) | Powder XRD |
| Rodrigues et al.55 | 170–250 | 4.9(3) | 11.7(4) | 7.7(2) | 24.5(3) | Neutron powder diffraction |
| Riedner et al.56 | 300–475 | 53(5) | 10(2) | 0(5) | 63(12) | Single Crystal XRD |
| Keyes et al.57 | 300–700 | 22(2) | 38(4) | 39(4) | 99(10) | Powder XRD |
| Sansone et al.55 | 300–600 | 1 | 11 | 8 | 20 | DFT |
The volumetric thermal expansion of bP obtained in this work is in excellent agreement with that reported by Henry et al.53 and Rodrigues et al.55 and in relatively good agreement with that reported by Faber et al.54 As for this study, the employed experimental method in ref. 53–57 was in situ XRD (neutron powder diffraction was used in ref. 55). A good agreement is also found with the density-functional theory (DFT) calculations of Sansone et al.58 However, strong deviations emerge with respect to the papers by Keyes et al.57 and Riedner et al.,56 likely due to a much smaller set of collected data points in these studies.
As expected, the smallest directional thermal expansion is found in the (010) plane, along the zig-zag [100] and the armchair [001] directions, where the atoms form covalently-bonded puckered layers. By comparison, the crystallographic b direction, normal to the layers, exhibits a nearly twice as large thermal expansion value compared to the a and c directions (Table 2). This is consistent with the presence of weak van der Waals-type interlayer interactions only along the crystallographic b direction. As previously reported by Henry et al.,53 we do not confirm the in-plane anisotropy suggested by the DFT calculations of Sansone et al.58 In contrast with Henry et al.,53 we did not observe a discontinuity in the slope of the linear expansion coefficients for the a and c parameters above 706 K. This could be due to the smaller temperature increment used in the present study which resulted in better data sampling and smaller error bars. The positive in-plane thermal expansion of bulk bP is in good agreement with ab initio first-principles calculations performed for monolayer, bilayer, and trilayer phosphorene.77 Indeed, it is reported that, at high temperatures, only the monolayer has negative thermal expansion, while the bilayer and trilayer systems exhibit positive thermal expansion.
Room temperature equations of state of hBN and bP
Hexagonal boron nitride
The pressure dependence of unit-cell parameters and volume of hBN from run 3 and literature are shown in Fig. 5.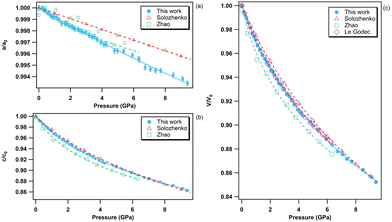 | ||
| Fig. 5 Pressure evolution of the relative lattice parameters (a) a/a0 and (b) c/c0 and (c) relative volume v/v0 of hBN in the 0–10 GPa pressure range at room temperature. The solid blue circles represent the data acquired in the present study upon compression. Empty symbols refer to the data reported in the literature. Red triangles: Solozhenko et al.;41 green squares: Zhao et al.;42 pink diamonds: Le Godec et al.52 The individual a- and c-axis data were fitted using a polynomial equation and the volume data using a third order Birch–Murnaghan equation of state.80 | ||
As presented in Fig. 5a, the a lattice parameter of hBN presents a very small variation in the 0–10 GPa pressure range, only reduced by 0.7% of its initial value over the investigated pressure range. By contrast, we have measured a much larger reduction of 14% along the c axis (20 times larger) in the same pressure interval (Fig. 5b). The strong compressibility anisotropy can be clearly appreciated in Fig. 6a. This observation is consistent with the characteristic layered structure of the material featuring strong intra-plane covalent bonds and weak van der Waals inter-plane interactions.
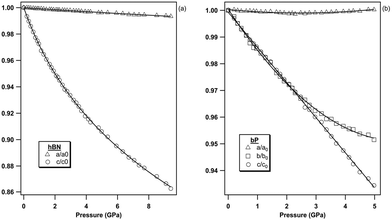 | ||
| Fig. 6 Pressure evolution of the lattice parameters of (a) hBN and (b) bP, normalized to their ambient pressure values to highlight their anisotropic compressive behavior. | ||
The equation of state (EOS) parameters of hBN have been derived using the EoSFit program78,79 by fitting the experimental data using a third-order Birch–Murnaghan EOS80 with the following expression:
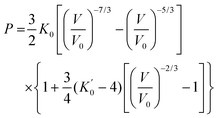 | (4) |
| Exp | P range (GPa) | V 0 (Å3) | K 0(GPa) | K′0 | Technique | EOS type |
|---|---|---|---|---|---|---|
| This work | 0–9.5 | 36.18 ± 0.06 | 27.4 ± 0.9 | 11.4 ± 0.8 | Powder XRD | 3rd order BM |
| Solozhenko et al.41 | 0–12 | 36.17 | 36.7 ± 0.5 | 5.6 ± 0.2 | Powder XRD | Murnaghan |
| Zhao et al.42 | 0–9.0 | — | 17.6 ± 0.8 | 19.5 ± 3.4 | Powder XRD | 3rd order BM |
| Le Godec et al.52 | 0–6.7 | — | 27.6 ± 0.5 | 10.5 ± 0.5 | Powder XRD | 3rd order BM |
| Axis | P range (GPa) | A | B | C | D | Technique | Polynomial fit |
|---|---|---|---|---|---|---|---|
| a axis | 0–9.5 | 2.504[9] | −0.00081[2] | 0.000012[2] | − | Powder XRD | 2nd order |
| c axis | 0–9.5 | 6.661[5] | −0.0284[3] | 0.0025[1] | 0.000107[6] | Powder XRD | 3rd order |
Black phosphorus
The pressure variation of the relative lattice parameters and unit-cell volume of bP at ambient temperature are presented together with literature data in Fig. 7.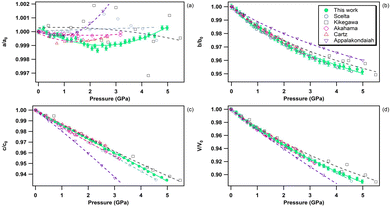 | ||
| Fig. 7 Relative lattice parameters [panels (a), (b) and (c)) and unit-cell volume variation (d) of bP in the 0–5 GPa pressure range at room temperature. The solid green circles represent the data obtained in the present study. The empty symbols refer to the data reported in the literature. Blue circles: Scelta et al.;43 black rectangles: Kikegawa et al.;44 pink diamonds: Akahama et al.;45 red upward triangles: Cartz et al.;46 and violet downward triangles: Appalakondaiah et al.47 The individual a-, b- and c-axis data were fitted using a polynomial equation and the volume data using a third order Birch–Murnaghan equation of state.80 | ||
As hBN, bP exhibits a strong anisotropic behavior (see Fig. 6b). The b and c axes of the orthorhombic lattice reduce by approximately 5%, while the a-axis is nearly incompressible in the entire stability field of bP up to 5 GPa. Using ab initio DFT calculations, Appalakondaiah et al.47 proposed an explanation for this mechanical behavior. Indeed, they showed that the elastic constant C11 is much larger than C22 and C33 (see ref. 47 for Cii index correspondence with the crystallographic directions), which implies that bP is stiffer against deformation along the a-axis (in-plane zig-zag) than along the b (interlayer) and c (in-plane arm-chair) axes. Owing to the very small volume change along a, very accurate XRD measurements and perfect hydrostatic conditions are required for quantitative analysis. We were able to observe a shallow relative a-axis contraction of 10−3 (0.1%) between 0 and ∼2.4 GPa, followed by an expansion of the same amount at higher pressure up to 5 GPa. As shown in Fig. 7, such behavior was not reported in previous experimental studies43–46 due to higher data point scattering, limited pressure range, or the presence of pressure gradients. It is also worth noting that, despite a significant difference in the absolute values, the DFT calculations in ref. 47 reproduce well the observed experimental trends under pressure. This behavior may be attributed to competitive effects between the layer puckering of the sheets and of the atomic repulsion.
The volumetric EOS and directional third-order polynomial parameters of bP are listed in Tables 5 and 6, respectively. As for hBN, a third-order Birch–Murnaghan EOS80 was employed to fit the experimental volume data. Due to the quasi-incompressible nature of the a-axis, the obtained polynomial coefficients B, C and D are close to zero. As detailed below, this unique feature can be exploited for accurate P, T metrology. In agreement with previous studies,43–46 the c axis varies quasi-linearly with pressure, while the b axis presents a standard non-linear behaviour. With the exception of Kikegawa et al.,44 the present volumetric EOS parameters V0, K0 and K′0 are in good agreement with those reported in the literature.
| Exp | P range (GPa) | V 0 (Å3) | K 0 (GPa) | K′0 | Technique | EOS type |
|---|---|---|---|---|---|---|
| a These parameters have been calculated from the data provided in the literature. | ||||||
| This work | 0–5 | 152.06 ± 0.16 | 29.8 ± 0.7 | 5.7 ± 0.5 | Powder XRD | 3rd order BM |
| Scelta et al.43 | 0–5 | 151.28 ± 0.16 | 33.3 ± 1.3 | 3.1 ± 0.6 | Powder XRD | Vinet |
| Kikegawa et al.44 | 0–5 | 151.2 ± 4.8 | 36 ± 2 | 4.5 ± 0.5 | Powder XRD | Murnaghan |
Akahama et al.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0–3.2 | 151.94 ± 0.02 | 29.1 ± 0.2 | 5.7 ± 0.2 | Powder XRD | 3rd order BM |
Cartz et al.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0–2.7 | 151.80 ± 0.17 | 32.8 ± 2.3 | 5.8 ± 1.9 | Powder XRD | 3rd order BM |
| Appalakondaiah et al.47 | 0–5 | 151.3 | 30.7 | — | DFT | — |
| Axis | P range (GPa) | A | B | C | D | Technique | Polynomial fit |
|---|---|---|---|---|---|---|---|
| a-axis | 0–5 | 3.314[1] | −0.0009[2] | 0.00014[8] | 0.000009[11] | Powder XRD | 3rd order |
| b-axis | 0–5 | 10.48[1] | −0.0163[6] | 0.0012[3] | 0.00003[4] | Powder XRD | 3rd order |
| c-axis | 0–5 | 4.375[2] | −0.01315[6] | — | — | Powder XRD | Linear |
A7 phase of phosphorus
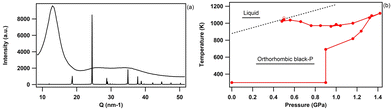
bP displays a series of pressure-induced first-order phase transitions.43 As shown in Fig. 8, upon compression orthorhombic bP undergoes a first-order phase transition to the A7 rhombohedral form (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). As previously reported,43 the onset of this phase transformation is observed at ∼5 GPa and is associated with a large volume contraction of 13% which corresponds to a major atomic rearrangement. This leads to the partial loss of the structural anisotropy of bP. The EOS parameters of the A7 phase of P are listed in Table 7 together with the literature data. Our results are in excellent agreement with those of Scelta et al.,43 but strongly deviate from those reported by Kikegawa et al.44 and Clark et al.81 This is again explained by the larger data point dispersion and the potential presence of significant pressure gradients as non-hydrostatic solid pressure media have been employed in these two studies. As mentioned earlier, helium was used as the pressure transmitting medium both in this study and that of Scelta et al.43
m). As previously reported,43 the onset of this phase transformation is observed at ∼5 GPa and is associated with a large volume contraction of 13% which corresponds to a major atomic rearrangement. This leads to the partial loss of the structural anisotropy of bP. The EOS parameters of the A7 phase of P are listed in Table 7 together with the literature data. Our results are in excellent agreement with those of Scelta et al.,43 but strongly deviate from those reported by Kikegawa et al.44 and Clark et al.81 This is again explained by the larger data point dispersion and the potential presence of significant pressure gradients as non-hydrostatic solid pressure media have been employed in these two studies. As mentioned earlier, helium was used as the pressure transmitting medium both in this study and that of Scelta et al.43
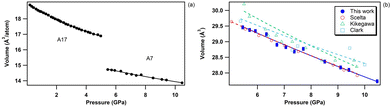 | ||
| Fig. 8 (a) Equation of state of bP at room temperature across the orthorhombic to rhombohedral (A7) first-order phase transition, observed at 5 GPa. (b) Unit-cell volume evolution of A7 rhombohedral P in the 5–10.5 GPa pressure range at room temperature. The solid blue circles represent the data acquired in the present study. The empty symbols refer to the data reported by Scelta et al.43 (red circles), Kikegawa et al.44 (green upward triangles) and Clark et al.81 (blue squares). The corresponding EOS fits are represented by lines. | ||
| Exp | P range (GPa) | V 0 (Å3 per atom) | K 0 (GPa) | K′ 0 | Technique |
|---|---|---|---|---|---|
| This work | 5–10.5 | 15.92 ± 0.06 | 64.8 ± 2.8 | 2.4 ± 0.4 | Powder XRD |
| Scelta et al.43 | 5–10 | 15.88 ± 0.02 | 68 ± 2 | 1.9 ± 0.3 | Powder XRD |
| Kikegawa et al.44 | 5.5–9.7 | 16.6 ± 0.2 | 46 ± 4 | 3.0 ± 0.6 | Powder XRD |
| Clark et al.81 | 3–10 | 15.97 ± 0.02 | 65.0 ± 0.6 | — | Powder XRD |
Exploiting the anisotropic thermo-elastic properties of bP for simultaneous P, T determination
As shown by Crichton and Mezouar,82 it is possible to simultaneously determine the pressure and temperature from the thermal equations of state of two materials subjected to the same P, T conditions. This method is commonly used for P, T metrology in large volume presses. Its precision depends on the contrast between the thermoelastic parameters (bulk modulus K0 and thermal expansion α) of the two materials. For example, NaCl and Au are good material choices because NaCl is much more compressible than Au, but has a much lower thermal expansion coefficient. In principle, this method could be applied to a single material with highly anisotropic thermo-elastic properties that could be used as a sensor for both P and T variables. As shown in Fig. 9, bP is an excellent candidate material for this type of application. Indeed, as discussed above, it is quasi-incompressible in one direction (Fig. 7a) and has a high linear thermal expansion coefficient (αa = 6.46(6)·10−6 K−1) along the a-axis (Fig. 4a and Table 2). This unique property allows the simultaneous determination of P and T with a good precision.Indeed, this remarkable feature makes bP the only known material that can be employed as a simultaneous P, T sensor. In practice, its a lattice parameter can be determined, for instance, from the (200) Bragg reflection, while the temperature can then be derived using the linear T dependence of a using the equation:
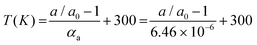 | (5) |
The pressure can then be derived from the third-order Birch–Murnaghan equation of state80 of bP (eqn (4) and Table 5). The precision of this method is ±15 K and ±0.1 GPa, which is sufficient for the determination of phase diagrams in the P, T range up to 5 GPa and 1700 K.
An example of application that aimed at determining a melting point of bP under pressure using the Paris–Edinburgh (PE) press63,64 is presented in Fig. 10. The PE press can generate pressures and temperatures in excess of 10 GPa and 2500 K and is ideally suited to determine P, T phase diagrams using in situ XRD. As shown in Fig. 10 (left panel), the melting of bP is clearly evidenced by the disappearance of the XRD reflections and appearance of a broad diffuse X-ray scattering signal associated with the loss of the crystalline order. Thanks to the established metrology, the P, T pathway in the phase diagram of bP and position of a melting point have been determined with a precision of ±15 K at 0.5 GPa. More details about this work will be presented in a future publication.
Conclusions
In this study, we employed in situ high-resolution X-ray diffraction to accurately determine the equations of state parameters, as well as the volumetric and directional thermal expansion coefficients, of hexagonal boron nitride (hBN) and black phosphorus (bP). Our investigation focused on the precise characterization of the non-linear variations of the unit-cell parameters of these 2D materials at different temperatures and pressures. In particular, small in-plane P and T unit cell variations were determined with unparalleled accuracy. These materials possess anisotropic properties due to their layered structure, making them relevant for various energy and technology applications. Our findings offer detailed insights into the structural behavior of hBN and bP at the nanoscale level under high-pressure and temperature conditions achievable with current industrial technology. Consequently, this information contributes to a better understanding and enhancement of the synthesis, stability, and application of these 2D nanostructured materials. Moreover, our data serve as a valuable experimental reference to refine theoretical calculations and gain a deeper understanding of the two-dimensional interactions present in these materials. Finally, we propose a novel method for high-pressure and high-temperature metrology, utilizing the highly anisotropic directional thermoelastic properties of bP. The high accuracy of this method is due to the high sensitivity of the pressure response of bP along the inter-plane crystallographic direction. This innovative approach could be advantageous for large volume press or diamond anvil cell experiments conducted within the low-pressure, high-temperature regime. The exceptional characteristics of bP enable its utilization as a single sensor for simultaneous determination of pressure and temperature through XRD analysis.Author contributions
The original idea was defined by M. M. Runs 1 and 2 were performed by H. M., G. G., T. P., M. C., M. S. R. and M. M. with equal contributions. Run 3 was performed by H. M., T. P., G. C., M. C. and M. S. R with equal contributions. The data were analysed and the figures were produced by H. M. with contributions from all the co-authors. The manuscript was written by M. M., H.M., F. D. and M. C. with contributions from all the co-authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Thanks are expressed to EC through the European Research Council (ERC) for funding the project PHOSFUN “Phosphorene functionalization: a new platform for advanced multifunctional materials” (Grant Agreement No. 670173) through an ERC Advanced Grant. Thanks are expressed also to the projects “GreenPhos – alta pressione” (CNR), “CHEMPRESS” (CNR), “SiPHOS” (CNR), HP-PHOTOCHEM (Cassa di Risparmio di Firenze) and PRIN 2017 KFY7XF FERMAT “FastElectRon dynamics in novel hybrid-2D MATerials” (MUR). The authors also acknowledge the European Synchrotron Radiation Facility for provision of synchrotron beamtime at the beamline ID27 and the Agence Nationale de la Recherche for financial support under Grant No. ANR-21-CE30-0032-01 (LILI).References
- C. Gautam and S. Chelliah, Methods of hexagonal boron nitride exfoliation and its functionalization: covalent and non-covalent approaches, RSC Adv., 2021, 11, 31284–31327 RSC.
- M. Peruzzini, et al., A perspective on recent advances in phosphorene functionalization and its applications in devices, Eur. J. Inorg. Chem., 2019, 11–12, 1476–1494 CrossRef PubMed.
- P. Chaikin and T. Lubensky, Principle of Condensed Matter Physics, Cambridge University Press, Cambridge, England, 1995 Search PubMed.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn, Nobel lecture: Electronic structure of matter-wave functions and density functionals, Rev. Mod. Phys., 1999, 71, 1253 CrossRef CAS.
- B. Mortazavi, E. V. Podryabinkin, I. S. Novikov, T. Rabczuk, X. Zhuang and A. V. Shapeev, Accelerating first-principles estimation of thermal conductivity by machine-learning interatomic potentials: A MTP/ShengBTE solution, Comput. Phys. Commun., 2021, 258, 107583 CrossRef CAS.
- Y. Cheng, X. Wu, Z. Zhang, Y. Sun, Y. Zhao, Y. Zhang and G. Zhang, Thermo-mechanical correlation in two-dimensional materials, Nanoscale, 2021, 13, 1425–1442 RSC.
- J. D. Bernal, The structure of graphite, Proc. R. Soc. London, Ser. A, 1924, 106, 749–773 CAS.
- R. S. Pease, Crystal structure of boron nitride, Nature, 1950, 165, 722–723 CrossRef CAS PubMed.
- Q. Cai, W. Gan, A. Falin, S. Zhang, K. Watanabe, T. Taniguchi, Y. Chen, E. J. G. Santos and L. H. Li, High thermal conductivity of high-quality monolayer boron nitride and its thermal expansion, Sci. Adv., 2019, 5, 0129 Search PubMed.
- R. Nikbakht and B. Jodoin, Thick Cu-hBN Coatings Using Pulsed Gas Dynamic Spray Process: Coating Formation Analysis and Characterization, J. Therm. Spray Technol., 2022, 31, 609–622 CrossRef.
- C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Boron nitride substrates for high-quality graphene electronics, Nat. Nanotechnol., 2010, 5, 722–726 CrossRef CAS PubMed.
- A. S. Mayorov, R. V. Gorbachev, S. V. Morozov, L. Britnell, R. Jalil, L. A. Ponomarenko, P. Blake, K. S. Novoselov, K. Watanabe, T. Taniguchi and A. K. Geim, Micrometer-Scale Ballistic Transport in Encapsulated Graphene at Room Temperature, Nano Lett., 2011, 11(6), 2396–2399 CrossRef CAS PubMed.
- A. K. Geim and I. V. Grigorieva, van der Waals heterostructures, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- L. H. Li, J. Cervenka, K. Watanabe, T. Taniguchi and Y. Chen, Strong oxidation resistance of atomically thin boron nitride nanosheets, ACS Nano, 2014, 8, 1457–1462 CrossRef CAS PubMed.
- A. Kovalčíková, J. Balko, C. Balázsi, P. Hvizdoš and J. Dusza, Influence of hBN content on mechanical and tribological properties of Si3N4/BN ceramic composites, J. Eur. Ceram. Soc., 2014, 34(14), 3319–3328 CrossRef.
- L. Wang, Y. Bai, Z. Ma, C. Ge, H. Guan and X. Zhang, Tribological performances of hexagonal boron nitride nanosheets via surface modification with silane coupling agent, SN Appl. Sci., 2021, 3, 368 CrossRef CAS.
- P. Madhukar, N. Selvaraj, C. S. P. Rao and G. B. Veeresh Kumar, Tribological behavior of ultrasonic assisted double stir casted novel nano-composite material (AA7150-hBN) using Taguchi technique, Composites, Part B, 2019, 175, 107136 CrossRef CAS.
- D. Berman, A. Erdemir and A. V. Sumant, Approaches for achieving superlubricity in two-dimensional materials, ACS Nano, 2018, 12(3), 2122–2137 CrossRef CAS PubMed.
- R. Zhang, Q. Ding, S. Zhang, Q. Niu, J. Ye and L. Hu, Construction of a continuously layered structure of hBN nanosheets in the liquid phase via sonication-induced gelation to achieve low friction and wear, Nanoscale, 2019, 11, 12553–12562 RSC.
- O. Popov, V. Vishnyakov, L. Fleming, M. Podgurskiy and L. Blunt, Reaction Sintering of Biocompatible Al2O3-hBN Ceramics, ACS Omega, 2022, 7(2), 2205–2209 CrossRef CAS PubMed.
- J. W. Mellor, A Comprehensive Treatise on Inorganic and Theoretical Chemistry, 1922, vol. VIII, pp. 744–754 Search PubMed.
- D. Corbridge, Phosphorus: Chemistry, Biochemistry and Technology, Taylor and Francis, New York, 6th edn, 2013 Search PubMed.
- P. W. Bridgman, Two new modifications of phosphorus, J. Am. Chem. Soc., 1914, 36(7), 1344–1363 CrossRef CAS.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Black phosphorus field-effect transistors, Nat. Nanotechnol., 2014, 9, 372–377 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, Phosphorene: an unexplored 2D semiconductor with a high role mobility, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- Y. Du, J. Maassen, W. Wu, Z. Luo, X. Xu and P. D. Ye, Auxetic black phosphorus: A 2D material with negative Poisson's ratio, Nano Lett., 2016, 16, 6701–6708 CrossRef CAS PubMed.
- J. W. Jiang, T. Rabczuk and H. S. Park, A Stillinger–Weber potential for single-layered black phosphorus, and the importance of cross-pucker interactions for a negative Poisson's ratio and edge stress-induced bending, Nanoscale, 2015, 7, 6059–6068 RSC.
- L. Vaquero-Garzon, R. Frisenda and A. Castellanos-Gomez, Anisotropic buckling of few-layer black phosphorus, Nanoscale, 2019, 11, 12080–12086 RSC.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Electronics and optoelectronics of two-dimensional transition metal dichalcogenides, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS PubMed.
- H. Asahina and A. Morita, Band structure and optical properties of black phosphorus, J. Phys. C: Solid State Phys., 1984, 17, 1839–1852 CrossRef CAS.
- A. S. Rodin, A. Carvalho and A. H. Castro Neto, Strain-induced gap modification in black phosphorus, Phys. Rev. Lett., 2014, 112, 176801 CrossRef CAS PubMed.
- X. Ling, H. Wang, S. Huang, F. Xia and M. S. Dresselhaus, The renaissance of black phosphorus, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4523–4530 CrossRef CAS PubMed.
- J. Lu, J. Yang, A. Carvalho, H. Liu, Y. Lu and C. H. Sow, Light-matter interactions in Phosphorene, Acc. Chem. Res., 2016, 49, 1806–1815 CrossRef CAS PubMed.
- D. Yuan, Y. Dou, Z. Wu, Y. Tian, K.-H. Ye, Z. Lin, S. X. Dou and S. Zhang, Atomically Thin Materials for Next-Generation Rechargeable Batteries, Chem. Rev., 2022, 122(1), 957–999 CrossRef CAS PubMed.
- K. Khan, A. K. Tareen, M. Iqbal, Z. Ye, Z. Xie, A. Mahmood, N. Mahmood and H. Zhang, Recent Progress in Emerging Novel MXenes Based Materials and their Fascinating Sensing Applications, Small, 2023, 19, 2206147 CrossRef CAS PubMed.
- A. Yang, D. Wang, X. Wang, D. Zhang, N. Koratkar and M. Rong, Recent advances in phosphorene as a sensing material, Nano Today, 2018, 20, 13–32 CrossRef CAS.
- C. X. Wang, C. Zhang, J. W. Jiang and T. Rabczuk, The effects of vacancy and oxidation on black phosphorus nanoresonators, Nanotechnology, 2017, 28, 135202 CrossRef PubMed.
- X. Yu, W. Liang, C. Xing, K. Chen, J. Chen, W. Huang, N. Xie, M. Qiu, X. Yan, Z. Xie and H. Zhang, Emerging 2D pnictogens for catalytic applications: status and challenges, J. Mater. Chem. A, 2020, 8, 12887–12927 RSC.
- V. L. Solozhenko, G. Will and F. Elf, Isothermal compression of hexagonal graphite-like boron nitride up to 12 GPa, Solid State Commun., 1995, 96, 1–3 CrossRef CAS.
- Y. Zhao, R. B. Von Dreele, D. J. Weidner and D. Schiferl, P-V-T Data of hexagonal boron nitride h BN and determination of pressure and temperature using thermoelastic equations of state of multiple phases, High Pressure Res., 1997, 15, 369–386 CrossRef.
- D. Scelta, A. Baldassarre, M. Serrano-Ruiz, K. Dziubek, A. B. Cairns, M. Peruzzini, R. Bini and M. Ceppatelli, The p-sc structure in phosphorus: bringing order to the high pressure phases of group 15 elements, Chem. Commun., 2018, 54, 10554–10557 RSC.
- T. Kikegawa and H. Iwasaki, An X-ray diffraction study of lattice compression and phase transition of crystalline phosphorus, Acta Crystallogr., 1983, B39, 158–164 CAS.
- Y. Akahama, M. Miyakawa, T. Taniguchi, A. Sano-Furukawa, S. Machida and T. Hattori, Structure refinement of black phosphorus under high pressure, J. Chem. Phys., 2020, 153, 014704 CrossRef CAS PubMed.
- L. Cartz, S. R. Srinivasa, R. J. Riedner, J. D. Jorgensen and T. G. Worlton, Effect of pressure on bonding in black phosphorus, J. Chem. Phys., 1979, 71, 1718 CrossRef CAS.
- S. Appalakondaiah, G. Vaitheeswaran, S. Lebègue, N. E. Christensen and A. Svane, Effect of van der Waals interactions on the structural and elastic properties of black phosphorus, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035105 CrossRef.
- R. S. Pease, An X-ray study of boron nitride, Acta Crystallogr., 1952, 5, 356–361 CrossRef CAS.
- W. Paszkowicz, J. B. Pelka, M. Knapp, T. Szyszko and S. Podsiadlo, Lattice parameters and anisotropic thermal expansion of hexagonal boron nitride in the 10–297.5 K temperature range, Appl. Phys. A, 2002, 75, 431–435 CrossRef CAS.
- V. L. Solozhenko and T. Peun, Compression and thermal expansion of hexagonal graphite-like boron nitride up to 7 GPa and 1800 K, J. Phys. Chem. Solids, 1997, 58(9), 1321–1323 CrossRef CAS.
- B. Yates, M. J. Overy and O. Pirgon, The anisotropic thermal expansion of boron nitride, Philos. Mag., 1975, 32(4), 847–857 CrossRef CAS.
- Y. Le Godec, D. Martinez-Garcia, M. Mezouar, G. Syfosse, J.-P. Itié and J.-M. Besson, Thermoelastic behavior of hexagonal graphite-like boron nitride, High Pressure Res., 2000, 17(1), 35–46 CrossRef.
- L. Henry, V. Svitlyk, M. Mezouar, D. Sifré, G. Garbarino, M. Ceppatelli, M. Serrano-Ruiz, M. Peruzzini and F. Datchi, Anisotropic thermal expansion of black phosphorus from nanoscale dynamics of Phosphorene layers, Nanoscale, 2020, 12, 4491–4497 RSC.
- In ref. 52 this work is reported as “Private Communication” by J. Faber. To our knowledge, this study was never published.
- J. E. F. S. Rodrigues, J. Gainza, F. Serrano-Sánchez, C. López, O. J. Dura, N. Nemes, J. L. Martinez, Y. Huttel, F. Fauth, M. T. Fernández-Diaz, N. Biškup and J. A. Alonso, Structural features, anisotropic thermal expansion, and thermoelectric performance in bulk black phosphorus synthesized under high pressure, Inorg. Chem., 2020, 59(20), 14932–14943 CrossRef CAS PubMed.
- R. Riedner, S. R. Srinivasa, L. Cartz, T. G. Worlton, R. Klinger and R. Beyerlein, Anisotropic thermal expansion and compressibility of black phosphorus, AIP Conf. Proc., 1974, 17, 8–20 Search PubMed.
- R. W. Keyes, The electrical properties of black phosphorus, Phys. Rev., 1953, 92, 580 CrossRef CAS.
- G. Sansone, A. J. Karttunen, D. Usvyat, M. Schütz, J. G. Brandenburg and L. Maschio, On the exfoliation and anisotropic thermal expansion of black phosphorus, Chem. Commun., 2018, 54(70), 9793–9796 RSC.
- M. Serrano-Ruiz, M. Caporali, A. Ienco, V. Piazza, S. Heun and M. Peruzzini, The role of water in the preparation and stabilization of high-quality phosphorene flakes, Adv. Mater. Interfaces, 2016, 3, 1500441 CrossRef PubMed.
- T. Poręba, D. Comboni, M. Mezouar, G. Garbarino and M. Hanfland, Tracking structural phase transitions via single crystal X-ray diffraction at extreme conditions: advantages of extremely brilliant source, J. Phys.: Condens. Matter, 2022, 35, 054001 CrossRef PubMed.
- A. Fitch, C. Dejoie, E. Covacci, G. Confalonier, O. Grendal, L. Claustre, P. Guillou, J. Kieffer, W. de Nolf, S. Petitdemange, M. Ruat and Y. Watier, ID22 - the high-resolution powder-diffraction beamline at ESRF, J. Synchrotron Radiat., 2023, 30, 1003–1012 CrossRef CAS PubMed.
- C. Dejoie, M. Coduri, S. Petitdemange, C. Giacobbe, E. Covacci, O. Grimaldi, P.-O. Autran, M. W. Mogodi, D. Š. Jung and A. N. Fitch, Combining a nine-crystal multi-analyser stage with a two-dimensional detector for high-resolution powder X-ray diffraction, J. Appl. Crystallogr., 2018, 51, 1721–1733 CrossRef CAS.
- J. M. Besson, G. Hamel, P. Grima, R. J. Nelmes, J. S. Loveday, S. Hull and D. Häusermann, A Large Volume Pressure Cell for High Temperatures, High Pressure Res., 1992, 8, 625 CrossRef.
- S. Klotz, Th. Strässle, G. Rousse, G. Hamel and V. Pomjakushin, Angle-dispersive neutron diffraction under high pressure to 10 GPa, Appl. Phys. Lett., 2005, 86, 031917 CrossRef.
- G. Morard, M. Mezouar, N. Rey, R. Poloni, A. Merlen, S. Le Floch, P. Toulemonde, S. Pascarelli, A. San Miguel, C. Sanloup and G. Fiquet, Optimization of Paris-Edinburgh press cell assemblies for in situ monochromatic X-ray diffraction and X-ray absorption, High Pressure Res., 2007, 27, 223 CrossRef CAS.
- M. Mezouar, T. Le Bihan, H. Libotte, Y. Le Godec and D. Häusermann, Paris-Edinbugh large-volume cell coupled with a fast imaging-plate system for structural investigation at high pressure and high temperature, J. Synchrotron Radiat., 1999, 6, 1115 CrossRef CAS.
- G. Morard, M. Mezouar, S. Bauchau, M. Álvarez-Murga, J.-L. Hodeau and G. Garbarino, High efficiency multichannel collimator for structural studies of liquids and low-Z materials at high pressures and temperatures, Rev. Sci. Instrum., 2011, 82, 023904 CrossRef CAS PubMed.
- G. Ashiotis, A. Deschildre, Z. Nawaz, J. P. Wright, D. Karkoulis, F. E. Picca and J. Kieffer, The fast azimuthal integration Python library: pyFAI, J. Appl. Crystallogr., 2015, 48, 510–519 CrossRef CAS PubMed.
- C. Prescher and V. B. Prakapenka, DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration, High Pressure Res., 2015, 35, 223–230 CrossRef CAS.
- B. H. Toby, EXPGUI, a graphical user interface for GSAS, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- A. Le Bail, H. Duroy and J. L. Fourquet, Ab initio structure determination of LiSbWO6 by X-ray powder diffraction, Mater. Res. Bull., 1988, 23, 447–452 CrossRef CAS.
- R. Letoullec, J. P. Pinceaux and P. Loubeyre, The membrane diamond anvil cell: A new device for generating continuous pressure and temperature variations, High Pressure Res., 1988, 1, 77–90 CrossRef.
- G. Shen, Y. Wang, A. Dewaele, C. Wu, D. E. Fratanduono, J. Eggert, S. Klotz, K. F. Dziuket, P. Loubeyre, O. V. Fat'yanov, P. D. Asimow, T. Mashimo, R. M. M. Wentzcovitch and members of the IPPS task group, Toward an international practical pressure scale: A proposal for an IPPS ruby gauge (IPPS-Ruby2020), High Pressure Res., 2020, 40(3), 299–314 CrossRef.
- M. A. Kriegel, K. M. Omambac, S. Franzka, F. J. Meyer zu Heringdorf and M. Horn-von Hoegen, Incommensurability and negative thermal expansion of single layer hexagonal boron nitride, Appl. Surf. Sci., 2023, 624, 157156 CrossRef CAS.
- Q. Cai, E. Janzen, J. H. Edgar, W. Gan, S. Zhang, E. J. G. Santos and L. H. Li, Isotope effect on the thermal expansion coefficient of atomically thin boron nitride, 2D Mater., 2021, 8, 34006 CrossRef CAS.
- S. Thomas, K. M. Ajith, S. Chandra and M. C. Valsakumar, Temperature dependent structural properties and bending rigidity of pristine and defective hexagonal boron nitride, J. Phys.: Condens. Matter, 2015, 27, 315302 CrossRef PubMed.
- G. Liu, H. Wang and G. L. Li, Layer effect on thermal expansion in blue phosphorene monolayer and few-layer, Phys. Lett. A, 2021, 419, 127726 CrossRef CAS.
- R. J. Angel, J. Gonzalez-Platas and M. Alvaro, EosFit7c and a Fortran module (library) for equation of state calculations, Z. Kristallogr. – Cryst. Mater., 2014, 229, 405–419 CrossRef CAS.
- J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. J. Angel, EosFit7-GUI: A new graphical user interface for equation of state calculations, analyses and teaching, J. Appl. Crystallogr., 2016, 49, 1377–1382 CrossRef CAS.
- F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- S. M. Clark and J. M. Zaug, Compressibility of cubic white, orthorhombic black, rhombohedral black, and simple cubic black phosphorus, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134111 CrossRef.
- W. A. Crichton and M. Mezouar, Noninvasive pressure and temperature estimation in large-volume apparatus by equation-of-state cross-calibration, High Temp. – High Pressures, 2002, 34, 235–242 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |