Ion imaging of spatially inhomogeneous nanoplasmas in NaCl particles

Abstract

Studying photoemission from free, unsupported aerosol particles is a powerful method for gaining insight into light–matter interactions at the nanoscale. We used single-shot velocity map imaging to experimentally measure kinetic energy and angular distributions of ions emitted following interaction of sub-micrometer NaCl particles with femtosecond pulses of near infrared (NIR, 800 nm) and ultraviolet (UV, 266 nm) light. We combined this with time-dependent simulations of light propagation through the particles and a rate equation approach to computationally address the origin of the observed ion emission. For both NIR and UV pulses, ion emission is caused by the formation of an under-dense nanoplasma with similar densities, although using an order of magnitude weaker UV intensities. Such conditions result in remarkably similar ion fragments with similar kinetic energies, and no obvious influence of the plasma formation mechanism (photoionization or collisional ionization). Our data suggests that Coulomb explosion does not play a significant role for ion emission, and we discuss alternative mechanisms that can lead to material ablation from under-dense nanoplasma. Finally, we show how finite size effects play an important role in photoemission through generation of spatially inhomogeneous nanoplasmas, which result in asymmetric ion emission that depends on particle size and laser wavelength. By utilizing the single-particle information available from our experiments, we show how finite size effects and inhomogeneous nanoplasma formation can be exploited to retrieve the size and orientation of individual submicrometer aerosol particles.

---

Introduction

Studying interactions of condensed phase samples with intense, ultrashort laser radiation has been an inexhaustible field of research for many decades. Material under the influence of intense laser radiation can show several interesting properties. For example, modification of a material's refractive index can enable sub-picosecond optical switching,¹ material can emit high-energy radiation (e.g. for extreme ultraviolet lithography²), and controlled ablation of material is useful for surgery and laser machining.³ Condensed phase samples in particulate form offer additional opportunities as the light field can be “tailored” inside and around the particle. Recently, studies on dielectric particles illustrated such advantages by reporting subwavelength transient refractive index reconfiguration,^4,5 appearance of photonic nanojets,⁶ controlled electron acceleration,^7–10 and spatially resolved mapping of photodissociation yields.^11,12

In this work, we investigate interactions of dielectric NaCl particles with intense, ultrashort pulses in the near-infrared (NIR) and ultraviolet (UV) regime. With a combined experimental and computational approach, we obtain a detailed insight into light–matter interactions on the nanoscale by following ion emission from individual particles. Namely, we show that light interacting with finite-sized particles leads to spatially inhomogeneous nanoplasma (NP) formation and enables detailed studies of the ablation mechanism, as well as determination of the size and orientation of individual particles.

We begin with a brief summary of a cascade of processes responsible for ion emission (for more details see ref. 13–16). The first step of material modification is photoionization (multiphoton or strong-field). After a certain number of electrons have left the target, subsequent electrons become trapped in the potential of the ionized particle forming a NP.¹⁵ Quasi-free electron absorption of light can initiate an avalanche of ionization events further increasing the quasi-free electron density. In certain cases, the plasma density reaches the critical value at which collective excitation leads to very effective deposition of laser energy into the particle^17–19 (typically associated with the damage threshold). Because of ultrashort pulse duration (femtoseconds), the energy exchange between the laser and the material is limited to electronic excitation, and further transfer of energy to the lattice takes place after the laser pulse has passed. Following ionization, NP typically expands hydrodynamically under the pressure of hot electrons,^20–22 leading to ion emission or electron-ion recombination. In specific cases where electrons are not effectively trapped in the NP (e.g. at higher photon energies), Coulomb explosion serves as an additional mechanism for ion emission.²³

Understanding the effect of quasi-free electron generation (ionization) on the outcome of the laser-particle interaction is therefore crucial. Previous work on NaCl particles explained the ion emission by the formation of a dense NP and extreme resonant heating.^17–19,24 However, less is understood on the precise ion emission mechanism, as well as the importance of Coulomb explosion and hydrodynamic expansion, at laser intensities where an under-dense NP is formed. For example, it was proposed that at such conditions bulk alkali halide crystals undergo laser damage by “cold ablation”, due to the strong Pauli repulsion forces.²⁵

In this paper, we extend previous work on NaCl particles^17–19,24 to address the ion emission mechanism in more detail. This is accomplished by the following:

(i) We use NIR intensities ∼2 × 10¹³ W cm⁻² to reach electron densities below and around the critical plasma density. With this, we investigate a regime where resonant plasma heating is not possible.

(ii) We use UV pulses (∼2 × 10¹² W cm⁻²) which let us address the influence of collisional ionization on the ion emission process (free-electron heating is negligible for UV pulses). Secondly, they provide means for the formation of a localized NP due to a stronger nanofocusing effect.

(iii) We record mass spectra and mass-gated velocity map images (VMIs) of cations and anions.

(iv) We employ single-shot analysis to address the effects of focal volume averaging^10,17 (see Methods section). By utilizing the single-particle information available from our experiments, we show how spatially inhomogeneous NP formation can be exploited to retrieve the size and orientation of individual sub-micrometer aerosol particles.

Results and discussion

Nanoplasma formation: simulations of laser-particle interactions

To provide some understanding of the ionization and NP formation processes and their influence on ion emission, we first turn to simulations. We calculate time-dependent light intensity distributions (internal and near-field of the particle) with the Finite-Difference Time-Domain (FDTD) method and employ a rate-equation approach to calculate spatial distributions of electron density following photoionization (described by the Keldysh formalism) and collisional ionization (effective rate). Details of the model are described in the Methods section. This approach follows previous work on laser ablation of solids^14,16 and more recently nano-sized particles.^4,6,17,20,26 Laser intensities and pulse durations (i.e. laser fluence) used in our work set us in a regime of relatively rare NPs (electron density n_e < 10²⁰ cm⁻³). For this reason, we simplify our approach by using only linear light propagation terms (not self-consistent⁶) since we do not expect significant changes in the refractive index at these plasma densities. The main goal of this section is to address the influence of focal volume averaging – i.e. distributions of particle size and laser intensity sampled within the ionization region.^10,17

Fig. 1 shows time-averaged light intensity distributions obtained from FDTD simulations for NIR (800 nm, panel a) and UV (266 nm, panel d) pulses interacting with 100 nm NaCl particles. The distribution is shown for a 2D slice through the center of the particle, with the electric field polarization being vertical and the laser propagation axis horizontal. We limit our analysis to the center slice as it exhibits the highest internal light intensity (see Fig. SI10† for a 3D visualization). The small size parameter (i.e. the ratio of particle size to laser wavelength) for NIR pulses leads to a dipole-like scattering, with a nearly homogeneous internal intensity distribution and pronounced maxima in the near field along the polarization axis. The increase in the size parameter for UV pulses leads to Mie-type behavior and the appearance of resonances referred to as nanofocusing. As a result, we observe an asymmetry along the laser propagation direction and light intensity enhancement in a hotspot at the side where light exits the particle and in its near field.

Fig. 1 Panels a and d: Time-averaged light intensity distributions in and around a 100 nm NaCl particle for NIR (a) and UV (d) pulses. Panels b and e: Corresponding electron densities calculated by the rate-equation approach. Panels c and f: Time-evolution of the electron density at the entrance (blue, see stars in panels b and e) and exit (red, see diamonds in panels b and e) side of the particle. Total electron density is shown as full lines, photoionization contribution as dashed-dotted lines and contributions from collisional ionization as dashed lines. Time-evolution of the pulse intensity is shown as shaded blue/red curves.

Time evolution of the internal intensity is then used in the rate equations to calculate the electron density distribution. The resulting electron distributions after the laser pulse is over are shown for NIR and UV pulses in Fig. 1b and e, respectively. They reflect the internal light distribution, but additionally increase the contrast between different regions of the particle due to the nonlinear nature of the ionization process. For NIR pulses, the electron density is maximal near particle surfaces perpendicular to the laser propagation axis (see diamonds and stars in Fig. 1b). The electron density is an order of magnitude lower at surfaces parallel to the laser propagation axis. For the UV case, nanofocusing leads to pronounced asymmetry along the laser propagation axis and higher electron density in the hotspot.

Time evolution of the laser intensity and total electron density at two positions inside the particles is shown for NIR and UV pulses in Fig. 1c and f, respectively. The positions of these points correspond to the maximal light intensity in the region near the particle surface (see black diamonds and stars in panels b and e). First, at times after the laser pulse has passed, we see that electron density is higher near the exiting surface of the light (red lines) because of asymmetry in the light distribution (see above). This asymmetry is more pronounced for UV pulses. Second, we separately show contributions of photoionization (dashed-dotted lines) and collisional ionization (dashed lines). For both NIR and UV pulses, photoionization (PI) is dominated by multiphoton processes due to a relatively large Keldysh parameter. For that reason, lower PI order in the UV case results in a photoionization cross section comparable to that for NIR pulses of significantly higher intensity. On the other hand, collisional ionization (CI) is only important for NIR pulses due to a large ponderomotive energy (U_p). Because of the lower intensity and shorter wavelength (U_p ∝ I·λ²), CI is negligible for UV pulses.

Analogous simulations for 200 nm and 300 nm particles are shown in Fig. SI11 and SI12.† With increasing particle size, nanofocusing becomes dominant in the NIR case, and translates into pronounced asymmetry in the electron density. Due to increasing light enhancement with increasing particle size,²⁷ electron densities reach values close to complete ionization (NaCl density is ∼10²² cm⁻³) for 300 nm particles. In the UV case, the electron densities also increase, and their distributions become more complex, as expected from their corresponding internal light distributions.

To address the influence of focal averaging, we summarize the interplay of wavelength, incident laser intensity, size-dependent light enhancement and resulting electron densities in Fig. 2. Electron densities after the laser pulse is over are shown as a function of the peak incident laser intensity for NIR (red) and UV (blue) interacting with 100 nm (panel a), 200 nm (panel b) and 300 nm (panel c) particles. Laser intensities and particle sizes are chosen in the region relevant for our experiment. Electron densities at the light exit side of the particle (nanofocusing region) are shown as full lines and at the light entrance side (shadowing region) as dashed lines. This figure was obtained by repeating the calculation presented in Fig. 1, and scaling the time-dependent laser intensity before solving the rate equations. This is possible because of our simplified two-step model (see Methods section). From Fig. 2 we see that:

(i) NP remains under-dense (n_e < n_c) for all three particle sizes, at UV intensities <1 × 10¹² W cm⁻². For NIR, under-dense NP is obtained for intensities <2 × 10¹³ W cm⁻², except for the largest particles (300 nm) where electron density approaches n_c due to nanofocusing (full line in panel c).

(ii) UV light produces asymmetry (along the laser propagation axis) in electron densities for all three particle sizes. This asymmetry is washed out as the electron density approaches the asymptote of complete single ionization (n_e = n_o). For NIR, comparable asymmetry is only obtained for the largest particles, while the smallest particles (100 nm) exhibit nearly symmetric electron density. These asymmetries are directly visible in the light intensity distributions (see Fig. 1 and Fig. S11 and S12†).

(iii) At peak intensities used in the experiment (blue/red vertical lines), we obtain comparable electron densities for NIR and UV, although the UV pulses have ∼10× lower incident light intensity.

(iv) Due to higher photon energy (lower photoionization order), electron density increases slower as a function of intensity for UV pulses. This leads to less drastic variations in the NP densities within the focal volume than in the case of NIR.

Fig. 2 Total electron densities as a function of incident laser intensity are shown for NIR (red) and UV (blue) pulses interacting with 100 nm (a), 200 nm (b) and 300 nm (c) particles. Electron densities at the exit side (nanofocusing region, see diamonds in Fig. 1) are shown as full lines and at the entrance side (shadowing region, see stars in Fig. 1) are shown as dashed lines. Critical plasma densities (n_c) for NIR and UV are indicated as dotted horizontal lines. Estimated peak intensities used in our experiment are indicated by shaded vertical lines.

In summary, these results indicate that different wavelengths and the effects of focal averaging (i.e. variation of particle size and laser intensity) lead to different regimes of NP formation spanning from under-dense to near-critical NPs that either form in a localized hotspot or throughout the whole particle. Specifically, we achieve two different experimental conditions by using NIR and UV pulses. First, in the UV case, a highly localized NP with electron densities below the critical plasma density is generated with minimal contribution from collisional ionization. Second, in the NIR case, either under-dense (small particles) or dense (large particles) NPs are generated with a strong influence from collisional ionization and are more likely to appear throughout the whole particle.

The question that remains is how these electron density distributions translate into experimentally measurable emission of ions? In the following sections, we present results on NP emission and discuss implications for the ion emission mechanism.

Nanoplasma disintegration: charged particle emission

Time-of-flight (TOF) spectra. We recorded the emission of both cations and anions (see Fig. SI13†) and assigned the fragments based on their time-of-flight (TOF). For both wavelengths, spectra are dominated by singly charged fragments and qualitatively similar to previous work using femtosecond laser ablation for aerosol mass spectrometry, which corroborates our assignment.²⁸ Cation spectra show dominant contributions from H⁺, Na⁺ and clusters [NaCl]_1–2Na⁺. No larger clusters were observed. Small contributions from H₂⁺ and H₃⁺ suggest that previously reported exotic catalytic properties of aerosolized nanoparticles²⁹ could be a general phenomenon extending to other particles (NaCl) and laser fields (multi-cycle, NIR and UV). Anion spectra show contributions from Cl⁻ and [NaCl]Cl⁻. In addition to the electron signal, at low m/z (see Fig. SI13†) we observe peaks whose origin is currently unclear. They possibly originate from ion fragments (e.g. H⁻) with rather high kinetic energy, multiply charged fragments, or delayed electron detachment from H⁻/H₂⁻ anions. We will further investigate their origin in an upcoming study.

In summary, ion TOF spectra show that both NIR and UV ionization lead to remarkably similar ion emission (similar fragments and their relative intensities). In addition, ion emission is dominated by singly charged ions, whose polarity is dictated by the corresponding electronegativity (e.g. Na⁺versus Cl⁻).

Ion emission energies. To obtain insight into the energetics of ion emission, we recorded VMIs of specific ions by time-of-flight gating of the imaging detector. Kinetic energy (KE) spectra for different ions were obtained by angular integration of the VMIs summed over many recorded laser shots. They are shown in Fig. 3 for NIR (panel a) and UV (panel b) pulses. It is important to note that due to the lack of cylindrical symmetry (see single-shot analysis in the next section) it is not possible to apply standard VMI reconstruction approaches.^30,31

Fig. 3 KE distributions obtained by angularly integrating VMIs for NIR (top) and UV (bottom) pulses. Different ions are shown as different coloured lines, see legend.

The spectra of specific ions are rather similar for both NIR and UV cases. The KEs of H⁺ show a broad distribution extending to >30 eV with KE ∼ 6.6 eV (NIR) and 9.4 eV (UV). These distributions qualitatively agree with previous work,^17,19,24 although exact values differ due to differences in particle size and laser intensity. For the simplest ablation product (Na⁺), the range of KE narrows to <20 eV with KE ∼ 2.6 eV (NIR) and 4.5 eV (UV). [NaCl]Na⁺ and [NaCl]₂Na⁺ cluster ions show further decrease in the KE range and distributions. In comparison to previous work,^17,19,24 here we extend ion emission studies to anions. The KE of Cl⁻ reaches up to ∼15 eV for both NIR and UV, just slightly lower than for Na⁺. KE distribution of [NaCl]Cl⁻ is comparable to cluster cations. In addition, we find that the contribution of near-zero KE ions (VMI centre spot) becomes more pronounced for heavier ion fragments. However, quantitative analysis of this signal is complicated without the appropriate VMI reconstruction. Similar emission energies of Na⁺ and Cl⁻ indicate that they gain energy by forces other than Coulomb interaction (opposite charge polarity).

Finally, we note that KE spectra of anions are weakly influenced by emission of electrons and fast anions, whose contribution can in principle be removed by single-shot analysis. Further analysis of such contributions is outside the scope of the current work and will be investigated in the future.

In summary, from the TOF and KE spectra we conclude that (i) ion emission is dominated by singly charged ions, whose polarity is dictated by the corresponding electronegativity (e.g. Na⁺versus Cl⁻) and (ii) both NIR and UV ionization lead to remarkably similar ion emission (similar fragments relative intensities and ion emission energies).

Such similarity of ion emission for UV and NIR pulses suggests that the ionization mechanism (photoionization vs. collisional ionization) does not play a significant role in the ion emission, but that the determining factor is the electron density of the NP.

Single-shot velocity map imaging of nanoplasma emission

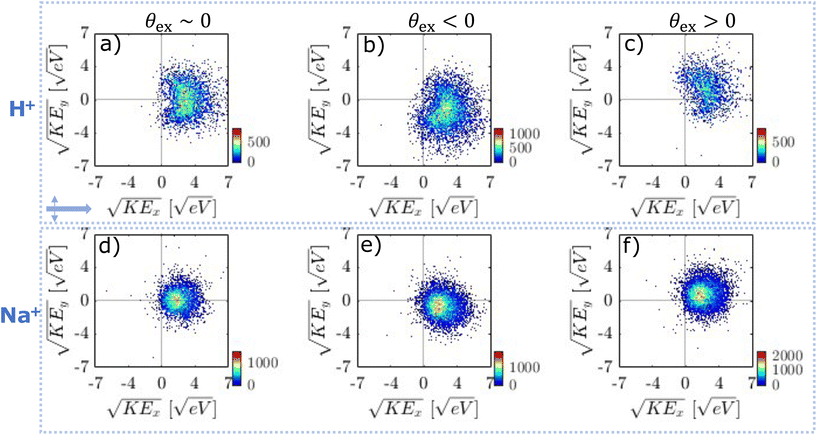
Focal volume averaging leads to significant shot-to-shot variations in ion emission because of different particle sizes and laser intensities probed. In addition, particle orientation becomes important for cubic particles.^17,24 It is important to analyse VMIs on a single-shot basis since focal volume effects can lead to different internal light intensities and in turn different plasma-generating conditions. Previously, this problem was approached either by controlling the peak intensity and using particles with a narrow size distribution,¹⁷ or by employing single-shot analysis and selecting frames based on the number of emitted ions.^32,33

Here we use single-shot velocity map imaging (ssVMI) to extract spatial information on the NP formation from ion VMIs. For this, we characterize ion emission by ssVMI in combination with mass-gating of the imaging detector based on specific ion TOF. We use four parameters to characterize emission on a shot-to-shot basis (see Methods section): (i) total ion yield (i.e. number of bright pixels), (ii) average KE, (iii) average emission angle (θ_ex, θ_en, θ_p) and (iv) asymmetry parameter α.

We start with a comparison of the obtained asymmetry parameters (α). In the UV case (Fig. SI14†), nearly all frames show asymmetric emission for all ions with α > 0.7. This suggests that under our experimental conditions and within the whole focal volume, UV ionization leads to spatially localized ion emission exclusively from the exit side of the particle. Considering simulations from Fig. 2, we can conclude that light intensity enhancement due to nanofocusing leads to sufficient electron density to emit ions only from the exit side of the particle (full lines). In contrast, NIR pulses (Fig. SI14†) result in asymmetry parameters ranging from −0.5 up to 1. NIR ionization leads to more complicated behaviour where ion emission asymmetry suggests NP formation throughout the whole particle. In addition, for both NIR and UV pulses average ion emission angle spans an angle of ±40° around the laser propagation axis (Fig. SI15†). This suggests that orientation of cubical NaCl particles plays a role in determining the ion emission (see below).

In the following, we discuss in more detail the single-shot analysis for both the UV case and the NIR case.

Spatially inhomogeneous nanoplasmas – UV. Fig. 4 shows VMIs of H⁺ (panels a–c) and Na⁺ (panels d–f) for UV pulses. The images were obtained by filtering the frames based on the average emission angle (Fig. SI15†). Panels (a) and (d) show ion emission from the exit side of the particle, while panels (b/e) and (c/f) show upwards and downwards direction emission, respectively. Analogous results are obtained from other cations and anions (not shown).

Fig. 4 Ion VMIs of H⁺ (top row) and Na⁺ (bottom row) filtered on different ion emission angles for the UV case. Panels a/d: emission with θ_ex ∼ 0, panels b/e emission with θ_ex < 0, panels c/f emission with θ_ex > 0.

First, the ion emission shows clear directionality. We assign this to the orientation of the cubical NaCl particles with respect to the laser propagation axis. The assignment is supported by simulations of light intensity distributions in rotated particles (see Fig. SI17–20†). In fact, we propose that this directionality in ion emission can be used to infer the particle size directly from the VMIs. This becomes clear with inspection of the angular distribution of light inside rotated cubical NaCl particles of different sizes (Fig. SI20†). In general, we observe an intensity hotspot that deviates from the laser propagation axis for all rotation angles except integer multiples of 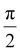due to symmetry. However, the deviation from the propagation axis is most pronounced for small particles (100 nm) and negligible for largest particles considered (300 nm). Because of this we conclude that directional ion emission originates from rotated particles smaller than 300 nm. To support this conclusion, we calculate the angular distribution of light intensity in the centre plane defined by the laser propagation and polarization axes and compare the result with the experimental VMI (for Na⁺) in Fig. 5. We find that the angular distribution of ion emission (full black lines) is qualitatively reproduced by the light distribution inside a 100 nm particle (full blue lines). Light distribution inside a rotated 300 nm particle (dashed blue lines) fails to reproduce the experimental data.

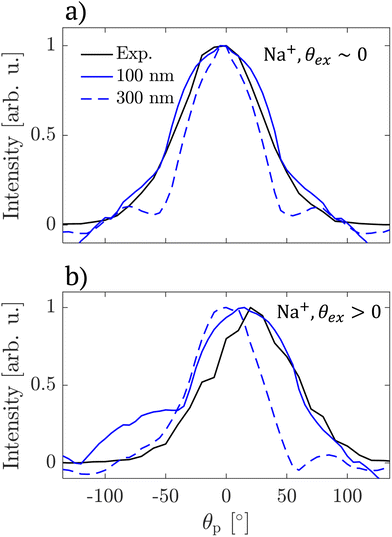Fig. 5 Angular distributions of Na⁺ ion emission intensity (black lines) and light distributions inside NaCl 100 nm (full blue lines) and 300 nm (dashed blue lines) particles calculated for rotated by 0° (panel a) and 15° (panel b) with respect to the laser propagation axis. Experimental angular distributions were obtained from VMIs shown in Fig. 4.

This finding regarding particle size together with simulations in Fig. 2 suggests that ion emission takes place below the critical plasma densities, at n_e ∼ 10¹⁹–10²⁰ cm⁻³, mainly due to the nanofocusing of light intensity in a localized hotspot inside the particle.

Spatially inhomogeneous nanoplasmas – NIR. In the NIR case, shot-to-shot variations in the ion emission patterns are significantly more complex than in the UV case. Below, we focus on (i) variation in ion KE, (ii) asymmetry along the laser propagation direction and (iii) emission angle and discuss possible origins of observed variations. We also note that certain ion emission features could originate from variation in particle morphology (non-cubical) and clusters of particles^12,32,34 (e.g. dimers). We do not consider these possibilities here and therefore the discussion remains qualitative.

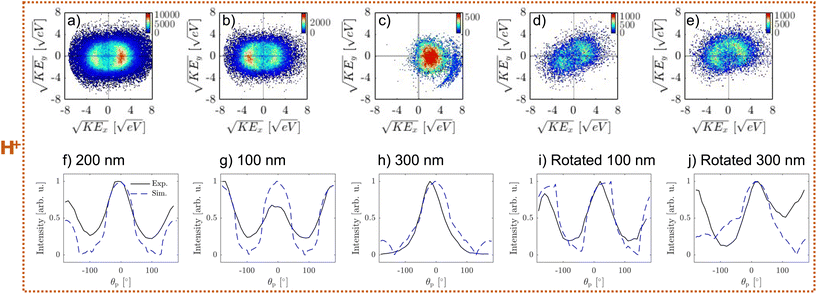
The complexity of ion emission patterns is illustrated in Fig. 6. Panel (a) shows the distribution of the average KE versus number of illuminated pixels (N_p) for H⁺ ion (analogous analysis for Na⁺ is shown in Fig. SI21,† similar results also hold for other ions). KE is constant for frames with between 10² and 10^3.2 illuminated pixels and starts to increase above 10^3.5 pixels. This increase is more pronounced for heavier ions (see Fig. SI21†). For the region of constant KE (black box in panel a), we show the distribution of KE as a function of the α parameter in panel (b). The majority of the frames lie within α values of 0 to 0.5, indicating weak nanofocusing. However, there are some frames that show strong nanofocusing (α ∼ 1), similar to the UV case. The increase in α is accompanied by the increase in KE. Finally, panel (c) shows the correlation of emission angles. The frames along the diagonal (i.e. along the dashed line) indicate correlation of the emission angles, i.e. simple rotation of the ion emission patterns (see Fig. 7d). However, frames along the anti-diagonal (i.e. perpendicular to the dashed line) are more surprising as they indicate more complicated light-particle interactions (see Fig. 7e).

Fig. 6 Single-shot analysis of H⁺ emission for the NIR case. Panel a: 2D histogram showing the number of frames with a specific number of illuminated pixels (x-axis) and average kinetic energy (y-axis). Panel b: 2D histogram showing the number of frames with specific asymmetry (x-axis) and average kinetic energy (y-axis). Panel c: 2D histogram showing the number of frames with specific combination of emission angles.

Fig. 7 Ion VMIs of H⁺ for the NIR case showing weak nanofocusing (a), shadowing (b), strong nanofocusing (c) and emission from rotated particles (panels d and e). Panels f–j: Angular distribution of H+ ion emission intensity (black lines) and simulated light distribution (blue dashed lines) inside NaCl particles for different cases of emission patterns (see text). Ion emission occurs at electron densities below the critical plasma density.

Representative VMIs for H⁺ are shown in Fig. 7. The frames, selected based on α, are shown in panels a–c: for weak nanofocusing (0 < α < 0.5, panel a), shadowing (−0.5 < α < 0, panel b), and strong nanofocusing (α > 0.5, panel c). All three cases show a similar ion KE distribution.

The first case (weak nanofocusing, panel a) can be explained by the nearly homogeneous light intensity distribution inside the 200 nm NaCl particles that is reflected in the weakly asymmetric NP density (see Fig. 1a and b). This is supported by the agreement between the angular distributions of ion emission (black line in Fig. 7f) and the angular light intensity distribution (blue line f).

The second case (shadowing, panel b) is surprising – we would expect a symmetric ion emission for the 100 nm NaCl particles (see blue line in Fig. 7g). We propose two possible explanations for this behaviour. The first possibility is due to the subtle effect of multiphoton ionization. At incident intensity of 20 TW cm⁻², the electron density shows a higher value at the entrance side (i.e. lower intensity) than the exit side (i.e. higher intensity) of the particle. This is due to the sharp decrease in the photoionization cross section at specific intensities (i.e. change in photoionization order as a function of laser intensity, for example see Fig. 2a in ref. 6). The second possibility is that light absorption of quasi-free electrons becomes significant within the pulse duration and leads to decreased intensity at the exit side of the particle. In the future, self-consistent simulations^4,6,17,20,26 will be required to further understand this behaviour.

Finally, we assign the third case (panel c) to ion emission from larger particles present in the focal region (e.g. 300 nm, see Fig. 1c). This is supported by the agreement between the angular distributions of ion emission (black line in Fig. 7h) and the light distribution (blue line Fig. 7h). Nanofocusing light enhancement enables electron density to reach the critical plasma density, forming a dense NP and facilitating ion emission. This is distinct from the behaviour of smaller particles and can be identified by the appearance of sharp high KE features in the VMI (Fig. 7c) that are likely related to previously reported shock wave formation.¹⁹

Analogously to the UV case, we also observe “rotated” ion emission patterns as shown in Fig. 7d and e. The simple “rotated” pattern (Fig. 7d) can be explained by ion emission from a rotated cubical NaCl particle of 100 nm (see Fig. 7i). The pattern in Fig. 7e cannot be explained by simple rotation of larger particles (300 nm, see Fig. 7j). It is possible that these patterns are caused by variations of particle morphology or coagulation.

In summary, our investigation of ion emission on a single-shot basis can be summarized with the following points:

(i) UV and NIR pulses lead to ion emission from spatially distinct NPs although they exhibit similar energetics.

(ii) Similar energetics of ion emission suggests that collisional ionization does not play a major role for ion emission and that the NP density is the determining factor for ion emission in under-dense NPs.

(iii) Under our experimental conditions, UV ionization leads to the formation of a spatially localized NP and in turn strongly asymmetric ion emission. NIR ionization leads to more symmetric ion emission which is attributed to NP formation throughout the whole particle.

(iv) We propose that ion emission patterns contain spatial information on laser-particle interactions, namely particle size and orientation within the focal volume.

Ion emission mechanism: discussion

Ion emission from under-dense NPs takes place below the critical plasma density which raises the question of the nature of the emission mechanism. Due to efficient electron trapping (large particle size and low electron KE)^23,24 and similar emission energies of cations and anions, it is likely that the emission does not take place by Coulomb explosion. An alternative explanation is a thermal emission mechanism, such as hydrodynamic expansion. However, our results do not support previously reported heating mechanisms. First, similarities between ion emission with NIR and UV pulses suggest that inverse bremsstrahlung heating does not play a major role.^35,36 Second, a low electron density (under-dense NP, below critical plasma density) excludes resonant laser heating.¹⁸ Third, multiphoton ionization with low-energy photons used here leads to virtually no excess energy following ionization. This makes heating mechanisms reported for high-energy photons (e.g. multi-body recombination, ionization heating) unlikely.^37,38 A plausible thermal emission mechanism can be found by considering formation of self-trapped excitons previously reported for NaCl³⁹ that can lead to increased light absorption and transfer of energy to the NP. Alternatively, non-thermal mechanisms relying on electronic (Pauli repulsion forces)²⁵ or lattice strain (defects due to self-trapped excitons)⁴⁰ were also shown to result in ion emission. Such mechanisms would explain the similar energetics we observed for cations and anions, as well as our observation of larger cluster ions.

While we cannot precisely determine the emission mechanism from the present data, we argue that electronic excitation in NaCl plays an important role for observing ion emission from the under-dense NP. With this we highlight the open questions about the mechanism of ion emission (i.e. ablation) at relatively low laser fluences where both ionization (i.e. generation of quasi-free electrons) and excitation (i.e. heating, Pauli repulsion or self-trapped excitons) play a role. We aim to further address the details of the ion emission mechanism in future studies.

Conclusions

We investigated emission of cations and anions following interaction of single, intense femtosecond NIR/UV pulses with NaCl particles by experiments and simulations. Experimentally, we used single-shot velocity-map imaging to record kinetic energy and angular distributions of individual ion species by gating the imaging detector based on their time-of-flight. To complement the experiment, we simulated the light-particle interactions and investigated effects of light confinement (Mie theory), photoionization and collisional ionization on electron and ion emission. In this way, we could address different aspects of the NP generation and explosion process.

We compared NPs generated with NIR and UV pulses by following emission of cations and anions. We showed that under-dense NPs of similar density can be generated with NIR and UV pulses, although requiring an order of magnitude lower UV intensity. In both cases we observed emission of the same ion fragments with similar energetics. Lighter ions (H⁺, Na⁺ and Cl⁻) appeared with higher KEs than heavier ions (clusters) and the KE does not depend on the ion charge polarity. From this, we exclude mechanisms that are responsible for ion emission in dense NPs (Coulomb explosion and resonant plasma heating).

Finally, from the angular distributions of emitted ions we find that they originate from spatially distinct NPs. This highlights the differences in light confinement within NaCl particles for NIR and UV pulses and how the resulting inhomogeneities can be used to form locally confined NPs. Furthermore, by analysing ion emission from an individual particle we can use these inhomogeneities in particle-light interactions to infer the variation in particle size and orientation within the focal volume. With this we would like to highlight the prospect of velocity-map imaging for studying morphologies of individual aerosol particles and consider it complementary to the ongoing progress of coherent-diffraction imaging (CDI).⁴¹ We expect that this work will motivate further studies of NP emission and believe that the findings discussed here are of broad interest in the context of engineering material ablation on the nanometer scale and characterizing unsupported, free particles in-vacuo.

Experimental methods

The experimental setup is based on our previous work.^30,42,43 Briefly, NaCl particles are generated by atomizing an aqueous solution of NaCl (100 mM) in a commercial Collision-type atomizer. The aerosol was directed through a silica-based diffusion dryer to dry the particles (relative humidity < 10% at the dryer exit). The resulting particle size distribution was measured with a scanning mobility particle sizer (SMPS) and shows a mean particle diameter of ∼124 nm and geometric standard deviation of 1.7 (see Fig. S1†). Dry particles were transferred into the vacuum chamber by an aerodynamic lens stack to form a particle beam. The particle beam was intersected by a focused (f = 500 mm) NIR or UV laser beam. Peak intensity of the NIR pulses (pulse length ∼40 fs, pulse energy ∼200 μJ, repetition rate 1 kHz) was determined from above threshold ionization (ATI) spectra of Xe (see Fig. S2†) to be 1.3 × 10¹³ W cm⁻². With the UV pulses we could not observe ATI of Xe which suggests significantly lower peak intensity. To determine the intensity of UV pulses (pulse length ∼70 fs, pulse energy ∼60 μJ, repetition rate 1 kHz) we therefore imaged the laser beam at the interaction point and calibrated the beam diameter with the known intensity of the NIR pulses. This resulted in UV peak intensity of 1.1 × 10¹² W cm⁻².

The velocity-map imaging (VMI) spectrometer consists of a three-plate extractor operated at the repeller/extractor voltage ratio of V_ext/V_rep = 0.71 with the third plate at ground. To measure ions of up to a few-10 eV kinetic energy V_rep was set to 12 kV. The polarity of the extractor was changed from positive to negative for cation and anion detection, respectively. Ions were detected on a single-shot basis using an imaging detector (MCP and phosphor) and a kHz camera.⁴⁴ The detector was gated using a fast high-voltage switch based on time-of-flight (TOF) for a specific ion. The TOF spectra were recorded from the current on the imaging detector while using the extraction ratio of V_ext/V_rep = 0.78.

Hit rate and focal volume averaging

With our experimental setup we record TOF mass spectra and VMIs for each laser shot. This allows for the investigation of shot-to-shot variations in ion and electron emission which is important for addressing the effects of focal averaging.^10,17 Focal averaging is used to describe a distribution of laser intensities and particle sizes that are present within the ionization volume.

From the single-shot TOF spectra, we find that peak intensities vary across several orders of magnitude. However, we observe the same dominant ion species independent of the hit strength, which is apparent from comparing TOF spectra with different integral ion yields (see Fig. SI3 and SI4†). Therefore, we conclude that similar conditions for ion emission are achieved within the focal volume.

From the TOF-gated VMIs, we determined the hit rate for each of the dominant ion species observed in the experiment. The hit rate is determined by counting the number of laser shots containing particle hits that result in more than 15 bright pixels. This value is chosen since most of plasma-forming particle hits result in >15 bright pixels and laser shots without particle hits have <15 bright pixels (see Fig. SI5–8†). The number of bright pixels is directly correlated to the total ion signal. We refrain from counting individual ions as centroiding is only possible for a limited number of illuminated pixels in each frame. From the hit rate analysis (see Fig. SI9†), we find that ∼18% (∼30%) of laser shots lead to electron emission in the NIR (UV) case. Hit rates for observing ions are significantly lower, <6% (<0.4%) for NIR (UV) pulses (ions in the UV case are scaled by a factor of 20 in the figure). The hit rate also varies between different ions, with the highest hit rates for H⁺ and Na⁺.

Although a comparison of absolute hit rates is not possible between NIR/UV pulses due to different beam diameters at the interaction region, the probability of observing ion fragments for each electron is clearly higher for NIR than UV pulses under our conditions. The higher photoionization (PI) rate for UV pulses leads to a wider intensity region over which one can expect electron emission without ion emission.

Single-shot analysis

We use four parameters to characterize ion emission on a shot-to-shot basis:

Total ion yield (N_p, i.e. number of bright pixels) is determined by simply counting the number of pixels with non-zero intensity value for each recorded laser shot.

Average kinetic energy (KE) is calculated for each frame as a weighted average of the radial coordinate of each pixel , where I_p is pixel intensity and r_p is its radial coordinate. Average radius is then transformed to KE by our VMI calibration 〈KE〉 = f_cal〈r〉².

Average emission angle θ is calculated from the azimuths (θ_p) of individual pixels. We calculate the angle relative to the laser propagation axis towards the exit side of the particle (θ_ex) and the entrance side of the particle (θ_en) separately as , where θ_p is the azimuth of each pixel.

The asymmetry parameter (α) is calculated as α = (I_ex − I_en)/(I_ex + I_en), where I_ex and I_en are the total intensities in the exit and entrance sides of the particle, respectively.

Simulation methods

The simulation approach is based on a two-step procedure: (i) simulation of the time-dependent light intensity distributions (internal and near-field of the particle) and (ii) calculation of the ionized electron density from a single rate equation that was previously used to explain femtosecond laser-induced damage (see for example ref. 14 and 16). This approach is possible for plasma below the critical density, where the interaction of light with the generated quasi-free electrons is still negligible. For dense plasmas it is necessary to implement a self-consistent approach, see ref. 6, 15 and 45. Furthermore, for particle sizes and kinetic energies relevant to this work the portion of electrons that directly leave the particle is negligible and we therefore take the ionized electron density to approximate the nanoplasma density.²³

In step (i), we solved Maxwell's equations using a Finite-Difference Time-Domain (FDTD) method (Lumerical). We used cubical NaCl particles with the refractive index of n = 1.54 (NIR) and n = 1.64 (UV) and laser pulse properties that match the experiment (for NIR: 800 nm and 40 fs, for UV: 266 nm and 70 fs).

In step (ii), we used the obtained time-dependent light field inside the particle to calculate the electron density. We used the following rate equation to describe time-dependent quasi-free electron density n_e(t)^{6,14,16,45,46}

where n₀ is the initial electron density (assuming only single ionization of each NaCl unit, n₀ = 1.6 × 10²² cm⁻³), n_a is the time-dependent density of the remaining bound electrons (n_a = n₀ − n_e) and ν_rec is the recombination rate. Because typical recombination times are longer than pulse durations used in this work, we neglected this contribution (ν_rec = 0). W_PI is the photoionization rate calculated from the Keldysh equation using the time dependent light intensity I(t).^16,47 The collisional (impact) ionization rate is defined according to ref. 14
where IE is the ionization energy of NaCl (IE = 8.2 eV), ε₀ is the ponderomotive energy that depends on the light intensity I(t), ω is the laser frequency and ν_ci is the effective electron–electron collision frequency (ν_ci = 1 fs⁻¹).

Data availability

Data required to reproduce the results presented in the paper can be found in the open access data collection of ETHZ at doi: https://doi.org/10.3929/ethz-b-000659712.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Saima Nafees, Jan Krohn and Stefan Feusi for their help with the experiment. We thank David Stapfer, Markus Steger and Dr Egor Chasovskikh for their technical support. This project has received funding from the European Unions Horizon 2020 research and innovation program from the European Research Council under the Grant Agreement No. 786636, and the research was supported by the NCCR MUST, funded by the Swiss National Science Foundation (SNSF), through ETH-FAST, and through SNSF project No. 200020_200306. C.W.W. acknowledges funding from the European sUnion's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 801459 - FP-RESOMUS - and the Swiss National Science Foundation through the NCCR MUST.

References

1. B. Dromey, S. Kar, M. Zepf and P. Foster, Rev. Sci. Instrum., 2004, 75, 645–649.
2. I. Fomenkov, D. Brandt, A. Ershov, A. Schafgans, Y. Tao, G. Vaschenko, S. Rokitski, M. Kats, M. Vargas, M. Purvis, R. Rafac, B. La Fontaine, S. De Dea, A. LaForge, J. Stewart, S. Chang, M. Graham, D. Riggs, T. Taylor, M. Abraham and D. Brown, Adv. Opt. Technol., 2017, 6, 173–186.
3. K. C. Phillips, H. H. Gandhi, E. Mazur and S. K. Sundaram, Adv. Opt. Photonics, 2015, 7, 684.
4. A. Rudenko, K. Ladutenko, S. Makarov and T. E. Itina, Adv. Opt. Mater., 2018, 6, 1701153.
5. Q. Liu, L. Seiffert, F. Süßmann, S. Zherebtsov, J. Passig, A. Kessel, S. A. Trushin, N. G. Kling, I. Ben-Itzhak, V. Mondes, C. Graf, E. Rühl, L. Veisz, S. Karsch, J. Rodrĺguez-Fernández, M. I. Stockman, J. Tiggesbäumker, K. H. Meiwes-Broer, T. Fennel and M. F. Kling, ACS Photonics, 2020, 7, 3207–3215.
6. A. Rudenko and J. V. Moloney, Adv. Photonics Res., 2020, 1, 2000029.
7. S. Zherebtsov, T. Fennel, J. Plenge, E. Antonsson, I. Znakovskaya, A. Wirth, O. Herrwerth, F. Sümann, C. Peltz, I. Ahmad, S. A. Trushin, V. Pervak, S. Karsch, M. J. J. Vrakking, B. Langer, C. Graf, M. I. Stockman, F. Krausz, E. Rühl and M. F. Kling, Nat. Phys., 2011, 7, 656–662.
8. F. Süßmann, L. Seiffert, S. Zherebtsov, V. Mondes, J. Stierle, M. Arbeiter, J. Plenge, P. Rupp, C. Peltz, A. Kessel, S. A. Trushin, B. Ahn, D. Kim, C. Graf, E. Rühl, M. F. Kling and T. Fennel, Nat. Commun., 2015, 6, 7944.
9. L. Seiffert, F. Süßmann, S. Zherebtsov, P. Rupp, C. Peltz, E. Rühl, M. F. Kling and T. Fennel, Appl. Phys. B: Lasers Opt., 2016, 122, 101.
10. Q. Liu, L. Seiffert, A. Trabattoni, M. C. Castrovilli, M. Galli, P. Rupp, F. Frassetto, L. Poletto, M. Nisoli, E. Rühl, F. Krausz, T. Fennel, S. Zherebtsov, F. Calegari and M. F. Kling, J. Optom., 2018, 20, 024002.
11. P. Rupp, C. Burger, N. G. Kling, M. Kübel, S. Mitra, P. Rosenberger, T. Weatherby, N. Saito, J. Itatani, A. S. Alnaser, M. B. Raschke, E. Rühl, A. Schlander, M. Gallei, L. Seiffert, T. Fennel, B. Bergues and M. F. Kling, Nat. Commun., 2019, 10, 1–7.
12. P. Rosenberger, P. Rupp, R. Ali, M. S. Alghabra, S. Sun, S. Mitra, S. A. Khan, R. Dagar, V. Kim, M. Iqbal, J. Schötz, Q. Liu, S. K. Sundaram, J. Kredel, M. Gallei, C. Costa-Vera, B. Bergues, A. S. Alnaser and M. F. Kling, ACS Photonics, 2020, 7, 1885–1892.
13. S. S. Mao, F. Quéré, S. Guizard, X. Mao, R. E. Russo, G. Petite and P. Martin, Appl. Phys. A, 2004, 79, 1695–1709.
14. E. G. Gamaly, A. V. Rode, B. Luther-Davies and V. T. Tikhonchuk, Phys. Plasmas, 2002, 9, 949.
15. T. Fennel, K.-H. Meiwes-Broer, J. Tiggesbäumker, P.-G. Reinhard, P. M. Dinh and E. Suraud, Rev. Mod. Phys., 2010, 82, 1793–1842.
16. P. Balling and J. Schou, Rep. Prog. Phys., 2013, 76, 036502.
17. E. Antonsson, F. Gerke, L. Merkel, I. Halfpap, B. Langer and E. Rühl, Phys. Chem. Chem. Phys., 2019, 21, 12130–12138.
18. E. Antonsson, C. Peltz, J. Plenge, B. Langer, T. Fennel and E. Rühl, J. Electron Spectrosc. Relat. Phenom., 2015, 200, 216–221.
19. D. D. Hickstein, F. Dollar, J. A. Gaffney, M. E. Foord, G. M. Petrov, B. B. Palm, K. E. Keister, J. L. Ellis, C. Ding, S. B. Libby, J. L. Jimenez, H. C. Kapteyn, M. M. Murnane and W. Xiong, Phys. Rev. Lett., 2014, 112, 1–5.
20. C. Peltz, C. Varin, T. Brabec and T. Fennel, Phys. Rev. Lett., 2014, 113, 133401.
21. C. Peltz, J. A. Powell, P. Rupp, A. Summers, T. Gorkhover, M. Gallei, I. Halfpap, E. Antonsson, B. Langer, C. Trallero-Herrero, C. Graf, D. Ray, Q. Liu, T. Osipov, M. Bucher, K. Ferguson, S. Möller, S. Zherebtsov, D. Rolles, E. Rühl, G. Coslovich, R. N. Coffee, C. Bostedt, A. Rudenko, M. F. Kling and T. Fennel, New J. Phys., 2022, 24, 043024.
22. L. Flückiger, D. Rupp, M. Adolph, T. Gorkhover, M. Krikunova, M. Müller, T. Oelze, Y. Ovcharenko, M. Sauppe, S. Schorb, C. Bostedt, S. Düsterer, M. Harmand, H. Redlin, R. Treusch and T. Möller, New J. Phys., 2016, 18, 043017.
23. M. Arbeiter and T. Fennel, New J. Phys., 2011, 13, 053022.
24. D. D. Hickstein, F. Dollar, J. L. Ellis, K. J. Schnitzenbaumer, K. E. Keister, G. M. Petrov, C. Ding, B. B. Palm, J. A. Gaffney, M. E. Foord, S. B. Libby, G. Dukovic, J. L. Jimenez, H. C. Kapteyn, M. M. Murnane and W. Xiong, ACS Nano, 2014, 8, 8810–8818.
25. M. Hada, D. Zhang, K. Pichugin, J. Hirscht, M. A. Kochman, S. A. Hayes, S. Manz, R. Y. N. Gengler, D. A. Wann, T. Seki, G. Moriena, C. A. Morrison, J. Matsuo, G. Sciaini and R. J. D. Miller, Nat. Commun., 2014, 5, 3863.
26. L. Seiffert, S. Zherebtsov, M. F. Kling and T. Fennel, Adv. Phys.: X, 2022, 7, 9–13.
27. P. Corral Arroyo, G. David, P. A. Alpert, E. A. Parmentier, M. Ammann and R. Signorell, Science, 2022, 376, 293–296.
28. R. Ramisetty, A. Abdelmonem, X. Shen, H. Saathoff, T. Leisner and C. Mohr, Atmos. Meas. Tech., 2018, 11, 4345–4360.
29. M. S. Alghabra, R. Ali, V. Kim, M. Iqbal, P. Rosenberger, S. Mitra, R. Dagar, P. Rupp, B. Bergues, D. Mathur, M. F. Kling and A. S. Alnaser, Nat. Commun., 2021, 12, 3839.
30. L. Ban, B. L. Yoder and R. Signorell, Annu. Rev. Phys. Chem., 2020, 71, 315–334.
31. D. K. Božanić, G. A. Garcia, O. Sublemontier, J. Pajović, V. Djoković and L. Nahon, J. Phys. Chem. C, 2020, 124, 24500–24512.
32. F. Sun, H. Li, S. Song, F. Chen, J. Wang, Q. Qu, C. Lu, H. Ni, B. Wu, H. Xu and J. Wu, Nanophotonics, 2021, 10, 2651–2660.
33. J. A. Powell, A. M. Summers, Q. Liu, S. J. Robatjazi, P. Rupp, J. Stierle, C. Trallero-Herrero, M. F. Kling and A. Rudenko, Opt. Express, 2019, 27, 27124.
34. X. Han, H. Huang, X. Huang, W. Cao, Q. Zhang and P. Lu, Adv. Opt. Mater., 2022, 2201260, 1–10.
35. T. Ditmire, T. Donnelly, A. M. Rubenchik, R. W. Falcone and M. D. Perry, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 3379–3402.
36. C. Jungreuthmayer, M. Geissler, J. Zangheilini and T. Brabec, Phys. Rev. Lett., 2004, 92, 133401.
37. M. Arbeiter and T. Fennel, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 1–7.
38. C. Jungreuthmayer, L. Ramunno, J. Zanghellini and T. Brabec, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 38, 3029–3036.
39. M. Henyk, F. Costache and J. Reif, Appl. Surf. Sci., 2002, 197–198, 90–95.
40. J. J. Kolodziej, B. Such, P. Czuba, F. Krok, P. Piatkowski, P. Struski, M. Szymonski, R. Bennewitz, S. Schär and E. Meyer, Surf. Sci., 2001, 482–485, 903–909.
41. M. J. Bogan, S. Boutet, H. N. Chapman, S. Marchesini, A. Barty, W. H. Benner, U. Rohner, M. Frank, S. P. Hau-Riege, S. Bajt, B. Woods, M. M. Seibert, B. Iwan, N. Timneanu, J. Hajdu and J. Schulz, Aerosol Sci. Technol., 2010, 44, i–vi.
42. L. Ban, T. E. Gartmann, B. L. Yoder and R. Signorell, Phys. Rev. Lett., 2020, 124, 13402.
43. L. Ban, H. Tang, B. L. Yoder and R. Signorell, Faraday Discuss., 2022, 236, 461–484.
44. F. Süßmann, S. Zherebtsov, J. Plenge, N. G. Johnson, M. Kübel, A. M. Sayler, V. Mondes, C. Graf, E. Rühl, G. G. Paulus, D. Schmischke, P. Swrschek and M. F. Kling, Rev. Sci. Instrum., 2011, 82, 093109.
45. A. Rudenko, J.-P. Colombier and T. E. Itina, Int. J. Numer. Model.: Electron. Netw. Devices Fields, 2018, 31, e2215.
46. J.-L. Déziel, L. J. Dubé and C. Varin, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 104, 045201.
47. L. V. Keldysh, Sov. Phys. JETP, 1965, 20.5, 1307–1314.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06368b

‡ These authors contributed equally.

---