 Open Access Article
Open Access ArticleThe multivariate interaction between Au and TiO2 colloids: the role of surface potential, concentration, and defects†
Kinran
Lau
 a,
Brian
Giera
a,
Brian
Giera
 b,
Stephan
Barcikowski
b,
Stephan
Barcikowski
 *a and
Sven
Reichenberger
*a and
Sven
Reichenberger
 *a
*a
aTechnical Chemistry I, University of Duisburg-Essen and Center for Nanointegration Duisburg-Essen (CENIDE), Essen, Germany. E-mail: stephan.barcikowski@uni-due.de; sven.reichenberger@uni-due.de
bCenter for Engineered Materials and Manufacturing, Lawrence Livermore National Laboratory, California, USA
First published on 2nd January 2024
Abstract
The established DLVO theory explains colloidal stability by the electrostatic repulsion between electrical double layers. While the routinely measured zeta potential can estimate the charges of double layers, it is only an average surface property which might deviate from the local environment. Moreover, other factors such as the ionic strength and the presence of defects should also be considered. To investigate this multivariate problem, here we model the interaction between a negatively charged Au particle and a negatively charged TiO2 surface containing positive/neutral defects (e.g. surface hydroxyls) based on the finite element method, over 6000 conditions of these 6 parameters: VPart (particle potential), VSurf (surface potential), VDef (defect potential), DD (defect density), Conc (salt concentration), and R (particle radius). Using logistic regression, the relative importance of these factors is determined: VSurf > VPart > DD > Conc > R > VDef, which agrees with the conventional wisdom that the surface (and zeta) potential is indeed the most decisive descriptor for colloidal interactions, and the salt concentration is also important for charge screening. However, when defects are present, it appears that their density is more influential than their potential. To predict the fate of interactions more confidently with all the factors, we train a support vector machine (SVM) with the simulation data, which achieves 97% accuracy in determining whether adsorption is favorable on the support. The trained SVM including a graphical user interface for querying the prediction is freely available online for comparing with other materials and models. We anticipate that our model can stimulate further colloidal studies examining the importance of the local environment, while simultaneously considering multiple factors.
1. Introduction
The conventional Derjaguin–Landau–Verwey–Overbeek (DLVO) theory describes colloidal interactions by balancing the van der Waals attraction and the electrostatic repulsion between the double layers. If the resulting energy barrier is larger than the thermal energy (kT), then the colloidal suspension is predicted to be kinetically stable against aggregation,1,2 which is usually the desired behavior. However, there are occasions when the irreversible collision of particles is preferred, such as adsorbing metal nanoparticles onto oxide supports. To facilitate this adsorption, a common strategy is to mix metal and oxide colloids at a pH value where the adsorbates and adsorbents are oppositely charged, such that they are attracted to each other (by both electrostatic and van der Waals contributions). Experimentally, this condition is fulfilled when the pH is between the isoelectric points (IEPs) of the two materials.3 The IEP is the pH when the particle has a net surface charge/zeta potential of zero. At a pH below the IEP, the material is positively charged, whereas at a pH above it, the material is negatively charged.4 Accordingly, by mixing the metal and oxide particles at a pH value between their IEPs, the two species are oppositely charged to encourage the electrostatically induced adsorption, while avoiding their self-agglomeration due to the repulsion between the same materials. As an example, Pt and TiO2 have IEPs at around 2.8 and 6.4 respectively, and hence a pH value of 5 would be appropriate to induce the adsorption between them with an attractive Coulomb force.5 Importantly, the IEP is an experimentally measurable quantity reflecting the surface charges of particles, and hence it is usually a convenient metric for predicting whether the interaction between particles is favorable or not.6–10However, even when both particles are negatively charged and experience electrostatic repulsion between them, adsorption might still be possible. Nanoparticles with an absolute zeta potential larger than ±30 mV generally possess an electrostatic energy barrier that is large enough to prevent the agglomeration and aggregation induced by the attractive van der Waals forces at room temperature.7–10 At 298 K, the thermal voltage ( ), which can be thought of as the potential equivalence of thermal energy (kT), is approximately 25.7 mV. This implies that if the absolute potential is smaller than 25.7 mV, particles following a Boltzmann distribution on average would possess sufficient kinetic energy to surpass the energy barrier, leading to coalescence.11 Consequently, the common criterion of ±30 mV is a conservative estimate, ensuring that the majority of particles in the Boltzmann distribution do not have adequate energy to overcome the barrier. On the contrary, with zeta potentials below this threshold, metal colloids can still be deposited onto a support because they are not repulsive enough. In this context, Wagener et al. studied the interaction between negatively charged Ag colloids and BaSO4 microparticles. The zeta potential of the BaSO4 support was kept constant at −2.5 mV, but that of the Ag nanoparticles was adjusted to more negative values by adding more citrate ligands to the mixture (−25 mV to −75 mV). It was observed that the adsorption between Ag and BaSO4 only occurred when the Ag colloids obtained a zeta potential less negative than −30 mV.12 However, it is also noted that the inclusion of surfactants in this case can complicate the interpretation because it also adds a small steric contribution to the question.
), which can be thought of as the potential equivalence of thermal energy (kT), is approximately 25.7 mV. This implies that if the absolute potential is smaller than 25.7 mV, particles following a Boltzmann distribution on average would possess sufficient kinetic energy to surpass the energy barrier, leading to coalescence.11 Consequently, the common criterion of ±30 mV is a conservative estimate, ensuring that the majority of particles in the Boltzmann distribution do not have adequate energy to overcome the barrier. On the contrary, with zeta potentials below this threshold, metal colloids can still be deposited onto a support because they are not repulsive enough. In this context, Wagener et al. studied the interaction between negatively charged Ag colloids and BaSO4 microparticles. The zeta potential of the BaSO4 support was kept constant at −2.5 mV, but that of the Ag nanoparticles was adjusted to more negative values by adding more citrate ligands to the mixture (−25 mV to −75 mV). It was observed that the adsorption between Ag and BaSO4 only occurred when the Ag colloids obtained a zeta potential less negative than −30 mV.12 However, it is also noted that the inclusion of surfactants in this case can complicate the interpretation because it also adds a small steric contribution to the question.
Although the zeta potential is usually a satisfactory descriptor for the electrostatic interaction between particles, it is only the weighted average potential at the shear/slipping plane of all the particles in the dispersion.13 It is known that the nanoenvironment around nanoparticles is different from the bulk, and the local surface potential might not be well represented by the global zeta potential.14 Following the DLVO theory, Au and P25 TiO2 colloids would have an energy barrier larger than kT in the electrostatically repulsive regime of pH 8.5, hindering the adsorption between them.3 Nevertheless, quantitative adsorption of Au onto TiO2 was observed up till 20 wt%,3 suggesting that the zeta potential and the traditional DLVO theory failed to capture the essence of this interaction. A possible reason for that is the deviation of the local environment from the bulk average. As an example, atomic force microscopy (AFM) experiments performed on single crystals of rutile TiO2 demonstrated that different facets do not share the same IEP, e.g. (110): 5.5–4.8 and (100): 3.7–3.2.15 Unsurprisingly, the bulk IEP of rutile TiO2 (5.2–6.8)4 matches well with the dominant facet of (110). However, it is notable that while (100) only occupies a small proportion of the exposed surfaces in rutile, the IEP of (100) is lower than the bulk value by as much as 2 units. This facet-dependent trend in IEP was also reported for SrTiO3 (110) and (100) in an independent AFM study by Su et al.16 Despite being on the same particle, (110) and (100) are expected to interact very differently with metal particles, and these distinctive facets cannot be collectively described by a single metric of zeta potential. Moreover, even within the same facet, the charge distribution does not necessarily have to be uniform across the whole surface due to the presence of point or volume defects. It was demonstrated by simulation studies that surface heterogeneity and roughness can significantly reduce the repulsive energy barrier compared to a perfect surface.17,18 Specifically for TiO2, defects such as oxygen vacancies are often referred to as the favorable adsorption sites for Au nanoparticles in the DFT and catalysis literature due to the distorted electron density near the surface.19–24 In addition, surface hydroxyls can also serve as local charge deviations,25–27 as well as affecting short-range contributions such as hydration forces.28,29 The pH of the system plays a crucial role in the behavior of surface hydroxyls. As the pH increases, more surface hydroxyls are deprotonated, leading to a more negatively charged oxide surface.30–34 However, the surface hydroxyls are only completely deprotonated at highly alkaline pH (e.g. 11–12), since the pKa of TiO2 basic hydroxyls is ∼9.35,36 This means that at moderately alkaline pH (e.g. 8–9), a considerable proportion of hydroxyls are still protonated and could serve as point defects, since they are less negative than the rest of the surface (formally neutral for terminal Ti–OH and positive for bridging Ti–OH–Ti). Furthermore, it is also suggested that the enriched electron density near the surface due to Ti3+/oxygen vacancies can further alter the abundance of surface hydroxyls.37 Clearly, the local environment exhibits a much more subtle surface potential than the zeta potential manages to describe, and this should be considered particularly in the repulsive regime when the interacting particles carry the same charge sign.
While it might be experimentally challenging to examine the local environment when the particles come into contact, it is relatively easier to model particles with local surface charges deviating from the rest of the surface, and simulate how they interact. As discussed, when both the adsorbing nanoparticle and the support are negatively charged, the zeta potential alone might not be a sufficient predictor for the interaction outcome. Therefore, other parameters have to be taken into account, such as the density and potential of defects on the support. To evaluate the effect of each factor, it is desirable to perform a parametric sweep across a wide range of physically realistic conditions. To keep this computationally feasible while capturing the essence of the interaction, we constructed an empirical model based on the finite element method. We specifically consider the Au/TiO2 system, which is a popular catalyst for reactions such as hydrogen production,38 alcohol oxidation,39–41 and CO oxidation.42–44 Particularly for CO oxidation, the Au/TiO2 interface has been identified as the active site for the reaction,45–48 and the strong metal–support interaction makes it a good catalyst.49,50 In our model (Fig. 1), we depict the interaction between a negatively charged sphere (Au) and a negative surface with positive/neutral defects (TiO2), where the point defects (e.g. surface OH groups) are local sites with a surface potential different from the normal surface. To obtain a comprehensive picture, a total of 6000 unique conditions are simulated by systematically varying the following parameters: VPart (particle potential), VSurf (surface potential), VDef (defect potential), DD (defect density), Conc (salt concentration), and R (particle radius). The van der Waals interactions between typical Au and TiO2 particles are also considered. Our results show that although the surface potential (VSurf and VPart) remains to be the most decisive factor, the defect density and the salt concentration in solution also seem to play a significant role in the adsorption between Au and TiO2. Using logistic regression and a support vector machine (SVM), we also determined the transition boundary between the “favorable” (below kT) and “unfavorable” (above kT) cases. Hence, it is possible to predict the outcome of the interaction more confidently by considering multiple parameters at the same time, rather than only the zeta potential. Our study highlights the importance of local surface deviations in colloidal interactions, and we hope this work will encourage further research into the effects of local environments.
 | ||
| Fig. 1 Model configuration of a negative particle (e.g. Au) interacting with a negative surface (e.g. TiO2) with positive/neutral defects. A defect density of 0.2 is illustrated in this example. | ||
2. Methods
2.1. Model configuration and parameter space
We consider the interaction between Au and TiO2 in an aqueous electrolyte solution, with a pH higher than the isoelectric points of both materials, but only at a mildly alkaline pH (e.g. 8). Under these conditions, both Au and TiO2 are overall negatively charged, but not all surface hydroxyls on TiO2 are deprotonated,30,31,35,51 and hence the remaining protonated species could serve as local charge deviations, which we refer to as defects. We model this particular Au/TiO2 system by a negative sphere coming into contact with a negative surface containing positive/neutral defects, which is depicted schematically in Fig. 1. When Au nanoparticles are adsorbed on TiO2, the former is typically much smaller (at least 10 times) than the latter, and therefore the curvature of TiO2 is also significantly smaller relative to the Au colloids. Accordingly, we model the TiO2 surface as a flat plane. More importantly, TiO2 particles have preferentially exposed facets, which result in a rod-like or elongated shape rather than being spherical. For instance, the most stable polymorph rutile TiO2 is mostly terminated by (110) surfaces followed by (011) surfaces as predicted by Wulff construction, resulting in shapes ranging from a needle-like crystal to a short blocky habit,52,53 which can be sufficiently described as a flat plane for Au nanoparticles much smaller than TiO2. We also only consider the case of diluted Au colloids so Au–Au interactions can be ignored. On the other hand, the defects are modeled by small cylinders with a radius (LD) of 0.5 nm and a height of 0.1 nm. These defects are tiny protrusions in the z-direction because the oxygen atoms of surface hydroxyls are roughly 0.1 nm above the remaining (110) surface as measured experimentally by scanning tunneling microscopy54 and atomic force microscopy.55 For simplicity, the defects are uniformly arranged in a 2D primitive square array with a lattice parameter of a, where the defect density (DD) is defined as | (1) |
On the idealized rutile (110) surface, the surface oxygen atoms are ordered in a similar but rectangular fashion.56 By tuning DD, it is possible to pack the defects more densely or sparsely to match the more realistic case.
In order to study the interaction between Au and TiO2 over an extensive range of realistic conditions, a parametric sweep was performed for these six factors: VPart (particle potential), VSurf (surface potential), VDef (defect potential), DD (defect density), Conc (salt concentration), and R (particle radius). A total of 6000 unique conditions are considered, and the parameter space is summarized in Table 1. Temperature is kept constant at 298 K throughout. Importantly, this parameter space is chosen to survey a large scope of physically relevant conditions. For example, both the particle and the flat surface have VPart and VSurf varied up to −51.4 mV, which is considerably repulsive given that an absolute zeta potential larger than ±30 mV is generally considered to be sufficient to resist particle agglomeration and aggregation.7–10 Similarly, the maximum VDef is set to be +51.4 mV for highly charged defects, while the minimum VDef of 0 mV represents neutral defects.
| Parameter | Values | Unit | |
|---|---|---|---|
| V Part | Particle potential | −51.4, −38.5, −25.7, −12.8 | mV |
| V Surf | Surface potential | −51.4, −38.5, −25.7, −12.8 | mV |
| V Def | Defect potential | 0.0, +12.8, +25.7, +38.5, +51.4 | mV |
| DD | Defect density | 0.1, 0.2, 0.25, 0.3, 0.35 | — |
| Conc | Salt concentration | 0.1, 0.5, 1.0 | mM |
| R | Particle radius | 0.5, 1.5, 2.5, 3.5, 4.5 | nm |
| D | Particle–surface separation | 0.1–4.1 (15 steps) | κ −1 (Debye length) |
The cases with minimal defects and the scenarios with full defect occupancy (DD = 0.1–0.35) are also considered. According to our definition of DD (eqn (1)), if all the surface oxygen atoms are protonated, this would give a DD of ∼0.37. (The surface density of unsaturated oxygen atoms is 5.2 nm−1 on rutile (110).57 The diameter of an oxygen atom is ∼0.3 nm.56 Therefore the maximum DD is  .) However, this extreme case should be highly unlikely at alkaline pH because the extent of deprotonation of surface OH increases with pH, so more moderate DD values (0.1, 0.2, 0.25, 0.3) are also investigated. In contrast to the defective (non-uniformly charged) surfaces, we also separately simulated a control model with only perfect (uniformly charged) surfaces (DD = 0). Details of the comparisons are provided in the ESI (Fig. S2–S6†). The objective is to identify the conditions where defects exert the largest influence at the nanoscale. To achieve this, we evaluated the interaction energy barriers when both perfect and defective surfaces have the same effective surface potential (VEff, the average potential of the entire surface). When defects play a more critical role, the deviations in the energy barriers are expected to be more pronounced between the two scenarios. To quantify this discrepancy, the coefficient of determination (R2) is calculated, where a smaller R2 value indicates a more significant impact of the defects. The results show that while there are some instances where the perfect surface offers a reasonable description of the defective surface with the same VEff, a considerable dispersion in the interaction energy barriers persists in most other cases, which can only be accounted for when defects are explicitly considered. Hence, defects are included as local charge deviations in our model.
.) However, this extreme case should be highly unlikely at alkaline pH because the extent of deprotonation of surface OH increases with pH, so more moderate DD values (0.1, 0.2, 0.25, 0.3) are also investigated. In contrast to the defective (non-uniformly charged) surfaces, we also separately simulated a control model with only perfect (uniformly charged) surfaces (DD = 0). Details of the comparisons are provided in the ESI (Fig. S2–S6†). The objective is to identify the conditions where defects exert the largest influence at the nanoscale. To achieve this, we evaluated the interaction energy barriers when both perfect and defective surfaces have the same effective surface potential (VEff, the average potential of the entire surface). When defects play a more critical role, the deviations in the energy barriers are expected to be more pronounced between the two scenarios. To quantify this discrepancy, the coefficient of determination (R2) is calculated, where a smaller R2 value indicates a more significant impact of the defects. The results show that while there are some instances where the perfect surface offers a reasonable description of the defective surface with the same VEff, a considerable dispersion in the interaction energy barriers persists in most other cases, which can only be accounted for when defects are explicitly considered. Hence, defects are included as local charge deviations in our model.
Conc spans salt concentrations commonly found in experiments (0.1, 0.5, 1.0 mM), and only symmetric monovalent electrolytes (e.g. NaCl) are considered, which means that the ionic strength (I) is equal to the salt concentration (c0): 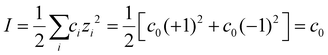 . We also note that it is the ionic strength which ultimately affects the Debye length, but not the salt concentration except for the case of symmetric monovalent salts. For R, the particle radius scales with the defect radius (R = 1–9 LD = 0.5–4.5 nm, where LD = 0.5 nm), so the actual physical size of defects is relatively less critical. To limit the simulation time, only one-eighth of the square prism is simulated (indicated by the solid black line in Fig. 1), and the rest of the model is generated by symmetry. Further simulation details and model snapshots can be found in the ESI (Fig. S1†).
. We also note that it is the ionic strength which ultimately affects the Debye length, but not the salt concentration except for the case of symmetric monovalent salts. For R, the particle radius scales with the defect radius (R = 1–9 LD = 0.5–4.5 nm, where LD = 0.5 nm), so the actual physical size of defects is relatively less critical. To limit the simulation time, only one-eighth of the square prism is simulated (indicated by the solid black line in Fig. 1), and the rest of the model is generated by symmetry. Further simulation details and model snapshots can be found in the ESI (Fig. S1†).
For each particular set of conditions, the particle is moved progressively towards the defect-containing surface (similar to how real particles might diffuse) to examine how the system energy changes (0.1–4.1 Debye lengths, 15 steps). In this work, only two energy components are considered: the electrostatic free energy (Fel) stemming from the electrical double layer, and the van der Waals energy (Evdw) resulting from the induced dipole interactions. Other contributions (e.g. hydrophobic forces and surface energies) are not included. While hydrophobic forces and surface energies might provide an additional thermodynamic driving force for the colloids to interact, they are only significant when the colloids are in close proximity. In other words, these energies are only crucial if the colloids have sufficient energy to first overcome the kinetic barrier to come close to each other. This kinetic barrier is computed by combining Fel and Evdw in this study.
2.2. Electrostatic free energy (Fel)
The electrostatic interaction between colloids in an aqueous medium is governed by the potential (φ or ψ) of the electrical double layer. We denote φ as the dimensional potential with a unit of V, and ψ as the dimensionless potential. The additional subscript of φ0 clarifies that this is the potential at the surface, but not that in the electrolyte. The potentials can be interconverted by multiplying/dividing by the thermal voltage (eqn (2)). At 298 K, 1 dimensionless potential translates to approximately 25.7 mV. | (2) |
For a more intuitive understanding, the dimensional potential φ is used predominantly throughout the text, which shares the same unit (V) with the experimentally measured zeta potential. However, it is often more convenient to express equations and run simulations with the dimensionless potential ψ, and therefore we present the equations here with a mixture of φ and ψ.
We calculate the potential and the corresponding electrostatic free energy following the expressions derived by Theodoor and Overbeek,58 and adapted by Krishnan.59 Since no assumptions were made for a particular geometry (e.g. perfect planes), these equations can be applied to our complicated surface with defects. The detailed derivation can be found in the above literature and also in the ESI.† Only the most important equations are presented here. Solving the Poisson–Boltzmann equation (eqn (3)) yields how the potential varies in the electrical double layer,
 | (3) |
∇2ψ = κ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh (ψ) sinh (ψ) | (4) |
 | (5) |
In this work, the non-linear Poisson–Boltzmann equation is solved numerically using the COMSOL Multiphysics® software via the finite element method,60 which yields a potential map in three dimensions. An example of that solution is visualized in Fig. 1, where the potential (φ) is indicated by different colors (e.g. navy blue when φ = −51.4 mV and light green when φ = 0 mV). A boundary condition of constant potential (φ = φ0) is applied to the surfaces of the particle, the normal surface, and the defects, while the continuity condition (n·∇φ = 0) is specified on the boundary of the model.
The computed spatial distribution of potential is subsequently used to calculate the electrostatic free energy (Fel), which is the sum of 3 energy components (eqn (6)).
| Fel = Uel − TΔS + Fchem | (6) |
 | (7) |
 | (8) |
The last contribution is the chemical free energy (Fchem) (eqn (9)), accounting for the change in free energy (chemical, non-electrical) due to the preferential adsorption of ions at the surface.
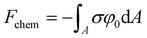 | (9) |
Substituting eqn (7)–(9) back to Fel gives eqn (10).
 | (10) |
Importantly, Fel consists of a surface integral and two volume integrals. The surface integral should be performed on all the surfaces. For our model, this would be the particle, the defects, and the normal surface. On the other hand, the volume integrals should be evaluated for the bulk electrolyte.
2.3. van der Waals energy (Evdw)
In addition to the electrostatic free energy Fel, the attractive van der Waals contributions are also considered. The system of Au and TiO2 is geometrically modeled by a sphere interacting with a plane. For such geometry, the attractive van der Waals energy is given by | (11) |
While the AH of TiO2 in water is fairly consistent in the literature (∼50 zJ),62,63 that of Au varies considerably depending on the study (∼100–300 zJ).64,65 For the sake of discussion, we initially limit ourselves to the mean value of 200 zJ as the AH of Au, but it is allowed to vary later when fitting the data with a support vector machine (0–150 zJ for Au/TiO2). Accordingly, the Hamaker constant describing the interaction between TiO2 and Au can be estimated by taking the geometric mean of the individual AH, i.e. . However, it is noted that changing the overall AH slightly does not affect the qualitative outcome, as indicated by the distributions of energy barriers with varying AH in Fig. S7.†
. However, it is noted that changing the overall AH slightly does not affect the qualitative outcome, as indicated by the distributions of energy barriers with varying AH in Fig. S7.†
2.4. Total interaction energy (Etot) and energy barrier
The total interaction energy (Etot) is given by the sum of the electrostatic free energy (Fel) and the van der Waals energy (Evdw) (eqn (12)).| Etot = Fel + Evdw | (12) |
For a particular set of parameters (VPart, VSurf, VDef, DD, Conc, R), Etot is evaluated at 15 distances (0.1–4.1 κ−1) between the particle and the surface to examine how the energy changes upon interaction. A representative example of how each individual energy component constitutes the total energy is illustrated in Fig. 2 (when VPart = −51.4 mV, VSurf = −51.4 mV, VDef = +12.8 mV, DD = 0.2, Conc = 1 mM, R = 2.5 nm). The whole dataset can be explored in our GitHub repository.
 | ||
| Fig. 2 The six parameters (VPart, VSurf, VDef, DD, Conc, R) determine the electrostatic free energy (Fel) and the van der Waals energy (Evdw), which are added up to give the total interaction energy (Etot). A representative example is shown here when VPart = −51.4 mV, VSurf = −51.4 mV, VDef = +12.8 mV, DD = 0.2, Conc = 1 mM, R = 2.5 nm. The maximum Etot is extracted as the energy barrier for each set of conditions. Further examples of how Fel and Evdw affect the final Etot are included in Fig. S8.† It is also shown that the 15 steps in particle–surface separations are sufficient to capture the energy barriers (details in section 5 of ESI†). | ||
Since we are only interested in the relative change in energy when the particle moves towards the surface, the energy when the particle and surface are significantly apart (>4 κ−1) and are essentially non-interacting is defined as zero. The energy curves for defects and the normal surface in Fig. 2 are fitted to an exponential expression for better analysis: E = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−bD), where a and b are the parameters fitted for each curve, with an average residual standard deviation of 0.14 and 0.16 for the fitted defective and surface curves respectively. Importantly, the resultant Etot is in the magnitude of thermal energy (kT, T = 298 K), and the maximum energy of Etot can be extracted as the energy barrier for interaction. This operation is repeated for all the 6000 simulated conditions to acquire the corresponding energy barrier. For the particular example in Fig. 2, the barrier is larger than kT. Further representative cases of how Fel and Evdw affect the final Etot are shown in Fig. S8.† It is also shown that the 15 steps in particle–surface separations are sufficient to capture the energy barriers (details in ESI, Fig. S9†).
exp(−bD), where a and b are the parameters fitted for each curve, with an average residual standard deviation of 0.14 and 0.16 for the fitted defective and surface curves respectively. Importantly, the resultant Etot is in the magnitude of thermal energy (kT, T = 298 K), and the maximum energy of Etot can be extracted as the energy barrier for interaction. This operation is repeated for all the 6000 simulated conditions to acquire the corresponding energy barrier. For the particular example in Fig. 2, the barrier is larger than kT. Further representative cases of how Fel and Evdw affect the final Etot are shown in Fig. S8.† It is also shown that the 15 steps in particle–surface separations are sufficient to capture the energy barriers (details in ESI, Fig. S9†).
3. Results and discussion
As depicted in Fig. 1, we consider the interaction between a negatively charged particle (Au) and a negatively charged plane with the presence of positive/neutral defects (TiO2). This configuration represents the scenario at mildly alkaline pH (e.g. 8), which is above the IEP of both materials, and therefore both Au and TiO2 are overall negatively charged. However, this moderately alkaline pH is only slightly above the IEP of TiO2, so not all surface hydroxyls on TiO2 are deprotonated.30,31,35,51 Hence, the remaining protonated species could serve as local positive/neutral charges, and we refer to these local charge deviations as defects. In our defect-containing model, we systematically varied a total of six parameters (VPart, VSurf, VDef, DD, Conc, R) in 6000 different combinations (Table 1). For each of these 6000 conditions, the total interaction energy is calculated by considering both the electrostatic free energy and van der Waals energy, in a fashion similar to the classical DLVO theory (Fig. 2, details in the Methods section). The resultant energy barriers are extracted from each case, and the distributions of these 6000 energy barriers are plotted by each parameter in Fig. 3(a).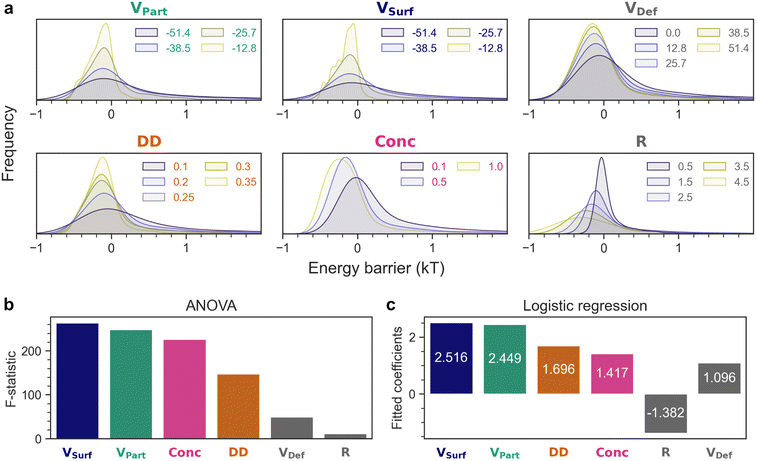 | ||
| Fig. 3 (a) Grouping the same set of 6000 energy barriers by different parameters to examine the effect of each factor. Feature importance determined by (b) ANOVA and (c) logistic regression. | ||
By examining how the energy barriers change in response to varying parameters, it is possible to evaluate the importance of VPart, VSurf, VDef, DD, Conc, R. For instance, if a factor is crucial for the interaction, changing its value should also shift the energy barrier significantly. By contrast, if a parameter has minimal effect on the outcome, the energy barrier should remain essentially the same. From Fig. 3(a), it is apparent that when modifying the value of each parameter, the distributions of energy barriers are all shifted to lower or higher kT values substantially, suggesting that all six factors contribute to the resultant energy barrier, though to a different extent. The effect of each parameter can be examined by varying it, and inspecting how the energy barriers change correspondingly:
• VPart, VSurf, VDef: For VPart and VSurf, traversing the surface potential from −12.8 mV to −51.4 mV results in a broader distribution of energy barriers and more values above kT, since there is more electrostatic repulsion when the particle and the surface are more negatively charged. On the contrary, when the defects become more positively charged (VDef from 0 mV to +51.4 mV), the energy barriers are reduced due to more electrostatic attraction.
• DD: Higher defect density (0.1–0.35) lowers the interaction energy barrier due to the neutral/positively charged defects.
• Conc: Higher salt concentrations (and ionic strengths) (0.1–1 mM) mean shorter Debye lengths and less repulsion between the surfaces due to the screening of charges.
• R: Larger particles (0.5–4.5 nm) lead to more electrostatic repulsion but also more van der Waals attraction (eqn (11)). The van der Waals contribution outweighs the electrostatic component in this case.
Although the behavior of each parameter follows what one might expect qualitatively, it would be desirable to quantify which factors are more decisive than others in determining the final interaction energy barrier, i.e. the feature importance. This is estimated by two separate methods here: ANOVA (analysis of variance) and logistic regression.
ANOVA compares the variances of different distributions and calculates the F-statistic to evaluate how likely the distributions are from the same population. In other words, a large F-statistic means the distributions do not resemble each other. Following this idea, if a parameter is more important, it should also shift the distributions of energy barriers more significantly, leading to more heterogeneous distributions and a larger value of F-statistic. By performing ANOVA on the distributions of energy barriers in Fig. 3(a), the F-statistics for each parameter can be obtained and are plotted in Fig. 3(b) in descending order: VSurf > VPart > Conc > DD > VDef > R. We shall comment on the feature importance estimated by ANOVA in greater detail after the discussion of logistic regression, but it is immediately obvious that VSurf (264) and VPart (248) are the most influential factors as manifested by the largest F-statistics, which supports the experimental intuition to use zeta potential as a first hint to infer colloidal stability. In addition, Conc (226) is also a decisive determinant for colloidal interactions followed by DD (147). On the contrary, VDef (50) and R (11) do not seem to affect the outcome significantly. Instead of comparing several distributions at once with ANOVA, a pairwise comparison of the distributions was also carried out by the Tukey's HSD (honestly significant difference) test (Fig. S10†), where the q-statistics suggest the effect of each parameter is even stronger when it is varied towards its extreme values (minimum or maximum).
While it is useful to calculate the exact interaction energy barrier, it is only meaningful when compared with the thermal energy (kT) available, which ultimately determines whether the interaction is favorable or not at a particular temperature. In other words, if the barrier is larger than kT, the interaction is considered “unfavorable”, and vice versa. However, we also note that colloids should exhibit a Boltzmann distribution of energies, and therefore simply comparing the energy barrier with kT might not be the most comprehensive metric, especially when they are of similar magnitude. Yet, by splitting the 6000 computed barriers into either “below kT” or “above kT” cases, this interaction problem essentially becomes a simple binary classification task, which is well-modeled by logistic regression. Similar to multivariate linear regression, logistic regression adds up all the variables (xi) with appropriate coefficients (βi) together with an intercept term (β0) to give y (eqn (13)). However, there is an additional step of feeding y into a sigmoid function to introduce non-linearity (eqn (14)). The resultant z takes a value between 0 and 1, and is therefore suitable for predicting the probability when there are only two distinct scenarios.
 | (13) |
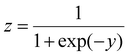 | (14) |
Putting this into the context of colloidal interactions, the calculated z is essentially the probability of “below kT” (and (1 − z) is the probability of “above kT”). The goal of logistic regression is to take the six parameters (VPart, VSurf, VDef, DD, Conc, R) as inputs, and predict whether it is more likely to be “below kT” or “above kT”. This prediction can be optimized by tuning the coefficients (βi) of the factors. The fitted coefficients are shown in Fig. 3(c) and eqn (15), where the magnitude represents the relative importance of each parameter. To prevent large absolute numbers from potentially dominating the results, the parameters are scaled by z-score normalization prior to fitting ( , μi and σi are the mean and standard deviation of the distribution). The extra ∥ ∥ symbol is used to denote a normalized quantity. Further details of logistic regression can be found in the ESI.†
, μi and σi are the mean and standard deviation of the distribution). The extra ∥ ∥ symbol is used to denote a normalized quantity. Further details of logistic regression can be found in the ESI.†
 | (15) |
The feature importance informed by logistic regression is as follows: VSurf > VPart > DD > Conc > R > VDef. Given that ANOVA analyzes the absolute energy barriers, while logistic regression collapses the whole interaction problem into a binary decision, it is not surprising that the feature importance estimated by both methods does not match exactly. Interestingly, although the exact order differs, ANOVA and logistic regression share the top four factors (VSurf, VPart, DD, Conc). VSurf and VPart are among the most influential descriptors, which agree well with the common experimental observation that the zeta potential of colloids is a reasonably good metric for predicting their stability.6–10 The salt concentration (Conc) is also an important determinant, which is in accordance with the classical double layer theory that ions screen the charges in the solution, and therefore a higher salt concentration (and ionic strength) leads to a shorter Debye length and lower stability of colloids. However, when defects are also taken into account, it appears that the exact potential of defects (VDef) does not play a pivotal role, but the defect density (DD) is much more crucial to the fate of the interaction. Nevertheless, it is noted that the interaction in question is ultimately a high-dimensional problem, and therefore no single factor can predict the outcome confidently, but a combination of parameters should be considered.
Since the top four factors (VSurf, VPart, DD, Conc) should be responsible for the majority of the results, it is therefore of interest to examine whether it is already sufficient to only consider these parameters, i.e. leaving out the two remaining ones (R, VDef). A common engineering approach is to handcraft certain dimensionless numbers out of the parameters in consideration, and visualize the data on a 2D plot to inspect whether the data points cluster. Several dimensionless numbers (e.g. and
and 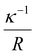 ) were constructed in an attempt to separate the data points into regions of “below kT” and “above kT” (Fig. S11†). However, none of them yields satisfactory clustering. Since the formulation of dimensionless numbers is confined by the intrinsic units of VSurf, VPart, DD, and Conc, these factors can only be assembled in a limited number of ways. To solve this problem, we exploit z-score normalization as a general way to combine parameters even though they do not necessarily have complementary units. Z-score normalization scales the inputs with respect to their standard deviations which have the same units, essentially rendering them dimensionless on their own (
) were constructed in an attempt to separate the data points into regions of “below kT” and “above kT” (Fig. S11†). However, none of them yields satisfactory clustering. Since the formulation of dimensionless numbers is confined by the intrinsic units of VSurf, VPart, DD, and Conc, these factors can only be assembled in a limited number of ways. To solve this problem, we exploit z-score normalization as a general way to combine parameters even though they do not necessarily have complementary units. Z-score normalization scales the inputs with respect to their standard deviations which have the same units, essentially rendering them dimensionless on their own (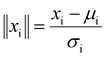 , where μi and σi are the mean and standard deviation of the distribution respectively). The mean and standard deviation for each variable are summarized in Table S3.† Importantly, with these dimensionless, normalized quantities, they can be simply added up together to construct dimensionless numbers, even though they might not have compatible units intrinsically.
, where μi and σi are the mean and standard deviation of the distribution respectively). The mean and standard deviation for each variable are summarized in Table S3.† Importantly, with these dimensionless, normalized quantities, they can be simply added up together to construct dimensionless numbers, even though they might not have compatible units intrinsically.
However, to form a meaningful dimensionless number, the normalized variables must be combined linearly with appropriate weights. A natural choice of such weights is the coefficients previously fitted by logistic regression (βi, summarized in (eqn 15) and Fig. 3(c)), since the logistic regression coefficients were obtained by processing normalized parameters in the first place. More specifically, we can add up the surface potential VSurf and the particle potential VPart with the logistic regression coefficients to construct the “Electrostatics” metric (2.516∥VSurf∥+2.449∥VPart∥). Similarly, the defect density DD and the salt concentration Conc can be considered together to formulate the “Environment” descriptor (1.696∥DD∥+1.417∥Conc∥). When these two descriptors (“Electrostatics” and “Environment”) are used as the selection criteria and plotted as the x and y axes in Fig. 4, the “below kT” and “above kT” cases are successfully clustered into distinctive regions as manifested by the separation of colors (green for “below kT” and red for “above kT”), which cannot be achieved if only individual parameters (VSurf, VPart, DD, Conc) are considered. The color of the data points represents the likelihood of “below kT”, which is evaluated by considering the overlapping points (N = 25 in Fig. 4) in this low-dimensional space, inevitably existing because only 4 out of 6 parameters are included here. Each point carries a label of either “below kT” (1) or “above kT” (0), and by taking the average of the labels at the overlapping points, the probability of “below kT” can be estimated. Notably in Fig. 4, the decision boundary between “above kT” and “below kT” is vividly visualized by the diagonal transition from red to yellow and eventually to green, indicating an increasing probability of “below kT” from the bottom left to the top right of the graph. The diagonal nature of this shift demonstrates that both the x and y axes are vital to the fate of colloidal interactions. If the results are mainly determined by the x-axis (y-axis), the boundary would have been a vertical (horizontal) one. Given that only ∼9% of the data points (554 out of 6000) are “above kT”, this graphical method is proven to be an effective way to separate the “below kT” and “above kT” cases by considering the top four factors together. Overall, a prediction for the interaction can be made by simply inputting the normalized numbers of ∥VSurf∥, ∥VPart∥, ∥DD∥, ∥Conc∥, and reading the color off the diagram: green for “below kT”, red for “above kT”, and yellow for the uncertain cases.
Although the graphical method in Fig. 4 manages to capture the transition from “above kT” to “below kT” by taking the four most important factors into account, the intermediate cases with higher uncertainty can only be decided by including the remaining parameters. Moreover, throughout the previous discussion, a constant Hamaker constant (AH) of 100 zJ is used to represent the average van der Waals attraction between TiO2 and Au, which might slightly deviate from it depending on the actual Au system. Consequently, we expanded the dataset by allowing the Hamaker constant to vary (0–150 zJ, steps of 10 zJ). Further simulations of perfect (uniformly charged) surfaces without defects (DD = 0 and VDef = 0) are also added to the dataset for comparative purposes. As a result, the extended dataset now encompasses a total of 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 conditions of seven parameters including the Hamaker constant (details in ESI†). To interact with this extensive dataset effectively, we fitted it to a support vector machine (SVM). The trained SVM model takes the seven factors (VPart, VSurf, VDef, DD, Conc, R, AH) as inputs, and returns “below kT” (spontaneous adsorption expected) or “above kT” (no adsorption expected) as the output, together with a decision function indicating the confidence of the prediction (a larger absolute value means higher confidence). An accuracy of 97% is achieved with a standard train/validation split of 80%/20%. Importantly, since our parameter space covers a large landscape of realistic conditions, and the SVM is trained based on these simulation data, it is also possible to predict the interaction between colloids for unseen but physically feasible cases, for perfect and defective surfaces. To facilitate the usability of the trained SVM, we prepared a Google Colab notebook with a simple graphical user interface, where users can enter a specific set of the seven parameters, and obtain a prediction for whether the interaction is favorable or not. This is made available in our GitHub repository.
160 conditions of seven parameters including the Hamaker constant (details in ESI†). To interact with this extensive dataset effectively, we fitted it to a support vector machine (SVM). The trained SVM model takes the seven factors (VPart, VSurf, VDef, DD, Conc, R, AH) as inputs, and returns “below kT” (spontaneous adsorption expected) or “above kT” (no adsorption expected) as the output, together with a decision function indicating the confidence of the prediction (a larger absolute value means higher confidence). An accuracy of 97% is achieved with a standard train/validation split of 80%/20%. Importantly, since our parameter space covers a large landscape of realistic conditions, and the SVM is trained based on these simulation data, it is also possible to predict the interaction between colloids for unseen but physically feasible cases, for perfect and defective surfaces. To facilitate the usability of the trained SVM, we prepared a Google Colab notebook with a simple graphical user interface, where users can enter a specific set of the seven parameters, and obtain a prediction for whether the interaction is favorable or not. This is made available in our GitHub repository.
While it might be a neat approach to treat the colloidal interaction as a simple problem of binary classification (“below kT” or “above kT”), it is worth noting the limitations of our model. First, the simulations are based on the Poisson–Boltzmann equation (eqn (3)), which means that our model also suffers from the inadequacies inherited from the theory. For instance, it is only a mean-field method with no ion-ion correlations considered.66 In addition, the Poisson–Boltzmann theory also tends to fail for highly charged regimes and multivalent electrolytes.67 Consequently, a symmetric monovalent salt (e.g. NaCl) has been deliberately assumed throughout this work, and hence the terms “salt concentration” and “ionic strength” are used interchangeably in the text. For simplicity, the Stern layer is also neglected, but it might be included in a similar way as described by Biesheuvel.68 Apart from the shortcomings of the Poisson–Boltzmann theory, we have only considered the effect of seven parameters (VPart, VSurf, VDef, DD, Conc, R, AH), and other factors which might potentially influence the outcome are not captured in our model, such as the morphology beyond a spherical particle. Despite these limitations, we employed this parametrized model based on the Poisson–Boltzmann theory due to its efficiency, where a simulation only took roughly ten seconds to run on average (details in ESI†). This enables a parametric sweep across a wide range of physically interesting conditions, which cannot be easily accomplished by more sophisticated yet computationally expensive methods (e.g. molecular dynamics and Monte Carlo).
Furthermore, it has to be noted that surfactants are not considered in our model, which are often used to stabilize the metal colloids against aggregation. Although our model can possibly account for the electrostatic contribution from the surfactants, the additional steric component of the surfactants might still prevent adsorption from happening. Therefore, to encourage the favorable interaction between metal and oxide particles, surfactant-free colloids should be used. Common approaches to remove surfactants include thermal treatment and repeated centrifugation with a mixture of good and poor organic solvents.69,70 However, it is not always trivial to eliminate the surfactants without changing the structure and keeping the colloids stable. An alternative method is to synthesize particles without the use of surfactants from the beginning. This can be done by techniques such as laser ablation in liquid, where a bulk metal target (e.g. Au) is irradiated by a pulsed laser to create nanoparticles in water which are only stabilized electrostatically.71 When comparing our model to experiments, it is expected that these surfactant-free particles would follow the predicted adsorption behavior better than the surfactant-stabilized counterparts.
Until now, we have limited ourselves to Au/TiO2 systems. However, since the factors (e.g.VSurf, DD, AH) are all empirical, it is expected that our model should largely generalize to similar metal/oxide materials, which could help understand the effect of the local environment on colloidal interactions. Experimentally, the zeta potential has always been the indicator of colloidal stability due to its ease of measurement. Yet, the zeta potential is only a weighted average of the potentials at the shear/slipping plane of all the particles in the dispersion.13 This global metric might not fully represent the local surface potential, which ultimately determines the adsorption behavior. As an example, it has been shown by AFM that the major (110) and minor (100) facets of rutile TiO2 have disparate IEPs separated by about two units, i.e. (110): 5.5–4.8 and (100): 3.7–3.2.15 This means that the surface (and zeta) potentials of these two facets are not the same at a particular pH, and are expected to interact differently with colloids. This facet-dependent interaction was demonstrated evidently by Su et al.16 when adsorbing silica nanoparticles on SrTiO3 supports. With dual scale AFM, the authors established that the IEPs of major (110) and minor (100) on SrTiO3 are ∼4 and ∼6 respectively. At a pH below their IEPs (3.5), negatively charged silica colloids were adsorbed on both facets which were positively charged. At a pH above their IEPs (10.8), no adsorption happened since all the silica, SrTiO3 (110) and (100) were negatively charged. Interestingly, in the intermediate pH range (4–6) between the IEP of (110) and (100), negatively charged silica colloids selectively adsorbed on the positively charged (100), but not the negatively charged (110). The bulk IEP value of SrTiO3 (∼3.5) would not have predicted this facet anisotropy. In our model, different facets can be potentially described by two separate cases: (110) with a lower IEP and VSurf, and (100) with a higher IEP and VSurf. Instead of only considering the case when (110) is negatively charged and (100) is positively charged, it would also be possible to predict the adsorption when both facets are slightly negatively charged.
Moreover, even within the same facet, the local surface potential does not necessarily have to be uniform across the entire surface due to the presence of defects, such as surface hydroxyls having a different charge than the rest of the surface. Using an OH-functionalized AFM tip, Wagner et al.72 directly probed the proton affinity of surface oxygen atoms on In2O3 (111), where the proton affinity of surface oxygen atoms is strongly correlated with the acidity (pKa) of the resultant surface hydroxyls. It was found that the four types of surface hydroxyls on In2O3 (111) had varied degrees of acidity. This means that they are likely to be protonated/deprotonated to a different extent at the same pH. In our model, this local environment of surface hydroxyls at different pH values could be captured by modifying the defect density (DD) and defect potential (VDef), and predictions can be made on whether a particular colloidal interaction is favorable. Overall, although the zeta potential is usually a reasonable initial estimate for colloidal interactions, it is the local environment which ultimately dictates the interaction outcome. We hope that our model will encourage further studies on examining the effect of facets and surface defects with well-defined methodology (e.g. quartz crystal microbalance and single crystals), as well as achieving the desired adsorption behavior by controlling the surface chemistry.
4. Conclusion
Colloidal interaction is ultimately a high-dimensional problem. Conventionally, the zeta potential is the most frequently used metric for predicting the stability of colloids in line with the established DLVO theory. The salt concentration and ionic strength are also known to affect the interaction following the Debye length relationship and the Schulze–Hardy rule. To gain more insights beyond the current understanding, it is important to consider all these well-studied factors together with other contributions which are relatively less explored, such as the effect of local defects.Herein, we simulate the interaction between negatively charged Au and TiO2 particles in the electrostatically repulsive regime based on the Poisson–Boltzmann equation and the finite element method, while varying a total of six parameters: VPart (particle potential), VSurf (surface potential), VDef (defect potential), DD (defect density), Conc (salt concentration), and R (particle radius). Defects were treated as local charge deviations compared to the regular surface. A possible identity of such defects is the surface hydroxyls on TiO2, which are less negative than the rest of the surface when protonated. The van der Waals contribution was included by using a mean value of Hamaker constant (AH) for Au/TiO2. A wide range of experimentally relevant conditions is covered by simulating 6000 unique combinations of these six parameters, and the interaction energy barrier for each case is extracted. By analyzing the distribution of interaction energies with ANOVA and logistic regression, the relative importance of each factor is inferred: VSurf > VPart > DD > Conc > R > VDef. The results demonstrate that the top four factors are VSurf, VPart, DD, and Conc, which agrees well with the conventional wisdom that the surface (and zeta) potential and the salt concentration (ionic strength) play a decisive role in the stability of colloids. Interestingly, when defects are included, it appears that the energy barrier can also be significantly lowered by a higher defect density (DD), while the defect potential (VDef) seems to have a minimal impact on the interaction outcome.
To examine whether it is sufficient to consider only the top four factors, the interaction can be framed as a classification problem: for Au colloids to adsorb on the TiO2 support, the energy barrier has to be smaller than the thermal energy (kT). Accordingly, the interaction energy barriers from the simulations can be divided into two groups relative to kT: “below kT” for favorable interactions and “above kT” for unfavorable interactions. This essentially simplifies the interaction problem to a binary classification task, which is well-modeled by logistic regression. Using the weights from logistic regression, the top four factors are combined to construct the “Electrostatics” (2.516∥VSurf∥+2.449∥VPart∥) and “Environment” (1.696∥DD∥+1.417∥Conc∥) descriptors, which successfully cluster the data points into regions of unfavorable (red), uncertain (yellow), and favorable (green) cases. However, even when combining the top four parameters, certain scenarios remain uncertain (yellow), and can only be confidently classified by taking the remaining parameters (R and VDef) into account. Hence, it is crucial to consider all the six parameters including the particle radius R and the defect potential VDef for an accurate prediction.
In the preceding discussion, the van der Waals Hamaker constant (AH) was fixed at the mean value for Au/TiO2 (100 zJ). However, to improve the generalizability of this model towards other materials, AH was also allowed to vary across the entire range of 0–150 zJ, yielding an expanded dataset with 116160 conditions encompassing seven parameters and their corresponding interaction energies. To predict the fate of the interaction while considering all parameters, a support vector machine (SVM) is trained with the extended dataset, which determines a decision boundary between “below kT” and “above kT” cases with 97% accuracy using a standard train/validation split of 80%/20%. The trained SVM model takes a total of seven variables (VPart, VSurf, VDef, DD, Conc, R, AH) as the input, and returns “below kT” or “above kT” as the output, together with a decision function indicating the confidence of the prediction. It is also noted that the model can be used for both seen and unseen cases, perfect and defective surfaces. To facilitate the usability of the trained SVM, we prepared a Google Colab notebook with a simple graphical user interface for querying the prediction given a set of parameters, where users can easily change different parameters and examine the effect.
Although the simulations are modeled after Au/TiO2 systems, the factors (e.g.VSurf and Conc) are all empirical, and therefore the model should largely generalize to similar metal/oxide materials. We anticipate that our results and tools can encourage further experimental and theoretical investigations into the effect of local surface chemistry (e.g. facets and defects) on colloidal interactions, rather than only assessing the established bulk metrics (e.g. zeta potential).
Abbreviations
| β 0 | Logistic regression intercept (—) |
| β i | Logistic regression coefficient (—) |
| n | Normal (—) |
| ΔS | Configurational entropy (J K−1) |
| ε 0 | Vacuum permittivity (F m−1) |
| ε r | Relative permittivity (—) |
| κ −1 | Debye length (m) |
| μ i | Mean of distribution (—) |
| ψ | Dimensionless potential (—) |
| ρ | Charge density (C m−3) |
| σ | Surface charge density (C m−2) |
| σ i | Standard deviation of distribution (—) |
| φ | Dimensional potential (V) |
| φ 0 | Dimensional surface potential (V) |
| a | Lattice parameter of defect array (nm) |
| A H | Hamaker constant (J) |
| c 0 | Number concentration of salt (number m−3) |
| Conc | Salt concentration (mM) |
| D | Particle–Surface separation (κ−1) |
| DD | Defect density (—) |
| e | Elementary charge (C) |
| E tot | Total interaction energy (J) |
| E vd w | van der Waals energy (J) |
| F chem | Chemical free energy (J) |
| F el | Electrostatic free energy (J) |
| I | Ionic strength (number m−3) |
| k | Boltzmann constant (J K−1) |
| L D | Defect radius (0.5 nm) |
| R | Particle radius (nm) |
| T | Temperature (K) |
| U el | Electrostatic potential energy (J) |
| V Def | Defect potential (mV) |
| V Part | Particle potential (mV) |
| V Surf | Surface potential (mV) |
Data availability
The whole dataset and the SVM model are available at https://github.com/kinranlau/COMSOL_colloid_interaction.Author contributions
All authors conceptualized the idea. K. L. ran the simulations and analyzed the data under the supervision of B. G. and S. R. K. L. drafted the manuscript. All authors wrote the final version of the manuscript. S. B. and S. R. acquired the funding for this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the German Research Foundation (DFG) projects 388390466 – CRC/TRR 247 and MA 8454/2-1. We thank Dr Bastian Mei for the helpful discussion on facet-dependent adsorption. K. L. acknowledges the PhD funding from the International Max Planck Research School for Interface Controlled Materials for Energy Conversion (IMPRS-SurMat). B. G. thanks DFG for the Mercator Fellowship. This work was performed in part under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07-NA27344, LLNL-JRNL-844847.References
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic press, Burlington (Mass.), 3rd edn, 2011 Search PubMed.
- H. Ohshima, Electrical Phenomena at Interfaces and Biointerfaces, John Wiley & Sons, Inc., 2012 Search PubMed.
- S. Reichenberger, G. Marzun, M. Muhler and S. Barcikowski, ChemCatChem, 2019, 11, 4489–4518 CrossRef CAS.
- M. Kosmulski, Adv. Colloid Interface Sci., 2016, 238, 1–61 CrossRef CAS.
- G. Marzun, C. Streich, S. Jendrzej, S. Barcikowski and P. Wagener, Langmuir, 2014, 30, 11928–11936 CrossRef CAS PubMed.
- D. Segets, R. Marczak, S. Schäfer, C. Paula, J.-F. Gnichwitz, A. Hirsch and W. Peukert, ACS Nano, 2011, 5, 4658–4669 CrossRef CAS PubMed.
- A. Sikora, D. Bartczak, D. Geißler, V. Kestens, G. Roebben, Y. Ramaye, Z. Varga, M. Palmai, A. G. Shard, H. Goenaga-Infante and C. Minelli, Anal. Methods, 2015, 7, 9835–9843 RSC.
- S. Samimi, N. Maghsoudnia, R. B. Eftekhari and F. Dorkoosh, Characterization and Biology of Nanomaterials for Drug Delivery, Elsevier, 2019, pp. 47–76 Search PubMed.
- S. Honary and F. Zahir, Trop. J. Pharm. Res., 2013, 12, 265–273 Search PubMed.
- N. Raval, R. Maheshwari, D. Kalyane, S. R. Youngren-Ortiz, M. B. Chougule and R. K. Tekade, Basic Fundamentals of Drug Delivery, Elsevier, 2019, pp. 369–400 Search PubMed.
- T. Hupfeld, A. Wegner, M. Blanke, C. Doñate-Buendía, V. Sharov, S. Nieskens, M. Piechotta, M. Giese, S. Barcikowski and B. Gökce, Adv. Opt. Mater., 2020, 8, 2000473 CrossRef CAS.
- P. Wagener, A. Schwenke and S. Barcikowski, Langmuir, 2012, 28, 6132–6140 CrossRef CAS.
- R. J. Hunter, Zeta Potential in Colloid Science: Principles and Applications, Academic Press, London, New paperback edn, 1988 Search PubMed.
- C. Pfeiffer, C. Rehbock, D. Hühn, C. Carrillo-Carrion, D. J. de Aberasturi, V. Merk, S. Barcikowski and W. J. Parak, J. R. Soc., Interface, 2014, 11, 20130931 CrossRef PubMed.
- J. W. Bullard and M. J. Cima, Langmuir, 2006, 22, 10264–10271 CrossRef CAS.
- S. Su, I. Siretanu, D. Ende, B. Mei, G. Mul and F. Mugele, Adv. Mater., 2021, 33, 2106229 CrossRef CAS.
- S. Bhattacharjee, C.-H. Ko and M. Elimelech, Langmuir, 1998, 14, 3365–3375 CrossRef CAS.
- M. Bendersky and J. M. Davis, J. Colloid Interface Sci., 2011, 353, 87–97 CrossRef CAS PubMed.
- A. Vijay, G. Mills and H. Metiu, J. Chem. Phys., 2003, 118, 6536–6551 CrossRef CAS.
- N. Kruse and S. Chenakin, Appl. Catal., A, 2011, 391, 367–376 CrossRef CAS.
- N. Siemer, A. Lüken, M. Zalibera, J. Frenzel, D. Muñoz-Santiburcio, A. Savitsky, W. Lubitz, M. Muhler, D. Marx and J. Strunk, J. Am. Chem. Soc., 2018, 140, 18082–18092 CrossRef CAS PubMed.
- N. Mintcheva, P. Srinivasan, J. B. B. Rayappan, A. A. Kuchmizhak, S. Gurbatov and S. A. Kulinich, Appl. Surf. Sci., 2020, 507, 145169 CrossRef CAS.
- N. Lopez, J. Catal., 2004, 225, 86–94 CrossRef CAS.
- J. Wan, W. Chen, C. Jia, L. Zheng, J. Dong, X. Zheng, Y. Wang, W. Yan, C. Chen, Q. Peng, D. Wang and Y. Li, Adv. Mater., 2018, 30, 1705369 CrossRef.
- J. V. Lauritsen, A. S. Foster, G. H. Olesen, M. C. Christensen, A. Kühnle, S. Helveg, J. R. Rostrup-Nielsen, B. S. Clausen, M. Reichling and F. Besenbacher, Nanotechnology, 2006, 17, 3436–3441 CrossRef CAS.
- A. Yurtsever, Y. Sugimoto, M. Abe and S. Morita, Nanotechnology, 2010, 21, 165702 CrossRef CAS PubMed.
- M. Miyazaki, Y. Sugawara and Y. J. Li, Langmuir, 2021, 37, 10588–10593 CrossRef CAS PubMed.
- J. J. Valle-Delgado, J. A. Molina-Bolívar, F. Galisteo-González, M. J. Gálvez-Ruiz, A. Feiler and M. W. Rutland, J. Chem. Phys., 2005, 123, 034708 CrossRef CAS.
- A. Klaassen, F. Liu, F. Mugele and I. Siretanu, Langmuir, 2022, 38, 914–926 CrossRef CAS.
- M. R. Hoffmann, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96 CrossRef CAS.
- M. Szekeres and E. Tombácz, Colloids Surf., A, 2012, 414, 302–313 CrossRef CAS.
- H. H. Kung, Transition Metal Oxides: Surface Chemistry and Catalysis, Elsevier, 1989, vol. 45, pp. 72–90 Search PubMed.
- T. Hiemstra, J. De Wit and W. Van Riemsdijk, J. Colloid Interface Sci., 1989, 133, 105–117 CrossRef CAS.
- J. P. Fitts, M. L. Machesky, D. J. Wesolowski, X. Shang, J. D. Kubicki, G. W. Flynn, T. F. Heinz and K. B. Eisenthal, Chem. Phys. Lett., 2005, 411, 399–403 CrossRef CAS.
- D. A. Sverjensky and N. Sahai, Geochim. Cosmochim. Acta, 1996, 60, 3773–3797 CrossRef CAS.
- T. Y. Yun and B. D. Chandler, ACS Appl. Mater. Interfaces, 2023, 15, 6868–6876 CrossRef CAS.
- K. Lau, F. Niemann, K. Abdiaziz, M. Heidelmann, Y. Yang, Y. Tong, M. Fechtelkord, T. C. Schmidt, A. Schnegg, R. K. Campen, B. Peng, M. Muhler, S. Reichenberger and S. Barcikowski, Angew. Chem., Int. Ed., 2023, 62, e202213968 CrossRef CAS PubMed.
- V. Kumaravel, S. Mathew, J. Bartlett and S. C. Pillai, Appl. Catal., B, 2019, 244, 1021–1064 CrossRef CAS.
- W. Dong, S. Reichenberger, S. Chu, P. Weide, H. Ruland, S. Barcikowski, P. Wagener and M. Muhler, J. Catal., 2015, 330, 497–506 CrossRef CAS.
- A. Lüken, M. Muhler and J. Strunk, Phys. Chem. Chem. Phys., 2015, 17, 10391–10397 RSC.
- A. Mahdavi-Shakib, J. Sempel, M. Hoffman, A. Oza, E. Bennett, J. S. Owen, A. Rahmani Chokanlu, B. G. Frederick and R. N. Austin, ACS Appl. Mater. Interfaces, 2021, 13, 11793–11804 CrossRef CAS.
- S. Overbury, V. Schwartz, D. Mullins, W. Yan and S. Dai, J. Catal., 2006, 241, 56–65 CrossRef CAS.
- J. Saavedra, C. Powell, B. Panthi, C. J. Pursell and B. D. Chandler, J. Catal., 2013, 307, 37–47 CrossRef CAS.
- I. X. Green, W. Tang, M. Neurock and J. T. Yates, Acc. Chem. Res., 2014, 47, 805–815 CrossRef CAS PubMed.
- D. Widmann and R. J. Behm, Angew. Chem., Int. Ed., 2011, 50, 10241–10245 CrossRef CAS PubMed.
- I. X. Green, W. Tang, M. Neurock and J. T. Yates, Science, 2011, 333, 736–739 CrossRef CAS.
- J. Saavedra, H. A. Doan, C. J. Pursell, L. C. Grabow and B. D. Chandler, Science, 2014, 345, 1599–1602 CrossRef CAS.
- Y. Y. Wu, N. A. Mashayekhi and H. H. Kung, Catal. Sci. Technol., 2013, 3, 2881 RSC.
- A. Y. Klyushin, M. T. Greiner, X. Huang, T. Lunkenbein, X. Li, O. Timpe, M. Friedrich, M. Hävecker, A. Knop-Gericke and R. Schlögl, ACS Catal., 2016, 6, 3372–3380 CrossRef CAS.
- A. Y. Klyushin, T. E. Jones, T. Lunkenbein, P. Kube, X. Li, M. Hävecker, A. Knop-Gericke and R. Schlögl, ChemCatChem, 2018, 10, 3985–3989 CrossRef CAS.
- H. P. Boehm, Discuss. Faraday Soc., 1971, 52, 264 RSC.
- M. Ramamoorthy, D. Vanderbilt and R. D. King-Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16721–16727 CrossRef CAS PubMed.
- A. S. Barnard and L. A. Curtiss, Nano Lett., 2005, 5, 1261–1266 CrossRef CAS.
- S. Wendt, R. Schaub, J. Matthiesen, E. Vestergaard, E. Wahlström, M. Rasmussen, P. Thostrup, L. Molina, E. Lægsgaard, I. Stensgaard, B. Hammer and F. Besenbacher, Surf. Sci., 2005, 598, 226–245 CrossRef CAS.
- Q. Zhang, J. Brndiar, M. Konôpka, H. F. Wen, Y. Adachi, M. Miyazaki, R. Turanský, R. Xu, Z. H. Cheng, Y. Sugawara, I. Štich and Y. J. Li, J. Phys. Chem. C, 2021, 125, 27607–27614 CrossRef CAS.
- Z. Dohnálek, I. Lyubinetsky and R. Rousseau, Prog. Surf. Sci., 2010, 85, 161–205 CrossRef.
- K. Bourikas, C. Kordulis and A. Lycourghiotis, Chem. Rev., 2014, 114, 9754–9823 CrossRef CAS PubMed.
- J. Theodoor and G. Overbeek, Colloids Surf., 1990, 51, 61–75 CrossRef.
- M. Krishnan, J. Chem. Phys., 2013, 138, 114906 CrossRef PubMed.
- COMSOL Multiphysics® v. 5.6, COMSOL AB.
- H. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- L. Bergström, Adv. Colloid Interface Sci., 1997, 70, 125–169 CrossRef.
- J. M. Fernández-Varea and R. Garcia-Molina, J. Colloid Interface Sci., 2000, 231, 394–397 CrossRef PubMed.
- V. Parsegian and G. H. Weiss, J. Colloid Interface Sci., 1981, 81, 285–289 CrossRef CAS.
- K. Jiang and P. Pinchuk, Nanotechnology, 2016, 27, 345710 CrossRef CAS PubMed.
- A. Cuetos, J. A. Anta and A. M. Puertas, J. Chem. Phys., 2010, 133, 154906 CrossRef.
- I. S. Sidhu, A. L. Frischknecht and P. J. Atzberger, ACS Omega, 2018, 3, 11340–11353 CrossRef CAS PubMed.
- P. Biesheuvel, J. Colloid Interface Sci., 2004, 275, 514–522 CrossRef CAS.
- W. Huang, Q. Hua and T. Cao, Catal. Lett., 2014, 144, 1355–1369 CrossRef CAS.
- T. Song, F. Gao, S. Guo, Y. Zhang, S. Li, H. You and Y. Du, Nanoscale, 2021, 13, 3895–3910 RSC.
- V. Amendola, D. Amans, Y. Ishikawa, N. Koshizaki, S. Scirè, G. Compagnini, S. Reichenberger and S. Barcikowski, Chem. – Eur. J., 2020, 26, 9206–9242 CrossRef CAS PubMed.
- M. Wagner, B. Meyer, M. Setvin, M. Schmid and U. Diebold, Nature, 2021, 592, 722–725 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: An additional description of the model, logistic regression and SVM; further equation derivations; data of varying Hamaker constants and Tukey's HSD tests. See DOI: https://doi.org/10.1039/d3nr06205h |
| This journal is © The Royal Society of Chemistry 2024 |

