Structure and dynamics of double-stranded DNA rotaxanes

Abstract

A DNA rotaxane, with its unique mechanically interlocked architecture consisting of a circular DNA molecule threaded onto a linear DNA axle, holds promise as a fundamental component for nanoscale functional devices. Nevertheless, its structural and dynamic behaviors, essential for advancing molecular machinery, remain largely unexplored. Using extensive all-atom molecular dynamics simulations, we investigated the behaviors of double-stranded DNA (dsDNA) rotaxanes, concentrating on the effects of shape distortion induced by torsional stress in small circular dsDNA containing 70–90 base pairs. We analyzed structural characteristics, including shape, intermolecular distances, and tilt angles, while also exploring dynamic properties such as translational diffusion and toroidal rotation. Our results indicate that shape distortion brings the circular and linear dsDNA components into closer proximity and causes a slight increase in translational diffusion yet a minor decrease in toroidal rotation. Nevertheless, there is no apparent evidence of coupling between translation and rotation. Overall, the insights from this study indicate that such shape distortion does not significantly alter their structure and dynamics. This finding provides flexibility for the design of DNA rotaxanes in nanoscale applications.

---

Introduction

A rotaxane is a mechanically interlocked structure composed of a circular molecule threaded onto a linear axle.^1–5 Over the last half-century, there has been significant advancement in the study of supramolecular rotaxanes, setting the stage for their application in molecular switches, machines, and sensors.^3–5 More recently, rotaxanes have been proposed as functional units for crafting novel polymer architectures, including main-chain polyrotaxanes and slide-ring gels.^6–8 The advent of DNA nanotechnology in recent years has opened the door to the development of DNA-based rotaxanes.^9–13 Specifically, double-stranded DNA (dsDNA) rotaxanes feature a small circular dsDNA molecule less than 200 base pairs (bp) in length and a linear dsDNA axle threading through the circular component. There has been substantial progress in the synthesis of dsDNA rotaxanes, and they have been proposed as nanoscale switches capable of responding to external triggers such as light.¹⁰

The versatility of rotaxanes stems from their capacity to govern the movement of the macrocycle along the linear axle.^3–5 Thanks to the non-covalent and topological link between circular and linear dsDNA molecules, the circular component exhibits the ability to move and rotate along the linear one. By customizing the circular component, for instance, through functionalization with stimuli-responsive polymers or DNA-binding proteins,¹⁴ it can serve as a processivity unit within nanoscale machinery. The development of such processive molecular systems necessitates a comprehensive understanding of the structure and dynamics of dsDNA rotaxanes. However, the structural and dynamic characteristics of the processive circular component in DNA rotaxanes have yet to be fully explored.

Here, we present extensive all-atom molecular dynamics (MD) simulations of dsDNA rotaxanes, which are formed through the mechanical interlocking of a small circular dsDNA molecule (ranging in length from 70 to 90 bp) with a linear dsDNA axle, as illustrated in Fig. 1. Hereinafter, we will refer to dsDNA as simply DNA, and the small circular DNA molecule as the DNA minicircle. In this work, we used DNA sequences of repeating AT/AT dinucleotides both for the linear DNA axle and the DNA minicircles. Double-stranded DNA, known for its stiffness and rigidity,¹⁶ can undergo structural disruption and shape distortion when sharply bent into small DNA minicircles. Such structural disruptions in small DNA minicircles less than 70–80 bp has been reported in experiments and MD simulations.^17–22 To mitigate the likelihood of such structural disruptions, using DNA sequences with high flexibility is advantageous. The sequences of repeating AT/AT dinucleotides are recognized for their high flexibility without any inherent structure bias.^23,24,49 Hence, these sequences are likely to be more stable in DNA minicircles where sharp bending is required. It is noted that in previous experiments on DNA rotaxanes^9,10,12 DNA minicircles contain short segments of AA/TT repeats, known as A-tracts, at several positions. These A-tracts are recognized to form intrinsically bent structures,^25,26 which aid in stabilizing the sharp bends of DNA minicircles. However, in our approach, we opted for the AT/AT dinucleotide sequences, which are inherently flexible and devoid of intrinsic structure. This choice was made to avoid potential design constraints that might arise from incorporating A-tracts. Specifically, we conducted MD simulations on DNA minicircles composed of several lengths of AT/AT repeats, while keeping the number of helical turns constant. Although these sequences are highly flexible, the sharp bending required to form small DNA minicircles may still lead to structural disruptions and shape distortions, depending on the torsional stress determined by their length and the number of helical turns. This allowed us to examine how torsional stress-induced DNA distortion affects the structure and dynamics of DNA rotaxanes.

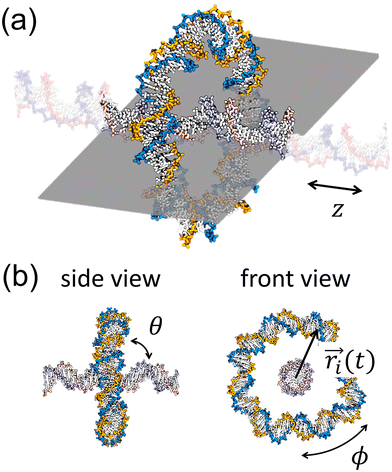Fig. 1 (a) A snapshot of a DNA rotaxane captured using the visualization software, VMD.¹⁵ In this figure, the DNA molecules have sequences of (AT)_n/(AT)_n with n = 41 and 16 for the circular and linear DNA molecules, respectively. This corresponds to lengths of 82 bp and 32 bp. The linear DNA molecule, aligned in the z direction, has its ends connected to each other by the application of periodic boundary conditions (PBC). A gray plane, drawn parallel to the linear DNA, serves as a guide to the eye. Transparent linear segments outside of the gray plane represent periodic images of the linear DNA segment. Water molecules and Na⁺ and Cl⁻ ions are hidden for ease of visualization. (b) Snapshots from the side and front views of a DNA rotaxane. The parameters defined in the figure are used to characterize the structure and dynamics of the rotaxane; θ represents the tilt angle between the minicircle and the linear axle, ϕ denotes the toroidal angle of the DNA minicircle, and 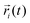is the vector from the linear axle to ith base pair of the minicircle.

Previously, several research groups have reported all-atom MD simulation studies involving small DNA minicircles with lengths ≤200 bp,^{20–22,27–33} examining structural features under various torsional states. Nonetheless, to the best of the authors’ knowledge, there has been no prior report on all-atom MD simulations of DNA rotaxanes. On the other hand, there has been several reports on computational studies on polyrotaxanes (mechanical interlocking of several circular molecules threaded by a linear axle) and polycatenanes (mutual mechanical interlocking of several circular molecules), employing generic polymer chain models to explore the general features of polyrotaxanes and polycatenanes depending on the model parameters.^34–39 All-atom MD simulations of DNA rotaxanes in this work can complement these approaches by providing more detailed information at all-atom level.

Results and discussion

In this work, DNA rotaxanes are composed of a linear DNA axle and a DNA minicircle, as shown in Fig. 1, both of which have sequences of repeating AT/AT dinucleotides. For the linear DNA axle, we used a 32 bp-long sequence of (AT)₁₆/(AT)₁₆ with both its ends connected to each other by imposing the periodic boundary condition (PBC), mimicking an infinitely long molecule. As for the DNA minicircle, four lengths were considered with the sequences of (AT)_n/(AT)_n with n = 35, 38, 41, and 45, corresponding to the number of base pairs of N_bp = 70, 76, 82, and 90, respectively. Given that torsional stress varies with N_bp while maintaining a fixed linking number (L_k, representing the number of helical turns in a DNA minicircle constrained in a plane), our selection of DNA lengths provides an opportunity to investigate the effects of torsional stress-induced DNA distortion on the structure and dynamics of DNA rotaxanes. The magnitude of torsional stress is quantified using the super helical density, σ, which is defined as σ = (L_k − L_k0)/L_k0, as listed in Table 1. In this equation, L_k0 represents the number of helical turns predicted based on the average twist angle of the corresponding linear molecule. When σ is close to 0, it indicates minimal torsional stress, while values less or greater than 0 signify under-twisting or over-twisting of the DNA minicircle, respectively. Among the four DNA minicircles, the one with N_bp = 82 and L_k = 8 exhibits a σ value of +0.025, which is closest to 0 and therefore experiences the least influence from torsional stress. In contrast, the minicircles with N_bp = 76 and 70 at the same L_k are significantly over-twisted, whereas the minicircle with N_bp = 90 is under-twisted.

Table 1 Summary of DNA minicircles investigated in this study. N_bp represents the number of base pairs, and L_k denotes the linking number as discussed in the text. The superhelical density σ is defined by σ = (L_k − L_k0)/L_k0, where L_k0 is the number of ideal helical turns, calculated using the average twist angle of the corresponding linear molecules. D_t and D_r are the translational and rotational diffusion coefficients, respectively, determined by linear fitting of the mean square displacement (MSD). D′_r converts D_r from units of degree² ns⁻¹ to cm² s⁻¹. Errors in D_t, D_r, and D′_r represent the standard deviations estimated from four independent simulations conducted for each DNA rotaxane

N bp	L k	σ	D t (10^−7 cm^2 s^−1)	D r (degree^2 ns^−1)	D′r (10^−7 cm^2 s^−1)
70	8	+0.201	2.7 ± 0.4	16.8 ± 0.4	6.1 ± 0.1
76	8	+0.106	2.8 ± 0.5	14.0 ± 1.5	6.4 ± 0.7
82	8	+0.025	2.4 ± 0.3	13.7 ± 0.7	7.7 ± 0.4
90	8	−0.066	2.7 ± 0.3	9.8 ± 1.0	6.2 ± 0.6

---

Fig. 2 illustrates two structural features of DNA rotaxanes: the shape of a DNA minicircle throughout the simulation and the distribution of the linear DNA axle in relation to the DNA minicircle. Initially, the focus is on the shape of the DNA minicircle, revealing its length dependence induced by torsional stress, as demonstrated in the final snapshots depicted in Fig. 2(a) and Fig. S1 of the ESI† and the helical axes illustrated in Fig. 2(b) and Fig. S2 of the ESI.† The helical axes, which trace the path of the DNA double helix, were obtained using the Curves+ software,⁴⁰ and its time-dependent variation is depicted by closed curves with varying color in Fig. 2(b).

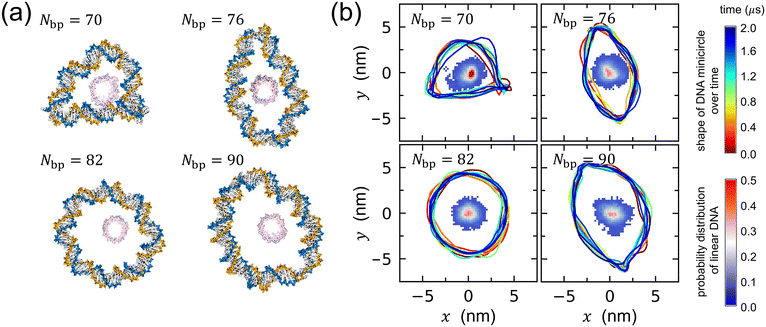Fig. 2 (a) Representative final snapshots of DNA rotaxanes captured using the visualization software, VMD.¹⁵ The labels N_bp = 70, 76, 82, and 90 in each panel denote the lengths of the DNA minicircles in the rotaxanes. Water molecules and Na⁺ and Cl⁻ ions are hidden for ease of visualization. (b) The temporal evolution of the DNA minicircle shape is visualized through closed curves with varying colors that represent time changes (refer to the upper color bar to the right of the figure for the time sequence), while the probability distribution of the linear DNA axle's position relative to the DNA minicircle is illustrated by the colored dots within each minicircle (refer to the lower color bar to the right of the figure). The helical axis of the minicircle, indicative of its shape, was calculated using the Curves+ software.⁴⁰ Although DNA minicircles rotate with time, the simulation trajectories were converted such that the DNA minicircle at later times is fitted to the initial structure and hence, it appears that the DNA minicircle does not rotate. The results in (a) and (b) are derived from one representative simulation out of four independent simulations conducted for each DNA rotaxane. All other results are presented in Fig. S1 and S2 of the ESI.†

When N_bp = 82, the DNA minicircle predominantly maintains a circular configuration, aligning with our earlier assertion that it experiences minimal torsional stress, as reflected in the smallest value of σ. However, for N_bp values other than 82, the shape deviates significantly from a perfect circle. DNA minicircles with N_bp ≤ 76 are over-twisted, leading to structural disruptions in the DNA double helix. This structure disruption results in an almond-like shape for N_bp = 76 and partial supercoiling at N_bp = 70 due to increased torsional stress. In contrast, minicircles with N_bp = 90 are under-twisted, resulting again in structural disruptions and adopting an elliptical shape. Previously, structural disruptions of small DNA minicircles have been reported under various torsional states by all-atom MD simulations.^{20–22,27,28,30,33} The structural disruptions observed in the DNA minicircles in this study qualitatively agree with findings from previous research.

Qunatitative identification of structural disruptions in small DNA minicircles has been previously achieved by observing sudden changes in the inter-base-pair roll angle²⁰ or through base-pair opening events.^21,22 In this work, we calculated the hydrogen bond distances between A–T bases in each base pair, which helped in identifying base-pair opening, and the roll angles between consecutive base pairs to gauge the extent of DNA bending. These calculations are detailed in Fig. S3–S6 of the ESI.† Hydrogen bond distances exceeding the range of 0.2–0.4 nm are indicative of base-pair opening, while large negative values of the roll angle are characteristic of kink formation in the DNA structure. Our results demonstrate that minicircles with N_bp = 82 typically exhibit zero or one kinked site. Conversely, minicircles with different N_bp values (N_bp ≠ 82) display two or three kinks. This finding correlates with largely circular shapes for N_bp = 82 and distorted shapes for those with other N_bp values.

Secondly, the spatial relationship between the DNA minicircle and the linear axle is visualized in Fig. 2(b) with the linear DNA axle's position marked by colored dots within the DNA minicircle. The simulation trajectories were adjusted so that the DNA minicircle in subsequent times is fitted to the initial structure. Hence, the distribution of the linear DNA axle is calculated relative to this fixed DNA minicircle. For N_bp = 82 and 90, the linear DNA axle remains relatively distant from the helical axis of the DNA minicircle, with an average minimum distance of 3.34 and 3.24 nm, respectively (see Fig. S7 of the ESI†). In contrast, for N_bp = 70 and 76, the linear axle occasionally moves closer to the DNA minicircle, with an average minimum distance of 2.62 and 2.57 nm, respectively (illustrated in Fig. S1 of the ESI†). Such results indicate that, at N_bp = 70 and 76, the interactions between the circular and linear DNA components can be notably pronounced during simulations.

The snapshots captured in Fig. 2(a) vividly depict the proximity of the linear DNA axle to the distorted DNA minicircle, particularly evident for N_bp = 70 and 76. The images suggest a conformation where the linear DNA axle appears to be compacted within the confines of the deformed DNA minicircle. We conducted separate MD simulations of a system containing only a DNA minicircle without a linear DNA axle. Notably, in one of the two 1 μs-long simulations of a DNA minicircle with N_bp = 70, we observed a supercoiled conformation, as illustrated in Fig. S8 of the ESI.† However, none of the four MD simulations of the DNA rotaxanes with N_bp = 70 manifested a supercoiled structure of the DNA minicircle. This discrepancy can likely be attributed to the electrostatic repulsion between the circular DNA and the interlaced linear DNA in the rotaxanes, which counteracts the formation of a supercoil. The presence of the linear DNA axle in the center acts as a spatial constraint, preventing the DNA minicircle from adopting a fully supercoiled conformation. Yet, torsional stress seems to propel the DNA minicircle into a constricted shape, intensifying its interactions with the linear DNA axle.

Given this intensified interaction, particularly for N_bp = 70 and 76, one might surmise that the linear DNA axle's helical structure could potentially influence the DNA minicircle's dynamics. It was hypothesized that there might be a correlation between the translational movement (variation along the z direction) and the toroidal rotation (angle ϕ variation) of the DNA minicircle as it traverses the linear DNA axle's double helix. However, further analysis reveals no substantive evidence to support the notion of such coupling between translational and rotational movements, as will be discussed below.

In addition, we calculated the tilt angle, θ, of the DNA minicircle relative to the linear axle, as defined in Fig. 1(b), to gain further insights into the structure of DNA rotaxanes. For the calculation of θ, we defined its complementary angle, θ′, as the angle between the principal axis of the DNA minicircle and the z axis, along which the linear DNA axle is aligned. The probability distribution of θ is presented in Fig. 3(a). In this calculation, we disregarded the orientation of the DNA minicircle's principal axis around the z axis. Simulation results indicate that the highest probability distributions for θ fall between 70° and 80°, rather than at 90° corresponding to the arrangement of the DNA minicircle perpendicular to the linear axle. This observation is attributed to the orientational entropy of the principal axis around the linear axle. As θ decreases from 90° or θ′ increases from 0°, the principal axis of the DNA minicircle has more potential orientations around the linear axle, proportional to the area element of dA = 2π sin θ′dθ′, which represents the area where the normalized principal axis of the DNA minicircle can point, given the principal axis in the range between θ′ and θ′ + dθ′ along the z axis.

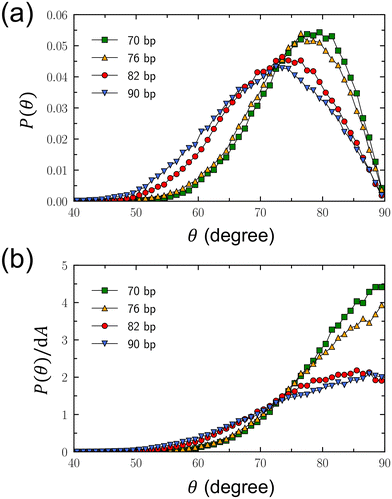Fig. 3 Characterization of tilt angle, θ, of the DNA minicircle relative to the linear DNA axle, which is aligned along the z axis as depicted in Fig. 1(b). (a) Probability distributions of θ. (b) Modified probability distributions of θ, calculated by dividing the probability distributions by the area element of dA = 2π sin θ′dθ′, where θ′ is the angle complementary to θ and is defined as the angle between the principal axis of the DNA minicircle and the linear axle.

An initial observation reveals that the probability distribution in Fig. 3(a) leans toward smaller angles as N_bp increases. Fundamentally, this shift can be understood based on the growth in size of the minicircles with increasing N_bp. Naturally, larger DNA minicircles possess greater freedom for tilting motion relative to the linear DNA axle. Intriguingly, however, the probability distributions are quite similar for N_bp values of 70 and 76, and again for 82 and 90. This pattern appears to be a results of the shape distortion observed in DNA minicircles. The minicircles with N_bp = 70 and 76 are predominantly elliptical, wrapping more tightly around the linear axle, thereby restricting the minicircle's tilting motion to the similar extent. Even though the minicircle with N_bp = 90 exhibits an elliptical shape, its larger size allows the tilting motion of the minicircle to some extent. This leads to a probability distribution for θ that appears similar with that of N_bp = 82.

To remove the influence of orientational entropy of the minicircle's principal axis around the linear axle, we adjusted this probability distribution by dividing it by the area element dA = 2π sin θ′dθ′. The modified probability distributions peak at θ = 90°, as shown in Fig. 3(b), corresponding to the DNA minicircle aligning perpendicular to the linear DNA axle. Notably, the modified probability distribution around θ = 90° is more constrained for N_bp = 70 and 76, whereas it is broader for N_bp = 82 and 90. This suggests greater freedom in tilting motion for N_bp = 82 and 90.

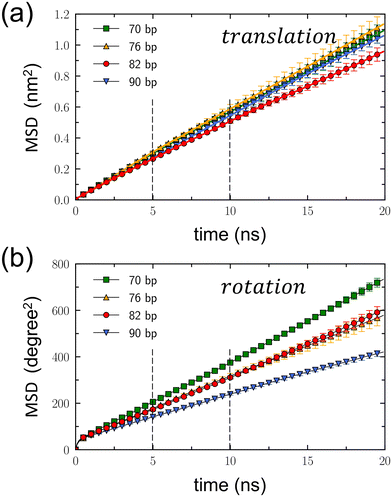
Dynamic properties of DNA rotaxanes were examined by assessing translational displacements and toroidal rotations of a DNA minicircle. Translational displacements were determined by monitoring changes in the minicircle's position z(t) along the z direction, as shown in Fig. S9–S12 of the ESI.† The translational mean square displacement (MSD), defined as 〈(z(t) − z(0))²〉, was calculated over time by adding all the trajectories from the four independent simulations for each DNA rotaxane, as shown in Fig. 4(a). Toroidal rotations were assessed by measuring variations in the angle ϕ around the linear axle, as shown in Fig. S13–S16 of the ESI.† The rotational MSD, defined as 〈(ϕ(t) − ϕ(0))²〉, was also computed by adding all the trajectories from the four independent simulations for each DNA rotaxane and is presented as a function of time in Fig. 4(b).

Fig. 4 Translational and rotational mean square displacements (MSD) of DNA minicircles. (a) Translational MSD, 〈(z(t) − z(0))²〉, plotted as a function of time. The dashed lines represent the time interval between 5 and 10 ns, during which the diffusion coefficients were calculated. This interval was selected based on the convergence of MSDs from four independent simulation sets for each N_bp within this range. (b) Rotational MSD, 〈(ϕ(t) − ϕ(0))²〉, as a function of time, with ϕ measured in degrees. Error bars are the standard deviation estimated from four independent simulations conducted for each DNA rotaxane. The dashed lines again highlight the time interval used for calculating the diffusion coefficients.

From the linear relation of MSD = 2Dt, the translational diffusion coefficient, D_t, was calculated by fitting the translational MSD to a linear line within the time interval between 5 and 10 ns, as presented in Table 1. This time interval, indicated by dashed lines in Fig. 4(a), was chosen because the translational MSDs calculated separately for the four simulations of each DNA rotaxane were converged well in this time interval, as is shown in Fig. S17 of the ESI.† While extending the duration of MD simulations to tens or hundreds of microseconds could enhance the convergence of the MSD over longer periods, such an undertaking exceeds our present computing resources. Therefore, we plan to address this in our future research efforts. Treating the toroidal rotation as 1-dimensional diffusive process, we also calculated the rotational diffusion coefficient D_r by fitting the rotational MSD to a linear line. The values of D_r were also obtained within the time interval between 5 and 10 ns and presented in Table 1. The rotational MSDs from the four simulations for each DNA rotaxane are presented in Fig. S18 of the ESI.†

Notably the translational diffusion coefficients, D_t, listed in Table 1 agree well with the experimental measurement, 3.2 × 10⁻⁷ cm² s⁻¹, for linear DNA fragments of 80 bp in aqueous solutions.⁴¹ This consistency validates the effectiveness of our model in simulating the diffusion of DNA molecules. In addition, there are a group of DNA-binding proteins that wrap around and move processively along DNA, called sliding clamps.^42,43 Recently, using the similar computational model,⁴³ the translational diffusion of a proliferating cell nuclear antigen (PCNA) protein, one of the sliding clamps, was estimated to be ∼3 × 10⁻⁸ cm² s⁻¹, an order of magnitude smaller than that of DNA minicircles calculated in this work. This disparity can be attributed to electrostatic interactions: a negatively charged DNA minicircles have repulsion from a negatively charged linear DNA axle, while a PCNA protein contains positively charged residues that create attractive interactions with a negatively charged DNA axle. Hence, it becomes evident that the translational diffusion of a DNA minicircle is significantly faster than that of a PCNA protein.

For all DNA minicircles examined in this work, the slopes of the translational MSD, as shown in Fig. 4(a), and the values of D_t, as presented in Table 1, are largely the same. However, an exception was found in the case of the DNA minicircle with N_bp = 82. This particular DNA minicircle exhibited a slight deviation in its translational MSD and a marginally smaller D_t value compared to the others. The errors of D_t were derived from the standard deviation of linear fits across the four simulations for each DNA rotaxane. Currently, the reason for the slightly reduced translational diffusion estimated for the DNA minicircle with N_bp = 82, relative to the others, remain unclear. However, given that the D_t values overlap within the error margins, a more definite conclusion may require even more extended simulations, possibly spanning several tens of microseconds.

On the other hand, both the slopes of the rotational MSD, illustrated in Fig. 4(b), and the D_r values, presented in Table 1, exhibit a decrease with the increasing value of N_bp. This trend reflects the extension of the contour length accompanying the increase in N_bp. As the DNA minicircle enlarges, a specific displacement during toroidal rotation yields a reduced angular variation (measured in degree). Consequently, for an equivalent spatial displacement during toroidal rotation, the resultant angular variation diminishes as N_bp increases. Notably, the D_r values for N_bp = 76 and 82 closely match. This suggests that the toroidal rotation of N_bp = 82 is faster than that of N_bp = 76, likely due to the shape distortion of the DNA minicircle with N_bp = 76.

To ensure an equitable comparison of rotational diffusion across DNA minicircles, independent of their sizes, we converted the rotational diffusion coefficient D_r (expressed in degree² ns⁻¹) into an alternative form D′_r (expressed in cm² s⁻¹). To convert the angular variation into a distance change during toroidal rotation, we applied a correction factor of (2π〈r〉/360)², where 〈r〉 represents the average size of the DNA minicircle. The resulting D′_r values are provided in Table 1. A comparison of the D′_r values among DNA minicircles reveals that the rotational diffusion is faster for the DNA minicircle with N_bp = 82 than the others. We hypothesize that this difference arises from variations in their shapes. Specifically, the minicircle with N_bp = 82 maintains a circular form, while those with different N_bp values become distorted into ellipses. In a scenario where an elliptical DNA minicircle undergoes toroidal rotation around its principal axis, the DNA base pairs must displace water molecules from their anticipated circular path, thereby impeding their movement. In contrast, during the toroidal rotation of a perfectly circular DNA structure, there are no water molecules obstructing the circular path of the DNA base pairs. Instead, the synchronized movements of adjacent base pairs create space for toroidal rotation.

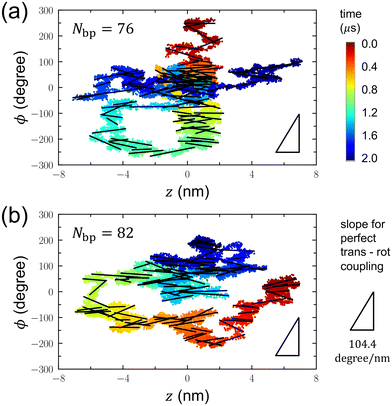
Considering the differential effects of DNA shape distortion on translation and rotation, we postulated the existence of a potential interplay between the translational motion of a DNA minicircle and its toroidal rotation along the helical structure of a linear DNA axle. To explore this potential coupling, we concurrently plotted variations in the z position and angle ϕ, as illustrated in Fig. 5. In this presentation, each data point corresponds to a (z, ϕ) pair for each time step throughout the 2 μs simulations. To enhance clarity, we applied linear fits to the (z, ϕ) variations at 20 ns intervals, represented by thick linear lines.

Fig. 5 Representative trajectories of a DNA minicircle in rotaxanes (depicted as colored scattered dots) in the space of the rotational angle, ϕ, and the position, z, along the linear axle. The color bar on the right reflects the time evolution. The triangle on the right serves as a guide to the eye, representing the slope for perfect coupling between translational and rotational motions, which is 104.4° nm⁻¹. This value corresponds to the helical pitch of the DNA double helix, relating to the backward–forward movement of a DNA minicircle along the major/minor grooves. Bold linear lines superimposed on the scattered plots show the linear fits of the (z, ϕ) variations over each 20 ns interval. The slopes of these fitted lines are substantially lower than 104.4° nm⁻¹, demonstrating a negligible coupling between translational and rotational movements.

If there is a coupling between translation and rotation along the double helix of a linear DNA axle, we would anticipate the slope of the linear fit to be (a helical turn)/(DNA length for a turn) = 360°/3.45 nm = 104.4° nm⁻¹. This anticipated value is denoted by the triangle at the bottom right of each panel. However, the slopes of the linear fits calculated within 20 ns intervals mostly fall significantly below this 104.4° nm⁻¹, suggesting the absence of translation-rotation coupling. This could be due to the large size of the DNA minicircle and the strong electrostatic repulsion between the DNA minicircle and the linear DNA axle. These factors are likely responsible for ensuring that the dynamics of the DNA minicircle remain uninfluenced by the helical structure of the linear DNA axle. Interestingly, recent MD simulations have also demonstrated weak coupling between translation and rotation for PCNA proteins.^42,43

Conclusion

In summary, we conducted extensive all-atom MD simulations on DNA rotaxanes, comprising a small DNA minicircle and a linear DNA axle. Our analysis delved into the structural and dynamic properties of these rotaxanes, focusing on the shape, spatial distribution, and tilt angles of the DNA minicircle in relation to the linear DNA axle, and its translational and rotational diffusive behaviors along this axle. A particular focus is the impact of shape distortion in the DNA minicircle induced by torsional stress. We achieved this by simulating DNA minicircles of varying lengths while keeping the linking number consistent. Notably, while the DNA minicircle with N_bp = 82 predominantly exhibited a circular form, those with N_bp = 70 and 76 and that with N_bp = 90 manifested over-twisted and under-twisted configurations, respectively. Shape distortion of the DNA minicircle into an elliptic shape led to a tighter spatial relationship between the circular and linear DNA components and causes a slight increase in translational diffusion yet a minor decrease in toroidal rotation. The reasons behind these observations are deferred to our future efforts. We also concluded from our results that there is no discernible coupling between translational and rotational motions.

Several other factors can influence the structure and dynamics of DNA rotaxanes, notably the DNA sequence and ion concentration. In our simulations, we exclusively used DNA molecules with repetitive AT/AT dinucleotide sequences. Altering these DNA sequences could modify the flexibility of the DNA, thereby affecting the stability of sharply bent DNA minicircles. Moreover, all simulations were conducted at a NaCl concentration of 0.150 M. It is important to note that changes in ion concentration can alter electrostatic interactions between DNA molecules, which may have consequential effects on the structure and dynamics of DNA rotaxanes. These elements will be taken into account in our future research.

The emerging field of nanoscale machinery, especially with DNA rotaxanes, presents significant promise. Utilizing DNA-binding proteins or harnessing sequence-specific hybridization with additional DNA strands could lead to the development of sophisticated DNA rotaxane-based devices.¹⁰ Selecting the appropriate sequence and length of DNA minicircles is crucial in the assembly of DNA rotaxanes, as it significantly influences their interaction with proteins or other DNA strands. Concerns might arise regarding the potential for structural disruptions and shape distortions in DNA minicircles due to specific DNA sequences and lengths. However, our research indicates that such structural disruptions do not markedly impact the overall structure and dynamics of DNA rotaxanes. This insight allows for greater flexibility in the design of dynamic DNA rotaxanes, enabling the selection of DNA minicircles’ sequence and length without undue worry about shape distortion.

Methods

All the simulations were performed using GROMACS v2019.5 software with the PARMBSC1 force field⁴⁴ and CUFIX correction⁴⁵ for DNA molecules. Water molecules were considered using the rigid TIP3P model and 0.150 M of Na⁺ and Cl⁻ ions were explicitly modeled using Joung and Cheatham parameters⁴⁶ with CUFIX correction.⁴⁵ The initial rotaxane structure was generated using the Nucleic Acid Builder (NAB) program in AmberTools16.⁴⁷ This structure consisted of a linear DNA axle threading through a DNA minicircle in a hexagonal simulation box, as shown in Fig. 1. The 32 bp-long linear DNA was aligned along the z direction, and the PBC was applied to connect both ends. For each simulation, an initial MD equilibration was carried out for 300 ns, at 300 K and 1 bar. The equations of motion were integrated numerically using a leapfrog algorithm with a time step of 2 fs. Temperature coupling employed the V-rescale method, while semi-isotropic Parrinelo-Raman pressure coupling was applied in the xy direction, with the z direction box size held constant. Thermostat and barostat time constants were set at 0.1 ps and 2.0 bar, respectively. Compressibility for pressure control in the lateral direction was set to 4.5 × 10⁻⁵ bar⁻¹. In the subsequent production runs, the same MD simulations were extended to a duration of 2μ each. Nevertheless, a weak restraint was applied to the linear DNA axle. This is to counteract the ease of rotation around its longitudinal axis that is induced by the application of PBC, which, without such a restraint, would result in an overly facile rotational behavior not typically observed in natural conditions. For each DNA rotaxane, we conducted four independent MD simulations, resulting in a cumulative duration of 8 μs for each DNA rotaxane. Our analysis primarily centered on characterizing the structural features of DNA rotaxanes and examining the dynamics of a DNA minicircle along a linear axle.^31,32Fig. 1 provides an overview of the simulation system and the parameters used to characterize the structure and dynamics of the rotaxane in this work, including the tilt angle θ between the minicircle and the linear axle and the toroidal angle ϕ of the DNA minicircle. Curvilinear helical axes of minicircles, presented in Fig. 2, were calculated using the Curves+ software.⁴⁰ Simulation inputs and data for production runs of all DNA rotaxanes in this work and representative movies are available from a github repository.⁴⁸

Author contributions

J. S. K. conceived and designed this work. Y. S. and J. S. K. developed the computational models. Y. S. conducted the computer simulations and data analysis. Y. S. and J. S. K. wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the National Research Foundation of Korea (NRF) under Grant No. NRF-2019R1A2C1084414 and NRF-2020R1A5A2019210.

References

1. I. T. Harrison and S. Harrison, J. Am. Chem. Soc., 1967, 5723–5724.
2. P. L. Anelli, N. Spencer and J. F. Stoddart, J. Am. Chem. Soc., 1991, 113, 5131–5133.
3. C. Cheng, P. R. McGonigal, S. T. Schneebeli, H. Li, N. A. Vermeulen, C. Ke and J. F. Stoddart, Nat. Nanotechnol., 2015, 10, 547–553.
4. E. R. Kay and D. A. Leigh, Angew. Chem., Int. Ed., 2015, 54, 10080–10088.
5. D. Sluysmans and F. Stoddart, Trends Chem., 2019, 1, 185–197.
6. L. F. Hart, J. E. Hertzog, P. M. Rauscher, B. W. Rawe, M. M. Tranquilli and S. J. Rowan, Nat. Rev., 2021, 6, 508–530.
7. K. Mayumi, C. Liu, Y. Yasuda and K. Ito, Gels, 2021, 7, 91.
8. L. Chen, X. Sheng, G. Li and F. Huang, Chem. Soc. Rev., 2022, 51, 7046–7065.
9. D. Ackermann, T. L. Schmidt, J. S. Hannam, C. S. Purohit, A. Heckel and M. Famulok, Nat. Nanotechnol., 2010, 5, 436–442.
10. F. Lohmann, D. Ackermann and M. Famulok, J. Am. Chem. Soc., 2012, 134, 11884–11887.
11. A. Cocconello, C.-H. Lu, J. Elbaz and I. Willner, Nano Lett., 2013, 13, 6275–6280.
12. S.-S. Jester and M. Famulok, Acc. Chem. Res., 2014, 47, 1700–1709.
13. Z. Yu, C. Julián, M. Matthies, P. Šulc and M. Famulok, J. Am. Chem. Soc., 2021, 143, 13292–13298.
14. J. Valero, N. Pal, S. Dhakal, N. G. Walter and M. Famulok, Nat. Nanotechnol., 2018, 13, 496–503.
15. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
16. J. P. Peters and L. J. Maher III, Q. Rev. Biophys., 2010, 43, 23–63.
17. Q. Du, A. Kotlyar and A. Vologodskii, Nucleic Acids Res., 2008, 36, 1120–1128.
18. A. Vologodskii and M. D. Frank-Kamenetskii, Nucleic Acids Res., 2013, 41, 6785–6792.
19. T. T. Le and H. D. Kim, Nucleic Acids Res., 2014, 42, 10786–10794.
20. F. Lankaš, R. Lavery and J. H. Maddocks, Structure, 2006, 14, 1527–1534.
21. S. A. Harris, C. A. Laughton and T. B. Liverpool, Nucleic Acids Res., 2008, 36, 21–29.
22. J. S. Mitchell and S. A. Harris, Phys. Rev. Lett., 2013, 110, 148105.
23. Y. Zhang and D. M. Crothers, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3161–3166.
24. S. Geggier and A. Vologodskii, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15421–15426.
25. P. J. Hagerman, Biopolymers, 1985, 24, 1881–1897.
26. H.-S. Koo, H.-M. Wu and D. M. Crothers, Nature, 1986, 320, 501–506.
27. M. Taranova, A. D. Hirsh, N. C. Perkins and I. Andricioaei, J. Phys. Chem. B, 2014, 118, 11028–11036.
28. T. Sutthibutpong, C. Matek, C. Benham, G. Slade, A. Noy, C. Laughton, J. Doye, A. Louis and S. Harris, Nucleic Acids Res., 2016, 44, 9121–9130.
29. M. Pasi, K. Zakrzewska, J. H. Maddocks and R. Lavery, Nucleic Acids Res., 2017, 45, 4269–4277.
30. T. S. Alexiou, P. V. Alatas, D. G. Tsalikis and V. G. Mavrantzas, Macromolecules, 2020, 53, 5903–5918.
31. M. Kim, S. Bae, I. Oh, J. Yoo and J. S. Kim, Nanoscale, 2021, 13, 20186–20196.
32. M. Kim, C. Hong, S. Lee and J. S. Kim, Bull. Korean Chem. Soc., 2022, 43, 523–528.
33. J. D. Curuksu, J. Chem. Phys., 2023, 159, 105101.
34. P. M. Rauscher, S. J. Rowan and J. J. de Pablo, ACS Macro Lett., 2018, 7, 938–944.
35. Y. Yasuda, M. Toda, K. Mayumi, H. Yokoyama, H. Morita and K. Ito, Macromolecules, 2019, 52, 3787–3793.
36. P. M. Rauscher, K. S. Schweizer, S. J. Rowan and J. J. de Pablo, Macromolecules, 2020, 53, 3390–3408.
37. G. Zhang and J. Zhang, Polymer, 2020, 196, 122475.
38. K. Li, Y. Wang, F. Guo, L. He and L. Zhang, Soft Matter, 2021, 17, 2557–2567.
39. P. Chiarantoni and C. Micheletti, Macromolecules, 2022, 55, 4523–4532.
40. R. Lavery, M. Moakher, J. H. Maddocks, D. Petkeviciute and K. Zakrzewska, Nucleic Acids Res., 2014, 37, 5917–5929.
41. E. Dauty and A. S. Verkman, J. Biol. Chem., 2005, 280, 7823–7828.
42. D. Daitchman, H. M. Greenblatt and Y. Levy, Nucleic Acids Res., 2018, 46, 5935–5949.
43. S. You, H.-G. Lee, K. Kim and J. Yoo, J. Chem. Theory Comput., 2020, 16, 4006–4013.
44. I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2016, 13, 55–58.
45. J. Yoo and A. Aksimentiev, Phys. Chem. Chem. Phys., 2018, 20, 8432–8449.
46. I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041.
47. D. Case, R. Betz, D. Cerutti, T. Cheatham III, T. Darden, R. Duke, T. Giese, H. Gohlke, A. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. Merz, G. Monard, H. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, D. Roe, A. Roitberg, C. Sagui, C. Simmerling, W. Botello-Smith, J. Swails, R. Walker, J. Wang, R. Wolf, X. Wu, L. Xiao and P. Kollman, AMBER 16, University of California, San Francisco., 2016.
48. https://github.com/junsookim76/DNA-Rotaxane-SI . date accessed on 02/06/24.
49. S. Bae and J. S. Kim, J. Chem. Theory Comput., 2021, 17, 7952–7961.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05846h

---