Quantifying intuition: Bayesian approach to figures of merit in EXAFS analysis of magic size clusters

Abstract

Analysis of the extended X-ray absorption fine structure (EXAFS) can yield local structural information in magic size clusters even when other structural methods (such as X-ray diffraction) fail, but typically requires an initial guess – an atomistic model. Model comparison is thus one of the most crucial steps in establishing atomic structure of nanoscale systems and relies critically on the corresponding figures of merit (delivered by the data analysis) to make a decision on the most suitable model of atomic arrangements. However, none of the currently used statistical figures of merit take into account the significant factor of parameter correlations. Here we show that ignoring such correlations may result in a selection of an incorrect structural model. We then report on a new metric based on Bayes theorem that addresses this problem. We show that our new metric is superior to the currently used in EXAFS analysis as it reliably yields correct structural models even in cases when other statistical criteria may fail. We then demonstrate the utility of the new figure of merit in comparison of structural models for CdS magic-size clusters using EXAFS data.

---

1 Introduction

Establishing the atomic structures of materials is a fundamental step in understanding their mechanical, electronic and optical properties and is essential for material applications. However, recovering the atomic structures of nanomaterials is particularly challenging using standard structural analysis techniques (e.g. X-ray and electron diffraction, Raman scattering, etc.) due to loss of periodicity at atomic level and potential presence of novel metastable atomic arrangements. This is especially true of the recently discovered ultra-small truly mono-disperse nanoparticles—magic-size clusters (MSCs).^1–3 As a consequence, several advanced structural methods such as X-ray absorption spectroscopy (XAS) and pair distribution function (PDF) analysis have been utilised to investigate atomic structure of MSCs.^4–6 XAS, in particular, has been shown to be sensitive to the atomic arrangements and structural changes in MSCs delivering information about sample stoichiometry and cluster symmetry discriminating between variety of structural models.⁶

This new class of nanoscale systems pushes XAS capabilities to the limit both in terms of the quality of the data required and of analysis methods for the two key parts of the X-ray absorption spectrum: X-ray absorption near edge structure (XANES) and extended X-ray absorption fine structure (EXAFS). The former is sensitive to the symmetry around the absorbing atom of interest (e.g. Cd in CdS MSCs⁶) and its oxidation state, while the latter provides information about local coordination numbers, interatomic distances and local atomic dynamics (see Fig. 1).

Fig. 1 EXAFS analysis is the study and interpretation of the fluctuations in the post-edge X-ray absorption spectrum. The fluctuations in the signal (in the purple highlight) are the result of interference of the outgoing photoelectron wave with the portion scattered by the neighboring atoms. The EXAFS equation used for modelling these oscillations. χ(k) is related to the plotted absorption μ(E) by the transform: , E₀ being absorption edge energy.

Analysis of EXAFS data typically involves background subtraction and normalisation followed by theoretical EXAFS calculations for a selected structural model (or a selection of model structures), comparisons of the calculated spectrum with the data and parameter refinement to obtain the best fit and the corresponding structural information.^7,8 Theoretical calculations and subsequent refinement are some of the most crucial steps and require a suitable atomistic model, thus implying some prior knowledge of the atomic structure or having an informed guess (e.g. based on molecular dynamics, DFT calculations or similar material, etc.). Recovering atomic structure of MSCs puts particularly stringent demands on model comparison in EXAFS because local atomic arrangements can be quite similar.⁹ When theoretical and experimental spectra are compared, in most EXAFS analysis programs (such as Artemis¹⁰ and Larch¹¹) there are a number of figures of merit (FoMs) available to provide quantitative model evaluation to answer the question of whether the model is a suitable match for the experimental data. However, none of the commonly used FoMs take into account parameter correlation. At the same time, it is well-known^12–14 that correlation can have significant negative consequence on data refinement (i.e. larger errors) and, most importantly, on model verification and selection.

This shortcoming of the EXAFS FoMs has long been recognised as a problem and in the latest development of the Artemis (one of the most commonly used EAXFS analysis package) a heuristic “happiness parameter” is offered to provide in-code indication of the fit quality. This parameter is based on decades of EAXFS analysis experience and includes, with varying weighting, an R-factor (a numerical measure of how well the fit over-plots the data), penalties for parameter correlations, restraints, the number of independent parameters, etc.¹⁵ While recognised as an important guide during data analysis, being a heuristic parameter, it has no firm basis in statistics and therefore cannot be quoted in publications.

In this article we introduce for the first time in EXAFS analysis an FoM that explicitly includes parameter correlations – the Bayes factor integral (BFI).¹⁶ We use EXAFS data for crystalline Ge at low temperature to demonstrate that the BFI is more sensitive than the typical FoMs used for EXAFS analysis to model choice. We then demonstrate that the BFI consistently points towards the correct structure as preferred model. We then use the BFI to compare a selection of models for a material with unknown structure: CdS magic sized clusters (MSCs 311 and 322).^5,6,17 With these examples, we introduce the BFI as a numerical metric for quantifying intuition in EXAFS model comparison.

2 Methods

2.1 Figures of merit in EXAFS analysis

Least-squares fitting (LS, the minimisation of the sums of squares of residuals to optimise a model) is a commonly used method to fit data, to estimate parameters and to make decisions about model selection. In EXAFS LS fitting, reported FoMs in Larch and Artemis are χ, χ_ν², R-factor, AIC and BIC.

The first is the well-known statistical value characterising the residuals between the model and experimental data. It is a simple statistical measure of how small the fit residuals are:

i.e. how closely does the model fit the data, however, it is has been well-established that the number of independent variables (fitting parameters) can significantly influence the value of χ². The total number of parameters available in EXAFS analysis is limited by the sampling theorem of the Fourier analysis¹⁸ (this is also known as the Nyquist criterion/theorem in EXAFS community). Therefore, the most commonly reported fitting statistic in EXAFS is the so-called reduced chi-squared, χ_ν², based on χ² but with a modification to include normalisation of χ² by degrees of freedom such that once the maximum number of free parameters allowed for the data (N_ind) is reached,¹⁸ it will become negative and provides a clear indication of over-fitting. The R-factor is another variation of the χ² criterion with a different normalisation factor.

The AIC and BIC are not found in Artemis, but are used as FoMs in Larch¹¹ to aid model comparison: both are based on the Likelihood function (rather than χ²) while also including a penalty term for adding parameters to the model (adding fitting parameters to a model—physically meaningful or not—normally increases the likelihood of the model while reducing the probability that the model is correct).

There are a number of problems with the figures of merit described above. They treat all parameters alike, whether physically-meaningful or not. Apart from the number of parameters approaching N_ind, there is not much help from these FoMs to tell whether one has a physically meaningful fit. Crucially, none of them include parameter correlations, while it is well documented^12–14 that parameter correlations indicate over-fitting and have significant consequences on the refinement errors and model selection. For example, in EXAFS analysis it is well-established that there exist correlations between fitting parameters even when N_ind ¹⁸ is not exceeded.^7,11,19–21 Both Artemis and Larch do provide functionality to calculate parameter correlations, but these are almost never used to assess the quality of the fit nor to aid model justification or selection. To compensate for that and to help guide users during the refinement in Artemis there is an inbuilt FoM that does include correlations: the Happiness parameter.¹⁵ However, it cannot be reported in publications since it has no mathematical basis: it is an empirical FoM that can be adjusted between fits to accord with the user's preferences. Hence, there is a need for a FoM rooted in statistics that does include parameter correlations.

2.2 Bayes theorem, Bayes factor and Bayes factor integral

The goal of EXAFS analysis can be described as “to find the best model parameters that fit the data” or, more generally, “to select the best model that fits the data”. This lends itself naturally to the Bayesian statistical analysis and the use of Bayes theorem:where P(M|D) represents the conditional probability of the model M, given the data D. In the case of multi-parameter fitting (including EXAFS) this can be rewritten as (see, for example²²):where w is the vector of parameter values. Models can then be compared by, for example, taking a ratio of their conditional probabilities P(w|D,M). This ratio of probabilities of two models (e.g. i and j) represents the odds ratio in favour of one model over the other:²³where I is prior information we have about the models. Using eqn (2) it is straightforward to show that:where BF_ij is the Bayes factor.²³ The ratio on the right hand side is the prior odds ratio of the two models and throughout this work we consider this to be unity (i.e. no preference of one model over another). Thus, to compare the models we need to compute P(D|M_i,I)—probability of the data given the model and prior information. However, expressions for P(D|M_i,I) can be rather complicated and for analysis involving many (in general correlated) parameters they include the evaluation of a multi-dimensional integral over the parameter space (the MLI – marginal likelihood integral). Assuming uniform top-hat priors and a Gaussian error distribution for independent identically distributed experimental data points gives (see for example,²³ p. 276):where _Δp_i are prior parameter ranges, n is the number of the data points, m is the number of the model parameters p = [p₁, p₂…p_m]^T and Cov_p is the parameter covariance matrix. Thus, although the Bayesian approach has already been demonstrated in application to EXAFS analysis^49,24 it has not been used to any significant extent, as far as we can tell, on account of its complexity. Indeed, parameter correlation is almost always the case in EXAFS and would normally require evaluation of the multidimensional integral in eqn (5). That can be addressed by constructing an orthonormal set of the model basis functions²³ (model parameters) so that the new parameters will have no correlation and hence the multidimensional integral can be replaced by the product of multiple single integrals. However, this would require redefining the problem in terms of the new (orthogonal) parameter set, repeating the fit and then back-transforming the new parameters to recover the original ones.

Here we propose a simple alternative FoM that requires only trivial modifications to the statistical procedures already existing in EXAFS analysis. We note that the multidimensional integral on the far right of the eqn (5) constitutes the volume in the parameter distribution space. We also note that Cov_p is symmetric positive definite, hence its diagonalization involves basis rotation. However, the volume (and also det(Cov_p)) does not change under rotation of the parameter space required for the transformation to the orthonormal basis. Hence, the following expression normally corresponding to the orthonormal parameter set can be used for calculation of P(D|M_i,I)—Bayes factor integral (BFI)—for a model with parameter correlations present:¹⁶

where Δp_i are the initial parameter ranges and L_max is the likelihood for the model. Thus defined BFI can then be used for model comparison (giving preference for a model with the larger value of BFI) following EXAFS data fitting without the need to redefine the problem in the new orthonormal parameter set. We call this BFI (rather than, for example, MLI) to distinguish from a more common case when the orthogonal parameter set is used to obtain eqn (6) (and therefore the Cov_p is a diagonal matrix). Crucially, the FoM in eqn (2) naturally incorporates the Occam factor:that accounts for parameter correlations as well as parameter ranges and provides a penalty for a model with significant parameter correlations and/or large initial parameter ranges (parameter uncertainty). However, since values of BFI can vary drastically, a more convenient way of evaluation is through comparison of ln(BFI) of the corresponding models. In such a case model evaluation is reduced to calculation of the ln(BFI) ratios—designated in this paper as ln(BF)—with the following scale^16,25 for ln(BF) values that differentiate between the models:

• <1 – barely worth considering,

• 1–2 – substantial,

• 2–5 – strong evidence,

• >5 – decisive.

We proceed below by testing this approach on a reference data set (crystalline Ge, c-Ge) before applying the procedure to the magic size clusters of CdS.

3 Results and discussion

3.1 The case of crystalline germanium

To verify the utility of BFI we first used the XAS data²⁶ for germanium collected at 12 K (the X-ray absorption spectrum is shown in Fig. 2). The data were selected on the account of their high quality. The structure of Ge at this temperature is well-established and has been verified by previous publications.^26–29 The data analysis was performed in Larch¹¹ for background removal, normalisation and the actual fitting of the models to the experimental data since we found Larch to provide the most comprehensive fitting statistics. Fig. 1 shows the EXAFS equation used to fit data where N is number of nearest neighbours, R is absorber–scatterer atom distance, S₀² is an amplitude reduction factor, σ² is Debye–Waller factor, F(k) is photoelectron scattering amplitude, λ(k) is photoelectron mean free path, and φ(k) is the phase shift. The latter three parameters (F(k), λ(k) and φ(k)) are calculated using the FEFF 9 code^30,31 and therefore are not refined.

Fig. 2 The Ge 12 K XAS spectrum used for fits.

Three structural models have been selected for comparison: (i) the actual structure of crystalline Ge at 12 K known to be a 4-coordinated face-centered diamond cubic type;^28,32 (ii) 6-coordinated high-pressure Ge phase VI structure (Cmma, model 2); (iii) 6-coordinated high pressure β-Sn structure of Ge³³ (I4/amd, models 3a, 3b). For model 3 two different refinements were carried out: one (model 3a) was for a single shell of 6 nearest neighbours, while for the other (model 3b) 3 shells of 2 atoms were used to reflect the actual nearest neighbour configuration in the β-Sn structure. This was also used to gauge the effect on the BFI of increasing the number of model parameters.

To enable a fair model comparison, for each model we only looked at the first peak in the R-space (corresponding to the GeGe bond length of 2.45 Å; the atomic shell structure beyond the first shell is very different in the three selected models) and we used single-scattering paths only (see Fig. 2). The data were fitted over the range of 2.00 Å⁻¹ < k < 22.93 Å⁻¹ in k-space (see Fig. 2). This ensured that only the first-shell EXAFS were fitted. Parameter ranges are given in Table 1 and are defined as follows. The amplitude reduction factor S₀² corrects for inelastic effects in the absorbing atom.³⁴ This is empirically established to be in the range 0.8–1, and is well-covered by 0.5 range. The shift in the edge position E₀ accounts for errors in experimental calibration and for empirical convention in determination of the absorption edge position^7,19—the range typically does not exceed 10 eV. Relative change in the nearest-neighbor interatomic distance ΔR is not expected to exceed 10% as the interatomic distances are determined by the covalent radii of elements and the pressure temperature conditions (as an example, 10% bond length variation is well above that expected on melting or under pressures as high as 10 GPa in a typical semiconductor material such as Ge²⁹). Mean squared relative displacements of atoms due to atomic vibrations σ² (and static disorder, if any) accounts for damping effects on χ(k). The initial value can be calculated using e.g. correlated Debye or Einstein approximations^35–37 and for c-Ge at 12 K this is around 0.003 Ų (ref. 26) hence the range of ±0.003 is selected to make it positive-definite. The number of nearest neighbours N was set according to the structural models and was not refined.

Table 1 Parameter ranges for all models

Parameter	Initial value	Range
S 0 ^2	0.9	0.5
E 0	0	10
ΔR	0	0.1
σ ^2	0.003	0.006

---

For model 1 (zinc blende structure), one single-scattering single-shell path was used to fit the spectrum. For model 2 (the high-pressure Cmma structure), the spectrum was fit with 3 single-scattering single-shell paths between (in total) 6 atoms in the first shell to describe the signal. For (β-Sn) model 3a, one single-scattering single-shell path was used at first, and then 3 single-scattering first shell paths were used (model 3b).

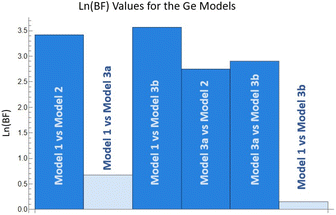
The summary of the results for the ln(BF) (the difference between ln(BFI) values) are shown in Fig. 3 and Table 2. One can see that model 1 is favoured over all other models except for 3a (the single path β-Sn fit): the ln(BF) between model 1 and all other models (except 3a) are found to be >3 providing strong evidence for model 1 being the preferred structure. The lnBF value between model 1 and 3a is 0.67 is slightly in favour of model 1 but not statistically significant according to the criteria outlined at the end of the previous section. However, the currently available fitting statistics FoMs found in the corresponding tables† favour other models: model 2 has lowest χ² and χ_ν², model 3b has the lowest value of R-factor, while AIC and BIC favour model 2 over model 1. This shows that reliance only on the currently used FoMs in EXAFS analysis can lead to an incorrect atomic structure model as the best solution. At the same time, we see that the BFI is able to deliver the correct result in this relatively complicated case – after all we used a single peak only in the EXAFS FT magnitude in order to differentiate between the models. Having verified the utility of the proposed BFI-based FoM in case of the reference system, in the next section we apply the Bayes approach to analysis of EXAFS of MSCs.

Table 2 Models and Ln(BF) values for the different Ge models

Model	Ln(BFI)
1	−6.65
2	−10.07
3a	−7.32
3b	−10.22

---

Fig. 3 Ln(BF) values for the Ge models.

3.2 Bulk CdS k-space fitting

Before proceeding on CdS MSCs we further tested the utility of the new FoM in k-space fitting of the bulk crystalline CdS. As reference data, bulk crystalline CdS EXAFS data at 90 K at Cd K-edge were fit in Larch.¹¹ The first shell (Cd–S scattering paths) in k-space was fit using several different structures respectively: a zinc blende (ZB), wurtzite (WZ),³⁸ NaCl-like³⁹ and cmcm sturcutres,⁴⁰ latter two being high-pressure derived structures.

K-Space noise (ε_k) was evaluated from the signal between 6.50 Å⁻¹ < k < 18.30 Å⁻¹ and the fit to the EXAFS data was carried out in the region 2.50 Å⁻¹ < k < 15.0 Å⁻¹, parameter ranges for the BFI calculations are shown in Table 3. The results of the fit are shown in the Table 4. The BFI-based FoMs support ZB and WZ structures significantly over the NaCl-like and cmcm models. This is consistent with our previous results where XPDF analysis of bulk CdS (and of regular CdS quantum dots) has shown CdS to be a mix of ZB and WZ structures.⁵

Table 3 Parameter values and ranges for all MSCs

Parameter	Initial value	Range
ΔR	0	0.1
E 0	0	10
S 0 ^2	0.9	0.5
σ ^2	0.006	0.006

---

Table 4 Ln(BFI) values for each model in the bulk CdS EXAFS fitting (1st shell)

Model	Ln(BFI)
ZB	−0.738
WZ	−1.31
NaCl-like	−2.04
cmcm	−2.31

---

3.3 Magic sized clusters

Magic sized clusters (MSCs) are ultra-small (<3 nm) colloidal semiconductor systems.⁴ They are materials of interest due to their monodisperse nature³ that suggests one can deliver atomic-level control of system size using colloidal synthesis route. Their atomic structure is still under debate as are the methods of their structural verification. One of the key challenges for the latter is the possibility for stable (and multiple meta-stable atomic arrangements) that are size- and temperature-dependent.^5,6,9

The MSCs under investigation in this work are CdS. These MSCs exhibit a sharp UV-vis absorption peak at 311 nm (MSC 311) but when heated to 60 °C (ref. 4) this peak shifts to 322 nm (MSC 322)⁶ and the shift is accompanied by atomic structure rearrangement as indicated by X-ray pair distribution function (xPDF) and XAS analysis.^5,6 Due to their small size leading to the lack of long-range order, establishing the atomic-level structure of MSCs is challenging⁴¹ and in this work we examine the sensitivity of our new EXAFS BFI-based FoM to the structural model selection. To this end we compared 4 models as candidates of possible structures of MSCs 311 and 322: (i) Cd₄₀S₁₉ with ZB structure, (ii) Cd₄₀S₂₀ with WZ structure, (iii) Cd₃₃S₃₂ β-Sn-like structure and (ii) Cd₃₇S₂₀ with an InP-like structure. The rationale for the model selection is as follows:

(i) Bulk CdS can possess WZ or ZB structure (while regular CdS quantum dots are known to exhibit both characters⁵). Hence, when constructing a model for an unknown atomic structure of MSCs, the atomic arrangement found in the bulk can be a starting point if there is no other information (this is frequently the case).

(ii) It has been observed²⁹ that average interatomic distances in small nanoparticles can be reduced compared to their bulk counterparts. This can be interpreted as an effective pressure on these systems. Such compression may results in distortion towards the β-Sn structure,⁴² hence it is reasonable to use it as one of the structural models.

(iii) It has recently been shown that an InP-like structure⁴³ provides the best fit to PDF⁵ data in CdS MSCs.

All clusters (except for InP-like cluster where the structure from our recent work^5,6 was used) have been cut as spherical regions of appropriate size from the corresponding bulk crystalline structure and were terminated with oxygen. This followed by the cluster geometry optimisation where we used two approaches: standard classical Universal Force Field⁴⁴ available in Avogadro⁴⁵ and via ab initio density functional theory methods using CP2K. In doing so we pursued two goals: comparison between classical and ab initio methods and evaluation of quantum effects in geometry relaxation in MSCs. Indeed, a number of recent investigations suggest that classical force fields may not always be appropriate in description of interatomic interactions in small nanoclusters⁴⁶ with some work showing sensitivity of local atomic dynamics in EXAFS to potential selection.⁴⁷ In the case of CP2K MOLOPT Cd basis set was used for Cd atoms (the excited atoms in the simulation) and for the S and O atoms a pseudo potential (DZVP-MOLOPT-GTH) was used. Again, since the InP-like structure has been experimentally obtained no further optimization was applied to it.

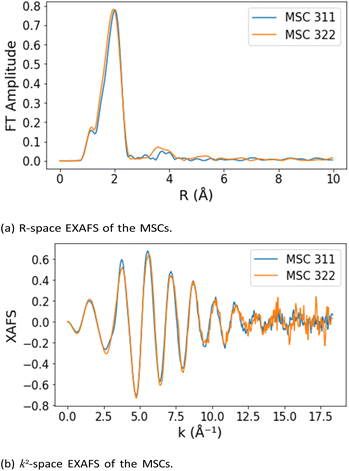
EXAFS data analysis has been carried out in Larch¹¹ and Mathematica 13.0 (for BFI calculations). The initial parameter values and their ranges for all models are given in Table 3 (if the standard errors returned by Larch exceed the half range set for _Δp_i terms, the range is corrected to 2 × standard error). While at low temperatures (90 K in our case) 3^rd cumulants for the atoms in the bulk of a nanoparticle are expected not to be significant, this may not be the case for the surface Cd–O coordination shell. The ln(BFI)s for and ln(BF)s between the candidate models were calculated using the same method as in the Ge model comparisons with the fits carried out in the range of 2–16 Å⁻¹, 2–14 Å⁻¹ for MSC 311 and 322 respectively. For the noise value used in EXAFS χ, χ_ν² calculations we used the standard deviation of the k space spectra for the MSC 311 and 322 data at 14.50–15 Å⁻¹ and 13–14 Å⁻¹ respectively, with scattering paths up to near 4 Å fitting up to the second peak in R-space corresponding to Cd–Cd scattering path close to 4 Å.

The results for ln(BFI) for relaxed model clusters for 311 and 322 MSCs are given in the Tables 5 and 6 below and summarised in Fig. 5 (where shades are used to differentiate between various structures according to the classification proposed at the end of the Methods section). One can see that for the MSC 311 and the models optimised with UFF it is ZB and InP-like models that fall within the category of “strong evidence” (i.e. ln(BF) > 2) with InP-like structure having slight advantage. The result is almost identical for DFT-based optimisation with ZB structure coming slightly on top in the ranking. For MSC 322 the results show the β-Sn-like structure being ranked the highest in both UFF and DFT cases (this is consistent with the results of our recent work⁶). We can also conclude, that both UFF and DFT-based geometry optimisations, although show small quantitative differences in model ranking, ultimately yield very similar results.

Table 5 MSC 311 Ln(BFI) results

Model	Ln(BFI)
(a) ln(BFI) values for UFF optimized models, MSC311.
Zinc blende	−3.0387
β-Sn	−4.2649
InP-like	−2.7893
Wurtzite	−5.0384
(b) ln(BFI) values for DFT optimized models, MSC311.
Zinc blende	−2.6579
β-Sn	−6.1064
InP-like	−2.7893
Wurtzite	−4.3887

---

Table 6 MSC 322 Ln(BFI) results

Model	Ln(BFI)
(a) ln(BFI) values for UFF optimized models, MSC322.
Zinc blende	−3.4749
β-Sn	−2.03393
InP-like	−3.8476
Wurtzite	−6.3588
(b) ln(BFI) values for DFT optimized models, MSC322.
Zinc blende	−3.9762
β-Sn	−2.8193
InP-like	−3.8476
Wurtzite	−5.2444

---

Thus, our findings indicate that the new FoM: (i) is pointing to the InP-like and ZB models as the most probable structures for MSC 311; (ii) pointing to β-Sn-like structure as a model for MSC 322; (iii) is detecting the difference between the EXAFS data of the two MSCs (as reflected in changing values of FoM and model preferences). This is a very significant finding considering the differences between the EXAFS signals for MSC 311 and 322 are very small (see Fig. 4) and the corresponding χ²-values are also quite close (see ESI†). The preference for InP-like structure for MSC 311, and for β-Sn-like for MSC 322 is consistent with our previous work^5,6 where it was shown to provide the best model to fit xPDF, EXAFS and XANES data. Thus, the result provide very strong support to using the new Bayesian FoM as a universal metric for model comparison and selection.

Fig. 4 MSC 311 and 322 data used for fits.

Fig. 5 Charts of the results for each MSC, darker colours indicate a higher statistical significance of the favoured model.

4 Conclusions

In this work we introduced the Bayesian-based statistical metric, the Bayes factor integral, for model comparison in EXAFS analysis. We showed for the first time that the new FoM provides a superior tool for model comparison in EXAFS by quantifying the intuitions about the parameter ranges and correlations through the Occam factor. We tested the new Bayesian FoM against reference EXAFS data for c-Ge and demonstrated that it is superior to the FoMs typically used in EXAFS analysis and reliably predicts the correct structure. In the process we showed that ignoring model parameter correlations may result in a selection of an incorrect structural model. We then applied the new FoM for the model comparison in analysis of MSCs where we demonstrated that it is sensitive to the differences between EXAFS signals of MSCs 311 and 322 and can point to the most probable structural models for these systems.

So far we utilised identical parameter ranges for all models of interest in all our tests (except for the range correction when the standard error ≥1/2Δp_i). Imposing model-specific constraints on parameter ranges routed in microscopic physics (e.g. from molecular-dynamics or ab initio simulations) in the calculation of BFI values should be an interesting direction to pursue. The results also show that the choice of cluster geometry optimization method has influence (albeit small) on the BFI-based model ranking—this should be a another avenue of study.

We note that the current approach is so far limited by the requirement of providing initial guess structures, while the ultimate goal of structural analysis of MSCs (and of nonperiodic/nanoscale systems in general) is developing new structural models for materials with unknown structures. Hence, further development of our approach should include automation of the BFI calculation to be used to inform model evolution in a variety of structure searching methods.^9,48

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

LH is grateful to Diamond Light Source and Queen Mary University of London for the joint studentship and funding to support this work.

References

1. K. Yu, Adv. Mater., 2012, 24, 1123–1132.
2. N. Kirkwood and K. Boldt, Nanoscale, 2018, 10, 18238–18248.
3. S. Kudera, M. Zanella, C. Giannini, A. Rizzo, Y. Li, G. Gigli, R. Cingolani, G. Ciccarella, W. Spahl, W. Parak and L. Manna, Adv. Mater., 2007, 19, 548–552.
4. B. Zhang, et al. , Nat. Commun., 2018, 9, 2499.
5. L. Tan, et al. , Nanoscale, 2019, 11, 21900–21908.
6. L. T. Ying Liu, et al. , Nanoscale, 2020, 12, 19325.
7. B. Ravel, Quantitative EXAFS Analysis, National Institute of Standards and Technology, 2015.
8. F. d'Acapito, Introduction to ab-initio methods for EXAFS data analysis, 2007.
9. L. Tan, C. J. Pickard, K. Yu, A. Sapelkin, A. J. Misquitta and M. T. Dove, J. Phys. Chem. C, 2019, 123, 29370–29378.
10. B. Ravel, Demeter Homepage, https://bruceravel.github.io/demeter/, 2006, [accessed 01/02/2023].
11. M. Newville, J. Phys.: Conf. Ser., 2013, 430, 012007.
12. K. C. Robben and C. M. Cheatum, J. Phys. Chem. B, 2021, 125, 12876–12891.
13. K. J. Hae, Korean J. Anesthesiol., 2019, 72, 558–569.
14. G. W. Stewart, Stat. Sci., 1987, 2, 68–84.
15. B. Ravel, 7.2. The heuristic happiness parameter, 2016, Accessed December 12, 2022. https://bruceravel.github.io/demeter/documents/Artemis/fit/happiness.html.
16. D. J. Dunstan, J. Crowne and A. J. Drew, Sci. Rep., 2022, 12, 993.
17. Y. Zhu, X. Wang, M. Liu, Y. Zhang, S. Zhang, G. Jiang, M. T. Dove, M. Zhang and K. Yu, Chem. Phys. Lett., 2021, 779, 138870.
18. E. A. Stern, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 9825–9827.
19. S. D. Kelly and B. Ravel, AIP Conf. Proc., 2007, 882 DOI:10.1063/1.2644451.
20. N. Binsted, M. T. Weller and J. Evans, Physica B: Condensed Matter, 1995, 208-209, 129–134.
21. P. Ghigna, M. Di Muri and G. Spinolo, J. Appl. Crystallogr., 2001, 34, 325–329.
22. D. J. C. MacKay, Neural Comput., 1991, 4, 415–447.
23. P. Gregory, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica® Support, Cambridge University Press, 2005.
24. H. J. Krappe and H. H. Rossner, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 184303.
25. R. E. Kass, A. E. Raftery and Bayes Factors, J. Am. Stat. Assoc., 1995, 90(430), 773–795.
26. A. V. Sapelkin and S. C. Bayliss, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 172104.
27. K. Takemura, Extended X-Ray Absorption Fine Structure Analysis of Crystalline Germanium at High Pressure, AGU Fall Meeting Abstracts, 2010ED41A-0622.
28. F. D. C. H. Bates and R. Roy, Science, 1965, 147, 860–862.
29. N. R. C. Corsini, et al. , Nano Lett., 2015, 15, 7334–7340.
30. J. J. Rehr, J. J. Kas, M. P. Prange, A. P. Sorini, Y. Takimoto and F. Vila, C. R. Phys., 2009, 10, 548–559.
31. M. Newville, FEFFIT: Using feff to model XAFS data, University of Chicago, 1998.
32. K. Takemura, U. Schwarz, K. Syassen, M. Hanfland, N.E. Christensen, D.L. Novikov and I. Loa, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(16), R10603–R10606.
33. T. K. Takemura, U. Schwarz, K. Syassen, N.E. Christensen, M. Hanfland, D.L. Novikov and I. Loa, Phys. Status Solidi B, 2001, 223, 385–390.
34. G. Bunker, Introduction to XAFS: A Practical Guide to X-ray Absorption Fine Structure Spectroscopy, Cambridge University Press, 2010, pp. 127–128.
35. I.-K. Jeong, R. H. Heffner, M. J. Graf and S. J. L. Billinge, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 67, 104301.
36. E. Sevillano, H. Meuth and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 4908–4911.
37. T. S. Tien, N. Van Nghia, C. S. Thang, N. C. Toan and N. B. Trung, Solid State Commun., 2022, 353, 114842.
38. C.-Y. Yeh, Z. W. Lu, S. Froyen and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 10086–10097.
39. H. Sowa, Solid State Sci., 2005, 7, 73–78.
40. H. Chen, Y. Zhu and B. Wu, Phys. B, 2011, 406, 4052–4055.
41. S. J. L. Billinge and I. Levin, Science, 2007, 316, 561–565.
42. N. R. C. Corsini, et al. , Nano Lett., 2015, 15, 7334–7340.
43. D. C. Gary, S. E. Flowers, W. Kaminsky, A. Petrone, X. Li and B. M. Cossairt, J. Am. Chem. Soc., 2016, 138(5), 1510–1513.
44. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
45. M. D. Hanwell, D. E. Curtis and D. C. Lonie, J Cheminform., 2012, 4, 17.
46. J. Timoshenko, Z. Duan, G. Henkelman, R. Crooks and A. Frenkel, Annu. Rev. Anal. Chem., 2019, 12, 501–522.
47. L. A. Mistryukova, N. P. Kryuchkov, V. N. Mantsevich, A. V. Sapelkin and S. O. Yurchenko, Phys. Rev. B, 2021, 104, 054108.
48. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
49. K. V. Klementev, J. Phys. D: Appl. Phys., 2001, 34, 15.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05110b

---