New approach for predicting crystal densities of energetic materials

Abstract

Predicting crystal density of energetic materials accurately critically impacts assessment of their detonation potential, with higher density directly improving energetic performance. This new approach will help in density prediction to enable accelerated computational material discovery. By refining Politzer's approach using rigorously validated B3LYP quantum calculations and Multiwfn's precise structural elucidation, our optimized protocol substantially enhances predictive accuracy, marking a significant leap over traditional approaches. This streamlined and efficient framework spearheads high-fidelity virtual screening to transformatively expedite the development of novel, potent energetic candidates. Moreover, this research accentuates the decisive impact of refined computational techniques on elucidating structure–property relationships early-on, paving the way to accelerated development of promising energetic materials. Future work may concentrate on expanding training datasets to further improve model robustness and computational efficiency. Overall, this transformative density prediction workflow delivers a more precise approach to fundamentally advanced energetic material innovation.

---

The pursuit of novel energetic materials is an intricate process encompassing design, synthesis, characterization, testing and scale-up, amounting to a costly R&D endeavour. Heightened costs stem from the advanced techniques required to safely design powerful yet stable explosives, hindering rapid advancements. Therefore, the scientific community has increasingly embraced computationally efficient quantum mechanics (QM) protocols offering expedited and economic performance estimates to help accelerate development while reducing dangers with a focus on structure–property evaluations. QM methods particularly excel at predicting critical detonation attributes through virtual screening, minimizing risky experiments. Specifically, QM methods can efficiently predict key detonation and propulsion figures-of-merit like density, enthalpy of formation, detonation pressures and velocities that enable preliminary screening.^1–3 When applied to density predictions, the computed density of prospective materials strongly informs detonation performance assessments, underpinning shock wave propagation and blast efficiency. Structure–density relationships quantify how intermolecular packing impacts bulk density values, although traditional divisions of molecular weight by molar volume overlook these interactions. Pioneering works derived structure-density links by correlating electrostatic potentials with statistical variance measures.^4,5 Extending this foundation through recent sophisticated improvements, approaches by Willer and coworkers,⁶ Pan-Lee,⁷ Rice-Byrd⁸ and Kim and coworkers,⁹ Keshavarz and coworkers¹⁰ and Klapötke and coworkers¹¹ have been introduced. Later, Ghule and coworkers compared the experimental densities with the densities obtained from these approaches¹² and found that the Politzer and Rice approaches give calculated values for density which are closer to the experimental densities. However, opportunities for enhanced predictive precision remain. This new approach suggests a refined density prediction model delivering noticeably improved accuracy through targeted reparameterization of Politzer's approach (Fig. 1). By incorporating contemporary density functional theory and multi-scale simulations, our density estimates excel preceding methods in reliability. The optimized protocol pioneers a simulation toolkit to further innovation in high-energy materials discovery.

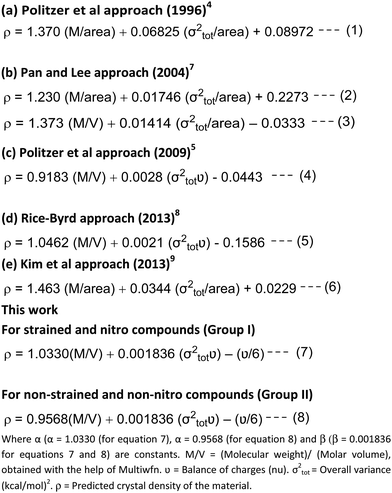Fig. 1 Recently developed methods and the present work.^4,5,7–9

Inspired by these approaches, we have further extended Politzer's approaches^4,5 for predicting crystal density more precisely using the B3LYP/6-311++G(d,p) level of DFT¹³ selected for its accurate portrayal of intermolecular interactions pivotal for density models (eqn (7) and (8)). Optimization and frequency analysis were pursued using the Gaussian 03 suite to ensure that the obtained structures represent true local minima.¹⁴ Subsequently, Multiwfn enabled rigorous quantitative elucidation of electron densities and molecular surfaces to derive electrostatic potentials (ESPs) for density prediction.¹⁵

Molecules were strategically selected based on the availability of reliable crystal density characterizations in the literature. Most studied compounds hold distinction in energetic materials, supplemented by recent publications.^16–31 For optimal density predictions, these are classified into two groups – strained or nitro-containing compounds (Group I, Schemes 1 and 2), and non-strained aliphatic/aromatic hydrocarbons (Group II, Scheme 3) based on their distinct intermolecular interaction profiles. These bespoke classification schemes account for variances in packing interactions, working to improve predictive accuracy.

Scheme 1 Group I (crystal density predicted using eqn (7)): (a) polycyclic strained/nitro compounds.

Scheme 2 Group I (crystal density predicted using eqn (7)): (b) polynitro compounds.

Scheme 3 Group II (crystal density predicted using eqn (8)): hydrocarbon and compounds without nitro group.

Crystal densities of compounds 1–24 (Schemes 1 and 2) were computed via eqn (7), selected specifically for strained and nitro-containing systems where intermolecular interactions substantially influence density. For non-strained aliphatic/aromatic hydrocarbons (compounds 25–36, Scheme 3), eqn (8) was pursued to account for their distinct packing effects.

For benchmarking, densities were additionally predicted using the preceding eqn (1), (2) and (4)–(6) established in the literature (Fig. 1).^4–8 These comparative results are tabulated in Tables 1 and 2 and depicted in Fig. 2–5.

Table 1 Comparison of crystal densities of compounds 1–24 (Group I) determined by our approach and using eqn (1), (2) and (4)–(6)

Compound	υ	M/V^b	υ × σtot^2^c	β × υ × σtot^2 ^d	ρ	ρ (Lit.)	Δ	ρ (eqn (1))	ρ (eqn (2))	ρ (eqn (4))	ρ (eqn (5))	ρ (eqn (6))
a υ = balance of charges (nu). b M/V = (molecular weight)/(molar volume), obtained with the help of Multiwfn. c Product of σtot^2 (overall variance kcal mol^−2) and υ (balance of charges). d Product of σtot^2 (overall variance kcal mol^−2), υ (balance of charges) and β. e ρ = crystal density of the material predicted according to eqn (7). f ρ (Lit.) = experimental crystal density. g Δ = difference between experimental crystal density and crystal density predicted according to eqn (7). h ρ (eqn (1)) = predicted crystal density according to eqn (1). i ρ (eqn (2)) = predicted crystal density according to eqn (2). j ρ (eqn (4)) = predicted crystal density according to eqn (4). k ρ (eqn (5)) = predicted crystal density according to eqn (5). l ρ (eqn (6)) = predicted crystal density according to eqn (6). α = 1.0330 and β = 0.001836 are constants.
1	0.0584	1.9601	13.9932	0.025691625	2.0407	2.0400	0.0007	1.9763	1.8972	1.7948	1.9214	2.0165
2	0.1758	1.8792	27.6664	0.050795492	1.9626	1.9850	−0.0223	1.8020	1.7383	1.7588	1.8655	1.8283
3	0.1089	1.8821	22.0477	0.040479687	1.9665	1.9590	0.0075	1.9986	1.9194	1.7457	1.8567	2.0423
4	0.1716	1.7897	29.4705	0.054107856	1.8742	1.8130	0.0612	1.9036	1.8350	1.6816	1.7756	1.9416
5	0.0943	1.7773	20.5503	0.037730516	1.8579	1.8140	0.0439	1.6467	1.5916	1.6453	1.7439	1.6561
6	0.0302	2.0004	4.8985	0.008993664	2.0703	1.9790	0.0913	2.0438	1.9664	1.8063	1.9445	2.0962
7	0.1143	1.2317	0.7875	0.001445813	1.2547	1.2900	−0.0352	1.0827	1.1159	1.0889	1.1316	1.0807
8	0.0092	2.2766	1.3556	0.002489028	2.3526	2.4290	−0.0763	1.9046	1.8306	2.0500	2.2260	1.9381
9	0.1397	1.7276	25.9716	0.047683894	1.8090	1.8300	−0.0209	1.5716	1.5154	1.6148	1.7033	1.5682
10	0.1273	1.7291	27.2892	0.050103045	1.8150	1.8100	0.0050	1.6081	1.5483	1.6199	1.7076	1.6073
11	0.1340	1.7690	33.0870	0.060747842	1.8657	1.9100	−0.0442	1.7599	1.6903	1.6728	1.7616	1.7744
12	0.2085	1.6404	22.4788	0.041271132	1.7010	1.6500	0.0510	1.5244	1.4946	1.5250	1.6047	1.5368
13	0.1979	1.7158	36.2283	0.066515159	1.8059	1.7800	0.0259	1.6192	1.5732	1.6327	1.7125	1.6322
14	0.2490	1.5677	26.7377	0.049090527	1.6270	1.5700	0.0570	1.4166	1.3906	1.4701	1.5376	1.4153
15	0.1372	1.7310	34.9834	0.064229596	1.8294	1.8560	−0.0265	1.6215	1.5578	1.6432	1.7258	1.6194
16	0.1815	1.6904	84.0449	0.154306495	1.8702	1.8900	−0.0197	1.6294	1.4726	1.7433	1.7863	1.5468
17	0.2468	1.7185	63.4310	0.116459334	1.8505	1.8340	0.0165	1.6113	1.5427	1.7114	1.7725	1.6032
18	0.1399	1.6509	20.1076	0.036917535	1.7189	1.6970	0.0219	1.5701	1.5441	1.5280	1.6107	1.5930
19	0.1820	1.7559	27.2569	0.050043700	1.8335	1.7670	0.0665	1.6093	1.5629	1.6444	1.7357	1.6205
20	0.0465	1.9699	6.1808	0.011347894	2.03850	2.0070	0.0315	1.8477	1.7898	1.7819	1.9152	1.8864
21	0.0836	1.9774	13.9262	0.025568522	2.0542	2.0060	0.0482	1.7385	1.6849	1.8105	1.9394	1.7637
22	0.1792	1.8882	41.7622	0.076675454	1.9973	1.9990	−0.0016	1.7522	1.6811	1.8065	1.9045	1.7642
23	0.1434	1.8509	24.1799	0.044394443	1.9324	1.9020	0.0304	1.7002	1.6416	1.7230	1.8285	1.7149
24	0.0446	1.8882	13.8161	0.025366341	1.9684	1.9400	0.0284	1.7659	1.6807	1.7283	1.8458	1.7677

---

Table 2 Comparison of crystal densities of compounds 25–36 (Group II) determined by our approach and using eqn (1), (2) and (4)–(6)

Compound	υ	M/V^b	υ × σtot^2^c	β × υ × σtot^2^d	ρ	ρ (Lit.)^f	Δ	ρ (eqn (1))	ρ (eqn (2))	ρ (eqn (4))	ρ (eqn (5))	ρ (eqn (6))
a υ = balance of charges (nu). b M/V = (molecular weight)/(molar volume), obtained with the help of Multiwfn. c Product of σtot^2 (overall variance kcal mol^−2) and υ (balance of charges). d Product of σtot^2 (overall variance kcal mol^−2), υ (balance of charges) and β. e ρ = crystal density of the material predicted according to eqn (8). f ρ (Lit.) = experimental crystal density. g Δ = difference between experimental crystal density and crystal density predicted according to eqn (7). h ρ (eqn (1)) = predicted crystal density according to eqn (1). i ρ (eqn (2)) = predicted crystal density according to eqn (2). j ρ (eqn (4)) = predicted crystal density according to eqn (4). k ρ (eqn (5)) = predicted crystal density according to eqn (5). l ρ (eqn (6)) = predicted crystal density according to eqn (6). α = 0.9568 and β = 0.001836 are constants.
25	0.0554	0.6218	0.3596	0.000660	0.5863	0.5170	0.0693	0.4795	0.5595	0.5277	0.4927	0.4235
26	0.0210	1.9500	0.5871	0.001078	1.8633	1.8230	0.0403	1.6517	1.6217	1.7480	1.8827	1.6839
27	0.0935	0.7484	0.4235	0.000778	0.7012	0.6900	0.0072	0.5855	0.6659	0.6441	0.6252	0.5466
28	0.1047	1.2332	32.9179	0.060437	1.2229	1.2300	−0.0071	1.2687	1.1096	1.1803	1.2007	1.1272
29	0.2456	1.2545	44.8608	0.082364	1.2417	1.2660	−0.0242	1.1445	1.0410	1.2333	1.2480	1.0322
30	0.2483	1.1979	87.9804	0.161532	1.2662	1.2600	0.0062	1.3910	1.0509	1.3020	1.2794	1.1098
31	0.2380	1.0846	8.9239	0.016384	1.0144	1.0160	−0.0015	0.9634	0.9906	0.9766	0.9948	0.9374
32	0.1358	0.9770	0.4493	0.000825	0.9129	0.8560	0.0569	0.8854	0.9400	0.8541	0.8644	0.8711
33	0.1911	1.7574	7.6850	0.014110	1.6637	1.6540	0.0097	1.5236	1.5034	1.5910	1.6961	1.5443
34	0.1966	1.3230	8.0502	0.014780	1.2478	1.2250	0.0228	1.1697	1.1810	1.1931	1.2424	1.1622
35	0.1929	1.2031	27.9871	0.051384	1.1703	1.1550	0.0153	1.1375	1.1005	1.1388	1.1588	1.0825
36	0.2494	1.3131	40.9579	0.075199	1.2900	1.3220	−0.0320	1.2406	1.2017	1.2762	1.3011	1.2002

---

Fig. 2 Plots of predicted crystal densities using our approach (eqn (7)) versus literature value calculated using eqn (1), (2) and (4)–(6).

Fig. 3 Plots of predicted crystal densities using our approach (eqn (8)) versus literature value calculated using eqn (1), (2) and (4)–(6).

Fig. 4 Difference in crystal densities of compounds 1–24 determined using eqn (1), (2) and (4)–(7) and experimental values.

Fig. 5 Difference in crystal densities of compounds 25–36 determined using eqn (1), (2), (4)–(6) and (8) and experimental values.

A good comparison of the results produced by eqn (1), (2), and (4)–(8) suggests that by refining Politzer's approach using rigorously validated B3LYP quantum calculations and Multiwfn's precise structural elucidation, our protocol substantially enhances predictive accuracy involving the individual contributions of ν/6, marking a significant leap over traditional approaches as listed in Tables 1 and 2, Fig. 2–5 and Tables S15 and S16 (ESI‡).

Conclusions

This study revealed that the predictions of the crystal density of organic compounds could be significantly improved by strategically modifying Politzer's approach. Compounds were categorized into two classes (Group I and Group II) based on the presence/absence of strain and nitro functionalities to optimize model parameters for these distinct chemical spaces. The universal constants α, β, and γ were replaced by 1.0330, 0.001836, and ν/6 specifically for Group I compounds, whereas values of 0.9568, 0.001836, and ν/6 were utilized for Group II systems. Notably, substituting γ with ν/6 to capture intrinsic charge differences between materials delivered superior density predictions over all preceding methods. This work not only enhances predictive accuracy, but pioneers a broadly applicable platform to accelerate the discovery of novel, high-performance energetic candidates.

S. L. investigation, methodology, conceptualization and manuscript writing. H. G. manuscript writing – review and editing. J. M. S. conceptualization, manuscript writing – review and editing, supervision.

Data availability

All data relevant to the work described here are available in the ESI,‡ or from the current literature.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We are grateful for the support from the Fluorine-19 fund.

Notes and references

1. J. P. Agrawal and R. D. Hodgson, Organic chemistry of explosives, John Wiley & Sons, Ltd, Chichester, 2007, p. 243.
2. (a) T. M. Klapötke, Chemistry of high-energy materials, De Gruyter, Berlin, 2nd edn, 2012; (b) S. Lal, H. Gao and J. M. Shreeve, Design and computational insight into two novel CL-20 analogues, BNMTNIW and BNIMTNIW: high performance energetic materials, New J. Chem., 2022, 46, 16693–16701.
3. (a) H. Gao and J. M. Shreeve, Azole-Based Energetic Salts, Chem. Rev., 2011, 111, 7377–7436; (b) L. Mallick, S. Lal, S. Reshmi, I. N. N. Namboothiri, A. Chowdhury and N. Kumbhakarna, Theoretical studies on the propulsive and explosive performance of strained polycyclic cage compounds, New J. Chem., 2017, 41, 920–930.
4. J. S. Murray, T. Brinck and P. Politzer, Relationships of molecular surface electrostatic potentials to some macroscopic properties, Chem. Phys., 1996, 204, 289–299.
5. P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro-Labbe, An electrostatic interaction correction for improved crystal density prediction, Mol. Phys., 2009, 107, 2095–2101.
6. R. L. Willer, Calculation of the density and detonation properties of C, H, N, O and F compounds: use in the design and synthesis of new energetic materials, J. Mex. Chem. Soc., 2009, 53, 108–119.
7. J.-F. Pan and Y.-W. Lee, Crystal density prediction for cyclic and cage compounds, Phys. Chem. Chem. Phys., 2004, 6, 471–473.
8. B. M. Rice and E. F. Byrd, Evaluation of electrostatic descriptors for predicting crystalline density, J. Comput. Chem., 2013, 34, 2146–2151.
9. C. K. Kim, S. G. Cho, C. K. Kim, M.-R. Kim and H. W. Lee, Prediction of physicochemical properties of organic molecules using semi-empirical methods, Bull. Korean Chem. Soc., 2013, 34, 1043–1046.
10. M. H. Keshavarz, H. Soury, H. Motamedoshariati and A. Dashtizadeh, Improved method for prediction of density of energetic compounds using their molecular structure, Struct. Chem., 2014, 2, 455–466.
11. S. Wahler and T. M. Klapötke, Research output software for energetic materials based on observational modelling 2.1 (RoseBoom2.1©), Mater. Adv., 2022, 3, 7976–7986.
12. (a) A. Nirwan, A. Devi and V. D. Ghule, Assessment of density prediction methods based on molecular surface electrostatic potential, J. Mol. Model., 2018, 24, 166; (b) P. Politzer and J. S. Murray, Electrostatic potentials at the nuclei of atoms and molecules, Theor. Chem. Acc., 2021, 140, 7; (c) F. A. Bulat, A. T. Labbé, T. Brinck, J. S. Murray and P. Politzer, Quantitative analysis of molecular surfaces: areas, volumes, electrostatic potentials and average local ionization energies, J. Mol. Model., 2010, 16, 1679–1691.
13. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. L. Caricato, X. H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Revision D.01 ed., Gaussian, Inc., Wallingford, CT, 2003.
15. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
16. J. V. Viswanath, K. J. Venugopal, N. V. S. Rao and A. Venkataraman, An overview on importance, synthetic strategies and studies of 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (HNIW), Def. Technol., 2016, 12, 401–418.
17. V. T. Ramakrishnan, M. Vedachalam and H. Boyer, 10-Dinitro-2,6,8,12-tetraoxa 4,10-diazatetracyclo[5.5.0.05,9.03,11] dodecane, Heterocycles, 1990, 31, 179–180.
18. J. Zhang, T. Hou, L. Zhang and J. Luo, 2,4,4,6,8,8-Hexanitro-2,6-diazaadamantane: A High-Energy Density Compound with High Stability, Org. Lett., 2018, 20, 7172–7176.
19. T.-J. Hou, H.-W. Ruan, G.-X. Wang and J. Luo, 2,4,4,8,8-Pentanitro-2-Azaadamantane: A High-DensityEnergetic Compound, Eur. J. Org. Chem., 2017, 6957–6960.
20. K. A. Lukin, J. Li, P. E. Eaton, N. Kanomata, J. Hain, E. Punzalan and R. Gilardi, Synthesis and chemistry of 1,3,5,7-tetranitrocubane including measurement of its acidity, formation of-nitro anions, and the first preparations of pentanitrocubane and hexanitrocubane, J. Am. Chem. Soc., 1997, 119, 9591–9602.
21. K. F. Biegasiewicz, J. R. Griffiths, G. P. Savage, J. Tsanaktsidis and R. Priefer, Cubane: 50 years later, Chem. Rev., 2015, 115, 6719–6745.
22. M. Sugiyama, M. Akiyama, Y. Yonezawa1, K. Komaguchi, M. Higashi, K. Nozaki1 and T. Okazoe, Electron in a cube: synthesis and characterization of perfluorocubane as an electron acceptor, Science, 2022, 377, 756–759.
23. T. G. Archibald, R. Gilardi, K. Baum and C. George, Synthesis and X-ray crystal sructure of 1,3,3-trinitroazetidine, J. Org. Chem., 1990, 55, 2920–2924.
24. S. Lal, R. J. Staples and J. M. Shreeve, FOX-7 derived nitramines: Novel propellants and oxidizers for solid rocket propulsion, Chem. Eng. J., 2023, 468, 143737.
25. S. Lal, R. J. Staples and J. M. Shreeve, Design and synthesis of high-performance planar explosives and solid propellants with tetrazole moieties, Org. Lett., 2023, 27, 5100–5104.
26. W. Huang, Y. Tang, G. H. Imler, D. A. Parrish and J. M. Shreeve, Nitrogen-Rich tetrazolo[1,5-b] pyridazine: promising building block for advanced energetic materials, J. Am. Chem. Soc., 2020, 142(7), 3652–3657.
27. S. Lal, R. J. Staples and J. M. Shreeve, Design and synthesis of phenylene-bridged isoxazole and tetrazole-1-ol based energetic materials of low sensitivity, Dalton Trans., 2023, 52, 3449–3457.
28. Q. Yu, P. Yin, J. Zhang, C. He, G. H. Imler, D. A. Parrish and J. M. Shreeve, Pushing the limits of oxygen balance in 1,3,4-oxadiazoles, J. Am. Chem. Soc., 2017, 139, 8816–8819.
29. W. Zhang, Y. Yang, Y. Wang, T. Fei, Y. Wang, C. Sun and S. Pang, Challenging the limits of the oxygen balance of a pyrazole ring, Chem. Eng. J., 2023, 451, 138609.
30. S. Lal, R. J. Staples and J. M. Shreeve, Energetic performance of trinitromethyl nitrotriazole (TNMNT) and its energetic salts, Chem. Commun., 2023, 59, 11276–11279.
31. S. Lal, R. J. Staples and J. M. Shreeve, Trinitromethyl-triazolone (TNMTO): a highly dense oxidizer, Dalton Trans., 2023, 52, 12341–12346.

---

Footnotes

† Dedicated to Professor Peter Politzer for his invaluable contribution to theoretical and computational chemistry.

‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nj01774a

---