Rate-enhancing PETase mutations determined through DFT/MM molecular dynamics simulations

Abstract

The PETase enzyme from the bacterium Ideonella sakaiensis can degrade polyethylene terephthalate (PET) back into its polymeric constituents at room temperature, making it an ecologically friendly tool for reducing PET pollution. Computational enzyme optimization is a fundamental tool to accelerate enzyme engineering towards the “green revolution” promised by the introduction of enzymatic catalysis in industry. The Asp83Asn mutant generates a sub-optimal reactive conformation that the mutation-induced transition state stabilization does not compensate for, and the barrier is raised by 1.9 kcal mol⁻¹. In contrast, the Asp89Asn mutant keeps a perfect reactive conformation, and the mutation stabilizes the transition state more than the reactants, lowering the barrier by 4.7 kcal mol⁻¹. We show that computer-based well-chosen single-residue substitutions in PETase can decrease the activation barrier significantly, facilitating the development of highly-efficient PETase mutants. The results of this work encourage future studies that aim for rational enzyme engineering on PETase and other enzymes.

---

1. Introduction

Computational simulations are widely used to determine enzyme reaction mechanisms with atomic detail.^3–9 Computational enzyme engineering is a logical step forward, as computer simulations can predict the effect of mutations in the reaction mechanism and rate-limiting barriers, helping to improve the catalytic efficiency of enzymes.^3,5,10–15 After two decades of methodologic development, assisted by increasing computer power, enzyme improvement and refinement increasingly rely on computational chemistry. Many computational tools are currently being automated to create promising and chemically realistic mutant candidates, complementing the experimental methodologies.^15–18

Current developments in enzyme engineering of PETase

Biodegradation of polyethylene terephthalate through enzymatic action is an excellent way to recycle this widely used polyester. Several PET hydrolases have been identified and characterized,^19–21 namely the IsPETase and IsMHETase enzymes from the bacterium Idonella Sakaiensis, which convert PET into its monomers,²² are particularly interesting.

Several studies have revealed the catalytic mechanism of PET degradation by IsPETase and created IsPETase mutants with improved catalytic activity, often assisted by docking and, more rarely, molecular dynamics calculations. Han et al.² performed site-directed mutagenesis experiments that identified the Ser-His-Asp catalytic triad; Austin et al.²³ narrowed the binding cleft of PETase by mutating two active site residues (S238F/W159H) for the corresponding residues in the homologous cutinases F209 and H129, producing a double mutant with a 3.8-fold improved PET degradation activity due to an increased binding affinity to the substrate; Joo et al.²⁴ observed that substituting Arg280 with a small hydrophobic residue (IsPETase^R280A) resulted in a more stable enzyme:substrate complex, able to bind longer substrates, such as PET film, and with increased PET degradation activity by 22.4% in 18 h and 32.4% in 36 h when PET film was used as the substrate; Ma et al.²⁵ focused on six critical residues around the substrate-binding groove to create novel high-efficiency PETase mutants through protein engineering, ultimately producing a mutant in which the K_m of the mutant enzyme was reduced by 3.8 times, while the k_cat/K_m value was 15.6-fold higher than the wild type.

The low thermal stability of IsPETase is another limitation for efficient PET degradation. Son et al.²⁶ used several IsPETase mutants screened for high thermal stability and improved PET degradation activity. Mutations at the β6–β7 connecting loop and the binding site generated a triple mutant variant IsPETase (S121E/D186H/R208A) that increased the melting temperature (T_m) value by 8.8 °C, and extended its activity for five days relatively to the wild type (which loses activity within a day).²⁶ Cui et al.¹⁵ have modeled a robust IsPETase through computational redesign using the greedy accumulated strategy for protein engineering (GRAPE). The resulting IsPETase exhibited a drastically higher melting temperature (by 31 °C) than the wild-type and strikingly enhanced degradation of PET over 300-fold towards 30% semicrystalline PET films at mild temperatures. Recently Bell et al.,²⁷ created a thermostable IsPETase variant (HotPETase, T_m = 82.5 °C) that can function at PET's glass transition temperature, using directed evolution. HotPETase could selectively deconstruct the PET component of a laminated multimaterial and depolymerize semicrystalline PET more quickly than previously reported PETases. In addition, Avilan et al. demonstrated that while mesophilic IsPETase variants often showed concentration-dependent inhibition, such inhibition could not be observed in the extremely thermostable HotPETase.²⁸

In conclusion, many PET engineering studies confirmed the possibility of fine-tuning the properties of PETases in general, and IsPETase in particular, towards an increase in enzyme efficiency and thermal stability.

The PETase substrate-binding and reaction mechanism has been widely studied experimentally and computationally.^2,24,29 Han et al.²⁰ and Chen et al.¹ proposed that PETase follows cutinases' classical hydrolysis reaction mechanism, an acylation/deacylation process conducted by a catalytic triad formed by Ser131-His208-Asp177. In the acylation stage, the His208-Asp177 interaction promotes a proton shuttle that activates the Ser131, generating an alkoxide nucleophile that attacks the carbonyl carbon of the scissile ester bond, forming an acyl–enzyme intermediate (Scheme 1). In the deacylation stage, a nucleophilic attack performed by a water molecule completes the cleavage of the ester bond of the acyl–enzyme intermediate via a second tetrahedral intermediate. Finally, the product is released, and the enzyme is regenerated. The backbone NH groups of Tyr58 and Met132 form an oxyanion hole that stabilizes the transition states, increasing enzyme activity.^2,24 Additionally, in the crystal structure of PETase (PDB ID: 5XH3), Trp156, a residue close to the active site and often referred to as the wobbly tryptophan, can adopt three different conformations, but substrate binding is only favored when the conformation of Trp156 allows the formation of T-stacking interactions between its indole sidechain and the benzene moiety of the acylated PET region.^1,2 The high flexibility of this residue enables the formation of π-stacking interactions that contribute to the stabilization of the substrate near the catalytic residues. After the ester bond cleavage, the product is rotated, pulled away, and released from the active center. Recently, the hydrolysis mechanism for PET degradation by IsPETase has been characterized using QM/MM molecular dynamics (MD) simulations and adiabatic mapping QM/MM.^30–33 The computational studies corroborated, in general, the proposal shown in Scheme 1. However, there is still controversy about the mechanism's fine details, as both a concerted and a stepwise mechanism with a short life intermediate were observed in different computational studies.^30–33 Nevertheless, the computations made at the highest level support a mechanism with single acylation and deacylation steps, each mediated by a tetrahedral transition state.^30–33 From a mechanistic perspective, the difference might seem irrelevant. However, for enzyme optimization, the accurate characterization of the rate-limiting transition state is critical to the success of the mutant predictions.

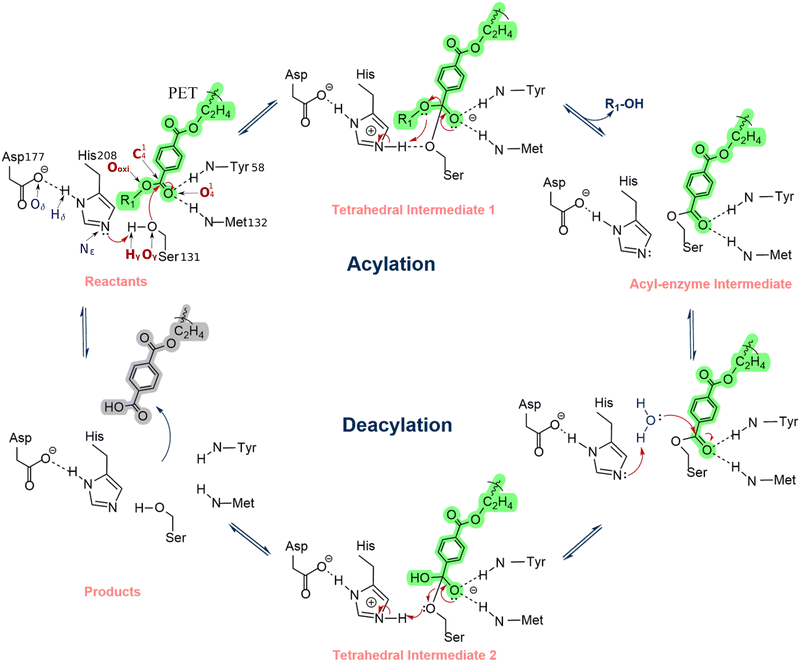Scheme 1 Reaction mechanism of PETase proposed by Han et al. and Chen et al.^1,2

Our previous simulations showed that the transition state (TS) of the acylation step (refer to Scheme 1) is rate-limiting.³³ Therefore, enzyme mutants that increase the reaction rate should facilitate the rearrangement of electron density at this step.^34,35 Accordingly, the electron density rearrangement between the reactant state and TS was analyzed. Two areas were particularly affected: an area centered at the PET dimer O₄¹ that became negative at the TS and an area centered at the protonated imidazole of His208 that became positive at the TS. Both regions were essentially neutral in the reactant state.

The substrate O₄¹ and the hydrogen that was transferred from Ser131 to His208 (H_ϒ in Scheme 1) were used as a positional reference for the two charge zones mentioned above (the salt bridge with Asp177 shields the interactions with the Hδ). These atoms were taken as a reference to identify charged residues within a 10 Å radius.

The transition state stabilizing macrodipole model takes advantage of the charge rearrangements between the reactant and the TS. If a positive residue is closer to the substrate O₄¹ than the His208 imidazole, it stabilizes the TS more than the reactant state and reduces the activation barrier.^35,36 On the other hand, if it is closer to the His208 imidazole than O₄¹, it stabilizes the reactant more than the TS, increasing the barrier. Negative residues decrease the barrier when they are closer to the His208 imidazole than O₄¹ and raise the barrier if they are closer to O₄¹ than the His208 imidazole. We carried out this analysis in our previous work,³³ and we identified Asp83 and Asp89 as residues that potentially increase the rate-limiting barrier, the reason why they have been considered for mutagenesis, specifically by Asn residues, to introduce the minimal perturbation that still eliminates their negative charge.

The electrostatic analysis described above is done considering the distances of the residues to the reference atoms in the wild-type enzyme. It is strictly valid under the assumption that the enzyme structure is kept after the introduction of mutations.³⁵ Nevertheless, if the mutations introduce local or global changes in the enzyme structure, the stabilization/destabilization tendencies can change, and some predictions may not materialize. Even though this is not very problematic within an enzyme optimization strategy, which is prepared to accommodate a significant attrition rate (i.e., testing many more mutations than the ones that finally work), it is desirable to maximize the prediction accuracy and minimize the attrition rate. Therefore, this paper explored the effect of two proposed mutations, incorporating the potential for (at least) local, sub-microsecond enzyme reorganization by simulating the mutants with classical MM and the rate-limiting acylation step with PBE/MM MD simulations. As the charge redistribution from the intermediate to the TS of the deacylation process is equivalent to that during the acylation step, similar electrostatic forces are likely at work throughout both steps. Therefore, it is very likely that the reaction barrier for the (non-rate limiting) deacylation process should also be favored by the mutations.

In addition, the study solidifies strategies for enzyme optimization in general and PETase optimization in particular.

2. Results and discussion

Molecular dynamics of the wild type and mutant PETases: Mutations at specific sites, namely accounting for conserved residues, may induce changes in the structure and function of a protein. The residues mutated in this work (Asp83 and Asp89) are located in flexible loops far from the binding and active site, as shown in Fig. 1; Asn83 is in the β-strand β4, and Asn89 is in the loop connecting β-strand β4 to the helix α2.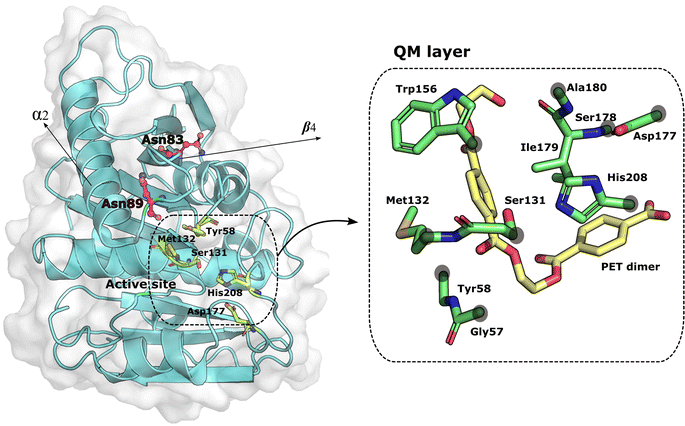

Fig. 1 PETase:PET complex. On the left, the mutated residues are represented as magenta balls and sticks. The residues that form the active site and the substrate are represented as green sticks. The distance between the mutations and the active site residues is around 7 Å. The structure of PETase was taken from the PDB ID: 5XH3. On the right, the residues of the QM layer are represented in green sticks and the PET dimer in yellow sticks. The gray circles above the residues indicate the placement of the link atoms.

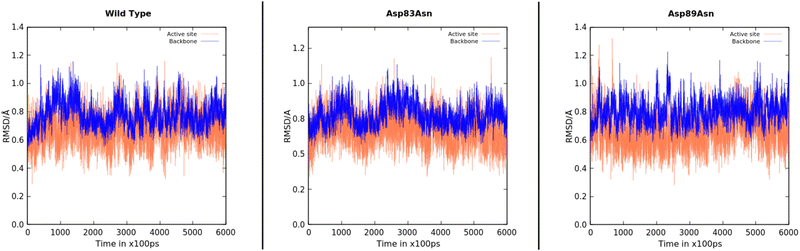
We performed 600 ns MD simulations of the wild-type and mutant PETases to investigate if the mutations induced conformational changes or changed the PETase flexibility. The simulations provide significant insights into the structure and stability of the protein after the mutations, showing that no extensive structural changes were caused by the mutations, even though we cannot exclude PETase rearrangements at a timescale longer than the simulation time. Fig. 2 depicts the evolution of the root-mean-square deviation (RMSD) over time for the three PETase:PET dimer models. The RMSD for each system was also calculated for the active site (Tyr58, Ser131, Met132, Asp177, His208). The stability of the enzyme conformation of PETase with respect to the wild type of all systems is converged within the timescale of the simulation, with an average RMSD below 1 Å, which indicated the folding and the active site of the mutant PETase forms was essentially well-preserved. In addition, enzyme residues with the most contacts with the PET dimer substrate (>70%), for the wild type, Asp83Asn, and Asp89Asn, were analyzed during the MD and QM/MM MD simulations, showing close interactions between the PET dimer and the catalytic Tyr58, as well as residues Trp156 and Ile179, for over 90% of the MD simulation in all cases (Fig. S3 in ESI†).

Fig. 2 RMSD plots for the 600 ns MD simulations of the wild type, Asp83Asn, and Asp89Asn PETases. The RMSD values were calculated using the backbone atoms (blue line) and the active site (coral line).

We then quantified the availability of catalytically competent structures during the simulations. We considered a conformation as catalytically competent when three critical interactions were formed at the active site: (i) two hydrogen bonds from the backbone-NH of Tyr58 and Met132 formed an oxyanion hole with the carbonyl oxygen of the PET dimer substrate (considered using heavy atom distances below 4.5 Å and 5 Å, respectively); (ii) the His208-imidazole accepted a hydrogen bond from Ser131–OγH and donated a hydrogen bond to Asp177 (considered using heavy atom distances below 4 Å and 3.5 Å, respectively); (iii) the Ser131 Oγ–C¹₄ distance was below 4.5 Å. Considering these criteria simultaneously, the prevalence of catalytically competent conformations followed the order Asp89Asn (25.1%) > Wild Type (9.2%) > Asp83Asn (8.5%). The complete distance distribution can be found in Fig. S2 of the ESI.†

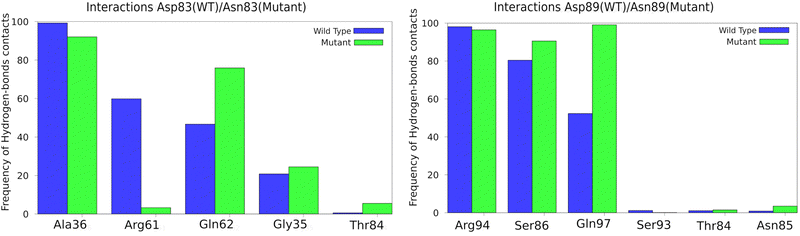
The protein structure around the mutations was analyzed to show if there were significant changes. Fig. 3 shows an analysis of hydrogen bonds in the environment of each mutated residue and the corresponding region in the wild type. A few changes were observed: for the Asp83Asn mutant, the interactions with Arg61 are more prevalent in the wild type than in the mutant (in line with our previous work,³³ this residue is expected to lower the barrier); for Gln62, the interaction is more prevalent in the mutant than in the wild type; for the Asp89Asn mutant, the interactions with Gln97 residue were less prevalent in the wild type. Moreover, other protein regions were also analyzed, and no local structural changes were found.

Fig. 3 Enzyme residues with the most contacts with the mutated residues in the MD simulations.

Reaction mechanisms at the PBE/MM MD level

To choose the starting structures for PBE/Amber studies, we used the GROMOS algorithm³⁷ implemented in the GROMACS package to cluster the MD trajectories for the Asp83Asn and Asp89Asn systems, using a cutoff value of 1.4 Å over the RMSD of the atoms involved in the critical distances for a catalytically-competent PETase. From the cluster with the shortest distances required for catalytically competent complex, we then selected as starting conformation that in which these distances assumed the shortest values. The starting structure used for the PBE/Amber studies may have a small impact on the calculated free energy barrier, even though most of the dependence is smoothed out by the MD sampling along the free energy profile. Nevertheless, it is important that it reflects a quasi-reactive conformation so that the reaction mechanism can be properly explored at the sub-nanosecond timescale.

We then carried out umbrella sampling simulations to study the acylation mechanism of both mutants. We obtained a converged free energy profile after 15 ps of simulation per umbrella window. To assess the convergence the of the umbrella sampling simulations, we analyzed the resulting free energy for different simulation blocks of 3 ps. After analysis, we chose to discard the first 3 ps of each simulation, using the remaining 12 ps production/window to calculate the final converged free energy profiles for the acylation reaction (Fig. 4d). The standard deviation for the free energy barrier was 0.11, 0.24, and 0.11 kcal mol⁻¹ for the wild-type, the Asp83Asn and Asp89Asn mutants (details in Fig. S4 in ESI†). The standard deviations are satisfactory in the face of the typical DFT error, which is often 2–3 kcal mol⁻¹ or higher.³⁸

Fig. 4 (a)–(c) Reactant, TS, and products for the acylation step. Distances (in Å) are shown in coral for the Asp83Asn complex, in black for the Asp89Asn complex, and magenta for the wild-type. (d) The free energy profile for the reactions. These structures were taken from a representative snapshot of the umbrella sampling QM/MM MD simulations ran for the Asp89Asn PET mutant, for the reactant (a), transition state (b) and products (c), respectively.

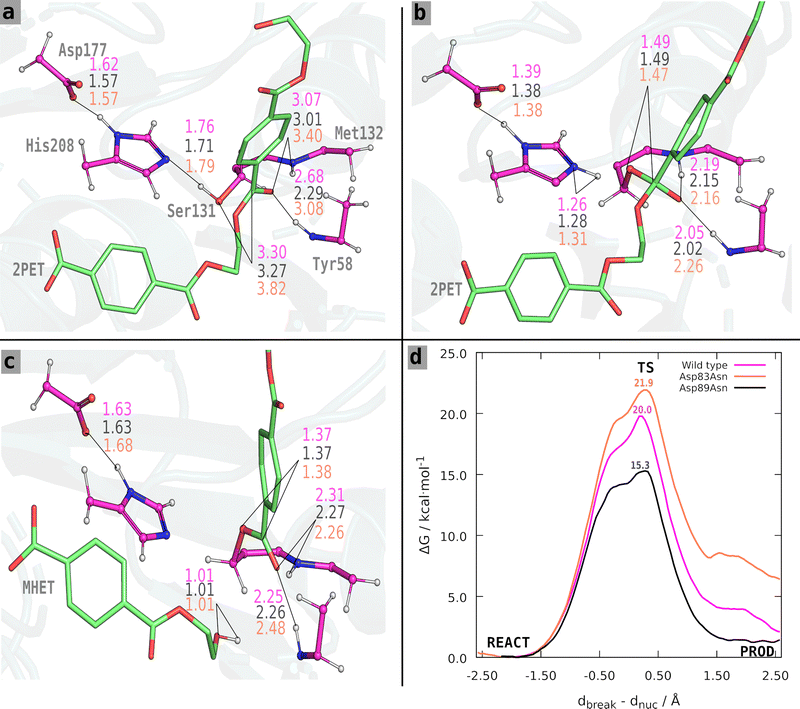
The Asp83Asn and Asp89Asn mutants share an acylation mechanism similar to the one described in the literature for the wild-type PETase.³³ However, after analyzing the structures of the reactant and TS of the wild type and mutants, we found slight differences in the fine organization of the active site that should account for the different results we observed. The average values for the critical catalytic distances along the reaction step are presented in Table S2a–c (ESI†) and Fig. 4. The free energy profile of each process is shown in Fig. 4. For the Asp83Asn mutant, the acylation occurs with a free energy barrier of 21.9 kcal mol⁻¹. The mutation was unfavorable because the free energy is slightly higher than the one calculated in the wild type (20.0 kcal mol⁻¹). For the mutant Asp89Asn, the acylation occurs with a free energy barrier of 15.3 kcal mol⁻¹, a favorable, lower value than the one calculated for the wild type.

The distances shown in Fig. 4 and Table S2a–c (ESI†) reveal a clear trend: besides the effect of the mutation, the barriers are significantly influenced by the reactant's structure of the wild type and mutants. The critical distances are very similar at the transition state and products for all systems; the relevant differences are found in the reactant state. The wild-type and Asp89Asn have similar critical distances, although Asp89Asn has a slightly shorter Ser131 Oγ–C¹₄ distance, shorter oxyanion hydrogen bonds, and a smaller barrier. Oppositely, the Asp83Asn mutant has a significantly larger Ser131 Oγ–C¹₄ distance and oxyanion hydrogen bonds compared to the wild-type and Asp89Asn, and has a higher free energy barrier. This observation agrees with several studies of the dependence between the activation free energy and the reactant structure. It has been shown in several different systems, such as the HIV-1 protease,^39,40 α-amylase,^41,42 2′-hydroxyphenyl-2-sulfinate desulfinase,⁴³ or the human transmembrane protease serine 2⁴⁴ that the activation barrier depends critically on the fine pre-organization of the active site. In an enoyl-thioester reductase, it was experimentally shown that a mutation causing a displacement of 1 Å in the substrate caused a change of six orders of magnitude in forming an otherwise undetectable side-product.⁴⁵ In short, the results confirm that the mutations predicted to stabilize the transition state over the reactant with the static transition state macrodipole stabilization method do have a catalytic effect if the enzyme does not suffer structural changes at least at the active-site level, which is the premise of the technique. However, when the assumption does not strictly hold, and active site rearrangements lead to an (even slightly) poorer catalytic conformation with longer critical reactive distances, the cost of the imperfect pre-organization may overcome the electrostatic benefits of the mutation, and the mutants become non-catalytic or slightly anticatalytic. Nevertheless, given the very high attrition rate of enzyme optimization, the transition state macrodipole stabilization method provides a clear advantage for enzyme evolution, used alone or in combination with directed evolution methods.

3. Materials and methods

Molecular dynamics simulations

As in our previous work, a PETase:PET dimer complex was assembled.³³ Two different PETase mutants were generated, where the residues Asp83 and Asp89 were mutated to asparagine. The tleap module of Amber 18⁴⁶ was used to assemble each system, using the ff14SB force field⁴⁷ to describe the enzyme and GAFF2⁴⁸ force field for the substrate. The total charge was neutralized with seven chloride ions. Each enzyme:substrate complex was centered in a periodic rectangular box with faces at a minimum distance of 12 Å from the limits of the enzyme:substrate complex and solvated with TIP3P⁴⁹ water molecules. The final systems had ca. 34 800 atoms. After proper setup and parameterization, the resulting systems were minimized following five MM minimization steps (details in ESI†). All molecular mechanics calculations were performed using the GROMACS software package.⁵⁰ After energy minimization, the complexes were gradually heated (annealing) from 0 to 300 K for 40 ps, followed by 60 ps at 300 K under constant volume and temperature (NVT ensemble) using the leap-frog integrator⁵¹ and modified Berendsen thermostat.⁵² After that, constant pressure and temperature (NPT ensemble) equilibration was performed to stabilize the system's pressure at 1 bar using the Berendsen barostat, first with restraints on the enzyme and substrate, for 3 ns with 2 fs time step, and after 5 ns with no constraints. Next, NPT molecular dynamics productions of each PETase mutant complex were performed for 600 ns with a 2 fs time step, using the Parrinello–Rahman barostat⁵³ for a reference pressure of 1 bar. The cutoff distance for the nonbonded interaction was set to 10 Å.⁵⁴ The covalent bonds containing hydrogen were constrained using the linear constraint solver algorithm (LINCS).^55,56 The particle-mesh Ewald method^57,58 was used to treat long-range electrostatic interactions beyond the cutoff. The pressure was controlled by the isotropic position scaling protocol applied in GROMACS. Temperature coupling was set with a velocity-rescaling thermostat⁵⁹ at 300 K and a coupling constant of 0.2 ps. All simulations were performed under periodic boundary conditions.

QM/MM molecular dynamics

QM/MM simulations were carried out for the rate-limiting acylation step. The CP2K⁶⁰ hybrid QM/MM scheme was used, with forces computed using the QUICKSTEP module⁶¹ that allows using both atom-centered Gaussian orbitals and plane waves as the basis set to solve the Kohn–Sham equations, and the classical force-field module FIST for MM calculations. The PBE^62,63 functional was used with a double ζ-valence polarization plane-wave basis-set (DZVP-GTH-PBE) and Goedecker–Teter–Hutter (GTH) pseudopotentials;^64,65 the plane-wave expansion cutoff was set at 300 Ry in the QM cell. All QM subsystems have a charge of −2 and a singlet spin multiplicity. The Amber ff14SB force field described the remaining atoms assigned to the MM part. Hydrogen atoms were used as “link atoms” to treat the boundary region between the QM and MM atoms.^5,66 The Gaussian expansion of the electrostatic potential method (GEEP)⁶⁷ was used to describe the long-range Coulomb behavior accelerating the calculation of the electrostatic interaction.

The initial structure for the PBE/MM MD simulations was extracted from the 600 ns classical MD simulation. We performed a clustering based on the RMSD of the active site atoms involved in the critical distances for the reaction mechanism. Out of the most populated cluster, we chose the starting coordinates taking into account the shortest distances between the Ser131 oxygen with the ester carbon of PET dimer, the distance between the Ser131 oxygen with the Nε of His208, and the distances between the oxyanion hole formed by the backbone of Tyr58 and Met132 with the carbonyl oxygen of the ester bond of the substrate, simultaneously.

Atoms participating directly or indirectly in the PETase acylation reaction were treated at the QM level whereas all other atoms were treated at the MM level. Thus, the QM region consisted of Gly57, Tyr58, Ser131, Met132, Trp156, Asp177, Ser178, Ile179, Ala180, His208, and the PET dimer substrate (refer to Fig. S1 in ESI†), while the MM region accounted for the remaining atoms. The total number of atoms for the QM level was 142 (Table S1 in ESI†). Each model was optimized with the LBFGS algorithm using first mechanical and after electrostatic embedding. Next, the optimized structures were equilibrated with MD in the NVT ensemble for 2 ps at 300 K using the CSVR thermostat⁵⁹ and a 1 fs integration step. Following that, PBE/MM steered MD was performed for 3 ps along the previously used reaction coordinate,³³ with a harmonic potential force constant of 50 kcal mol⁻¹ Å⁻² and a target growth of 0.002 fs⁻¹ on the following reaction coordinate, RC (atom names in Scheme 1): RC = d(PET dimer(C¹₄–O_oxi)) − d(Ser(131-O_γ)-PET dimer(C¹₄)), where d(PET dimer(C¹₄–O_oxi)) represents the breaking of the PET dimer–ester bond (d_break) and d(Ser(131-O_γ)-PET dimer(C¹₄)) represents the nucleophilic attack by Ser131 (d_nuc).

Umbrella sampling

We have chosen structures from the steered MD runs to define the starting reaction coordinate points for the windows of the umbrella sampling simulations⁶⁸ that allow for calculating the reaction free energy profile. The reaction coordinate reference values are separated by 0.1 Å, with harmonic biasing restraints centered at the reference values and a force constant of 100 or 200 kcal mol⁻¹ Å⁻². The US simulations ran for 15 ps in each window. Table S1 (ESI†) shows the number of windows used in each system, which depends on the specific reaction coordinate. For each of the windows, a harmonic potential was chosen based on the potential energy at each of the reference points along the RC and added to the system's Hamiltonian. QM/MM MD simulations were performed for all windows (the RC distribution for each window per simulation is represented in Fig. S5 of the ESI†).⁶⁹ Finally, we used the weighted histogram analysis method (WHAM)⁷⁰ to recover the unbiased reaction coordinate populations and the free energy along the reaction coordinate with a convergence tolerance of 0.0001 kcal mol⁻¹ using 100 bootstrap data sets.

4. Conclusions

The catalytic mechanism of PETase had been studied before by us³³ and others.^{30–32,71,72} It was concluded that the acylation process is the rate-limiting step. In this study, we used a solid level of theory by combining extensive classical and PBE/Amber MD simulations for the wild type and two different PETase mutants (Asp83Asn and Asp89Asn) previously pointed out as potentially rate-enhancing by the static transition state macrodipole stabilization method, to see how promising these mutations are and to which extent does the incorporation of structural rearrangements upon mutation affect the results.

The Asp83Asn mutation did not have a good effect since the free energy barrier was higher than that of the wild type by 1.9 kcal mol⁻¹. In the case of the Asp89Asn mutant, its activation free energy decreased by 5 kcal mol⁻¹ compared to the wild type. The principal reason for the difference was that the reactant state critical catalytic distances were pretty favorable in the Asp89Asn mutant but slightly less fortunate in the Asp83Asn mutant. The latter detrimental rearrangement overcomes the electrostatic stabilization the mutation provides, resulting in a net free energy increase. The high sensibility of activation energies concerning the fine structural details of the reactant state is well-known and is an additional variable to consider in enzyme optimization. Computational protein design has emerged as a leading and vital research area in biochemistry; thus, our results significantly contribute to the rational design of enzymes with improved function in general and PETase mutants to make PET biodegradation a viable industrial application method in particular. The present work validates the favorable mutations discussed before and provides a deeper understanding of enzyme optimization's delicate mechanisms.

Author contributions

Carola Jerves: conceptualization, methodology, formal analysis, research, validation, visualization, writing – original draft,. Rui P. P. Neves: validation, resources, data curation, writing – review & editing, visualization. Saulo L. da Silva: writing – review & editing. Maria J. Ramos: methodology, resources, visualization, writing – review and editing. Pedro A. Fernandes: conceptualization, funding acquisition, methodology, project administration, resources, visualization, writing – review and editing. All authors have read and agreed to the published version of the manuscript. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by UIDB/50006/2020 and UIDP/50006/2020 with funding from FCT/MCTES through national funds. We thank the University of Porto and the University of Cuenca for allowing scientific collaboration through Addendum to the Cultural and Scientific Agreement for FCJV. R. P. P. N. thanks FCT for funding through the Individual Call to Scientific Employment Stimulus (Ref. 2021.00391.CEECIND/CP1662/CT0003). We further thank PRACE for granting us access to MareNostrum at Barcelona Supercomputing Center (BSC), Spain, through Project 2019215204.

Notes and references

1. C. C. Chen, X. Han, T. P. Ko, W. D. Liu and R. T. Guo, FEBS J., 2018, 285, 3717–3723.
2. X. Han, W. D. Liu, J. W. Huang, J. T. Ma, Y. Y. Zheng, T. P. Ko, L. M. Xu, Y. S. Cheng, C. C. Chen and R. T. Guo, Nat. Commun., 2017, 8, 2106.
3. S. F. Sousa, A. J. M. Ribeiro, R. P. P. Neves, N. F. Bras, N. M. F. S. A. Cerqueira, P. A. Fernandes and M. J. Ramos, WIREs Comput. Mol. Sci., 2017, 7, e1281.
4. N. F. Brás, J. T. S. Coimbra, R. P. P. Neves, N. M. F. S. A. Cerqueira, S. F. Sousa, P. A. Fernandes and M. J. Ramos, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2015 DOI:10.1016/B978-0-12-409547-2.10833-9.
5. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
6. E. Kraka and D. Cremer, Acc. Chem. Res., 2010, 43, 591–601.
7. S. Ahmadi, L. B. Herrera, M. Chehelamirani, J. Hostas, S. Jalife and D. R. Salahub, Int. J. Quantum Chem., 2018, 118, e25558.
8. M. G. Quesne, T. Borowski and S. P. de Visser, Chem. – Eur. J., 2016, 22, 2562–2581.
9. M. W. van der Kamp and A. J. Mulholland, Biochemistry, 2013, 52, 2708–2728.
10. M. Musil, H. Konegger, J. Hong, D. Bednar and J. Damborsky, ACS Catal., 2019, 9, 1033–1054.
11. Y. Li, K. Song, J. Zhang and S. Y. Lu, Catalysts, 2021, 11, 286.
12. R. Lonsdale, J. N. Harvey and A. J. Mulholland, Chem. Soc. Rev., 2012, 41, 3025–3038.
13. K. Swiderek, I. Tunon and V. Moliner, WIREs Comput. Mol. Sci., 2014, 4, 407–421.
14. N. M. F. S. A. Cerqueira, P. A. Fernandes and M. J. Ramos, Chem. Phys. Chem., 2018, 19, 669–689.
15. Y. L. Cui, Y. C. Chen, X. Y. Liu, S. J. Dong, Y. E. Tian, Y. X. Qiao, R. Mitra, J. Han, C. L. Li, X. Han, W. D. Liu, Q. Chen, W. Q. Wei, X. Wang, W. B. Du, S. Y. Tang, H. Xiang, H. Y. Liu, Y. Liang, K. N. Houk and B. Wu, ACS Catal., 2021, 11, 1340–1350.
16. M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354–2377.
17. C. E. Sequeiros-Borja, B. Surpeta and J. Brezovsky, Briefings Bioinf., 2021, 22, bbaa150.
18. J. A. Keith, V. Vassilev-Galindo, B. Q. Cheng, S. Chmiela, M. Gastegger, K. R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872.
19. K. Hiraga, I. Taniguchi, S. Yoshida, Y. Kimura and K. Oda, EMBO Rep., 2019, 20, e49365.
20. I. Taniguchi, S. Yoshida, K. Hiraga, K. Miyamoto, Y. Kimura and K. Oda, ACS Catal., 2019, 9, 4089–4105.
21. E. Erickson, J. E. Gado, L. Avilán, F. Bratti, R. K. Brizendine, P. A. Cox, R. Gill, R. Graham, D.-J. Kim, G. König, W. E. Michener, S. Poudel, K. J. Ramirez, T. J. Shakespeare, M. Zahn, E. S. Boyd, C. M. Payne, J. L. DuBois, A. R. Pickford, G. T. Beckham and J. E. McGeehan, Nat. Commun., 2022, 13, 7850.
22. S. Yoshida, K. Hiraga, T. Takehana, I. Taniguchi, H. Yamaji, Y. Maeda, K. Toyohara, K. Miyamoto, Y. Kimura and K. Oda, Science, 2016, 351, 1196–1199.
23. H. P. Austin, M. D. Allen, B. S. Donohoe, N. A. Rorrer, F. L. Kearns, R. L. Silveira, B. C. Pollard, G. Dominick, R. Duman, K. El Omari, V. Mykhaylyk, A. Wagner, W. E. Michener, A. Amore, M. S. Skaf, M. F. Crowley, A. W. Thorne, C. W. Johnson, H. L. Woodcock, J. E. McGeehan and G. T. Beckham, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4350–E4357.
24. S. Joo, I. J. Cho, H. Seo, H. F. Son, H. Y. Sagong, T. J. Shin, S. Y. Choi, S. Y. Lee and K. J. Kim, Nat. Commun., 2018, 9, 382.
25. Y. Ma, M. D. Yao, B. Z. Li, M. Z. Ding, B. He, S. Chen, X. Zhou and Y. J. Yuan, Engineering, 2018, 4, 888–893.
26. H. F. Son, I. J. Cho, S. Joo, H. Seo, H. Y. Sagong, S. Y. Choi, S. Y. Lee and K. J. Kim, ACS Catal., 2019, 9, 3519–3526.
27. E. L. Bell, R. Smithson, S. Kilbride, J. Foster, F. J. Hardy, S. Ramachandran, A. A. Tedstone, S. J. Haigh, A. A. Garforth, P. J. R. Day, C. Levy, M. P. Shaver and A. P. Green, Nat. Catal., 2022, 5, 673–681.
28. L. Avilan, B. R. Lichtenstein, G. König, M. Zahn, M. D. Allen, L. Oliveira, M. Clark, V. Bemmer, R. Graham, H. P. Austin, G. Dominick, C. W. Johnson, G. T. Beckham, J. E. McGeehan and A. R. Pickford, ChemSusChem, 2023, 16, e202202277.
29. T. Fecker, P. Galaz-Davison, F. Engelberger, Y. Narui, M. Sotomayor, L. P. Parra and C. A. Ramirez-Sarmiento, Biophys. J., 2018, 114, 1302–1312.
30. M. N. Zheng, Y. W. Li, W. L. Dong, W. X. Zhang, S. S. Feng, Q. Z. Zhang and W. X. Wang, ACS Sustainable Chem. Eng., 2022, 10, 7341–7348.
31. S. Feng, Y. Yue, M. Zheng, Y. Li, Q. Zhang and W. Wang, ACS Sustainable Chem. Eng., 2021, 9, 9823–9832.
32. S. Boneta, K. Arafet and V. Moliner, J. Chem. Inf. Model., 2021, 61, 3041–3051.
33. C. Jerves, R. P. P. Neves, M. J. Ramos, S. da Silva and P. A. Fernandes, ACS Catal., 2021, 11, 11626–11638.
34. A. J. M. Ribeiro, D. Santos-Martins, N. Russo, M. J. Ramos and P. A. Fernandes, ACS Catal., 2015, 5, 5617–5626.
35. R. P. P. Neves, M. J. Ramos and P. A. Fernandes, J. Chem. Inf. Model., 2023, 63, 20–26.
36. A. V. Pinto, P. Ferreira, R. P. P. Neves, P. A. Fernandes, M. J. Ramos and A. L. Magalhaes, ACS Catal., 2021, 11, 10416–10428.
37. X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed., 1999, 38, 236–240.
38. M. Bursch, J. M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735.
39. A. R. Calixto, M. J. Ramos and P. A. Fernandes, Chem. Sci., 2019, 10, 7212–7221.
40. J. T. S. Coimbra, R. P. P. Neves, A. V. Cunha, M. J. Ramos and P. A. Fernandes, Chem. – Eur. J., 2022, 28, e202201066.
41. D. Santos-Martins, A. R. Calixto, P. A. Fernandes and M. J. Ramos, ACS Catal., 2018, 8, 4055–4063.
42. R. P. P. Neves, P. A. Fernandes and M. J. Ramos, J. Chem. Inf. Model., 2022, 62, 3638–3650.
43. J. P. M. Sousa, R. P. P. Neves, S. F. Sousa, M. J. Ramos and P. A. Fernandes, ACS Catal., 2020, 10, 9545–9554.
44. L. M. C. Teixeira, J. T. S. Coimbra, M. J. Ramos and P. A. Fernandes, J. Chem. Inf. Model., 2022, 62, 2510–2521.
45. R. G. Rosenthal, B. Vogeli, T. Wagner, S. Shima and T. J. Erb, Nat. Chem. Biol., 2017, 13, 745–749.
46. D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. Salomon-Ferrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, Amber 18, University of California, San Francisco, 2018.
47. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
48. D. Vassetti, M. Pagliai and P. Procacci, J. Chem. Theory Comput., 2019, 15, 1983–1995.
49. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
50. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25.
51. W. F. Van Gunsteren and H. J. C. Berendsen, Mol. Simul., 1988, 1, 173–185.
52. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
53. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
54. H. G. Petersen, J. Chem. Phys., 1995, 103, 3668–3679.
55. B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122.
56. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
57. P. P. Ewald, Ann. Phys., 1921, 64, 253–287.
58. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
59. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
60. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, WIREs Comput. Mol. Sci., 2014, 4, 15–25.
61. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
62. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
63. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
64. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
65. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
66. F. Maseras and K. Morokuma, J. Comput. Chem., 1995, 16, 1170–1179.
67. T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2005, 1, 1176–1184.
68. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
69. Q. Liao, in Progress in Molecular Biology and Translational Science, ed. B. Strodel and B. Barz, Academic Press, 2020, vol. 170, pp. 177–213.
70. A. Grossfield, WHAM: the weighted histogram analysis method, Rochester, NY, 2013, p. 14642.
71. E. Shrimpton-Phoenix, J. B. O. Mitchell and M. Bühl, Chem. – Eur. J., 2022, 28, e202201728.
72. R. García-Meseguer, E. Ortí, I. Tuñón, J. J. Ruiz-Pernía and J. Aragó, J. Am. Chem. Soc., 2023, 145, 19243–19255.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nj04204a. Most relevant trajectories and statistical innefiency analysis are available at the public repository Zenodo, https://doi.org/10.5281/zenodo.10136888.

---