Asymmetric edge supercurrents in MoTe₂ Josephson junctions

Abstract

To investigate the higher order topology in MoTe₂, the supercurrent interference phenomena in Nb/MoTe₂/Nb planar Josephson junctions have been systematically studied. By analyzing the obtained interference pattern of the critical supercurrents and performing a comparative study of the edge-touched and untouched junctions, it's found that the supercurrent is dominated by the edges, rather than the bulk or surfaces of MoTe₂. An asymmetric Josephson effect with a field-tunable sign is also observed, indicating the nontrivial origin of the edge states. These results not only provide initial evidence for the hinge states in the higher order topological insulator MoTe₂, but also demonstrate the potential applications of MoTe₂-based Josephson junctions in rectifying the supercurrent.

---

1. Introduction

The discovery of topological insulators (TIs) has triggered extensive studies of topological materials in the fields of condensed matter physics and materials science.^1–7 One essential feature of 3D TI is the presence of topologically protected 2D surface states due to the nontrivial topology of the bulk electronic states. This is the well-known bulk-boundary correspondence of topological materials. Recently this correspondence has been extended to higher order topological insulators (HOTIs).^8,9 For an nth-order 3D TI, it will possess gapless boundary states at 3-n dimensions. Theoretical studies have predicted some materials to be second order TIs with 1D hinge states, such as bismuth,¹⁰ Cd₃As₂,^11,12 and layered transition metal dichalcogenides MoTe₂ and WTe₂.¹³ However, the experimental detection of these hinge states is challenging, especially when the bulk is also metallic. Up to now, scanning tunneling microscopy and supercurrent interference experiments are the two most effective way to probe the hinge states in HOTIs.^14–18 In particular, anisotropic edge supercurrent which can persist in magnetic fields up to a few Tesla has been reported in the study of WTe₂-based Josephson junctions, pointing to the existence of helical hinge states in WTe₂.^16,19

As a member of the XTe₂ (X = W, Mo) family of transition metal dichalcogenides, MoTe₂ exhibits many similar properties to WTe₂, such as the 2D quantum spin Hall effect with helical edge states and the 3D type-II Weyl semimetal phase with Fermi arc surface states.^20–23 But distinctive from WTe₂, MoTe₂ can become superconducting below 0.1 K.²⁴ A recent Little-Parks experiment even reveals the emergence of edge superconductivity in MoTe₂ below its superconducting transition temperature (T_c).²⁵ But whether this edge superconductivity is related to the 1D hinge state remains unclear. Besides, the study of Josephson supercurrent interference above T_c aiming to clarify the higher order topology in MoTe₂ is also rare. In view of these, we have fabricated Nb/MoTe₂/Nb planar Josephson junctions (JJs) and carried out systematic investigation of the supercurrent interference in perpendicular magnetic fields above T_c. By analyzing the obtained interference pattern of the critical supercurrents, we uncover the dominant edge contribution to the supercurrent, instead of the bulk/surface ones. A comparative study of the edge-touched and untouched JJs also confirms the dominant role of edge states in carrying the Josephson supercurrent. Furthermore, the Nb/MoTe₂/Nb JJs are found to exhibit a pronounced asymmetric Josephson effect (AJE), with the magnitude and sign of the asymmetry between positive and negative critical currents highly tunable by the applied magnetic field. All these results suggest the existence of hinge states in MoTe₂ above T_c. Based on the field-tunable AJE, the application of MoTe₂ JJs in superconducting diodes can also be envisaged.^26–33

2. Experimental

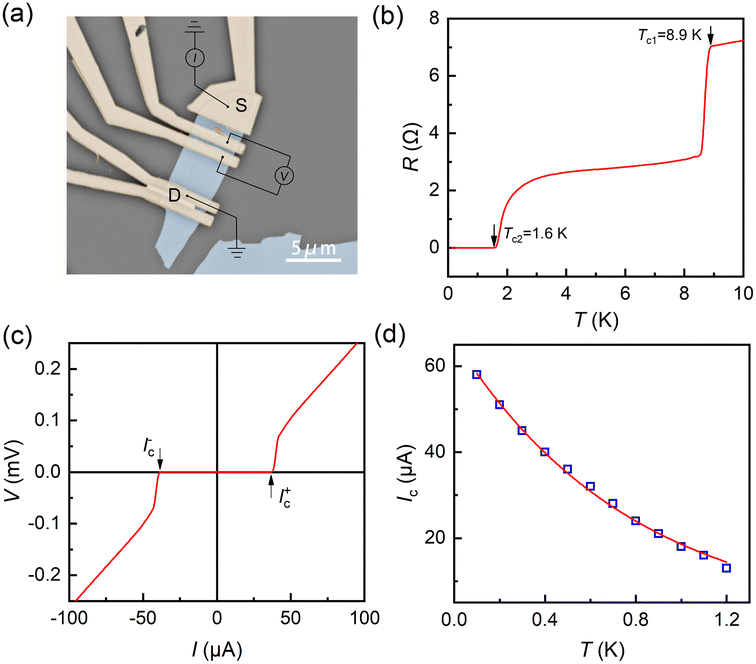
The MoTe₂ crystals were grown by the Te-flux method. The powder and single crystal X-ray diffraction measurements have confirmed the 1T′ phase of MoTe₂ at room temperature. The MoTe₂ flakes were exfoliated from bulk crystals and subsequently transferred onto a silicon substrate covered with a 280 nm thick insulating SiO₂ layer. By employing electron beam lithography and pulsed laser deposition (PLD) techniques, a pair of superconducting niobium electrodes (120 nm) were fabricated on the MoTe₂ flakes, forming Nb/MoTe₂/Nb planar Josephson junctions. To enhance the electrical transparency of the Nb/MoTe₂ interface, an argon ion source was utilized for surface cleaning of the MoTe₂ flake before the in situ deposition of Nb electrodes via PLD. Fig. 1(a) shows the image of a typical Nb/MoTe₂/Nb Josephson junction, featuring a gap (L) of approximately 400 nm between the two Nb electrodes. In studying the transport properties of the junction, a current (I) was input via source (S) and drain (D) electrodes and the resultant voltage (V) was measured between the two Nb electrodes, as indicted in Fig. 1(a). The Nb/MoTe₂/Nb Josephson junctions were systematically investigated within a cryogenic dilution refrigerator under varying temperature (T) and magnetic field (B) conditions. The differential resistance curves were recorded using a Keithley 6221 AC/DC current source and 2182A nanovoltmeter.

Fig. 1 (a) An image of the planar MoTe₂ Josephson junction. The thickness (t) of the MoTe₂ flake is 34 nm and the junction has a width (W) of 4.7 μm and a length (L) of 400 nm. (b) The temperature dependence of the resistance of the Josephson junction. The Nb superconducting transition occurs around T_c1 = 8.9 K and the Josephson supercurrent appears below T_c2 = 1.6 K. (c) The voltage (V)–current (I) curve recorded at 0.5 K in zero magnetic field. (d) The temperature dependence of the critical supercurrent I_c. The data can be well fitted to the long ballistic model, as indicated by the red fitting curve.

3. Results and discussion

The temperature dependence of the resistance of the Josephson junction is shown in Fig. 1(b). As the temperature decreases, two distinct and well-defined resistance drops are observed. The first drop, occurring around T_c1 = 8.9 K, corresponds to the superconducting transition of the Nb electrodes. Subsequently, the second resistance drop emerges, indicating the onset of supercurrent flow within the junction. Below T_c2 = 1.6 K, the resistance reaches zero, signifying the establishment of a Josephson superconducting state. Fig. 1(c) shows the V(I) curve of the junction at T = 0.5 K. Note that the current was always swept from zero to positive or negative values to mitigate any potential heating effect. The curve distinctly exhibits a zero-resistance state within a current range between I_c⁺ and I_c−, as indicated by arrows in Fig. 1(c). Therefore, I_c⁺ and I_c− represent the critical Josephson supercurrents in the positive and negative current directions, respectively. In the absence of magnetic fields, I_c⁺ = |I_c−| = I_c. The temperature dependence of the critical supercurrent I_c is depicted in Fig. 1(d). We observe an exponential growth of I_c with decreasing T, a distinctive feature of long ballistic Josephson junctions where I_c ∝ exp(−k_BT/δE) and δE ≈ v_F/2πL.^34–37 As shown by the red curve in Fig. 1(d), the data can be well fitted to the above equation, yielding a Fermi velocity v_F ∼ 3.2 × 10⁵ m s⁻¹ and δE ∼ 0.0417 meV. A similar phenomenon has been observed in previous studies of graphene.³⁸

We further investigate the Josephson effect of the Nb/MoTe₂/Nb junctions in perpendicular magnetic fields. Fig. 2(a) shows the junction's differential resistance as a function of the magnetic field and current bias at T = 1.2 K. Similar to Fig. 1(c), the current bias is also swept from zero to positive values. In the blue region, the differential resistance approaches zero, implying the supercurrent flowing through the Josephson junction. The boundary of the blue region, i.e., the I_c⁺(B) curve, exhibits obvious oscillations as the field varies. This oscillatory behavior is a manifestation of the supercurrent interference in perpendicular fields.³⁹ As is known, for a Josephson junction with uniform supercurrent distribution, the interference pattern is described by with ϕ = BL_effW and L_eff = L + 2λ. W, L, λ, and ϕ₀ represent the junction width, the length, the magnetic field penetration depth of Nb, and the magnetic flux quantum, respectively. Such a Fraunhofer pattern is illustrated in the inset of Fig. 2(a). It's obvious that the measured interference pattern in Fig. 2(a) deviates much from the standard Fraunhofer pattern, with the former showing a much slower decay of critical supercurrents with increasing fields than the latter. This discrepancy suggests a nonuniform supercurrent distribution in the Nb/MoTe₂/Nb junction.

Fig. 2 (a) 2D color map of the differential resistance versus the current bias and magnetic field at 1.2 K. The inset shows the standard Fraunhofer pattern. (b) The supercurrent density distribution of the Josephson junction exhibits the presence of edge states with characteristic widths of 480 nm and 380 nm, respectively. The inset shows the distribution derived from the Fraunhofer pattern.

To derive the spatial distribution of supercurrents within the Josephson junction, we adopt the method proposed by Dynes and Fulton to analyze the obtained interference pattern in Fig. 2(a).⁴⁰ A comprehensive procedure for the Dynes–Fulton analysis is available in the ESI.† The red curve in Fig. 2(b) shows the derived distribution of supercurrents along the width direction of the Josephson junction. Two prominent current peaks are clearly observed at the left and right edges of our sample, the locations of which are indicated by vertical dashed lines in Fig. 2(b). The different peak heights imply the asymmetric coupling of the edges with the Nb electrodes. The half maximum widths of these two peaks are about 480 and 380 nm, respectively. But it's noted that the observed edge supercurrent is larger than the maximum supercurrent that a single ballistic hinge state can carry. Similar phenomena were also observed in previous studies of higher order topological insulators, such as bismuth and WTe₂.^19,41,42 This might reflect the presence of multiple hinge states at the edges due to the existence of terraces on the edge or the multiple orbital effect, or to the subtle inductance effects.^41,42 Compared with the edge contribution to the supercurrent, the bulk contribution is almost negligible. This is thus very different from the uniform distribution of supercurrents derived from the Fraunhofer pattern using the same Dynes–Fulton method, as shown in the inset of Fig. 2(b). Note that similar phenomena have been also observed in other MoTe₂ Josephson junctions (Fig. S2, ESI†).

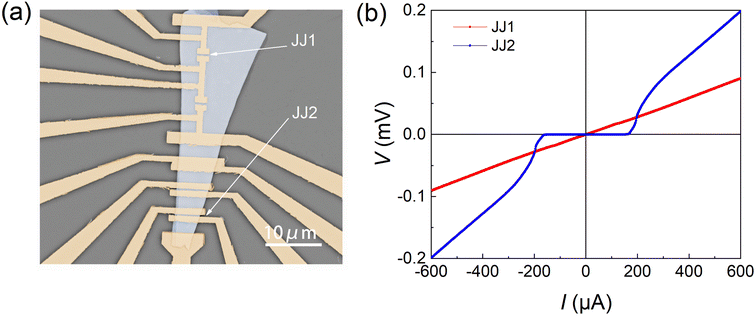
To provide more direct evidence for the existence of edge supercurrent in Nb/MoTe₂/Nb junctions, we have also fabricated two different types of Josephson junctions (JJ1 and JJ2) with comparable junction lengths (L = 236 and 295 nm) as shown in Fig. 3(a). JJ1 is an edge-untouched Josephson junction. Since the Nb electrodes are at least 2 μm away from the edge of the MoTe₂ flake, much larger than the half maximum width of the edge supercurrent peaks as derived in Fig. 2(b), there will be little edge contribution to the supercurrent of JJ1. But similar to the Josephson junction shown in Fig. 1(a), JJ2 is an edge-touched one, with Nb electrodes crossing the flake edge. Therefore, edge supercurrent can only appear in JJ2 if it is present. Fig. 3(b) shows the V(I) curves of these two junctions at T = 0.6 K. It's clear that edge-touched JJ2 exhibits the supercurrent behavior as observed in Fig. 1(c). In contrast, edge-untouched JJ1 displays an almost linear V(I) curve, without any indication of Josephson supercurrents. Since both junctions were fabricated on the same MoTe₂ flake with the same nanofabrication process flow, the different transport behaviors between JJ1 and JJ2 strongly indicate the dominant contribution of edge states to the observed supercurrent in JJ2. Note that we have also fabricated a Josephson junction with the Nb electrodes only contacting the edge of the MoTe₂ flake. It also exhibits Josephson supercurrents at low temperatures, consistent with the edge supercurrent picture.

Fig. 3 (a) An image of the edge-untouched (JJ1) and touched (JJ2) planar MoTe₂ Josephson junctions. The thickness of the MoTe₂ flake is 75 nm and the junction length is 236 and 295 nm for junctions JJ1 and JJ2, respectively. (b) The voltage (V)–current (I) curves of junctions JJ1 and JJ2 obtained at 0.6 K in zero magnetic field.

Besides the intriguing edge supercurrent, it's also found that the Josephson effect is not symmetric with respect to the current direction. Fig. 4(a) shows the measured positive (I_c⁺) and negative (I_c−) critical supercurrents as a function of perpendicular magnetic fields at T = 1.2 K. For comparison, the absolute value of I_c− is plotted in Fig. 4(a). The I_c⁺(B) and |I_c−(B)| curves almost overlap with each other with |B| > 5 mT. But in low fields, one can clearly observe the deviation between these two curves. To quantify the asymmetry between I_c⁺ and I_c−, we have calculated ΔI_c = I_c⁺(B) − |I_c−(B)| and presented it in Fig. 4(b). It's seen that the asymmetry ΔI_c mainly appears in low fields and gradually vanishes with increasing fields. Furthermore, the asymmetry ΔI_c also exhibits interesting sign changes as the field changes. Therefore, the field-tunable asymmetric Josephson effect (AJE) is realized in our Nb/MoTe₂/Nb junctions.

Fig. 4 (a) Field dependence of the critical supercurrents in positive (I_c⁺) and negative (|I_c−|) current directions at 1.2 K. (b) Field dependence of the critical supercurrent asymmetry defined by ΔI_c = I_c⁺(B) − |I_c−(B)| at 1.2 K.

The observed edge superconductivity implies the presence of edge states in the MoTe₂ flakes. Previous studies have revealed that monolayer MoTe₂ is a 2D topological insulator, exhibiting the quantum spin Hall effect with helical edge states.²⁰ But the flake thickness is above 30 nm in our work, thus excluding the quantum spin Hall effect as the physical origin of the edge state we observed in Nb/MoTe₂/Nb junctions. The second possibility of the edge state is the side surface Fermi arc states of MoTe₂. As a type-II WSM, MoTe₂ has been revealed to host Fermi arc surface states.²² But as shown in Fig. 2(b) and 3, the edge states dominate the supercurrent transport in Nb/MoTe₂/Nb junctions, with negligible bulk/surface contributions. If it's the side surface Fermi arc states that give rise to the edge states, one would also expect to observe supercurrent flowing through the top surface states, as discussed in the study of hinge states in WTe₂.¹⁶ This is apparently inconsistent with the negligible bulk/surface supercurrent as shown in Fig. 2(b) and 3. Therefore, the edge state is unlikely to arise from the Fermi arc states of WSM. It has been reported recently in the study of Cd₃As₂ Josephson junctions that the non-Hermitian skin effect might also result in edge supercurrent.⁴³ According to this study, the edge supercurrent density peak can exhibit a large full-width-at-half-maximum of up to 1.6 μm and the left/right peak ratio shows a rapid decrease toward 1 as the sample temperature approaches the critical transition temperature of supercurrent. But in our study, the characteristic peak width is only about 300–400 nm. Besides, the peak ratio of our junction is still as large as 2.8 at T = 1.2 K, a temperature very close to T_c2. These discrepancies seem to suggest the minor role of the non-Hermitian skin effect in the observed edge supercurrent in our MoTe₂ Josephson junctions.

After ruling out the above three possibilities, we tend to ascribe the observed edge state to the 1D hinge state of HOTI.¹³ As pointed out in previous theoretical studies, transition metal dichalcogenides including MoTe₂ and WTe₂ are promising HOTI candidates.¹³ Experimental signatures of hinge states have also been revealed in the transport study of WTe₂.^16,19,44 We are also aware that an intriguing dimensional reduction of supercurrent transport has been reported in the study of Dirac semimetal Cd₃As₂-based Josephson junctions.¹⁷ By increasing the junction length, one can finally realize the hinge state dominated supercurrent with negligible bulk/surface contribution. This situation is just the same as what we have observed in Fig. 2(b) and 3(b). Besides this, the observation of the AJE in Fig. 4 further indicates the non-sinusoidal current phase relation of the Nb/MoTe₂/Nb junction, suggesting the nontrivial origin of the observed edge states.¹⁹ All these lead us to believe that the edge state is most likely associated with the 1D hinge state of HOTI.

It's worth pointing out that edge superconductivity has also been revealed in MoTe₂ below its superconducting transition temperature T_c.²⁵ But the physical origin of this edge superconductivity remains unclear. Whether it's related to the hinge state of the higher order topological insulator still needs to be verified. We have considered two different ways to tackle this issue. The first one is based on the S/N/S Josephson junctions, just like the Nb/MoTe₂/Nb junctions in this work. But when the bulk superconductivity (S′) of MoTe₂ emerges below T_c, the Josephson junction will change to an S/S′/S junction, the physics of which is not solely governed by the Josephson supercurrent anymore. This might result in the failure of the Dynes–Fulton method to derive the spatial distribution of supercurrent density. The second one is based on the Hall bar device with normal metal electrodes, similar to the devices used in the study of edge superconductivity in superconducting MoTe₂.²⁵ We might study the nonlocal transport properties of the device to see if the edge state still persists with temperatures raised above T_c, as inspired by the study of helical edge states in 2D topological insulators.⁴⁵ But the bulk state of MoTe₂ is metallic, which dominates the transport properties instead of the edge state. Therefore, we are now still looking for other more feasible ways to clarify the physical origin of the edge superconductivity of MoTe₂ below T_c and its possible connection to the hinge state.

As the edge state dominates the supercurrent in our Josephson junction, the total Josephson current can be generally described as , where I_Ln and I_Rn represent the Josephson currents carried by the left and right edge states at the nth order, Φ is the field-induced magnetic phase in MoTe₂, and φ is the phase difference between the two Nb electrodes.⁴⁶ If I_Ln = I_Rn, the equation can be reduced to 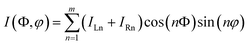, suggesting the occurrence of the symmetric Josephson effect. But as shown in Fig. 2(b), the supercurrent density at the left edge is apparently much larger than the one at the right edge. Under the condition I_Ln ≠ I_Rn, the Josephson supercurrent I(Φ,φ) is not symmetric for both Φ and φ anymore.⁴⁶ This explains the emergence of the AJE in our MoTe₂ Josephson junctions with asymmetric edge supercurrent.⁴⁶ The asymmetry between positive and negative critical supercurrents I_c⁺ and I_c− indicates that the Nb/MoTe₂/Nb junctions can be implemented to realize the rectification of supercurrents, i.e., the supercurrent only flows in the positive (or negative) direction for −I_c < I < I_c⁺ if I_c⁺ > −I_c− (or I_c− < I < −I_c⁺ if I_c⁺ < −I_c−). Such a nonreciprocal supercurrent transport has been termed the superconducting diode effect and attracted lots of attention recently, not only because of intriguing physics behind this phenomenon, but also because of potential applications in low-dissipation superconducting electronics.^26–33 Based on the results shown in Fig. 4, the rectification efficiency defined by can reach up to 13.8%. It is smaller than the highest value (35%) obtained so far in Nb/Pt/Nb planar JJs,³⁰ but still much larger than that (3%) of the [Nb/V/Ta]_n superlattice.²⁶

4. Conclusions

We have successfully revealed the existence of asymmetric edge states in Nb/MoTe₂/Nb Josephson junctions. Instead of the bulk/surface states of MoTe₂, it is these peculiar edge states that dominate the Josephson supercurrent through the junctions. Besides this, we also observe an asymmetric Josephson effect with the field-tunable sign of the asymmetry, suggesting the non-sinusoidal current phase relation of the junctions. Our work provides initial evidence for the hinge states in HOTI MoTe₂. The observation of the AJE further indicates the potential application of MoTe₂-based Josephson junctions in low dissipation superconducting electronics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (No. 2022YFA1403700), the Natural Science Foundation of Guangdong Province (No. 2021A1515010046), the Science, Technology and Innovation Commission of Shenzhen Municipality (No. ZDSYS20190902092905285 and No. GXWD20201230110313001), Guangdong province 2020KCXTD001, and the Center for Analysis and Test of Southern University of Science and Technology.

References

1. L. Fu, C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2007, 98, 106803.
2. M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045.
3. X. L. Qi and S. C. Zhang, Rev. Mod. Phys., 2011, 83, 1057.
4. H. Zhang, C. X. Liu, X. L. Qi, X. Dai, Z. Fang and S. C. Zhang, Nat. Phys., 2009, 5, 438.
5. S.-Y. Xu, I. Belopolski, N. Alidoust, M. Neupane, G. Bian, C. Zhang, R. Sankar, G. Chang, Z. Yuan, C.-C. Lee, S.-M. Huang, H. Zheng, J. Ma, D. S. Sanchez, B. Wang, A. Bansil, F. Chou, P. P. Shibayev, H. Lin, S. Jia and M. Z. Hasan, Science, 2015, 349, 613.
6. B. Yan and C. Felser, Annu. Rev. Condens. Matter Phys., 2017, 8, 337.
7. S. Jia, S. Y. Xu and M. Z. Hasan, Nat. Mater., 2016, 15, 1140.
8. W. A. Benalcazar, B. A. Bernevig and T. L. Hughes, Science, 2017, 357, 61.
9. F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig and T. Neupert, Sci. Adv., 2018, 4, eaat0346.
10. J. Langbehn, Y. Peng, L. Trifunovic, F. von Oppen and P. W. Brouwer, Phys. Rev. Lett., 2017, 119, 246401.
11. S. A. A. Ghorashi, T. Li and T. L. Hughes, Phys. Rev. Lett., 2020, 125, 266804.
12. R. Chen, T. Liu, C. M. Wang, H. Z. Lu and X. C. Xie, Phys. Rev. Lett., 2021, 127, 066801.
13. Z. Wang, B. J. Wieder, J. Li, B. Yan and B. A. Bernevig, Phys. Rev. Lett., 2019, 123, 186401.
14. F. Schindler, Z. Wang, M. G. Vergniory, A. M. Cook, A. Murani, S. Sengupta, A. Y. Kasumov, R. Deblock, S. Jeon, I. Drozdov, H. Bouchiat, S. Guéron, A. Yazdani, B. A. Bernevig and T. Neupert, Nat. Phys., 2018, 14, 918.
15. L. Aggarwal, P. Zhu, T. L. Hughes and V. Madhavan, Nat. Commun., 2021, 12, 4420.
16. Y.-B. Choi, Y. Xie, C.-Z. Chen, J. Park, S.-B. Song, J. Yoon, B. J. Kim, T. Taniguchi, K. Watanabe, J. Kim, K. C. Fong, M. N. Ali, K. T. Law and G.-H. Lee, Nat. Mater., 2020, 19, 974.
17. C. Z. Li, A. Q. Wang, C. Li, W. Z. Zheng, A. Brinkman, D. P. Yu and Z. M. Liao, Phys. Rev. Lett., 2020, 124, 156601.
18. H. Xue, Y. Yang, F. Gao, Y. Chong and B. Zhang, Nat. Mater., 2019, 18, 108.
19. A. Kononov, G. Abulizi, K. Qu, J. Yan, D. Mandrus, K. Watanabe, T. Taniguchi and C. Schönenberger, Nano Lett., 2020, 20, 4228.
20. X. Qian, J. Liu, L. Fu and J. Li, Science, 2014, 346, 1344.
21. S. Tang, C. Zhang, D. Wong, Z. Pedramrazi, H.-Z. Tsai, C. Jia, B. Moritz, M. Claassen, H. Ryu, S. Kahn, J. Jiang, H. Yan, M. Hashimoto, D. Lu, R. G. Moore, C.-C. Hwang, C. Hwang, Z. Hussain, Y. Chen, M. M. Ugeda, Z. Liu, X. Xie, T. P. Devereaux, M. F. Crommie, S.-K. Mo and Z.-X. Shen, Nat. Phys., 2017, 13, 683.
22. K. Deng, G. Wan, P. Deng, K. Zhang, S. Ding, E. Wang, M. Yan, H. Huang, H. Zhang, Z. Xu, J. Denlinger, A. Fedorov, H. Yang, W. Duan, H. Yao, Y. Wu, S. Fan, H. Zhang, X. Chen and S. Zhou, Nat. Phys., 2016, 12, 1105.
23. Y. Wu, D. Mou, N. H. Jo, K. Sun, L. Huang, S. L. Bud'ko, P. C. Canfield and A. Kaminski, Phys. Rev. B, 2016, 94, 121113.
24. Y. Qi, P. G. Naumov, M. N. Ali, C. R. Rajamathi, W. Schnelle, O. Barkalov, M. Hanfland, S.-C. Wu, C. Shekhar, Y. Sun, V. Süβ, M. Schmidt, U. Schwarz, E. Pippel, P. Werner, R. Hillebrand, T. Förster, E. Kampert, S. Parkin, R. J. Cava, C. Felser, B. Yan and S. A. Medvedev, Nat. Commun., 2016, 7, 11038.
25. W. Wang, S. Kim, M. Liu, F. A. Cevallos, R. J. Cava and N. P. Ong, Science, 2020, 368, 534.
26. F. Ando, Y. Miyasaka, T. Li, J. Ishizuka, T. Arakawa, Y. Shiota, T. Moriyama, Y. Yanase and T. Ono, Nature, 2020, 584, 373.
27. Y. Y. Lyu, J. Jiang, Y. L. Wang, Z. L. Xiao, S. Dong, Q. H. Chen, M. V. Milošević, H. Wang, R. Divan, J. E. Pearson, P. Wu, F. M. Peeters and W. K. Kwok, Nat. Commun., 2021, 12, 1.
28. H. Wu, Y. Wang, Y. Xu, P. K. Sivakumar, C. Pasco, U. Filippozzi, S. S. P. Parkin, Y. J. Zeng, T. McQueen and M. N. Ali, Nature, 2022, 604, 653.
29. C. Baumgartner, L. Fuchs, A. Costa, S. Reinhardt, S. Gronin, G. C. Gardner, T. Lindemann, M. J. Manfra, P. E. Faria Junior, D. Kochan, J. Fabian, N. Paradiso and C. Strunk, Nat. Nanotechnol., 2022, 17, 39.
30. K. R. Jeon, J. K. Kim, J. Yoon, J. C. Jeon, H. Han, A. Cottet, T. Kontos and S. S. P. Parkin, Nat. Mater., 2022, 21, 1008.
31. B. Pal, A. Chakraborty, P. K. Sivakumar, M. Davydova, A. K. Gopi, A. K. Pandeya, J. A. Krieger, Y. Zhang, M. Date, S. Ju, N. Yuan, N. B. M. Schröter, L. Fu and S. S. P. Parkin, Nat. Phys., 2022, 18, 1228.
32. B. Turini, S. Salimian, M. Carrega, A. Iorio, E. Strambini, F. Giazotto, V. Zannier, L. Sorba and S. Heun, Nano Lett., 2022, 22, 8502.
33. J. X. Lin, P. Siriviboon, H. D. Scammell, S. Liu, D. Rhodes, K. Watanabe, T. Taniguchi, J. Hone, M. S. Scheurer and J. I. A. Li, Nat. Phys., 2022, 18, 1221.
34. I. O. Kulik, J. Exp. Theor. Phys., 1969, 30, 944.
35. J. Bardeen and J. L. Johnson, Phys. Rev. B, 1972, 5, 72.
36. A. V. Svidzinskiǐ, T. N. Antsygina and E. N. Bratus, J. Exp. Theor. Phys., 1972, 34, 860.
37. A. V. Svidzinsky, T. N. Antsygina and E. N. Bratus', J. Low Temp. Phys., 1973, 10, 131.
38. I. V. Borzenets, F. Amet, C. T. Ke, A. W. Draelos, M. T. Wei, A. Seredinski, K. Watanabe, T. Taniguchi, Y. Bomze, M. Yamamoto, S. Tarucha and G. Finkelstein, Phys. Rev. Lett., 2016, 117, 237002.
39. A. Barone and G. Paterno, Physics and Applications of the Josephson Effect, Wiley, New York, 1982.
40. R. C. Dynes and T. A. Fulton, Phys. Rev. B, 1971, 3, 3015.
41. A. Murani, A. Kasumov, S. Sengupta, Y. A. Kasumov, V. T. Volkov, I. I. Khodos, F. Brisset, R. Delagrange, A. Chepelianskii, R. Deblock, H. Bouchiat and S. Guéron, Nat. Commun., 2017, 8, 15941.
42. M. Endres, A. Kononov, H. S. Arachchige, J. Yan, D. Mandrus, K. Watanabe, T. Taniguchi and C. Schönenberger, Nano Lett., 2023, 23, 4654.
43. C. G. Chu, J. J. Chen, A. Q. Wang, Z. B. Tan, C. Z. Li, C. Li, A. Brinkman, P.-Z. Xiang, N. Li, Z. C. Pan, H. Z. Lu, D. Yu and Z. M. Liao, Nat. Commun., 2023, 14, 6162.
44. C. Huang, A. Narayan, E. Zhang, X. Xie, L. Ai, S. Liu, C. Yi, Y. Shi, S. Sanvito and F. Xiu, Natl. Sci. Rev., 2020, 7, 1468.
45. M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X. L. Qi and S. C. Zhang, Science, 2007, 318, 766.
46. C. Z. Chen, J. J. He, M. N. Ali, G. H. Lee, K. C. Fong and K. T. Law, Phys. Rev. B, 2018, 98, 075430.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00884c

‡ These authors contributed equally to this work.

---