Open Access Article
Open Access ArticleKinetics of primary mechanochemical covalent-bond-forming reactions
Yerzhan S.
Zholdassov
 abc,
Ryan W.
Kwok
abc,
Ryan W.
Kwok
 bc,
Milan A.
Shlain
abc,
Monil
Patel
bc,
Milan A.
Shlain
abc,
Monil
Patel
 ab,
Mateusz
Marianski
ab,
Mateusz
Marianski
 abcd and
Adam B.
Braunschweig
abcd and
Adam B.
Braunschweig
 *abcd
*abcd
aAdvanced Science Research Center at the Graduate Center of the City University of New York, 85 St Nicholas Terrace, New York, NY 10031, USA. E-mail: abraunschweig@gc.cuny.edu
bDepartment of Chemistry, Hunter College, 695 Park Ave, New York, NY 10065, USA
cPhD Program in Chemistry, Graduate Center of the City University of New York, 365 5th Ave, New York, NY 10016, USA
dPhD Program in Biochemistry, Graduate Center of the City University of New York, 365 5th Ave, New York, NY 10016, USA
First published on 22nd February 2024
Abstract
Mechanical activation of reactions can reduce significantly the amounts of solvent and energy required to form covalent organic bonds. Despite growing interest in the field of mechanochemistry and increasing reports of mechanochemical synthesis of organic molecules, the fundamental question of how stresses activate covalent-bond-forming (CBF) reactions remains unresolved. This question remains unresolved because of the difficulties involved in measuring the applied forces and the reaction times in mechanochemical reactors, and the challenges related to deconvoluting microscopic (primary) and macroscopic (secondary) processes in the analysis of reaction kinetics. Here we discuss the use nanoscopic probe-microscope tips to explore the kinetics of CBF reactions. Because these experiments examine reactions on monolayers, surfaces, or nanoscopic particles, they circumvent secondary processes to isolate how stress affects the rates of the primary, CBF events. The major result of these studies is an emerging consensus that stress accelerates reactions by distorting organic molecules and in doing so, lowers reaction activation energies and alters reaction trajectories. This new understanding of how stresses activate reactions can be used to predict the outcomes of CBF mechanochemical reactions, which will lead to the wider adoption of sustainable mechanochemical processes by the synthetic community.
Introduction
Mechanochemistry is the use of mechanical energy to form or rupture chemical bonds, and is an alternative to conventional chemical syntheses that use solvothermal methods involving heating reactants in a solvent bath to activate chemical transformations.1–3 Mechanochemical methods have already been used to generate organometallic compounds,4,5 active pharmaceutical ingredients,6–8 nanoparticles,9,10 metal–organic frameworks,11,12 and stimuli-responsive materials.13 In addition to the wide range of materials that have been made, mechanochemical methods can produce chemicals that are difficult to obtain using solvothermal processes,14 or, in other instances, result in product distributions that differ from those obtained when the same reaction is carried out using conventional solvothermal methods.15,16 Perhaps the most compelling attribute of mechanochemical reactions is that they are significantly more sustainable than their solvothermal counterparts17 because the mechanochemical reactions often proceed with lower relative energy demand than solvothermal syntheses and without toxic solvents.2 Because of these advantages over solvothermal conditions – including faster reactions, access to alternative reaction products, and increased sustainability – the interest in mechanochemistry amongst synthetic chemists is growing rapidly. In the last two decades, the number of publications appearing under the search term “mechanochemistry” or “mechanochemical” has increased from 227 in 2002 to 2046 in 2022 according to Science Direct (Fig. 1), confirming the growing interest in mechanochemistry.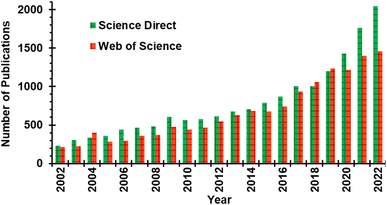 | ||
| Fig. 1 Mechanochemistry-related publication from 2002 to 2022 in Science Direct and Web of Science search engines. Title search queries were limited to “mechanochemistry” or “mechanochemical”. | ||
Despite the advantages of mechanochemical reactions and the growing interest in using them in chemical fabrication, they have not yet been widely adopted by the synthetic community and incorporated into manufacturing processes for several reasons. These include unfamiliarity with the reactors used to carry out mechanochemical reactions, a lack of appreciation for mechanochemistry's substantial sustainability benefits, and a poor understanding of how mechanochemical conditions alter reaction trajectories to dictate reaction selectivities – in other words, what distribution of products will form under mechanochemical reaction conditions. Here, we first briefly discuss how these reactions are performed and detail the sustainability benefits of mechanochemistry. Understanding selectivity, however, is more challenging. The question of reaction selectivities – specifically, why product ratios differ between mechanochemical conditions and solvothermal conditions – is not yet well-understood. Selectivity is a very important problem in mechanochemistry because grasping the molecular-scale origins of selectivity can lead directly to the understanding of how stresses affect reaction trajectories, and this knowledge could be used to develop predictive models that anticipate products and energy landscapes for reactions that have not yet been performed. As a direct consequence of solving the selectivity question, sustainable, mechanochemical reaction conditions could be designed to attain particular products.
Understanding selectivities in chemical reactions is typically approached through the measurement of reaction kinetics to determine activation energies (Eas) and transition state geometries,18 however the measurement of kinetics in mechanochemical reactions has unique challenges that do not occur when studying reactions in solution. The first challenge arises because the rates of mechanochemical reactions in mills or extruders are affected by coupled macroscopic and microscopic processes occurring in tandem (Fig. 2). The macroscopic processes – referred to here as the ‘secondary reactions’ – involve, for example, grinding powders into smaller pieces to expose reactive sites that had been buried inside solid particles. The microscopic process, or ‘primary reaction’, refers to the formation of covalent chemical bonds, like new C–C bonds, which are the same bond-forming processes that are typically followed when studying reaction kinetics in solution. These two terms have been used previously in the literature,19 and are interdependent in ball-mills and extruders. As such, understanding the contribution of force on molecular-scale processes requires disentangling microscopic/primary and macroscopic/secondary processes, which may not always be possible. The second challenge is experimental, in that tracking the reactions under stress can be extremely difficult and requires specialized instrumentation. For example, many of the reaction vessels for mills are stainless steel and cannot be interrogated spectroscopically. Even if the tracking problem is overcome,20–24 certain parameters that are essential for the kinetic modeling of mechanically driven reactions, such as the magnitude and direction of the force applied to the reactants, F, or the time a reactant is under stress, t, can be difficult to determine accurately.25 Consequently, there do not yet exist widely adopted methods to measure the kinetics of mechanochemical reactions. Although evidence has shown that mechanochemical conditions alter reaction pathways,26–31 the fundamental question of how force changes the primary mechanochemical reaction to alter the trajectory that a reaction follows along the energy landscape from reactants to products has not yet been resolved to the satisfaction of the mechanochemistry community. To address this, here we discuss how recent, tip-based experiments have been used to isolate the kinetics of primary covalent bond-forming (CBF) mechanochemical reactions on surfaces, and how these studies have provided insight into the unique role force has on the outcomes of mechanochemical reactions carried out in mills and extruders. These tip-based studies also can explain the selectivities of mechanochemical reactions in some cases, although it is too early to determine whether the results of these studies provide more general guidance beyond the particular reactions described. Although mechanochemistry has broad applications throughout chemical synthesis,32 the focus of this review is on CBF mechanochemical reactions. This review focuses specifically on how force affects primary mechanochemical CBF reactions, and how our understanding has been furthered as a result of tip-based experimental techniques. For discussions of mechanochemical bond rupture,27 combining mechanochemistry with sonochemical, thermochemical, photochemical or electrochemical activation,33,34 polymer mechanochemistry,35,36 molecular modeling of reactions under external force,37 or a more general overview of mechanochemistry,38–42 we refer interested readers to the recent reviews on those subjects.
Discussion
Mechanochemical reactors
Mechanochemical syntheses are carried out in reactors that exert stress and shearing forces on the reagents, such as milling devices, like ball mill43,44 and planetary mill reactors,25 or in twin-screw extruders.45,46 Each of these reactors has a different working principle, energy efficiency, and applies a unique combination of impact, compression, and shear forces on the reactive contents.47 The milling vials in shaker mills (Fig. 3A) are filled with grinding balls and the reactive chemicals, and the vials oscillate back and forth, causing the balls to impact the molecules with a frequency that governs the efficiency and a speed of the grinding process. In doing so, it mixes reagents, reduces particle sizes, and activates reactions through impact and shear forces generated by the balls. In planetary ball mills (Fig. 3B), the milling vial is placed on a rotating plate.25,48 The milling jar and plate rotate in opposite directions around their respective axes. As the underlying plate rotates, it causes the grinding balls inside the milling vial to rotate around their own axis. This combination of the two rotational motions causes the grinding balls to impact with high force and create frictional forces within the material being ground. Sometimes the materials of which the balls and vials are composed can take an active role as catalysts in the primary chemical reactions as well.49–52 Twin-screw extruders (Fig. 3C) operate by feeding materials into the extruder, which are then conveyed along the barrel by screws that intermesh with each other. As the material is transported, it is mixed and ground between the screws, and the resulting product is extruded through an aperture located at the device's end. Screw extruders are particularly interesting tools for scaling-up mechanochemical reactions53 – while mill instruments can generally only be run in batches, extruders can be run continuously54 and produce products at rates of hundreds of g hr−1. | ||
| Fig. 3 Common mechanochemical reactors. (A) Ball-mill, and (B) planetary mill reactors for batch synthesis. (C) Twin-screw extruder for continuous mechanochemical production. | ||
Mechanochemical sustainability
One aspect of mechanochemistry that is particularly compelling to the chemical industry is the sustainability benefits of reactions performed mechanochemically compared to performing the same transformation under solvothermal conditions. The majority of CBF reactions performed in research laboratories or by the chemical industry use solvents to solubilize molecules and to tune the reaction trajectory, and these solvents typically account for 80–90% of reaction mass.55 These solvents themselves are costly and might require preliminary conditioning, such as degassing and drying, before the reaction can be performed. Often these solvents are toxic, flammable, or environmentally detrimental, and their storage and disposal is a growing concern since 80–85% of all chemical waste is solvents. One approach to minimizing the negative impact of toxic solvents is to replace harmful solvents with “greener” alternatives,56 however these changes may attenuate reaction yields and purities. Another challenge that occurs because of the solvents in reactions is that the chemical industry consumes 37% of all manufacturing energy, in part because of the need to heat, cool, and remove solvents involved in the reactions.57 So, between their toxicity, waste, and energy demands, there are strong drivers to reduce solvent usage or eliminate them altogether.Mechanochemistry is a promising approach to eliminating the dependence of CBF reactions upon organic solvents because CBF mechanochemical reactions are carried out solvent-free or using only stoichiometric equivalents of solvents under conditions termed “liquid-assisted grinding” (LAG).58–60 In a solvent-free mechanochemical reaction in a mill, solid reagents and grinding bearings are added to a milling vial and the vial is then shaken.2 LAG59,60 is a variant of these methods, where only small amounts of solvent (<1–2 stoichiometric equivalents) are added to the system to improve the reactivity.60 It should be noted that running the reaction mechanochemically does not eliminate solvents that may be needed for purification, but improvements in selectivity and conversion that have been observed mechanochemically16 could also reduce solvent usage in isolation processes as well.61
Mechanochemical selectivity
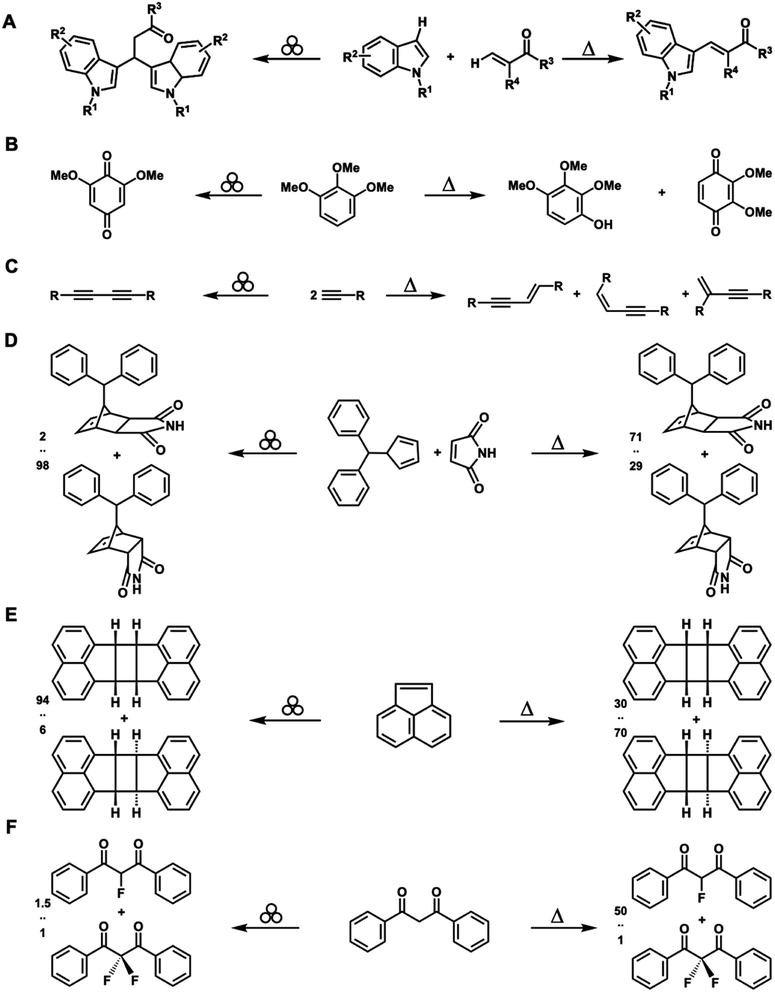
In addition to reducing the solvent and energy demands of synthesis, one of the most compelling aspects of CBF mechanochemical reaction conditions is that they may sometimes produce different products than those obtained using other forms of activation, including heat, light, or electrochemical potential.16 For example, Jia et al. studied the mechanism of the Pd-catalyzed oxidative coupling of indoles with acrylates under neat grinding and compared the results to those obtained under solvothermal conditions.62 Using DMF as a solvent, the reaction yielded exclusively 3-vinylindoles, whereas under neat milling conditions, β,β-diindolyl propionates were obtained as a major product (Fig. 4A). Sommer and co-workers have reported oxidation of methoxylated aromatic chemicals63 in the presence of Oxone®. In aqueous media, 1,2,3-trimethoxybenzene is converted to 2,3,4-trimethoxyphenol along with byproducts. Alternatively, neat grinding conditions provided 2,6-dimethoxybenzoquinone as a single product at higher total conversion (Fig. 4B). Many other examples of mechanically altered selectivity exist, which have been reviewed elsewhere,16,64 including in the synthesis of biaryls via C–H/C–H arylation,65 halogenation of organometallic complexes,66 dimerization of alkynes67 (Fig. 4C), pericyclic reactions44,68,69 (Fig. 4D), and photomechanochemical reactions15 (Fig. 4E). LAG has also led to different product distributions than those for solvent-free mechanochemical and solvothermal conditions.64 Recently, Howard et al. studied the fluorination of dibenzoylmethane with Selectfluor® reagents (Fig. 4F).70 The reaction in MeCN proceeded in 88% yield in 3.5 hours with selectivity for monofluorinated![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) difluorinated product >50
difluorinated product >50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Under neat grinding, a higher yield (95%) was achieved at shorter time (2 h) with a selectivity of 1.5
1. Under neat grinding, a higher yield (95%) was achieved at shorter time (2 h) with a selectivity of 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monofluorinated
1 monofluorinated![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) difluorinated product. Interestingly, the addition of a small amount of MeCN (10% of total volume of all materials in milling vial) led to 98% yield with a selectivity of 50
difluorinated product. Interestingly, the addition of a small amount of MeCN (10% of total volume of all materials in milling vial) led to 98% yield with a selectivity of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monofluorinated
1 monofluorinated![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) difluorinated product. Why these different selectivities arise under mechanochemical conditions compared to solvothermal conditions is still a matter of considerable debate and may not be explained by current mechanochemical kinetic theories.
difluorinated product. Why these different selectivities arise under mechanochemical conditions compared to solvothermal conditions is still a matter of considerable debate and may not be explained by current mechanochemical kinetic theories.
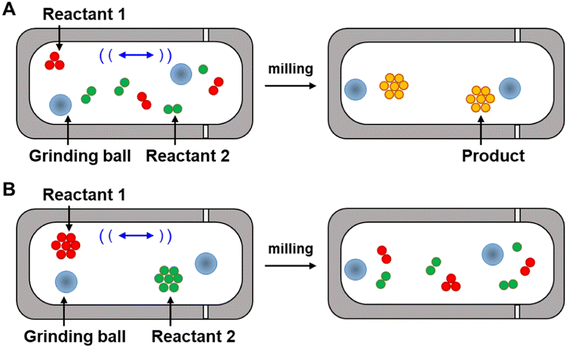
In some of these cases, theories have been presented as to why differences in selectivity are observed between solvothermal and mechanochemical conditions. Whether these theories are correct or not, the following must be true of the primary reaction for the selectivity to be altered: changes in product distribution in mechanochemical conditions compared to solvothermal conditions occur because the mechanochemical conditions change the favored trajectory the primary reaction takes across its energy landscape. In other words, the application of stresses alters the structures and energies of the reaction reagents and transition states of the preferred reaction pathway. To measure the changes in the reaction pathways, the Ea of reactions should be determined from kinetics experiments.18,71 Kinetic measurements of mechanochemical reactions have led to two primary theories to explain the rate accelerations that occur because of mechanochemical conditions, which we refer to here as the ‘hot-spot theory’ and the ‘mixing efficiency theory’. Below we describe each theory, and their limitations in explaining increased rates and the changes in selectivity of mechanochemical reactions compared to when the same reaction is carried out under strictly solvothermal conditions.
Hot-spot theory
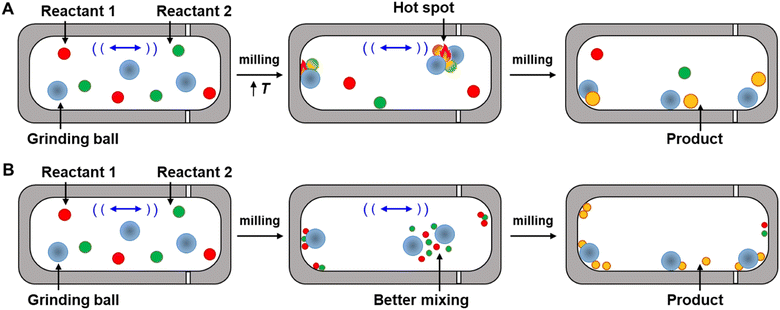
Hot spots were first proposed by Bowden and Yoffe in their investigations on impact explosives in the 1950s.72,73 This theory states that kinetic energy is dissipated into the milling medium during collision, and, as a result, extremely high temperatures can occur at the location of impact (Fig. 5A). The temperatures of these hot-spots have been hypothesized to be >1000 K (ref. 74) and to last for a few milliseconds before dissipating,75 and it is further hypothesized that these increases in temperature provide the energy to overcome the reaction activation barrier. The hot spot theory, however, has been questioned by recent experimental studies. Delogu et al. investigated the phase transition of metals and metal oxides under milling.76 These metals and metal oxides can undergo transitions between different structures under thermal activation. For example, the face-centered cubic α-phase of Ca transforms into the body-centered cubic β-phase at 720 K, while CuI γ-phase undergoes structural phase transitions, first to a β-phase and then to a α-phase structure at 650 and 672 K, respectively. However, no changes in phase were detected during milling of these materials even though the temperatures required for this conversion in both cases could presumably be accessed under hot-spot conditions. The recent development of mechanochemical reactors with the ability to control temperature precisely77 or monitor temperature in situ78 have also been used to test the hot-spot theory. The experiments revealed that the mechanical impact occurring within the reactor can increase temperature, but these increases are closer to 10 °C.79 It is worth noting, however, that these experiments may be insensitive to sharp rises in local temperatures at the site of impact from ball collisions. To measure the temperature of the balls, since the temperature rise during the milling that are hypothesized to be the result of ball-to-ball, ball-to-powder, and ball-to-wall collisions, Gerasimov et al. used calorimetric techniques to estimate the local temperatures of the balls during the milling, and found the temperatures as high as 600 °C can occur on the surface of the balls.80 As such, the roles of localized hot-spots and temperature spikes on increasing the rates of reactions remains unresolved but suggest that increased temperature could have a role in increasing reaction rates. However, because the activation here remains thermal, the transition state energies and structures would not differ from those that arise under typical thermal activation, and, as such, hot-spot theory does not account for changes in selectivities that occur in mechanochemical reactions.Mixing efficiency theory
Butyagin divided mechanochemical reactions into two groups based on their kinetics.19 In the first case, the rate of the mechanochemical process is determined by the rate of the primary chemical reaction that is under a constant field of mechanical stress. Mechanical energy is absorbed quickly when a constant stress is applied, and the stress is distributed evenly along the reaction system. In this model, the dependence of reaction rate on external stress should be defined mainly by the characteristics of the primary chemical reaction. The second class of reactions consist of a multistep process, involving both the mechanochemical deformation of matter (secondary reaction) and the primary chemical reaction. In this case the deformation of matter involves grinding neat reactants into smaller particles. Mixing of these particles increases diffusion and contact between reactants, and in turn, opportunities for the reaction to occur. By milling powders, grain sizes are reduced, which increases the surface-to-volume ratio, and in turn, the amount of reagent available for reacting (Fig. 5B). The roles of diffusion and grinding on reaction rates have been studied by several research groups. Boldyreva81–83 and others have studied the mixing efficiency of powders.19,26,84 They concluded that many factors affect the mixing efficiency, such as mixing time, mixing method, particle size and shapes, density, and rigidity of particles, and the formation of surface charges or fluid phases. They also found that pre-grinding of one or more reactants is often required before mixing two reactants together, otherwise particle segregation may occur instead of homogeneous mixing. They conclude, for example, that “if it is necessary to mix needle-shaped and spherical particles, preliminary grinding of the needle-shaped particles is required”.83 In another example, Calvet and Baltas studied the Diels–Alder reaction between diphenyl fulvene and maleimide by ball milling.44 They reported a significant acceleration of the reaction was observed with pre-ground starting materials compared to when the same reaction was carried out without pre-grinding, revealing that the smaller particles reacted faster and that the rate acceleration was associated with the increased surface area. These studies show that the mixing efficiency theory has some merit, and that secondary reactions that reduce particle size do indeed affect the kinetics of mechanochemical reactions. However, according to this theory, the reactions are still thermally activated, and this theory does not explain why the stresses within mechanochemical reactors alter the selectivities, transition states, and trajectories of primary mechanochemical reactions, so isolating the role of stress on primary reactions will still require experiments that can disentangle primary and secondary processes in CBF mechanochemical reactions.Mechanochemical bond rupture
Probing the kinetics of CBF mechanochemical reactions requires methods that can disentangle the rates of grinding, or other secondary processes, from those of the primary reactions. In addition, any such technique must be able to measure the stresses exerted between the reactants so the role of force on the reaction and the time the reaction is under stress can be probed quantitatively, thereby providing values that can be incorporated into kinetic models. These parameters, however, have proven difficult to quantify in mills and extruders, even when these reactors have been modified so the reactions occurring within them can be probed spectroscopically during the course of the reaction. Until these experimental prerequisites – the ability to measure stresses and reaction times accurately – can be met, the understanding of mechanochemical mechanisms will be incomplete and the rates and selectivities of mechanochemical reactions cannot be modeled and anticipated.One area in where there has been substantial success in disentangling how force affects reaction energies is in the study of the mechanically driven bond-rupture of mechanophores. The kinetics of bond rupture of mechanophores85,86 – molecules that selectively respond to applied mechanical energy – has been studied far more extensively than mechanochemical bond formation, and has been reviewed elsewhere.87–89 Mechanochemical bond rupture is being discussed briefly here only to demonstrate that the quantitative understanding of mechanochemical bond-rupture can inform how mechanochemical bond-formation can be studied. Mechanical energy has been applied to mechanophores through sonication,90 laser pulses,85 sliding along the surface with an atomic force microscope (AFM) probe,86,91 and pulling AFM probes.92,93 The latter has been the most broadly used as AFMs are widely available and can control precisely the stress applied and pulling rate that cause the mechanophore to rupture.
A landmark in the investigation of covalent bond-rupture in organic mechanophores was the 2007 report by Hickenboth et al. who studied the mechanically driven ring opening of a polymer-functionalized benzocyclobutene (BCB) mechanophore using sonication.90 It was hypothesized that pulling stress would cause an electrocyclic opening of the butene ring, and the researchers sought to determine the stereochemistry of the resulting products. They discovered that both the trans and cis isomers of the 1,2-disubstituted BCB undergo an electrocyclic ring opening reaction upon sonication, resulting in identical E,E-isomer products, despite the fact that the E,E product from the cis-isomer starting material is thermally forbidden under the Woodward–Hoffmann rules.94 This is in contrast to reactions initiated solely by light or heat in the absence of sonication, where the cis and trans isomers produce different products – those that are predicted by the Woodward–Hoffmann rules. These experiments showed that pulling on the reactants produced products distributions that violate these rules. The authors then rationalize the unique mechanoselectivity of the ring opening of BCB under mechanochemical conditions. They propose that the E,E-isomer arises upon sonication because a new, distorted state precedes the transition state when the molecules are being pulled upon. This distorted intermediate directs the mechanically driven reactions along a different reaction trajectory than would be followed under thermal reaction conditions. These new, mechanochemical trajectories favor the E,E-isomer as product, regardless of which BCB isomer was used as the starting material. The Martínez group modelled the response of BCB to applied external mechanical force,95 and confirmed that the application of mechanical energy significantly affects the trajectory that the primary mechanochemical reaction takes across the reaction landscape, and in turn produces a transition state that favors the E,E-product. Despite the elegance of this work and the new theories about mechanical activation that arose from these results, the drawback of using sonication to apply force is that the magnitude and direction of the stresses applied to the mechanophores is difficult to determine, which limits the ability to probe quantitatively the effect of forces on the kinetics of mechanochemical reactions.
AFM96 is known for its nanoscale imaging capabilities97 and its ability to create nanoscale structures.98,99 Its versatility is demonstrated by the fact that it can operate in a variety of environments,100,101 including ultrahigh-vacuum, ambient atmosphere,102,103 and in aqueous104 and organic solvents,86 making it well-suited for studying a wide range of processes. Importantly, AFM can apply different forms of mechanical force, including shear force91,100,105 pulling force,106 and compression.107,108 Because of these attributes, AFM-based methods have been used extensively to study the rupture of mechanically sensitive bonds in mechanophores. Another important advantage of AFM methods is that the force applied to the mechanophores, and the pulling rate can be controlled precisely. Several probe-based methods have been developed to study bond rupture, including nanoshaving,109–111 nanodissection,112 and nanografting,113,114 but the two primary AFM-based methods have emerged for studying how stresses affect bond rupture are single-molecule force spectroscopy (SMFS)92,93 and sliding the tip across the surface under load.86,91 How these experiments operate, and the knowledge gained regarding mechanophore bond-rupture are detailed below.
Using SMFS to study mechanochemical bond-rupture involves embedding mechanophores within polymer chains and adsorbing the opposing ends of the polymer chain onto the rigid substrate and onto an AFM tip, respectively (Fig. 6A). It is necessary that a sufficiently high adhesion force between the polymer chain and the AFM probe and the polymer chain and the substrate exist so that when stress is applied, the mechanophore is the weakest link and ruptures before the bonds between the polymer and the surfaces break. Retraction of the tip at a constant velocity gives rise to a force vs. chain extension curve (Fig. 6B). The bond cleavage of an individual mechanophore induces only small chain extensions, which may be difficult to detect. As such, SMFS experiments often embed multiple mechanophores within the polymer chains or involve the attachment of multiple chains between the probe and the substrate to increase signal. SMFS can apply forces ranging from a few piconewtons to several hundred nanonewtons.115 This sensitivity permits the determination of the force required to rupture the bonds in the mechanophores and also investigates how the structure and conformation of the mechanophore impact the mechanical activation energy. For example, Wang et al. reported the force-induced acceleration of the electrocyclic ring opening of gem-dichlorocyclopropanes (gDCC),106 and found that the reaction rates are affected by the stereochemistry of the α-alkene group on the gDCC, despite the two isomers having effectively identical force-free ring-opening reaction rates. It was discovered that the force required to open the E-alkene-substituted gDCC was ∼400 pN lower than that required in the corresponding Z-isomer (Fig. 6B). The experimental data revealed that the activation lengths – the change in bond length from ground state to transition state – was lower for the Z isomers than the E isomers, resulting in a lower susceptibility to stress for Z isomer, thereby requiring greater force to drive the ring-opening reaction. The same authors also conducted a systematic investigation into the contrasting reactivity of BCB116 (Fig. 6C). They found that the symmetry forbidden disrotatory ring opening of BCB occurs in the SMFS experiments, and that mechanochemical reactivity was different than solvothermal reactivity, as was observed when the same systems were ruptured using sonication.90 Additionally, using AFM methods, the authors could determine the activation force for the mechanochemically driven ring-opening (1490 pN), demonstrating the impressive ability of AFM platforms to measure mechanochemical events quantitatively.
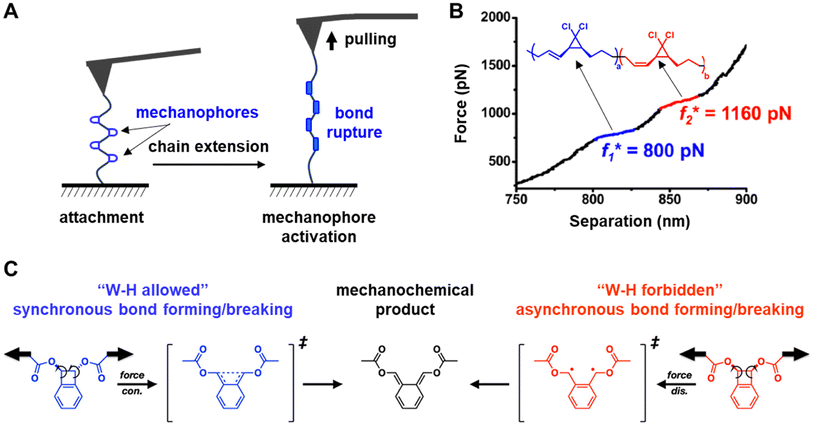 | ||
Fig. 6 (A) Single-molecule force spectroscopy (SMFS) with an atomic force microscope (AFM). (B) Force curves of the SMFS-induced rupture of gem-dichlorocyclopropane (gDCC) isomers with 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio at a retraction rate of 300 nm s−1. (C) Benzocyclobutene (BCB) showcasing both a symmetry allowed thermal conrotatory pathway and a symmetry forbidden thermal disrotatory ring-opening pathway. Under mechanochemical pulling, both cis and trans isomers favor the E,E-produce. Adapted from ref. 106 with permission from the American Chemical Society, Copyright 2014, and ref. 116 with permission from the American Chemical Society, Copyright 2021. 1 ratio at a retraction rate of 300 nm s−1. (C) Benzocyclobutene (BCB) showcasing both a symmetry allowed thermal conrotatory pathway and a symmetry forbidden thermal disrotatory ring-opening pathway. Under mechanochemical pulling, both cis and trans isomers favor the E,E-produce. Adapted from ref. 106 with permission from the American Chemical Society, Copyright 2014, and ref. 116 with permission from the American Chemical Society, Copyright 2021. | ||
The second method of studying the rupture of chemical bonds using AFM involves removing surface-anchored molecules by applying a high load and sliding the tip across the surface (Fig. 7A). The bond-rupture is subsequently monitored by measuring changes in the surface properties in areas where the load was applied, often using the very same tip that caused the bond cleavage to analyze the surface. The changes to surface properties, such as changes in topography,86,117 optical properties,86,118 and friction,91,105 can be used to extract kinetic data and determine bond strength (Fig. 7B). In one example, the change in friction of a graphene layer was used to quantify the removal of covalently bound chemical groups from the graphene surface upon applying different loads with a tip.91 Since the modified graphene interacts more strongly with the probe than with the pristine graphene, bond rupture results in decreased friction.119 Therefore, the relative difference in friction between functionalized and pristine graphene can be used to determine the degree of chemical functionalization.120 As an example, the Felts group studied the kinetics of graphene oxide (GO) reduction by applying heat and stress with an AFM tip.100 First, they studied oxygen removal from graphene driven by tip heating, with temperatures ranging from 310 to 355 °C (Fig. 7C). They defined the dependence between reaction rate k and relative friction, f as a first-order process (eqn (1)):
Δf(t) = A0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−kt + y0 e−kt + y0 | (1) |
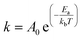 | (2) |
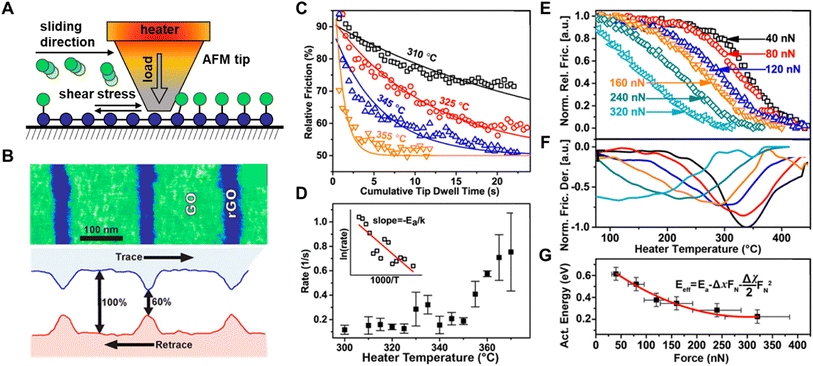 | ||
| Fig. 7 (A) Scanning AFM tip removes chemical groups from a graphene oxide by applying normal load and/or temperature and measures the removal with lateral friction measurements. (B) Friction force map of the reduced graphene oxide patterns. (C) Relative friction drop as a function of cumulative tip dwell time at various heater temperatures. (D) Reaction rate as a function of temperature; inset shows the Arrhenius plot. (E) Ramp heating rate (760 °C min−1) curves at varying tip force. The friction data obtained were normalized for the purpose of analyses. (F) Normalized relative friction derivative showing a shift in maximum removal toward lower temperatures for increasing tip force. (G) Effective energy (Eeff) as a function of tip force. Adapted from ref. 105 with permission from the American Chemical Society, Copyright 2017. | ||
They found that adding force during sliding lowers the Ea. Fig. 7E shows friction measured during sliding an AFM probe at T between 50 and 450 °C and tip loads ranging from 40 to 320 nN. The dependence of Eeff on F can be estimated from eqn (3):
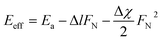 | (3) |
Although our interest here is in mechanochemical bond-formation, these studies using SMFS and AFM sliding to understand bond rupture suggest that AFM-based techniques can be used to quantify the kinetics of primary mechanochemical reactions, where the precise application of force can be used to obtain quantitative kinetic data. They serve as a roadmap to how the kinetics of primary CBF mechanochemical reactions can be interrogated using AFM techniques, where applying precise forces to understand the role of stress on the reaction kinetics that can be incorporated into predictive quantitative models. In addition, the hypothetical distorted state that precedes bond-rupture under pulling force, first proposed by Hickenboth90et al., may have an analogue in bond-forming CBF events, and understanding similarities between bond-formation and bond-rupture under stress could help clarify the unexplained mechanochemical mechanisms that lead to alternate selectivities.
Analysis of CBF primary mechanochemical reactions by tip-based methods
Taking lessons from investigations into mechanochemical bond-rupture, researchers have turned to tip-based methods to understand how force can drive CBF mechanochemical reactions. Tip-based methods are ideal for studying CBF mechanochemical reactions because the stresses applied to the reactants and the reaction times can be controlled precisely, and they can interrogate reactions occurring on monolayers, surfaces, or other nanoscale systems that do not require grinding into smaller structures before the primary reaction can occur. As such, tip-based methods can be used to study mechanochemical reactions where only the primary reaction occurs. This is advantageous over investigating CBF mechanochemical reactions in macroscopic reactors, like mills or extruders, because, with AFM, the secondary processes can be circumvented, and the complications in the kinetic analysis that arise from the convolution of primary and secondary reactions are mitigated. Overall, this can result in a simpler kinetic analysis where bond formation rates are dependent only upon the primary reaction. Here we will discuss these studies of CBF mechanochemical reactions using tip-based methods and how they are leading towards a consensus of how stress affects reaction rates and selectivities.Polymer pen lithography121 (PPL) is a variant of tip-based lithography that uses massively parallel arrays of elastomeric pyramids to pattern surfaces. In PPL, the tip arrays are coated with ink and mounted onto the piezo actuator of an AFM, which is used to repeatedly bring the arrays into contact with the surface to create a pattern (Fig. 8A). Unlike other popular nanolithography methods, like electron-beam lithography or ion-beam lithography, those tip-based methods do not use ionizing radiation that would denature or destroy soft matter to form patterns, rather the ink is gently transferred from the tips, typically through an aqueous meniscus that forms between the tips and the surface.99 Like dip-pen nanolithography, where a rigid AFM tip is used to deliver the ink to the surface,99 the feature dimensions of patterns created by PPL can be dependent upon the time the tips and surface are in contact. However, because the PPL tips are elastomeric, they are compressed when pushed into the surface, resulting in square features whose edge-lengths are dependent not on the dwell-time but rather upon the force exerted between the tips and the surface.122 As such, PPL arrays are ideal for studying the kinetics of force-accelerated reactions on surfaces because the force can be determined from the area of the printed feature, and the reaction time is controlled precisely by the piezoactuators that hold the tip-array. In addition, because these arrays can contain thousands of tips printing in parallel, each feature is printed thousands of times resulting in higher fidelity datasets for more accurate fittings. Consequently, the adoption of PPL for interrogating mechanochemical reactions has led directly to a greater understanding of how forces drive CBF reactions.
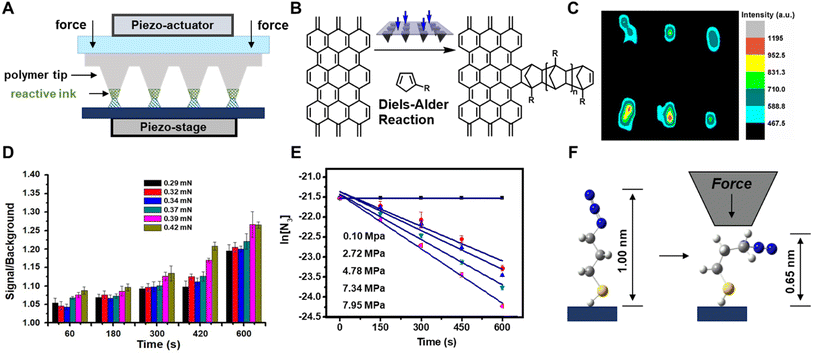 | ||
| Fig. 8 (A) Polymer pen lithography uses elastomeric tips to transfer molecules (green) onto a surface via an aqueous meniscus (blue) and apply mechanical stress by compression. (B) Diels–Alder reaction between functionalized cyclopentadiene and a SLG surface. (C) Raman mapping image (1324 cm−1, D-band) of 2 × 3 dot arrays of cyclopentadiene covalently immobilized onto the SLG. (D) Signal-to-background of the printed features of dye-labelled alkyne increases with p and t. (E) Plots of ln([azide]) vs. t at different p, whose slope provides reaction rate constants, k. (F) Molecular distortion of the azide monolayer as a result of the uniaxial force. Adapted from ref. 123 with permission from the American Chemical Society, Copyright 2013; and ref. 133 with permission from the American Chemical Society, Copyright 2014. | ||
The first demonstration of the ability of PPL arrays to drive mechanochemical reactions involved the covalent functionalization of the graphene basal plane using force-accelerated Diels–Alder reactions.123 Graphene has been championed as a promising material for sensors, transistors, and energy-harnessing devices,124 however the inability to functionalize covalently the conjugated basal plane of graphene has hindered the realization of many of these proposed technologies. Covalent reactions with the basal plane require disrupting the conjugation of the relatively inert graphene lattice, and so reactions that typically proceed with alkenes do not typically react with graphene double bonds. A reaction that had been shown to proceed for functionalizing graphene lattices in solutions at high temperatures is the Diels–Alder reaction between a diene and the graphene flakes as a dienophile.125,126 Although those reported solution conditions would be difficult to reproduce on immobilized substrates, they suggested a compelling route to pattern graphene substrates mechanochemically. As early as 1963 it was found that applied pressure increases the rate of Diels–Alder reactions in solution,127 so the Braunschweig group reasoned that PPL tips could apply force between a graphene substrate and tips coated with an appropriate diene, and the Diels–Alder reaction would proceed via the same pressure-accelerated mechanism123 (Fig. 8B). To this end, the Braunschweig group prepared electrochemically active and Raman-active cyclopentadienes that could potentially react with graphene in a Diels–Alder reaction and used those as inks. PPL arrays were coated with those diene inks by solubilizing them within a polyethylene glycol (PEG) matrix, and patterns were generated by pressing the inked PPL tips into the surface with a force of ∼100 mN. Raman microscopy, AFM, cyclic voltammetry, and molecular modeling confirmed that patterns formed as a result of covalent bond formation, with the Raman spectra showing an increase in sp3 character of the surface, as would be expected from a Diels–Alder process on graphene (Fig. 8C). Importantly, the reaction did not proceed in the absence of force. In addition to demonstrating the first method to pattern covalently the graphene basal plane, this work demonstrated that PPL arrays could be used to drive mechanochemical reactions on surfaces, while providing the ability to researchers to precisely monitor reaction force and reaction time, capabilities which continue to elude most in situ mechanochemical experiments. Additionally, in this experiment – the mechanically driven patterning of graphene – the Braunschweig group showed that reactions that are known to be sensitive to pressure in solution are likely also mechanically active.
Building upon this result, the Braunschweig group used PPL-based mechanochemical printing to address an unresolved question in mechanochemistry. Specifically, contradicting reports had arisen in the literature as to whether the 1,3-dipolar cycloaddition reaction between an alkyne and an azide, a reaction known as the Huisgen cycloaddition,128,129 could be induced to proceed on surfaces by applying pressure between the reactants. Using microcontact printing, the Reinhoudt130 and Ravoo131 groups had reported that the reaction does proceed upon the application of pressure, whereas the Stoddart group attributed the progress of the reaction in the Reinhoudt and Ravoo experiments to metal catalysts leeching from the stamp.132 In all three studies, the authors had been unable to precisely determine the reaction force, leaving the question of whether force acted on the reaction unresolved. To determine whether force could be used to induce the Huisgen reaction on surfaces, the Braunschweig group prepared azide monolayers on SiO2 and Au substrates, which would react with fluorescent and redox-active inks, respectively, that were delivered to the surface with PPL arrays.133 Again, because the azides were present as monolayers, and the alkynes were solubilized in a PEG matrix and present in great excess, no secondary mechanochemical processes were considered to be significant in the reaction. With PPL, patterns were created where the force and the reaction time at each feature could be independently controlled, and the reaction progress as a function of force (0.29–0.42 μN) and time (0–600 s) was monitored by determining the grafting density, Γ, at each feature (Fig. 8D). They found that Γ increased monotonically with both force and time, and this observation was used to explain the contradiction in the literature: at low force, the reaction does not progress, so the lack of observed reactivity was likely the result of insufficient force exerted upon the reactants.
The quantitative data from these experiments was used to understand how force affects the reaction progress. The relationship between pressure and reaction rate was first suggest by van't Hoff (eqn (4)),
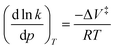 | (4) |
To further investigate the values and meaning of ΔV‡ in primary mechanochemical reactions and why they are larger than the ΔV‡ observed for reactions in solution that are run under hydrostatic pressure, PPL was used to study the Diels–Alder reaction between anthracene monolayers and a series of fluorescently labelled dienophiles that varied in steric and electronic structure.134 The Diels–Alder reaction was chosen because it has been widely studied in solution, so the relationships between reaction rates, electronic structure, and steric bulk in solution are well understood.135–137 Also, the Diels–Alder reaction is accelerated by increasing p in solution138 and has been successfully carried out in ball-mill reactors.44 In the latter case, however, the rate is dependent on both primary and secondary processes, so activation parameters of the primary reaction, such as Ea and ΔV‡, could not be determined. Using a similar approach as was used for studying the Huisgen reaction described above, the Braunschweig group created fluorescent patterns by pushing the fluorescently labelled dienophile inks into the anthracene monolayer using PPL tips (Fig. 9A and B). The fluorescence intensity of the patterns was used to track reaction progress and measure k (Fig. 9C). Using a kinetic model (eqn (5)),
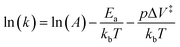 | (5) |
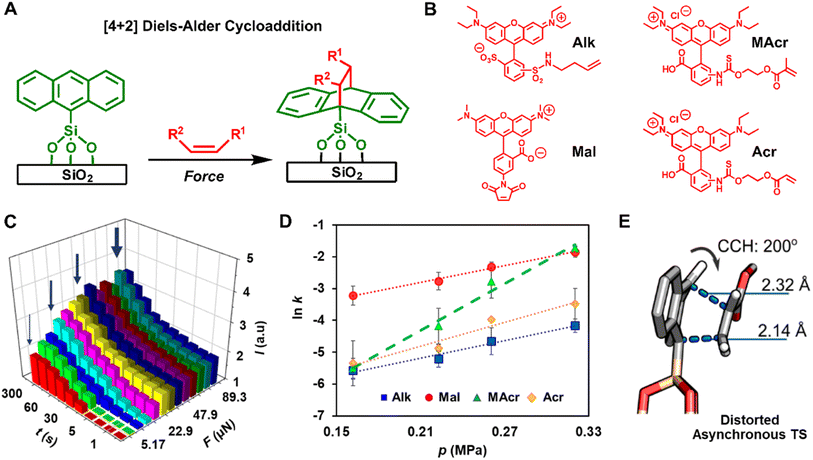 | ||
Fig. 9 (A) The Diels–Alder reaction between a dienophile and a diene (anthracene) immobilize on a silica surface. (B) The investigated set of dienophiles with varying stereoelectronic properties. (C) Normalized fluorescence intensity (I is fluorescence of feature/fluorescence of background) of the reacted molecules as a function of F and t. The wide arrows indicate high F, and narrow arrows indicate low F. (D) Plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus p for different reactants, the slope of which provides ΔV‡, whereas y-intercept provides Ea. (E) Distorting the CCH coordinate causes change to the geometry and energetics of the reaction transition state. Adapted from ref. 134 with permission from The American Association for the Advancement of Science, Copyright 2023. k versus p for different reactants, the slope of which provides ΔV‡, whereas y-intercept provides Ea. (E) Distorting the CCH coordinate causes change to the geometry and energetics of the reaction transition state. Adapted from ref. 134 with permission from The American Association for the Advancement of Science, Copyright 2023. | ||
The mechanism of the tip-driven reaction was analyzed by multiscale modeling, where it was assumed that the tips caused uniaxial stresses that resulted in bending of the immobilized anthracene, and the changes in the reaction energies as a result of this bending was analyzed. It was found that bending specific bonds (Fig. 9E) of the immobilized dienophile raises the reactant energy, ΔERd, and the transition state energy, ΔETSd, but the transition state energy rose less than the reagent energy resulting in a lower overall reaction energy (Fig. 10). To achieve this effect, the force must deform the reagents along a specific coordinate which differs from the solvothermal reaction trajectory. In case of the reported reaction, the bending of the top H atom of the anthracene towards the dienenophile destabilizes the weak, van der Waals reaction complex. At the same time, the same distortion has a weaker effect on the energy of the transition state because of a decrease in Pauli's repulsion energy between the diene's and dienophile's occupied molecular orbitals. Thus, the difference in the distortion energies, ΔΔE = ΔETSd − ΔERd, is negative which results in lowering of the activation energy.
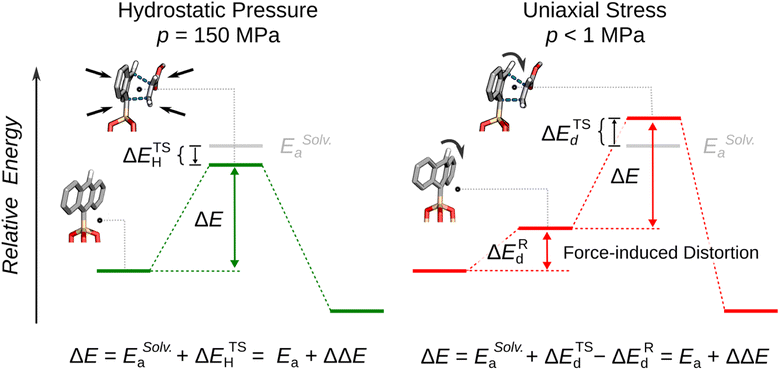 | ||
| Fig. 10 Under hydrostatic pressure, the reaction energy ΔE is equal to the sum of activation energy ΔEaSolv. and energy of the transition state, ETSH. Under uniaxial mechanical compression the reaction energy ΔE is equal to the sum of activation energy ΔESolv.a and the modified by the difference between distortion energy of the reactants, ΔERd and the distortion energy of the transition state, ΔETSd. Adapted from ref. 134 with permission from The American Association for the Advancement of Science, Copyright 2023. | ||
This mechanism – molecular distortion because of uniaxial stress lowering reaction energy – explains several unresolved questions in mechanochemistry. First, it explains why ΔV‡ are significantly higher for reactions in mechanochemical reactors than those carried out in solvent under hydrostatic pressure. Only in the former does molecular distortion occur, and relatively small amounts of uniaxial stress (<1 MPa) could cause those bends, so a small uniaxial stress could cause significant acceleration of the reaction rate. However, at least one reactant must be affixed by proximity to an interface so the distortion can occur when the stress is applied to the molecule, which is why these large accelerations are observed in mechanochemical reactors and not hydrostatic pressure. Second, this mechanism also explains the unique selectivities that are often observed under mechanochemical conditions. The underlying potential energy surface (PES) which defines the reaction trajectory is altered by the uniaxial stress which yields force-modified PES (FMPES).27 The changes to the conformations and energies of reagents and transition states on the modified PES are significant in that they may affect the primary trajectory the reaction takes across the energy landscape. Under this specific condition, applied force may make the trajectory for a different product more energetically favorable than the trajectory towards the major product that is obtained under solvothermal conditions.
This model of mechanochemical reactivity can also be extended beyond the Diels–Alder reaction because many molecules will be distorted and, in turn, destabilized as a result of molecular distortion that occurs under uniaxial stress, leading to increased reactivity, and suggests that the number of mechanically active reactions could be far greater than previously anticipated. For instance, Liu et al. recently studied force-induced [1,3]-aryl shifts within 1,4-dimethoxy-2,5-cyclohexadiene derivatives (Fig. 11) through the use of molecular bows in solution.139 Although the [1,3]-aryl shift can be realized by two consecutive [1,2]-aryl shifts, the second shift is only observed in the presence of a molecular “bowstring”. Molecular modeling showed that the bowstring causes uniaxial stress in the ring and the amount of stress increases after the first shift, but it is relieved as the reaction proceeds through the transition state of the second shift. In other words, the stress raises the energy of the intermediate formed after the first shift more than more than the transition state connecting it with the final product of the [1,3]-aryl shift.
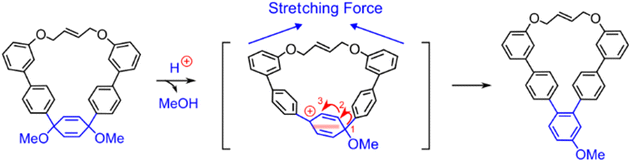 | ||
| Fig. 11 Force-induced [1,3]-aryl shift within 1,4-dimethoxy-2,5-cyclohexadiene derivatives. The shift occurs as two consecutive [1,2]-aryl shifts, where the second shift is promoted by the intramolecular strain. Adapted from ref. 139 with permission from John Wiley & Sons, Inc., Copyright 2023. | ||
Tip-induced force has also been used in combination with other stimuli, such as heat,105 electrical potential,140 and light141 to study CBF reactions on surfaces, and these efforts have helped explain how mechanical energy operates within the complex energy landscape of CBF reactions. For example, Raghuraman et al. studied the relationship between applied mechanical force and applied voltage on the rate of oxygenation of multilayered graphene using conductive AFM probes.140 The reaction was monitored by tracking changes in the friction of the surface, which increased in oxygenated areas relative to unmodified graphene (Fig. 12A). They found that applied voltage between the tip and surface primarily affected the splitting of water into H+ and OH− ions, while the applied load affects the reaction of the OH− with the graphene surface (Fig. 12B) because the onset voltage for OH− deposition decreases with increasing applied load. In this case the Eeff is a thermal barrier affected both by the mechanical force and the voltage, and the rate of this reaction will proceed according to an Arrhenius relationship (eqn (6)):
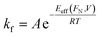 | (6) |
 | ||
| Fig. 12 (A) Conductive AFM tip in contact with graphene surface causes local anodic oxidation through an aqueous meniscus. The voltage bias between the tip and surface splits H2O into H+ and OH− groups, which migrate towards the oppositely charged surfaces. (B) Voltage ramps. Relative friction as a function of voltage for 10, 100, 200, 300 and 700 nN applied tip loads. (C) Effective energy barrier as a function of applied tip load. Insets show force per atom when contact mechanics and electrostatic forces are included. (D) The stress-assisted formation surface-bound structures on the substrate in the presence of ZDDP. (E) AFM height profile. (F) Corresponding cross sections from (E). Adapted from ref. 140 with permissions from the Royal Society of Chemistry, Copyright 2018; and ref. 142 with permissions from the American Chemical Society, Copyright 2018. | ||
The authors argue that the applied electric field, V, acts along the mechanochemical force FN and pushes the reactant state towards the transition state structure, thereby sufficiently lowering the activation barrier for the reaction to proceed (Fig. 12C).
Khare et al. have introduced a nanoscale additive manufacturing technique called “Nanotribological Printing”,142 wherein structures are formed at the interface between a substrate and an AFM probe. The molecules are dispersed in a carrier liquid surrounding the AFM probe and diffuse into the contact during sliding. They dispersed zinc dialkydithiophosphate (ZDDP) in carrier oil in 0.8 wt% and exposed this solution to normal and shear force with a pyramidal Si AFM probe on a Si substrate (Fig. 12D). The applied stresses activates the formation of surface-bound structures (Fig. 12E). Successive line scans were performed with increasing values of applied normal load over 200 cycles. As shown in Fig. 12F, ZDDP-derived patterns increase in height with increasing normal load.
Although technically involving bond-rupture, a study by Ducker et al.141 that combines tip-applied force in combination with photoirradiation provides further insight into how compressive force affects reactivity. In this study, they examined the photochemical cleavage of a nitroveratryloxycarbonyl (NVOC) protecting groups from aminosilane monolayers by simultaneously irradiating the surfaces while compressing the monolayers with tips. They showed that with this method they were able to create lines in the monolayers of selectively deprotected regions, as narrow as ∼20 nm, where the NVOC groups were removed. An interesting aspect of this study is that, while compressing the monolayers, they were able to significantly lower the energy barrier for photodeprotection from 3.1 eV to 1.2 eV – so the NVOC could be removed with visible photons – as a result of the compressive force on the monolayers. They note that the charge transfer p–p* transition is the energetic barrier of the photodeprotection reaction. The compression of the adsorbate layer decreases the N–N separation, which changes the energies of molecular orbitals and reduces this energy barrier, even under modest loading. Thus, this is another example of uniaxial stress causing a distorted state that leads to a lowering of the reaction energy, and adds to the growing body of evidence that the uniaxial stresses that occur under mechanochemical conditions cause changes in conformation that lower reaction energy barriers.
Another example to support this thesis was reported by Hawthorne et al.143 and does not involve nanoscopic tips, but rather uses a distorted surface to arrive at the same conclusion. In this work, the authors studied the reaction between 4-nitrobenzenediazonium tetrafluoroborate (4-NBD) and the basal plane of graphene, as well as the basal plane of a graphene layer that had been strained by depositing it over a layer of 6 nm diameter silica beads. The 4-NBD can react with graphene via a diazonium reaction. The authors found that the strained graphene that was draped over the silica beads had a significantly higher rate of reaction than the basal plane of unstrained graphene. In this case, draping the graphene over the silica beads has the same role as a tip that applies force has, i.e. straining and distorting the surface away from its ground state conformation and, in turn, increasing its reactivity. The authors argue that the strain decreases the sp2 character of the graphene lattice, which lowers the activation barrier, and renders the surface more reactive towards the 4-NBD.
Theoretical modeling of molecular distortions under stress
Computational techniques have contributed to the development of theories of mechanochemistry that account for macro-, meso-, and molecular-scale effects. Each of these scales presents a unique set of challenges for computational studies, leading to the development of computational toolsets to tackle these challenges, such as finite element analysis,144,145 kinetic Monte Carlo,146 coarse grain methods,147 reactive force fields,148 parallel tempering,149 atomistic molecular dynamics (MD),28 metadynamics ab initio MD150 and density functional theory (DFT).151–153 Each of these methods has been reviewed recently, and here we will focus on the application of quantum methods that model the effect of molecular distortion on molecular reactivity.The relationship between force and a mechanochemical reaction's rate can be inferred from Bell theory.37 To a first order approximation, the rate of the chemical reaction under external force can be calculated as (eqn (7)):
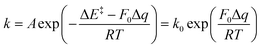 | (7) |
Quantum chemical methods allow us to investigate the influence of molecular distortion on chemical reactions, and DFT, as a result of its accuracy and computational tractability, is the most commonly used method to study reaction mechanisms. Perhaps the most intuitive approach to include the effect of force in quantum mechanical treatment of mechanochemical conditions is the constrained geometries simulate external force (CoGEF) method.154,155 As the name suggest, the methods applies arbitrary constraints to the molecular geometry to mimic the effect of the molecular deformation caused by an external force (eqn (8)):
| VCoGEF(x, q) = VBO(x) − λ(q(x) − q0) | (8) |
Alternatively, the external force can be included during geometry optimization.156 An example of such class of methods is external force is explicitly included (EFEI) method,95,157 which transforms the PES with a constant, explicit force (eqn (9)):
| VEFEI(x, F0) = VBO(x) − F0q(x) | (9) |
| ΔE‡(F0) = VEFEI(xTS, F0) − VEFEI(xR, F0), | (10) |
Both methods have been applied extensively in polymer mechanochemistry with a focus on bond rupture, which involves constraining end-to-end bond distances to simulate the effect of force. These methods have been repeatedly validated in the scientific literature,158–162 however, the application of both methods requires defining a molecular coordinate along which the pulling occurs. This coordinate can span multiple molecular degrees of freedom – molecular bonds, angles, and dihedral angles – and the resulting distribution and magnitude of mechanical forces throughout the system depends on the choice of an appropriate coordinate system. Several different coordinate systems,37,163–165 which can be divided into redundant and non-redundant sets of coordinates, have been proposed, but the outcome of the analysis strongly depends on the coordinate system. Recently, this problem has been addressed by Baron et al.,166,167 who explained the acceleration of the Diels–Alder reaction in a ball-mill reactor by expressing the molecular distortion using a basis set of vibrational modes.
The challenge of defining the coordinate of the uniaxial force is amplified during study of mechanochemical CBF reaction where, in contrast to stretching, a pushing force is involved. The pushing force opens up new trajectories of mechanical activation, but they may not align with a deformation of a specific bond. Instead, the force is allowed to act along additional degrees of freedom, which likely occurs in mechanochemical reactors, and multiple coordinates are deformed simultaneously, which poses a combinatorial problem for PES evaluation. The challenge that arises is that any arbitrary selection of distortion coordinates, such as bending only a single H atom in the Diels–Alder reaction, might oversimplify the system and omit the sampling of the true reaction trajectory. Sampling all potentially relevant coordinates, however, is not computationally feasible, as the number of calculations increases exponentially with the number of coordinates.
Finally, it should be noted that the described quantum mechanical treatment involves only static calculations on a molecular PES that addresses the ‘primary reaction’. A consequence of this static approach is that the effects of temperature fluctuations and entropy,76 nuclear quantum effects,168 and non-adiabatic effects169 are not included. While MD and AIMD methods can address the effect of the temperature and entropy, as well as be able to sample relevant reaction coordinates, they still suffer from increased computational costs and other limitations. A more comprehensive computational toolset investigating force-based reactivity must go beyond Born–Oppenheimer surfaces, but such a toolset has yet to be applied for the investigation of microscale molecular distortion on the rates and selectivities of CBFs. The complete multiscale computational toolset, however, should include the ‘secondary reaction’, such as mixing and grinding powders into smaller pieces.
Open questions in CBF mechanochemical reactions
The tip-based studies of mechanically driven CBF reactions have led to an emerging consensus on how mechanochemical conditions – the application of uniaxial stress to a chemical reaction – drives primary CBF reactions towards products: uniaxial stress distorts and destabilizes bonds, thereby lowering the reaction energy. This paradigm suggests that the chemical reactions that are susceptible to mechanochemical conditions could be far greater than previously anticipated and provides an explanation of the anomalous mechanochemical selectivity that has been observed experimentally because the distorted transition state is different than the transition state involved when using other modes of activation (e.g. solvothermal, electrochemical, photochemical). With this new understanding of the mechanisms of mechanochemical understanding, several new questions about CBF mechanochemical reactions can be considered. These include: Are CBF mechanochemical reactions reversible? And can we create kinetic models that consider both primary and secondary reactions?Reversibility of CBF mechanochemical reactions
Based on the literature, it appears that at least some mechanochemical CBF reactions are reversible, and that the direction of the reaction is dependent on how the mechanical energy is applied. Take for example the Diels–Alder reaction, where dienes and dienophiles are reacted to produce cyclohexenes, and its reverse, the retro-Diels–Alder reaction. Both reactions can be driven mechanochemically,134,170 suggesting that at least one mechanochemical reaction is reversible, but how does one control the direction of the reaction? Answering this question illustrates the unique aspect of mechanical energy compared to thermal energy or even hydrostatic pressure in that mechanochemical reactors can control the direction of uniaxial stress relative to the reaction trajectory, whereas other activation forms do not have this directionality. Pulling with AFM tips apply uniaxial stress in a direction that favors bond rupture, whereas pushing forces that occur in mills, extruders, or when tips are used to push upon a surface, applies uniaxial stress in the opposite direction. So, the direction of the reaction – as in Diels–Alder reaction or retro-Diels–Alder reaction – under mechanochemical conditions is determined by the directions of the uniaxial stress relative to the reaction coordinate. It is important to note that the forward and reverse reactions of the Diels–Alder/retro-Diels–Alder reactions, and likely any other reversible mechanochemical reaction pair, have important similarities and differences.134 The mechanochemical reaction pairs are similar in that they form a mechanically distorted state that precedes the transition state as uniaxial stress is applied, and that their transition state structures differ from those of their thermally driven counterparts. As a result of the distorted transition state, the reaction energy is lower than that of the thermally driven reactions, such that uniaxial stress causes a significant acceleration of the reaction rates. While both the forward and reverse reactions proceed through strained transition states, the structures and energies of their transition states differ significantly.Combining primary and secondary reaction kinetics
It is increasingly clear that the rates of mechanochemical reactions in macroscopic reactors – ball mills, planetary mills, and extruders – are dependent on the rates of both primary and secondary processes. While some kinetic models have been developed,171–174 models that consider both processes have not yet been successfully applied to describe the kinetics of mechanochemical reactions. While selectivity can now be explained, until new kinetic models emerge that combine primary and secondary processes, the rates and energetics of mechanochemical reaction kinetics cannot be anticipated. However, we anticipate that as more knowledge and data is generated regarding primary mechanochemical processes, these data can be combined with the substantial literature on secondary processes to develop unified mechanochemical kinetic models that account for both primary and secondary processes on reaction rates.Conclusions
Mechanochemistry has the potential to revolutionize the synthesis of organic compounds by reducing solvent and energy usage substantially, and providing products that may not be accessible by conventional solvothermal methods. However, the inability to understand mechanochemical kinetics has hindered the development of predictive models to explain the outcomes of mechanochemical reactions, and, in turn, the wider adoption of mechanochemistry by synthetic chemists. Here we discussed emerging literature from the use of scanning probe tips and computational studies to investigate the kinetics of primary mechanochemical reactions. What we find is that there is an emerging consensus that suggests that mechanochemical acceleration and unique product selectivities in CBFs arise because molecules are distorted in mechanochemical reactors. The result of this distortion is that mechanochemical CBF reactions proceed via a different trajectory than their solvothermal counterparts, and that this distortion causes a decrease of reaction energies. Although these studies reveal how uniaxial stresses affect primary mechanochemical mechanisms, several fundamental questions remain unresolved. For instance, the question of how crystal polymorphism may affect the selectivity of mechanochemical reactions. The most pressing of these questions, however, is how the primary and secondary processes together dictate the overall rates, energies, and selectivities of mechanochemical reactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. M. and A. B. B. are grateful to the National Science Foundation (NSF) Center for the Mechanical Control of Chemistry (CCI CHE-2023644 and CCI CHE-2303044) for generous support. A. B. B. also acknowledges support from NSF award DBI-2032176 and the NSF Center for Interface Design and Engineered Assembly of Low Dimensional Systems HRD-2112550. R. W. K. and M. S. thank National Science Foundation Research Traineeship Program (2151945) for their support.References
- F. Cuccu, L. De Luca, F. Delogu, E. Colacino, N. Solin, R. Mocci and A. Porcheddu, Mechanochemistry: New Tools to Navigate the Uncharted Territory of “Impossible” Reactions, ChemSusChem, 2022, 15(17), e202200362 CrossRef CAS PubMed.
- J.-L. Do and T. Friščić, Mechanochemistry: A Force of Synthesis, ACS Cent. Sci., 2017, 3(1), 13–19 CrossRef CAS PubMed.
- W. Ostwald and W. H. Morris, The Fundamental Principles of Chemistry: An Introduction to All Text-Books of Chemistry, Longmans, Green, and Co., 1909 Search PubMed.
- Y. X. Shi, K. Xu, J. K. Clegg, R. Ganguly, H. Hirao, T. Friščić and F. García, The First Synthesis of the Sterically Encumbered Adamantoid Phosphazane P4(NtBu)6: Enabled by Mechanochemistry, Angew. Chem., Int. Ed., 2016, 55(41), 12736–12740 CrossRef CAS PubMed.
- N. R. Rightmire and T. P. Hanusa, Advances in organometallic synthesis with mechanochemical methods, Dalton Trans., 2016, 45(6), 2352–2362 RSC.
- D. Tan, L. Loots and T. Friščić, Towards medicinal mechanochemistry: evolution of milling from pharmaceutical solid form screening to the synthesis of active pharmaceutical ingredients (APIs), Chem. Commun., 2016, 52(50), 7760–7781 RSC.
- E. Colacino, A. Porcheddu, I. Halasz, C. Charnay, F. Delogu, R. Guerra and J. Fullenwarth, Mechanochemistry for “no solvent, no base” preparation of hydantoin-based active pharmaceutical ingredients: nitrofurantoin and dantrolene, Green Chem., 2018, 20(13), 2973–2977 RSC.
- I. Sović, S. Lukin, E. Meštrović, I. Halasz, A. Porcheddu and F. Delogu, et al., Mechanochemical Preparation of Active Pharmaceutical Ingredients Monitored by In Situ Raman Spectroscopy, ACS Omega, 2020, 5(44), 28663–28672 CrossRef PubMed.
- T. Tsuzuki and P. G. McCormick, Mechanochemical synthesis of nanoparticles, J. Mater. Sci., 2004, 39(16), 5143–5146 CrossRef CAS.
- T. Tsuzuki, Mechanochemical synthesis of metal oxide nanoparticles, Commun. Chem., 2021, 4(1), 143 CrossRef CAS PubMed.
- M. Klimakow, P. Klobes, A. F. Thünemann, K. Rademann and F. Emmerling, Mechanochemical Synthesis of Metal−Organic Frameworks: A Fast and Facile Approach toward Quantitative Yields and High Specific Surface Areas, Chem. Mater., 2010, 22(18), 5216–5221 CrossRef CAS.
- C.-A. Tao and J.-F. Wang, Synthesis of Metal Organic Frameworks by Ball-Milling, Crystals, 2021, 11(1), 15 CrossRef CAS.
- C. Hu, P. van Bonn, D. E. Demco, C. Bolm and A. Pich, Mechanochemical Synthesis of Stimuli Responsive Microgels, Angew. Chem., Int. Ed., 2023, 62, e202305783 CrossRef CAS PubMed.
- N. R. Rightmire, T. P. Hanusa and A. L. Rheingold, Mechanochemical Synthesis of [1,3-(SiMe3)2C3H3]3(Al,Sc), a Base-Free Tris(allyl)aluminum Complex and Its Scandium Analogue, Organometallics, 2014, 33(21), 5952–5955 CrossRef CAS.
- S. Biswas, S. Banerjee, M. A. Shlain, A. A. Bardin, R. V. Ulijn and B. L. Nannenga, et al., Photomechanochemical control over stereoselectivity in the [2 + 2] photodimerization of acenaphthylene, Faraday Discuss., 2023, 241, 266–277 RSC.
- J. G. Hernández and C. Bolm, Altering Product Selectivity by Mechanochemistry, J. Org. Chem., 2017, 82(8), 4007–4019 CrossRef PubMed.
- K. J. Ardila-Fierro and J. G. Hernández, Sustainability Assessment of Mechanochemistry by Using the Twelve Principles of Green Chemistry, ChemSusChem, 2021, 14(10), 2145–2162 CrossRef CAS PubMed.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006 Search PubMed.
- P. Y. Butyagin, Kinetics and nature of mechanochemical reactions, Russ. Chem. Rev., 1971, 40(11), 901 CrossRef.
- P. A. Julien, I. Malvestiti and T. Friščić, The effect of milling frequency on a mechanochemical organic reaction monitored by in situ Raman spectroscopy, Beilstein J. Org. Chem., 2017, 13, 2160–2168 CrossRef CAS PubMed.
- A. A. L. Michalchuk and F. Emmerling, Time-Resolved In Situ Monitoring of Mechanochemical Reactions, Angew. Chem., Int. Ed., 2022, 61(21), e202117270 CrossRef CAS PubMed.
- I. Halasz, S. A. J. Kimber, P. J. Beldon, A. M. Belenguer, F. Adams and V. Honkimäki, et al., In situ and real-time monitoring of mechanochemical milling reactions using synchrotron X-ray diffraction, Nat. Protoc., 2013, 8(9), 1718–1729 CrossRef PubMed.
- A. D. Katsenis, A. Puškarić, V. Štrukil, C. Mottillo, P. A. Julien and K. Užarević, et al., In situ X-ray diffraction monitoring of a mechanochemical reaction reveals a unique topology metal-organic framework, Nat. Commun., 2015, 6(1), 6662 CrossRef CAS PubMed.
- C. Leroy, S. Mittelette, G. Félix, N. Fabregue, J. Špačková and P. Gaveau, et al., Operando acoustic analysis: a valuable method for investigating reaction mechanisms in mechanochemistry, Chem. Sci., 2022, 13(21), 6328–6334 RSC.
- C. F. Burmeister and A. Kwade, Process engineering with planetary ball mills, Chem. Soc. Rev., 2013, 42(18), 7660–7667 RSC.
- V. V. Boldyrev and E. G. Avvakumov, Mechanochemistry of inorganic solids, Russ. Chem. Rev., 1971, 40(10), 847 CrossRef.
- J. Ribas-Arino and D. Marx, Covalent mechanochemistry: theoretical concepts and computational tools with applications to molecular nanomechanics, Chem. Rev., 2012, 112(10), 5412–5487 CrossRef CAS PubMed.
- J. Yeon, X. He, A. Martini and S. H. Kim, Mechanochemistry at solid surfaces: polymerization of adsorbed molecules by mechanical shear at tribological interfaces, ACS Appl. Mater. Interfaces, 2017, 9(3), 3142–3148 CrossRef CAS PubMed.
- W. Sakai, L. Gonnet, N. Haruta, T. Sato and M. Baron, Theoretical study on the mechanochemical reactivity in Diels–Alder reactions, Phys. Chem. Chem. Phys., 2024, 26, 873–878 RSC.
- R. Rana, R. Bavisotto, K. Hou, N. Hopper and W. T. Tysoe, Surface Chemistry at the Solid-Solid Interface; Selectivity and Activity in Mechanochemical Reactions on Surfaces, Chem.: Methods, 2021, 1(7), 340–349 CAS.
- S. Romero Garcia, Y. S. Zholdassov, A. B. Braunschweig and A. Martini, Reactive Simulations of Silica Functionalization with Aromatic Hydrocarbons, Langmuir, 2023, 40, 561–567 CrossRef PubMed.
- T. Friščić, C. Mottillo and H. M. Titi, Mechanochemistry for Synthesis, Angew. Chem., Int. Ed., 2020, 59(3), 1018–1029 CrossRef PubMed.
- V. Martinez, T. Stolar, B. Karadeniz, I. Brekalo and K. Užarević, Advancing mechanochemical synthesis by combining milling with different energy sources, Nat. Rev. Chem, 2023, 7(1), 51–65 CrossRef CAS PubMed.
- J. Stojaković, B. S. Farris and L. R. MacGillivray, Vortex grinding for mechanochemistry: application for automated supramolecular catalysis and preparation of a metal–organic framework, Chem. Commun., 2012, 48(64), 7958–7960 RSC.
- M. A. Ghanem, A. Basu, R. Behrou, N. Boechler, A. J. Boydston and S. L. Craig, et al., The role of polymer mechanochemistry in responsive materials and additive manufacturing, Nat. Rev. Mater., 2021, 6(1), 84–98 CrossRef CAS.
- P. A. May and J. S. Moore, Polymer mechanochemistry: techniques to generate molecular force via elongational flows, Chem. Soc. Rev., 2013, 42(18), 7497–7506 RSC.
- T. Stauch and A. Dreuw, Advances in Quantum Mechanochemistry: Electronic Structure Methods and Force Analysis, Chem. Rev., 2016, 116(22), 14137–14180 CrossRef CAS PubMed.
- R. T. O'Neill and R. Boulatov, The many flavours of mechanochemistry and its plausible conceptual underpinnings, Nat. Rev. Chem, 2021, 5(3), 148–167 CrossRef PubMed.
- A. A. L. Michalchuk, E. V. Boldyreva, A. M. Belenguer, F. Emmerling and V. V. Boldyrev, Tribochemistry, Mechanical Alloying, Mechanochemistry: What is in a Name?, Front. Chem., 2021, 9, 685789 CrossRef CAS PubMed.
- S. Pagola, Outstanding Advantages, Current Drawbacks, and Significant Recent Developments in Mechanochemistry: A Perspective View, Crystals, 2023, 13(1), 124 CrossRef CAS.
- S. L. Craig, Concluding remarks: Fundamentals, applications and future of mechanochemistry, Faraday Discuss., 2023, 241, 485–491 RSC.
- E. Boldyreva, Spiers Memorial Lecture: mechanochemistry, tribochemistry, mechanical alloying – retrospect, achievements and challenges, Faraday Discuss., 2023, 241, 9–62 RSC.
- J. M. Andersen and J. Mack, Decoupling the Arrhenius equation via mechanochemistry, Chem. Sci., 2017, 8(8), 5447–5453 RSC.
- L. Gonnet, A. Chamayou, C. André-Barrès, J.-C. Micheau, B. Guidetti and T. Sato, et al., Elucidation of the Diels–Alder Reaction Kinetics between Diphenylfulvene and Maleimide by Mechanochemistry and in Solution, ACS Sustain. Chem. Eng., 2021, 9(12), 4453–4462 CrossRef CAS.
- D. E. Crawford, A. Porcheddu, A. S. McCalmont, F. Delogu, S. L. James and E. Colacino, Solvent-Free, Continuous Synthesis of Hydrazone-Based Active Pharmaceutical Ingredients by Twin-Screw Extrusion, ACS Sustain. Chem. Eng., 2020, 8(32), 12230–12238 CrossRef CAS.
- B. D. Egleston, M. C. Brand, F. Greenwell, M. E. Briggs, S. L. James and A. I. Cooper, et al., Continuous and scalable synthesis of a porous organic cage by twin screw extrusion (TSE), Chem. Sci., 2020, 11(25), 6582–6589 RSC.
- E. Colacino, M. Carta, G. Pia, A. Porcheddu, P. C. Ricci and F. Delogu, Processing and Investigation Methods in Mechanochemical Kinetics, ACS Omega, 2018, 3(8), 9196–9209 CrossRef CAS PubMed.
- A. Stolle, R. Schmidt and K. Jacob, Scale-up of organic reactions in ball mills: process intensification with regard to energy efficiency and economy of scale, Faraday Discuss., 2014, 170, 267–286 RSC.
- D. A. Fulmer, W. C. Shearouse, S. T. Medonza and J. Mack, Solvent-free Sonogashira coupling reaction via high speed ball milling, Green Chem., 2009, 11(11), 1821–1825 RSC.
- W. Pickhardt, S. Grätz and L. Borchardt, Direct Mechanocatalysis: Using Milling Balls as Catalysts, Chemistry, 2020, 26(57), 12903–12911 CrossRef CAS PubMed.
- R. A. Haley, J. Mack and H. Guan, 2-in-1: catalyst and reaction medium, Inorg. Chem. Front., 2017, 4(1), 52–55 RSC.
- C. G. Vogt, S. Grätz, S. Lukin, I. Halasz, M. Etter, J. D. Evans and L. Borchardt, Direct Mechanocatalysis: Palladium as Milling Media and Catalyst in the Mechanochemical Suzuki Polymerization, Angew. Chem., Int. Ed., 2019, 58(52), 18942–18947 CrossRef CAS PubMed.
- Q. Cao, D. E. Crawford, C. Shi and S. L. James, Greener Dye Synthesis: Continuous, Solvent-Free Synthesis of Commodity Perylene Diimides by Twin-Screw Extrusion, Angew. Chem., 2020, 132(11), 4508–4513 CrossRef.
- D. E. Crawford, C. K. G. Miskimmin, A. B. Albadarin, G. Walker and S. L. James, Organic synthesis by Twin Screw Extrusion (TSE): continuous, scalable and solvent-free, Green Chem., 2017, 19(6), 1507–1518 RSC.
- C. Sansom, Solvents and Sustainability, Chemistry World, 2018 Search PubMed.
- C. J. Clarke, W.-C. Tu, O. Levers, A. Bröhl and J. P. Hallett, Green and Sustainable Solvents in Chemical Processes, Chem. Rev., 2018, 118(2), 747–800 CrossRef CAS PubMed.
- 2018 Manufacturing Energy Consumption Survey, US Energy Information Administration, 2021 Search PubMed.
- T. Friščić, S. L. Childs, S. A. A. Rizvi and W. Jones, The role of solvent in mechanochemical and sonochemical cocrystal formation: a solubility-based approach for predicting cocrystallisation outcome, CrystEngComm, 2009, 11(3), 418–426 RSC.
- P. Ying, J. Yu and W. Su, Liquid-Assisted Grinding Mechanochemistry in the Synthesis of Pharmaceuticals, Adv. Synth. Catal., 2021, 363(5), 1246–1271 CrossRef CAS.
- Z.-J. Jiang, Z.-H. Li, J.-B. Yu and W.-K. Su, Liquid-Assisted Grinding Accelerating: Suzuki–Miyaura Reaction of Aryl Chlorides under High-Speed Ball-Milling Conditions, J. Org. Chem., 2016, 81(20), 10049–10055 CrossRef CAS PubMed.
- Y.-J. Tan, Z. Zhang, F.-J. Wang, H.-H. Wu and Q.-H. Li, Mechanochemical milling promoted solvent-free imino Diels–Alder reaction catalyzed by FeCl3: diastereoselective synthesis of cis-2,4-diphenyl-1,2,3,4-tetrahydroquinolines, RSC Adv., 2014, 4(67), 35635–35638 RSC.
- K.-Y. Jia, J.-B. Yu, Z.-J. Jiang and W.-K. Su, Mechanochemically activated oxidative coupling of indoles with acrylates through C–H activation: synthesis of 3-vinylindoles and β, β-diindolyl propionates and study of the mechanism, J. Org. Chem., 2016, 81(14), 6049–6055 CrossRef CAS PubMed.
- S. Collom, P. Anastas, E. Beach, R. Crabtree, N. Hazari and T. Sommer, Differing selectivities in mechanochemical versus conventional solution oxidation using Oxone, Tetrahedron Lett., 2013, 54(19), 2344–2347 CrossRef CAS.
- J. L. Howard, M. C. Brand and D. L. Browne, Switching chemoselectivity: using mechanochemistry to alter reaction kinetics, Angew. Chem., 2018, 130(49), 16336–16340 CrossRef.
- S.-J. Lou, Y.-J. Mao, D.-Q. Xu, J.-Q. He, Q. Chen and Z.-Y. Xu, Fast and selective dehydrogenative C–H/C–H arylation using mechanochemistry, ACS Catal., 2016, 6(6), 3890–3894 CrossRef CAS.
- J. G. Hernández, N. A. Macdonald, C. Mottillo, I. S. Butler and T. Friščić, A mechanochemical strategy for oxidative addition: remarkable yields and stereoselectivity in the halogenation of organometallic Re (I) complexes, Green Chem., 2014, 16(3), 1087–1092 RSC.
- L. Chen, M. Regan and J. Mack, The choice is yours: using liquid-assisted grinding to choose between products in the palladium-catalyzed dimerization of terminal alkynes, ACS Catal., 2016, 6(2), 868–872 CrossRef CAS.
- Z. Zhang, Z.-W. Peng, M.-F. Hao and J.-G. Gao, Mechanochemical Diels-Alder cycloaddition reactions for straightforward synthesis of endo-norbornene derivatives, Synlett, 2010, 2895–2898 CrossRef CAS.
- A. Rammohan, A. P. Krinochkin, A. F. Khasanov, D. S. Kopchuk and G. V. Zyryanov, Sustainable Solvent-Free Diels–Alder Approaches in the Development of Constructive Heterocycles and Functionalized Materials: A Review, Top. Curr. Chem., 2022, 380(5), 43 CrossRef CAS PubMed.
- J. L. Howard, Y. Sagatov, L. Repusseau, C. Schotten and D. L. Browne, Controlling reactivity through liquid assisted grinding: the curious case of mechanochemical fluorination, Green Chem., 2017, 19(12), 2798–2802 RSC.
- M. G. Evans and M. Polanyi, Some applications of the transition state method to the calculation of reaction velocities, especially in solution, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- F. Bowden and A. Yoffe, Fast Reactions in Solids, Butterworths Scientific Publications, 1958 Search PubMed.
- F. P. Bowden and A. D. Yoffe, Initiation and Growth of Explosion in Liquids and Solids, CUP Archive, 1985 Search PubMed.
- G. Heinicke, Tribochemistry, ed. L. M. Belyaev and Y. N. Martyshev, Akad.-Verlag, Berlin, 1984, vol. 460, p. 6 Search PubMed.
- P. G. Fox, Mechanically initiated chemical reactions in solids, J. Mater. Sci., 1975, 10(2), 340–360 CrossRef CAS.
- F. Delogu and G. Cocco, Weakness of the “hot spots” approach to the kinetics of mechanically induced phase transformations, J. Alloys Compd., 2008, 465(1), 540–546 CrossRef CAS.
- F. Fischer, K.-J. Wenzel, K. Rademann and F. Emmerling, Quantitative determination of activation energies in mechanochemical reactions, Phys. Chem. Chem. Phys., 2016, 18(33), 23320–23325 RSC.
- L. Batzdorf, F. Fischer, M. Wilke, K. J. Wenzel and F. Emmerling, Direct in situ investigation of milling reactions using combined X-ray diffraction and Raman spectroscopy, Angew. Chem., 2015, 127(6), 1819–1822 CrossRef.
- H. Kulla, M. Wilke, F. Fischer, M. Röllig, C. Maierhofer and F. Emmerling, Warming up for mechanosynthesis – temperature development in ball mills during synthesis, Chem. Commun., 2017, 53(10), 1664–1667 RSC.
- Y.-S. Kwon, K. B. Gerasimov and S.-K. Yoon, Ball temperatures during mechanical alloying in planetary mills, J. Alloys Compd., 2002, 346(1–2), 276–281 CrossRef CAS.
- E. Boldyreva, Mechanochemistry of inorganic and organic systems: what is similar, what is different?, Chem. Soc. Rev., 2013, 42(18), 7719–7738 RSC.
- A. A. Michalchuk, I. A. Tumanov, V. A. Drebushchak and E. V. Boldyreva, Advances in elucidating mechanochemical complexities via implementation of a simple organic system, Faraday Discuss., 2014, 170, 311–335 RSC.
- O. Lapshin, E. Boldyreva and V. Boldyrev, Role of mixing and milling in mechanochemical synthesis, Russ. J. Inorg. Chem., 2021, 66, 433–453 CrossRef CAS.
- C. W. Yip and J. A. Hersey, Perfect powder mixtures, Powder Technol., 1977, 16(2), 189–192 CrossRef CAS.
- J. Sung, M. J. Robb, S. R. White, J. S. Moore and N. R. Sottos, Interfacial Mechanophore Activation Using Laser-Induced Stress Waves, J. Am. Chem. Soc., 2018, 140(15), 5000–5003 CrossRef CAS PubMed.
- A. R. Sulkanen, J. Sung, M. J. Robb, J. S. Moore, N. R. Sottos and G.-y Liu, Spatially selective and density-controlled activation of interfacial mechanophores, J. Am. Chem. Soc., 2019, 141(9), 4080–4085 CrossRef CAS PubMed.
- J. Li, C. Nagamani and J. S. Moore, Polymer Mechanochemistry: From Destructive to Productive, Acc. Chem. Res., 2015, 48(8), 2181–2190 CrossRef CAS PubMed.
- C. L. Brown and S. L. Craig, Molecular engineering of mechanophore activity for stress-responsive polymeric materials, Chem. Sci., 2015, 6(4), 2158–2165 RSC.
- Y. Chen, G. Mellot, D. van Luijk, C. Creton and R. P. Sijbesma, Mechanochemical tools for polymer materials, Chem. Soc. Rev., 2021, 50(6), 4100–4140 RSC.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Biasing reaction pathways with mechanical force, Nature, 2007, 446(7134), 423–427 CrossRef CAS PubMed.
- J. R. Felts, A. J. Oyer, S. C. Hernández, K. E. Whitener Jr, J. T. Robinson, S. G. Walton and P. E. Sheehan, Direct mechanochemical cleavage of functional groups from graphene, Nat. Commun., 2015, 6(1), 6467 CrossRef CAS PubMed.
- G. R. Gossweiler, T. B. Kouznetsova and S. L. Craig, Force-rate characterization of two spiropyran-based molecular force probes, J. Am. Chem. Soc., 2015, 137(19), 6148–6151 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, R. Boulatov and S. L. Craig, Mechanical gating of a mechanochemical reaction cascade, Nat. Commun., 2016, 7(1), 13433 CrossRef PubMed.
- G. Gill, The application of the Woodward–Hoffmann orbital symmetry rules to concerted organic reactions, Q. Rev., Chem. Soc., 1968, 22(3), 338–389 RSC.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, First principles dynamics and minimum energy pathways for mechanochemical ring opening of cyclobutene, J. Am. Chem. Soc., 2009, 131(18), 6377–6379 CrossRef CAS PubMed.
- G. Binnig, C. F. Quate and C. Gerber, Atomic Force Microscope, Phys. Rev. Lett., 1986, 56(9), 930–933 CrossRef PubMed.
- L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, The chemical structure of a molecule resolved by atomic force microscopy, Science, 2009, 325(5944), 1110–1114 CrossRef CAS PubMed.
- G. Liu, S. H. Petrosko, Z. Zheng and C. A. Mirkin, Evolution of dip-pen nanolithography (DPN): From molecular patterning to materials discovery, Chem. Rev., 2020, 120(13), 6009–6047 CrossRef CAS PubMed.
- A. B. Braunschweig, F. Huo and C. A. Mirkin, Molecular printing, Nat. Chem., 2009, 1(5), 353–358 CrossRef CAS PubMed.
- R. W. Carpick and M. Salmeron, Scratching the Surface: Fundamental Investigations of Tribology with Atomic Force Microscopy, Chem. Rev., 1997, 97(4), 1163–1194 CrossRef CAS PubMed.
- C. Carbonell, D. Valles, A. M. Wong, A. S. Carlini, M. A. Touve and J. Korpanty, et al., Polymer brush hypersurface photolithography, Nat. Commun., 2020, 11(1), 1244 CrossRef CAS PubMed.
- D. J. Valles, Y. S. Zholdassov, J. Korpanty, S. Uddin, Y. Naeem and D. R. Mootoo, et al., Glycopolymer Microarrays with Sub-Femtomolar Avidity for Glycan Binding Proteins Prepared by Grafted-To/Grafted-From Photopolymerizations, Angew. Chem., Int. Ed., 2021, 60(37), 20350–20357 CrossRef CAS PubMed.
- A. M. Wong, D. J. Valles, C. Carbonell, C. L. Chambers, A. Y. Rozenfeld, R. W. Aldasooky and A. B. Braunschweig, Controlled-height brush polymer patterns via surface-initiated thiol-methacrylate photopolymerizations, ACS Macro Lett., 2019, 8(11), 1474–1478 CrossRef CAS PubMed.
- Y. S. Zholdassov, D. J. Valles, S. Uddin, J. Korpanty, N. C. Gianneschi and A. B. Braunschweig, Orthogonal Images Concealed Within a Responsive 6-Dimensional Hypersurface, Adv. Mater., 2021, 33(21), 2100803 CrossRef CAS PubMed.
- S. Raghuraman, M. B. Elinski, J. D. Batteas and J. R. Felts, Driving surface chemistry at the nanometer scale using localized heat and stress, Nano Lett., 2017, 17(4), 2111–2117 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. S. Kean, L. Fan, B. D. Mar, T. J. Martínez and S. L. Craig, A remote stereochemical lever arm effect in polymer mechanochemistry, J. Am. Chem. Soc., 2014, 136(43), 15162–15165 CrossRef CAS PubMed.
- S. Tan, R. L. Sherman and W. T. Ford, Nanoscale compression of polymer microspheres by atomic force microscopy, Langmuir, 2004, 20(17), 7015–7020 CrossRef CAS PubMed.
- W. Cai, J. T. Bullerjahn, M. Lallemang, K. Kroy, B. N. Balzer and T. Hugel, Angle-dependent strength of a single chemical bond by stereographic force spectroscopy, Chem. Sci., 2022, 13(19), 5734–5740 RSC.
- G.-Y. Liu, S. Xu and Y. Qian, Nanofabrication of self-assembled monolayers using scanning probe lithography, Acc. Chem. Res., 2000, 33(7), 457–466 CrossRef CAS PubMed.
- J. E. Headrick, M. Armstrong, J. Cratty, S. Hammond, B. A. Sheriff and C. L. Berrie, Nanoscale patterning of alkyl monolayers on silicon using the atomic force microscope, Langmuir, 2005, 21(9), 4117–4122 CrossRef CAS PubMed.
- S. Xu and G.-y. Liu, Nanometer-scale fabrication by simultaneous nanoshaving and molecular self-assembly, Langmuir, 1997, 13(2), 127–129 CrossRef CAS.
- G. Kaupp, Mechanochemistry: the varied applications of mechanical bond-breaking, CrystEngComm, 2009, 11(3), 388–403 RSC.
- M. Liu, N. A. Amro and G.-y Liu, Nanografting for surface physical chemistry, Annu. Rev. Phys. Chem., 2008, 59, 367–386 CrossRef CAS PubMed.
- A. Pawlicki, E. Avery, M. Jurow, B. Ewers, A. Vilan, C. M. Drain and J. Batteas, Studies of the structure and phase transitions of nano-confined pentanedithiol and its application in directing hierarchical molecular assemblies on Au (1 1 1), J. Phys.: Condens. Matter, 2016, 28(9), 094013 CrossRef PubMed.
- N. Willis-Fox, E. Rognin, T. A. Aljohani and R. Daly, Polymer mechanochemistry: manufacturing is now a force to be reckoned with, Chem, 2018, 4(11), 2499–2537 CAS.
- C. L. Brown, B. H. Bowser, J. Meisner, T. B. Kouznetsova, S. Seritan, T. J. Martinez and S. L. Craig, Substituent effects in mechanochemical allowed and forbidden cyclobutene ring-opening reactions, J. Am. Chem. Soc., 2021, 143(10), 3846–3855 CrossRef CAS PubMed.
- C. I. Drexler, K. B. Moore III, C. P. Causey and T. J. Mullen, Atomic force microscopy characterization and lithography of cu-ligated mercaptoalkanoic acid “Molecular Ruler” multilayers, Langmuir, 2014, 30(25), 7447–7455 CrossRef CAS PubMed.
- A. R. Sulkanen, M. Wang, L. A. Swartz, J. Sung, G. Sun and J. S. Moore, et al., Production of Organizational Chiral Structures by Design, J. Am. Chem. Soc., 2022, 144(2), 824–831 CrossRef CAS PubMed.
- S. Kwon, J.-H. Ko, K.-J. Jeon, Y.-H. Kim and J. Y. Park, Enhanced nanoscale friction on fluorinated graphene, Nano Lett., 2012, 12(12), 6043–6048 CrossRef CAS PubMed.
- Q. Liang, P. A. Newman, J. S. Daniel, S. Reimann, B. D. Hall, G. Dutton and L. J. Kuijpers, Constraining the carbon tetrachloride (CCl4) budget using its global trend and inter-hemispheric gradient, Geophys. Res. Lett., 2014, 41(14), 5307–5315 CrossRef CAS.
- F. Huo, Z. Zheng, G. Zheng, L. R. Giam, H. Zhang and C. A. Mirkin, Polymer pen lithography, Science, 2008, 321(5896), 1658–1660 CrossRef CAS PubMed.
- X. Liao, A. B. Braunschweig, Z. Zheng and C. A. Mirkin, Force-and Time-Dependent Feature Size and Shape Control in Molecular Printing via Polymer-Pen Lithography, Small, 2010, 6(10), 1082–1086 CrossRef CAS PubMed.
- S. Bian, A. M. Scott, Y. Cao, Y. Liang, S. Osuna, K. Houk and A. B. Braunschweig, Covalently patterned graphene surfaces by a force-accelerated Diels–Alder reaction, J. Am. Chem. Soc., 2013, 135(25), 9240–9243 CrossRef CAS PubMed.
- M. Massetti, F. Jiao, A. J. Ferguson, D. Zhao, K. Wijeratne and A. Würger, et al., Unconventional thermoelectric materials for energy harvesting and sensing applications, Chem. Rev., 2021, 121(20), 12465–12547 CrossRef CAS PubMed.
- S. Sarkar, E. Bekyarova, S. Niyogi and R. C. Haddon, Diels−Alder chemistry of graphite and graphene: graphene as diene and dienophile, J. Am. Chem. Soc., 2011, 133(10), 3324–3327 CrossRef CAS PubMed.
- S. Sarkar, E. Bekyarova and R. C. Haddon, Chemistry at the Dirac point: Diels–Alder reactivity of graphene, Acc. Chem. Res., 2012, 45(4), 673–682 CrossRef CAS PubMed.
- C. Walling and H. J. Schugar, Organic Reactions under High Pressure. VII. Volumes of Activation for Some Diels-Alder Reactions, J. Am. Chem. Soc., 1963, 85(5), 607–612 CrossRef CAS.
- V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, A stepwise Huisgen cycloaddition process: copper (I)-catalyzed regioselective “ligation” of azides and terminal alkynes, Angew. Chem., 2002, 114(14), 2708–2711 CrossRef.
- M. Breugst and H.-U. Reissig, The Huisgen Reaction: Milestones of the 1,3-Dipolar Cycloaddition, Angew. Chem., Int. Ed., 2020, 59(30), 12293–12307 CrossRef CAS PubMed.
- D. I. Rozkiewicz, D. Jańczewski, W. Verboom, B. J. Ravoo and D. N. Reinhoudt, “Click” chemistry by microcontact printing, Angew. Chem., Int. Ed., 2006, 45(32), 5292–5296 CrossRef CAS PubMed.
- J. Mehlich and B. J. Ravoo, Click chemistry by microcontact printing on self-assembled monolayers: a structure–reactivity study by fluorescence microscopy, Org. Biomol. Chem., 2011, 9(11), 4108–4115 RSC.
- W. F. Paxton, J. M. Spruell and J. F. Stoddart, Heterogeneous catalysis of a copper-coated atomic force microscopy tip for direct-write click chemistry, J. Am. Chem. Soc., 2009, 131(19), 6692–6694 CrossRef CAS PubMed.
- X. Han, S. Bian, Y. Liang, K. Houk and A. B. Braunschweig, Reactions in elastomeric nanoreactors reveal the role of force on the kinetics of the Huisgen reaction on surfaces, J. Am. Chem. Soc., 2014, 136(30), 10553–10556 CrossRef CAS PubMed.
- Y. S. Zholdassov, L. Yuan, S. R. Garcia, R. W. Kwok, A. Boscoboinik and D. J. Valles, et al., Acceleration of Diels-Alder reactions by mechanical distortion, Science, 2023, 380(6649), 1053–1058 CrossRef CAS PubMed.
- J. J. Dudkowski and E. I. Becker, Electronic effects and rates in the Diels-Alder reaction, J. Org. Chem., 1952, 17(2), 201–206 CrossRef CAS.
- I. Benghiat and E. I. Becker, Electronic Effects and Rates in the Diels-Alder Reaction1, J. Org. Chem., 1958, 23(6), 885–890 CrossRef.
- H. Chen, E. Yao, C. Xu, X. Meng and Y. Ma, Unusual regio-and stereo-selectivity in Diels–Alder reactions between bulky N-phenylmaleimides and anthracene derivatives, Org. Biomol. Chem., 2014, 12(28), 5102–5107 RSC.
- V. D. Kiselev, High-Pressure Influence on the Rate of Diels–Alder Cycloaddition Reactions of Maleic Anhydride with Some Dienes, Int. J. Chem. Kinet., 2013, 45(9), 613–622 CrossRef CAS.
- L. Jiang, Z. Peng, Y. Liang, Z. B. Tang, K. Liang, J. Liu and Z. Liu, Strain-Driven Formal [1, 3]-Aryl Shift within Molecular Bows, Angew. Chem., Int. Ed., 2023, 62(42), e202312238 CrossRef CAS PubMed.
- S. Raghuraman, M. Soleymaniha, Z. Ye and J. R. Felts, The role of mechanical force on the kinetics and dynamics of electrochemical redox reactions on graphene, Nanoscale, 2018, 10(37), 17912–17923 RSC.
- R. E. Ducker, O. S. Brügge, A. J. Meijer and G. J. Leggett, Tribochemical nanolithography: selective mechanochemical removal of photocleavable nitrophenyl protecting groups with 23 nm resolution at speeds of up to 1 mm s−1, Chem. Sci., 2023, 14(7), 1752–1761 RSC.
- H. Khare, N. Gosvami, I. Lahouij, Z. Milne, J. McClimon and R. W. Carpick, Nanotribological printing: a nanoscale additive manufacturing method, Nano Lett., 2018, 18(11), 6756–6763 CrossRef CAS PubMed.
- N. Hawthorne, S. Banerjee, Q. Moore, A. M. Rappe and J. D. Batteas, Studies of the Reactivity of Graphene Driven by Mechanical Distortions, J. Phys. Chem. C, 2022, 126(41), 17569–17578 CrossRef CAS.
- R. Steck, P. Niederer and M. K. Tate, A finite element analysis for the prediction of load-induced fluid flow and mechanochemical transduction in bone, J. Theor. Biol., 2003, 220(2), 249–259 CrossRef CAS PubMed.
- H. Wang and E.-H. Han, Computational simulation of corrosion pit interactions under mechanochemical effects using a cellular automaton/finite element model, Corros. Sci., 2016, 103, 305–311 CrossRef CAS.
- H. Kobayashi, Y. Suzuki, T. Sagawa, M. Saito and A. Fukuoka, Selective Synthesis of Oligosaccharides by Mechanochemical Hydrolysis of Chitin over a Carbon-Based Catalyst, Angew. Chem., Int. Ed., 2023, 62(3), e202214229 CrossRef CAS PubMed.
- X.-Y. Ji and X.-Q. Feng, Coarse-grained mechanochemical model for simulating the dynamic behavior of microtubules, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84(3), 031933 CrossRef PubMed.
- J. Müller and B. Hartke, ReaxFF reactive force field for disulfide mechanochemistry, fitted to multireference ab initio data, J. Chem. Theory Comput., 2016, 12(8), 3913–3925 CrossRef PubMed.
- J. W. Steed, 21st century developments in the understanding and control of molecular solids, Chem. Commun., 2018, 54(94), 13175–13182 RSC.
- P. Dopieralski, J. Ribas-Arino, P. Anjukandi, M. Krupicka and D. Marx, Unexpected mechanochemical complexity in the mechanistic scenarios of disulfide bond reduction in alkaline solution, Nat. Chem., 2017, 9(2), 164–170 CrossRef CAS PubMed.
- B. S. Pladevall, A. de Aguirre and F. Maseras, Understanding ball milling mechanochemical processes with DFT calculations and microkinetic modeling, ChemSusChem, 2021, 14(13), 2763–2768 CrossRef CAS PubMed.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Implementing the mechanical force into the conceptual DFT framework: understanding and predicting molecular mechanochemical properties, Phys. Chem. Chem. Phys., 2019, 21(14), 7378–7388 RSC.
- X. Geng, X. Liu, X. Ding, Q. Zhou, T. Huang and Y. Duan, Mechanochemical bromination of unburned carbon in fly ash and its mercury removal mechanism: DFT study, J. Hazard. Mater., 2022, 423, 127198 CrossRef CAS PubMed.
- M. K. Beyer, The mechanical strength of a covalent bond calculated by density functional theory, J. Chem. Phys., 2000, 112(17), 7307–7312 CrossRef CAS.
- P. E. Marszalek, A. F. Oberhauser, Y. P. Pang and J. M. Fernandez, Polysaccharide elasticity governed by chair-boat transitions of the glucopyranose ring, Nature, 1998, 396(6712), 661–664 CrossRef CAS PubMed.
- W. Kauzmann and H. Eyring, The Viscous Flow of Large Molecules, J. Am. Chem. Soc., 1940, 62(11), 3113–3125 CrossRef CAS.
- J. Ribas-Arino, M. Shiga and D. Marx, Understanding Covalent Mechanochemistry, Angew. Chem., Int. Ed., 2009, 48(23), 4190–4193 CrossRef CAS PubMed.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough and S. L. Potisek, et al., Force-induced activation of covalent bonds in mechanoresponsive polymeric materials, Nature, 2009, 459(7243), 68–72 CrossRef CAS PubMed.
- M. J. Kryger, A. M. Munaretto and J. S. Moore, Structure–mechanochemical activity relationships for cyclobutane mechanophores, J. Am. Chem. Soc., 2011, 133(46), 18992–18998 CrossRef CAS PubMed.
- T. Shiraki, C. E. Diesendruck and J. S. Moore, The mechanochemical production of phenyl cations through heterolytic bond scission, Faraday Discuss., 2014, 170, 385–394 RSC.
- M. J. Robb, T. A. Kim, A. J. Halmes, S. R. White, N. R. Sottos and J. S. Moore, Regioisomer-specific mechanochromism of naphthopyran in polymeric materials, J. Am. Chem. Soc., 2016, 138(38), 12328–12331 CrossRef CAS PubMed.
- I. M. Klein, C. C. Husic, D. P. Kovács, N. J. Choquette and M. J. Robb, Validation of the CoGEF method as a predictive tool for polymer mechanochemistry, J. Am. Chem. Soc., 2020, 142(38), 16364–16381 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, A quantitative quantum-chemical analysis tool for the distribution of mechanical force in molecules, J. Chem. Phys., 2014, 140(13), 134107 CrossRef PubMed.
- T. Stauch and A. Dreuw, On the use of different coordinate systems in mechanochemical force analyses, J. Chem. Phys., 2015, 143(7), 074118 CrossRef PubMed.
- W. Li and A. Ma, Some studies on generalized coordinate sets for polyatomic molecules, J. Chem. Phys., 2015, 143(22), 224103 CrossRef PubMed.
- N. Haruta, P. F. M. de Oliveira, T. Sato, K. Tanaka and M. Baron, Force-induced dissolution of imaginary mode in mechanochemical reaction: dibenzophenazine synthesis, J. Phys. Chem. C, 2019, 123(35), 21581–21587 CrossRef CAS.
- W. Sakai, L. Gonnet, N. Haruta, T. Sato and M. Baron, Origin of Stereoselectivity in a Mechanochemical Reaction of Diphenylfulvene and Maleimide, J. Phys. Chem. A, 2023, 127(28), 5790–5794 CrossRef CAS PubMed.
- M. Bocus, R. Goeminne, A. Lamaire, M. Cools-Ceuppens, T. Verstraelen and V. Van Speybroeck, Nuclear quantum effects on zeolite proton hopping kinetics explored with machine learning potentials and path integral molecular dynamics, Nat. Commun., 2023, 14(1), 1008 CrossRef CAS PubMed.
- T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang and B. Nebgen, et al., Non-adiabatic Excited-State Molecular Dynamics: Theory and Applications for Modeling Photophysics in Extended Molecular Materials, Chem. Rev., 2020, 120(4), 2215–2287 CrossRef CAS PubMed.
- R. Stevenson and G. De Bo, Controlling reactivity by geometry in retro-Diels–Alder reactions under tension, J. Am. Chem. Soc., 2017, 139(46), 16768–16771 CrossRef CAS PubMed.
- F. K. Urakaev and V. V. Boldyrev, Mechanism and kinetics of mechanochemical processes in comminuting devices: 1. Theory, Powder Technol., 2000, 107(1), 93–107 CrossRef CAS.
- F. K. Urakaev and V. V. Boldyrev, Mechanism and kinetics of mechanochemical processes in comminuting devices: 2. Applications of the theory. Experiment, Powder Technol., 2000, 107(3), 197–206 CrossRef CAS.
- M. Carta, L. Vugrin, G. Miletić, M. J. Kulcsár, P. C. Ricci, I. Halasz and F. Delogu, Mechanochemical Reactions from Individual Impacts to Global Transformation Kinetics, Angew. Chem., Int. Ed., 2023, 62(33), e202308046 CrossRef CAS PubMed.
- A. Boscoboinik, D. Olson, H. Adams, N. Hopper and W. T. Tysoe, Measuring and modelling mechanochemical reaction kinetics, Chem. Commun., 2020, 56(56), 7730–7733 RSC.
| This journal is © The Royal Society of Chemistry 2024 |