Design principle of disordered rocksalt type overlithiated anode for high energy density batteries

Abstract

Rechargeable lithium–ion batteries with high energy density and fast-charging capability are vital for commercial applications. Disordered rocksalt (DRX) materials with a cation/anion ratio greater than one, achieved through additional lithium insertion, have emerged as promising high-rate anode candidates. Inspired by the previously reported Li_3+xV₂O₅ (0 ≤ x ≤ 2) anode, a comprehensive search was conducted for all potential redox centers using high-throughput density functional theory (DFT) computations. This study examined 23 redox centers in a prototype formula Li_3+xV₂O₅ (0 ≤ x ≤ 2) with the DRX structure, analyzing aspects such as voltage curve, theoretical capacity, energy density, phase stability, electronic conductivity, and volumetric change during cycling. Promising candidates were identified with redox centers including V, Cr, Nb, Mn, and Fe, marking them as potential anode materials. Additionally, this research revealed the origin of the low voltage in DRX anodes and proposed a method to optimize the average voltage by tuning the relative energies among structures with varying lithium contents. This work provides compositional design principles for the new promising DRX anode of LIBs with high energy density, fast-charging capability, and good cycling stability.

---

New concepts

We introduced a new concept for estimating the average voltage of a broad range of Li–ion battery anode materials. This concept uses the relative energy between the overlithiated state and the stoichiometric state. It applies to materials with a cation/anion ratio larger than one and a disordered rocksalt (DRX) structure. The concept is based on about 7680 density functional theory calculations across 23 metals and 13Li contents per formula unit. Additionally, we have identified ten material systems that outperform the state-of-the-art Lithium Titanate commercialized anode. Given the vast design space of overlithiated DRX materials, this concept will significantly accelerate the discovery of novel intercalation electrodes.

Introduction

Rechargeable lithium–ion batteries (LIBs) with high energy density, fast-charging capability, cycling stability, and safety are required to satisfy the increasing global energy demand.^1–5 The disordered rock-salt (DRX) oxides recently emerged as promising intercalation anodes.^6–10 The lower lithium–ion intercalation voltage of the DRX anode contributes to the higher energy density of LIBs.^6,8,11,12 Recently, DRX Li_3+xV₂O₅ (0 ≤ x ≤ 2)⁶ has been reported as a promising DRX anode with an average intercalation voltage of 0.58 V. Such anodes in general operate at the composition with cation/anion ratio larger than 1.0, which is referred to as overlithiated DRX.¹³ As a result of overlithiation, the lithium–ion diffusivity will be greatly enhanced, which leads to extraordinary rate performance for fast charging applications.^6,14 The origin of high ionic conductivity stems from the face-sharing local structures that are enforced by overlithiation,^8,13,14 which is the key to high lithium–ion diffusivity in several cases even without overlithiation.^15,16

Understanding overlithiated disordered rock-salt (DRX) compounds is essential, as DRX-type Li_3+xV₂O₅ has demonstrated reversible cycling between 0.01 V and 2 V with a specific capacity of ∼255 mAh g⁻¹.⁶ This material exhibits excellent rate capability and maintains stable performance over 1000 charge–discharge cycles with negligible capacity decay, leading to its recent commercialization. Additionally, our recent computational and experimental work¹³ has confirmed that various overlithiated DRX compounds can be directly synthesized through the solid-state synthesis method. Therefore, it reveals that there is an overlooked potential of the overlithiated DRX compounds.

Given the promises for building DRX anodes with overlithiation composition design, the viable chemical space is still largely unknown. In this work, 23 redox centers (e.g. Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Ge, Zr, Nb, Mo, Rh, Ru, Sn, Sb, Te, Hf, Ta, W, Re, Ir, Ce) were thoroughly evaluated concerning the possibility of acting as promising anode materials when intercalating from Li₃M₂O₅ to Li₅M₂O₅. For each redox center, the average voltage, theoretical capacity, and energy density of 23 systems are calculated by even sample of Li content ranging from 3Li per O₅ (Li₃M₂O₅) to 5Li per O₅ Li (Li₅M₂O₅) and at least 16 types of different ordered structures are sampled for each Li content. Taking Li_4+xTi₅O₁₂ (LTO) (0 ≤ x ≤ 3)¹⁵ as a reference, there are some promising anode materials with similar or higher energy densities. Among these, several new anode compositions are presented that are comparable to or better than state-of-art Li_3+xV₂O₅ (0 ≤ x ≤ 2)⁶ in terms of performance, stability, volumetric change, cost, and electronic conductivity. Additionally, the voltage curves of selected low voltage and high voltage DRX Li_3+xM₂O₅ anode are presented. Furthermore, we also established a straightforward way to understand the origin and tunability of average voltage for overlithiated DRX anodes.

Results and discussion

High energy density anode is a crucial requirement for the next generation of LIBs.^17–20 DRX anode has been regarded as a high energy density anode due to its high theoretical capacity and low voltage.^6,7 To discover more promising DRX anodes with high energy density and find the fundamental mechanism of high-performance overlithiated DRX anode, 23 redox centers, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Ge, Zr, Nb, Mo, Rh, Ru, Sn, Sb, Te, Hf, Ta, W, Re, Ir, and Ce, were systematically evaluated when lithium–ion intercalation from Li₃M₂O₅ to Li₅M₂O₅. The typical structure of Li_3+xM₂O₅ is demonstrated in Fig. 1(a), the extra Li is assumed to be inserted into the tetrahedron sites according to previous reports.^6,13 Building on the DFT computed average voltage and capacity, the Ragone plot^21–23 that correlates theoretical capacity and average voltage with energy density is shown in Fig. 1(b). The average voltage of the cathode is assumed to be 4 V in the calculations, which is achievable in state-of-the-art Ni-rich cathodes.^6,24,25 Compared with the reported LTO¹⁵ with a theoretical capacity of 175.14 mAh g⁻¹ and average voltage of 1.55 V, the theoretical capacity of 11 DRX Li_3+xM₂O₅ compounds (where M = Cu, Ni, Co, Fe, Ge, Mn, Cr, Ru, Rh, V, and Nb) are higher.¹⁵ Among those promising candidates, Mn, Cr, Nb, and V-based anodes stand out among all candidates with the highest energy densities (>600 Wh kg⁻¹). Particularly, V shows the highest theoretical capacity of 264.44 mAh g⁻¹ and energy density of 930.22 Wh kg⁻¹ respectively (Table S1, ESI†). The calculated theoretical capacity of 264.44 mAh g⁻¹ is close to the experimentally measured capacity value of ∼255 mAh g⁻¹.⁶ While Nb shows the lowest theoretical accessible voltage as 0.19 V, even though the energy density is relatively lower at 711.60 Wh kg⁻¹ due to the much larger molar mass of Nb. Moreover, Ru, Rh, Ge, Fe, and Mn also show larger energy density compared with reported LTO, with energy densities being 535.21 Wh kg⁻¹, 469.17 Wh kg⁻¹, 527.79 Wh kg⁻¹, 519.74 Wh kg⁻¹, and 663.02 Wh kg⁻¹ respectively. Additionally, Li_3+xM₂O₅ compounds that contain Sn, Co, Ni, and Sb are very close to the energy density of the LTO anode. Nevertheless, Li_3+xM₂O₅ compounds with certain metals, e.g. Mo, W, and Ce also display very competitive voltage with limited capacity. On the other hand, Ti, Zr, Hf, and Ta-based Li_3+xM₂O₅ turn out to be electrochemically inactive at all.

Fig. 1 Overview of high throughput screening DFT data: (a) the atomic structure of Li_3+xM₂O₅ (0 ≤ x ≤ 2); (b) Ragone plot of the average voltage, theoretical capacity, and energy density of all searched DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2) (M = Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Ge, Zr, Nb, Mo, Rh, Ru, Sn, Sb, Te, Hf, Ta, W, Re, Ir, Ce) and reported Li_4+xTi₅O₁₂ (0 ≤ x ≤ 3).¹⁵

A promising anode material for lithium–ion batteries (LIBs) should ideally have a near-zero low intercalation voltage to maximize energy density. Consequently, the voltage curves of various DRX anode materials are analyzed through high-throughput screening of density functional theory (DFT) data. The analysis focuses on understanding the low voltage characteristics of DRX Li_3+xM₂O₅ materials. The selected voltage curves are depicted in Fig. 2, organized by the magnitude of the average voltage. Specifically, Fig. 2(a) showcases candidates with voltages close to 0 V, including materials with M as Ce, Re, Nb, V, Ru, and Cr, while Fig. 2(b) features candidates with average voltages above 1.5 V, comprising materials with M as Cu, Ni, Co, Fe, Te, and Sb. The average voltages for these selected low and high-voltage DRX Li_3+xM₂O₅ (M = Ce, Re, Nb, V, Ru, Cr, Cu, Ni, Co, Fe, Te, and Sb) are as follows: 0.21 V, 1.22 V, 0.19 V, 0.48 V, 0.98 V, 1.14 V, 2.87 V, 2.41 V, 2.26 V, 1.94 V, 1.85 V, and 1.71 V respectively, as listed in Table S1 (ESI†). Additionally, the intercalation voltage curves for other DRX Li_3+xM₂O₅ materials not included in Fig. 2 (M = Ti, Mn, Ge, Zr, Rh, Sn, Hf, Ta, W, Ir, and Mo) are presented in Fig. S1 (ESI†). Among all examined DRX Li_3+xM₂O₅ materials, DRX Li_3+xNb₂O₅ exhibits the lowest voltage, and the intercalation voltage for all DRX anode materials decreases during the lithiation process.

Fig. 2 Analysis of selected compounds with low voltage and high voltage: (a) the voltage curve of Li_3+xM₂O₅ with relative low average voltage (M = Ce, Re, Nb, V, Ru, and Cr); (b) the voltage curve of Li_3+xM₂O₅ with relative high average voltage (M = Cu, Ni, Co, Fe, Te, and Sb); (c) and (d) the intercalation convex hull of selected low and high voltage DRX Li_3+xM₂O₅ (M = Ce, Re, Nb, V, Ru, Cr, Cu, Ni, Co, Fe, Te, and Sb); (e) and (f) the stability (E_hull) of selected low and high voltage DRX Li_3+xM₂O₅ (M = Ce, Re, Nb, V, Ru, Cr, Cu, Ni, Co, Fe, Te, and Sb).

To further study the stability of DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2) anode during lithiation, the intercalation convex hull of all searched DRX Li_3+xM₂O₅ (M = Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Ge, Zr, Nb, Mo, Rh, Ru, Sn, Sb, Te, Hf, Ta, W, Re, Ir, and Ce) anodes are calculated (Fig. 2c and d and Fig. S2, ESI†). Fig. 2(c) and (d) shows the intercalation convex hull of selected low voltage Li_3+xM₂O₅ (M = Ce, Re, Nb, V, Ru, Cr) and high voltage Li_3+xM₂O₅ (M = Cu, Ni, Co, Fe, Te, and Sb). The more complete convex hull with metastable compounds is shown in Fig. S3 (ESI†). Cr compounds feature the deepest convex hull around x = 4.0, followed by Re and Ce in Fig. 2(c). On the other hand, Ru and Nb have a flat intercalation hull, which leads to no step as shown in the voltage curve of Fig. 2(a). It is also noted that the E_hull values do not necessarily form a convex hull, particularly for DRX Li_3+xCe₂O₅, Li_3+xV₂O₅, Li_3+xCu₂O₅, and Li_3+xTe₂O₅ systems. This is owing to the variation of competing phases during the intercalation process, which can be further supported by Fig. S4–S6 (ESI†).

Furthermore, the energy above hull (E_hull) of selected low voltage DRX Li_3+xM₂O₅ (M = Ce, Re, Nb, V, Ru, Cr) and high voltage DRX Li_3+xM₂O₅ (M = Cu, Ni, Co, Fe, Te, and Sb) are evaluated in Fig. 2(e) and (f), while the competing phase at each composition is listed in Table S2 (ESI†). In general, it can be inferred from Fig. 2(e) that all compounds have E_hull values increasing rapidly after intercalation from Li₃M₂O₅. For example, Li₃V₂O₅ starts with an E_hull value of 21.02 meV per atom and then climbs to 190.28 meV per atom at the state of Li₅V₂O₅. All other compounds in general have the same trend as Li₅V₂O₅. In contrast, for compounds with high voltage in Fig. 2(f), there is no clear trend of E_hull values. Particularly, the E_hull value of Li_3+xCu₂O₅ drops for Cu based system and the E_hull value of Sb based system first decreases and then increases during intercalation. There are also other systems, i.e., Li_3+xCo₂O₅, Li_3+xTe₂O₅, and Li_3+xNi₂O₅ based systems, showing similar E_hull values across all ranges of Li contents. Such divergent trends of E_hull values reveal potential fundamental differences in relative energies between low-voltage and high-voltage compounds. The correlation between relative energy among different lithiation states and average voltage will be explained more details in the discussion section.

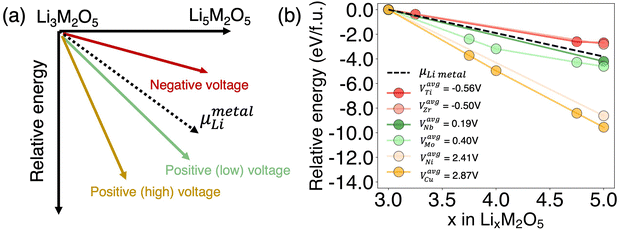
As known to all, a promising DRX anode is expected to have positive voltage that is close to zero. As revealed by comparing Fig. 2(e) and (f), the average voltage seems to be correlated to relative energy among different lithiation states. From the definition of voltage, the actual potential is determined by the relative stability of at least two lithiated states, rather than the stability of a single composition (complete formula available in computational method). Moreover, it should be highlighted that the stability of overlithiated DRX is very sensitive to the metal ion radius, as well as the compatibility of specifical metal ions in DRX structure,¹³ regardless of the actual redox potential. Such feature further highlights the importance of relative stability as a descriptor for voltage rather than using the metal redox potential. The influence of relative stability on average voltage can be illustrated by the schematic in Fig. 3(a). By aligning the energy taking the pristine state Li₃M₂O₅ as a reference, the relative energy of all other states Li_3+xM₂O₅ (0 ≤ x ≤ 2) can be illustrated by the y-axis in Fig. 3(a) as “relative energy”. Therefore, the slope of the plot indicates the chemical potential of Li in Li_3+xM₂O₅ (0 ≤ x ≤ 2). In other words, a more negative slope indicates a higher average voltage during the intercalation process.

Fig. 3 (a) Schematic of three types of intercalation voltages with different trends of relative energy; (b) the computed relative voltage for selected DRX anode compositions Li_3+xM₂O₅ (0 ≤ x ≤ 2) (M = Ti, Zr, Nb, Mo, Ni, and Cu).

The optimal voltage can be achieved by controlling the relative stability below and close to the black dash color as shown in Fig. 3(a), which corresponds to the chemical potential of Li metal. When the relative energy is too high for overlithiated DRX with respect to typical DRX (indicated with red arrow), the intercalation will not happen given Li has a higher chemical potential than Li metal. When overlithiated DRX is overly stabilized compared to typical DRX (indicated with yellow arrow), or when the relative energy is too low, the average voltage will be too high to be a good anode. If the average voltage is high enough, such overlithiated DRX may be good cathode candidates. As a result, the optimal range of relative energy can be represented by the green arrow in Fig. 3(a). The real data of selected chemical systems are plotted in Fig. 3(b). Two overlithiated DRX materials are selected for each group, e.g., negative, low positive voltage, and high positive voltage, respectively. The exact computed average voltage is shown as legend, which confirms that a more negative slope implies a higher average voltage during the intercalation process.

To further assess the practical application of the identified overlithiated DRX Li_3+xM₂O₅ anodes, the energy density, phase stability, electronic conductivity, maximum volume change, and cost as estimated for five promising systems. A direct comparison across different metal chemistry is presented in Fig. 4 and more details are provided in Fig. S7 (ESI†). Particularly, the band gap is calculated with Heyd–Scuseria–Ernzerhof (HSE06) level of theory.^26–28 The lower band gap is used as a proxy for better electronic conductivity. To evaluate the pros and cons of several promising candidates, Fig. 4(a) shows that energy density, stability, electronic conductivity, volumetric change, and cost are typically considered to optimize for a high-performance anode. The top five Li_3+xM₂O₅ systems with the highest energy density are selected for detailed analysis. Such systems are Li_3+xV₂O₅, Li_3+xCr₂O₅, Li_3+xNb₂O₅, Li_3+xMn₂O₅, and Li_3+xFe₂O₅ respectively, which show 930.22 Wh kg⁻¹, 749.05 Wh kg⁻¹, 711.60 Wh kg⁻¹, 663.02 Wh kg⁻¹, and 519.74 Wh kg⁻¹ correspondently. In addition to the energy densities in Fig. 4(b), the energy above hull (E_hull) values for Li₃M₂O₅ are demonstrated in Fig. 4(c), the average band gaps are demonstrated in Fig. 4(d), maximum volume changes are shown in Fig. 4(e), and cost per kilogram is presented in Fig. 4(f).

Fig. 4 (a) schematic of the typical metric to evaluate good anode, e.g., high energy density, good stability, good electronic conductivity, small volume change, and low cost; (b) the energy density, (c) E_hull of Li₃M₂O₅, (d) average band gap, (e) maximum volumetric change, and (f) cost of promising DRX Li_3+xM₂O₅ (M = V, Cr, Nb, Mn, and Fe).

It can be inferred that except for Nb, all other four systems show reasonable stability, considering that a typical DRX that can be synthesized with solid-state reaction has around 50 meV per atom of E_hull value²⁹ (Table S3, ESI†). On the other hand, Nb based system seems to have extraordinary electronic conductivity than all other four systems due to a much smaller band gap of 0.99 eV compared with 1.69 eV, 2.15 eV, 1.82 eV, and 1.89 eV respectively. When comes to volumetric change, all five systems show much large volume change due to lithiation process, mainly because overlithiation tends to create short Li–metal bonds that forces the system to expand. The volume expansion percentage calculation of DRX Li_3+xM₂O₅ is based on pristine Li₃M₂O₅. Among all five systems, Li_3+xFe₂O₅ seems to have the smallest value of maximum volume change during lithiation process, which is still substantial at 20.10%. Even though the volume change of all five overlithiation DRX anode systems is much larger than typical cathodes,^30,31 it is still close to the range of 13–30% volume change of carbon-based anodes^32–34 and much smaller compared to 300–400% volume change of silicon-based anodes.^35–38 With such consideration, the DRX anodes are quite reasonable in terms of volume change as anode materials. Furthermore, as the discovery of DRX-based anodes is still at its primary stage, it is also possible to further reduce the volume change or its impact by doping,³⁹ hierarchically structures design,⁴⁰ coating,^41,42 and solid electrolyte interphase (SEI) interface design.⁴³ Finally, it should be noted that Li_3+xV₂O₅ and Li_3+xNb₂O₅ tend to be the most expensive systems in terms of cost in Fig. 4(f).

Conclusions

In summary, 23 redox centers of overlithiated DRX Li_3+xM₂O₅ were systematically evaluated for their voltage, theoretical capacity, energy density, phase stability, electronic conductivity, and volumetric change during cycling. The predicted DRX Li_3+xV₂O₅⁶ has been experimentally reported. It displayed that DRS Li_3+xV₂O₅ can be cycled reversibly between 0.01 V and 2 V with a specific capacity of ∼255 mAh g⁻¹, which is close to our calculated theoretical capacity of 264.44 mAh g⁻¹ for Li_3+xV₂O₅. The reported experimental average voltage of 0.58 V for DRX Li_3+xV₂O₅ is close to our calculated average voltage of 0.48 V. Therefore, the high-throughput DFT computations of DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2) anode agree well with the reported experimental value. In addition to the explored Li_3+xV₂O₅, Li_3+xNb₂O₅ system is shown as a promising anode system with low voltage, and high electronic conductivity, but its cost is higher and it's more challenging to synthesize. Li_3+xCr₂O₅ system also shows very competitive energy density and good rate performance in general, furthermore, there is no obvious disadvantage in terms of electronic conductivity, volume change, and price. Moreover, both Li_3+xFe₂O₅ and Li_3+xMn₂O₅ show reasonable performance as well. They have unique advantages being the cheapest transition metal on the periodic table. It is also worth noting that both Fe and Mn-based DRX systems show reasonable stability at various oxidation states. The energy density can be further increased by careful compositional optimization. It also revealed that the origin of the low voltage of DRX anode and proposed ‘relative energy’ to describe the correlation between voltage and phase stability of overlithiated DRX anode. The computed relative energies confirmed the principle that lithiated DRX should have reasonable stability to ensure low and positive average voltage. Therefore, this work provides compositional design principles for the new promising DRX anode of LIBs with high energy density, fast-charging capability, and good cycling stability.

Computational methods

The high throughput density functional theory (DFT) calculations were carried out using the Vienna ab initio simulation package⁴⁴ and the projector-augmented wave (PAW) method,^45,46 with spin polarization consideration. A reciprocal mesh discretization of 25 Å⁻¹ has been used for each calculation. The threshold energy difference for electronic self-consistent convergence in the total free energy was set to 1 × 10⁻³ eV. A plane wave energy cutoff of 520 eV was used for all calculations. Li_3+xM₂O₅ structures are created with Li content ranging from 24 Li to 40 Li with M being one of the 23 selected metals. We derived all structures by creating partial occupancy through a rocksalt structure and then randomly sampling different ordered states with low electrostatic energies for DFT calculations and for constructing the convex hull. This method has been widely used in the past decades for battery calculations.⁴⁷ We also used the homemade script based on pymatgen⁴⁸ to automate all calculations and data processing. In addition, to evaluate the electronic conductivity of promising DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2), the band gap is calculated with the implementation of the HSE (Heyd–Scuseria–Ernzerhof) exchange–correlation functional.^26,27 The band gap calculation is tested with different K-point densities. We found that the computed band gap values converge after using a 15 Å⁻¹ density of larger value. Therefore, all band gap calculations using HSE with 15 Å⁻¹K mesh.

The theoretical capacity of all DRX is calculated within the effective lithiation/delithiation range. The formula of theoretical capacity is as follows:²³

where F is the Faraday constant, n is the number of electron transfers, and M represents the molar mass (g mol⁻¹) of Li₃M₂O₅.

The volume changes are calculated on the structures on the intercalation convex hull. When quantifying voltage, energy density, relative energy, and the volume change of DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2), the pristine Li₃M₂O₅ is used as a reference.

The voltage of DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2) during lithiation/delithiation can be expressed as follows:²³

V = −(E(Li_3+xM₂O₅) − E(Li₃M₂O₅) − μ_Lix)/x(0 ≤ x ≤ 2)

where E(Li_3+xM₂O₅) is the total energy of Li_3+xM₂O₅ per formula unit, E(Li₃M₂O₅) is the total energy of Li₃M₂O₅ per formula unit, and μ_Li is the chemical potential of lithium–ion. After obtaining the average voltage of anode, the energy density of DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2) anode-based batteries is then calculated as follows:

Energy density = C_Theory × (V_cathode − V_anode)

where C_Theory is the theoretical capacity within effective lithiation/delithiation range, V_cathode is the average voltage of reference cathode, and V_anode is the average voltage of DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2) within positive voltage range during lithiation/delithiation. In this work, we considered one reference 4 V of Ni-rich cathodes (V_cathode = 4 V).

The correlation between voltage and relative structure stability is described by the relative energy. The relative energy formula of Li_3+xM₂O₅ (0 ≤ x ≤ 2) is as follows:

E_{relative energy} = E(Li_3+xM₂O₅) − E(Li₃M₂O₅) (0 ≤ x ≤ 2)

where E(Li_3+xM₂O₅) is the total energy of Li_3+xM₂O₅ per formula unit and E(Li₃M₂O₅) is the total energy of Li₃M₂O₅ per formula unit. Therefore, from voltage and relative energy formulas, it is obvious that the relative energy term E_{relative energy} determines the theoretical average voltage. Physically, this can be understood as the stability of the metastable overlithiated state will determine the average voltage of the DRX Li_3+xM₂O₅ (0 ≤ x ≤ 2) when utilized as an anode.

Data availability

The data that support the findings of this study are available from the author upon reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work was supported by the startup funding from Florida State University. The Computational resources were provided by the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS), the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science and the U.S. Department of Energy under contract no. DE-AC02-05CH11231 and Research Computing Center (RCC) at Florida State University. The computation and data processing were also supported by the supercomputing resources from the Department of Energy's Office of Energy Efficiency and Renewable Energy at the National Renewable Energy Laboratory.

References

1. Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang and T. Chen, Promises and challenges of next-generation “beyond Li–ion” batteries for electric vehicles and grid decarbonization, Chem. Rev., 2020, 121(3), 1623–1669.
2. M. Armand and J.-M. Tarascon, Building better batteries, Nature, 2008, 451(7179), 652–657.
3. A. Manthiram, An outlook on lithium ion battery technology, ACS Cent. Sci., 2017, 3(10), 1063–1069.
4. J. B. Goodenough and K.-S. Park, The Li–ion rechargeable battery: a perspective, J. Am. Chem. Soc., 2013, 135(4), 1167–1176.
5. M. S. Whittingham, Electrical energy storage and intercalation chemistry, Science, 1976, 192(4244), 1126–1127.
6. H. Liu, Z. Zhu, Q. Yan, S. Yu, X. He, Y. Chen, R. Zhang, L. Ma, T. Liu and M. Li, A disordered rock salt anode for fast-charging lithium–ion batteries, Nature, 2020, 585(7823), 63–67.
7. P. Barnes, Y. Zuo, K. Dixon, D. Hou, S. Lee, Z. Ma, J. G. Connell, H. Zhou, C. Deng and K. Smith, Electrochemically induced amorphous-to-rock-salt phase transformation in niobium oxide electrode for Li–ion batteries, Nat. Mater., 2022, 21(7), 795–803.
8. X. Guo, C. Chen and S. P. Ong, Intercalation chemistry of the disordered rocksalt Li₃V₂O₅ anode from cluster expansions and machine learning interatomic potentials, Chem. Mater., 2023, 35(4), 1537–1546.
9. D. Mikhailova, A. Voss, S. Oswald, A. Tsirlin, M. Schmidt, A. Senyshyn, J. Eckert and H. Ehrenberg, Lithium insertion into Li₂MoO₄: reversible formation of Li₃MoO₄ with a disordered rock-salt structure, Chem. Mater., 2015, 27(12), 4485–4492.
10. R. Clément, Z. Lun and G. Ceder, Cation-disordered rocksalt transition metal oxides and oxyfluorides for high energy lithium–ion cathodes, Energy Environ. Sci., 2020, 13(2), 345–373.
11. A. R. Armstrong, C. Lyness, P. M. Panchmatia, M. S. Islam and P. G. Bruce, The lithium intercalation process in the low-voltage lithium battery anode Li_1+xV_1−xO₂, Nat. Mater., 2011, 10(3), 223–229.
12. Y. Qin, H. Zhao, M. Hua, J. Gao, J. Lu, S. Zhang, X. Lin, J. Sun, L. Yin and R. Wang, Pseudocapacitive lithium-rich disordered rock salt vanadium oxide with 3D lithium–ion transport pathways for high-performance lithium–ion capacitor, J. Power Sources, 2023, 588, 233722.
13. Y. Chen, Z. Lun, X. Zhao, K. P. Koirala, L. Li, Y. Sun, C. A. O’Keefe, X. Yang, Z. Cai and C. Wang, Unlocking Li superionic conductivity in face-centred cubic oxides via face-sharing configurations, Nat. Mater., 2024, 1–8.
14. Z. Jadidi, T. Chen, L. Barroso-Luque and G. Ceder, Kinetics of Li transport in vanadium-based disordered rocksalt structures, Chem. Mater., 2023, 35(21), 9225–9234.
15. W. Zhang, D.-H. Seo, T. Chen, L. Wu, M. Topsakal, Y. Zhu, D. Lu, G. Ceder and F. Wang, Kinetic pathways of ionic transport in fast-charging lithium titanate, Science, 2020, 367(6481), 1030–1034.
16. H. Ji, J. Wu, Z. Cai, J. Liu, D.-H. Kwon, H. Kim, A. Urban, J. K. Papp, E. Foley and Y. Tian, Ultrahigh power and energy density in partially ordered lithium–ion cathode materials, Nat. Energy, 2020, 5(3), 213–221.
17. F. N. U. Khan, M. G. Rasul, A. Sayem and N. Mandal, Maximizing energy density of lithium–ion batteries for electric vehicles: a critical review, Energy Rep., 2023, 9, 11–21.
18. C. Wang, C. Yang and Z. Zheng, Toward practical high-energy and high-power lithium battery anodes: present and future, Adv. Sci., 2022, 9(9), 2105213.
19. Y. Son, T. Lee, B. Wen, J. Ma, C. Jo, Y.-G. Cho, A. Boies, J. Cho and M. De Volder, High energy density anodes using hybrid Li intercalation and plating mechanisms on natural graphite, Energy Environ. Sci., 2020, 13(10), 3723–3731.
20. B. Zhu, X. Wang, P. Yao, J. Li and J. Zhu, Towards high energy density lithium battery anodes: silicon and lithium, Chem. Sci., 2019, 10(30), 7132–7148.
21. I. Beyers, A. Bensmann and R. Hanke-Rauschenbach, Ragone plots revisited: a review of methodology and application across energy storage technologies, J. Energy Storage, 2023, 73, 109097.
22. J. Woods, A. Mahvi, A. Goyal, E. Kozubal, A. Odukomaiya and R. Jackson, Rate capability and Ragone plots for phase change thermal energy storage, Nat. Energy, 2021, 6(3), 295–302.
23. L. Wang, J. Wang and B. Ouyang, Computational Investigation of MAX as Intercalation Host for Rechargeable Aluminum–Ion Battery, Adv. Energy Mater., 2023, 13(46), 2302584.
24. H. Liu, Z. Xie, W. Qu, E. Dy, S. Niketic, S. Brueckner, K. Tsay, E. Fuller, C. Bock and N. Zaker, High-voltage induced surface and intragranular structural evolution of Ni-rich layered cathode, Small, 2022, 18(19), 2200627.
25. L. David, D. Mohanty, L. Geng, R. E. Ruther, A. S. Sefat, E. Cakmak, G. M. Veith, H. M. Meyer III, H. Wang and D. L. Wood III, High-Voltage Performance of Ni-Rich NCA Cathodes: Linking Operating Voltage with Cathode Degradation, ChemElectroChem, 2019, 6(22), 5571–5580.
26. J. Heyd and G. E. Scuseria, Efficient hybrid density functional calculations in solids: assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional, J. Chem. Phys., 2004, 121(3), 1187–1192.
27. J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional, J. Chem. Phys., 2005, 123(17), 174101.
28. D.-H. Seo, A. Urban and G. Ceder, Calibrating transition-metal energy levels and oxygen bands in first-principles calculations: accurate prediction of redox potentials and charge transfer in lithium transition-metal oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(11), 115118.
29. H. Ji, A. Urban, D. A. Kitchaev, D.-H. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi and J. C. Kim, Hidden structural and chemical order controls lithium transport in cation-disordered oxides for rechargeable batteries, Nat. Commun., 2019, 10(1), 592.
30. X. Zhao, Y. Tian, Z. Lun, Z. Cai, T. Chen, B. Ouyang and G. Ceder, Design principles for zero-strain Li–ion cathodes, Joule, 2022, 6(7), 1654–1671.
31. X. Zhao and G. Ceder, Zero-strain cathode materials for Li–ion batteries, Joule, 2022, 6(12), 2683–2685.
32. S. Schweidler, L. de Biasi, A. Schiele, P. Hartmann, T. Brezesinski and Jr Janek, Volume changes of graphite anodes revisited: a combined operando X-ray diffraction and in situ pressure analysis study, J. Phys. Chem. C, 2018, 122(16), 8829–8835.
33. K. Dai, Z. Wang, G. Ai, H. Zhao, W. Yuan, X. Song, V. Battaglia, C. Sun, K. Wu and G. Liu, The transformation of graphite electrode materials in lithium–ion batteries after cycling, J. Power Sources, 2015, 298, 349–354.
34. N. Kobayashi, Y. Inden and M. Endo, Silicon/soft-carbon nanohybrid material with low expansion for high capacity and long cycle life lithium–ion battery, J. Power Sources, 2016, 326, 235–241.
35. H. Schmidt, B. Jerliu, E. Hüger and J. Stahn, Volume expansion of amorphous silicon electrodes during potentiostatic lithiation of Li–ion batteries, Electrochem. Commun., 2020, 115, 106738.
36. B. Jerliu, E. Huger, L. Dorrer, B.-K. Seidlhofer, R. Steitz, V. Oberst, U. Geckle, M. Bruns and H. Schmidt, Volume expansion during lithiation of amorphous silicon thin film electrodes studied by in-operando neutron reflectometry, J. Phys. Chem. C, 2014, 118(18), 9395–9399.
37. C. R. Becker, K. E. Strawhecker, Q. P. McAllister and C. A. Lundgren, In situ atomic force microscopy of lithiation and delithiation of silicon nanostructures for lithium ion batteries, ACS Nano, 2013, 7(10), 9173–9182.
38. C. Cao, H.-G. Steinrück, B. Shyam, K. H. Stone and M. F. Toney, In situ study of silicon electrode lithiation with X-ray reflectivity, Nano Lett., 2016, 16(12), 7394–7401.
39. S. Hoshino, A. M. Glushenkov, S. Ichikawa, T. Ozaki, T. Inamasu and N. Yabuuchi, Reversible three-electron redox reaction of Mo³⁺/Mo⁶⁺ for rechargeable lithium batteries, ACS Energy Lett., 2017, 2(4), 733–738.
40. K. X. Wang, X. H. Li and J. S. Chen, Surface and interface engineering of electrode materials for lithium–ion batteries, Adv. Mater., 2015, 27(3), 527–545.
41. K. Du, A. Gao, L. Gao, S. Sun, X. Lu, C. Yu, S. Li, H. Zhao and Y. Bai, Enhancing the structure stability of Ni-rich LiNi_0.6Co_0.2Mn_0.2O₂ cathode via encapsulating in negative thermal expansion nanocrystalline shell, Nano Energy, 2021, 83, 105775.
42. C. Zhao, C. Wang, X. Liu, I. Hwang, T. Li, X. Zhou, J. Diao, J. Deng, Y. Qin and Z. Yang, Suppressing strain propagation in ultrahigh-Ni cathodes during fast charging via epitaxial entropy-assisted coating, Nat. Energy, 2024, 9(3), 345–356.
43. C. Cui, X. Fan, X. Zhou, J. Chen, Q. Wang, L. Ma, C. Yang, E. Hu, X.-Q. Yang and C. Wang, Structure and interface design enable stable Li-rich cathode, J. Am. Chem. Soc., 2020, 142(19), 8918–8927.
44. J. Hafner and G. Kresse, The vienna ab initio simulation program VASP: an efficient and versatile tool for studying the structural, dynamic, and electronic properties of materials, Properties of Complex Inorganic Solids, Springer, 1997, pp. 69–82.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
46. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
47. A. Urban, D.-H. Seo and G. Ceder, Computational understanding of Li–ion batteries, npj Comput. Mater., 2016, 2(1), 1–13.
48. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): a robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319.

---

Footnote

† Electronic supplementary information (ESI) available: The supplementary information document and the original data of all DRX anode materials calculations are available online. See DOI: https://doi.org/10.1039/d4mh00715h

---