Rethinking tolerance factor analysis for chalcogenide perovskites

Abstract

Tolerance factor analysis has been widely used to predict suitable compositions for oxide and halide perovskites. However, in the case of the emerging chalcogenide perovskites, the predictions from the tolerance factor have failed to align with experimental observations. In this work, we reconsider how tolerance factor is being applied, specifically adjusting for the effect of increased covalency of bonding on the ionic radii. Further, we propose a series of screening steps based on the octahedral factor, tolerance factor, and electronegativity difference to better predict the formation of sulfide perovskites.

---

New concepts

This work seeks to change how tolerance factor analysis is applied to chalcogenide perovskites. The tolerance factor and other geometric screening methods have been used broadly for oxide and halide perovskites. However, the translation of these methods to chalcogenide perovskites has, so far, failed to explain experimental observations. Here, we consider how the fundamental assumptions behind radius ratio rules and the tolerance factor necessitate careful consideration of what data best represents sulfide materials. With this improved geometric analysis, we then identify that further non-geometric factors help dictate which combinations of cations form sulfide perovskites. Together, these findings change the perception of the potential compositional space of chalcogenide perovskites and lead to new candidate materials for this crystal structure.

Perovskites with the composition ABX₃ are one of the most heavily studied classes of materials, particularly in the case of oxide and halide perovskites. While the diverse group of oxide perovskites (generally with wide bandgaps) have been studied for a wide variety of applications, the recent emergence of organic–inorganic halide perovskites with narrower bandgaps and excellent optoelectronic properties led to the surge of perovskite-based solar cells and semiconductor devices.¹ Yet, fundamental challenges in halide perovskite stability have resulted in a widespread investigation into methods to enhance the stability of halide perovskites or to find new perovskites and perovskite-inspired materials that have excellent optoelectronic properties but enhanced stability.^2–4 As such, there has been substantial effort to quickly screen the compositional space for combinations of ions that might allow for the formation of a perovskite material.

The perovskite crystal structure is based around a corner-sharing network of BX₆ octahedra, with the A-cations filling the resulting cavities. As a simple screening procedure to determine which combinations of A, B, and X ions can form the perovskite crystal structure, geometrically derived dimensionless numbers have been defined. The most famous of these dimensionless numbers is the tolerance factor, t, which is defined based on r_A, r_B, and r_X, which are the ionic radii of the A, B, and X ions, respectively.⁵

In essence, the tolerance factor considers if the A-cation has an appropriate size to stabilize the BX₆ octahedral network. If the value of t is greater than 1, it predicts that the A-cation is too big, and a non-perovskite crystal structure will form. If the value of t is exactly 1, it predicts that the A-cation is the perfect size, and a cubic perovskite will form. Values slightly below 1 (the exact definition varies but approximately between 0.8–1) predict that the octahedral network will distort to accommodate a smaller A-cation, resulting in a distorted perovskite.^6–9 Finally, for values well below 1 (generally below 0.8), the A-cation is much too small, and a non-perovskite crystal structure is formed.

A second dimensionless number that is also useful in screening for perovskite compounds is referred to as the octahedral factor, μ, and is the ratio of the B-cation radius to the X-anion radius.

The octahedral factor considers if the B-cation and X-anion are appropriately sized to form BX₆ octahedra, an important consideration given the requisite of this unit in the perovskite structure. This is predicted to occur when values of μ fall between 0.414 and 0.732.^10,11 While in the context of perovskites this value is referred to as the octahedral factor, it is really just a specific example of the radius ratio rules which can be used to predict the coordination number for a given cation–anion combination.^12–15 The values in Table 1 show the predicted coordination number around a B-cation depending on the radius ratio with an X-anion.

Table 1 Predicted coordination based on the radius ratio

r B/rX	Coordination number	Packing/coordination type
1.0	12	Hexagonal or cubic closest packing
0.732–1.0	8	Cubic
0.414–0.732	6	Octahedral
0.225–0.414	4	Tetrahedral
0.155–0.225	3	Triangular
0–0.155	2	Linear

---

This combination of tolerance factor and octahedral factor have generally been successful for the screening of oxide, fluoride, and chloride perovskite materials, which make up the bulk of the known and heavily studied perovskites.^6,11 Chalcogenide perovskites (mostly sulfide perovskites) have recently emerged as an interesting class of materials for optoelectronic applications due to their better stability than the organic–inorganic halide perovskites and their lower bandgaps than the oxide perovskites.^3,16 As such, tolerance factor analysis was quickly used to screen for candidate chalcogenide perovskite materials. However, simple application of tolerance factor and octahedral factor suggests there should be few chalcogenide perovskites, which fails to accurately connect with the growing number of experimentally synthesized ABS₃ perovskites.^17,18

To better understand where these predictions are going wrong, we can first consider attempts to predict which B-cations are suitable for sulfide perovskites. Because the sulfide anion is larger than the oxide anion, it is intuitive that large +4 cations would be of interest for sulfide perovskites. Considering d and p block elements that commonly take this oxidation state, this could include Ti⁴⁺, Zr⁴⁺, Hf⁴⁺, Mo⁴⁺, W⁴⁺, and Sn⁴⁺. Tiwari et al. used Shannon ionic radii to calculate the octahedral factor for a wide range of +4 cations.¹⁷ The reported μ values for these cations with a S²⁻ anion were 0.33, 0.39, 0.39, 0.35, 0.36, and 0.38, respectively.¹⁷ As none of these values cross the lower threshold of 0.414, this result implies that all of these B-cations are too small to have octahedral coordination with sulfide anions. However, in each of the binary TiS₂, ZrS₂, HfS₂, MoS₂, WS₂, and SnS₂, the +4 metal has 6-fold coordination with the S²⁻ anions, showing that these octahedral factor calculations do not track with experimental observations.

Next, we can consider tolerance factor calculations in the context of chalcogenide perovskites, which has been covered in several reports.^17–21 As discussed by Jess et al., using the traditional tolerance factor analysis for known ABS₃ materials results in a variety of perovskite and non-perovskite materials falling within the 0.83 to 1 tolerance factor range that should translate chalcogenide perovskites.²² For example, from these calculations all of BaZrS₃, BaSnS₃, PbZrS₃, and PbSnS₃ have an appropriate tolerance factor to form a distorted perovskite. But experimentally only BaZrS₃ takes the perovskite crystal structure, while BaSnS₃, PbZrS₃, and PbSnS₃ take the needle-like crystal structure. This indicates that on its own, tolerance factor analysis is incapable of distinguishing between chalcogenide perovskites and other related chalcogenide materials.

Going a step further, Sopiha et al. used both the tolerance factor and octahedra factor to make a 2D map to highlight the challenge of finding a combination of A- and B-cations that satisfy both the tolerance factor and octahedral factor to form a sulfide perovskite.¹⁸ None of the combinations they considered passed a strict threshold of 0.414 < μ < 0.732 and 0.85 < t < 1. This would lead to the expectation that chalcogenide perovskites are exceedingly rare. But while the number of known chalcogenide perovskites is much smaller than the number of oxide perovskites, there are more chalcogenide perovskites than would be expected based on this combined tolerance factor and octahedral factor analysis.

In this work we seek to remedy this disconnect by reconsidering how tolerance factor analysis is applied to the screening of sulfide perovskites. In doing so, we emphasize two key areas of consideration. The first of these is the criticality of using the correct radii for a given system. Ionic radii are not fixed values. While it is widely understood that the ionic radius can change with oxidation state and coordination number, this value can also change based on the ionic-covalent nature of the specific bond. Second, while the tolerance factor and octahedral factor can screen “geometrically”, it is also useful to consider screening “chemically” in the prediction of sulfide perovskites. Considering these two points together better explains the known compositional space for chalcogenide perovskites and provides new direction for researchers searching for undiscovered perovskite materials.

To have a data set to study the screening of chalcogenide perovskites, a search for ABS₃ materials was performed on the Materials Project database. Excluding persulfides, 100 ABS₃ materials were found that were on or within 0.05 eV of the convex hull.²³ When multiple crystal structures were listed for a given ABS₃ composition, the crystal structure with the lowest energy was selected. These materials are shown in Table S1 (ESI†). This table also notes the common crystal structures found in this dataset, including distorted perovskite (DP), needle-like (NL), hexagonal (Hex), NdYbS₃-type, and CeTmS₃-type. The distorted perovskites are further classified as 2–4, 3–3, or 4–2 depending on the charges of the A- and B-cations, respectively. No 1–5 or 5–1 sulfide perovskites were listed in the Materials Project database, despite these combinations of cations satisfying charge balance. This table also lists the coordination-number of the B-cations, since BS₆ octahedra are a core feature of the perovskite crystal structure and are the focus of the octahedral factor calculation. It should be noted that a major assumption of this analysis is that the computational data obtained from Materials Project is reflective of reality. This assumption is discussed further and validated below.

The first major requirement for geometric screening of chalcogenide perovskites is to have correct sizes for the constituent ions. Incorrect radii will inherently lead to flawed geometric calculations. As has been discussed above, the mismatch between octahedral calculations in the literature and actual experimental observations is an indication that the wrong radii are being used in the case of chalcogenide perovskites. Shannon's ionic radii are the most widely used values for the sizes of ions in the literature and have been the primary source for chalcogenide perovskite screening. It is readily apparent in this data that changes in the oxidation state and the coordination number of the ions will cause a change in the ionic radius. However, a less readily apparent factor that will also impact the ionic radius is the ionic-covalent nature of the specific bond. In the most widely utilized data set, Shannon meticulously calculated all the ionic radii from experimental data on the crystal structures of metal oxides and metal florides.^24,25 However, as Brehm et al. and Jess et al. pointed out, the more covalent nature of metal sulfide bonds compared to metal oxide bonds means that these ionic radii derived from metal oxide data will not be correct for metal sulfides.^22,26 Both Brehm et al. and Jess et al. proceeded to develop a modified tolerance factor where one or more electronegativity difference terms are included, and in both cases improved predictions were obtained. However, this type of modification means that the tolerance factor no longer has a geometric interpretation as was initially intended. A more fundamental approach to solving this problem is instead to obtain corrected radii specifically for metal sulfides.

Luckily, Shannon also realized this problem and later published a less complete dataset for crystal radii derived from metal sulfide experimental data.²⁷ In addition to adjusting the cationic radii, there is also an important distinction that this work uses the crystal radius of 6-coordinated S²⁻ of 1.70 Å rather than the ionic radius of 1.84 Å. In this work, we have used this sulfide-derived crystal radii dataset, filling in the gaps with extrapolation and approximation where needed (Table S2, ESI†). In doing so we denote μ^S and t^S as the octahedral factor and tolerance factor calculations that utilize sulfide-derived radii.

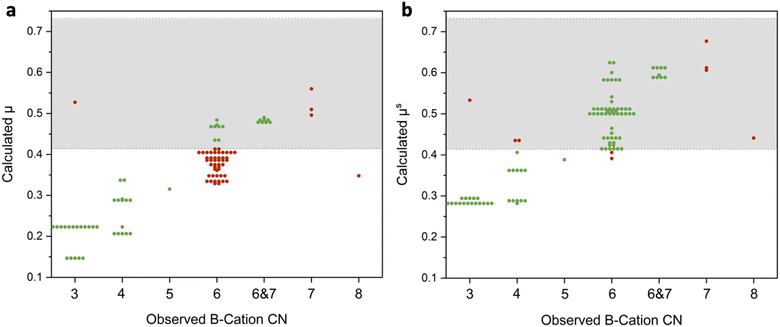
Our first step was to determine if these revised radii lead to improved geometric predictions. This can be done by comparing how accurate octahedral factor predictions are with the oxide-derived ionic radii and with the sulfide-derived crystal radii. These octahedral factor calculations for the set of materials used in this study are shown in Fig. 1 with green circles representing correct predictions and red circles representing incorrect predictions. As seen in Fig. 1a, octahedral factor calculations based on the oxide-derived radii have poor predictive ability, only correctly predicting the coordination around the B-cation as <6, =6, or >6 in 49 out of the 100 materials. Diving into these predictions further, these calculations do tend to be correct for materials where the B-cation has coordination numbers less than 6. However, when considering the materials where the B-cation has a coordination number of exactly 6 or a mixture of 6- and 7-fold coordination, the calculation incorrectly predicts that the cation is too small for this degree of coordination in 46 out of the 63 materials.

Fig. 1 Scatter plots comparing the observed coordination number for the B-cations of the 100 ABS₃ materials (based on computational structures from Materials Project) compared to the calculated octahedral factor based on (a) oxide derived radii and (b) sulfide derived radii. Correct predictions are marked with a green circle and incorrect predictions are marked with a red circle.

On the other hand, a large improvement in the predictive ability of the octahedral factor is obtained when using sulfide-derived radii (Fig. 1b). Overall, 91 out of the 100 materials had the correct prediction for B-cation coordination of <6, =6, or >6. In particular, materials that had some degree of B-cations with 6-fold coordination were correctly identified in 61 out of 63 examples. While there are still some limitations in this sulfide-derived dataset (see Discussion S1 in the ESI†), the switch to sulfide-derived data leads to markedly enhanced predictive ability. Overall, this allows us to arrive at the conclusion that these sulfide-derived radii better match the actual sizes of the ions in these materials and should therefore be used for geometric predictions of the sulfides.

Utilizing the octahedral factor with sulfide-derived radii as the first screening step, 67 candidate materials were predicted to have BX₆ octahedra (noting that a handful of these did not actually have BX₆ octahedra in their crystal structure). As a second step of the screening procedure, the tolerance factor was calculated using sulfide-derived radii (designated as t^S). Given the use of radii that more accurately reflect the size of the ions in the crystals, it is expected that improved geometric screening via tolerance factor can be achieved. In line with this prediction, 21 out of the 22 chalcogenide perovskites that passed the octahedral factor screening had t^S values between 0.865 and 0.965 (Fig. 2). The other chalcogenide perovskite which didn’t fall in this region (LaLuS₃) had a t^S value of 0.84 which is near the expected distorted perovskite region, depending on how that range is defined. This suggests that the correction to the radii has improved the tolerance factor predictions. However, counter to this idea, 20 materials that don’t take the distorted perovskite crystal structure also had t^S values in the range of 0.865 to 0.965, with 13 of them taking the needle-like crystal structure. This suggests that the combination of tolerance factor and octahedral factor as geometric screening methods is still not satisfactory for differentiating chalcogenide perovskites and a third screening step is necessary. It should be noted that the finding that a simple use of tolerance factor is unable to accurately separate perovskite and non-perovskite materials is consistent with other classes of ABX₃ materials, particularly those with anions that are less electronegative, such as iodides.^6,28

Fig. 2 Scatter plot for the 67 materials that passed the modified octahedral factor screening comparing their calculated tolerance factor, t^S and their electronegativity difference, χ_diff, and sorted by their crystal structure.

Interestingly, researchers have improved the groupings with tolerance factor when multiplied by some term that accounts for electronegativity difference, despite the fact that this no longer allows for a geometric interpretation of the resulting value.^22,26 This could suggest that rather than accounting for changes in the radii of the ions as was initially intended, this electronegativity term is acting as a screening method based on the chemistry of the ions. For example, the electronegativity differences between the anions and cations can affect charge localization and impact cation–cation repulsion, which could in turn lead to certain crystal structures being favored. Therefore, we added a screening step based on the electronegativity difference between the anions and cations, χ_diff.

The scatter plot in Fig. 2 establishes a two-dimensional map of the 67 materials that passed the octahedral factor screening step based on their t^S and their χ_diff. The results show excellent grouping of the different crystal structures. Notably, this χ_diff aids in distinguishing between the distorted perovskites and the needle-like materials. Taking the constraints of t^S between 0.865 and 0.965 and χ_diff above 1.025 effectively groups 18 of the 22 chalcogenide perovskites that passed the μ^S constraint. Additionally, only one material that does not have a chalcogenide perovskite crystal structure falls within this region (CeLuS₃). There are also notable groupings of other crystal structures. Hexagonal materials have a larger t^S value and a high χ_diff value. On the other hand, NdYbS₃-type and CeTmS₃-type materials have a lower t^S value and a high χ_diff value. Interestingly, the needle-like materials have a large spread in their t^S values but all have a low χ_diff value.

It is also worth considering the effectiveness of this three-step screening procedure as a whole. A total of 100 ABS₃ materials were considered, 24 of which take a distorted perovskite crystal structure. Only 19 materials were classified to fit within the constraints of 0.414 < μ^S < 0.732, 0.865 < t^S < 0.965, and χ_diff > 1.025, and 18 of those were correctly predicted as distorted perovskites. Therefore 18 out of 24 perovskites and 75 out of 76 non-perovskites were correctly classified by this procedure.

At this point, it is important to verify that the dataset obtained from Materials Project is reflective of reality. Table S4 (ESI†) compares the crystal structures obtained from Materials Project to the crystal structures listed in ICSD for the 67 materials contained in Fig. 2. There is strong agreement between the two sources. In some cases, ICSD shows multiple crystal structures for a given material. In these cases, the Materials Project is useful in identifying which is the thermodynamically favorable crystal structure.

Consideration should be given to the meaning behind this procedure and its implication for chalcogenide perovskites. The first two screening steps (μ^S and t^S) are purely geometric with the intention of utilizing more accurate radii. While geometric dimensionless numbers have been highly successful for predicting oxide perovskites, these metrics alone fail to satisfactorily identify sulfide perovskites. Therefore, an additional screening step based on the chemical nature of the constituent ions was added (χ_diff), which improves the predictive ability of this screening. In particular, it notes that sulfide perovskites tend to have a larger electronegativity difference between their cations and the sulfide anion. This is interesting as the more electronegative oxide anion allows for a large χ_diff with a diversity of cations, which correlates with the observation that there is a huge number of known oxide perovskites. Additionally, a selenide perovskite (LaScSe₃) was recently discovered which would also have a χ_diff above the threshold designated in this study.²⁹ That being said, we do not propose a specific mechanism by which large electronegativity difference would enable a perovskite crystal structure. Instead, we can put forward a few potential hypotheses for this finding:

• In materials with a small χ_diff and relatively covalent bonding nature there could be reduced charge localization. That may minimize the impact of cation–cation repulsion and allow for non-perovskite crystal structures which have smaller cation–cation distances.

• As χ_diff decreases the covalency of the bond increases which may negate the hard-sphere assumption that is built into geometric screening methods. Therefore, for materials with a small χ_diff, the determined ionic radii may no longer be representative and tolerance factor analysis may not be valid.

• The χ_diff factor may just be following some other periodic table trend that is more connected to the fundamental factors determining the crystal structure.

The majority of chalcogenide perovskite research has so far focused on BaZrS₃, which has proven to have good stability and a bandgap that could be useful in tandem photovoltaics.^30–36 However, the ongoing search for chalcogenide perovskites could unearth new materials with interesting properties for a variety of applications. Ultimately, this sort of screening based on easy to obtain data is better considered as a useful first step rather than some perfect end-all-be-all methodology. Still, it can point researchers in the right direction in attempts to discover new chalcogenide perovskites.

In considering these three screening criteria together, we performed a preliminary search to find hitherto unidentified distorted perovskites by limiting to cations from elements on the left side of the periodic table (Table 2). This includes the alkali metals, alkaline earth metals, early transition metals, and the metals of the lanthanide and actinide series. Because of the radioactivity of the actinide series, chalcogenide perovskites of these metals are not likely to be useful in semiconductor applications. Similar radioactivity arguments could be used to remove promethium and any elements with atomic numbers of 84 or more. While elemental abundance arguments might be presumed to eliminate the “rare earth” lanthanides, they are actually more abundant than some other elements used in the semiconductor industry like indium, silver, cadmium, and tellurium. It is frequently observed that the lanthanides form sulfides perovskites with scandium, with this constituting the majority of the known 3–3 perovskites.¹⁸ However, EuScS₃ was not present in the Materials Project database. While europium often takes the +2 oxidation state, the +3 oxidation state is also possible making this an intriguing option for a new 3–3 perovskite. Other 3–3 perovskites may also exist based on lanthanide A-cations and either yttrium, titanium, or niobium as the B-cation.

Table 2 Preliminary search for unidentified sulfide perovskites

Suggested composition	Calculated μ^S	Calculated t^S	Calculated χdiff
EuScS3	0.51	0.89	1.04
SmHfS3	0.50	0.93	1.05
SmZrS3	0.50	0.93	1.05
CaTiS3	0.43	0.95	1.04
NaTaS3	0.44	0.93	1.06

---

Considering the +4 B-cations, zirconium and hafnium have already been observed in combination with most of the likely +2 A-cations (barium, strontium, calcium, and europium).^18,37–39 Samarium can also take the +2 oxidation state and would satisfy the need for a large A-cation meaning SmZrS₃ and SmHfS₃ might take the perovskite crystal structure. Other +4 cations that could be of interest include titanium and cerium. Titanium is notably smaller than zirconium and hafnium, so in combination with barium it produces hexagonal BaTiS₃. Perhaps the smaller calcium would enable CaTiS₃ to take the distorted perovskite structure.

There are very few +5 cations that are likely to have the size and electronegativity combination to enable a chalcogenide perovskite, so it is expected that 1–5 sulfide perovskites would be rare. The best B-cation candidate for these 1–5 perovskites would be tantalum, and even this in on the small side. CsTaS₃ is reported in a hexagonal crystal structure.⁴⁰ However, pairing tantalum with a smaller alkali metal might satisfy the above criteria, making NaTaS₃ an intriguing option for the first 1–5 sulfide perovskites. KTaS₃ and RbTaS₃ would fall near the border of the distorted perovskite and hexagonal regions, close enough that errors from the extrapolation method for determining the alkali cation radii could impact the predictions. We note that our initial attempt to synthesize NaTaS₃ and KTaS₃via high temperature solid-state reactions was unsuccessful. However, challenging synthesis has been a hallmark of chalcogenide perovskites, and these new perovskites may just require a careful and creative search to find appropriate synthesis conditions.

We also note that the data presented here could reasonably be extended to identifying likely cations that could be alloyed into known sulfide perovskites. Additionally, the similar size and electronegativity of the selenide anion compared to the sulfide anions means that the cation radii and methods used in this work could be used as a first approximation for identifying selenide perovskites. In a similar way, this work could also be extended as a first approximation of alloyed sulfoselenide perovskites. However, more accurate predictions would likely be possible when using data derived from metal selenide materials.

In conclusion, this study seeks to enhance screening procedures for sulfide perovskite. To do this, we utilize the well-established tolerance factor and octahedral factor, but attempt to correct the radii of the ions to account for the more covalent nature of the metal sulfur bonds. Additionally, we identify that even with these improved radii, geometric factors alone fail to distinguish between the ABS₃ materials that take the distorted perovskite crystal structure and the needle-like crystal structure. Therefore, an additional chemical screening method based on electronegativity differences was introduced which drastically enhanced the identification of sulfide perovskites from the tested dataset. With these three screening parameters, we can direct researchers in the pursuit of new chalcogenide perovskites.

Author contributions

J. W. T. – conceptualization, methodology, formal analysis, investigation, visualization, writing – original draft, writing – review & editing. S. A. – investigation, validation, writing – review & editing. R. A. – conceptualization, writing – review & editing, supervision, funding acquisition.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful for the financial support from the National Science Foundation through Grants 1735282-NRT (SFEWS) and 10001536 (INFEWS).

Notes and references

1. B. V. Lotsch, Angew. Chem., Int. Ed., 2014, 53, 635–637.
2. B. P. Finkenauer, Y. Zhang, K. Ma, J. W. Turnley, J. Schulz, M. Gómez, A. H. Coffey, D. Sun, J. Sun, R. Agrawal, L. Huang and L. Dou, J. Phys. Chem. C, 2023, 127, 930–938.
3. Y.-Y. Sun, M. L. Agiorgousis, P. Zhang and S. Zhang, Nano Lett., 2015, 15, 581–585.
4. Y.-T. Huang, S. R. Kavanagh, D. O. Scanlon, A. Walsh and R. L. Z. Hoye, Nanotechnology, 2021, 32, 132004.
5. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
6. W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548.
7. S. Burger, M. G. Ehrenreich and G. Kieslich, J. Mater. Chem. A, 2018, 6, 21785.
8. Q. Sun and W.-J. Yin, J. Am. Chem. Soc., 2017, 139, 30.
9. Z. Li, X. Wu, L. Chen, G. Pilania, P. V. Balachandran, C. Kim and T. Lookman, Front. Mater., 2016, 3, 19.
10. C. Li, K. C. K. Soh and P. Wu, J. Alloys Compd., 2004, 372, 40–48.
11. C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr., Sect. B, 2008, B64, 702–707.
12. G. F. Hüttig, Z. anorg. allg. Chem., 1920, 114, 24.
13. A. Magnus, Z. anorg. allg. Chem., 1922, 124, 289–321.
14. V. M. Goldschmidt, Trans. Faraday Soc., 1929, 25, 253–283.
15. W. B. Jensen and D. Davenport, J. Chem. Educ., 2010, 87, 587–588.
16. J. W. Turnley and R. Agrawal, Chem. Commun., 2024, 60, 5245.
17. D. Tiwari, O. S. Hutter and G. Longo, J. Phys. Energy, 2021, 3, 034010.
18. K. V. Sopiha, C. Comparotto, J. A. Márquez and J. J. S. Scragg, Adv. Opt. Mater., 2022, 10, 2101704.
19. W. Meng, B. Saparov, F. Hong, J. Wang, D. B. Mitzi and Y. Yan, Chem. Mater., 2016, 28, 821–829.
20. N. A. Moroz, C. Bauer, L. Williams, A. Olvera, J. Casamento, A. A. Page, T. P. Bailey, A. Weiland, S. S. Stoyko, E. Kioupakis, C. Uher, J. A. Aitken and P. F. P. Poudeu, Inorg. Chem., 2018, 57, 55.
21. A. Swarnkar, W. J. Mir, R. Chakraborty, M. Jagadeeswararao, T. Sheikh and A. Nag, Chem. Mater., 2019, 31, 565–575.
22. A. Jess, R. Yang and C. J. Hages, Chem. Mater., 2022, 34, 6894–6901.
23. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 11002.
24. R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925.
25. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
26. J. A. Brehm, J. W. Bennett, M. R. Schoenberg, I. Grinberg and A. M. Rappe, J. Chem. Phys., 2014, 140, 224703.
27. R. D. Shannon, Industrial Chemistry Library, Academic Press Inc., 1981, vol. 2, pp. 53–70.
28. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693.
29. H. Zhang, X. Wu, K. Ding, L. Xie, K. Yang, C. Ming, S. Bai, H. Zeng, S. Zhang and Y.-Y. Sun, Chem. Mater., 2023, 35, 4128–4135.
30. J. W. Turnley, K. Catherine Vincent, A. A. Pradhan, I. Panicker, R. Swope, M. C. Uible, S. C. Bart and R. Agrawal, J. Am. Chem. Soc., 2022, 144, 18234–18239.
31. S. Agarwal, J. W. Turnley, A. A. Pradhan and R. Agrawal, J. Mater. Chem. C, 2023, 11, 15817–15823.
32. R. Yang, A. D. Jess, C. Fai and C. J. Hages, J. Am. Chem. Soc., 2022, 144, 15928–15931.
33. C. Comparotto, P. Ström, O. Donzel-Gargand, T. Kubart and J. J. S. Scragg, ACS Appl. Energy Mater., 2022, 5, 6335–6343.
34. T. Gupta, D. Ghoshal, A. Yoshimura, S. Basu, P. K. Chow, A. S. Lakhnot, J. Pandey, J. M. Warrender, H. Efstathiadis, A. Soni, E. Osei-Agyemang, G. Balasubramanian, S. Zhang, S. F. Shi, T. M. Lu, V. Meunier and N. Koratkar, Adv. Funct. Mater., 2020, 30, 2001387.
35. S. Niu, J. Milam-Guerrero, Y. Zhou, K. Ye, B. Zhao, B. C. Melot and J. Ravichandran, J. Mater. Res., 2018, 33, 4135–4143.
36. K. C. Vincent, S. Agarwal, J. W. Turnley and R. Agrawal, Adv. Energy Sustainable Res., 2023, 4, 2300010.
37. A. Clearfield, Acta Crystallogr., 1963, 16, 135–142.
38. R. Lelieveld and D. J. W. Ijdo, Acta Crystallogr., 1980, B36, 2223–2226.
39. A. A. Pradhan, M. C. Uible, S. Agarwal, J. W. Turnley, S. Khandelwal, J. M. Peterson, D. D. Blach, R. N. Swope, L. Huang, S. C. Bart and R. Agrawal, Angew. Chem., Int. Ed., 2023, 62, e202301049.
40. M. A. Pell, G. V. M. Vajenine and J. A. Ibers, J. Am. Chem. Soc., 1997, 119, 5186–5192.

---

Footnote

† Electronic supplementary information (ESI) available: Materials and crystal radii data, discussion on data limitations. See DOI: https://doi.org/10.1039/d4mh00689e

---