 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-supervised graph neural networks for polymer property prediction†
Qinghe
Gao‡
a,
Tammo
Dukker‡
a,
Artur M.
Schweidtmann
 a and
Jana M.
Weber
a and
Jana M.
Weber
 *b
*b
aProcess Intelligence Research Group, Department of Chemical Engineering, Delft University of Technology, Van der Maasweg 9, Delft 2629 HZ, The Netherlands
bPattern Recognition and Bioinformatics, Department of Intelligent Systems, Delft University of Technology, Van Mourik Broekmanweg 6, 2628 XE Delft, The Netherlands. E-mail: J.M.Weber@tudelft.nl
First published on 29th August 2024
Abstract
The estimation of polymer properties is of crucial importance in many domains such as energy, healthcare, and packaging. Recently, graph neural networks (GNNs) have shown promising results for the prediction of polymer properties based on supervised learning. However, the training of GNNs in a supervised learning task demands a huge amount of polymer property data that is time-consuming and computationally/experimentally expensive to obtain. Self-supervised learning offers great potential to reduce this data demand through pre-training the GNNs on polymer structure data only. These pre-trained GNNs can then be fine-tuned on the supervised property prediction task using a much smaller labeled dataset. We propose to leverage self-supervised learning techniques in GNNs for the prediction of polymer properties. We employ a recent polymer graph representation that includes essential features of polymers, such as monomer combinations, stochastic chain architecture, and monomer stoichiometry, and process the polymer graphs through a tailored GNN architecture. We investigate three self-supervised learning setups: (i) node- and edge-level pre-training, (ii) graph-level pre-training, and (iii) ensembled node-, edge- & graph-level pre-training. We additionally explore three different transfer strategies of fully connected layers with the GNN architecture. Our results indicate that the ensemble node-, edge- & graph-level self-supervised learning with all layers transferred depicts the best performance across dataset size. In scarce data scenarios, it decreases the root mean square errors by 28.39% and 19.09% for the prediction of electron affinity and ionization potential compared to supervised learning without the pre-training task.
Design, System, ApplicationOur manuscript on “Self-supervised graph neural networks for polymer property prediction” is a graph-based machine learning method to improve molecular property prediction in scarce data domains. We develop node-level, edge-level, and graph-level self-supervised learning strategies for weighted directed message passing graph neural networks. We show how our method improves the performance of a state-of-the art property predictor when limited data is available. Thus, the method is useful for screening and design efforts in scarce data domains. The molecular systems are co-polymers based on combinations of almost 700 distinct monomer chemistries, varying monomer stoichiometries (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1 1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 3 3, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), and three distinct chain-architectures. The properties of interest are electron affinity and ionisation potential. The immediate application potential of the work is to improve photocatalyst design for the production of green hydrogen. Ultimately, our work can be further employed for any co-polymer property prediction task which can be modelled through GNNs. 1), and three distinct chain-architectures. The properties of interest are electron affinity and ionisation potential. The immediate application potential of the work is to improve photocatalyst design for the production of green hydrogen. Ultimately, our work can be further employed for any co-polymer property prediction task which can be modelled through GNNs.
|
1 Introduction
The rise of many novel technologies demands the development of innovative polymers, with applications such as polymer-based organic batteries,1 polymer photocatalysts that aid hydrogen generation,2 or more sustainable plastics.3 However, navigating the vast chemical space to identify polymers with optimal properties poses a considerable challenge. Consequently, various computational methods have been proposed to assist preliminary screening tasks.One widely recognized class of methods is quantitative structure–property relationships (QSPR),4 which link molecules' physical or chemical properties to their structural information through the use of predefined molecular descriptors and linear or nonlinear regression techniques. Nonetheless, QSPR models carry intrinsic limitations. For instance, significant domain expertise is required to select appropriate molecular descriptors and potentially sub-optimal choices impact their prediction capacity. Additionally, the feature selection process needs to be repeated for each target property. These limitations are addressed by end-to-end learning methods in machine learning (ML), bypassing the need for manual selection of descriptors and enabling the models to discern relevant features autonomously. Here, the algorithms learn a molecular fingerprint directly from the molecular representation without the need for descriptor selection. Graph neural networks (GNNs) have recently emerged as a key end-to-end learning technique for molecular property prediction tasks, as they leverage the graphical representation of molecules.5 Particularly, atoms are represented as nodes, and bonds are represented as edges. GNNs have shown to be very successful in a broad range of molecular prediction tasks, such as predicting combustion-related properties,6 predicting the growth of Escherichia coli for new antibiotic discovery,7 and protein function8 or protein–protein interaction tasks.9
Despite the success of GNNs in molecular machine learning, extending them to polymer property prediction remains challenging. The reasons for that are twofold. Firstly, polymer structures are difficult to model accurately. They exhibit an inherent hierarchical complexity and they are not one uniquely defined molecular structure but are composed of an ensemble of similar molecules.10 Secondly, unlike in the domains of small molecules and ordered materials, where numerous large (>100K) and open-source databases exist,11,12 there is an absence of accessible polymer property data.13–15 The recent work by Aldeghi et al.,10 has represented polymers with selected higher-order structural information as a stochastic graph, making them applicable for GNNs. However, the second obstacle, the lack of sufficient polymer property data is still challenging. The measurements of polymer properties in the community rely highly on the instruments in the experiments. However, those instruments have few open interfaces and data models, hindering further developments of large property databasets.16–18
To address the scarcity of labeled data, several strategies have been proposed, including transfer learning19,20 and multi-task learning.21,22 For instance, Zhang et al.19 pre-trained a transformer model on a dataset of 1 billion small molecules and subsequently fine-tuned the model with a small amount of labeled polymer property data (ranging from 300 to 3000 samples). The resulting accuracies were comparable to those achieved by the TransPolymer23 and polyBERT24 models, without the expensive generation and pretraining on large-scale augmented polymer datasets. Furthermore, the objective of a multi-task training approach is to enhance the performance and generalization of a model by concurrently training it on multiple related tasks, thereby leveraging shared information and representations. Gurnani et al.21 introduced multi-task GNNs for predicting 34 polymer properties. Their results indicated that, for datasets with fewer than 300 samples, the proposed models generally outperform the benchmark models.
Self-supervised learning (SSL) is another method for learning from limited data and currently helps solve data scarcity challenges in many fields like computer vision25,26 and natural language processing.27 SSL first designs a predictive learning task within the unlabelled data itself such that the model learns universal features and semantics, which subsequently contribute to the downstream supervised task with less labeled training data. A common SSL technique, for example, is to create a pseudo label from the unlabelled data structure. Unlike other training strategies that incorporate pseudo-labels into the input to enhance performance,28 SSL pre-trains the model using pseudo-labels to extract initial semantic information from unlabeled data. This approach reduces the amount of labeled data needed for subsequent fine-tuning tasks. Taking computer vision as an example,29 one can rotate an image and task the model with predicting the rotation angle. Thereby the model learns certain features from images and their orientation in space; semantics that are useful for the downstream task of interest. In the field of graph-based molecular property prediction, such tasks are commonly designed according to the structure of the molecular graph. For example, Zhang et al.30 leveraged node and edge masking as an SSL technique to pre-train GNNs, which improves the performance of predicting properties of organic semiconductors. Zang et al.31 implemented a hierarchical molecular graph neural network (HMGNN) with multi-level SSL techniques to achieve superior molecular property prediction results on both classification and regression tasks. With various successful applications in small molecular property prediction30–32 and proteins,33,34 SSL is a promising technique for prediction tasks in the sparse data domain of polymer informatics. Several studies19,23,24,33 have leveraged large language models (LLMs) for polymer property prediction tasks in an SSL manner. For example, polyBERT is pre-trained using masked language modeling (MLM) on approximately 80 million polymer strings, generated from about 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 original polymers. During fine-tuning, the pre-trained transformer weights are frozen and employed to provide polymer embeddings, which serve as inputs to a multi-layer perceptron for multitask property prediction. While these studies achieve similar performance, they are limited by using the PSMILES language, which only specifies the repeating unit and neglects important structural information such as chain architecture, stoichiometry, and monomer bonding, crucial for determining polymer properties.
800 original polymers. During fine-tuning, the pre-trained transformer weights are frozen and employed to provide polymer embeddings, which serve as inputs to a multi-layer perceptron for multitask property prediction. While these studies achieve similar performance, they are limited by using the PSMILES language, which only specifies the repeating unit and neglects important structural information such as chain architecture, stoichiometry, and monomer bonding, crucial for determining polymer properties.
We propose self-supervised GNNs for polymer property prediction. In particular, we utilize the state-of-the-art polymer graph representation and tailored GNN model from Aldeghi et al.10 as foundation, and investigate three self-supervised learning setups: (i) pre-training with node- and edge-level pseudo tasks, (ii) pre-training with graph-level pseudo tasks, and (iii) ensembled node-, edge-, and graph-level pre training. Additionally, we investigate various strategies for transferring the model architecture to augment the predictive accuracy, providing a novel perspective in the realm of polymer property prediction.
2 Methods
This section introduces the methodologies employed throughout our work. First, the graph representation of polymers is introduced in section 2.1 and the GNN architecture with tailored message-passing layers is illustrated in section 2.2 (adapted from Aldeghi et al.10). Then, three different strategies of self-supervised learning are explained: node- and edge-level, graph-level task, and node- and edge- and graph-level task consecutively. Moreover, we outline our weight transferal strategies. Finally, we introduce the details of the polymer datasets and the training procedure.2.1 Polymer graphs
We make use of a polymer representation that combines the graph representation of monomers with stochastic edges according to linking probabilities. We denote the graph representation of a polymer p with nodes as atoms v ∈ N and edges as bonds evu ∈ E connecting two nodes v and u. Specifically, there are two directed bonds between nodes v and u: bond evu and bond euv. Two directed edges allow for a wider variety of polymer structures. For example, as Fig. 1 shows, they can capture the impact of terminal ends when required such as oligomer with termini, and different possibilities of two atoms being adjacent to one another such as graft copolymers. Moreover, a feature vector and a stochastic weight are assigned to each node and each directed edge. We denote the feature vector and the stochastic weight of node v with fv ∈ FN and wv ∈ WN, respectively. fv contains specific information for atoms such as the atom type and wv represents the stochiometric ratio of the corresponding monomer. Similarly, for the directed edge from node v to node u, a feature vector fevu ∈ FE and a stochastic weight wvu ∈ WE are attached. fevu contains specific information for bonds such as the bond type. wv ∈ (0, 1] is an associated weight value reflecting the probability of that bond occurring within the respective polymer topologies. Notably, within the monomer, the edge weight is set to 1. While for the directed edges connecting different monomers, the weights vary as shown in Fig. 1. Typical features are given in Table 1 for atoms and in Table 2 for bonds. The feature-enriched graph of a polymer p is then denoted by G(p) = {V, E, FN, FE, WN, WE}.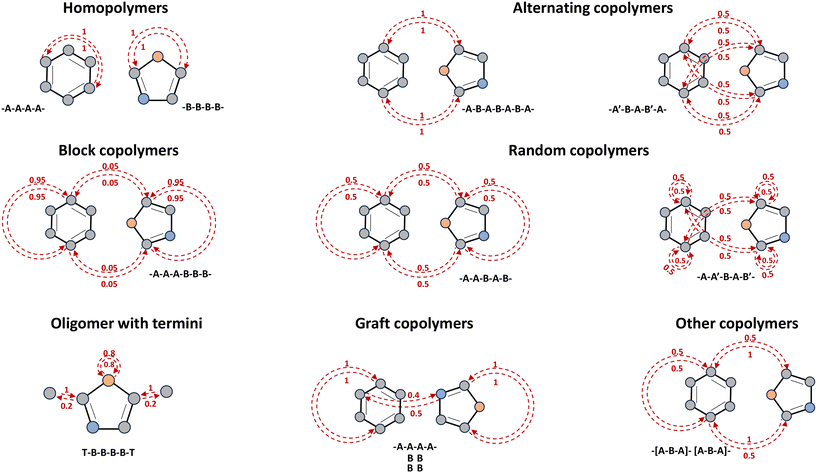 | ||
| Fig. 1 Overview of polymer topologies (adapted from Aldeghi et al.10). The red dashed lines represent the direct edges which are assigned to corresponding weights between zero and one. The weights of incoming edges indicate the possibility that the originating node (atom) is adjacent to the target node (atom). For instance, in the case of graft copolymers, there is a 40% chance that the atoms on monomer A will be neighboring atoms on monomer B (two of five monomers A are connected to monomers B), whereas the atoms on monomer B have a 50% chance of being adjacent to atoms on monomer A (two out of four monomers B are connected to the monomers A). The text underneath of each topology represents an example of the corresponding polymer sequence, where A and B are different monomers. The polymer sequence depicts a tail-to-head orientation, e.g., –A–B– represents the tail of monomer A links to the head of monomer B, and –A′–B– indicates the head of monomer A connects to the head of monomer B. | ||
| Feature | Description |
|---|---|
| Atom type | Type of atom |
| Chiral tag | Type of chirality |
| Degree | Number of bonded neighbors in the graph |
| Is aromatic | Whether the atom is part of an aromatic system |
| Hybridization | Type of hybridization such as sp, sp2 |
| Charge | Formal charge of the atom |
| #Hs | Number of bonded hydrogen atoms |
| Mass | Atom mass |
| Feature | Description |
|---|---|
| Bond type | Single, double, triple, or aromatic |
| Conjugated | Whether the bond is conjugated |
| Is in a ring | Whether the bond is part of a ring |
| Stereo | None, any, E/Z, or cis/trans |
2.2 Graph neural networks
GNNs can learn desired target predictions from a featured graph representation. Fig. 2 shows an example of the GNN architecture that is used in this work for supervised learning-only training. GNNs consist of two phases: the message passing phase, which contains convolutional operations, and the readout phase, which forms the fingerprint and predicts the target task. In the following subsection, we will introduce these two phases separately.In the message passing phase, graph convolution is utilized to extract the structural information from the polymer graph. Importantly, the weighted direct message passing neural network (wD-MPNN) is used as the graph convolutional layer. Fig. 3 shows the four steps in wD-MPNN to extract structural information from polymers. In the first step, taking node v as an example, the edge feature fevu from node v to node u is updated into h0vu as eqn (1) shows.
 | (1) |
 | (2) |
 | (3) |
 | ||
| Fig. 3 Four steps visualization of wD-MPNN.10 First, the hidden edge features are initialized by concatenating originating atom features with edge features and then passing through a single fully connected layer. Second, hidden edge features are updated through L steps of edge-centered message passing. Within l ∈ L steps, the neighboring hidden edge features are combined by the weighted sum, and then the results are added to the center hidden edge features h0vu and passed through a fully connected layer. Third, the center atom features fv are updated through the concatenation of the weighted sum of incoming hidden edge features and the original atom features. The results are then passed through a single fully connected layer. Finally, a polymer fingerprint is obtained by taking the weighted average or sum of the updated atom feature vectors. | ||
In the readout phase, the learned information from the previous steps in the hidden nodes is aggregated into a polymer fingerprint by taking the weighted average/sum as eqn (4) shows, where N is the number of nodes in the graph, wv are the associated stochastic weights of each node.
 | (4) |
Finally, the polymer fingerprint h is mapped into the property of interest. For GNNs, a multi-layer perception (MLP) is used to compute the property: ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = MLP(h).
= MLP(h).
2.3 Self-supervised learning
Fig. 4 illustrates the general framework of SSL: the pre-training phase where pseudo-tasks are designed for larger, yet unlabelled, datasets and the fine-tuning phase where the actual target labels are used for training purposes. During the pre-training phase, the encoder (message-passing layers in our case) is trained by polymer graphs with pseudo labels. These pseudo labels are obtained from the featured polymer graph topology. The aim is to design tasks for which no labeled data, i.e., physical properties, are needed to calculate these pseudo labels. Then, the pre-trained message-passing layers (including steps 1–4 in Fig. 3) are further fine-tuned with or partially with an additional new readout training (e.g., new fully connected layers) by the downstream task with a small amount of labeled data in the second phase. Three SSL techniques are used in this work: (i) node- and edge-level, (ii) graph-level task, and (iii) node- and edge-level with consecutive graph-level tasks. | ||
| Fig. 4 General framework of SSL.37 The message passing layers are first trained with SSL tasks. Then the trained message passing layers are transferred with/partially with a new readout training (e.g., new fully connected layers) to train with target labels for downstream tasks. | ||
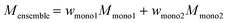 | (5) |
2.4 Polymer dataset
We develop our method on the polymer dataset presented by Aldeghi et al.,10 encompassing 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966 polymers, composed of nine A monomers and 862 B monomers. These polymers are categorized based on three distinct chain architectures: alternating, random, and block, and are further characterized by three stoichiometric ratios, namely 1
966 polymers, composed of nine A monomers and 862 B monomers. These polymers are categorized based on three distinct chain architectures: alternating, random, and block, and are further characterized by three stoichiometric ratios, namely 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 3
3, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Furthermore, the dataset contains electron affinity (EA) and ionization potential (IP) as molecular properties, i.e., target labels. Both properties were derived through density functional theory (DFT) simulations.
1. Furthermore, the dataset contains electron affinity (EA) and ionization potential (IP) as molecular properties, i.e., target labels. Both properties were derived through density functional theory (DFT) simulations.
2.5 Training procedure
First, we trained two GNN models via a supervised learning paradigm, targeting both the EA and IP labels (in the following referred to as baseline training). Subsequently, we perform three SSL techniques: (i) node- and edge-level, (ii) graph-level task, (iii) node-, edge-, and graph-level tasks. The polymer dataset is randomly shuffled and 40% of the dataset is used for SSL pre-training tasks. We then transferred the message-passing layers and subsequently conducted exploratory analyses across varying dataset sizes for fine-tuning, spanning 0.08%, 0.16%, 0.24%, 0.32%, 0.4%, 0.8%, 1.6%, 2.4%, 3.2%, 4%, 8%, 16%, 24%, 32%, and up to 40%, allowing us to explore the performance of SSL under varying label availability scenarios. The baseline models are only trained with the same fine-tuning datasets ranging from 0.08% to 40% in a supervised-only manner. Finally, the evaluation of the GNN models is conducted on the remaining 20% of the dataset. The Adam optimizer is used with a 10−3 learning rate and a batch size of 64 across 100 training epochs is used. The GNN architectures incorporate three edge-focused message passing layers with a hidden dimension calibrated at 300. Additionally, three fully connected layers are used to map the fingerprints to the prediction task.3 Results and discussion
In this section, we present the results from our three SSL techniques: (i) node- and edge-level, (ii) graph level task, and (iii) a sequential application of node- and edge-level followed by the graph-level task. We also outline the results with different layer transferal strategies.3.1 SSL results
Fig. 7, Tables 3 and 4 illustrate the model performance metrics R2 and RMSE regarding electron affinity and ionization potential. The corresponding values and 95% confidence interval values are also detailed in the ESI.† In the small labeled data regimes (e.g., <0.4%), node and edge-level SSL, as well as node-, edge- & graph-level SSL, demonstrate similar performance across all evaluated models for both EA and IP according to the R2 and RMSE. For instance, for node-, edge- & graph-level SSL, an increase of 32.21% and 23.21% in R2 is observed for both EA and IP, respectively, compared with baseline models in the smallest fine-tuning dataset (0.08%). Similarly, for node- and edge-level SSL, R2 is improved by 38.66% and 38.04%, respectively, followed by graph-level SSL in the smallest fine-tuning dataset. Therefore, in the small labeled data regimes, SSL significantly enhances the prediction performance.| Dataset size | R 2 of EA | R 2 of IP | ||||||
|---|---|---|---|---|---|---|---|---|
| Baseline | NE | G | NEG | Baseline | NE | G | NEG | |
| 0.08% | 0.357 | 0.495 | 0.413 | 0.472 | 0.418 | 0.577 | 0.511 | 0.515 |
| 0.16% | 0.383 | 0.413 | 0.418 | 0.461 | 0.417 | 0.533 | 0.522 | 0.508 |
| 0.24% | 0.583 | 0.616 | 0.619 | 0.695 | 0.541 | 0.793 | 0.619 | 0.759 |
| 0.32% | 0.555 | 0.644 | 0.585 | 0.706 | 0.546 | 0.800 | 0.645 | 0.744 |
| 0.4% | 0.631 | 0.704 | 0.643 | 0.744 | 0.646 | 0.813 | 0.695 | 0.812 |
| 0.8% | 0.664 | 0.779 | 0.709 | 0.805 | 0.762 | 0.850 | 0.791 | 0.869 |
| 1.6% | 0.789 | 0.878 | 0.824 | 0.883 | 0.868 | 0.920 | 0.894 | 0.926 |
| 2.4% | 0.867 | 0.912 | 0.867 | 0.919 | 0.927 | 0.947 | 0.924 | 0.943 |
| 3.2% | 0.918 | 0.949 | 0.912 | 0.946 | 0.955 | 0.967 | 0.942 | 0.960 |
| 4% | 0.949 | 0.969 | 0.939 | 0.961 | 0.968 | 0.976 | 0.963 | 0.968 |
| 8% | 0.982 | 0.987 | 0.979 | 0.983 | 0.985 | 0.989 | 0.987 | 0.988 |
| 16% | 0.991 | 0.992 | 0.989 | 0.991 | 0.992 | 0.994 | 0.993 | 0.993 |
| 24% | 0.993 | 0.995 | 0.993 | 0.994 | 0.994 | 0.995 | 0.995 | 0.995 |
| 32% | 0.994 | 0.995 | 0.995 | 0.995 | 0.994 | 0.996 | 0.995 | 0.996 |
| 40% | 0.995 | 0.996 | 0.995 | 0.996 | 0.996 | 0.997 | 0.996 | 0.997 |
| Dataset size | RMSE of EA | RMSE of IP | ||||||
|---|---|---|---|---|---|---|---|---|
| Baseline | NE | G | NEG | Baseline | NE | G | NEG | |
| 0.08% | 0.479 | 0.424 | 0.457 | 0.433 | 0.372 | 0.317 | 0.341 | 0.340 |
| 0.16% | 0.469 | 0.456 | 0.455 | 0.436 | 0.372 | 0.332 | 0.337 | 0.342 |
| 0.24% | 0.386 | 0.370 | 0.369 | 0.329 | 0.330 | 0.222 | 0.299 | 0.239 |
| 0.32% | 0.398 | 0.356 | 0.385 | 0.323 | 0.329 | 0.218 | 0.290 | 0.247 |
| 0.4% | 0.362 | 0.324 | 0.357 | 0.302 | 0.290 | 0.211 | 0.269 | 0.211 |
| 0.8% | 0.346 | 0.280 | 0.322 | 0.263 | 0.238 | 0.189 | 0.223 | 0.177 |
| 1.6% | 0.273 | 0.208 | 0.250 | 0.204 | 0.177 | 0.138 | 0.159 | 0.133 |
| 2.4% | 0.217 | 0.177 | 0.217 | 0.169 | 0.132 | 0.112 | 0.134 | 0.116 |
| 3.2% | 0.170 | 0.134 | 0.177 | 0.138 | 0.103 | 0.089 | 0.116 | 0.098 |
| 4% | 0.134 | 0.105 | 0.146 | 0.117 | 0.086 | 0.075 | 0.094 | 0.087 |
| 8% | 0.080 | 0.069 | 0.085 | 0.077 | 0.060 | 0.051 | 0.057 | 0.054 |
| 16% | 0.057 | 0.052 | 0.063 | 0.056 | 0.044 | 0.037 | 0.042 | 0.040 |
| 24% | 0.051 | 0.044 | 0.049 | 0.047 | 0.036 | 0.033 | 0.035 | 0.033 |
| 32% | 0.045 | 0.042 | 0.044 | 0.042 | 0.031 | 0.029 | 0.031 | 0.029 |
| 40% | 0.042 | 0.037 | 0.041 | 0.038 | 0.030 | 0.028 | 0.027 | 0.027 |
In the data regimes from 0.4% to 4%, node- and edge-level SSL, as well as node-, edge- & graph-level SSL, still boost the performance for both R2 and RMSE compared with baseline models. However, graph-level SSL exhibits less significant improvements and even negative contributions compared with baseline models. A potential reason is that the chosen pseudo label (ensemble molecular weight) has a discrepancy with target labels EA and IP.
As for larger labeled data regimes (e.g., >4%), the differences between the models become smaller (potentially neglectable) regarding both performance metrics and property labels. A plausible explanation is that with larger fine-tuning dataset availability, the graph semantics can be learned directly through the target label in the supervised fine-tuning phase, which improves the final prediction together with the pre-training SSL phase.
We further analyzed the error distribution of all four models for predicting EA and IP (see Fig. 8). First, it is evident that all error distributions follow a long-tail pattern, indicating that while the majority of predictions are accurate (low RMSE), there are a few significant outliers. In the smallest labeled data regime (0.08%), both for EA and IP, graph-level pre-training contributes minimally to performance improvement, as indicated by error distributions close to those of the baseline models. In contrast, the node-, edge-level, and combined node-, edge-, and graph-level SSL models demonstrate superior performance, with error distributions peaking over 500 with slightly lower RMSE and being narrower for both EA and IP. Notably, for EA, all models struggle to predict polymers containing pyromellitic dianhydride (PMDA) as Fig. 8 shows. This difficulty likely arises from PMDA's strong electron-withdrawing properties due to the presence of anhydride groups, complicating EA predictions. Additionally, only 63 out of 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966 samples contain PMDA, and this data scarcity contributes to poor generalization. Conversely, for IP, there is no common failure pattern in the predictions for specific polymers. In the larger labeled data regime (24%), significant improvements are observed for both EA and IP, with RMSE distributions becoming narrower. For both properties, SSL models continue to outperform baseline models, demonstrated by higher peaks with slightly lower RMSE and narrower error distributions. Overall, node- and edge-level SSL, as well as node-, edge- & graph-level SSL, exhibit consistently better performance than the baseline supervised-learning results even in the biggest labeled data regime. For example, the R2 still increases by 0.1% and 0.1% for both EA and IP for node-, edge- & graph-level SSL.
966 samples contain PMDA, and this data scarcity contributes to poor generalization. Conversely, for IP, there is no common failure pattern in the predictions for specific polymers. In the larger labeled data regime (24%), significant improvements are observed for both EA and IP, with RMSE distributions becoming narrower. For both properties, SSL models continue to outperform baseline models, demonstrated by higher peaks with slightly lower RMSE and narrower error distributions. Overall, node- and edge-level SSL, as well as node-, edge- & graph-level SSL, exhibit consistently better performance than the baseline supervised-learning results even in the biggest labeled data regime. For example, the R2 still increases by 0.1% and 0.1% for both EA and IP for node-, edge- & graph-level SSL.
3.2 Transferring fully connected layers
In this section, we present and discuss the impact of the layer transfer strategy within SSL for both graph-level SSL and node-, edge- & graph-level, respectively. Fig. 9, Tables 5 and 6 show the RMSE results with our three different transfer strategies for both EA and IP. Here we only show the RMSE results as the R2 renounces in the same trend. In the labeled data regimes <4%, we observe a pronounced difference when transferring all layers (strategy c) for the prediction of the label EA in contrast to the baseline model and the two other strategies where fewer layers are transferred. This holds both for graph-level SSL and node-, edge- & graph-level SSL. For example, the RMSE significantly decreases by 15.10% and 20.79% compared to strategy a, where only message-passing layers are transferred, for both graph-level SSL and node-, edge- & graph-level SSL, respectively. Strategy a and b also outperform the baseline models in all low data availability scenarios, yet less significantly than strategy c. On the other hand, when predicting the IP, the three strategies for graph-level SSL have a similar performance in terms of RMSE and show a less significant improvement over the baseline model. For node-, edge-, and graph-level SSL, all three strategies still exhibit a similar performance but improve the prediction significantly compared to the baseline model. For example, the RMSE of strategy c decreases by 19.09% compared to the baseline model in the smallest data scenario (0.08%). This indicates that during the node- & edge-level SSL pre-training, the learned semantics are additionally embedded in the message passing layers, which significantly contributes to predicting the target labels in the downstream tasks.| Dataset size | RMSE of EA | RMSE of IP | ||||||
|---|---|---|---|---|---|---|---|---|
| Baseline | G | G2 | G3 | Baseline | G | G2 | G3 | |
| 0.08% | 0.479 | 0.457 | 0.426 | 0.388 | 0.372 | 0.341 | 0.338 | 0.341 |
| 0.16% | 0.469 | 0.455 | 0.439 | 0.388 | 0.372 | 0.337 | 0.340 | 0.343 |
| 0.24% | 0.386 | 0.369 | 0.359 | 0.348 | 0.330 | 0.299 | 0.287 | 0.285 |
| 0.32% | 0.398 | 0.385 | 0.366 | 0.353 | 0.329 | 0.290 | 0.294 | 0.287 |
| 0.4% | 0.362 | 0.357 | 0.347 | 0.320 | 0.290 | 0.269 | 0.264 | 0.267 |
| 0.8% | 0.346 | 0.322 | 0.314 | 0.268 | 0.238 | 0.223 | 0.231 | 0.214 |
| 1.6% | 0.273 | 0.250 | 0.253 | 0.187 | 0.177 | 0.159 | 0.154 | 0.151 |
| 2.4% | 0.217 | 0.217 | 0.198 | 0.152 | 0.132 | 0.134 | 0.118 | 0.124 |
| 3.2% | 0.170 | 0.177 | 0.158 | 0.139 | 0.103 | 0.116 | 0.104 | 0.102 |
| 4% | 0.134 | 0.146 | 0.135 | 0.116 | 0.086 | 0.094 | 0.087 | 0.094 |
| 8% | 0.080 | 0.085 | 0.080 | 0.079 | 0.060 | 0.057 | 0.063 | 0.058 |
| 16% | 0.057 | 0.063 | 0.058 | 0.059 | 0.044 | 0.042 | 0.043 | 0.047 |
| 24% | 0.051 | 0.049 | 0.051 | 0.048 | 0.036 | 0.035 | 0.039 | 0.039 |
| 32% | 0.045 | 0.049 | 0.044 | 0.043 | 0.031 | 0.031 | 0.033 | 0.033 |
| 40% | 0.042 | 0.041 | 0.040 | 0.040 | 0.030 | 0.027 | 0.030 | 0.030 |
| Dataset size | RMSE of EA | RMSE of IP | ||||||
|---|---|---|---|---|---|---|---|---|
| Baseline | NEG | NEG2 | NEG3 | Baseline | NEG | NEG2 | NEG3 | |
| 0.08% | 0.479 | 0.433 | 0.395 | 0.343 | 0.372 | 0.340 | 0.333 | 0.301 |
| 0.16% | 0.469 | 0.436 | 0.389 | 0.338 | 0.372 | 0.342 | 0.320 | 0.289 |
| 0.24% | 0.386 | 0.329 | 0.325 | 0.277 | 0.330 | 0.239 | 0.235 | 0.222 |
| 0.32% | 0.398 | 0.323 | 0.311 | 0.270 | 0.329 | 0.247 | 0.245 | 0.226 |
| 0.4% | 0.362 | 0.302 | 0.311 | 0.253 | 0.290 | 0.211 | 0.211 | 0.200 |
| 0.8% | 0.346 | 0.263 | 0.258 | 0.225 | 0.238 | 0.177 | 0.185 | 0.171 |
| 1.6% | 0.273 | 0.204 | 0.204 | 0.166 | 0.177 | 0.133 | 0.133 | 0.129 |
| 2.4% | 0.217 | 0.169 | 0.160 | 0.133 | 0.132 | 0.108 | 0.107 | 0.110 |
| 3.2% | 0.170 | 0.138 | 0.136 | 0.112 | 0.103 | 0.093 | 0.093 | 0.090 |
| 4% | 0.134 | 0.117 | 0.115 | 0.098 | 0.086 | 0.087 | 0.084 | 0.080 |
| 8% | 0.080 | 0.077 | 0.076 | 0.072 | 0.060 | 0.054 | 0.053 | 0.055 |
| 16% | 0.057 | 0.056 | 0.052 | 0.054 | 0.044 | 0.039 | 0.039 | 0.042 |
| 24% | 0.051 | 0.047 | 0.046 | 0.045 | 0.036 | 0.033 | 0.033 | 0.034 |
| 32% | 0.045 | 0.042 | 0.041 | 0.041 | 0.031 | 0.029 | 0.029 | 0.030 |
| 40% | 0.042 | 0.038 | 0.038 | 0.039 | 0.030 | 0.028 | 0.028 | 0.028 |
In the labeled data regime (e.g., >4%), the impact of transferring fully connected layers becomes less significant: the importance of SSL decreases as shown by the performance curves approaching each other. For node-, edge- & graph-level SSL, strategy c is still consistently better than the baseline models for both EA and IP. However, for IP, we do observe a slightly negative contribution (4%) from strategy c compared to the baseline model for graph-level SSL. A plausible explanation is that graph-level SSL indeed has a negative contribution in the larger labeled data regime as we observed before. The chosen pseudo label from the pre-training phase is not sufficiently informative for the target label IP, and the learned semantics stored in the fully connected layer introduce extra bias during the pre-training and thereby hinder further learning in fine-tuning.
To sum it up, the extent of transferred weights impacts the overall performance of SSL in the two case studies investigated in our work. In small fine-tuning dataset scenarios (e.g., <0.4%), all transferal strategies perform better than the baseline models in both prediction tasks and both SSL scenarios. For both EA and IP, strategy c where most layers were transferred demonstrates the best performance, which decreases the RMSE by 28.39% and 19.09% respectively, compared to the baseline models for node-, edge- & graph-level SSL. In larger fine-tuning dataset scenarios, the differences become less pronounced as the impact of SSL decreases. Here, scenario c, where most layers are transferred, also showed to perform slightly worse than the baseline model for IP. Thus, we showed that next to the design of the molecular-topology based pseudo-tasks, additional design decisions on the extent of layer transfer are important for designing best performing SSL pipelines.
4 Conclusions
We propose a first SSL framework using GNNs for polymer property prediction to address the challenge of improved learning from small polymer datasets. We employ a state-of-the-art polymer graph representation and a wD-MPNN architecture to process polymer graphs. Our contribution investigates three different SSL techniques: (i) node- and edge-level SSL, (ii) graph-level SSL (iii) node-, edge- & graph-level SSL. Furthermore, we explore the impacts of different weight transfer strategies for the fully connected layers. The results show that SSL indeed boosts R2 32.21% and 23.21% for EA and IP respectively, especially when labeled data is extremely limited (0.08%) for the fine-tuning phase (our two smallest data size scenarios). Additionally, SSL can still contribute to augmenting the R2 by 0.1% and 0.1% for EA and IP, even in the largest labeled data regime. Moreover, we highlighted the impact of layer transferal during SSL, where transferring all fully connected layers was advantageous in small data scenarios. Overall, the ensemble node-, edge- & graph-level SSL with all transferred layers depicts the best performance. It decreases the RMSE by 28.39% and 19.09% for EA and IP, respectively. Our results contribute to well-reasoned and improved SSL pipelines in the field of polymer property prediction. Our current study introduces a single graph pseudo label and one node/edge masking strategy. Future research could explore the extension to multiple graph pseudo labels and diverse node/edge masking strategies. Additionally, subsequent work may consider integrating various datasets to evaluate the robustness of the proposed SSL framework. Moreover, a promising future investigation is the integration of SSL with quantitative structure–activity relationship (QSAR) or QSPR modeling for predicting polymer properties. For instance, one approach could involve masking a specific property within the descriptors and predicting the masked property during the pre-training phase. This pre-trained model could then be fine-tuned using the target property dataset.Data availability
This study was carried out using publicly available data (dataset with electron affinity and ionization potential values for 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966 copolymers) from polymer-chemprop-data at https://github.com/coleygroup/polymer-chemprop-data. The data supporting this article have been included as part of the ESI.†
966 copolymers) from polymer-chemprop-data at https://github.com/coleygroup/polymer-chemprop-data. The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.References
- S. Muench, A. Wild, C. Friebe, B. Häupler, T. Janoschka and U. S. Schubert, Polymer-Based Organic Batteries, Chem. Rev., 2016, 116(16), 9438–9484, DOI:10.1021/acs.chemrev.6b00070.
- Y. Wang, A. Vogel, M. Sachs, R. S. Sprick, L. Wilbraham, S. J. A. Moniz and R. Godin, et al. Current understanding and challenges of solar-driven hydrogen generation using polymeric photocatalysts, Nat. Energy, 2019, 4(9), 746–760, DOI:10.1038/s41560-019-0456-5.
- Y. Zhu, C. Romain and C. K. Williams, Sustainable polymers from renewable resources, Nature, 2016, 540(7633), 354–362, DOI:10.1038/nature21001.
- L. P. Hammett, Some Relations between Reaction Rates and Equilibrium Constants, Chem. Rev., 1935, 17(1), 125–136, DOI:10.1021/cr60056a010.
- E. Heid, K. P. Greenman, Y. Chung, S. C. Li, D. E. Graff, F. H. Vermeire and H. Wu, et al. Chemprop: A machine learning package for chemical property prediction, J. Chem. Inf. Model., 2023, 64(1), 9–17 CrossRef PubMed.
- A. M. Schweidtmann, J. G. Rittig, A. König, M. Grohe, A. Mitsos and M. Dahmen, Graph Neural Networks for Prediction of Fuel Ignition Quality, Energy Fuels, 2020, 34(9), 11395–11407, DOI:10.1021/acs.energyfuels.0c01533.
- J. M. Stokes, K. Yang, K. Swanson, W. Jin, A. Cubillos-Ruiz, N. M. Donghia and C. R. MacNair, et al. A Deep Learning Approach to Antibiotic Discovery, Cell, 2020, 180(4), 688–702.e13, DOI:10.1016/j.cell.2020.01.021.
- R. You, S. Yao, H. Mamitsuka and S. Zhu, DeepGraphGO: graph neural network for large-scale, multispecies protein function prediction, Bioinformatics, 2021, 37(Supplement 1), i262–i271, DOI:10.1093/bioinformatics/btab270.
- H. Zhou, W. Wang, J. Jin, Z. Zheng and B. Zhou, Graph Neural Network for Protein–Protein Interaction Prediction: A Comparative Study, Molecules, 2022, 27(18), 6135, DOI:10.3390/molecules27186135.
- M. Aldeghi and C. W. Coley, A graph representation of molecular ensembles for polymer property prediction, Chem. Sci., 2022, 13(35), 10486–10498, 10.1039/d2sc02839e.
- L. Ruddigkeit, R. v. Deursen, L. C. Blum and J. L. Reymond, Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17, J. Chem. Inf. Model., 2012, 52(11), 2864–2875, DOI:10.1021/ci300415d.
- J. J. Irwin and B. K. Shoichet, ZINC – A Free Database of Commercially Available Compounds for Virtual Screening, J. Chem. Inf. Model., 2004, 45(1), 177–182, DOI:10.1021/ci049714+.
- C. Kim, A. Chandrasekaran, T. D. Huan, D. Das and R. Ramprasad, Polymer Genome: A Data-Powered Polymer Informatics Platform for Property Predictions, J. Phys. Chem. C, 2018, 122(31), 17575–17585, DOI:10.1021/acs.jpcc.8b02913.
- S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu and M. Yamazaki, PoLyInfo: Polymer Database for Polymeric Materials Design, in 2011 International Conference on Emerging Intelligent Data and Web Technologies, IEEE, 2011 Search PubMed.
- Y. Amamoto, Data-driven approaches for structure-property relationships in polymer science for prediction and understanding, Polym. J., 2022, 54(8), 957–967, DOI:10.1038/s41428-022-00648-6.
- T. B. Martin and D. J. Audus, Emerging Trends in Machine Learning: A Polymer Perspective, ACS Polym. Au, 2023, 3(3), 239–258, DOI:10.1021/acspolymersau.2c00053.
- R. A. Patel, C. H. Borca and M. A. Webb, Featurization strategies for polymer sequence or composition design by machine learning, Mol. Syst. Des. Eng., 2022, 7(6), 661–676, 10.1039/d1me00160d.
- Y. Zhao, R. J. Mulder, S. Houshyar and T. C. Le, A review on the application of molecular descriptors and machine learning in polymer design, Polym. Chem., 2023, 14(29), 3325–3346, 10.1039/d3py00395g.
- P. Zhang, L. Kearney, D. Bhowmik, Z. Fox, A. K. Naskar and J. J. Gounley, Transferring a molecular foundation model for polymer property predictions, arXiv, 2023, preprint, DOI:10.48550/arXiv.2310.16958.
- H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi and J. Morikawa, et al. Predicting Materials Properties with Little Data Using Shotgun Transfer Learning, ACS Cent. Sci., 2019, 5(10), 1717–1730, DOI:10.1021/acscentsci.9b00804.
- R. Gurnani, C. Kuenneth, A. Toland and R. Ramprasad, Polymer Informatics at Scale with Multitask Graph Neural Networks, Chem. Mater., 2023, 35(4), 1560–1567, DOI:10.1021/acs.chemmater.2c02991.
- O. Queen, G. A. McCarver, S. Thatigotla, B. P. Abolins, C. L. Brown, V. Maroulas and K. D. Vogiatzis, Polymer graph neural networks for multitask property learning, npj Comput. Mater., 2023, 9(1), 90, DOI:10.1038/s41524-023-01034-3.
- C. Xu, Y. Wang and A. B. Farimani, TransPolymer: a Transformer-based language model for polymer property predictions, npj Comput. Mater., 2023, 9(1), 64, DOI:10.1038/s41524-023-01016-5.
- C. Kuenneth and R. Ramprasad, polyBERT: a chemical language model to enable fully machine-driven ultrafast polymer informatics, Nat. Commun., 2023, 14(1), 4099, DOI:10.1038/s41467-023-39868-6.
- I. Misra and L. v. d. Maaten, Self-Supervised Learning of Pretext-Invariant Representations, in 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, 2020 Search PubMed.
- S. Azizi, B. Mustafa, F. Ryan, Z. Beaver, J. Freyberg, J. Deaton and A. Loh, et al. Big Self-Supervised Models Advance Medical Image Classification, in 2021 IEEE/CVF International Conference on Computer Vision (ICCV), IEEE, 2021 Search PubMed.
- Z. Lan, M. Chen, S. Goodman, K. Gimpel, P. Sharma and R. Soricut, ALBERT: A Lite BERT for Self supervised Learning of Language Representations, arXiv, 2019, preprint, DOI:10.48550/arXiv.1909.11942.
- C. Brozos, J. G. Rittig, S. Bhattacharya, E. Akanny, C. Kohlmann and A. Mitsos, Predicting the Temperature Dependence of Surfactant CMCs Using Graph Neural Networks, J. Chem. Theory Comput., 2024, 20(13), 5695–5707, DOI:10.1021/acs.jctc.4c00314.
- S. Gidaris, P. Singh and N. Komodakis, Unsupervised Representation Learning by Predicting Image Rotations, arXiv, 2018, preprint, DOI:10.48550/arXiv.1803.07728.
- Z. Zhang, Q. Liu, H. Wang, C. Lu and C. K. Lee, Motif-based Graph Self-Supervised Learning for Molecular Property Prediction, arXiv, 2021, preprint, DOI:10.48550/arXiv.2110.00987.
- X. Zang, X. Zhao and B. Tang, Hierarchical Molecular Graph Self-Supervised Learning for property prediction, Commun. Chem., 2023, 6(1), 34, DOI:10.1038/s42004-023-00825-5.
- S. Chithrananda, G. Grand and B. Ramsundar, ChemBERTa: Large-Scale Self-Supervised Pretraining for Molecular Property Prediction, arXiv, 2020, preprint, DOI:10.48550/arXiv.2010.09885.
- A. X. Lu, H. Zhang, M. Ghassemi and A. Moses, Self-Supervised Contrastive Learning of Protein Representations By Mutual Information Maximization, BioRxiv, 2020, preprint, DOI:10.1101/2020.09.04.283929.
- R. Krishnan, P. Rajpurkar and E. J. Topol, Self-supervised learning in medicine and healthcare, Nat. Biomed. Eng., 2022, 6(12), 1346–1352, DOI:10.1038/s41551-022-00914-1.
- M. Simonovsky and N. Komodakis, Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural Message Passing for Quantum Chemistry, arXiv, 2017, preprint, DOI:10.48550/arXiv.1704.01212.
- Y. Xie, Z. Xu, J. Zhang, Z. Wang and S. Ji, Self-Supervised Learning of Graph Neural Networks: A Unified Review, arXiv, 2021, preprint, DOI:10.48550/arXiv.2102.10757.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4me00088a |
| ‡ Contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |






