Tuning the mechanical properties of molecular perovskites by controlling framework distortions via A-site substitution

Abstract

Molecular perovskites are important materials in the area of barocalorics, improper ferroelectrics and ferroelastics, where the search for principles that link composition, structure and mechanical properties is a key challenge. Herein, we report the synthesis of a new series of dicyanamide-based molecular perovskites [A]Ni(C₂N₃)₃, where the A-site cation (A⁺) is a range of alkylated piperidinium cations. We use this new family to explore how A⁺ cations determine their mechanical response by measuring the bulk modulus (B) – using high-pressure powder X-ray diffraction. Within the series, we find a positive correlation between the network distortions of the pseudocubic [Ni(C₂N₃)₃]⁻ network and B. Furthermore, we show that we can tune framework distortions, and therefore B, by synthesising A-site solid solutions. The applied methodology is a blueprint for linking framework distortions and mechanical properties in network materials and guides us toward principles for designing macroscopic properties via systematic compositional changes in molecular perovskites.

---

Introduction

The substitution of atoms by molecules in the structure motifs of all-inorganic materials is a powerful approach for designing new materials. It opens up a large chemical design space for studying application-oriented¹ and fundamental² structure–property relationships, while still allowing the use of established principles³ from inorganic solid-state chemistry to guide materials discovery. For instance, in coordination polymers that crystallise in an AMX₃ perovskite motif, such as [CH₃NH₃]Mn(N₃)₃⁴ and [C₁₀H₂₀N]Cd(C₂N₃)₃,⁵ here referred to as molecular perovskites, properties such as ferroelastic,⁶ (improper) ferroelectric^1,7,8 and multiferroic^9,10 behaviour, their glass-forming abilities^11,12 and their application as barocalorics^13,14 are linked to the molecular nature of the A- and X-site. In molecular perovskites, a ReO₃-type [MX₃]⁻ network is formed by the M-site cation (M²⁺) and X-site anion (X⁻) with the A-site cation (A⁺) sitting in the void of the pseudocubic [MX₃]⁻ network for charge balance (Fig. 1).

Fig. 1 Schematic of the perovskite structure of [A]Ni(C₂N₃)₃ materials studied in this work. Emphasis is given to the various A⁺ cations [DIP]⁺ (a), [PEP]⁺ (b), [DEP]⁺ (c) and [DPP]⁺ (d), as incorporated in the distorted 3D ReO₃-type [Ni(C₂N₃)₃]⁻ network. C atoms are shown in the darker colour, N atoms in the lighter colour, distorted NiN₆ octahedra in grey. The X⁻ = [C₂N₃]⁻ are simplified as linear linker shown as grey bars and H atoms are not shown for clarity.

In molecular perovskites, the use of molecular ions as building units introduces new chemical and structural degrees of freedom that can couple to external stimuli,^15,16 producing phenomena such as temperature and pressure-driven A-site order–disorder phase transitions,^17,18 unconventional octahedral tilts and shifts that can couple to break inversion symmetry,^1,19,20 melting processes as a response to heating¹¹ and a new type of polymorphism.²¹ Given their role as model systems for understanding structure–property relationships,^1,22 investigating their mechanical properties, such as the bulk modulus (B), Young's modulus, hardness and material stability, becomes increasingly important. Since the material's crystal chemistry ultimately determines its properties, studies related to the mechanical properties address both our fundamental interest in the search for structure–property principles and operational concerns such as material processability and material longevity. Furthermore, a low B has recently been implicated to improve the barocaloric performance in molecular materials.²³ The compositional variability of molecular perovskites enables us,²⁴ therefore, to identify the underlying structure chemical principles that determine B, and therewith, to enhance a material's solid-state cooling performance.

A few principles of how composition determines the mechanical properties of molecular perovskites have already been established. For instance, nanoindentation and high-pressure diffraction studies on materials such as [(CH₃)₂NH₂]M(HCOO)₃ (with M²⁺ = Ni²⁺, Co²⁺, Zn²⁺ and Mn²⁺),^25,26 [C(NH₂)₃]M(HCOO)₃ (with M²⁺ = Co²⁺ and Mn²⁺)²⁷ and [Pr₄N]M(C₂N₃)₃ (with [Pr₄N]⁺ = tetrapropylammonium, M²⁺ = Ni²⁺, Co²⁺ and Mn²⁺)²⁸ have demonstrated that a smaller size of M²⁺ paired with a larger ligand field stabilisation energy (LFSE) leads to a larger Young's modulus and B. These findings agree with our recent results, where we observed a decreasing B as a function of increasing Shannon ionic radius of M²⁺.²⁹

Looking at the role of A⁺, its capability to form hydrogen bonding interactions^20,30 (HBIs) to the [MX₃]⁻ network has been found to be an important factor. For instance, the mechanical properties are tunable across the solid solution [NH₃NH₂]_1−x[NH₃OH]_xZn(HCOO)₃³¹via HBIs, i.e. the choice of A⁺.^32,33 More recently, this strategy has been used to introduce ferroelasticity in [Et₃P(CH₂)₂Cl]_1−x[Et₃P(CH₂)₂F]_xMn(C₂N₃)₃.³⁴ Yet, our understanding of the interplay between the A⁺ and active framework distortions of the [MX₃]⁻ is only developing.^35–38

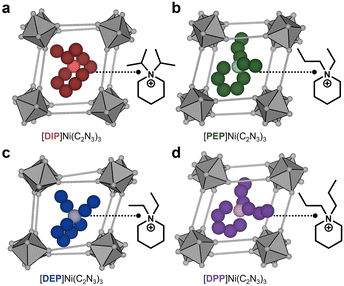
In the pursuit to fill this gap, we have synthesised a new series of [A]Ni(C₂N₃)₃ molecular perovskites with A⁺ = diisopropyl-piperidinium ([DIP]⁺ = [C₁₁H₂₄N]⁺), ethyl-propyl-piperidinium ([PEP]⁺ = [C₁₀H₂₂N]⁺), diethyl-piperidinium ([DEP]⁺ = [C₉H₂₀N]⁺) and dipropyl-piperidinium ([DPP]⁺ = [C₁₁H₂₄N]⁺) (Fig. 1). The absence of acidic hydrogen atoms in all A⁺ excludes contributions from HBIs. Furthermore, by keeping M²⁺ = Ni²⁺ in the series, we have minimised the effect of M²⁺ cation size and LFSE, and hence, the chemical bond strength in the [Ni(C₂N₃)₃]⁻ network on the structure and properties of the molecular perovskites. Therefore, this series allows us to isolate the impact of the size and shape of the A⁺ cation on the distortions of the 3D [MX₃]⁻ network and their ramifications on the mechanical properties, which we measured via high-pressure powder X-ray diffraction (HPPXRD) by using B as a proxy. In addition – by employing a solid solution approach – we investigated to which extent B can be fine-tuned via A⁺ substitution.

Results and discussion

Synthesis and characterisation

In the first step, we designed a range of A⁺ to produce a series of molecular perovskites that can be used to determine how structural and pressure responsive properties are altered by small chemical changes. In this pursuit, we synthesised a series of piperidinium derivatives ([DIP]⁺, [PEP]⁺, [DEP]⁺ and [DPP]⁺), where different alkyl chain modifications of the piperidinium nitrogen enable studying the impact of small variations in size and/or shape (Fig. 1). All A⁺ were synthesised via nucleophilic substitution of halides, see ESI† for details (Fig. S1–S5 and S11–S18). For instance, [DEP]⁺ was obtained from the reaction of diethylamine and 1,5-dibromopentane in acetonitrile. Single crystals of the [A]Ni(C₂N₃)₃ series were obtained by a mild-solution crystallisation route that has previously been used for the synthesis of related materials,^5,21 see ESI† for details (S-5). In a typical reaction, the precursor materials [A]Br, Na(C₂N₃) and Ni(NO₃)₂·6H₂O are dissolved in water, mixed and then left to crystallise overnight in a refrigerator. An overview of all synthesised compounds in this work is given in Table 1.

Table 1 A⁺ size and shape as captured by the volume of A⁺ (V_A⁺) and the globularity factor (G); both were calculated via CrystalExplorer17 based on 300 K SCXRD data. V_cell is the crystallographic volume of SCXRD data at 300 K. A_p is the parent-cell normalised distortion amplitude as a measure for framework distortions. The bulk moduli (B) calculated via EOSFit and volumes (V₀, at zero pressure and temperature) obtained from experimental HPPXRD are also shown

[A]Ni(C2N3)3	A^+ = [DIP]^+	[PEP]^+	[DEP]^+	[DPP]^+
V A^+/Å^3	227.25	202.18	190.56	225.87
G	0.87	0.83	0.88	0.81
Space group	P21/c	P21/c	P21/c	C2/c
V cell/Å^3	2163.4(5)	2028.08(14)	2021.16(14)	2079.38(10)
A p/Å	1.81	2.01	2.10	4.23
B(2^nd)/GPa	8.2 ± 0.1	8.5 ± 0.1	8.8 ± 0.2	10.5 ± 0.2
V 0(2^nd)/Å^3	2157.1 ± 0.5	2030.3 ± 0.6	2025.9 ± 0.2	2073.8 ± 0.6

---

Single crystal X-ray diffraction (SCXRD) at 100 and 300 K was used to determine the structure of all perovskite materials. All compounds in the [A]Ni(C₂N₃)₃ series crystallise with the targeted AMX₃ perovskite structure (Fig. 1). [DIP]Ni(C₂N₃)₃, [PEP]Ni(C₂N₃)₃ and [DEP]Ni(C₂N₃)₃ crystallise in the monoclinic space group P2₁/c, see ESI† for details of data collection and crystal structure solution (S-7, Tables S1–S3 and Fig. S7–S9). In contrast, [DPP]Ni(C₂N₃)₃ crystallises in the space group C2/c (Table S4 and Fig. S10, ESI†). To quantify the extent of network distortions across the series, we have applied an established group theoretical analysis^39–41 to SCXRD data of 300 K for all compounds. In this approach, the structures are first simplified to the underlying octahedral network and subsequently compared to an idealised cubic parent network. By using ISODISTORT,⁴⁰ the active distortions are then identified and described via their irreducible representation and amplitude. The latter enables the calculation of the overall parent-cell normalised distortion amplitude of the network (A_p), providing a rigorous measure for network distortions across our series, see Table 1 for A_p values of the different compounds at 300 K and ESI† for further tilt analysis details (S-69 and Table S22–S24).

To determine relationships between the size and shape of A⁺ and the resulting network distortions (Fig. 1), atomic coordinates from SCXRD data at 300 K were used to extract the geometry of A⁺. Following previous reports,⁴² we use the globularity (G) as a measure for the asphericity of A⁺, where G = 1 for a sphere. For this, we used DFT calculations to obtain the A⁺ surface (S_m,A⁺), the A⁺ volume (V_A⁺) as enclosed by S_m,A⁺, and the surface of an idealised sphere (S_sp,A⁺) with V_A⁺ (Table S27, ESI†). Then, the A⁺ globularity (G = S_sp,A⁺/S_m,A⁺) was calculated (Table 1). By using CrystalExplorer17,⁴³ we obtained G > 0.8 for all A⁺, which agrees with previous results from the literature for A⁺ of dicyanamide-based molecular perovskites.⁴² A similar trend in G with slightly smaller values is obtained when using Gaussian16⁴⁴ for calculating S_m,A⁺, S_sp,A⁺ and V_A⁺, see ESI† for details (Tables S27 and S30). No correlation between A_p, V_A⁺ and G is observed (Table 1), while the importance of G in dictating A_p becomes apparent when considering [DPP]⁺ and [DIP]⁺. Both cations have a similar V_A⁺ but are different in G. [DPP]⁺ shows the significantly smaller G, and among the here investigated series of [A]Ni(C₂N₃)₃, the A_p of [DPP]Ni(C₂N₃)₃ is by far the largest. Therefore, we hypothesise that the observed network distortions in [DPP]Ni(C₂N₃)₃ are a direct ramification of the interplay between A⁺ and the 3D [Ni(C₂N₃)₃]⁻ network, highlighting the templating role of A⁺ and the possibility of tuning network distortions via chemical modifications on A⁺. For instance, for symmetric functionalisation of the piperidine backbone, we find A_p increasing with the length of the alkyl chains, e.g. from ethyl ([DEP]⁺) to propyl ([DPP]⁺). Hence, small alkyl chain modifications on the nitrogen atom of piperidinium, and thus its shape, evidently have an impact on A_p of the 3D [Ni(C₂N₃)₃]⁻ network (Fig. 1) and, as we will see in the following, on the resulting pressure responsiveness.

The phase purity of powder samples of [A]Ni(C₂N₃)₃ was verified using laboratory PXRD and Pawley analysis (Fig. S28–S31, ESI†). Furthermore, thermal analysis (TGA/DSC) showed decomposition temperatures (T_d) between 570 and 600 K (Fig. S20–S23, ESI†). These are at the upper end of previously reported T_d of dicyanamide-based molecular perovskites.^21,45,46 In parts, we rationalise this by the stability of the here employed A⁺, which has previously been suggested as an important factor determining T_d;⁴⁷ however, T_d is a generally complex quantity, which depends upon many parameters, including crystal chemistry factors and analytic concerns.^45,48,49 In the DSC curves, several heat events related to 1^st and 2^nd order phase transitions were observed (Fig. S24–S27, ESI†), while no evidence of melting before T_d was found;¹¹ however, the nature of these phase transitions is beyond the focus of this study. Here, we employ our new [A]Ni(C₂N₃)₃ family as model compounds to study the relation between A⁺ and B.

Molecular perovskites under high pressure

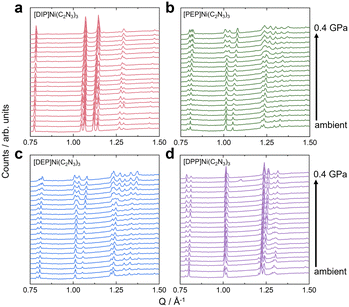
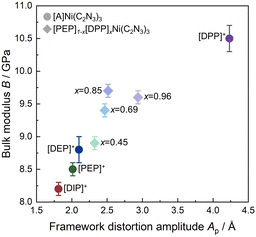
HPPXRD was used to obtain B for all compounds (Table 1). Given the expected subtle differences in the materials' pressure response, we have used a custom-built HPPXRD setup⁵⁰ to collect HPPXRD data with finely spaced pressure points, step size of Δp = 0.02 GPa, up to a maximum pressure of p_max. = 0.4 GPa (Fig. 2 and Fig. S34–S37, ESI†). Visual inspection of the HPPXRD data (Fig. 2) reveals pressure-driven phase transitions at pressures of p_trs. = 0.3 GPa ([DIP]Ni(C₂N₃)₃), p_trs. = 0.28 GPa ([PEP]Ni(C₂N₃)₃) and p_trs. = 0.3 GPa ([DEP]Ni(C₂N₃)₃). Accordingly, Pawley profile fits⁵¹ were performed up to p_trs., or p_max. = 0.4 GPa for [DPP]Ni(C₂N₃)₃, for obtaining lattice parameters and V(p) data, see ESI† for full details of the Pawley profile fits (Tables S11–S14 and Fig. S47–S50). B was calculated for each [A]Ni(C₂N₃)₃ compound by fitting a Birch–Murnaghan (B–M) equation of state to the V(p) data. For a better comparison with literature data, both 2^nd and 3^rd order B–M equation of state fits were performed using EOSFit,⁵² see ESI† for the results and all fits of the V(p) and F(f) plots (Fig. S64–S67). Similar results were obtained by using PASCal (Table S28, ESI†).⁵³ Only fits using 2nd order B–M equation of state show standard errors in fitted B comparable to those observed for the standard material Ni(dmgH)₂ (dmgH⁻ = dimethylglyoximate), σB = ± 0.09 GPa. Much larger uncertainties for a 3^rd order B–M fit suggest overparametrisation, see ESI† (S-66).

Fig. 2 HPPXRD data (λ = 0.4246 Å) of [A]Ni(C₂N₃)₃ with A⁺ = [DIP]⁺ (a), [PEP]⁺ (b), [DEP]⁺ (c), and [DPP]⁺ (d), collected in the pressure range between ambient pressure and 0.4 GPa. The data are shown as stacking plots, where intensities have been normalised.

We observe a monotonically decreasing B along the series B (A⁺ = [DPP]⁺) = 10.5 ± 0.2 GPa, B (A⁺ = [DEP]⁺) = 8.8 ± 0.2 GPa, B (A⁺ = [PEP]⁺) = 8.5 ± 0.1 GPa and B (A⁺ = [DIP]⁺) = 8.2 ± 0.1 GPa. We would like to note that deriving B by using the same pressure range for each compound results in the same trend but with a slightly larger σ. Across the here investigated series of compounds, we find a correlation between A_p and B (Fig. 3). The more distorted the framework is at p = ambient, the stiffer it is (Table 1). Since framework distortions summarised in A_p are some of the lowest-energy pathways for pressure-induced structural changes, a smaller A_p provides a larger margin for pressure-induced network distortions as a response to hydrostatic pressure, and thus a larger compressibility, i.e. a smaller B. This interpretation links A_p(↑) and B(↑) along the [A]Ni(C₂N₃)₃ series, providing a heuristic understanding of the observed pressure response within this series (Fig. 3). Given that A_p is very sensitive to chemical functionalisation of the piperidine backbone, we here show that chemical changes of A⁺ are highly effective for manipulating B.

Fig. 3 Bulk modulus (B) including error bars as a function of the parent-cell normalised amplitude over all active framework distortion modes (A_p) for the [A]Ni(C₂N₃)₃ family with varying A⁺ and molecular solid solutions [PEP]_1-x[DPP]_xNi(C₂N₃)₃.

We note that using A_p as a measure for available distortion pathways only accounts for distortion energies when treating the 3D framework isolated from A⁺. Any directional interactions, such as HBIs between A⁺ and the 3D network, give A⁺ a more active role and thus produce larger variability in B, as found in [(CH)₃NH₂]M(HCOO)₃ (M²⁺ = Mn²⁺, Fe²⁺ and Cu²⁺)⁵⁴ and [C(NH₂)₃]M(HCOO)₃ (M²⁺ = Mn²⁺, Co²⁺ and Cd²⁺),^55,56 with B varying between 21.3 and 27.2 GPa. HBIs thus strengthen the overall framework by making any network distortions energetically more demanding, resulting in an increase of B overall.

Furthermore, considering the series [(C₃H₇)₃CH₃N]M(C₂N₃)₃ with varying framework cation M²⁺ (M²⁺ = Mn²⁺, Co²⁺ and Ni²⁺) where A_p decreases but B increases,²⁹e.g. B (M²⁺ = Mn²⁺) = 7.1 ± 0.2 GPa and A_p (M²⁺ = Mn²⁺) = 2.36, B (M²⁺ = Co²⁺) = 9.9 ± 0.3 GPa and A_p (M²⁺ = Co²⁺) = 2.17 and B (M²⁺ = Ni²⁺) = 10.9 ± 0.2 GPa and A_p (M²⁺ = Ni²⁺) = 2.09, it is evident that crystal chemistry factors other than A_p can be decisive in determining B. For instance, when going from Mn²⁺ to Co²⁺ and Ni²⁺, the 3D network is stiffened and overall, B increases. Any network distortions increase in energy, and thus, A_p is reduced, making the change in chemical bond strength the dominating factor in this comparison.

Bulk moduli of A-site solid solutions

To further explore the tunability of B via targeted changes of A_p, we have synthesised the solid solutions [PEP]_1−x[DPP]_xNi(C₂N₃)₃ with x = 0, 0.45, 0.69, 0.85, 0.96 and 1. For their synthesis, the stoichiometry of precursor salts [PEP]Br and [DPP]Br has been varied and mixed with Na(C₂N₃) and Ni(NO₃)₂·6H₂O in water as a solvent, see ESI† (S-6). Independent of the applied precursor stoichiometry, we only obtained members of the solid solution with x ≥ 0.45. In previous studies, a full solid solution, i.e. 0 ≤ x ≤ 1, has only been found in one example where chemically similar A⁺ were used.³⁴ Therefore, we rationalise the here observed x range by the difference in crystallisation kinetics due to the chemical difference of A⁺. ¹H NMR spectroscopy on acid-digested samples has been used to determine the chemical composition x (Table S9 and Fig. S19, ESI†). We confirmed the formation of a solid solution using laboratory PXRD measurements of a mixture of the parent materials [PEP]Ni(C₂N₃)₃ and [DPP]Ni(C₂N₃)₃ (Fig. S32, ESI†). We determined the lattice parameters using Pawley refinements, using P2₁/c for x = 0 – 0.96 (Fig. S44 and S51–S54, ESI†) and C2/c for x = 1 (Fig. S46, ESI†). We observe a monotonic expansion of the volume from 2029.7(4) ų (x = 0) to 2076.9(4) ų (x = 1) with increasing x at ambient pressure (Table S15, ESI†).

We then used HPPXRD, using the same methodology, to determine B as a function of x (Fig. S68–S71, ESI†). Within standard errors, we observe an increasing B as a function of x in [PEP]_1−x[DPP]_xNi(C₂N₃)₃ (Tables S20 and S29, ESI†). This points at a close to ideal solid solution behaviour⁵⁷ and suggests the absence of strong coupling effects,⁵⁸e.g. behaviour that could arise from the ordering of [PEP]⁺ and [DPP]⁺.

Furthermore, we have performed Rietveld-based structural refinements for x = 0.45, 0.69, 0.85 and 0.96 based on a simplified structural model for extracting the network geometry and framework distortion modes, see ESI† for the employed strategy of structure refinement (S-59) and for results (Table S26). Visual inspection of the PXRD pattern and differences curve of the Rietveld fits suggests that the results should be treated with care; however, for all compounds, A_p lies between 2.013 (x = 0) and 4.232 (x = 1), suggesting tunability of A_pvia A⁺ substitution (Fig. 3). Thus, by employing the solid solution approach, it is possible to fine-tune B in a window as fine as B = 8.5 (x = 0) − 10.5 (x = 1) GPa.

Conclusion

In conclusion, we have synthesised a new series of [A]Ni(C₂N₃)₃ molecular perovskites, showing that framework distortions are sensitive towards small chemical changes of A⁺. Subsequently, we applied this series to establish a link between the size and globularity of A⁺, the active distortion modes in the [Ni(C₂N₃)₃]⁻ framework and the pressure responsiveness of the molecular perovskites for the first time. In the absence of HBIs and changes in chemical bond strength within the network, we conclude that A_p is the decisive parameter in defining the compressibility of a molecular perovskite. Additionally, we show tunability of A_p, and thus B, through the synthesis of A-site solid solutions. Such a tunability of B via chemical modifications advances our understanding of underlying composition–structure–property relations and paves the way for the targeted design of molecular perovskites’ mechanical properties for applications such as barocalorics.^13,23 Additionally, the here applied methodology to link network distortions and the pressure responsiveness is of general nature, with implications for the analysis of the high-pressure responsiveness of closely related material families, including metal–organic frameworks, covalent organic frameworks and hydrogen-bonded frameworks.

Focusing on molecular perovskites, our results have important ramifications on how to think and approach the challenge of designing molecular perovskites with targeted mechanical properties and, more generally, targeted network distortions. Evidently, A⁺ templates framework distortions, and when aiming for large distortions, A⁺ should be chosen that largely diverges from a sphere. For A⁺ based on alkylated ammonium or phosphonium, a chemical functionalisation that enables the formation of conformers with large anisotropies seems fruitful. This suggests the use of a more rigorous conformational analysis prior to the synthesis of A⁺ cations.⁵⁹ In parallel, robust criteria for describing the asphericity of A⁺ should be tested, where we consider G as an important yet only qualitative measure since any templating effect can be expected to be related to asphericity and volume. Such developments have the potential to bring related fields to fruition, such as the targeted design of active distortion modes, with implications for the synthesis of improper ferroelectrics.¹

Author contributions

S. M. Kronawitter: methodology, validation, formal analysis, investigation, data curation, writing – original draft, review and editing, visualisation. S. Park: data curation, investigation. S. A. Hallweger, E. Myatt, J. Pitcairn, M. J. Cliffe, D. Daisenberger: investigation, review and editing. G. Kieslich: conceptualisation, writing – review and editing, supervision, resources, project administration.

Data availability

The data supporting this article have been included as part of the ESI.† Furthermore, all crystallographic data have been deposited at the CCDC, see 2309035, 2309036, 2309038, 2309039, 2309042, 2309043, 2309049 and 2309050.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We want to acknowledge beamtime at the Diamond Light Source (UK), Beamline I15 (CY30815-2). S. M. K., S. A. H. and G. K. acknowledge support from the DFG through research grants (450070835, 493871295) and the Heisenberg program (524525093). Thanks to Melvin Resch for his contributions to the synthesis of the solid solutions.

Notes and references

1. H. L. B. Boström, M. S. Senn and A. L. Goodwin, Nat. Commun., 2018, 9, 2380.
2. S. Yuan, A. Stroppa and A. E. Phillips, APL Mater., 2023, 11, 061114.
3. G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715.
4. X.-H. Zhao, X.-C. Huang, S.-L. Zhang, D. Shao, H.-Y. Wei and X.-Y. Wang, J. Am. Chem. Soc., 2013, 135, 16006–16009.
5. S. Burger, S. Kronawitter, H. L. B. Boström, J. K. Zaręba and G. Kieslich, Dalton Trans., 2020, 49, 10740–10744.
6. Z.-B. Liu, L. He, P.-P. Shi, Q. Ye and D.-W. Fu, J. Phys. Chem. Lett., 2020, 11, 7960–7965.
7. K. Li, Z.-G. Li, J. Xu, Y. Qin, W. Li, A. Stroppa, K. T. Butler, C. J. Howard, M. T. Dove, A. K. Cheetham and X.-H. Bu, J. Am. Chem. Soc., 2022, 144, 816–823.
8. A. Sieradzki, M. Mączka, M. Simenas, J. K. Zaręba, A. Gągor, S. Balciunas, M. Kinka, A. Ciupa, M. Nyk, V. Samulionis, J. Banys, M. Paluch and S. Pawlus, J. Mater. Chem. C, 2018, 6, 9420–9429.
9. P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 13625–13627.
10. A. Stroppa, P. Barone, P. Jain, J. M. Perez-Mato and S. Picozzi, Adv. Mater., 2013, 25, 2284–2290.
11. B. K. Shaw, A. R. Hughes, M. Ducamp, S. Moss, A. Debnath, A. F. Sapnik, M. F. Thorne, L. N. McHugh, A. Pugliese, D. S. Keeble, P. Chater, J. M. Bermudez-Garcia, X. Moya, S. K. Saha, D. A. Keen, F.-X. Coudert, F. Blanc and T. D. Bennett, Nat. Chem., 2021, 13, 778–785.
12. S. M. Kronawitter, S. A. Hallweger, J. Meyer, C. Pedri, S. Burger, A. Alhadid, S. Henke and G. Kieslich, APL Mater., 2023, 11, 31119.
13. J. M. Bermúdez-García, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga and M. A. Señarís-Rodríguez, Nat. Commun., 2017, 8, 15715.
14. J. Salgado-Beceiro, A. Nonato, R. X. Silva, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, E. Stern-Taulats, M. A. Señarís-Rodríguez, X. Moya and J. M. Bermúdez-García, Mater. Adv., 2020, 1, 3167–3170.
15. H. L. B. Boström and A. L. Goodwin, Acc. Chem. Res., 2021, 54, 1288–1297.
16. C. L. Hobday and G. Kieslich, Dalton Trans., 2021, 50, 3759–3768.
17. W. Wei, W. Li, K. T. Butler, G. Feng, C. J. Howard, M. A. Carpenter, P. Lu, A. Walsh and A. K. Cheetham, Angew. Chem., Int. Ed., 2018, 57, 8932–8936.
18. R. X. Silva, R. R. Hora, A. Nonato, A. García-Fernández, J. Salgado-Beceiro, M. A. Señarís-Rodríguez, M. S. Andújar, A. P. Ayala and C. W. A. Paschoal, Spectrochim. Acta, Part A, 2023, 289, 122198.
19. S. G. Duyker, J. A. Hill, C. J. Howard and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 11121–11123.
20. M. Ma̧czka, M. Kryś, S. Sobczak, D. L. M. Vasconcelos, P. T. C. Freire and A. Katrusiak, J. Phys. Chem. C, 2021, 125, 26958–26966.
21. S. Burger, S. Grover, K. T. Butler, H. L. B. Boström, R. Grau-Crespo and G. Kieslich, Mater. Horiz., 2021, 8, 2444–2450.
22. D. Boldrin, Appl. Phys. Lett., 2021, 118, 170502.
23. B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S.-I. Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510.
24. J. M. Bermúdez-García, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, J. Phys. Chem. Lett., 2017, 8, 4419–4423.
25. J.-C. Tan, P. Jain and A. K. Cheetham, Dalton Trans., 2012, 41, 3949–3952.
26. S. Sobczak, A. Chitnis, M. Andrzejewski, M. Mączka, S. Gohil, N. Garg and A. Katrusiak, CrystEngComm, 2018, 20, 5348–5355.
27. G. Feng, D. Gui and W. Li, Cryst. Growth Des., 2018, 18, 4890–4895.
28. L.-J. Ji, S.-J. Sun, Y. Qin, K. Li and W. Li, Coord. Chem. Rev., 2019, 391, 15–29.
29. S. Grover, S. Burger, K. T. Butler, K. Hemmer, P. Vervoorts, G. Kieslich and R. Grau-Crespo, CrystEngComm, 2023, 25, 3439–3444.
30. K. L. Svane, A. C. Forse, C. P. Grey, G. Kieslich, A. K. Cheetham, A. Walsh and K. T. Butler, J. Phys. Chem. Lett., 2017, 8, 6154–6159.
31. G. Kieslich, S. Kumagai, A. C. Forse, S. Sun, S. Henke, M. Yamashita, C. P. Grey and A. K. Cheetham, Chem. Sci., 2016, 7, 5108–5112.
32. W. Li, A. Thirumurugan, P. T. Barton, Z. Lin, S. Henke, H. H.-M. Yeung, M. T. Wharmby, E. G. Bithell, C. J. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2014, 136, 7801–7804.
33. G. Kieslich, A. C. Forse, S. Sun, K. T. Butler, S. Kumagai, Y. Wu, M. R. Warren, A. Walsh, C. P. Grey and A. K. Cheetham, Chem. Mater., 2016, 28, 312–317.
34. L. He, P.-P. Shi, M.-M. Zhao, C.-M. Liu, W. Zhang and Q. Ye, Chem. Mater., 2021, 33, 799–805.
35. I. E. Collings, J. A. Hill, A. B. Cairns, R. I. Cooper, A. L. Thompson, J. E. Parker, C. C. Tang and A. L. Goodwin, Dalton Trans., 2016, 45, 4169–4178.
36. M. Mączka, S. Sobczak, M. Kryś, F. F. Leite, W. Paraguassu and A. Katrusiak, J. Phys. Chem. C, 2021, 125, 10121–10129.
37. A. Sieradzki, A. Nowok, S. Sobczak, K. Roszak, A. Szeremeta, M. Maczka, A. Katrusiak and S. Pawlus, Research Square, 2023 DOI:10.21203/rs.3.rs-3657532/v1.
38. J. Y. Lee, S. Ling, S. P. Argent, M. S. Senn, L. Cañadillas-Delgado and M. J. Cliffe, Chem. Sci., 2021, 12, 3516–3525.
39. H. T. Stokes, D. M. Hatch and B. J. Campbell, ISODISTORT, ISOTROPY Software Suite, https://iso.byu.edu.
40. B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614.
41. H. L. B. Boström, CrystEngComm, 2020, 22, 961–968.
42. J. García-Ben, A. García-Fernández, P. Dafonte-Rodríguez, I. Delgado-Ferreiro, U. B. Cappel, S. Castro-García, M. Sánchez-Andújar, J. M. Bermúdez-García and M. A. Señarís-Rodríguez, J. Solid State Chem., 2022, 316, 123635.
43. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
44. M. J. Frisch, G. W. Trucks and H. B. Schlegel, Gaussian 16 Rev. B.01, Wallingford, CT, 2016.
45. J. García-Ben, L. N. McHugh, T. D. Bennett and J. M. Bermúdez-García, Coord. Chem. Rev., 2022, 455, 214337.
46. L. Zhou, X. Zheng, P.-P. Shi, Z. Zafar, H.-Y. Ye, D.-W. Fu and Q. Ye, Inorg. Chem., 2017, 56, 3238–3244.
47. C. Ye, L. N. McHugh, C. Chen, S. E. Dutton and T. D. Bennett, Angew. Chem., Int. Ed., 2023, 62, e202302406.
48. Y. Wang and W. J. Thomson, Thermochim. Acta, 1995, 255, 383–390.
49. N. Khan, D. Dollimore, K. Alexander and F. Wilburn, Thermochim. Acta, 2001, 367–368, 321–333.
50. N. J. Brooks, B. L. L. E. Gauthe, N. J. Terrill, S. E. Rogers, R. H. Templer, O. Ces and J. M. Seddon, Rev. Sci. Instrum., 2010, 81, 64103.
51. G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357–361.
52. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, J. Appl. Crystallogr., 2016, 49, 1377–1382.
53. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
54. I. E. Collings, M. Bykov, E. Bykova, M. Hanfland, S. van Smaalen, L. Dubrovinsky and N. Dubrovinskaia, CrystEngComm, 2018, 20, 3512–3521.
55. Z. Yang, G. Cai, C. L. Bull, M. G. Tucker, M. T. Dove, A. Friedrich and A. E. Phillips, Philos. Trans. R. Soc., A, 2019, 377, 20180227.
56. H. Gao, C. Li, L. Li, W. Wei, Y. Tan and Y. Tang, Dalton Trans., 2020, 49, 7228–7233.
57. K. T. Jacob, S. Raj and L. Rannesh, Int. J. Mater. Res, 2007, 98, 776–779.
58. N. L. Evans, P. M. M. Thygesen, H. L. B. Boström, E. M. Reynolds, I. E. Collings, A. E. Phillips and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 9393–9396.
59. A. M. Mroz, L. Turcani and K. E. Jelfs, Electron. Struct., 2023, 5, 45004.

---

Footnote

† Electronic supplementary information (ESI) available: Details to material synthesis and characterisation (SCXRD, PXRD, NMR, TGA, DSC, HPPXRD and DFT). CCDC 2309035, 2309036, 2309038, 2309039, 2309042, 2309043, 2309049 and 2309050. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ma00587b

---