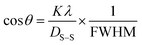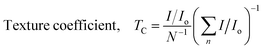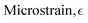DOI:
10.1039/D4MA00513A
(Paper)
Mater. Adv., 2024,
5, 6618-6629
Sustainable synthesis and characterization of nano-triple superphosphate from solid marine wastes
Received
19th May 2024
, Accepted 8th July 2024
First published on 9th July 2024
Abstract
Today, it is vitally important to develop an environmentally sound source for the manufacturing of phosphate fertilizers, as the availability of mineral rock phosphate is diminishing day by day. The present study focuses on the utilization of solid marine wastes from snail and cockle shells to synthesize nano-triple superphosphates (TSPs). The exothermic reaction processes between calcium carbonate (CaCO3) (from snail and cockle shells) and suitable amounts of orthophosphoric acid (H3PO4) (60% w/w) resulted in the sustainable production of triple superphosphates in a quantitative proportion of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Each of the freshly produced substances has been studied using a variety of techniques such as X-ray diffraction (XRD), scanning electron microscopy (SEM), energy dispersive X-ray (EDX) analysis, and Fourier-transform infrared spectroscopy (FT-IR) which confirmed the fact that each of the resulting substances are TSPs which are suitable to be applied as plant nutrients. The crystallite size has been estimated using various models and assumptions (linear straight-line method, Moshi–Scherrer model, Williamson–Hall model, size–strain plot, Halder–Wagner model, and Sahadat–Scherrer model), where the Halder–Wagner model yielded the most appropriate results (D = 32.25 nm, 58.82 nm, 21.73 nm). EDX analysis confirmed the formation of pure TSPs with higher weight percentages of calcium (19.22–24.52%) and phosphorus (27.16–28.13%) and the Rietveld refinement technique verified that the synthesized TSP materials are nearly 100% pure. The microscopic particles progressed to produce spherical and plate-shaped structures, according to SEM examination. The beneficial studies suggest that using marine snail or cockle shells as an initial resource for TSP manufacture in fertilizer manufacturing industries may substitute the usage of non-sustainable phosphate and calcium resources.
2. Each of the freshly produced substances has been studied using a variety of techniques such as X-ray diffraction (XRD), scanning electron microscopy (SEM), energy dispersive X-ray (EDX) analysis, and Fourier-transform infrared spectroscopy (FT-IR) which confirmed the fact that each of the resulting substances are TSPs which are suitable to be applied as plant nutrients. The crystallite size has been estimated using various models and assumptions (linear straight-line method, Moshi–Scherrer model, Williamson–Hall model, size–strain plot, Halder–Wagner model, and Sahadat–Scherrer model), where the Halder–Wagner model yielded the most appropriate results (D = 32.25 nm, 58.82 nm, 21.73 nm). EDX analysis confirmed the formation of pure TSPs with higher weight percentages of calcium (19.22–24.52%) and phosphorus (27.16–28.13%) and the Rietveld refinement technique verified that the synthesized TSP materials are nearly 100% pure. The microscopic particles progressed to produce spherical and plate-shaped structures, according to SEM examination. The beneficial studies suggest that using marine snail or cockle shells as an initial resource for TSP manufacture in fertilizer manufacturing industries may substitute the usage of non-sustainable phosphate and calcium resources.
Introduction
The global need for food and fiber is projected to rise by 40% by 2050, for 6.9 to 9.3 billion people.1 To meet the demands of the growing global population, it is predicted that both the food supply and agricultural output will rise.2 However, declining rural labor combined with growing industrial sectors may hinder the cultivation from expanding as expected. According to a report, we lose approximately a thousand tonnes of soil surface per second as well as depleting twenty thousand hectares of agricultural land annually. The process of erosion caused nearly a billion hectares of agricultural land to be unfit for cultivation.3,4 As the worldwide population expands, analysts are currently concentrating on raising yields of food while utilizing limited farmland. Synthetic fertilizers like potassium, nitrogen, and phosphorus-based fertilizers have been widely used to assist in agricultural output.5,6 Fertilizers including phosphorus, nitrogen, and potassium are necessary to maintain the productivity of crops in the context of agriculture. Fertilizing agricultural lands is a highly effective method for improving the output and has led to significant increases in agricultural yield. Fertilizers are classified based on their ingredients, potentiality, as well as additional characteristics. Every single fertilizer provides sufficient nutrients, additives, and components to promote nutritious and rapid growth of plants and or crops.7,8 Fertilizers made of inorganic substances improve agricultural productivity and enable the survival of hundreds of millions of consumers in the latter half of the 21st century.9 But such improvements have been accomplished at significant expense. People cause disruptions to the worldwide phosphorus chain by utilizing large amounts of phosphate deposits in the ecosystem.10 The following has led to extensive contamination from nutrients in waterways, streams, and seas, as well as the destruction of the limited resources formed over a long time.11,12 Nowadays, farming relies on fossil-based phosphorus obtained from phosphate minerals, which could reduce world phosphate resources within 50–100 years. The consumption of phosphorus is likely to be augmented, but the global supply will reach its maximum by 2030.13–15 Although rock phosphate is one of the easy options to be used as a source material for the synthesis of P-fertilizers, nevertheless effective alternative source coupled with sustainable synthesis protocol is now the priority in the pursuit of new research. One issue with using mineral phosphate is that it has a delayed time required to react. Traditionally, superphosphate is synthesized by reacting rock phosphate with sulfuric acid, which takes time to complete.16,17 However, the potential utilization of phosphorus is barely of worldwide concern. So, it is very important to think about alternative methods or sources of raw materials to produce phosphate fertilizers.13,18,19 Corals, snails, and cockles are typical marine species that can be used to synthesize TSP. These sources are more sustainable than other sources since they can reduce the harmful effects on the ecosystem.20,21 It is crucial to get rid of organic and inorganic wastes, or sustainably convert them, since their existence in nature, even in minimal amounts, endangers the wellness of humans and the ecosystem.22 Based on the pollutant's ultimate removal or conversion, various methods are applied to numerous types of waste. It has been evaluated how well pharmaceutical wastes, pesticides, and heavy metals can be extracted and preconcentrated from organic and environmental specimens using sorbents that consist of nanomaterials.23 Marine snails or cockles are particularly interesting for industrial uses as the majority of marine species are composed mostly of pure calcium carbonate with little or no organic substances.24 Large volumes of priceless shells are generated every year from marine species, creating a problem for the handling of waste. If these enormous amounts of solid trash are burned, buried, or dumped back into the ocean, it might have negative environmental effects.25 Successful oversight of ocean resources is crucial for balancing commercial growth and sustainability. In the twenty-first century, nations everywhere are focusing on managing maritime resources and combining them.26 Nations’ regular operations now incorporate maritime handling of resources. So, human civilizations rely on aquatic ecosystems for existence and progress. Aquatic resources contribute significantly to the nation's economy and growth in GDP, according to a comprehensive investigation.27,28 Thus, utilizing cockles and marine snail shells to produce TSP can be a sustainable way to minimize the need for phosphate rock. In this research, we report a sustainable approach to synthesize different triple superphosphates by utilizing the shells of marine snails and cockles. The produced TSP samples were characterized by XRD, SEM, EDX, and FT-IR analysis.
Materials and methods
Materials
Cardium sp., Conch sp., and Turritella sp. shells were gathered from the wetland area of Kolatoli Beach in the Cox's Bazar district of Bangladesh. The collected shells were immersed in hot water at 80 °C for 3 hours to eliminate any contaminants and sand adhering to their surface. Subsequently, the shells were subjected to a drying process in a drier at a temperature of 105 °C. We obtained concentrated orthophosphoric acid from E-Merck, Germany, through local vendor SF Scientific, Dhaka, Bangladesh, and utilized it in the absence of any additional refining. The double distilled water utilized in the synthesis process was prepared by the Glass Research Division (GRD) of BCSIR.
Methods
Preparation of triple superphosphate from Turritella sp. shell.
TSP synthesis was carried out using a batch mode methodology on a small scale in the laboratory. To begin the synthesis process, 85% acid was diluted with DI water in a measuring cylinder to yield a 60% (w/w) solution of orthophosphoric acid. Turritella sp. trash shells were ground into a fine powder utilizing a high-frequency ball mill (Pulverisette 5 classic line planetary ball mill) that ran for three hours at 450 rpm. This process aimed to enhance the surface area of the shells to facilitate chemical reactions. The milled powder was subsequently segregated on a 200-mesh screen. The acid, which was initially prepared, later was combined with the finely ground snail shell while keeping an appropriate molar proportion. The blend was agitated incessantly up to the time that the reaction reached its culmination. Eqn (1) represents the complete synthesis procedure:| | | CaCO3 (powder) + H3PO4 + H2O → Ca(H2PO4)2·H2O + heat | (1) |
In this case, a single water molecule was enclosed within the crystals of TSP, while the excess water was eliminated due to the heat produced in the process reaction. No additional heat-up or straining measures were employed in this technique. Within 30 hours, the material was fully dried under normal atmospheric conditions. The synthesized TSP was subsequently placed in a sampling bag for further examination.
Preparation of triple superphosphate from Cardium sp. shell.
For Cardium-based TSP, the same procedure was used. After ball milling and screening the Cardium sp. trash shells, the resulting calcium carbonate powder and a 60% (w/w) orthophosphoric acid solution were used to produce TSP. The formed TSP sample was allowed to dry under a room atmosphere.
Preparation of triple superphosphate from Conch sp. shell.
The same process was used for conch-based TSP as well. The TSP fertilizer was made by mixing the powdered shell with 60% orthophosphoric acid and then drying it at room temperature. Finally, the TSP sample was placed in a sampling bag so that it could be further examined.
XRD investigation.
The crystallographic study of the produced materials has been successfully conducted using Rigaku Smart Lab XRD equipment. The data were gathered by establishing a 2θ range of 5 to 70° with increments of 0.01. The temperature during the data collection was 22 °C, and the flow rate of the cooling water was maintained at 4.5–4.8 litres per minute. The equipment utilized a copper material (CuKa, λ = 1.5406 Å) to generate X-rays, with an operating current of 50 mA and a voltage of 40 kV. Data from the substances were acquired using the Bragg–Brentano para-focusing geometric analysis, which was also used for standardization using an appropriate silicon standard. The distinct phases of the components that had been made were identified.
FT-IR spectroscopic analysis.
Attenuated total reflection system-equipped IR-Prestige 21 equipment (Shimadzu, Japan) was used to identify the functional bands in the components. From 400 to 4000 cm−1, the spectrum was measured as a percentage of transmittance. A spectral resolution of 4 cm−1 and 30 scans were used for this.
Scanning electron microscopy (SEM) analysis.
TSP particles were analyzed microstructurally and elementally using a high-resolution field emission scanning electron microscopy (FESEM) apparatus (Model JEOL JSM-7610F) with EDX capability. The photographs were obtained at a speeding voltage of 15 kV.
Results and discussion
Identification of the crystalline phase
The substance's crystallographic assessment has been performed using powder X-ray diffraction records. The diffractogram is illustrated in Fig. 1 where the XRD pattern of the formed TSP was remarkably similar to the typical ICDD standard (card no. # 04-011-3010). The findings validated the form of the produced substance as calcium–phosphate-based TSP. The illustration depicts the X-ray diffractograms for each of the properly synthesized materials. The illustrations revealed by XRD of Turritella, Cardium, and Conch-based TSPs were comparable, but with differing strong peaks. The crystal arrangement of Turritella-based Ca(H2PO4)2·H2O showed three distinct peaks at 2θ = 7.49°, 22.83°, and 24.04°, representing the (010), (021), and (−120) reflections, correspondingly. Similarly, the X-ray diffraction patterns of Cardium and Conch-based TSP showed three strong intensity peaks at 2θ = 7.50°, 22.84°, and 24.06° and 2θ = 7.51°, 22.85°, and 24.06° corresponding to the (010), (021), and (−120) planes. Almost similar data were found in other literature.16 Formulas (2)–(7) have been applied to determine several crystallographic characteristics, including the crystallite size, microstrain, relative intensity, preference growth, dislocation density, and crystallinity index. More details associated with these mathematical expressions are discussed in earlier research studies.29–32 The values of the crystallographic parameters are registered in Table 1.
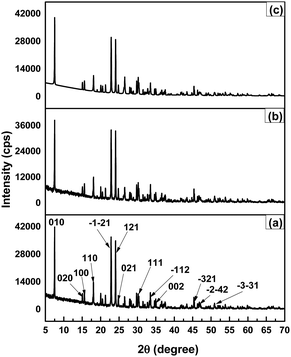 |
| | Fig. 1 X-ray diffractogram of triple superphosphates obtained from (a) Turritella, (b) Cardium, and (c) Conch shells. The scanning range used to obtain the data was 5–70°. | |
Table 1 Crystallographic parameters of produced TSP samples
| Sample |
Dislocation density, δ |
Crystallinity index, CI |
Crystallite size, D (nm) |
|
| TSP (Turritella sp.) |
0.123 |
2.79 |
88.42 |
0.0019 |
| TSP (Cardium sp.) |
0.132 |
2.81 |
86.26 |
0.0021 |
| TSP (Conch sp.) |
0.103 |
2.98 |
98.24 |
0.0017 |
Crystallite size (using the Scherrer formula),
| | 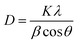 | (2) |
Crystallinity index,
| | 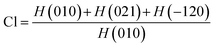 | (3) |
Dislocation density,
| | 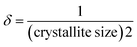 | (4) |
Microstrain,
| | 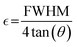 | (5) |
Relative intensity,
| |  | (6) |
Preference growth,
| | 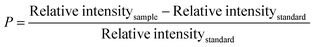 | (7) |
where
D = size of the crystallites,
K = shape parameter with a 0.90 value,
λ = wavelength,
θ = angle of diffraction (in degree),
β = full width at half maxima in radians, and
H = peak heights at respective planes.
Preference growth refers to the development of a crystal plane following a reaction under specific reaction circumstances. This makes it an important characteristic for characterizing substances through crystallography. Preference growth is capable of being expressed by evaluating the RI of a sufficient plane to the other three significant ones. The RI of the (010) plane has been determined for every one of them concerning the (021), (120), and (020) planes. The (010) plane had an estimated preference growth of −0.41 (Turritella), −0.37 (Cardium), and −0.25 (conch) when compared to the (021), (120), and (020) planes. The relative intensity of the (020) plane was also assessed in comparison with the (010), (021), and (−120) planes. From the RI of the reference and sample, it has been found that the (020) plane has a preference growth of −0.18 (Turritella), −0.072 (Cardium), and −0.31 (Conch). The results demonstrate that the growth along the (020) (Cardium) plane seems more thermally advantageous than other planes. The negative signs imply a decreased preference for the plane during the sample development according to the defined reaction criteria.
Determination of the crystallite size, stress, and strain
Linear straight-line method (LSLM) of the Scherrer equation.
The Scherrer equation pertains to the diffraction peak mentioned in eqn (8).33 This equation is commonly employed for determining the size of the crystallites. The equation may be illustrated as| | 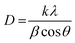 | (8) |
where k can be termed as the shape factor, that is for the spheroidal crystal, 0.90; λ is the wavelength; β is said to be the full width at half maximum (FWHM) of highly intensified peaks of diffraction given in radians; and θ is the angle of diffraction in degrees.
Eqn (8)'s measurement of crystallite size was further verified through the application of the linear straight-line method of Scherrer's formula, incorporating all peaks to infer the size of the crystallites. In comparison with a linear formula, Scherrer's formula (eqn (8)) is reconfigured to be:
| | 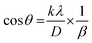 | (9) |
The crystallite size was determined through the utilization of this equation and the subsequent construction of a graph in which the
x-axis was demonstrated as 1/
β and the
y-axis was denoted by cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ, and the graphs are presented in
Fig. 2. The crystallite size calculation,
D, is simplified by using the slope of the mentioned equation, denoted as
kλ/
D, and the obtained values are shown in
Table 2. In this instance, the value of
D that has been measured will be significantly greater than the value obtained using the conventional form of the Scherrer equation. When applying the least-squares technique to fit data based on the linear straight-line model of Scherrer's equation, the
y-intercept is considered to have no physical value.
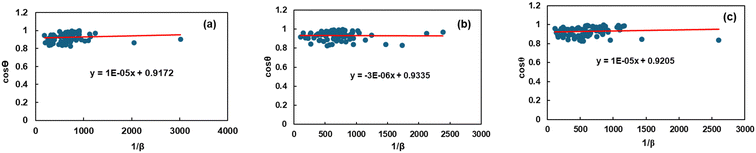 |
| | Fig. 2 Graphical illustration of the linear straight-line method (LSLM) of Scherrer's equation to calculate the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Table 2 Obtained crystallite size, stress, strain, and energy density of different snail and cockle-based TSPs
| Model name |
Crystallite size, D (nm); strain, 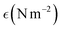
; energy density, u (J m−3); stress, σ |
| TSP (Turritella sp.) |
TSP (Cardium sp.) |
TSP (Conch sp.) |
| Linear straight-line method |
D = 13865 |
D = 46218 |
D = 13865 |
| Monshi–Scherrer model |
D = 106.65 |
D = 92.43 |
D = 89.45 |
| Williamson–Hall model |
UDM |
ε = 0.0003 |
ε = 0.0008 |
ε = 0.0004 |
|
D = 126.04 |
D = 86.65 |
D = 99.03 |
| USDM |
σ = 2 × 107 |
σ = 3 × 106 |
σ = 2 × 107 |
|
D = 126.04 |
D = 86.65 |
D = 99.03 |
| UDEDM |
u = 50.28 |
u = 8.62 |
u = 59.34 |
|
D = 126.04 |
D = 86.65 |
D = 99.03 |
| Size–strain plot |
D = 106.65 |
D = 81.55 |
D = 66.02 |
|
ε = 0.0044 |
ε = 0.0048 |
ε = 0.0044 |
| Halder–Wagner model |
D = 32.25 |
D = 58.82 |
D = 21.73 |
|
ε = −0.0028 |
ε = 0.0048 |
ε = −0.0034 |
| Sahadat–Scherrer model |
D = 138.65 |
D = 126.04 |
D = 126.04 |
Monshi–Scherrer (M–S) model.
The Monshi–Scherrer approach, based on the Scherrer equation, is a commonly employed model for evaluating the crystallite size. The Monshi–Scherrer model aims to minimize mistakes and takes into account all peaks when estimating the crystallite size.34 Logarithm was applied to both sides of the Scherrer equation (eqn (12)) and after modification, resulting in eqn (10)–(12). Eqn (12) is commonly referred to as the Monshi–Scherrer equation.29,30| | 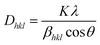 | (10) |
or,| | 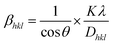 | (11) |
| | 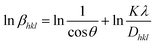 | (12) |
By plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βhkl on the Y-axis and
βhkl on the Y-axis and  on the X-axis (Fig. 3), the mean size of the crystallites was calculated (shown in Table 2) using the gradient of the constructed equation.
on the X-axis (Fig. 3), the mean size of the crystallites was calculated (shown in Table 2) using the gradient of the constructed equation.
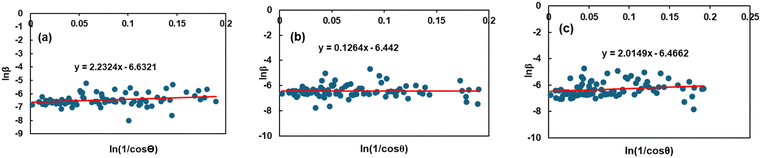 |
| | Fig. 3 Graphical representation of Monshi–Scherrer's equation to estimate the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Williamson–Hall (W–H) model
The formula proposed by Scherrer does not explain the inherent strain that forms in nanocrystals due to point errors, grain boundaries, triple interfaces, or assembling failures within the lattice; it only takes into consideration the effect of crystallite diameter on the XRD peak width.35 It is possible to determine the inherent tension and measurement of crystallite size using the Warren–Averbach approach, the Williamson–Hall strategy, and other techniques that consider the impact of strain on the XRD peak expansion. A very simple and easy one of these is the Williamson–Hall (W–H) method.36 According to this method, the X-ray diffraction peak undergoes physical line broadening as a result of the dimensions and internal microstrain of the materials. The overall spreading may be expressed as| | | βtotal = βsize + βstrain | (13) |
The average crystallite size and microstrain were determined in the current study by employing modified W–H equations, including UDM, USDM, and UDEDM, which are elaborated in the subsequent sections.
Uniform deformation model (UDM).
The uniform deformation model (UDM) takes into account the uniform tension that is found in nanocrystals as a consequence of crystal defects along the crystallographic direction.37 The peak width in the diffraction diagram was caused by defects. Defects can manifest as flaws and distortions. The broadening caused by these faults can be determined by the strain38| | 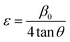 | (14) |
Two observations can be made from eqn (10) and (14); first, the strain varies as tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, while the crystallite size varies as 1/cos
θ, while the crystallite size varies as 1/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Both strain and crystallite size are meant to contribute to line broadening, and they are not interdependent. As both the size and strain exhibit a combined result, the sum of eqn (8) and (14) yields the total peak broadening βhkl = βD + βS and is given by,
θ. Both strain and crystallite size are meant to contribute to line broadening, and they are not interdependent. As both the size and strain exhibit a combined result, the sum of eqn (8) and (14) yields the total peak broadening βhkl = βD + βS and is given by,| | 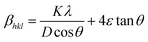 | (15) |
or equivalently,| | 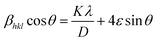 | (16) |
Eqn (15) or (16) is referred to as the Williamson–Hall equation (W–H) and portrays the uniform deformation model (UDM).39 In this model, the crystal is thought to be isotropic because the strain should be the same in all structural directions. For each of the observed diffraction points, a graph has been generated with 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ measurements on the horizontal axis and β
θ measurements on the horizontal axis and β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ measurements on the vertical axis (Fig. 4). The figure displays that the strain within the lattice (ε) is shown by the slope of the uniform line, while the graph's y-intercept relates to the dimension of the crystallite (D) (given in Table 2). The lattice shrinkage or enlargement in the nanocrystals is the main cause of the lattice strain since size confinement drastically alters the structure of the atoms compared to their massive equivalent. However, because of the size, numerous flaws are also produced in the lattice arrangement, which leads to intrinsic strain. It has been found that a negative strain can be created as a consequence of the lattice shrinkage, rendered in the determination of lattice parameters.40 However, because of the lattice expansion the slope of the UDM plot can be positive.41
θ measurements on the vertical axis (Fig. 4). The figure displays that the strain within the lattice (ε) is shown by the slope of the uniform line, while the graph's y-intercept relates to the dimension of the crystallite (D) (given in Table 2). The lattice shrinkage or enlargement in the nanocrystals is the main cause of the lattice strain since size confinement drastically alters the structure of the atoms compared to their massive equivalent. However, because of the size, numerous flaws are also produced in the lattice arrangement, which leads to intrinsic strain. It has been found that a negative strain can be created as a consequence of the lattice shrinkage, rendered in the determination of lattice parameters.40 However, because of the lattice expansion the slope of the UDM plot can be positive.41
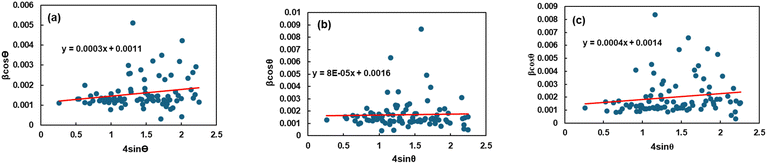 |
| | Fig. 4 Graphical illustration of uniform deformation model (UDM) to determine the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Uniform stress deformation model (USDM).
An anisotropic method is chosen because the expectations of homogeneity and isotropy are frequently not met. This means that the correct value of the strain ε needs to be substituted into the W–H equation.42 Hook's law, which upholds a direct relationship regarding stress and strain as shown by the equation σ = Yε, wherein Y is a measure of Young's modulus and σ represents stress, is used in the uniform stress deformation model (USDM) to determine the strain. Hooke's Law applies to tiny strains.43 Using the estimation of Hooke's law on eqn (16) results in:| | 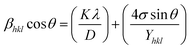 | (17) |
The uniform deformation stress (σ) can be obtained by illustrating 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/Y through the horizontal axis and β
θ/Y through the horizontal axis and β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ through the y-axis; the crystallite size (D) is indicated by the intercept on the y-axis (Fig. 5). With their modulus of elasticity (Y), the strain may be calculated.
θ through the y-axis; the crystallite size (D) is indicated by the intercept on the y-axis (Fig. 5). With their modulus of elasticity (Y), the strain may be calculated.
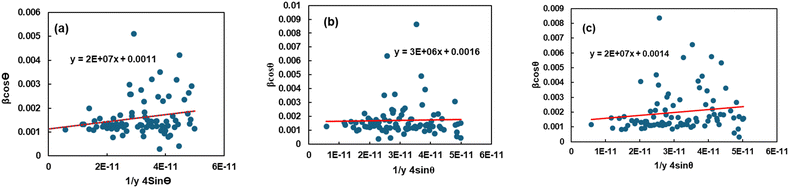 |
| | Fig. 5 Depiction of the uniform stress deformation model (USDM) to calculate the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Uniform deformation energy density model (UDEDM).
The calculation of the energy density of a crystalline material was performed utilizing the uniform deformation energy density model (UDEDM). Eqn (19) implies that crystals must exhibit homogeneity and isotropy. The density of the energy, u, can be determined using the formulawhich involves Hooke's law. Eqn (10) can be transformed based on the relationship between energy and strain.43| | 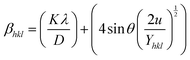 | (19) |
The x- and y-axes have been positioned with the values of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (2/Yhkl)1/2 and βhklcos
θ (2/Yhkl)1/2 and βhklcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, accordingly (Fig. 6). Table 2 provides the directional energy density (u) and the size of the crystallite (D) computed from the slope and the y intersection, respectively.
θ, accordingly (Fig. 6). Table 2 provides the directional energy density (u) and the size of the crystallite (D) computed from the slope and the y intersection, respectively.
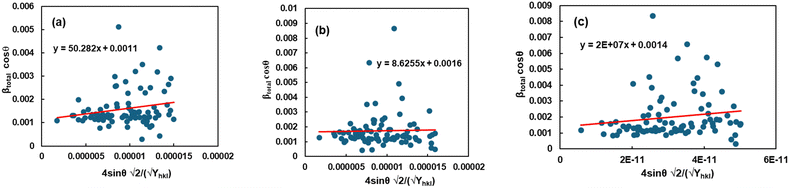 |
| | Fig. 6 Graphical representation of the uniform deformation energy density model (UDEDM) to evaluate the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Size–strain plot (SSP).
The Williamson–Hall approach takes into account the broadening of peaks with the diffraction angle (2θ), attributing it to a combination of size-induced broadening and strain-induced broadening. On the other hand, certain approaches focused on peak pattern assessment. The XRD peak appearance can be observed using the size–strain plot (SSP) method as a combination of Gaussian and Lorentzian characteristics. This approach uses a Gaussian distribution to describe the strain-expanded feature and a Lorentz variable to express the size-extended XRD feature.44 So, the overall broadening of SSP can be illustrated aswhere βL represents the peak broadening caused by the Lorentz function and βG represents the peak broadening caused by the Gaussian function. The SSP approach consistently yields superior results for isotropic broadening by prioritizing low-angle reflections, which offer higher accuracy and precision compared to higher angles. XRD data quality decreases at higher angles due to the increased overlap of peaks.
So, the crystallite size can be calculated using the following equation:45
| | 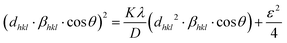 | (21) |
A graph was created by plotting (
dhkl2·
βhkl·cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ) on the
X-axis and (
dhkl·
βhkl·cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ)
2 on the
Y-axis for each diffraction peak using
eqn (21) (
Fig. 7). The calculated crystallite size and strain are given in
Table 2.
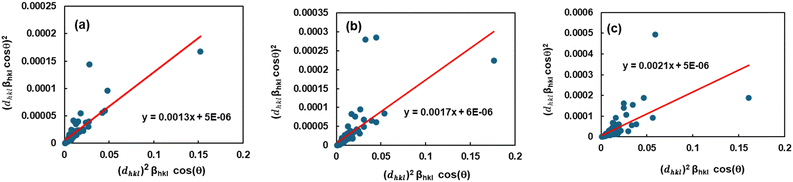 |
| | Fig. 7 Depiction of the size–strain plot to calculate the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Halder–Wagner (H–W) method.
The SSP approach assumes a Gaussian function for strain widening and a Lorentzian function for size broadening of the XRD peak profile. This is not a Gaussian or Lorentzian operation, as the shape of the XRD peak areas lines up with the Gaussian distribution effectively, but the tail portion collapses off rapidly rather than connecting the XRD peak area. In reality, the profile's tails accommodate the Lorentz operation very nicely, although they fail to correspond to the XRD peak profile.46,47 Peak expansion is thought to be an identical Voigt function since it is a conjunction of the Lorentzian product and the Gaussian product.44,47,48 That is why the Halder–Wagner approach is utilized to get around this problem. Therefore, the entire measurement at half the maximum of the physical feature for the Voigt function could be represented as follows, implementing the Halder–Wagner approach:| | | βhkl2 = βL·βhkl + βG2 | (22) |
where βL and βG are the Lorentzian and Gaussian functions' full widths at half maximum, respectively. One benefit of this approach is that it places greater emphasis on the peaks in the low and mid-angle range, where there is very little overlap between the diffracting peaks. The Halder–Wagner (H–W) method can be used concurrently to determine both the average crystallographic size and lattice strain. An alternate equation has been proposed in the Halder–Wagner (HW) approach in the following form:47| | 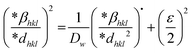 | (23) |
where β* is the integral width for a reciprocal lattice point and d* is the distance between the planes. The lattice strain is given by εHW, and the Halder–Wagner crystallite size is given by DHW. β* and d* are demonstrated using the following equations:| | 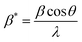 | (24) |
| | 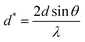 | (25) |
The Halder–Wagner (H–W) plot was constructed to determine DHW and ε, using the relationship between 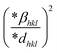 and
and  . DHW may be calculated by analyzing the slope of the plotted line, whereas the value of ε can be obtained from the intercept (Fig. 8).
. DHW may be calculated by analyzing the slope of the plotted line, whereas the value of ε can be obtained from the intercept (Fig. 8).
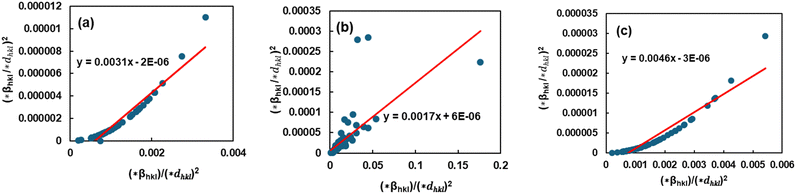 |
| | Fig. 8 Graphical illustration of the Halder–Wagner model to estimate the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Sahadat–Scherrer (S–S) model.
A new updated model called the Sahadat–Scherrer model was developed to more accurately compute the crystallite size, addressing the limitations of other models. Eqn (26), which was derived from the Scherrer equation, represents an algebraic equation corresponding to this model. As a result of the straight line traversing the origin, the model becomes more precise. cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ was plotted along the y-axis and 1/FWHM along the x-axis to generate a plot (Fig. 9) based on this model. An intercept was fabricated by passing through the origin after constructing a straight line. By matching this intercept to the y = mx equation, the size of the crystallite was calculated. The Sahadat–Scherrer equation can be written as29
θ was plotted along the y-axis and 1/FWHM along the x-axis to generate a plot (Fig. 9) based on this model. An intercept was fabricated by passing through the origin after constructing a straight line. By matching this intercept to the y = mx equation, the size of the crystallite was calculated. The Sahadat–Scherrer equation can be written as29| | 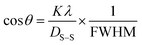 | (26) |
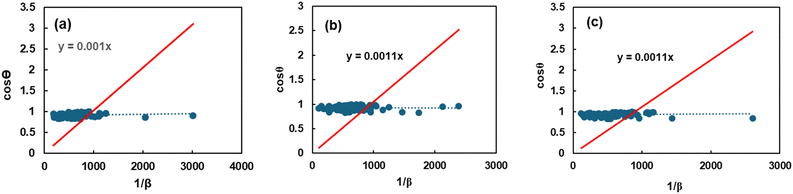 |
| | Fig. 9 Graphical representation of the Sahadat–Scherrer model to calculate the crystallite properties of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. | |
Rietveld refinement.
To determine and clarify the fraction of the TSP phase that makes up the produced substance, Rietveld refinement has been applied where around 1% calcium phosphate phase and 99% TSP component were identified during the Rietveld refinement of all the samples. Furthermore, following this assessment, the lattice parameters (a, b, and c) underwent refinement. The TSP phase developed the lattice parameters, a = 6.23 Å, b = 11.85 Å, and c = 5.60 Å, which seemed highly comparable to the observed values reported in the literature.21 Following Rietveld refining, the lattice parameters correlated with the typical card number, #009-0347, precisely.
Texture coefficient.
The texture coefficient (Tc) in crystallized substances can be employed to figure out the preferred arrangement of crystals from X-ray diffraction data. The highest value of the intensity for one of the crystals, obtained from a PDF records card that corresponds to the diffraction pattern from X-rays of the materials, is Io (hkl). The texture coefficient within the (hkl) plane is denoted by Tc (hkl). The diffraction peak number is n, and the overall quantity of appearances noticed is N.| | 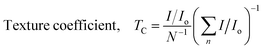 | (27) |
The results of the texture coefficient of the corresponding planes are shown in Table 3. The data indicate that the (0 2 1) and (−1 2 0) planes are texturing since they provide the highest texture coefficient values. Thus, the crystal planes' development may align with the texturing planes (021 and −120). The fact that all three of the TSP samples have the same texturing plane indicates that there didn't appear to be any significant variations in the alignment of the XRD patterns and SEM images.
Table 3 Texture coefficient of the TSP samples
| TSP sample |
Plane (hkl) |
Texture coefficient, (Tc) |
Remark |
| TSP (Turritella) |
0 1 0 |
0.635730177 |
(0 2 1) and (−1 2 0) texturing |
| 0 2 1 |
1.426257921 |
| −1 2 0 |
1.153195552 |
| −1 3 0 |
0.882562488 |
| 0 −2 2 |
0.902253863 |
|
|
| TSP (Cardium) |
0 1 0 |
0.720382233 |
(0 2 1) and (−1 2 0) texturing |
| 0 2 1 |
1.504199858 |
| −1 2 0 |
1.083761932 |
| −1 3 0 |
0.858940985 |
| 0 −2 2 |
0.832714993 |
|
|
| TSP (Conch) |
0 1 0 |
0.860313522 |
(0 2 1) and (−1 2 0) texturing |
| 0 2 1 |
1.508459467 |
| −1 2 0 |
1.219541669 |
| −1 3 0 |
0.884109555 |
| 0 −2 2 |
0.527575787 |
FT-IR analysis for functional groups.
The standard means of identifying substances in materials is the IR spectrum analysis, which identifies various functional components inside the structures of the molecules. The produced molecule, Ca(H2PO4)2·H2O, is commonly referred to as TSP in the agricultural industry. The desired compound's composition includes CaO, H2PO4− ion, and H2O molecules.49,50 The spectrum of the produced materials is expected to be characterized using the basic vibrational behaviors of the compounds. The structural elements of the prepared samples were investigated through FT-IR analysis. The FT-IR spectrum is shown in Fig. 10 where TSP contains Ca-oxide, –OH, and phosphate groups, resulting in IR spectral lines. Bending oscillations of O–P–O sections have been identified at 420–625 cm−1, whereas vibrations associated with stretching were observed at 923–1155 cm−1. Fig. 10 demonstrates an infrared spectrum of the major phosphate modes about 970 cm−1. The spectrum appears to reveal water molecule splitting oscillations at 1620 cm−1. Ca–O molecules exhibit distinctive spectral peaks at 853 and 670 cm−1. The spectrum line originated at 2352 cm−1 due to the auto appearance of CO2 in the ATR FT-IR configuration. The absence of any unexpected foreign functional groups in the FT-IR spectrum is consistent with the results of EDX and Rietveld refinement. The objective of the study was to produce pure TSP sustainably and the data from XRD (Fig. 1) and FT-IR (Fig. 10) indicate the development of pure and nanocrystalline TSP.
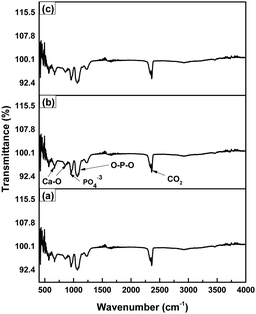 |
| | Fig. 10 FT-IR spectrum of TSP from (a) Turritella, (b) Cardium, and (c) Conch shells. The spectrum has been assessed as a percentage of transmittance over a wavenumber range of 400 and 4000 cm−1. | |
Microstructure analysis.
The structural study of the TSP samples has been carried out via SEM analysis. Additionally, the pictures collected at various levels of magnification are shown in Fig. 11. The particle shape and size (smaller and larger) of the TSP samples are among the various things that are displayed in the SEM analysis findings. The uneven shape and variable size of the particles characterize the morphology of TSP. The TSP micrographs show mixing characteristics in particle morphology. The particles persisted in groupings, resulting in spherical and plate-shaped formations. The formation of plate-like structures for TSP was found in other literature studies.16,49,51 Since the synthesis parameters for TSP formation remained identical across the separate portions, there seemed to be no substantial fluctuations in the SEM pictures, making them consistent with the FT-IR spectrum inspection and XRD pattern alignment as XRD and FT-IR figures are quite similar for all three samples. The size distributions of TSP did not appear homogeneous because the microscopic components stayed clustered. The pictorial representation demonstrated that there was certainly no regularity within the dimensions of the particles based on examination, and the majority of the particle forms resembled plate-shaped, together with just a few spherical-like appearances. One significant piece of evidence suggesting the controlled release of TSP in soil water is particle aggregation. Additionally, the aggregates of the TSP samples include a significant number of holes, which is advantageous for water routes. The estimation of preference growth indicated that the surfaces of crystalline TSP were not thermodynamically recommended by the process circumstances and exhibited unsteady development with negative values. The visual illustration of TSP components validated the findings for their development preference growth with low thickness and length.
 |
| | Fig. 11 SEM images of TSP obtained from (a and b) Cardium, (c and d) Turritella, and (e and f) Conch shells. The images were collected at a speeding voltage of 15 kV. | |
EDX analysis.
Fig. 12 displays the results of EDX obtained for the produced TSP samples. The EDX figures showed that TSP was present, with weight percentages of 21.1% calcium, 27.85% phosphorus, and 51.05% oxygen (for Cardium); 19.22% calcium, 28.13% phosphorus, and 52.65% oxygen (for Turritella); and 24.52% calcium, 27.16% phosphorus, and 48.31% oxygen (for Conch). Therefore, the development of plant growth may benefit from TSP generated with a larger percentage of calcium and phosphorus. Since the produced TSP is in a pure phase, we may anticipate that using this kind of fertilizer at the farmer level won't have any negative effects, such as the heavy metals' carcinogenic effects.52,53Table 4 provides the EDX results of TSP produced from different snail and cockle shells.
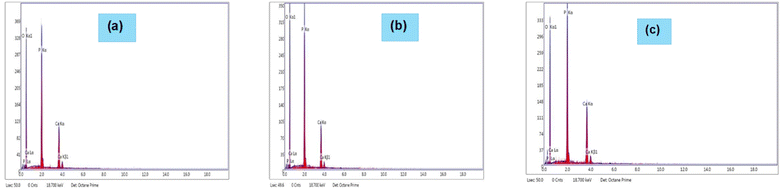 |
| | Fig. 12 EDX illustration of TSP obtained from (a) Cardium, (b) Turritella, and (c) Conch shells. | |
Table 4 Atomic and weight percentages of Ca, O, and P. A voltage and current of 15 kV and 768 A were used to obtain the EDX data
| Sample |
Element |
Weight (%) |
Atomic (%) |
| TSP (Cardium) |
O |
51.05 |
69.12 |
| P |
27.85 |
19.48 |
| Ca |
21.10 |
11.4 |
|
|
| TSP (Turritella) |
O |
52.65 |
70.34 |
| P |
28.13 |
19.41 |
| Ca |
19.22 |
10.25 |
|
|
| TSP (Conch) |
O |
48.31 |
66.98 |
| P |
27.16 |
19.45 |
| Ca |
24.52 |
13.57 |
Conclusions
Through a waste recovery process, TSP was effectively produced from waste snail and cockle shells for sustainable use in industry. Waste from snail and cockle shells may now be turned into valuable TSP with the help of an inexpensive and simple method. Multiple analytical approaches (XRD, FT-IR, SEM, and EDX) were used to confirm the synthesized TSP and no unusual performance or difficulties were encountered throughout the whole procedure. The XRD method offers significant insights regarding the formation of the crystalline phase of triple superphosphate. The synthesized TSP's crystallite sizes were found to be 88.42 nm (Turritella), 86.26 nm (Cardium), and 98.24 nm (Conch) according to the Scherrer formula. On the other hand, FT-IR analysis shows the presence of all functional groups in the structure of the synthesized materials. While Rietveld refinement verified that the synthesized TSP is in pure form with around 99% of its chemical composition, EDX analysis reveals that the generated TSP samples contain a significant amount of Ca, P, and O. The images obtained from SEM showed that there is no consistency in the arrangement of the particles in any of the three samples. Most of the particles are plate-shaped, with only a small number having spherical characteristics. The investigation suggests using Turritella sp., Cardium sp., and Conch sp. shells as a calcium source or as a base substance for phosphate-fertilizer and 60% (w/w) phosphoric acid to reduce manufacturing expenses by avoiding the need for additional drying. Using such substances as plant nutrients maximizes the supply of phosphorus. This additionally helps the ecosystem by reducing marine waste. The research provides important details for improving TSP manufacturing throughout the chemical sector. It proposes using snail or cockle shells instead of phosphate rocks or calcium minerals, which have fewer supplies. Future research aimed at synthesizing and assessing the performance of TSP fertilizers will benefit from the fundamental basis and fresh direction provided by this study.
Author contributions
Md. Kawcher Alam synthesized and characterized the produced TSP, analyzed the data, and wrote the draft and original manuscript. Md. Sahadat Hossain conceived and designed the experiment and analyzed the data. Mohammad Saimon Islam assisted in writing the draft. Newaz Mohammed Bahadur and Samina Ahmed supervised the findings of this work. Samina Ahmed supervised the overall work and managed the required facilities.
Data availability
Data will be made available on request.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors are grateful to the Bangladesh Council of Scientific and Industrial Research (BCSIR) authority for financial support through R&D projects (ref. no. 39.02.0000.011.14.134.2021/900; date: 30.12.2021) and (ref. no. 39.02.0000.011.14.157.2022/172; date: 10.11.2022). Md. Kawcher Alam wishes to thank the Department of Applied Chemistry and Chemical Engineering, Noakhali Science and Technology University, Noakhali, Bangladesh for approving the M. S. Thesis program.
References
-
G. C. Banik and D. Mukhopadhyay, in Input Use Efficiency for Food and Environmental Security, ed. R. Bhatt, R. S. Meena and A. Hossain, Springer Nature Singapore, Singapore, 2021, pp. 541–566 Search PubMed.
- W. M. Stewart and T. L. Roberts, Proc. Eng., 2012, 46, 76–82 CrossRef.
- G. Hazra, IJMER, 2014, 3, 190–208 Search PubMed.
- G. Hazra and T. Das, Glob. J. Sci. Front. Res. B: Chem., 2014, 14, 4 Search PubMed.
- S. Tang, J. Zhou, W. Pan, T. Sun, M. Liu, R. Tang, Z. Li, Q. Ma and L. Wu, Appl. Soil Ecol., 2023, 181, 104661 CrossRef.
- S. M. Yahaya, A. A. Mahmud, M. Abdullahi and A. Haruna, Pedosphere, 2023, 33, 385–406 CrossRef CAS.
- J. A. Camargo and Á. Alonso, Environ. Int., 2006, 32, 831–849 CrossRef CAS PubMed.
- R. Prasad, J. Trop. Agric., 2009, 47, 1–17 CAS.
- R. N. Roy, A. Finck, G. J. Blair and H. L. S. Tandon, Guide Integr. Nutr. Manag. FAO Fertil. Plant Nutr. Bull, 2006, 16, 201–214 Search PubMed.
-
R. Hassan, R. Scholes and N. Ash, Ecosystems and human well-being: current state and trends, 2005 Search PubMed.
- N. Cosme and M. Z. Hauschild, Ecol. Indic., 2016, 69, 453–462 CrossRef CAS.
- D. Scavia, J. D. Allan, K. K. Arend, S. Bartell, D. Beletsky, N. S. Bosch, S. B. Brandt, R. D. Briland, I. Daloğlu and J. V. DePinto, J. Gt. Lakes Res., 2014, 40, 226–246 CrossRef CAS.
- D. Cordell, J.-O. Drangert and S. White, Glob. Environ. Change, 2009, 19, 292–305 CrossRef.
-
P. Heffer and M. Prud’homme, 78th IFA annual conference, Paris, 2010, vol. 31, pp. 1–13 Search PubMed.
-
P. Heffer and M. Prud’homme, 36th IFA Enlarged Council Meeting, New Delhi (India), 2010, pp. 2–4 Search PubMed.
- M. S. Hossain, M. A. A. Shaikh, M. F. Ahmed and S. Ahmed, Mater. Adv., 2023, 4, 2384–2391 RSC.
- Z. Huang, S. Zhang, H. Wang, R. Liu, C. Cheng, Z. Liu, Z. Guo, X. Yu, G. He, G. Ai and W. Fu, J. Agric. Food Chem., 2020, 68, 11114–11120 CrossRef CAS PubMed.
-
A. N. Sharpley, P. J. A. Withers, C. W. Abdalla and A. R. Dodd, in Agronomy Monographs, ed. J. Thomas Sims and A. N. Sharpley, American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America, Madison, WI, USA, 2015, pp. 1069–1101 Search PubMed.
- I. Steen, Phosphorus Potassium, 1998, 217, 25–31 Search PubMed.
- Z. Zuliantoni, W. Suprapto, P. H. Setyarini and F. Gapsari, Results Eng., 2022, 14, 100390 CrossRef CAS.
-
S. Seesanong, C. Seangarun, B. Boonchom, C. Sron, S. Thompho, P. Rungrojchaipon, W. Boonmee and N. Laohavisuti, 2023 DOI:10.21203/rs.3.rs-2897225/v1.
- M. Soylak, O. Ozalp and F. Uzcan, Trends Environ. Anal. Chem., 2021, 29, e00109 CrossRef CAS.
- Q. Salamat, F. Tatardar, R. Moradi and M. Soylak, Anal. Lett., 2024, 0, 1–41 Search PubMed.
- A. Shafiu Kamba, M. Ismail, T. A. Tengku Ibrahim and Z. A. B. Zakaria, J. Nanomater., 2013, 2013, 1–9 CrossRef.
- A. G. Potortì, L. Messina, P. Licata, E. Gugliandolo, A. Santini and G. Di Bella, Sustainability, 2024, 16, 706 CrossRef.
- K. Vijai Anand, M. Reshma, M. Kannan, S. Muthamil Selvan, S. Chaturvedi, A. E. Shalan and K. Govindaraju, J. Nanostruct. Chem., 2021, 11, 409–422 CrossRef CAS.
- R. González-Val and F. Pueyo, Econ. Model., 2019, 83, 150–159 CrossRef.
- H. Zhang and S. Chen, Mar. Econ. Manage., 2022, 5, 69–83 CrossRef.
- M. S. Hossain, S. A. Jahan and S. Ahmed, Results Chem., 2023, 5, 100822 CrossRef.
- Md Sahadat Hossain and S. Ahmed, J. Saudi Chem. Soc., 2023, 27, 101649 CrossRef CAS.
- M. Z. U. Al Mamun, M. S. Hossain, S. P. Moulick, M. Begum, R. A. Sathee, M. S. Hossen, F. Jahan, M. M. Rashid, F. Islam and R. H. Bhuiyan, Heliyon, 2023, 9, e18012 CrossRef CAS PubMed.
- M. K. Alam, M. S. Hossain, N. M. Bahadur and S. Ahmed, J. Mol. Struct., 2024, 137820 CrossRef CAS.
- P. Scherrer, Nach Ges Wiss Gottingen, 1918, 2, 8–100 Search PubMed.
- A. Monshi, M. R. Foroughi and M. R. Monshi, World J. Nano Sci. Eng., 2012, 02, 154–160 CrossRef.
- R. Das and S. Sarkar, Curr. Sci., 2015, 775–778 Search PubMed.
- R. Jacob and J. Isac, Int. J. Chem. Stud., 2015, 2, 12–21 Search PubMed.
- W. H. Hall, Proc. Phys. Soc., London, Sect. A, 1949, 62, 741 CrossRef.
- G. K. Wiiliamson, Acta Metall., 1953, 1, 22–31 CrossRef.
- B. Rajesh Kumar and B. Hymavathi, J. Asian Ceram. Soc., 2017, 5, 94–103 CrossRef.
- A. K. Zak, W. A. Majid, M. E. Abrishami and R. Yousefi, Solid State Sci., 2011, 13, 251–256 CrossRef.
- S. Sarkar and R. Das, Micro Nano Lett., 2018, 13, 312–315 CrossRef CAS.
- P. Shunmuga Sundaram, T. Sangeetha, S. Rajakarthihan, R. Vijayalaksmi, A. Elangovan and G. Arivazhagan, Phys. B, 2020, 595, 412342 CrossRef CAS.
- Y. T. Prabhu, K. V. Rao, V. S. S. Kumar and B. S. Kumari, World J. Nano Sci. Eng., 2014, 4, 21–28 CrossRef CAS.
- D. Balzar and H. Ledbetter, J. Appl. Crystallogr., 1993, 26, 97–103 CrossRef.
- V. Mote, Y. Purushotham and B. Dole, J. Theor. Appl. Phys., 2012, 6, 6 CrossRef.
- A. Hepp and C. Baerlocher, Aust. J. Phys., 1988, 41, 229–236 CrossRef CAS.
- N. C. Halder and C. N. J. Wagner, Acta Crystallogr., 1966, 20, 312–313 CrossRef CAS.
- L. Motevalizadeh, Z. Heidary and M. E. Abrishami, Bull. Mater. Sci., 2014, 37, 397–405 CrossRef CAS.
- S. Seesanong, C. Seangarun, B. Boonchom, N. Laohavisuti, K. Chaiseeda and W. Boonmee, ACS Omega, 2021, 6, 22065–22072 CrossRef CAS PubMed.
- K. Nasri, C. Chtara, H. Chekir and H. Elfeki, J. Adv. Chem., 2014, 9, 1943–1952 CrossRef.
- S. Seesanong, C. Seangarun, B. Boonchom, C. Sronsri, N. Laohavisuti, K. Chaiseeda and W. Boonmee, Minerals, 2022, 12, 254 CrossRef CAS.
- C.-H. Lai, C.-H. Lin, C.-C. Liao, K.-Y. Chuang and Y.-P. Peng, RSC Adv., 2018, 8, 3041–3050 RSC.
- S. Karimian, S. Shekoohiyan and G. Moussavi, RSC Adv., 2021, 11, 8080–8095 RSC.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Mohammad Saimon
Islam
b,
Newaz Mohammed
Bahadur
b and
Samina
Ahmed
a,
Mohammad Saimon
Islam
b,
Newaz Mohammed
Bahadur
b and
Samina
Ahmed
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Each of the freshly produced substances has been studied using a variety of techniques such as X-ray diffraction (XRD), scanning electron microscopy (SEM), energy dispersive X-ray (EDX) analysis, and Fourier-transform infrared spectroscopy (FT-IR) which confirmed the fact that each of the resulting substances are TSPs which are suitable to be applied as plant nutrients. The crystallite size has been estimated using various models and assumptions (linear straight-line method, Moshi–Scherrer model, Williamson–Hall model, size–strain plot, Halder–Wagner model, and Sahadat–Scherrer model), where the Halder–Wagner model yielded the most appropriate results (D = 32.25 nm, 58.82 nm, 21.73 nm). EDX analysis confirmed the formation of pure TSPs with higher weight percentages of calcium (19.22–24.52%) and phosphorus (27.16–28.13%) and the Rietveld refinement technique verified that the synthesized TSP materials are nearly 100% pure. The microscopic particles progressed to produce spherical and plate-shaped structures, according to SEM examination. The beneficial studies suggest that using marine snail or cockle shells as an initial resource for TSP manufacture in fertilizer manufacturing industries may substitute the usage of non-sustainable phosphate and calcium resources.
2. Each of the freshly produced substances has been studied using a variety of techniques such as X-ray diffraction (XRD), scanning electron microscopy (SEM), energy dispersive X-ray (EDX) analysis, and Fourier-transform infrared spectroscopy (FT-IR) which confirmed the fact that each of the resulting substances are TSPs which are suitable to be applied as plant nutrients. The crystallite size has been estimated using various models and assumptions (linear straight-line method, Moshi–Scherrer model, Williamson–Hall model, size–strain plot, Halder–Wagner model, and Sahadat–Scherrer model), where the Halder–Wagner model yielded the most appropriate results (D = 32.25 nm, 58.82 nm, 21.73 nm). EDX analysis confirmed the formation of pure TSPs with higher weight percentages of calcium (19.22–24.52%) and phosphorus (27.16–28.13%) and the Rietveld refinement technique verified that the synthesized TSP materials are nearly 100% pure. The microscopic particles progressed to produce spherical and plate-shaped structures, according to SEM examination. The beneficial studies suggest that using marine snail or cockle shells as an initial resource for TSP manufacture in fertilizer manufacturing industries may substitute the usage of non-sustainable phosphate and calcium resources.
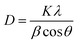
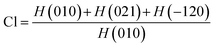
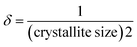
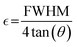

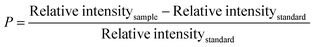
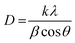
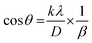
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, and the graphs are presented in Fig. 2. The crystallite size calculation, D, is simplified by using the slope of the mentioned equation, denoted as kλ/D, and the obtained values are shown in Table 2. In this instance, the value of D that has been measured will be significantly greater than the value obtained using the conventional form of the Scherrer equation. When applying the least-squares technique to fit data based on the linear straight-line model of Scherrer's equation, the y-intercept is considered to have no physical value.
θ, and the graphs are presented in Fig. 2. The crystallite size calculation, D, is simplified by using the slope of the mentioned equation, denoted as kλ/D, and the obtained values are shown in Table 2. In this instance, the value of D that has been measured will be significantly greater than the value obtained using the conventional form of the Scherrer equation. When applying the least-squares technique to fit data based on the linear straight-line model of Scherrer's equation, the y-intercept is considered to have no physical value.

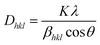
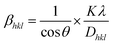
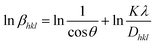
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βhkl on the Y-axis and
βhkl on the Y-axis and  on the X-axis (Fig. 3), the mean size of the crystallites was calculated (shown in Table 2) using the gradient of the constructed equation.
on the X-axis (Fig. 3), the mean size of the crystallites was calculated (shown in Table 2) using the gradient of the constructed equation.
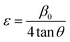
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, while the crystallite size varies as 1/cos
θ, while the crystallite size varies as 1/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Both strain and crystallite size are meant to contribute to line broadening, and they are not interdependent. As both the size and strain exhibit a combined result, the sum of eqn (8) and (14) yields the total peak broadening βhkl = βD + βS and is given by,
θ. Both strain and crystallite size are meant to contribute to line broadening, and they are not interdependent. As both the size and strain exhibit a combined result, the sum of eqn (8) and (14) yields the total peak broadening βhkl = βD + βS and is given by,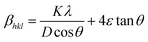
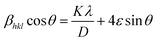
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ measurements on the horizontal axis and β
θ measurements on the horizontal axis and β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ measurements on the vertical axis (Fig. 4). The figure displays that the strain within the lattice (ε) is shown by the slope of the uniform line, while the graph's y-intercept relates to the dimension of the crystallite (D) (given in Table 2). The lattice shrinkage or enlargement in the nanocrystals is the main cause of the lattice strain since size confinement drastically alters the structure of the atoms compared to their massive equivalent. However, because of the size, numerous flaws are also produced in the lattice arrangement, which leads to intrinsic strain. It has been found that a negative strain can be created as a consequence of the lattice shrinkage, rendered in the determination of lattice parameters.40 However, because of the lattice expansion the slope of the UDM plot can be positive.41
θ measurements on the vertical axis (Fig. 4). The figure displays that the strain within the lattice (ε) is shown by the slope of the uniform line, while the graph's y-intercept relates to the dimension of the crystallite (D) (given in Table 2). The lattice shrinkage or enlargement in the nanocrystals is the main cause of the lattice strain since size confinement drastically alters the structure of the atoms compared to their massive equivalent. However, because of the size, numerous flaws are also produced in the lattice arrangement, which leads to intrinsic strain. It has been found that a negative strain can be created as a consequence of the lattice shrinkage, rendered in the determination of lattice parameters.40 However, because of the lattice expansion the slope of the UDM plot can be positive.41
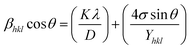
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/Y through the horizontal axis and β
θ/Y through the horizontal axis and β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ through the y-axis; the crystallite size (D) is indicated by the intercept on the y-axis (Fig. 5). With their modulus of elasticity (Y), the strain may be calculated.
θ through the y-axis; the crystallite size (D) is indicated by the intercept on the y-axis (Fig. 5). With their modulus of elasticity (Y), the strain may be calculated.
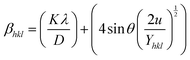
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (2/Yhkl)1/2 and βhklcos
θ (2/Yhkl)1/2 and βhklcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, accordingly (Fig. 6). Table 2 provides the directional energy density (u) and the size of the crystallite (D) computed from the slope and the y intersection, respectively.
θ, accordingly (Fig. 6). Table 2 provides the directional energy density (u) and the size of the crystallite (D) computed from the slope and the y intersection, respectively.
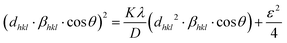
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) on the X-axis and (dhkl·βhkl·cos
θ) on the X-axis and (dhkl·βhkl·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 on the Y-axis for each diffraction peak using eqn (21) (Fig. 7). The calculated crystallite size and strain are given in Table 2.
θ)2 on the Y-axis for each diffraction peak using eqn (21) (Fig. 7). The calculated crystallite size and strain are given in Table 2.
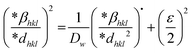
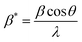
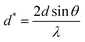
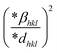 and
and  . DHW may be calculated by analyzing the slope of the plotted line, whereas the value of ε can be obtained from the intercept (Fig. 8).
. DHW may be calculated by analyzing the slope of the plotted line, whereas the value of ε can be obtained from the intercept (Fig. 8).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ was plotted along the y-axis and 1/FWHM along the x-axis to generate a plot (Fig. 9) based on this model. An intercept was fabricated by passing through the origin after constructing a straight line. By matching this intercept to the y = mx equation, the size of the crystallite was calculated. The Sahadat–Scherrer equation can be written as29
θ was plotted along the y-axis and 1/FWHM along the x-axis to generate a plot (Fig. 9) based on this model. An intercept was fabricated by passing through the origin after constructing a straight line. By matching this intercept to the y = mx equation, the size of the crystallite was calculated. The Sahadat–Scherrer equation can be written as29