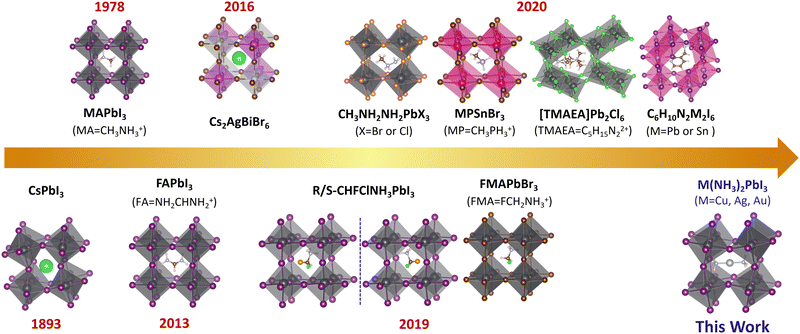
Open Access Article
Open Access ArticleThree-dimensional lead iodide perovskites based on complex ions†
Hebin
Wang‡
a,
Yinye
Yu‡
bcd,
Haolin
Lu
a,
Teng
Wang
a,
Yuki
Haruta
 e,
Xingzhan
Wei
c,
Guichuan
Xing
e,
Xingzhan
Wei
c,
Guichuan
Xing
 f,
Makhsud I.
Saidaminov
f,
Makhsud I.
Saidaminov
 g,
Yecheng
Zhou
g,
Yecheng
Zhou
 *b and
Guankui
Long
*b and
Guankui
Long
 *a
*a
aSchool of Materials Science and Engineering, National Institute for Advanced Materials, Renewable Energy Conversion and Storage Center (RECAST), Nankai University, 300350, Tianjin, China. E-mail: longgk09@nankai.edu.cn
bSchool of Materials Science and Engineering, Sun Yat-sen University, Guangzhou 510006, China. E-mail: zhouych29@mail.sysu.edu.cn
cMicro-nano Manufacturing and System Integration Center, Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, Chongqing 400714, China
dUniversity of Chinese Academy of Sciences, No. 19A Yuquan Road, Shijingshan District, Beijing 100049, China
eDepartment of Chemistry, University of Victoria, Victoria, British Columbia V8P 5C2, Canada
fInstitute of Applied Physics and Materials Engineering, University of Macau, Avenida da Universidade, Taipa, Macau, 999078, China
gDepartment of Chemistry, Department of Electrical & Computer Engineering, and Centre for Advanced Materials and Related Technologies (CAMTEC), University of Victoria, Victoria, British Columbia V8P 5C2, Canada
First published on 2nd September 2023
Abstract
Lead-halide perovskites have demonstrated outstanding optical, electrical, and spintronic properties and have made significant breakthroughs in many fields, especially in solar cells. Although substantial efforts have been devoted to developing novel 3D perovskites with a lower band gap towards the application in perovskite solar cells, none of them succeeded. Here we propose three novel 3D lead iodide perovskites with complex ions, Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3. Based on the optimized structures, formation and dissociation energies, phonon spectra, and ab initio molecular dynamics simulations, it is found that Ag(NH3)2PbI3 and Au(NH3)2PbI3 are kinetically and thermodynamically stable. Furthermore, Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit large absorption coefficients, suitable optical band gaps and small electron effective masses, which are very promising towards application in perovskite solar cells.
Introduction
The lead-halide perovskites with ABX3 structures have attracted attention owing to their unique optical, electrical, and spintronic properties towards applications in solar cells,1–11 light-emitting diodes,9,12–14 photodetectors,15–18 field-effect transistors,19 lasers,20,21etc. The power conversion efficiency (PCE) of lead-halide perovskite solar cells has exceeded 25%,2 which is comparable to that of the commercialized silicon-based solar cells. Taking the crystal structure into account, perovskites can be categorized by the arrangement of metal halide octahedra into different dimensionalities such as three-dimensional (3D),22–25 two-dimensional (2D),4,26–28 one-dimensional (1D),29,30 and zero-dimensional (0D).31–34 The dimensionality can be tuned by the size of the A-site cations. The cations can also influence the electronic properties of perovskite through distortions and symmetry breaking.35–42 To understand the unique optical and charge transport properties of 3D perovskites, not only structural but also electronic dimensionality – the connectivity of the conduction band (CB) and valence band (VB),43 is important. Structural 3D does not always lead to electronic 3D (such as Cs2AgBiBr643), while electronic 3D can only be achieved in 3D perovskites. The electronic dimensionality is determined by complex factors, such as the structural dimensionality, structural distortion, and the contribution of the A-site cations and inorganic framework to the VBM and CBM.43 The 3D electronic structure could ensure the isotropic charge transport in the crystal lattice. For 3D perovskites with 3D electronic connectivity, the charges can freely move along three dimensions since both the VB and CB are dispersive along all directions rather than restricted to one or two directions in electronically low-dimensional perovskites. Considering the randomly oriented grains in the perovskite thin film and the need for effective hole and electron transport between electrodes, the excellent isotropic transport of electronic 3D perovskites could ensure effective charge transport and hence high power conversion efficiency.For solar cell applications, there are three types of widely investigated 3D lead iodide perovskites: CH3NH3PbI3 (MAPbI3), NH2CHNH2PbI3 (FAPbI3) and CsPbI3, with band gaps of 1.57 eV, 1.48 eV and 1.73 eV, respectively.44 But according to the Shockley–Queisser limit, a 1.34 eV band gap leads to the best performing solar cells;45 therefore, it is highly needed to develop novel 3D perovskites with a lower band gap. However, such an ideal 3D lead iodide perovskite has not been developed although various novel 3D perovskites have been proposed, as shown in Fig. 1. For example, double perovskites like Cs2AgBiBr646–48 and (CH3NH3)2BiKCl649 were reported, but they have indirect band gaps (2.19 eV and 3.04 eV) and 0D electronic structure,43 and the highest power conversion efficiency is only 2.5% for these double perovskite-based solar cells.50 Later, Xiong et al. synthesized methylphosphonium (CH3PH3+, MP+)-based hybrid organic–inorganic perovskites (MPSnBr3, with a large band gap of 2.62 eV), which were proven to be structural 3D based on single crystal X-ray diffraction.51 Mączka et al. reported novel 3D lead chloride and bromide perovskites with large band gaps of 3.40 eV and 2.58 eV based on 2-methylhydrazin-1-ium (CH3NHNH3+).52 Long et al. proposed the 3D chiral lead iodide perovskite (CHFClNH3PbI3), which was proven to be both kinetically and thermodynamically stable based on theoretical calculations.24 Zhong et al. experimentally reported the first halogenated-methylammonium-based 3D lead halide perovskite (FMAPbBr3) with a band gap of 2.03 eV.53 Recently, a series of unique 3D lead halide perovskites based on diammonium and edge-shared (Pb2X10)6− octahedra dimers were also reported.54–59 For example, Xiong et al. developed a 3D ferroelectric lead-based perovskite ([TMAEA]Pb2Cl6, TMAEA = 2-trimethylammonioethylammonium), which exhibits a large band gap of 3.43 eV and spontaneous polarization of 1 μC cm−2.54 Kanatzidis et al. reported 3D lead-based perovskites ((xAMPY)Pb2I6, x = 3 or 4, AMPY = aminomethylpyridinium) with indirect band gaps of 2.05 eV (x = 3) and 2.12 eV (x = 4).55 However, all these experimentally reported novel 3D lead halide perovskites exhibit large band gaps (>2.0 eV), which could not harvest enough photons towards high-performance perovskite solar cells.
In this work, we introduce three complex ions, [Cu(NH3)2]+, [Ag(NH3)2]+ and [Au(NH3)2]+, to construct novel 3D lead-based perovskites. Based on the optimized structures, formation and dissociation energies, phonon spectra, and ab initio molecular dynamics simulations (AIMD), it is found that Ag(NH3)2PbI3 and Au(NH3)2PbI3 are both kinetically and thermodynamically stable. Most importantly, these two perovskites are not only structural 3D but also electronic 3D. With high absorption coefficients, low band gaps, and small hole and electron effective masses, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are very promising towards potential applications in perovskite solar cells.
Results and discussion
The geometric structures of the proposed lead-based perovskites with complex ions, [Cu(NH3)2]+, [Ag(NH3)2]+ and [Au(NH3)2]+, are optimized and shown in Fig. 2. The 3D structures are not destroyed after the introduction of complex ions, indicating that [Cu(NH3)2]+, [Ag(NH3)2]+ and [Au(NH3)2]+ are successfully embedded into the perovskite lattice framework without destroying the 3D structure. In order to further confirm this, the new tolerance factors (τau) proposed by Bartel et al. were calculated.60,61 As shown in Table S1 (ESI†), the calculated τau is 3.57, 3.58 and 3.57 for Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3, respectively, which is almost the same as that of FAPbI3 (3.64), further confirming that the proposed lead iodide perovskites could maintain their 3D structures. The average Pb–I bond lengths of Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are 3.28, 3.24 and 3.26 Å, respectively, which is comparable with that of 3.22 Å in γ-MAPbI3.24 To further estimate the distortion of the three perovskites with complex ions, the bond length distortion index (D), the bond angle variance (σ2) and the angle of the Pb–I–Pb bond (in-plane of (010)) were calculated. D and σ2 estimate the distortion degree of the [PbI6]4− octahedra, and the Pb–I–Pb bond angle (in-plane of (010)) estimates the degree of octahedral tilting in the perovskites. As shown in Table S4 and Fig. S1 (ESI†), the D values of Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are much larger than that of γ-MAPbI3, while σ2 is in the order of Cu(NH3)2PbI3 < Ag(NH3)2PbI3 < γ-MAPbI3 < Au(NH3)2PbI3. The tilting distortions of Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are much smaller than that of γ-MAPbI3. The stability of these proposed 3D perovskites with complex ions is further investigated by the phonon spectra, formation and dissociation energies, and ab initio molecular dynamics simulations, as shown below.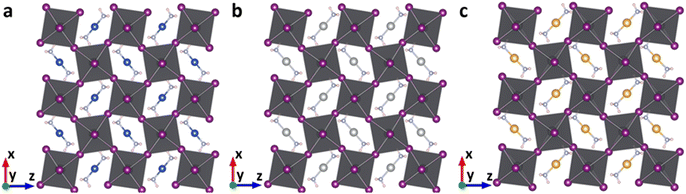 | ||
| Fig. 2 The optimized geometric structures of Cu(NH3)2PbI3 (a), Ag(NH3)2PbI3 (b) and Au(NH3)2PbI3 (c). | ||
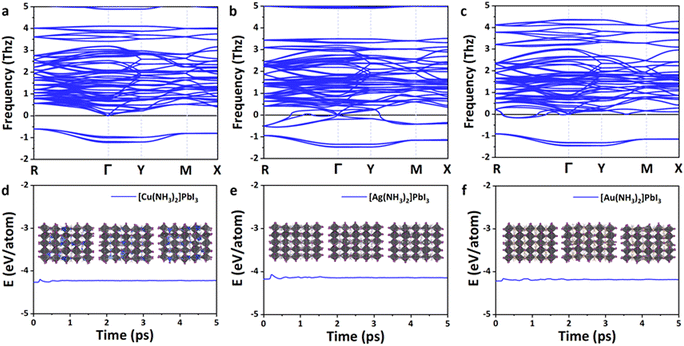
As shown in Fig. 3a–c, all these perovskites exhibit a similar phonon spectrum, and only very small imaginary frequencies (<2 THz) are found. These small imaginary modes are a very common feature for lead-based perovskites62 and have been confirmed by the soft mode in experiments (e.g., MAPbBr3)63 and theoretical calculations (e.g., α-MAPbI3).64–69 The origin of the imaginary frequencies is potentially due to the anharmonicity,64,65 which is caused by the rotations and tilting of the octahedra,62,66 or dynamic stabilization.67–72 The vibration modes that arise from the imaginary phonon frequencies were also analyzed. As shown in Fig. S2 (ESI†), the I(5) atom of Cu(NH3)2PbI3 vibrates along the y-direction, the I(7) atom of Ag(NH3)2PbI3 vibrates along the y-direction, and the I(10) atom of Au(NH3)2PbI3 vibrates along the z-direction. The three zero frequency translation modes at the Γ point could also be observed. Therefore, the proposed 3D lead iodide perovskites with complex ions are basically thermodynamically stable.
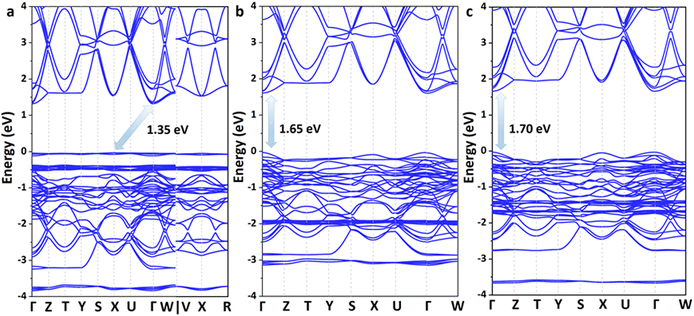
Then, the formation and dissociation energies of these lead iodide perovskites were calculated based on eqn (1) and (2),
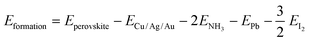 | (1) |
 | (2) |
In order to further confirm the kinetic stability of these lead iodide perovskites, ab initio molecular dynamics simulations were then performed at 300 K for 5 ps. As shown in Fig. 3d–f, the energies of these 3D lead iodide perovskites fluctuate significantly in the first 2 ps but remain stable in the next 3 ps. The octahedral frameworks are not destroyed during the AIMD simulations for Ag(NH3)2PbI3 and Au(NH3)2PbI3, which indicates that these two perovskites are dynamically stable. However, the structure of Cu(NH3)2PbI3 during AIMD simulation is destroyed, and Cu–I bonds are formed (Fig. S3, ESI†), which indicates that Cu(NH3)2PbI3 is not kinetically stable. Based on the above discussions, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are both thermodynamically and kinetically stable. Nevertheless, their suitability as a material platform for solar cells still needs further investigation.
Excellent solar cell materials should have an appropriate band gap, a high carrier mobility and a large optical absorption coefficient. Therefore, the electronic and optical properties of these lead iodide perovskites were further investigated. According to the Shockley–Queisser limit, the band gap of the best absorber should be in the optimal range of 0.85–1.85 eV; thus, the theoretical power conversion efficiency of solar cells could exceed 25%.45 The band structures of these 3D perovskites are calculated based on the Perdew–Burke–Ernzerhof (PBE) functional73 together with spin polarization and shown in Fig. 4 and Fig. S4–S7 (ESI†). The conduction band minimum (CBM) and valence band maximum (VBM) of Ag(NH3)2PbI3 and Au(NH3)2PbI3 are all located at the Γ point, which indicates that they exhibit direct band gaps. In contrast, Cu(NH3)2PbI3 exhibits an indirect band gap with the CBM located at the Γ point and the VBM located at the X point. These three perovskites exhibit almost the same conduction bands with three degenerate conduction band minima near the Γ point (CB1, CB2 and CB3) but different valence bands. The valence band of Cu(NH3)2PbI3 is almost flat, which could not facilitate hole transport. Among these perovskites, Cu(NH3)2PbI3 exhibits the smallest band gap of 1.34 eV, while Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit slightly larger band gaps of 1.65 eV and 1.70 eV, respectively. Since the energy of the Cu 3d orbit is distinctly lower than that of the Ag 4d and Au 5d orbits (Fig. S8, ESI†), it contributes mainly to the VBM of Cu(NH3)2PbI3. Thus, Cu(NH3)2PbI3 exhibits a different valence band compared with Ag(NH3)2PbI3 and Au(NH3)2PbI3. In order to ensure the reliability of our calculation, the electronic structures of these perovskites were also calculated by the Plane-Wave self-consistent field (PWscf) with the PBE functional considering the spin–orbit coupling (SOC) and the scalar relativistic (SR) effect,74,75 and almost the same band gaps were obtained (1.33 eV, 1.62 eV and 1.64 eV for Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3, respectively, Fig. S5, ESI†). However, while calculating the band structures with the PBE functional and considering the SOC only, the proposed perovskite exhibits a much smaller band gap (0.54 eV, 0.73 eV and 0.70 eV for Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3, respectively, Fig. S6, ESI†) which may be due to the error compensation between the SOC and SR is transformed into the bandgap. On the other hand, the absorption coefficient is another important parameter for solar cells, and a direct band gap in the optimal absorption range does not always guarantee that it has a larger absorption coefficient. The absorption spectra of these three perovskites were then calculated and are shown in Fig. S9 (ESI†). Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3 all have much larger absorption coefficients than that of α- and β-MAPbI3 in the visible range, which indicates that these proposed 3D perovskites exhibit much stronger photon harvesting ability towards solar cell applications.76 Moreover, the optical transition of these three perovskites was also estimated through calculating the transition dipole moment (TDM).77,78 As shown in Fig. S10 (ESI†), the direct VB-CB transitions of Ag(NH3)2PbI3 and Au(NH3)2PbI3 are more favorable than that of Cu(NH3)2PbI3. Given the discussion of stability, band structures, absorption coefficients and optical transition, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are good candidates towards high-performance perovskite solar cells.
 | ||
| Fig. 4 The calculated band structures of the 3D perovskite with complex ions based on the PBE functional: Cu(NH3)2PbI3 (a), Ag(NH3)2PbI3 (b) and Au(NH3)2PbI3 (c). | ||
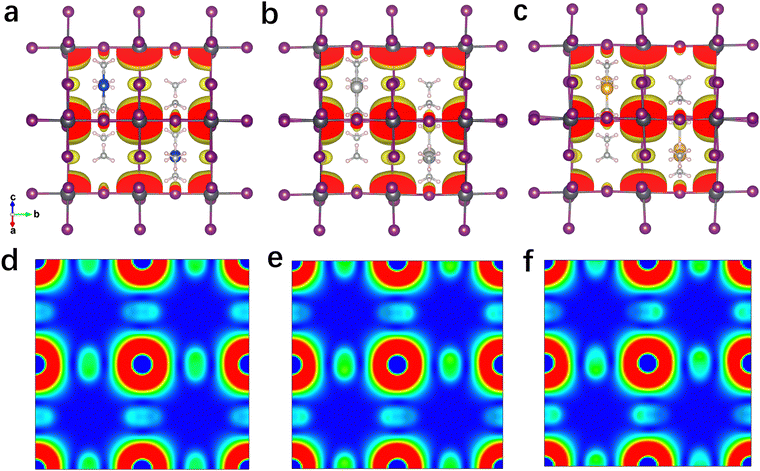
The projected density of states (PDOS) of these 3D perovskites are further calculated and shown in Fig. S11 (ESI†). The VBM of Cu(NH3)2PbI3 is mainly contributed by the Cu 3d orbit, while the CBM consists of the Pb 6p orbit and I 5p orbit. In contrast, the VBM of Ag(NH3)2PbI3 is mainly contributed by both the I 5p orbit and Ag 4d orbit, while it is mainly contributed by the I 5p orbit for Au(NH3)2PbI3. The CBM compositions of Ag(NH3)2PbI3 and Au(NH3)2PbI3 are similar to that of Cu(NH3)2PbI3. Thus, the electronic transition of Ag(NH3)2PbI3 should displace the electronic density from the A-site cation and I to Pb. For the electronic transition from the A-site cation to Pb, it is widely observed in low-dimensional perovskite with large conjugated cations.27 This depends on the energy discrepancy between the VB (or HOMO) of the cation and the inorganic framework (as shown in Fig. S13, ESI†).79 In order to further confirm the PDOS distribution of these perovskites, the electron densities at the VBM and CBM are calculated and shown in Fig. 5 and Fig. S15–S19 (ESI†). Consistent with the PDOS discussed above, the electron density at the VBM of Cu(NH3)2PbI3 is mainly localized on the Cu atom, which is mainly located on the I atom and Ag atom for Ag(NH3)2PbI3, and only on the I atom for Au(NH3)2PbI3, respectively. Meanwhile, the electron densities of Ag(NH3)2PbI3 and Au(NH3)2PbI3 at CBM1, CBM2 and CBM3 consist of the Pb 6p orbit and I 5p orbit (Fig. S15–S17, ESI†). As shown in Fig. 5d–f, the electron densities (the planes sliced for the electron densities are shown in Fig. S14, ESI†) at the CBM of Ag(NH3)2PbI3 and Au(NH3)2PbI3 demonstrate that the electron clouds indeed disperse along the Pb–I skeleton in three directions, which indicates an isotropic electron transport feature and 3D electronic connectivity. Different from the transport of electrons, holes are moving along the halide → complex ion → halide direction. Therefore, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are not only structural 3D but also electronic 3D, which is further confirmed by the effective electron and hole masses discussed below. The spin polarization was also considered while calculating the band structure and DOS, and the same results were obtained for spin-up and spin-down (as shown in Fig. S7 and S10, ESI†).
The electron and hole effective masses of these 3D lead iodide perovskites are then calculated based on eqn (3),
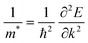 | (3) |
 and their harmonic mean values are calculated from Γ to T, Γ to W and Γ to X corresponding to the three directions of the inorganic perovskite framework (Table S5 and Fig. S21–S24, ESI†). Among these three directions, the minimal electron effective masses among the degenerated CBs (0.25 me, 0.26 me and 0.27 me) as well as their harmonic mean electron effective masses are of the same magnitude (0.66 me, 0.72 me and 0.69 me) for Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3, respectively, which further confirms the isotropic electron transport feature and 3D electronic connectivity of these three perovskites. The hole effective masses and their harmonic mean values of these perovskites along the inorganic perovskite framework (from Γ to T, Γ to W and Γ to X for Ag(NH3)2PbI3 and Au(NH3)2PbI3, respectively, and from X to V, X to R and X to Γ for Cu(NH3)2PbI3) were also calculated. The hole effective masses along the Γ–X direction of Ag(NH3)2PbI3 (31.63 me) and Au(NH3)2PbI3 (23.64 me) are much larger than other directions (∼2.90 me for Ag(NH3)2PbI3 and 2.55 me for Ag(NH3)2PbI3), which is similar to that of γ-MAPbI3 (11.98 me for [010] vs. 1.18 me for [100] and 1.05 me for [001] direction).76,80 In contrast, Cu(NH3)2PbI3 shows large harmonic mean hole effective masses along all three directions, Γ–T (19.59 me), Γ–W (19.62 me) and Γ–X (9.7 me).76 Therefore, based on the hole effective masses (Table S5 and Fig. S21, ESI†) and charge density mapping as discussed above, it is confirmed that Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit a 2D hole transport feature, while Cu(NH3)2PbI3 could not facilitate hole transport in all three directions. This is also consistent with the flat valence band of Cu(NH3)2PbI3, as shown in Fig. 4a. The 2D hole transport feature of Ag(NH3)2PbI3 and Au(NH3)2PbI3 may originate from the linear profile of the cations. The cations are arranging in the xz plane (Fig. 2) and holes are moving along the halide → complex ion → halide direction. Thus, Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit anisotropic hole transport (Fig. S23, ESI†). Based on the above discussion, Cu(NH3)2PbI3 could not be adopted as the light absorber of solar cells owing to both poorer stability and slower hole transport. Meanwhile, Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit a modest harmonic mean hole and electron effective mass together with optimized band gaps and large absorption coefficients, which is promising towards application in high-performance perovskite solar cells.76
and their harmonic mean values are calculated from Γ to T, Γ to W and Γ to X corresponding to the three directions of the inorganic perovskite framework (Table S5 and Fig. S21–S24, ESI†). Among these three directions, the minimal electron effective masses among the degenerated CBs (0.25 me, 0.26 me and 0.27 me) as well as their harmonic mean electron effective masses are of the same magnitude (0.66 me, 0.72 me and 0.69 me) for Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3, respectively, which further confirms the isotropic electron transport feature and 3D electronic connectivity of these three perovskites. The hole effective masses and their harmonic mean values of these perovskites along the inorganic perovskite framework (from Γ to T, Γ to W and Γ to X for Ag(NH3)2PbI3 and Au(NH3)2PbI3, respectively, and from X to V, X to R and X to Γ for Cu(NH3)2PbI3) were also calculated. The hole effective masses along the Γ–X direction of Ag(NH3)2PbI3 (31.63 me) and Au(NH3)2PbI3 (23.64 me) are much larger than other directions (∼2.90 me for Ag(NH3)2PbI3 and 2.55 me for Ag(NH3)2PbI3), which is similar to that of γ-MAPbI3 (11.98 me for [010] vs. 1.18 me for [100] and 1.05 me for [001] direction).76,80 In contrast, Cu(NH3)2PbI3 shows large harmonic mean hole effective masses along all three directions, Γ–T (19.59 me), Γ–W (19.62 me) and Γ–X (9.7 me).76 Therefore, based on the hole effective masses (Table S5 and Fig. S21, ESI†) and charge density mapping as discussed above, it is confirmed that Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit a 2D hole transport feature, while Cu(NH3)2PbI3 could not facilitate hole transport in all three directions. This is also consistent with the flat valence band of Cu(NH3)2PbI3, as shown in Fig. 4a. The 2D hole transport feature of Ag(NH3)2PbI3 and Au(NH3)2PbI3 may originate from the linear profile of the cations. The cations are arranging in the xz plane (Fig. 2) and holes are moving along the halide → complex ion → halide direction. Thus, Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit anisotropic hole transport (Fig. S23, ESI†). Based on the above discussion, Cu(NH3)2PbI3 could not be adopted as the light absorber of solar cells owing to both poorer stability and slower hole transport. Meanwhile, Ag(NH3)2PbI3 and Au(NH3)2PbI3 exhibit a modest harmonic mean hole and electron effective mass together with optimized band gaps and large absorption coefficients, which is promising towards application in high-performance perovskite solar cells.76
Conclusions
In summary, 3D lead iodide perovskites based on complex ions, Cu(NH3)2PbI3, Ag(NH3)2PbI3 and Au(NH3)2PbI3, are demonstrated for the first time in this work. Ag(NH3)2PbI3 and Au(NH3)2PbI3 are found to be both kinetically and thermodynamically stable based on structural optimization, phonon spectra, ab initio molecular dynamics simulations, formation and dissociation energies. In particular, Ag(NH3)2PbI3 and Au(NH3)2PbI3 are not only structural 3D but also electronic 3D. Moreover, these two perovskites exhibit large absorption coefficients, suitable band gaps, and small hole and electron masses, which are very promising towards application in perovskite solar cells. These findings could throw light on the development of novel electronic 3D perovskites with superior optical and electrical properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. Long, H. Wang, H. Lu and T. Wang acknowledge the financial support from the NSFC (52103218, 92256202, 12261131500) of China, the Fundamental Research Funds for the Central Universities, Nankai University (Grant Number: 023-63233038), and the Opening Project of State Key Laboratory of Polymer Materials Engineering (Sichuan University) (Grant No. sklpme2021-05-02). Y. Zhou and Y. Yu thank the funding from NSFC (No. 22103097) of China, The Science and Technology Bureau of Guangzhou (grant No. 202102020495). X. Wei acknowledges the financial support from the National Key R&D Program of China (2017YFE0131900). All theoretical calculations were performed at the National Supercomputer Center in Guangzhou.Notes and references
- M. Grätzel, Nat. Mater., 2014, 13, 838–842 CrossRef.
- J. Jeong, M. Kim, J. Seo, H. Lu, P. Ahlawat, A. Mishra, Y. Yang, M. A. Hope, F. T. Eickemeyer, M. Kim, Y. J. Yoon, I. W. Choi, B. P. Darwich, S. J. Choi, Y. Jo, J. H. Lee, B. Walker, S. M. Zakeeruddin, L. Emsley, U. Rothlisberger, A. Hagfeldt, D. S. Kim, M. Grätzel and J. Y. Kim, Nature, 2021, 592, 381–385 CrossRef.
- N. J. Jeon, H. Na, E. H. Jung, T.-Y. Yang, Y. G. Lee, G. Kim, H.-W. Shin, S. Il Seok, J. Lee and J. Seo, Nat. Energy, 2018, 3, 682–689 CrossRef.
- H. Tsai, W. Nie, J.-C. Blancon, C. C. Stoumpos, R. Asadpour, B. Harutyunyan, A. J. Neukirch, R. Verduzco, J. J. Crochet, S. Tretiak, L. Pedesseau, J. Even, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, Nature, 2016, 536, 312–316 CrossRef PubMed.
- D. Bi, C. Yi, J. Luo, J.-D. Décoppet, F. Zhang, S. M. Zakeeruddin, X. Li, A. Hagfeldt and M. Grätzel, Nat. Energy, 2016, 1, 16142 CrossRef.
- E. Eperon Giles, T. Leijtens, A. Bush Kevin, R. Prasanna, T. Green, T.-W. Wang Jacob, P. McMeekin David, G. Volonakis, L. Milot Rebecca, R. May, A. Palmstrom, J. Slotcavage Daniel, A. Belisle Rebecca, B. Patel Jay, S. Parrott Elizabeth, J. Sutton Rebecca, W. Ma, F. Moghadam, B. Conings, A. Babayigit, H.-G. Boyen, S. Bent, F. Giustino, M. Herz Laura, B. Johnston Michael, D. McGehee Michael and J. Snaith Henry, Science, 2016, 354, 861–865 CrossRef PubMed.
- J. Bie, D.-B. Yang, M.-G. Ju, Q. Pan, Y.-M. You, W. Fa, X. C. Zeng and S. Chen, JACS Au, 2021, 1, 475–483 CrossRef.
- J. Dai, L. Ma, M. Ju, J. Huang and X. C. Zeng, Phys. Chem. Chem. Phys., 2017, 19, 21691–21695 RSC.
- W. Xu, Q. Hu, S. Bai, C. Bao, Y. Miao, Z. Yuan, T. Borzda, A. J. Barker, E. Tyukalova, Z. Hu, M. Kawecki, H. Wang, Z. Yan, X. Liu, X. Shi, K. Uvdal, M. Fahlman, W. Zhang, M. Duchamp, J.-M. Liu, A. Petrozza, J. Wang, L.-M. Liu, W. Huang and F. Gao, Nat. Photonics, 2019, 13, 418–424 CrossRef.
- S. Yun, X. Zhou, J. Even and A. Hagfeldt, Angew. Chem., Int. Ed., 2017, 56, 15806–15817 CrossRef.
- W. Yan, Z. Wang, Y. Gong, S. Guo, J. Jiang, J. Chen, C. Tang, R. Xia, W. Huang and H. Xin, Org. Electron., 2019, 67, 208–214 CrossRef.
- Z. Xiao, Z. Song and Y. Yan, Adv. Mater., 2019, 31, 1803792 CrossRef.
- M. Yuan, L. N. Quan, R. Comin, G. Walters, R. Sabatini, O. Voznyy, S. Hoogland, Y. Zhao, E. M. Beauregard, P. Kanjanaboos, Z. Lu, D. H. Kim and E. H. Sargent, Nat. Nanotechnol., 2016, 11, 872–877 CrossRef PubMed.
- R. Fu, W. Zhao, L. Wang, Z. Ma, G. Xiao and B. Zou, Angew. Chem., Int. Ed., 2021, 60, 10082–10088 CrossRef PubMed.
- V. Adinolfi, O. Ouellette, M. I. Saidaminov, G. Walters, A. L. Abdelhady, O. M. Bakr and E. H. Sargent, Adv. Mater., 2016, 28, 7264–7268 CrossRef PubMed.
- H. Wei and J. Huang, Nat. Commun., 2019, 10, 1066 CrossRef.
- Q. Lin, A. Armin, P. L. Burn and P. Meredith, Nat. Photonics, 2015, 9, 687–694 CrossRef.
- S. Yakunin, D. N. Dirin, Y. Shynkarenko, V. Morad, I. Cherniukh, O. Nazarenko, D. Kreil, T. Nauser and M. V. Kovalenko, Nat. Photonics, 2016, 10, 585–589 CrossRef.
- W. Yu, F. Li, L. Yu, M. R. Niazi, Y. Zou, D. Corzo, A. Basu, C. Ma, S. Dey, M. L. Tietze, U. Buttner, X. Wang, Z. Wang, M. N. Hedhili, C. Guo, T. Wu and A. Amassian, Nat. Commun., 2018, 9, 5354 CrossRef PubMed.
- H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Nat. Mater., 2015, 14, 636–642 CrossRef PubMed.
- Y. Jia, R. A. Kerner, A. J. Grede, B. P. Rand and N. C. Giebink, Nat. Photonics, 2017, 11, 784–788 CrossRef.
- J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, Chem. Rev., 2020, 120, 7867–7918 CrossRef PubMed.
- W.-J. Yin, T. Shi and Y. Yan, J. Phys. Chem. C, 2015, 119, 5253–5264 CrossRef CAS.
- G. Long, Y. Zhou, M. Zhang, R. Sabatini, A. Rasmita, L. Huang, G. Lakhwani and W. Gao, Adv. Mater., 2019, 31, 1807628 CrossRef PubMed.
- Z.-J. Wang, L.-K. Wu, N. Wang, Q.-Q. Hu, J.-R. Li and H.-Y. Ye, Dalton Trans., 2023, 52, 2799–2803 RSC.
- G. Long, C. Jiang, R. Sabatini, Z. Yang, M. Wei, L. N. Quan, Q. Liang, A. Rasmita, M. Askerka, G. Walters, X. Gong, J. Xing, X. Wen, R. Quintero-Bermudez, H. Yuan, G. Xing, X. R. Wang, D. Song, O. Voznyy, M. Zhang, S. Hoogland, W. Gao, Q. Xiong and E. H. Sargent, Nat. Photonics, 2018, 12, 528–533 CrossRef CAS.
- Y. Gao, E. Shi, S. Deng, S. B. Shiring, J. M. Snaider, C. Liang, B. Yuan, R. Song, S. M. Janke, A. Liebman-Peláez, P. Yoo, M. Zeller, B. W. Boudouris, P. Liao, C. Zhu, V. Blum, Y. Yu, B. M. Savoie, L. Huang and L. Dou, Nat. Chem., 2019, 11, 1151–1157 CrossRef CAS.
- T. M. Koh, B. Febriansyah and N. Mathews, Chemistry, 2017, 2, 326–327 CrossRef CAS.
- D. Fu, Z. Hou, Y. He, J.-C. Liu, H.-P. Lv and Y.-Y. Tang, Chem. Mater., 2022, 34, 3518–3524 CrossRef CAS.
- H. Wang, J. Li, H. Lu, S. Gull, T. Shao, Y. Zhang, T. He, Y. Chen, T. He and G. Long, Angew. Chem., Int. Ed., 2023, e202309600 CAS.
- R. Zhang, X. Mao, Y. Yang, S. Yang, W. Zhao, T. Wumaier, D. Wei, W. Deng and K. Han, Angew. Chem., Int. Ed., 2019, 58, 2725–2729 CrossRef CAS PubMed.
- X.-G. Zhao, J.-H. Yang, Y. Fu, D. Yang, Q. Xu, L. Yu, S.-H. Wei and L. Zhang, J. Am. Chem. Soc., 2017, 139, 2630–2638 CrossRef CAS.
- G. Long, R. Sabatini, M. I. Saidaminov, G. Lakhwani, A. Rasmita, X. Liu, E. H. Sargent and W. Gao, Nat. Rev. Mater., 2020, 5, 423–439 CrossRef.
- L. Etgar, Energy Environ. Sci., 2018, 11, 234–242 RSC.
- K. Drużbicki, R. Lavén, J. Armstrong, L. Malavasi, F. Fernandez-Alonso and M. Karlsson, J. Phys. Chem. Lett., 2021, 12, 3503–3508 CrossRef.
- A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, M. K. Nazeeruddin, M. Grätzel and F. De Angelis, Nano Lett., 2014, 14, 3608–3616 CrossRef CAS PubMed.
- C. Motta, F. El-Mellouhi, S. Kais, N. Tabet, F. Alharbi and S. Sanvito, Nat. Commun., 2015, 6, 7026 CrossRef CAS.
- K. Drużbicki, R. S. Pinna, S. Rudić, M. Jura, G. Gorini and F. Fernandez-Alonso, J. Phys. Chem. Lett., 2016, 7, 4701–4709 CrossRef.
- A. Filippetti, P. Delugas, M. I. Saba and A. Mattoni, J. Phys. Chem. Lett., 2015, 6, 4909–4915 CrossRef CAS.
- A. Ray, B. Martín-García, A. Moliterni, N. Casati, K. M. Boopathi, D. Spirito, L. Goldoni, M. Prato, C. Giacobbe, C. Giannini, F. Di Stasio, R. Krahne, L. Manna and A. L. Abdelhady, Adv. Mater., 2022, 34, 2106160 CrossRef CAS.
- G. Saleh, G. Biffi, F. Di Stasio, B. Martín-García, A. L. Abdelhady, L. Manna, R. Krahne and S. Artyukhin, Chem. Mater., 2021, 33, 8524–8533 CrossRef CAS.
- K. Frohna, T. Deshpande, J. Harter, W. Peng, B. A. Barker, J. B. Neaton, S. G. Louie, O. M. Bakr, D. Hsieh and M. Bernardi, Nat. Commun., 2018, 9, 1829 CrossRef PubMed.
- Z. Xiao, W. Meng, J. Wang, D. B. Mitzi and Y. Yan, Mater. Horiz., 2017, 4, 206–216 RSC.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- M. R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 2579–2585 CrossRef CAS PubMed.
- A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141 CrossRef CAS PubMed.
- E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Chem. Mater., 2016, 28, 1348–1354 CrossRef CAS.
- F. Wei, Z. Deng, S. Sun, F. Xie, G. Kieslich, D. M. Evans, M. A. Carpenter, P. D. Bristowe and A. K. Cheetham, Mater. Horiz., 2016, 3, 328–332 RSC.
- M. T. Sirtl, R. Hooijer, M. Armer, F. G. Ebadi, M. Mohammadi, C. Maheu, A. Weis, B. T. van Gorkom, S. Häringer, R. A. J. Janssen, T. Mayer, V. Dyakonov, W. Tress and T. Bein, Adv. Energy Mater., 2022, 12, 2103215 CrossRef CAS.
- H.-Y. Zhang, X.-G. Chen, Z.-X. Zhang, X.-J. Song, T. Zhang, Q. Pan, Y. Zhang and R.-G. Xiong, Adv. Mater., 2020, 32, 2005213 CrossRef CAS.
- Ma M
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) czka, M. Ptak, A. G
czka, M. Ptak, A. G![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) gor, D. Stefańska, J. K. Zarȩba and A. Sieradzki, Chem. Mater., 2020, 32, 1667–1673 CrossRef.
gor, D. Stefańska, J. K. Zarȩba and A. Sieradzki, Chem. Mater., 2020, 32, 1667–1673 CrossRef. - S. Huang, P. Huang, L. Wang, J. Han, Y. Chen and H. Zhong, Adv. Mater., 2019, 31, 1903830 CrossRef CAS.
- H.-Y. Zhang, X.-J. Song, H. Cheng, Y.-L. Zeng, Y. Zhang, P.-F. Li, W.-Q. Liao and R.-G. Xiong, J. Am. Chem. Soc., 2020, 142, 4604–4608 CrossRef CAS.
- X. Li, Y. He, M. Kepenekian, P. Guo, W. Ke, J. Even, C. Katan, C. C. Stoumpos, R. D. Schaller and M. G. Kanatzidis, J. Am. Chem. Soc., 2020, 142, 6625–6637 CrossRef CAS PubMed.
- Y.-Y. Tang, Y.-H. Liu, H. Peng, B.-B. Deng, T.-T. Cheng and Y.-T. Hu, J. Am. Chem. Soc., 2020, 142, 19698–19704 CrossRef CAS PubMed.
- D. Umeyama, L. Leppert, B. A. Connor, M. A. Manumpil, J. B. Neaton and H. I. Karunadasa, Angew. Chem., Int. Ed., 2020, 59, 19087–19094 CrossRef CAS PubMed.
- P. Fu, S. Hu, J. Tang and Z. Xiao, Front. Optoelectron., 2021, 14, 252–259 CrossRef.
- X. Li, M. Kepenekian, L. Li, H. Dong, C. C. Stoumpos, R. Seshadri, C. Katan, P. Guo, J. Even and M. G. Kanatzidis, J. Am. Chem. Soc., 2022, 144, 3902–3912 CrossRef CAS PubMed.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693 CrossRef CAS PubMed.
- A. E. Fedorovskiy, N. A. Drigo and M. K. Nazeeruddin, Small Methods, 2020, 4, 1900426 CrossRef CAS.
- N. A. Benedek and C. J. Fennie, J. Phys. Chem. C, 2013, 117, 13339–13349 CrossRef CAS.
- I. P. Swainson, C. Stock, S. F. Parker, L. Van Eijck, M. Russina and J. W. Taylor, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 100303 CrossRef.
- F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goñi, A. M. A. Leguy, P. R. F. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308 CrossRef.
- A. Marronnier, G. Roma, S. Boyer-Richard, L. Pedesseau, J.-M. Jancu, Y. Bonnassieux, C. Katan, C. C. Stoumpos, M. G. Kanatzidis and J. Even, ACS Nano, 2018, 12, 3477–3486 CrossRef CAS.
- A. N. Beecher, O. E. Semonin, J. M. Skelton, J. M. Frost, M. W. Terban, H. Zhai, A. Alatas, J. S. Owen, A. Walsh and S. J. L. Billinge, ACS Energy Lett., 2016, 1, 880–887 CrossRef CAS.
- I. Maeng, S. Lee, H. Tanaka, J.-H. Yun, S. Wang, M. Nakamura, Y.-K. Kwon and M.-C. Jung, NPG Asia Mater., 2020, 12, 53 CrossRef CAS.
- A. M. A. Leguy, A. R. Goñi, J. M. Frost, J. Skelton, F. Brivio, X. Rodríguez-Martínez, O. J. Weber, A. Pallipurath, M. I. Alonso, M. Campoy-Quiles, M. T. Weller, J. Nelson, A. Walsh and P. R. F. Barnes, Phys. Chem. Chem. Phys., 2016, 18, 27051–27066 RSC.
- C. Gehrmann and D. A. Egger, Nat. Commun., 2019, 10, 3141 CrossRef.
- T. Sun, D.-B. Zhang and R. M. Wentzcovitch, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094109 CrossRef.
- O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180301 CrossRef.
- R. Comin, M. K. Crawford, A. H. Said, N. Herron, W. E. Guise, X. Wang, P. S. Whitfield, A. Jain, X. Gong, A. J. H. McGaughey and E. H. Sargent, Phys. Rev. B, 2016, 94, 094301 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- E. Mosconi, P. Umari and F. De Angelis, Phys. Chem. Chem. Phys., 2016, 18, 27158–27164 RSC.
- P. Umari, E. Mosconi and F. De Angelis, Sci. Rep., 2014, 4, 4467 CrossRef PubMed.
- Y. Zhou, F. Huang, Y.-B. Cheng and A. Gray-Weale, Phys. Chem. Chem. Phys., 2015, 17, 22604–22615 RSC.
- Z. Wang, A. M. Ganose, C. Niu and D. O. Scanlon, J. Mater. Chem. C, 2019, 7, 5139–5147 RSC.
- W. Meng, X. Wang, Z. Xiao, J. Wang, D. B. Mitzi and Y. Yan, J. Phys. Chem. Lett., 2017, 8, 2999–3007 CrossRef CAS PubMed.
- Y. Gao, Z. Wei, S.-N. Hsu, B. W. Boudouris and L. Dou, Mater. Chem. Front., 2020, 4, 3400–3418 RSC.
- J. Feng and B. Xiao, J. Phys. Chem. Lett., 2014, 5, 1278–1282 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00202k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |