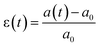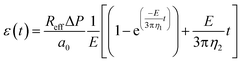Deformation under flow and morphological recovery of cancer cells

Abstract

The metastatic cascade includes a blood circulation step for cells detached from the primary tumor. This stage involves significant shear stress as well as large and fast deformation as the cells circulate through the microvasculature. These mechanical stimuli are well reproduced in microfluidic devices. However, the recovery dynamics after deformation is also pivotal to understand how a cell can pass through the multiple capillary constrictions encountered during a single hemodynamic cycle. The microfluidic system developed in this work allows single cell recovery to be studied under flow-free conditions following pressure-actuated cell deformation inside constricted microchannels. We used three breast cancer cell lines – namely MCF-7, SK-BR3 and MDA-MB231 – as cellular models representative of different cancer phenotypes. Changing the size of the constriction allows exploration of moderate to strong deformation regimes, the latter being associated with the formation of plasma membrane blebs. In the regime of moderate deformation, all cell types display a fast elastic recovery behavior followed by a slower viscoelastic regime, well described by a double exponential decay. Among the three cell types, cells of the mesenchymal phenotype, i.e. the MDA-MB231 cells, are softer and the most fluid-like, in agreement with previous studies. Our main finding here is that the fast elastic recovery regime revealed by our novel microfluidic system is under the control of cell contractility ensured by the integrity of the cell cortex. Our results suggest that the cell cortex plays a major role in the transit of circulating tumor cells by allowing their fast morphological recovery after deformation in blood capillaries.

---

Introduction

The role of cell mechanics in the successive steps leading to metastatic cancers¹ is more and more documented.² Migrating cells from a primary tumor experience strong deformation in their path toward the blood vessels.³ The environment of the bloodstream is then a source of shear stress and confinement.^4,5 Finally, the step of extravasation requires cell squeezing across the endothelial barrier.⁶In vitro approaches using microfluidic tools have highlighted the transformation and sorting effects of blood stream mechanical stressors on circulating tumors cells (hereafter referred to as CTCs). Cells exposed to shear stress display subsequent increased migration capabilities^7,8 and over-expression of epithelial–mesenchymal transition^9,10 or stemness¹¹ genes. Furthermore, shear stress applied for hours favors the survival of soft, stem cell like phenotypes showing high metastatic potential compared to stiffer cells.¹²

Mechanical stimuli encountered in blood circulation are however not limited to shear stress. Because the diameters of vessels in the capillary bed are much smaller than cell and even nucleus sizes,^13,14 circulating cells are repetitively squeezed in the microvasculature (see ref. 15 for a review). Eventually, capillary occlusion through cell arrest may occur. Interestingly, the mechanics of CTCs opens a new field of mechanobiology addressing strong and fast flow-induced deformation, distinct from the phenomenon of spontaneous migration under confinement which has been studied for a decade.^16,17 This regime of large deformation under flow has been studied using microfluidic-based models including constricted microchannels.^18–21 We have reported in a previous study that the time required for a cell to cross multiple successive constrictions was mainly determined by the time needed to enter through the first constriction.²² This observation is a consequence of the finite time of cell shape recovery, higher than the time necessary to reach the next constriction. Quite importantly, the viscoelastic relaxation time of CTCs might influence the transit and arrest of CTCs in capillaries,⁴ a phenomenon essential for extravasation. By devising a device including 80 μm long relaxation chambers in-between constrictions, Kamyabi et al.²³ were able to follow cell shape relaxation occurring with about 10 ms duration, thanks to the use of a high speed camera (1000 fps). This relaxation step occurs however under shear stress and cell motion. More recently, Yan et al.²⁴ succeeded in monitoring cell recovery under free-flow conditions by manually stopping the flow each time a cell escaped from the constrictions.

The present work focuses on new methodological developments for the study of cell morphological relaxation. The novelty of our work lies in the immediate release of hydrodynamic stresses after flow-induced deformation, together with cell immobilization in traps, providing unprecedented access to cell morphological recovery. This new methodology is then applied, in a proof-of-concept approach, to circulating cancer cells of three different types, to demonstrate the potential and limitations of this new system. Finally, this work highlights the role of the actomyosin cortex in cell recovery, which appears to be responsible for their initial elastic behavior.

Specifically, the journey of a cell in our original device occurs in several steps. Cells are first pushed by a pressure gradient into constrictions in which they next progress by deforming. They are then released into a relaxation chamber characterized by uniform pressure and filled with nest-like traps to immobilize them and track their morphological relaxation by fast camera imaging. Importantly, we designed the constrictions as slits in order to achieve significant cell deformation while avoiding cell blebbing. We will refer to this device as Pachinko in the following, because of its analogy to the popular Japanese game.

Design and running principle of the Pachinko microfluidic system

The Pachinko microfluidic chip

The overall design of the microfluidic device is described in Fig. 1a. It includes three inlet/outlet ports and three main compartments: a flowing channel between inlet 1 and outlet 2, a recovery chamber connected to outlet 3, and a set of three identical microchannels (constrictions) connecting the main channel to the recovery chamber. Each constriction is composed of a 60 μm-long narrowing of the channel with a circle arc profile. This shape was selected on the basis of a previous study²² to produce a smooth deformation profile, similar to what is observed at the level of mural cells (e.g. pericytes) under both static and dynamic conditions (during e.g. capillary diameter regulation for cerebrovascular blood flow control).^25,26 At the narrowest part of the constriction, the cross section is a 6 μm-wide and 15 μm-high rectangle (Fig. 1b and ESI,† section 2, Fig. S1). This characteristic lowest dimension falls in the range of typical diameters found in the microvasculature of various mammals,^26,27 including humans,²⁸ while providing significant deformation of the cell. It is also achievable using standard microfabrication techniques in contrast to circular channels which would require more sophisticated methods.²⁹

Fig. 1 Design and operating principle of the Pachinko device. (a) Image and overall design of the microfluidic device. The simulated pressure profile (values in mbar) in the microfluidic device is indicated. (b) Constriction and cell nest dimensions. (c) Principle of cell deformation and recovery in the device. (d) Reconstructed representative image of a cell in different parts of the device (light blue overlay: cell nucleus stained with Hoechst). (e) Pressure profile with simulated streamlines through a single constriction and adjacent nests. Most of the pressure gradient is located in the constriction (pressure drop ΔP ≈ 6 mbar), ensuring cell recovery under negligible hydrodynamic forces (due to a pressure drop of about 0.1 mbar across a trapped cell, see Fig. S2†).

The cell suspension is injected into the device through inlet 1, thus establishing a flow of cells in the main channel. The pressure difference between the main channel and the recovery chamber creates a pressure profile that drives cells to enter constrictions. There, they will undergo flow-induced deformation before crossing the constriction and getting trapped into one of the nests arranged in a staggered pattern. We set the pressure difference between the main channel and outlet to 10 mbar, in order to achieve a cell arrest time in the range of seconds, i.e. close to the order of magnitude of arrest times reported for CTCs in blood capillaries in vivo.³⁰

The pressure and velocity profiles in the microfluidic chip have been determined by numerical simulations. Due to the negligible size of the three constrictions in parallel compared to the main channel and the recovery chamber, the majority of the pressure drop is located at the constriction level, thus ensuring that the cell is free of any significant pressure gradient in the main channel and in the recovery chamber (Fig. 1e and ESI,† section 3, Fig. S2 and Table S1). The pressure drop applied along the narrowest part of the constriction, estimated to be approximately ΔP_h = 6 mbar, creates a hydrodynamic force that will push the cell, squeezing it between the channel walls (see Fig. 1d), until the cell is deformed enough to be released in the recovery chamber. Note that the surface of the channels is passivated using pLL-PEG to minimize the friction between the cells and the PDMS surface. The cell will then follow the streamlines and end up in one of the single cell nests where it can recover from the deformation. The pressure difference applied on the cell in a trap is estimated to be 0.1 mbar (Fig. S2†) and is thus negligible compared to ΔP_h. Note that as the cell membrane is being curved in the constriction, a pressure difference ΔP_c is created which opposes cell deformation and counteracts the hydrostatic pressure difference ΔP_h. Laplace law gives the equation which relates ΔP_c with the cell membrane cortical tension τ₀ and the front and back radius of the cell (R_front and R_back, respectively) in the constriction: ΔP_c = τ₀(1/R_front− 1/R_back).^31,32 Taking an estimate of τ₀≈ 50 pN μm⁻¹ (ref. 33) for cancer cells, we found that ΔP_c≈ 0.05 mbar at the cell entry and decreases as the cell progresses in the constriction (ESI,† section 4 and Fig. S3). Thus we can neglect the membrane curvature induced pressure difference and consider that cells experience in the constriction a pressure drop of ΔP ≈ 6 mbar.

Dynamics of cell morphology upon flow-induced deformation

Briefly, cells are stained with a membrane dye (DIL) to detect the outline of the whole cell (see the Materials and methods section). The trajectory of a cell can be divided into three parts (see Fig. 2a): travel in the main channel (points A and B), then deformation and transit through the constriction (points C and D), followed by recovery in the single cell nest (points E–I). In each frame, a region of interest around the cell is segmented to reveal the shape of the cell (represented by its 2D projection). The segmented image properties are measured to determine the cell deformation versus time, which is computed from the elliptical fit of the segmented shape (Fig. 2b, see ESI† movie). As a proxy for cell deformation and shape recovery, we use the elongation parameter ε defined as the length of the ellipse major axis a normalized to its initial value a₀ before the cell entry into the constriction:
We also measure the aspect ratio , with a(t) and b(t) as the major and minor axis lengths, which increases from 1 for a spherical cell to values above 1 for elongated cells. Fig. 2c displays an example of the dynamics of both parameters during the journey of a typical cell in the Pachinko device. The main regimes of ε(t) variation, defined by yellow, red and purple letters, reflect the history of the cell in the three compartments of the device. In the main channel (points A–C), ε = ε₀ is constant and equal to 0 by definition. Similarly, AR = AR₀ is constant and close to 1, which reflects that a spherical floating cell displays a projected shape close to a perfect circle. In the constriction (points C and D), the deformation increases rapidly as the cell is pushed in-between the walls, reaching the maximum ε_max (equivalently AR_max) value. In the cell nest (points E–I), the deformation relaxes toward an asymptotic ε_∞ (equivalently AR_∞) value. To capture all of the recovery, we record for a duration of 50 s after the cell exits the constriction. Beyond this time, we noticed that the cell shape no longer evolves.

Fig. 2 Cell trajectory and morphological analysis in the Pachinko device. (a) Trajectory of a representative cell. The cell initially flowing in the main channel (A) is deviated (B) into the constriction where it is pushed and deformed under flow-induced forces (C and D) before a final recovery step in a nest (E–I). (b) Representative images of the cell (DIL staining) at the different time points A–I shown in (a) (scale bar = 10 μm). Images display the raw and segmented shapes as well as the corresponding elliptic fit (major axis a, minor axis b). (c) Cell elongation ε(t) (blue) and aspect ratio AR(t) (orange) versus time as the cell flows through the microfluidic device, highlighting the time points A–I. The arrest time of the cell inside the constriction is defined as the duration between C and D.

Finally, let's note that approximately 30% of cells ended up alone in a nest. Cells escaping the nest array chamber, or multiple cells ending up in a single cell nest were discarded from the analysis.

Results

The method described above has been applied to three breast cancer cell lines: SK-BR-3, MCF-7 and MDA-MB-231. Each cell line represents one of the three main subtypes of this disease: SK-BR-3 cells originate from HER2+ cancer,³⁴ MCF-7 from estrogen and progesterone receptor positive tumors, while MDA-MB-231 cells display none of these markers and are therefore categorized as “triple-negative”. These subtypes correlate with different levels of aggressiveness, with the triple-negative breast cancer being the most aggressive and more prone to induce metastasis.³⁵

Deformation regime

Our device has been mainly designed for the study of the recovery regime. The circle arc shape of the constriction, in contrast to long and uniform deformation channels developed in ref. 20,and 36–38, involves complex deformation and friction force patterns whose exact modelisation is outside the scope of this study. However, temporal monitoring of cell deformation in these constrictions may still provide useful comparisons between cell lines.

We first consider the cell arrest time, defined as the residence time within the constriction. It should be noted that, due to the double flared shape of our constriction and its short length (relative to the cell diameter), this arrest time differs from the entry or the transit time as defined in the literature for funnel-shaped constrictions opening into a long and narrow channel.^20,36–38 Actually, our arrest time is a combination of both, reflecting the fact that cells are never arrested in the constriction but move slowly until their velocity displays an abrupt change upon cell release.

For each cell line, arrest times range from around 100 s for the slowest cells down to 20 ms for the fastest (Fig. 3 and Materials and methods section). A large variability in arrest time is observed for all three cell lines analyzed, in particular for MDA-MB-231 cells.

Fig. 3 Cell arrest in the constriction displays high variability within each cell line. (a) Box plot of the arrest time for each cell line. The indicated value refers to the cell line median arrest time. (b) Scatter plots of the arrest time as a function of cell diameter. Contours of highest point density are represented for each cell line (MCFs n = 37, SKs n = 85, MDAs, n = 59). Top and side plots around the central scatter plot represent the density of cell diameters (top) or arrest times (right, ‘all’). The gray-shaded side plot (right, ‘size bin’) represents the density of cell arrest times selected within the size bin of 15.5–16.5 μm (highlighted in gray in the central plot) for whole cells.

Arrest time is firstly correlated to cell diameter. The median arrest time of SK-BR-3 cells is 180 ms, which is significantly smaller than the median arrest time of MDA-MB-231 (680 ms) and MCF-7 cells (920 ms), without any significant difference between the latter two (Fig. 3a).

The arrest time correlates with the cell size at the population level as SK-BR-3 cells are on average smaller compared to the other two cell lines. The median diameter for SK-BR-3 cells is 15.9 μm, while the median diameters of MDA-MB-231 and MCF-7 have both been measured at 16.8 μm (ESI,† section 5 and Fig. S4). On average, the larger the cell is, the longer it takes to cross the constriction (Fig. 3b).

Other studies using flow-induced deformation in constrictions of similar dimensions have reported a correlation between the cell size and arrest time,³⁹ or between the cell buoyant mass (which is related to its volume) and arrest time.³⁶ Our results therefore confirm previous data.

Arrest time is a read-out of cell mechanical properties. The scatter plot of Fig. 3b indicates however that cell size is not the only relevant parameter to determine the arrest time. Indeed, some of the bigger cells can cross the constriction very rapidly, and inversely small cells can spend up to a few seconds in the constriction.

To compare between cells of a given size, we binned the data of Fig. 3b by cell size, performing a sliding approach with a bin size of 1 μm (ESI,† section 6 and Fig. S5). Interestingly, a hierarchy between cell types emerges. A typical example of such a window is shown on the right of Fig. 3b. The arrest time for MDA-MB-231 and SK-BR-3 cells distributes over the lowest values, conversely that of MCF-7 over the highest ones. In other terms, MDA-MB-231 and SK-BR-3 cells appear to be more deformable than MCF-7 cells. Our results are in line with other studies comparing the deformability of circulating MCF-7 and MDA-MB-231 cells.^40–42 Although the mechanical properties of SK-BR-3 cells are less documented, our results confirm previous work from our group, showing no significant difference between the arrest times of SK-BR-3 and MDA-MB-231 cells in an identical constriction geometry.²²

Cells progress linearly through the constriction. We next examined the position of the center of mass and longitudinal extent of cells during their journey into the constriction (Fig. 4a). To compare cells of different arrest times, we normalized the time spent in the constriction by their arrest time, so that each cell enters the constriction at time 0 and exits at time 1. Overall, the cell rapidly enters the constriction, then it linearly progresses through the narrow 6 μm wide opening until most of the cell has crossed the neck of the constriction (Fig. 4b).

Fig. 4 Spatio-temporal dynamics of cells during their passage through the constriction. (a) Position of the cell center (±95% CI) relative to the center of the constriction as the cell crosses the constriction. Upper and lower curves represent respectively the back and front position of the cell. For each cell, the time has been normalized by 1/arrest time to overlay curves. Only curves with at least 50 points were considered for this graph (MCFs n = 17, SKs n = 20, MDAs n = 24). (b) Outline of a whole cell (the same as that represented in Fig. 2) at different time points as it progresses through the constriction.

The arrest of the cell in the constriction is thus a continuous transit and not a full stop. Remarkably, for all cell lines, cell release from the constriction occurred as soon as the center of mass of the cell has passed the neck of the constriction (Fig. 4a).

The rheological analysis of the deformation regime reveals that MCF-7 cells are less deformable. We next studied the rheological parameters of cell deformation. We consider these objects as viscoelastic, meaning that they can be modeled by the association of elastic “springs” and viscous “dashpots” (see for instance ref. 43 for an overview of these rheological models). The simplest combination of springs and dashpots that allows us to adequately fit our data is the serial association of a Kelvin–Voigt element, built from a spring (Young modulus E) and a dashpot (viscosity η₁) in parallel, and a pure viscous regime (viscosity η₂). This combination of mechanical elements also known as Jeffrey's model is described in Fig. 5a. Short-time scale deformation is governed by the viscoelastic deformation of the Kelvin–Voigt element, while long-time scale deformation is governed by the linear elongation of the dashpot element. In this framework, the elongation ε(t) (see Fig. 5a) is ruled by the following equation:⁴⁴
where a₀ is the initial major axis length, R_eff is the equivalent radius of the constriction (see ESI,† section 1), ΔP is the pressure difference applied on the constriction, and E, η₁, and η₂ are the rheological parameters described in Fig. 5a.

Fig. 5 Deformation curves. (a) Deformation curves are well described by Jeffrey's model (see the main text for a description). The graph shows an example of the time variation of the elongation ε obtained for a cell arrested for a few seconds in the constriction, highlighting the viscous regime. (b) Mean curves for the three cell lines and fits of the viscoelastic regime set over a time range of 2 s. The viscous regime was not fitted as the majority of the cells escaped before reaching this regime. Error bars represent 95% confidence intervals (MCFs n = 31, SKs n = 46, MDAs n = 29).

It is important to note that most of the cells cross the constrictions in less than a few seconds. In other terms, the number of cells which can be analyzed decreases dramatically beyond a 5 s window. We have thus decided to confine our analysis on the viscoelastic regime at the short time scale by fitting the data with the Kelvin–Voigt model on time scales below 2 s (Fig. 5b).

The parameters deduced from this analysis are reported in Table 1. They are characterized by a low viscosity and an elastic modulus on the order of kPa, in agreement with other studies dealing with flow-induced deformation.^32,42,45

Table 1 Parameters obtained from Jeffrey's model fits, using R_eff = 6.27 μm and ΔP = 6 mbar. Values represent fitting parameters and 95% confidence interval

	MCF-7	SK-BR-3	MDA-MB-231
τ	0.28 s [0.24–0.32]	0.36 s [0.32–0.40]	0.66 s [0.56–0.77]
E	1.90 kPa [1.74–2.06]	1.15 kPa [1.08–1.22]	1.16 kPa [1.10–1.22]
η 1	0.056 kPa s [0.045–0.068]	0.044 kPa s [0.037–0.051]	0.081 kPa s [0.068–0.095]

---

Overall, Table 1 and Fig. 5 indicate that MCF-7 cells are relatively less deformable than SK-BR-3 and MDA-MB-231 cells, as indicated by their larger Young modulus E (Table 1) and lower maximal deformation (Fig. 5b). These observations are consistent with other results in the literature⁴⁰ and with the larger arrest time of MCF-7 cells measured with our Pachinko device (Fig. 3).

Recovery regime

We then turned our attention to the morphological fate of cells when trapped in the nests of the recovery chamber after their passage through the constrictions.

In order to compare cells of different sizes and different maximal elongation, we normalize the elongation by its maximal value for each cell (Fig. 6a) to define the normalized deformation as:

The starting time t = 0 of the recovery regime corresponds to the last frame before the cell exits the constriction, i.e. in most cases to the maximum deformation ε_max. Fig. 6a displays a typical example of the variation of ε_Norm(t). It can be decomposed into an almost instantaneous recovery, happening faster than our frame rate of observation (≤20 ms), followed by a slower shape relaxation. To identify the time constants governing cell recovery, we here chose to describe this slow decay as a viscoelastic (VE) regime according to a generalized fractional Kelvin–Voigt model:^43,46

ε_Norm(t) = ∑a_ie^(−t/τ_i)

Alternatively, fitting with a timescale-free power law model was also performed (ESI† section 7) according to⁴⁷
with C as a constant.

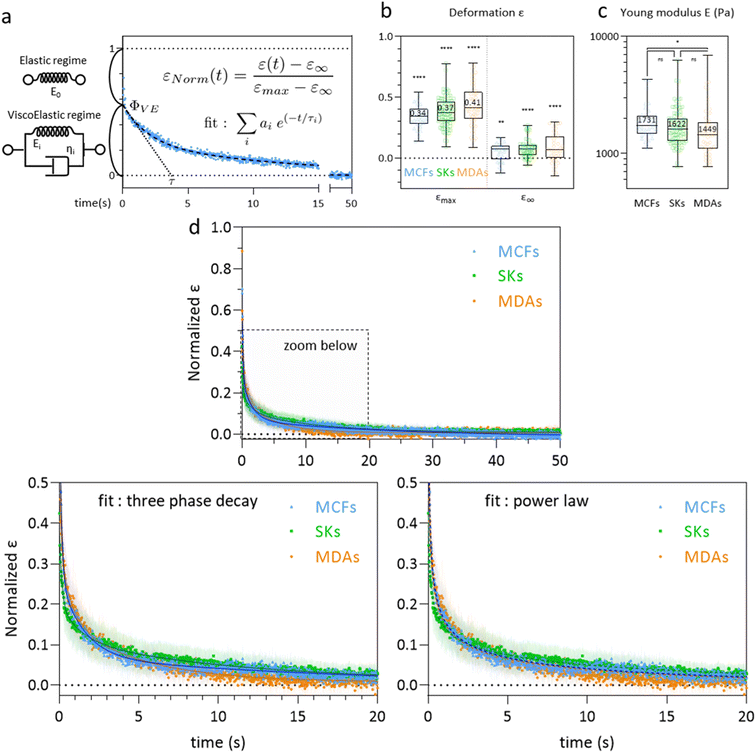Fig. 6 Recovery at the whole cell level. (a) The graph shows the time variation of the normalized deformation ε_Norm(t) = (ε(t) − ε_∞)/(ε_max− ε_∞) during recovery, which can be modeled by an instantaneous elastic regime, followed by a slower regime of total amplitude Φ₀. The latter can be described by a sum of Kelvin–Voigt elements of characteristic decay time τ_i. (b) Cell deformation measured in the constriction (ε_max, MCFs n = 36, SKs n = 85, MDAs n = 59) and after recovery (ε_∞, MCFs n = 30, SKs n = 56, MDAs n = 44). Statistical difference to ε₀ = 0 is shown. (c) Distribution of E_tot = E₀ + E_fast + E_medium + E_slow for the three cell lines. Statistical comparison between the cell lines is presented (MCFs n = 36, SKs n = 85, MDAs n = 59). (d) Mean normalized ε curves after exiting the constriction (taken as starting point t = 0). Bottom graphs display zoomed-in views over the first 20 seconds. Error bars represent the confidence interval at 95% (MCFs n = 25, SKs n = 51, MDAs n = 37). Fitting curves represent the three-phase decay (bottom left) or power law (bottom right) fits of the mean curves. Corresponding parameters (with confidence interval at 95%) are reported in Table 2.

Cells recover almost entirely from the deformation. Although recovery from the deformation induced in the constriction is almost complete, the mean values of ε_∞ show a small but significant difference with the initial value ε₀ = 0 (Fig. 6b). The observation may be attributed to cell plasticity, a behavior already reported after similar deformation under flow for SK-BR-3 and MDA-MB-231 cell lines.²² Assuming an elastic modulus of ≈1 kPa for the softer cells, the small pressure difference of 0.1 mbar across a trap (Fig. S2†) would result in a deformation of ≈1% through Hooke's law. The remaining pressure difference that cells undergo in the recovery chamber is thus not able to explain alone the magnitude of their residual deformation.

Cell recovery displays two regimes of different nature. As described previously in Fig. 6a, each cell recovery curve can be divided into an instantaneous recovery occurring in less than 20 ms, followed by a slower shape relaxation. This was observed for the three cell lines analyzed here (Fig. 6d). We want to emphasize here that the instantaneous recovery does not originate from an eventual flipping of the cell at the exit of the constriction which would anyway yield the same maximal elongation. Only a tilt of the cell over the height of the recovery chamber could affect this parameter. But a simple geometric calculation would then show that this would minimize ε_max by only around 10%. Finally, we performed experiments with isotropic square constrictions of similar section area to 6 × 15 μm² constrictions (i.e. 9 × 9 μm²) and observed again this instantaneous recovery (Fig. S8†).

At the whole cell level, the latter regime appears to be best described with a three-phase exponential decay equation (ESI† section 7 and Fig. S6 for a comparison with one-phase decay, two-phase decay and power law fits) corresponding to a viscoelastic behavior (Fig. 6a). The addition of more phase decays did not improve the quality of the fits, we thus chose to limit the fit to a sum of three exponential decays labelled fast, medium and slow. The general form of the equation thus becomes:

ε_Norm(t) = a_fast e^{(−t/τ_fast)} + a_medium e^{(−t/τ_medium)} + a_slow e^{(−t/τ_slow)}

with a_i as the amplitudes of the three exponential decays and τ_i (i = fast, medium, slow) as their characteristic times. The order of magnitude of about 100 ms obtained for the fast exponential decay for all cell lines (i.e. 110 ms for MCF-7, 113 ms for SK-BR-3 and 56 ms for MDA-MB-231 cells) has led us not to distinguish it from the recovery phase that takes place in less than 20 ms at the exit of the constriction, and to associate these two phases of recovery with an elastic regime. We then define Φ_VE = a_medium + a_slow as the fraction of the viscoelastic (VE) regime in the total recovery. Table 2 displays the results of these fits for each cell line.

Table 2 Parameters obtained from the three phase decay and power law fits of the cell recovery and deduced rheological parameters. Values represent median and [95% confidence intervals]

Three phase decay fit
	MCF-7	SK-BR-3	MDA-MB-231
a medium	20.4% [19.7–21.1]	9.49% [8.89–10.1]	20.3% [18.8–21.8]
τ medium	1.46 s [1.38–1.55]	1.23 s [1.11–1.38]	0.58 s [0.52–0.66
a slow	8.24% [8.04–8.44]	10.6% [10.3–10.9]	16.5% [15.8–17.2]
τ slow	24.0 s [21.6–27.0]	10.8 s [10.5–11.3]	4.68 s [4.49–4.87]
R ^2	0.968	0.977	0.962
Φ VE	28.6% [27.7–29.5]	20.1% [19.2–21.0]	36.8% [34.6–39.0]
E tot	1.76 kPa [1.57–1.96]	1.62 kPa [1.45–1.78]	1.45 kPa [1.19–1.62]
E elastic	1.26 kPa [1.12–1.40]	1.30 kPa [1.15–1.42]	0.92 kPa [0.75–1.03]
E viscoelastic	0.50 kPa [0.45–0.56]	0.33 kPa [0.29–0.36]	0.53 kPa [0.43–0.60]
η medium	0.53 kPa s [0.46–0.60]	0.19 kPa s [0.16–0.22]	0.17 kPa s [0.13–0.20]
η slow	3.48 kPa s [2.96–4.07]	1.87 kPa s [1.65–2.07]	1.12 kPa s [0.91–1.27]

---

Power law fit
	MCF-7	SK-BR-3	MDA-MB-231
n	0.35 [0.345–0.355]	0.18 [0.174–0.186]	0.33 [0.327–0.342]
R ^2	0.962	0.971	0.925

---

The graphs of Fig. 6d do not show striking differences between the cell lines. We however observe that the viscoelastic regime contributes more to the recovery in MDA-MB-231 cells (Φ_VE = 37% of the whole recovery compared to 29% and 20% for MCF-7 and SK-BR-3 cells, respectively), almost equally distributed along the medium and slow decay. The characteristic decay times are also lower in MDA-MB-231 indicating that MDA-MB-231 cells relax faster towards their equilibrium shape.

The power law fits (ESI† section 7 and Fig. 6d) overlap nicely with the three phase decay fits. They allow for an overall fit of the curves, without any distinction between elastic and viscoelastic regimes. The power law exponents obtained for each cell line are n_MCFs = 0.35, n_SKs = 0.18 and n_MDAs = 0.33 for MCF-7, SK-BR-3 cells and MDA-MB-231 cells, respectively. The lower value for SK-BR-3 cells reflects the lower contribution of the viscoelastic regime to the relaxation of SK-BR-3 cells, consistent with the lower value of Φ_VE in these cells.

To go deeper into the analysis of the whole cell recovery, we sought to deduce the rheological parameters of the three cell types. Assuming that in the constriction, cells experience a stress of magnitude ΔP ≈ 6 mbar, Hooke's law leads to the relation ΔP ≈ E_totε_max where E_tot = E₀ + E_fast + E_medium + E_slow and ε_max is the maximal longitudinal deformation. Though it was defined ad hoc for elastic materials only, we'll use it here to give an approximation of the apparent Young modulus E_tot of our viscoelastic cells. Fig. 6c shows a trend in the distributions of E_tot: MCF-7 cells have the highest median value and MDA-MB-231 the lowest, all of the order of 1 kPa and not significantly different from each other. From the value of E_tot, we could deduce the values of the Young modulus associated with the elastic and viscoelastic regimes (i.e. E_elastic = E₀ + E_fast and E_viscoelastic = E_medium + E_slow, see Table 2). The elastic regime (values of the Young modulus of the order of 1 kPa) is the most discriminant between cell types in terms of Young modulus, with again MDA-MB-231 cells showing the lowest values. Oppositely, E_viscoelastic is similar for the three cell lines and of the order of a few hundred Pa, i.e. much lower than E_elastic except for MDA-MB-231 cells.

More generally, the cell viscosity in recovery can reach very large values, in particular for the slowest decay η_slow (i.e. 3.48 kPa s for MCF-7 cells). Strikingly, MDA-MB-231 cells exhibit the lowest viscosity, the lowest recovery elastic modulus and the lowest relaxation times among the three cell lines, which underlines their relatively high deformability, as expected from their mesenchymal phenotype and their higher metastatic potential.

Role of the cell cortex integrity in shape recovery

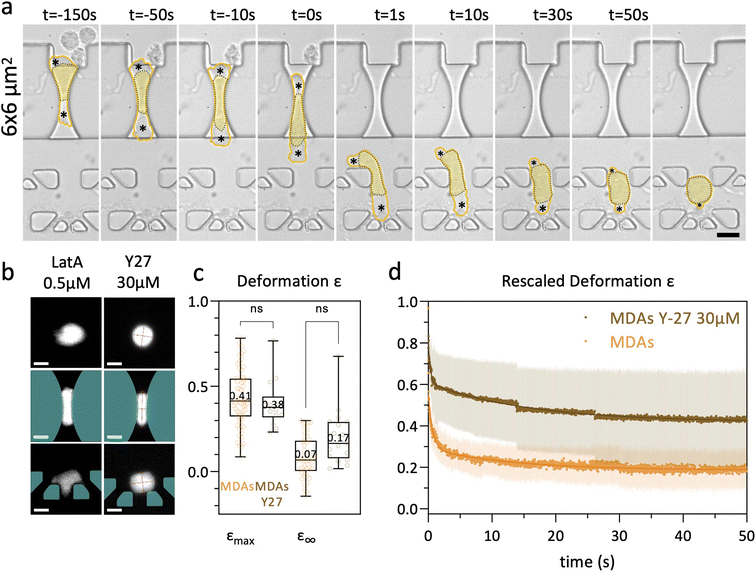
The results shown so far have been obtained under moderate deformation, with no detectable cell damage such as blebbing of the plasma membrane. We focus here on the role played by the cell actomyosin cortex underlying the plasma membrane during the elastic recovery highlighted in the previous sections. We address this through mechanical and pharmacological perturbations of the actomyosin cortex. As all cells display an elastic regime, with no striking differences between cell types, we choose to perform these experiments on the MDA-MB-231 cell line.

The occurrence of membrane blebs in a large deformation regime suppresses the elastic recovery regime. To induce larger cell deformation, we used constrictions with a 6 × 6 μm² square cross-section. The higher mechanical constraints induced membrane blebbing (Fig. 7a), suggesting that the deformation here is strong enough to disrupt the attachment of the cell cortex to the membrane. In the first set of experiments, we observed the presence of membrane blebs in 43 out of the 51 cells (84%) recorded going through the 6 × 6 μm² square constriction. Cells which did not present blebs were among the smallest cells observed. Strikingly, the elastic recovery regime was lost under these conditions. Instead, we observe a slow healing of blebs, compatible with the timescale of a few minutes associated with bleb retraction.⁴⁸

Fig. 7 Role of the actin cytoskeleton and actomyosin contractility in cell shape recovery following large deformation. (a) Images of a MDA-MB-231 cell through a square 6 × 6 μm² constriction (scale bar = 20 μm). The overall contour of the cell is delimited in yellow and encompasses the area of membrane blebs (*) located beyond the dark dotted line. (b) Representative images of cells treated with either 0.5 μM latrunculin A or 30 μM Y-27632 (scale bar = 10 μm). (c) Cell deformation measured in the constriction (ε_max, MDAs Y-27 n = 14, non-treated MDAs n = 59) and after recovery (ε_∞, MDAs Y-27 n = 17, non-treated MDAs n = 44). Data were statistically different to ε₀ = 0 (not shown, with at least ***). (d) Mean rescaled ε curves after exiting the constriction (taken as starting point t = 0). Error bars represent the confidence interval at 95% (MDAs Y-27 n = 14, non-treated MDAs n = 34).

Actin depolymerization prevents cell recovery. To further investigate the role of the cell cortex integrity in elastic recovery, we applied pharmacological perturbation on the cell cortex to depolymerize actin or impair cell cortex contractility.

MDA-MB-231 cells were treated with 0.5 μM latrunculin A (LatA) for 30 min. This concentration induces partial F-actin depolymerization on adherent MDA-MB-231 cells (ESI† section 8 and Fig. S7), in agreement with other studies.⁴⁹ LatA treated cells display a shorter arrest time (median 300 ms, i.e. less than half the median value observed under the control conditions, see Fig. S9†), thus supporting the role of the actin cytoskeleton in the resistance to deformation. Then, instead of progressively recovering their initial disc-shaped appearance into the nest, LatA treated cells tend to spread between trap structures, adopting indented shapes (see Fig. 7b). This prevented us to perform elliptical fits, and hence to compute recovery curves. This observation highlights the need for an intact actin cytoskeleton to observe recovery following induced deformation.

Myosin II inhibition leads to partial recovery. We next explored whether contractility was required using the ROCK inhibitor Y-27632 (Y-27). MDA-MB-231 cells were treated with 30 μM Y-27632 for 30 min. These conditions are associated with an increase in the spreading area of cells (see Fig. S7†), which suggests significant inhibition of actomyosin activity, as expected in this range of concentrations.⁵⁰

Even though maximal deformation levels were similar, the remaining deformation ε_∞ was higher for Y-27 treated cells (though not significant) compared to the control conditions. Y-27 treated cells kept an elongation of 0.17, against 0.07 for non-treated cells (Fig. 7c). The higher residual deformation observed in Y-27 treated cells suggests that actomyosin contractility participates in cell shape recovery.

To highlight long-term differences in the recovery, we define the rescaled deformation as:

The mean recovery curves are shown in Fig. 7d for treated and control cells. Both curves are composed of a first elastic regime followed by a viscoelastic regime, but Y-27 treated cells display lower and incomplete recovery. A three-phase exponential decay fit, as presented previously, yields a slow characteristic time of τ_slow = 9.91 s for Y-27 treated cells, emphasizing a slower viscoelastic recovery than that observed for non-treated MDA-MB-231 cells (τ_slow = 4.68 s).

Discussion and conclusion

The present study demonstrates the ability of a custom-made device, including constricted micro-channels and single cell traps placed in a flow-free recovery chamber, to study the morphological recovery of cells after fast deformation under flow. Using this device, we obtained new insights into the morphological adaptation of cancer cells to mechanical stressors and physical constraints such as those encountered in blood circulation. Most of our study was performed using a constriction geometry leading to significant cell deformation of about 40% but without observable disruption of the attachment of the cell cortex to the plasma membrane.

Even if the principle of the operating mode of the Pachinko device is simple, obtaining the recovery mechanical parameters of cells meets several challenges. We first need to image individual cells during their entire journey from the inlet to the traps, i.e. before entering the constriction, inside the constriction, and within a trap after their escape from the constriction. These multiple requirements are particularly challenging as many events can occur to lead us to discard a cell: first the cell must not flow too rapidly (leading to a blurred image in the main channel, or to an arrest time below our framerate in the constrictions), it should not be attached to another cell before and within the constriction, and finally the cell must recover in an empty trap that should remain as such for 50 s while many other cells continue to flow into our device. We estimate that less than 30% of cells are exploitable. On top of that, the track's reconstruction, segmentation and fitting procedure require manual reviewing and adjustments (e.g. of initial fitting parameters) when necessary, as mentioned in the dedicated Materials and methods sub-sections. This is why this system could be qualified as moderate-throughput, which is nevertheless sufficient to obtain about 10–15 exploitable cells per experiment, which typically lasts around 1 hour.

We have shown that MCF-7, SK-BR-3 and MDA-MB-231 breast cancer cells mostly recover their spherical shape after deformation, with residual deformation more pronounced in SK-BR-3 and MDA-MB-231 as compared to MCF-7 cells. Let's note that plastic deformation has also been reported in breast cancer lines after deformation,²⁴ and was associated with cytoskeletal damage accumulation particularly in high metastatic potential cancer cells. Strikingly, the major part of this recovery takes place within 100 ms. It is followed by a slower recovery regime, well described by a two exponential decay expressing the visco-elastic behavior of cells on a time scale of tens of seconds. The order of magnitude of the speed of circulating blood cells of about 1 mm s⁻¹ (ref. 51) would result in a full recovery length in the centimeter range. Such a slow recovery might avoid repetitive, large amplitude cycles of deformation–relaxation for cells encountering successive capillary constrictions, while the elastic-like relaxation occurring on much shorter lengths would, in contrast, relax partly and almost instantaneously the cell strain. Both effects might contribute to protecting cells during their transit in the circulation.

Our main finding is that cell recovery relies on the presence of actin filaments as well as on the integrity of the actomyosin cortex lining the inside of the plasma membrane. We indeed found that (i) depolymerizing F-actin filaments using latrunculin A suppresses the process of recovery itself, leading to plastic cell behavior, and (ii) inhibition of the myosin light chain phosphorylation using the ROCK inhibitor Y-27632 limits the amplitude of the elastic regime, restraining in turn the amplitude of the total recovery. Our observations are in line with evidence that the elastic modulus dominates over the viscous modulus at high frequency⁵² due to cortical tension. The actomyosin cortex, an active gel responsible for the most part of the tension of the cell envelope,⁵³ ensures the storage and relaxation of elastic energy.^32,54 We thus cannot totally exclude the contribution of active mechanisms in the regime of elastic recovery. Similarly, and although the passive viscous properties of the cytoplasm⁵⁵ and of the entangled cytoskeleton⁵⁶ alone could account for the post-elastic regime of recovery, we cannot rule out from our experiments an active contribution of the cell cortex in the viscoelastic recovery regime of amplitude Φ_VE.

The approach followed in this study has considered cell recovery independent of their prior deformation. A more elaborate analysis could however consider the entirety of the cell history (deformation and recovery), similar to the work of Bonakdar et al.⁵⁷ The time constants of the viscoelastic regimes are much higher in recovery than in deformation. These differences might be interpreted by considering the role of the nucleus, whose diameter is larger than the smallest size of our constrictions. The nucleus is expected to resist deformation in the constrictions, while it should interfere less with cell recovery. It would be interesting in future studies to monitor the deformation and recovery of isolated nuclei, enucleated cells and nuclei in their natural cellular environment. However, beyond these differences, MDA-MB-231 cells are, among the three cell lines, softer and the most fluid-like in both deformation and recovery.^58,59 An increase in softness is a recognized signature of tumorigenesis,^12,43 and a fluid-like behavior might be an asset for survival in the circulation, enhancing the probability of the occurrence of metastasis.⁶⁰ Our study deals with originally adherent cells which we have detached from their substrate and suspended to mimic the behavior of circulating tumor cells. It has been reported that suspended cells display significant differences regarding elasticity,⁶¹ myosin II activity⁶² and the lamin A/C post-transcriptional level⁶³ as compared to their adherent counterparts. In line with these results, we have established that the level of p-MLC (phosphomyosin II light chain) in our 3 breast cell lines was lower in suspended cells, which seems to indicate a decrease in their contractility (Fig. S10†).

A remaining open question is that of a possible change in volume of cells in the regime of fast deformation studied here. Some recent results obtained on volume monitoring by the fluorescence exclusion method (FXm) on a time scale of tens of milliseconds suggest that cells can reduce their volume on these time scales (see Fig. 7G of Venkova et al.⁵⁰). This volume loss is associated with an increase in membrane tension as well as with the loss of water and small solutes. The recovery rate expected from volume loss is on the order of minutes,⁵⁰i.e. well beyond the recovery characteristic times measured in the present study. However, volume loss could contribute also to shorter timescales in both deformation and recovery by e.g. reducing the cell apparent modulus. Further technological developments would be necessary to address the important question of suspended cell volume adaptation to fast deformation and release.

Overall, our work gives new insights not only into flow-induced deformation of suspended cells but also into their shape recovery, which are both critical cellular events during the journey of CTCs in blood circulation. A natural extension of our work, which would initially avoid the challenges raised by the rarity of CTCs among an overwhelming quantity of surrounding normal blood cells requiring advanced sorting techniques,⁶⁴ will be to flow CTC cell lines⁶⁵ into our Pachinko device.

Materials and methods

Photolithography

The microfluidic device layout was etched on a photosensitive resin-coated chrome-glass substrate (Nanofilm) following standard techniques to obtain the adequate mask of the device. A thin 15 μm layer of negative photoresist SU-8 (SU-82015, Kayaku Advanced Materials) was spin-coated on a silicium wafer (3000 g, 30 s), baked rapidly (3 min, 90 °C), and then exposed through the chrome mask (140 mJ cm⁻²). The wafer was baked (4 min, 90 °C), developed in PGMEA to dissolve unexposed resin, and then baked once more at 200 °C. The exact height of the device was measured with a mechanical profilometer (Dektam 6 M profilometer, Veeco). The wafer surface was rendered hydrophobic by silanization under vacuum with (tridecafluoro-1,1,2,2-tetrahydrooctyl)trichlorosilane (AB111444, abcr) after activation via plasma cleaning.

Soft lithography and microfluidic chip coating

PDMS mix (10 : 1 base : curing agent, Sylgard 184, Dow Corning) was prepared, degassed, and poured over the resin structures of the silanized silicium wafer (height ≈ 5 mm). PDMS was degassed under vacuum for 15 min so that it perfectly matches the resin structures, and then cured at 70 °C for 3 h. PDMS was removed from the wafer mold, and individual chips were cut apart. Inlets and outlets were punched out at a 1.5 mm diameter. PDMS was cleaned using 70% ethanol and isopropanol, and then dried with a nitrogen air gun. PDMS chips and fluorodishes were plasma-cleaned and then immediately bonded together to seal the microfluidic chip. On the day of the experiment, microfluidic chips were washed with 70% ethanol and then PBS, then passivated by injecting 100 μL of 1 mg mL⁻¹ solution of pLL-PEG (pLL(20)-g[3.5]-PEG(5), Susos) for 30 min, and then rinsed with PBS.

Numerical simulations

Simulations were performed using the Microfluidics module of COMSOL Multiphysics 5.5. The device geometry was imported and meshed finely (minimal element size 0.172 μm, Fig. S2†). The Navier–Stokes equation was applied to simulate fluid behaviour in the microfluidic chip. Laminar flow was assessed due to the characteristic dimensions of the system. Channel height was taken into consideration using the shallow channel approximation of the laminar flow module. Pressure and velocity field distributions were exported to confirm the hypothesis that the pressure drop is located at the constrictions (see Fig. 1e and S2 and S3†).

Cell culture

All three MDA-MB-231, SK-BR-3 and MCF-7 cell lines were cultured in Dulbecco's modified Eagle medium (DMEM GlutaMax, ThermoFisher 10566016), supplemented with 10% of fetal bovine serum (FBS, Gibco 10 270–106) and 1% of penicillin–streptomycin (10 000 U ml⁻¹ penicillin, 10 000 μg mL⁻¹ streptomycin, Gibco 151140-122). The cells were maintained in growth-enhanced treated culture flasks at 37 °C under a 5% CO₂ atmosphere. The cells were passaged routinely before reaching confluency, and media were renewed every couple of days.

Cell staining and treatments

The cells were plated in a 6-well plate so that they reach 70–90% confluency on the day of the experiment. The culture medium was removed and replaced with 1 mL of 20 μg mL⁻¹ lipophilic tracer DIL (1,1′-dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate, ThermoFisher D3911) dissolved in culture medium, and left to incubate for 1 hour at 37 °C. Alternatively, cells were stained with 5 μM calcein AM (Invitrogen C3099) in culture medium for 30 min at 37 °C. The dye containing medium was removed and the cells were washed with 1 mL PBS before being harvested with 500 μL trypsin (Gibco 12 605) for 5 min at 37 °C. The cell suspension was spun at 500g for 5 min, and then resuspended at ≈400 000 cells per mL in serum-free DMEM supplemented with 25 mM HEPES (Sigma H0887)) and 2000 U mL⁻¹ DNAse (Sigma D4513).

Optionally, either 30 μM Y-27632 (Tocris 1254) or 0.5 μM latrunculin A (Sigma L5163) was added to the preparation. The cells were left to incubate for 30 min at 37 °C before being injected into the microfluidic Pachinko device.

Cell injection in the Pachinko device

The cell suspension was placed in an Eppendorf tube mounted with a p-cap (Fluigent) connected to inlet 1 of the microfluidic chip through a fluidic tube (ID 0.02 in, OD 0.06 in, Tygon ND-100-80, Cole-Parmer). Outlets 2 & 3 were connected to Eppendorf tubes containing experiment media without cells. The cell suspension and medium were kept at 37 °C on a hot plate for the whole duration of the experiment. Inlet 1 and outlet 2 pressure values were set to 12 and 8 mbar, respectively, to initiate a flux of cells in the device main channel. The pressure in outlet 3 was initially kept at 10 mbar to prevent cells from entering constrictions and then decreased to 0 mbar to allow cells to enter (Fig. 1a).

Acquisition

Cell fluorescence as the cell moves through the device was recorded through a 10× objective on an inverted microscope mounted with a CMOS camera (acA1920-150um Basler AG, pixel size 4.8 μm × 4.8 μm) to record. Stained cells were acquired at 50 Hz with 5 ms exposure for at least 50 s. Exposure times and frame rates were adjusted to maximize the contrast of the fluorescent object while minimizing the blur due to cell motion at high speed through the device. The framerate was increased as much as possible within the limits of the camera to achieve the highest temporal resolution possible for each fluorescent marker, i.e. 20 ms for whole cell fluorescence.

Cell trajectory reconstruction

Sequences of the fluorescent cell or nucleus moving through the device were binned using ImageJ. Cell tracks were reconstructed using the TrackMate plugin in ImageJ⁶⁶ (see an example in Fig. 2a). Briefly, cells were detected with a threshold based method, and then the detected spots were linked in each successive image (linear motion LAP tracker) to reconstruct tracks. The parameters of the detection and tracking algorithms were adjusted to each sequence. Tracks were manually reviewed and corrected for punctual errors in track reconstruction. Track coordinates were exported to Matlab (R2020a, MathWorks) for downstream analysis.

Cell arrest time determination

Only complete tracks (i.e. with images before and after deformation in the constriction) were selected for the analysis. Entry and exit time points were defined as the index of the first image where the cell y-position exceeds respectively the constriction entry and exit y-coordinate. The arrest time of a cell was determined as the elapsed time between the entry and exit time points. For the fastest cells which can cross the constriction in less than 1 frame, we attribute to these cells an arrest time corresponding to the inverse of the acquisition frame rate, i.e. 20 ms.

Image analysis and segmentation

For each cell track, for each time point in the cell track, a region of interest around the cell position was drawn in the original images. The selected section of the image was binarized: DIL-stained membrane images were segmented with 2 thresholds calculated using Otsu's method, to account for fluorescence intensity heterogeneity in the cell. Non-background layers were merged together to recreate the cell binarized region. Images were filtered to keep the biggest structure in the image. The major and minor axes of the ellipse that have the same normalized second central moments as the binarized region were measured (see an example in Fig. 2b).

Cell parameter extraction

The diameter of the cell can be estimated by measuring the average area of the shape in the main channel assuming that the 2D projection of the cell is a circle through the relation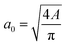 between the cell diameter a₀ and the binarized region area A. The elongation ε and aspect ratio AR of the cell or nucleus were defined with the major axis a and the minor axis length b as and where a₀ is the average value of the diameter measured in the main channel.

Maximal ε_max and end value ε_∞ were determined for each cell using the Matlab Cftool application interface and used to compute the normalized deformation 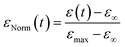. Incomplete and blurry images were manually excluded from the analysis based on visual examination of corresponding images.

Contour plots

Contour and density plots were generated for each cell line data set using Python gaussian kernel density estimation. For better visualisation, one density level was overlaid in scatter plots to indicate the region of highest point density. The Kernel density plot for each parameter was added on the right and on top of the graph to represent this parameter distribution.

Mean recovery curves and fits

For each cell, normalized elongation values of the cell during recovery were imported into GraphPad Prism9 software (GraphPad Software Inc., USA) (with time t = 0 s taken as the last image of the cell in the constriction). For each cell line, mean curves and the corresponding 95% confidence interval were plotted. These mean curves were used to fit according to the developed models described in the text and in ESI† section 7.

Statistical analysis

All statistical evaluations were conducted using the GraphPad Prism9 software (GraphPad Software Inc., USA). Independent groups were compared using the non-parametric Mann–Whitney test (arrest times, diameters, Young modulus), or Wilcoxon matched-pairs rank test in the case of paired data (ε_maxvs. ε_∞). Significance is reported as follows: *: p ≤ 0.05, **^:p ≤ 0.005, ***^:p ≤ 0.005, ****^:p ≤ 0.001.

Western blotting

Cells were collected, lysed with RIPA buffer (RIPA lysis and extraction buffer, Thermo Fisher Scientific) supplemented with protease and phosphatase inhibitor cocktail (Halt™ protease and phosphatase inhibitor cocktail (100×), Thermo Fisher Scientific) and EDTA solution (0.5 M EDTA (100×), Thermo Fisher Scientific), incubated on ice for 5 min, passed through a 1 mL syringe (Terumo) with a 25G needle (Terumo) ten times, incubated on ice for another 5 min and centrifuged at 16 000g for 5 min at 4 °C. Equal amounts of the supernatant were then mixed with 2× Laemmli sample buffer (Sigma) and boiled at 95 °C for 10 min. Proteins were then separated using sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE, 4–12% bis-Tris gel, Life Technologies) and transferred onto a nitrocellulose membrane using the dry transfer Trans-blot Turbo transfer system (BioRad). Membranes were blocked with 5% BSA (Euromedex) in tris-buffered saline (Interchim) containing 0.1% Tween (Sigma) (TBS-Tween) for 1 h at room temperature, after which primary antibodies diluted in TBS-Tween 5% BSA were added for overnight incubation at 4 °C. The membranes were subsequently washed in TBS-Tween after which secondary horseradish peroxidase (HRP) conjugated antibodies were added to 5% BSA in TBS-Tween and incubated for 2 h at room temperature. After extensive washing in TBS-Tween, the SuperSignal West Pico PLUS (Thermo Fisher Scientific) reagent was used and the chemiluminescence signal was recorded on a ChemiDoc Touch 2 imager (BioRad). The primary antibodies used for p-MLC2 detection were phospho-myosin light chain 2 (Thr18/Ser19) (polyclonal rabbit, Cell Signaling, #3674S), and for GAPDH – GAPDH (14C10) (monoclonal rabbit, Cell Signaling, #2118S). The secondary antibodies used were goat anti-rabbit IgG (H + L), HRP (polyclonal goat, Invitrogen, #65-6120).

Data availability

The data supporting this article have been included as part of the ESI† (S12–S14).

Author contributions

J.-L. V., H. C., K. T. and C. V. conceived the principle of the presented device. K. T. produced a set of preliminary experiments that form the basis of this paper. E. G. performed all experiments and analyzed the data, helped by E. S. and N. A. E. G. set up the mathematical modeling and conceptual framework of data analysis, while C. V., J.-B. M. and M. P. provided critical feedback. K. V. provided support to E. G. and N. A. regarding pharmacological experiments, immunostaining and immunoblotting. E. G. and C. V. wrote the manuscript. All authors discussed the results and contributed to the final manuscript. C. V. supervised the project and the findings of this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work benefited from the technical contribution of the joint service unit CNRS UAR 3750. The authors would like to thank the engineers of this unit for their advice during the development of the experiments. This work was supported by the European Research Council Advanced Grant 321107 “CellO”, the Institut Pierre-Gilles de Gennes (“Investissements d'avenir” program ANR-10-IDEX-0001-02 PSL and ANR-10-LABX-31, and ANR-10-EQPX-34), the ITMO Cancer PCSI 2020 program (grant number 20CP101-00), the ITMO Cancer PCSI 2022 program (grant number 22CP073), the JST FOREST Program (grant number JPMJFR212D) and “Ligue Contre le Cancer” for the 4th year PhD funding of Emile Gasser.

Notes and references

1. S. Valastyan and R. A. Weinberg, Cell, 2011, 147, 275–292.
2. V. Gensbittel, M. Kräter, S. Harlepp, I. Busnelli, J. Guck and J. G. Goetz, Dev. Cell, 2021, 56, 164–179.
3. G. P. de Freitas Nader, S. Agüera-Gonzalez, F. Routet, M. Gratia, M. Maurin, V. Cancila, C. Cadart, A. Palamidessi, R. N. Ramos and M. San Roman, et al. , Cell, 2021, 184, 5230–5246.
4. J. Perea Paizal, S. H. Au and C. Bakal, Br. J. Cancer, 2021, 124, 58–65.
5. B. L. Krog and M. D. Henry, Biomechanics in Oncology, 2018, pp. 209–233.
6. A. Labernadie and X. Trepat, Curr. Opin. Cell Biol., 2018, 54, 57–65.
7. S. Ma, A. Fu, G. G. Y. Chiew and K. Q. Luo, Cancer Lett., 2017, 388, 239–248.
8. S. Ma, A. Fu, S. Lim, G. G. Y. Chiew and K. Q. Luo, Free Radical Biol. Med., 2018, 129, 46–58.
9. Y. Xin, K. Li, M. Yang and Y. Tan, Int. J. Mol. Sci., 2020, 21, 8115.
10. K. F. Fuh, R. D. Shepherd, J. S. Withell, B. K. Kooistra and K. D. Rinker, Breast Cancer Res., 2021, 23, 1–17.
11. S. K. Dash, B. Patra, V. Sharma, S. K. Das and R. S. Verma, Lab Chip, 2022, 2200–2211.
12. J. Lv, Y. Liu, F. Cheng, J. Li, Y. Zhou, T. Zhang, N. Zhou, C. Li, Z. Wang and L. Ma, et al. , EMBO J., 2021, 40, e106123.
13. I. MacDonald, S. Aharinejad, E. Schmidt and A. Groom, Microvasc. Res., 1995, 49, 64–77.
14. L. Ding, M. Sunamura, T. Kodama, J. Yamauchi, D. Duda, H. Shimamura, K. Shibuya, K. Takeda and S. Matsuno, Br. J. Cancer, 2001, 85, 431–438.
15. A. S. Azevedo, G. Follain, S. Patthabhiraman, S. Harlepp and J. G. Goetz, Cell Adhes. Migr., 2015, 9, 345–356.
16. P. Vargas, E. Terriac, A.-M. Lennon-Duménil and M. Piel, J. Visualized Exp., 2014, e51099.
17. P. M. Davidson, J. Sliz, P. Isermann, C. Denais and J. Lammerding, Integr. Biol., 2015, 7, 1534–1546.
18. P. Preira, T. Leoni, M.-P. Valignat, A. Lellouch, P. Robert, J.-M. Forel, L. Papazian, G. Dumenil, P. Bongrand and O. Théodoly, Int. J. Nanotechnol., 2012, 9, 529–547.
19. S. H. Au, B. D. Storey, J. C. Moore, Q. Tang, Y.-L. Chen, S. Javaid, A. F. Sarioglu, R. Sullivan, M. W. Madden, R. O'Keefe, D. A. Haber, S. Maheswaran, D. M. Langenau, S. L. Stott and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4947–4952.
20. B. Nath, A. Raza, V. Sethi, A. Dalal, S. S. Ghosh and G. Biswas, Sci. Rep., 2018, 8, 1–10.
21. H. Chen, J. Guo, F. Bian and Y. Zhao, Smart Med., 2022, 1, e20220001.
22. H. A. Cognart, J.-L. Viovy and C. Villard, Sci. Rep., 2020, 10, 1–14.
23. N. Kamyabi, Z. S. Khan and S. A. Vanapalli, Cell. Mol. Bioeng., 2017, 10, 563–576.
24. Z. Yan, X. Xia, W. C. Cho, D. W. Au, X. Shao, C. Fang, Y. Tian and Y. Lin, Adv. Healthcare Mater., 2022, 11, 2101657.
25. C. M. Peppiatt, C. Howarth, P. Mobbs and D. Attwell, Nature, 2006, 443, 700–704.
26. S. Grubb, C. Cai, B. O. Hald, L. Khennouf, R. P. Murmu, A. G. Jensen, J. Fordsmann, S. Zambach and M. Lauritzen, Nat. Commun., 2020, 11, 1–12.
27. X. Wang, M. Hossain, A. Bogoslowski, P. Kubes and D. Irimia, Nat. Commun., 2020, 11, 1–12.
28. B. Müller, S. Lang, M. Dominietto, M. Rudin, G. Schulz, H. Deyhle, M. Germann, F. Pfeiffer, C. David and T. Weitkamp, Developments in X-ray Tomography VI, 2008, pp. 89–98.
29. K. Terao, M. Gel, A. Okonogi, A. Fuke, T. Okitsu, T. Tada, T. Suzuki, S. Nagamatsu, M. Washizu and H. Kotera, Sci. Rep., 2014, 4, 4123.
30. G. Follain, N. Osmani, A. S. Azevedo, G. Allio, L. Mercier, M. A. Karreman, G. Solecki, M. J. G. Leòn, O. Lefebvre and N. Fekonja, et al. , Dev. Cell, 2018, 45, 33–52.
31. E. Evans and A. Yeung, Biophys. J., 1989, 56, 151–160.
32. J. Dupire, P. H. Puech, E. Helfer and A. Viallat, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14798–14804.
33. K. Tsujita, R. Satow, S. Asada, Y. Nakamura, L. Arnes, K. Sako, Y. Fujita, K. Fukami and T. Itoh, Nat. Commun., 2021, 12, 5930.
34. D. G. Hicks and S. Kulkarni, Am. J. Clin. Pathol., 2008, 129, 263–273.
35. X. Dai, H. Cheng, Z. Bai and J. Li, J. Cancer, 2017, 8, 3131–3141.
36. S. Byun, S. Son, D. Amodei, N. Cermak, J. Shaw, J. H. Kang, V. C. Hecht, M. M. Winslow, T. Jacks, P. Mallick and S. R. Manalis, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 7580–7585.
37. H. W. Hou, Q. S. Li, G. Y. H. Lee, A. P. Kumar, C. N. Ong and C. T. Lim, Biomed. Microdevices, 2009, 11, 557–564.
38. C. Jebane, A.-A. Varlet, M. Karnat, L. M. Hernandez-Cedillo, A. Lecchi, F. Bedu, C. Desgrouas, C. Vigouroux, M.-C. Vantyghem and A. Viallat, iScience, 2023, 26, 107714.
39. M. Urbanska, H. E. Muñoz, J. Shaw Bagnall, O. Otto, S. R. Manalis, D. Di Carlo and J. Guck, Nat. Methods, 2020, 17, 587–593.
40. L. Pang, S. Shen, C. Ma, T. Ma, R. Zhang, C. Tian, L. Zhao, W. Liu and J. Wang, Analyst, 2015, 140, 7335–7346.
41. Y.-N. Chang, Y. Liang, W. Gu, J. Wang, Y. Qin, K. Chen, J. Li, X. Bai, J. Zhang and G. Xing, ACS Omega, 2019, 4, 8318–8323.
42. Y. Feng, H. Chai, W. He, F. Liang, Z. Cheng and W. Wang, Small Methods, 2022, 6, 2200325.
43. C. Alibert, B. Goud and J. B. Manneville, Biol. Cell, 2017, 109, 167–189.
44. P. M. Davidson, G. R. Fedorchak, S. Mondésert-Deveraux, E. S. Bell, P. Isermann, D. Aubry, R. Allena and J. Lammerding, Lab Chip, 2019, 19, 3652–3663.
45. S. Hu, R. Wang, C. M. Tsang, S. W. Tsao, D. Sun and R. H. Lam, RSC Adv., 2018, 8, 1030–1038.
46. A. Bonfanti, J. L. Kaplan, G. Charras and A. Kabla, Soft Matter, 2020, 16, 6002–6020.
47. N. Desprat, A. Richert, J. Simeon and A. Asnacios, Biophys. J., 2005, 88, 2224–2233.
48. G. T. Charras, M. Coughlin, T. J. Mitchison and L. Mahadevan, Biophys. J., 2008, 94, 1836–1853.
49. S. Kwon, S. Han and K. Kim, Oncol. Rep., 2023, 50, 200.
50. L. Venkova, A. S. Vishen, S. Lembo, N. Srivastava, B. Duchamp, A. Ruppel, A. Williart, S. Vassilopoulos, A. Deslys, J. M. Garcia Arcos, A. Diz-Muñoz, M. Balland, J. F. Joanny, D. Cuvelier, P. Sens and M. Piel, eLife, 2022, 11, 1–41.
51. U. Baran, L. Shi and R. K. Wang, J. Biophotonics, 2015, 8, 46–51.
52. K. Hosseini, A. Frenzel and E. Fischer-Friedrich, Biophys. J., 2021, 120, 3516–3526.
53. J. Prost, F. Jülicher and J.-F. Joanny, Nat. Phys., 2015, 11, 111–117.
54. A. X. Cartagena-Rivera, J. S. Logue, C. M. Waterman and R. S. Chadwick, Biophys. J., 2016, 110, 2528–2539.
55. M. I. Arjona, J. Najafi and N. Minc, Curr. Opin. Cell Biol., 2023, 85, 102278.
56. P. A. Pullarkat, P. A. Fernández and A. Ott, Phys. Rep., 2007, 449, 29–53.
57. N. Bonakdar, R. Gerum, M. Kuhn, M. SpÃűrrer, A. Lippert, W. Schneider, K. E. Aifantis and B. Fabry, Nat. Mater., 2016, 15, 1090–1094.
58. M. Tabatabaei, M. Tafazzoli-Shadpour and M. M. Khani, Biorheology, 2019, 56, 207–219.
59. J. Guck, S. Schinkinger, B. Lincoln, F. Wottawah, S. Ebert, M. Romeyke, D. Lenz, H. M. Erickson, R. Ananthakrishnan, D. Mitchell, J. Kas, S. Ulvick and C. Bilby, Biophys. J., 2005, 88, 3689–3698.
60. L. Hanin, J. Theor. Biol., 2023, 572, 111582.
61. Y. Nematbakhsh, K. T. Pang and C. T. Lim, Convergent Sci. Phys. Oncol., 2017, 3, 034003.
62. C. J. Chan, A. E. Ekpenyong, S. Golfier, W. Li, K. J. Chalut, O. Otto, J. Elgeti, J. Guck and F. Lautenschläger, Biophys. J., 2015, 108, 1856–1869.
63. X. Zhang and Y. Lv, Biochim. Biophys. Acta, Mol. Cell Res., 2017, 1864, 2272–2282.
64. M. S. Tretyakova, M. E. Menyailo, A. A. Schegoleva, U. A. Bokova, I. V. Larionova and E. V. Denisov, Int. J. Mol. Sci., 2022, 23, 15979.
65. Y. Shimada, T. Sudo, S. Akamatsu, T. Sunada, A. Myomoto, K. Okano and K. Shimizu, J. Pers. Med., 2022, 12, 666.
66. J.-Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S10, Table S1, and raw data files (ESI 12–14). See DOI: https://doi.org/10.1039/d4lc00246f

---