Toward 3D printed microfluidic artificial lungs for respiratory support

Abstract

Microfluidic artificial lungs (μALs) are a new class of membrane oxygenators. Compared to traditional hollow-fiber oxygenators, μALs closely mimic the alveolar microenvironment due to their size-scale and promise improved gas exchange efficiency, hemocompatibility, biomimetic blood flow networks, and physiologically relevant blood vessel pressures and shear stresses. Clinical translation of μALs has been stalled by restrictive microfabrication techniques that limit potential artificial lung geometries, overall device size, and throughput. To address these limitations, a high-resolution Asiga MAX X27 UV digital light processing (DLP) 3D printer and custom photopolymerizable polydimethylsiloxane (PDMS) resin were used to rapidly manufacture small-scale μALs via vat photopolymerization (VPP). Devices were designed in SOLIDWORKS with 500 blood channels and 252 gas channels, where gas and blood flow channels were oriented orthogonally and separated by membranes on the top and bottom, permitting two-sided gas exchange. Successful devices were post-processed to remove uncured resin from microchannels and assembled with external tubing in preparation for gas exchange performance testing with ovine whole blood. 3D printed channel dimensions were 172 μm-tall × 320 μm-wide, with 62 μm-thick membranes and 124 μm-wide support columns. Measured outlet blood oxygen saturation (SO₂) agreed with theoretical models and rated flow of the device was 1 mL min⁻¹. Blood side pressure drop was 1.58 mmHg at rated flow. This work presents the highest density of 3D printed microchannels in a single device, one of the highest CO₂ transfer efficiencies of any artificial lung to date, and a promising approach to translate μALs one step closer to the clinic.

---

Introduction

Clinical artificial lungs, known as hollow-fiber oxygenators, are utilized in thousands of extracorporeal membrane oxygenation (ECMO) and cardiopulmonary bypass (CPB) cases per year. From 2018–2022 there were 97 881 ECMO cases registered with the Extracorporeal Life Support Organization (ELSO)¹ and in 2021 alone, upwards of 200 000 CPB cases were reported by the Society of Thoracic Surgeons Adult Cardiac Surgery Database.²

Current artificial lungs are restricted to critical care settings and require constant monitoring by a large, specialized team of personnel due to high risks and complications with extracorporeal circuits.^3,4 Bleeding and coagulation, which could lead to embolism or device failure, are the most common hurdles with extracorporeal life support systems.⁵ These risks stem from hemocompatibility challenges with the hollow-fiber oxygenators used in the clinic.^3,4 During oxygenation, the blood traverses a dense bundle of gas-permeable hollow fibers, experiencing non-physiological flow paths and shear stresses, triggering the blood coagulation cascade and inflammatory responses in the patient.^4,6,7

Further, this design has suboptimal gas exchange relative to the native lungs. In the alveolar microenvironment where oxygenation occurs, capillaries are about 10 μm across and their cell walls are around 1–3 μm thick.⁴ Membranes of commercial hollow-fiber lungs are an order of magnitude higher, varying from 25–50 μm depending on the device.^4,8 The blood flow path between adjacent fibers is hundreds of microns, resulting in large diffusion distances that restrict gas exchange efficiency and relies on passive mixing to achieve relevant oxygenation.^4,7,9,10

To address these limitations, microfluidic artificial lungs (μALs) are designed with features on the size and scale of the alveolar capillaries.^8,9,11 Relative to traditional hollow-fiber oxygenators, fabricating microfluidic devices that can better mimic the complex microenvironment of the natural lung promises improvements in gas exchange efficiency, hemocompatibility, biomimetic blood flow networks, physiologically relevant blood vessel pressures and shear stresses, as well as portability.^4,10,12 Research groups have demonstrated the advantages of applying microfluidic approaches to construct membrane oxygenators,^13–16 but clinical translation of these approaches is impeded by current microfabrication techniques.

Soft lithography is the most common approach for fabrication of microfluidic devices, and has historically favored polydimethylsiloxane (PDMS) for its sub-micron fidelity when casted in a mold.^17–19 However, this process is slow and laborious, limiting device throughput. Various other planar methods have been used to fabricate microfluidics such as glass etching and micromilling, but like soft lithography, confine device designs to the XY plane.²⁰ To achieve clinically relevant blood flows, these geometrically constrained μALs must be scaled-up by stacking or combining tens to thousands of devices with tubing and connections, increasing blood priming volumes (filling volume), and potentially decreasing hemocompatibilty.^10,16,21,22 Maintaining low pressure drops is a also a challenge which restricts the size of these planar, 2D μALs and requires many devices to be assembled together to increase flow rate.¹⁰

The rapid growth of the 3D printing industry and development of higher-resolution systems and materials has enabled successful fabrication of microfluidics.^23–27 UV light based vat photopolymerization (UV-VPP) 3D printing via digital light processing (DLP) alleviates the challenges associated with traditional, planar microfabrication. It is also preferred over other extrusion-based 3D printing approaches due to its high resolution, part fidelity, open material systems, fast printing speeds, and larger build volumes.^25,28,29

PDMS is favored for the fabrication of μALs because of its gas permeability to O₂ and CO₂, elasticity, optical clarity, chemical inertness,¹⁹ and prevention of blood plasma leakage.⁹ Currently, there is not a commercially available PDMS-based resin that is capable of 3D printing truly micron-scale channels and membranes via UV-VPP. To address this, we previously presented a gas-permeable photopolymerizable PDMS resin for UV-VPP capable of 3D printing high-resolution microfluidic devices.^23,24

3D printing also offers the design freedom of fabricating microfluidic devices that are no longer restricted to planar geometries. Generating internal features, e.g. microchannels, in the x, y, and z planes mitigates the need to externally combine multiple devices with additional tubing and connections to increase blood flow rates (illustrated in Fig. 1). In addition to streamlining the fabrication process, 3D printing potentially enables the creation of more densely packed microchannels, reducing overall device size and allowing for gas diffusion into the blood channels from two or more sides, potentially further increasing efficiency (Fig. 1C and D). Finally, 3D printing should allow for the creation of truly 3D vascular and artificial lung geometries that are simply not possible with other manufacturing technologies.

Fig. 1 CAD rendering for the 3D printed μAL showing the complete device (A), cross sections through the gas flow channels (B) and blood flow channels (C) and a closeup of the blood and gas flow channels (D). The closeup shows the arrays of orthogonal blood and gas flow channels. A thin PDMS gas diffusion membrane separates each blood flow channel from each gas flow channel, enabling gas exchange via the top and bottom of the blood channel.

Previous achievements towards 3D printed artificial lungs have paved the way for this work. Bhattacharjee et al. created a photopolymerizable PDMS resin for 3D printed membranes, but membranes were >330 μm due to limitations of the material's resolution.³⁰ Other groups have generated structures with triply periodic minimal surfaces (TPMS) as gas exchange modules via 3D printing with PDMS directly³¹ and printing a dissolvable mold for casting PDMS membranes.³² In both cases, diffusion distances were much larger than is physiologically relevant, 1000 μm (ref. 31) and 800 μm,³² limiting their translation to clinically relevant gas exchange requirements as an artificial lung. Beyond PDMS-based devices, Grigoryan et al. 3D printed an artificial lung construct with the hydrogel poly(ethylene glycol) (PEGDA) to create biomimetic multivascular networks capable of tidal ventilation.³³ This work elegantly highlights 3D printing's functionality to generate complex 3D topologies for microfluidics. However, the gas exchange efficiencies of these devices (rated blood flow‡ <25 μL min⁻¹) were insufficient for clinical oxygenators due to the low permeability of PEGDA (∼10× smaller than PDMS)³⁴ and large diffusion distances (>300 μm to 1 mm).

Combining the advantages of microfluidics to mimic the size-scale of alveolar capillaries, a custom high-resolution PDMS resin for UV-VPP, and the geometric freedom of 3D printing, this paper presents the first small-scale, truly 3D microfluidic artificial lung for respiratory support. The design, fabrication, and performance of this next generation μAL are presented in this paper and portray a promising path for overcoming the fabrication challenges of creating clinically relevant μALs and for creating truly 3D microvasculature networks.

Results

μAL fabrication and characterization

A previously developed custom 3D printing resin formula²⁴ enabled the fabrication of a small-scale microfluidic artificial lung for respiratory support via 3D printing (Fig. 2). The 3D printed μAL presented herein contained 500 blood channels, each nominally 200 × 297 × 7344 μm, and 252 gas channels, each nominally 200 × 297 × 13 311 μm. Channels are separated laterally by 162 μm-wide support columns, and vertically on the top and bottom by 50 μm-thick membranes (Fig. S1†), resulting in the highest density of 3D printed microchannels to date and enabling gas diffusion in 2 directions. Fluid is simultaneously distributed to the array of channels via an open, pyramidal plenum and exits the device in the same manner (Fig. 1B and C, Video S2†). The total priming volume of this device is 510 μL with the inlet and outlet distribution regions accounting for 290 μL of this volume.

Fig. 2 Two 3D-printed μALs are attached to the build platform of the printer immediately after a build (A). Top view of μAL after post-processing of the device to remove uncured resin from the microchannels and after assembling the part with inlet and outlet tubing (B). Zoomed-in view of microchannel array inside the μAL (C).

True (as-printed) channel dimensions were determined via microscopic examination to be 172 μm-tall × 320 μm-wide, with 62 μm-thick membranes and 124 μm-wide support columns (Fig. S2†).

Micro computed tomography (microCT) was used to visualize the patent microchannels throughout the device (Fig. S3, Video S1†), where on average 72% ± 2% of blood channels and 59% ± 6% of gas channels were patent (i.e. cleared of uncured resin).

The roughness of the microchannel side walls, calculated as the root mean square height, is s_q = 4.9 μm and the roughness on the top and bottom of the channels is s_q = 0.4 μm (Fig. S4†).

Mathematical modelling of 2-sided gas exchange performance

After accounting for the as-printed channel dimensions, the properties of the experimental blood, and the loss of gas-exchange surface area due to channel patency, previously developed models^10,35,36 predicted a rated blood flow of 1.4 mL min⁻¹, capillary pressure drop at rated flow was 0.18 mmHg, and shear in the capillaries at rated flow was 2.5 dyn cm⁻². With 100% channel patency, theoretical rated flow is 3.3 mL min⁻¹, capillary pressure drop is 0.30 mmHg at rated flow, and capillary shear stress is 4.3 dyn cm⁻².

Using the printed channel dimensions and assuming 100% channel patency, but using typical properties for human blood, the theoretical rated flow is 6.0 mL min⁻¹, capillary pressure drop is 0.55 mmHg, and shear in the capillaries is 7.7 dyn cm⁻².

Computational fluid dynamics simulations

Computational fluid dynamics (CFD) was used to visualize the shear stresses, pressure drop and flow trajectories through the μAL (Fig. 3) using actual dimensions of the printed part at 6 mL min⁻¹ blood flow and assuming 100% channel patency. The shear stress in the device ranges from 0.04–33.26 dyn cm⁻² and the shear stress in the capillaries ranges from 5.58–11.11 dyn cm⁻². The simulated pressure drop across the device is 0.59 mmHg, and flow trajectories across the device ranges from 0.03–87.34 mm s⁻¹.

Fig. 3 CFD at 6 mL min⁻¹ rated flow illustrating shear stress (A) through the internal channels and distribution regions of the μAL, device pressure drop (B), and flow trajectories (C) are presented as a cut-plot of the top-down view of the device.

In vitro characterization

μALs were tested in vitro using anticoagulated, whole ovine blood to determine gas exchange performance and pressure drop (Fig. 4). Pure oxygen was used as the sweep gas.

Fig. 4 Blood testing of the μAL (A), saturated oxygen content vs. blood flow (B), partial pressure of CO₂vs. blood flow (C), gas transfer vs. blood flow (D), CO₂ transfer vs. sweep flow (E), and pressure drop vs. blood flow (F). Sweep gas flow to blood flow ratio was 4 : 1, unless otherwise noted in the plot.

Fig. 4B shows mean measured outlet blood oxygen saturation (SO₂) as a function of blood flow rate for 4 μALs (open diamonds). Incoming or inlet blood SO₂ was 64.8 ± 1.7% (thick solid line in Fig. 4B). The plot displays the traditional relationship between outlet SO₂vs. blood flow for an artificial lung, where small flow rates equate to large blood residence time in the μAL, permitting the blood to be fully saturated. As flow rate increases toward the device's rated blood flow, outlet SO₂ decreases as decreased blood residence time inside the μAL does not permit full saturation of blood with oxygen. Theoretical performance is shown with a solid line and agrees well with measured values, after adjusting for channel patency and properties of the experimental blood. The approximate rated blood flow is 1 mL min⁻¹. Theoretical performance assuming all blood and gas flow channels are patent is shown as the dashed green line. Theoretical performance assuming 100% channel patency and with normal human blood instead of ovine blood is shown as a dotted green line.

Measured outlet partial pressure of carbon dioxide (P_CO2) increased with increasing blood flow and asymptotically approached the measured inlet blood CO₂ (Fig. 4C). At low flow rates, long blood residence times permit a larger portion of the CO₂ dissolved in blood to be removed, resulting in smaller outlet blood P_CO2 values. The opposite is true at larger blood flow rates. Inlet blood P_CO2 (wide solid line, Fig. 4C) was 68.8 ± 1.3 mmHg, similar to that seen in lung disease patients with severe hypercarbia.

Measured CO₂ and O₂ transfer increased roughly linearly with blood flow rate over the range of flows tested (see Fig. S6† for % volume transfer plot). Measured O₂ exchange efficiency per gas exchange area was 78 mL min⁻¹ m⁻² at the rated flow. Maximum measured O₂ exchange efficiency was 255 mL min⁻¹ m⁻² at a blood flow rate of 5 mL min⁻¹.

Measured CO₂ transfer increased roughly linearly with the sweep gas flow rate, with a maximum measured value of 0.34 mL min⁻¹ at a sweep gas to blood flow ratio of 16 : 1. This corresponds to a 6.8% CO₂ vol% transfer or a CO₂ transfer per gas exchange surface area of 668 mL min⁻¹ m⁻², one of the highest reported for any artificial lung to date,^14,37 after adjusting gas exchange surface area for channel patency (see Fig. S6† for % CO₂ volume transfer plot).

A linear fit of the raw pressure drop data, P_d, was determined to be:

P_d = Q × 2.53 mmHg mL⁻¹ min + 1.21 mmHg

where Q is the blood flow rate (mL min⁻¹). The y-offset of 1.21 mmHg was likely due to change in the height of the tubing after zeroing the pressure sensor. Approximately 240 mm of 1/16 inch ID tubing, and 330 mm of 1/8 inch ID tubing was included in the flow path, which accounts for 0.95 mmHg of pressure drop per mL min⁻¹. After accounting for these factors, the resistance of the lung itself was calculated at 1.58 mmHg mL⁻¹ min. The resulting theoretical pressure drop for the tubing, device, and pressure offset equates to a P_d = 2.3 mmHg at 1 mL min⁻¹. Theoretical calculations of total pressure drop in Fig. 3 underestimate measured pressure drop, even after accounting for the tubing and patency of the artificial capillaries.

Discussion

μAL fabrication and characterization

The nature of DLP UV-VPP 3D printing is known to produce channel dimensions smaller than those in the CAD model²⁴ and is dependent upon the ability of the photopolymer resin and printer's light source to generate high-fidelity parts.

The channel dimensions in this μAL design were chosen based on manufacturability. Smaller channel dimensions were achievable²⁴ in simpler devices, but repeatability was insufficient for a μAL with many such channels. 200 × 297 μm channel dimensions were chosen to achieve physiologic shear and pressure drop in the capillaries while ensuring ease of clearing uncured resin from the device during post-processing. The number of blood and gas channels, 500 and 252 respectively, were chosen to demonstrate the ability to print a large matrix of microchannels, provide a sufficient rated blood flow for facile testing, be well within the build volume of the 3D printer, and ensure a reasonable printing time for repeatability. Studies are underway to understand the limits of printing smaller channels, to increase patency via improved methods to remove uncured resin, and to increase printing speed by optimizing printing parameters while ensuring adequate print yield.

Layer-by-layer fabrication of DLP 3D printing can also result in non-uniform or rough surfaces. The surface roughness of the microchannels in the μAL was dictated by the orientation in which the part was printed (Fig. 2A). The side wall roughness is due to the layer-by-layer stacking that forms the support pillars and microchannels. The top and bottom of the channels have much smoother surfaces as they are formed against the build tray film. Printing with thinner build layers would reduce this side wall roughness,³⁸ but at the cost of longer build times. Regardless, the variation in side-wall roughness compared to the top and bottom of the channels warrants investigation into the hemocompatibility of these 3D printed microchannels.

Regarding hemocompatibility, a recent study demonstrated that the resin used in this publication is non-cytotoxic after a post-fabrication solvent extraction, permitting the proliferation of HepG2 cells comparable to or better than traditional cell culture wells.²⁴ More detailed and longer studies with other cell types and blood will be investigated in the future to validate cytocompatibility and understand blood coagulation in these devices as it is known that the hydrophobic nature of PDMS leads to protein adsorption on surfaces.³⁹ Previous works have demonstrated the success in mitigating or delaying protein adsorption via surface modifications to PDMS channels.^40–42 We anticipate that post-printing surface coatings or inclusion of hydrophilic and/or zwitterionic molecules in the 3D printing resin formula^43–46 can successfully address the challenges of blood clotting in these 3D printed μALs.

Mathematical modelling of 2-sided gas exchange performance

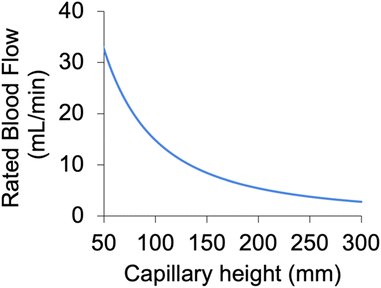
Each blood layer is sandwiched between two gas layers, facilitating two-sided gas exchange from both the top and bottom of the artificial capillaries (illustrated in Fig. 1). This doubles the surface area for gas exchange and halves the average distance O₂ must diffuse in the blood to bind to hemoglobin, increasing rated blood flow by ∼3.5×. The mathematical model predicted the rated flow (with human blood) to be 6.0 mL min⁻¹, assuming 100% channel patency, whereas the theoretical rated flow of a device with the same geometries, but only 1-sided gas exchange would have been 1.7 mL min⁻¹.

The presented mathematical model was also used to predict the impact of blood channel (i.e. artificial capillary) height on device performance (Fig. 5 and S7†). Predicted rated blood flow as a function of artificial capillary height is shown in Fig. 5 for a fixed build volume (equivalent to the build volume of the device in Fig. 2). As can be seen, decreasing capillary height significantly increases the rated blood flow achievable in a given build volume, both through reducing diffusion distances for oxygen and through the increased number of smaller channels that can fit in a given volume (increasing surface area for gas exchange). For this reason, decreasing artificial capillary height will be a priority in the future for pushing the technology to larger blood flows and thus toward the clinic. As we have previously shown,^10,47 reducing artificial capillary height can dramatically decrease the device's blood contacting surface area and blood priming volume, reducing overall device size and potentially increasing blood compatibly (due to less foreign surface exposed to blood). Smaller artificial capillaries come with other challenges, however, mainly due to pressure drop increases proportional to the inverse of capillary height cubed (H_C⁻³). Thus, in order to maintain a physiologic pressure drop, numerous small diameter artificial capillaries should be combined in parallel, potentially leading to complex and/or large blood distribution networks. These tradeoffs will need to be explored in future 3D printed μALs.

Fig. 5 Predicted rated flow (mL min⁻¹) for μAL performance vs. capillary height.

The effect of membrane thickness on performance was also modelled (Fig. S8†) and displayed only a minor impact on gas exchange and rated blood flow, especially when compared with the impact of decreasing the blood channel height. For example, halving the blood channel height increases rated flow by 2.6× (160%), but halving membrane thickness only increases rated flow by 1.3× (30%). Shrinking membrane thickness further may also reduce mechanical reliability.

Computational fluid dynamics simulations

The simulation makes many assumptions to make computation more manageable, including that the blood is homogeneous and exhibits laminar flow. In reality, the manufactured device has many manufacturing artifacts, imperfections in texture and shape, uncleared channels, and deformation under pressure likely causing flow anomalies not predicted in simulations. Further, unlike the simulation, blood is a heterogeneous mixture and changes in properties as it travels through the device (for example, as capillary size decreases, blood experiences a shear-thinning effect⁴⁸). Blood viscosity also varies between species (e.g. human versus ovine) at low shear rates due to hematocrit levels and inflexibility of the sheep's erythrocytes relative to human.⁴⁹ These simulations are meant firstly as a prediction of how the device will perform prior to empirical testing, and secondly as a tool to visualize flow and pressure patterns within the 3D printed μAL.

CFD-simulated pressure drop at a blood flow of 6 mL min⁻¹ for a fully patent device was 0.59 mmHg, comparable to the 0.11 mmHg predicted by the mathematical model. This difference is likely because the mathematical model does not take into account the blood inlet/outlet distribution regions and any flow disturbance or change in flow direction that occurs as the blood exits the tubing into the device's blood distribution region.

The CFD visualization (Fig. 3) demonstrates that shear in the inlet/outlet region varies widely, with an overall small stress (0.04–33.26 dyn cm⁻²) and is comparable to physiologic conditions (0.9–15.3 dyn cm⁻²).⁴⁰ Such small shear stresses may allow for the accumulation of blood clotting factors, initiating coagulation in these regions. Future designs should improve on these distribution regions to provide a more uniform and physiologic shear and thus to reduce coagulation risk.

In vitro characterization

Measured O₂ exchange with whole ovine blood closely matched theory after accounting for the properties of the blood and the channel patency. Channels blocked by uncured resin (as probed via microCT) reduced gas exchange area to ∼42% of the designed structure (i.e. the product of measured blood channel and gas channel patency), reducing rated flow by ∼2.4× according to theory. Removing all uncured resin from the large array of parallel microchannels is a priority for future devices and the subject of continued optimization.

The experimental blood also impacted measured gas exchange performance. Fitting the experimental blood to the Hill equation,⁵⁰ resulted in a p₅₀ (the oxygen partial pressure at which blood is 50% saturated) of 37 mmHg, an effective blood solubility of 9.3 × 10⁻⁴ mL O₂ per mL mmHg⁻¹, and an effective blood diffusivity of 7.3 × 10⁻⁷ cm² s⁻¹. For reference, normal human blood has a p₅₀ of 27 mmHg, an effective blood solubility of 7.9 × 10⁻⁴ mL O₂ per mL mmHg⁻¹, and an effective blood diffusivity of 1.4 × 10⁻⁶ cm² s⁻¹.³⁵ Theory thus predicts a significant increase in rated blood flow when using normal human blood (Fig. 4B).

The discrepancy between the empirically measured pressure drop and mathematical theory (Fig. 4F) is believed to be due to the following: 1) the mathematical model does not account for the blood distribution regions; 2) changes in flow direction and flow anomalies in the distribution regions are not considered in the model; and, 3) the sidewall and floor/ceiling surface roughness are not considered in the mathematical model.

Despite deviation from the mathematical predictions, the pressure drop in this device at rated flow, 1.58 mmHg, is small relative to traditionally fabricated μALs and hollow fiber devices, where pressure drops range from 10–100 s mmHg (ref. 10, 13, 14 and 37) and 63–231 mmHg respectively (Table 1). Traditional μAL fabrication techniques have made it difficult to create devices with small pressure drops and large flow rates because increasing total gas exchange surface area requires increasing either the length of the channels and/or the number of channels. However, to maintain low pressure drops, channel length restricts the size of the device in the XY plane, ultimately requiring traditional μALs to stack many layers with external tubing connections to achieve larger flow rates. Highlighted in Table 1, the 3D printed μAL presented in this publication was able to maintain a physiologically relevant pressure drop and priming volume by printing a dense array of channels in the Z-plane, all contained within the device and converging to a singular inlet and singular outlet. This eliminates the need for additional tubing and assembly while maintaining low pressure drop.

Table 1 Comparison of commercial membrane oxygenators and microfluidic artificial lungs

Device/publication	O2 exchange efficiency	CO2 exchange efficiency	Pressure drop	Channel height	Priming volume
	(mL min^−1 m^−2)	(mL min^−1 m^−2)	(mmHg)	(μm)	(mL)
a Gas supply is air.
Quadrox-i Neonatal^52	237	192	63	—	38
Novalung iLA^53	177	—	17	200	175
Sorin EOS ECMO^54	192	133	231	—	150
Lachaux, J., et al.^37	431	651	69	105	0.82
Thompson, A., et al.^14	153	303	66	10	0.03
3D printed μAL	78	668	1.58	200	0.51
Native lung^10	100^a	100^a	10	10	—

---

CO₂ removal in Fig. 4D offer insights into device performance, future optimization, and potential first clinical application. As the sweep gas flow to blood flow ratio increases, CO₂ removal increases approximately linearly. This signifies that for this μAL, CO₂ exchange is not limited by diffusion of CO₂ through the blood and membrane, but instead by the removal of CO₂ by the sweep gas. Hollow fiber ALs also demonstrate this behavior, but their CO₂ removal typically begins to level off and stop increasing after a sweep to blood flow ratio around 8 : 1.⁵¹ At a sweep to blood flow ratio of 16 : 1, the presented device achieves excellent CO₂ exchange efficiency (Fig. 4E). This high CO₂ exchange efficiency compared to previous μALs is likely due to testing at higher sweep to blood flow ratios, the higher CO₂ permeability of our PDMS resin compared to Sylgard 184,^23,24 and two-sided diffusion. Given the excellent CO₂ removal efficiency, a possible first clinical application for this μAL technology will be for extracorporeal CO₂ removal, a main need for many advanced or end stage lung disease patients.

Experimental

Resin formulation

A custom high-resolution PDMS resin for UV-VPP was prepared following previously established methods.²⁴ A resin composed of 80.0 w/w% methacryloxypropyl terminated polydimethylsiloxane, 125–250 cSt (DMS-R22; Gelest, Inc., Morrisville, PA, USA), 18.71 w/w% [7–9% (methacryloxypropyl)methylsiloxane]-dimethylsiloxane copolymer (RMS-083; Gelest, Inc., Morrisville, PA, USA), 0.80 w/w% 2,4,6-trimethyl benzoyl diphenylphosphine oxide (TPO-L), gifted as a sample from PL Industries of Esstech, Inc. (Essington, PA, USA), 0.40 w/w% 2-isopropylthioxanthone (ITX; VWR International, Radnor, PA, USA), and 0.09 w/w% Sudan I (Sigma-Aldrich, St. Louis, MO, USA) were weighed on a Quintix 125D-1S Semi-Micro Balance (Sartorius Lab Instruments GmbH & Co. KG, Goettingen, Germany) to the selected w/w% of material. Components were combined and mixed by hand, heated for 2 h at 70 °C on a VMS-C7 S1 hot plate (VWR International, Radnor, PA, USA), and then sonicated with a Q700 Sonicator (Qsonica LLC, Newtown, CT, USA) to ensure uniform mixing and particle size reduction.

Material characterization

3D printing resolution and viscosity were previously studied to determine printability of this material on an ASIGA MAX X 27 UV printer (Asiga, Alexandria, Australia).²⁴ Gas permeability to O₂ and CO₂, mechanical properties (namely Young's modulus and elongation at break), optical transparency, and cytocompatibility of this material were also investigated for their PDMS-like properties and translation for creating microfluidic devices.²⁴

Mathematical modelling of 2-sided gas exchange performance

Previously developed mathematical models^10,35,36 were performed in Excel and used to predict gas exchange, shear, and pressure drop based on the true dimensions of the printed channels. Dimensioned channels can be found in Fig. S2.† Theoretical outlet SO₂ was calculated using empirically derived blood diffusivity and solubility compared to human blood (Fig. S9†), using previously established models.⁵⁵ Please see Table S1† for a list of equations and constants.

Device structure and design

μALs were designed in SOLIDWORKS (Dassault Systèmes, Waltham, MA, USA). The as-drawn device design consists of alternating layers of 200 μm gas channels and 200 μm blood channels, oriented orthogonally in the XY plane, and separated in the z plane by 50 μm membranes to create a dense 3D array. Each channel is divided from the adjacent ones by a support wall, holding up the membrane layer above and keeping the channel patent. Inlet and outlet blood flow is distributed to the blood channels simultaneously by an open pyramidal plenum and gas is passed through the device in the same manner. Exit holes of 0.0625 inch diameter join the plenum distribution regions to external tubing ports for post-processing and assembly. The device design is presented in Fig. 1 as a SOLIDWORKS 3D rendering and is dimensioned in Fig. S1.†

This unique design allows all of the blood channels to be vertically sandwiched between membranes with a gas channel on each side, enabling two-sided diffusion. This improves gas-exchange efficiency since gas diffusion with the blood can be achieved through both the top and bottom of the blood channel.

Overall dimensions of the μAL were selected based on the properties of the 3D printer and material system. Channel widths and spacings were scaled to a factor of 27 μm to match the 27 μm X and Y pixel resolution of the 3D printer. Channel heights were selected to be 200 μm for the ability to remove uncured resin trapped inside the microchannels after printing. 50 μm membranes were selected as thinner membranes can tear due to separation forces on the part during printing⁵⁶ and can lead to build failures.

3D printing

All μALs and builds were printed using the Asiga MAX X27 UV printer (Asiga, Alexandria, Australia 2015). The printer has a 385 nm light source (wavelength range 370–400 nm), with an X and Y pixel resolution of 27 μm, and a Z (vertical) resolution of 1 μm and uses digital light processing (DLP) technology. Asiga Composer Software version 1.3.8 (Asiga, Alexandria, Australia 2015) was the interface used for all STL files and establishing print parameters.

Glass slides, which were silanized with 3-(trimethoxysilyl)propyl methacrylate (Sigma Aldrich, St. Louis, MO, USA) following the procedure as described by A. Urrios et al.,⁵⁷ were adhered to the build platform using a UV epoxy (Proto Glass, Proto Products, Ashland City, TN, USA) before the start of each print. The build platform was calibrated with the glass slide attached before printing began.

Post-processing, tubing assembly, and flushing channels

μALs were removed from the build platform and sonicated for 5 minutes in IPA using a Cole Parmer Ultrasonic cleaner (model 08849-00; purchased from Cole Parmer, Vernon Hills, IL, USA) to remove uncured resin. A 0.0625 inch inner diameter LIVEO™ Silicone Laboratory tubing (purchased from VWR, Radnor, PA, USA) was then attached at the inlet and outlet ports, using DOWSIL 3140 MIL-A-46146 RTV Coating. The RTV glue was allowed to dry at room temperature overnight before attaching 1/16′′ female/male Luer lock to hose barb adapters (purchased from Cole Parmer).

Following tubing assembly, trapped, uncured resin was flushed from the internal channels of the device. A gravity driven, open circuit with IPA was used to apply a relatively fixed pressure to the filled channels and simultaneously dilute the trapped resin until the fluid was released and enough channels were cleared for IPA to easily flow through the device. Once fluid flow was established on the open circuit, the devices were assembled onto a closed ethanol circuit on a Masterflex Roller Pump (Avantor by VWR, Radnor, PA, USA) to flush the remaining channels (Fig. S10†). Ethanol was flowed through the device at 0.2 mL min⁻¹ and slowly ramped up 0.1 mL min⁻¹ every hour until fluid flow of 1 mL min⁻¹ was achieved. Patent channels were determined by passing food dyed water through the device using the roller pump (Video S3†) and the device was kept in the ethanol circuit at 1 mL min⁻¹ until all channels were cleared.

Surface roughness

Surface roughness of the 3D printed μAL was measured using a laser confocal microscope, Olympus OLS 4000 LEXT (Olympus IE, Waltham, MA, USA). Channel walls and top and bottom surfaces were imaged and processed using the LEXT OLS 4100 software (version 3.1.14) at the Lurie Nanofabrication Lab at the University of Michigan.

Measurements of the surface roughness were acquired using the stitch function of the LEXT software and the 20× lens, creating a 2 × 2 surface quadrant. The 20× lens experiences a height error of 0.793%, producing an accurate reading of the variability of surface height.⁵⁸ Image correction was utilized in correcting any incline or curvature in the samples. The root mean squared height (s_q) was reported and is equivalent to the standard deviation of the roughness profile across the stitched image.⁵⁹

microCT

μALs (n = 3) were imaged at the University of Michigan Dental School MicroCT Core. Specimens were placed in a 34 mm diameter specimen holder and scanned using a microCT system (μCT100 Scanco Medical, Bassersdorf, Switzerland). Scan settings were: voxel size 16 μm, 55 kVp, 109 μA, 0.5 mm AL filter, 1000 projections/180° and integration time 500 ms. Images were generated using Dragonfly software (Version 2022.2 for Windows, Object Research Systems (ORS) Inc, Montreal, Canada, 2020).

TIFF images were analysed to reconstruct a 3D rendering of the μAL, enabling visualization of patent and occluded microchannels inside the device (Fig. S3, Video S1†). Patent and occluded channels were quantified by counting the channels in each layer of the sliced microCT images. Plots and statistical analysis (average, standard deviation, and percentage) were performed in Excel.

Computational fluid dynamics

After μALs were manufactured, some were cut apart and observed under a microscope to determine their actual dimensions, see Fig. S2† for dimensioned images.

The CAD model was updated in SOLIDWORKS to reflect actual dimensions, and computational fluid dynamics (CFD) was used to predict pressure drop and visualize flow. SOLIDWORKS Flow simulation add-in was used to generate velocity, pressure, and shear profiles. Blood was modelled as a non-Newtonian fluid with a density of 1060 kg m⁻³. The viscosity model used was the power-law model, where the power law index is 0.7991, the minimum dynamic viscosity is 0.0030 Pa s, and the maximum viscosity is 0.0122 Pa s. Boundary conditions are an inlet volume flow of 2.5 × 10⁻⁸ m³ s⁻¹, and outlet environment pressure of 760.0 mmHg. The mesh used to conduct the CFD studies was generated using the automatic mesh feature in flow simulation, where increasing the increments from 1 to 7 results in more refined mesh element sizes. Mesh-independent results were achieved at a mesh setting of 2 and used across all the CFD studies.

In vitro blood tests

In vitro blood tests were performed following the ISO 7199:1996 standard, adapted for testing with microfluidic devices. Ovine blood with anticoagulant, citrate phosphate dextrose solution (CPD), was purchased from Lampire Biological Laboratories (Pipersville, PA, USA). The CPD formulation information provided by Lampire is as follows: 26.3 g L⁻¹ Na-citrate, 25.2 g dextrose, 3 g L⁻¹ citric acid, and 2.2 g L⁻¹ Na phosphate in deionized water.⁶⁰ The ratio of blood to CPD is 14 parts CPD to 86 parts blood.⁶⁰

To condition the blood before testing with the microfluidic lung, blood in a blood bag was recirculated through a commercially available hollow-fiber membrane oxygenator, the Hilite 800 LT (Xenios AG, Stolberg, Germany). Blood was recirculated and sweep gas (a mixed gas stream of CO₂ and N₂) through the Hilite oxygenator was adjusted to achieve an oxygen saturation of 65 ± 5% O₂ saturation.

During blood conditioning and testing, the blood bag is kept in a Polyscience water bath (model WB20; Polyscience, Niles, Illinois, USA) heated to 37 °C and connected to the Hilite 800 LT oxygenator using silicone tubing 0.125′′ ID × 0.250′′ OD tubing purchased from Avantor by VWR (Radnor, PA, USA). The tubing is connected to a Masterflex Roller Pump (Avantor by VWR, Radnor, PA, USA) and blood is passed through the oxygenator at 100 mL min⁻¹. Simultaneously, a second roller pump is used to flow water from the 37 °C water bath into the commercial oxygenator to maintain the physiological temperature of the blood during conditioning and testing. The N₂ and CO₂ gas tanks are regulated by Omega mass flow meters (model FMA5508; Omega, Norwalk, CT, USA) to achieve a flow rate ratio of 10 : 1 N₂ to CO₂. The total flow rate of the combined N₂ and CO₂ (mL min⁻¹) gas mixture is equal to the blood flow rate through the oxygenator, 100 mL min⁻¹. As the color of blood begins to darken, indicating oxygen removal, blood gas levels are measured with a handheld iSTAT blood gas analyzer (Abbott, Orlando, FL, USA) using an EG6+ cartridge (Abbott, Orlando, FL, USA). Blood gas levels are measured every 10 minutes until 65 ± 5% O₂ saturation is achieved. Following titration, hematocrit (HCT) levels measured via the iSTAT are validated by collecting 1 mL of blood from the blood reservoir with a syringe and transferring to a 1.5 mL centrifuge tube (n = 2). Samples are spun at speed 6 for 10 minutes using a Micro-Centrifuge (Model 59A; Fisher Scientific, Waltham, MA, USA) to separate plasma and blood cells to calculate the HCT.

Once blood is conditioned to 65 ± 5% O₂ saturation, the μAL is connected to the blood circuit to begin oxygenation testing. Blood oxygenation was tested (n = 4 devices) at the flow rates of 0.5, 1.0, 2.0, and 5.0 mL min⁻¹, and with O₂ sweep flow rates of 2, 4, 8, and 20 mL min⁻¹. During testing, pressure drop measurements across the device were collected using a Hewlett Packard (Palo Alto, CA, USA) M1176A Model 66 clinical pressure monitor. A custom CO₂ sensor,⁶¹ in line with the gas exhaust, measures the resulting exhaust CO₂ levels. Once oxygenated blood has travelled through the tubing to the sampling port, blood is collected into a EG6+ cartridge and analysed with the iSTAT machine. Tests are repeated with each adjusted blood flow and corresponding O₂ sweep flow. All measured values were combined into means and standard deviations in Microsoft Excel for each testing condition. Images and additional details of the blood testing circuit can be found in Fig. S5.†

Conclusions

We have demonstrated the ability to create the first μALs for respiratory support via additive manufacturing, overcoming a major hurdle to advancing μALs toward the clinic. This achievement is in part due to the rapid advancements in the additive manufacturing industry, which soon may enable complex microfluidic devices with large-scale flow (L min⁻¹).

Presently, higher-throughout UV-VPP systems lack in material selection, especially for PDMS. Whereas higher-resolution systems like two-photon photolithography (2PP) are capable of fabricating devices with smaller internal feature sizes and complex geometries in PDMS,^62,63 they are limited in throughput due to small build volumes and slow build times.^64,65 As UV-VPP systems continue to improve and high-resolution photopolymer resins become more commercially available beyond 2PP, larger-scale 3D printed μALs should be realized.

For the next-generation of μALs, higher-resolution 3D printing can improve hemocompatibility of these devices through the creation of more biomimetic geometries with 1) cylindrical, rather than rectangular channels, 2) facile printing with thinner layers and therefore smoother surfaces, and 3) hierarchical branching architectures to mimic more physiologically relevant blood flows. To achieve clinical relevance, future work will be focused on increasing device size while reducing microchannel heights to improve gas-exchange efficiency.

While acknowledging potential challenges, such as surface roughness and blood clotting, the work presented herein underscores the promise of 3D printing as a legitimate approach for the development of microfluidic artificial lungs with unconstrained geometries, optimized performance, and reduced size.

Author contributions

Conceptualization, E. F. and J. P.; data curation, E. F., C. K., K. R., A. Z., M. A., J. P.; formal analysis, E. F., C. K., K. R., A. Z., M. A., S. M., J. P.; funding acquisition, J. P.; investigation, E. F., J. P.; methodology, E. F., C. K., K. R., A. Z., M. A., S. M., J. P., project administration, E. F. and J. P.; resources, E. F. and J. P., supervision, E. F. and J. P., validation, E. F., C. K., K. R., A. Z., M. A., S. M., J. P., visualization, E. F., C. K., K. R., A. Z., M. A., J. P.; writing – original draft, E. F. C. K., K. R., A. Z.; writing – review & editing, E. F., A. Z., S. M., J. P.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Thank you to Navid Shaikh for his CO₂ measurement system that was used during device testing, Tyler Teague at ProtoProducts for his 3D-printing technical support, and Laura Brubacher, for her support and revisions to this manuscript. Thank you to the University of Michigan School of Dentistry MicroCT Core which is funded in part by NIH/NCRR S10RR026475-01. This work was supported in part by SPiRE Award I21RX002403 from the United States Department of Veterans Affairs (VA) Rehabilitation Research and Development (RRD) Service, grant R01HL144660 from the United States National Institutes of Health, and VA RRD Merit Award I01RX003920. The contents do not represent the views of the United States Government or the U.S. Department of Veterans Affairs.

Notes and references

1. Registry Dashboard|ECMO|Extracorporeal Membrane Oxygenation, https://www.elso.org/registry/elsoliveregistrydashboard.aspx, (accessed January 15, 2023).
2. K. M. Kim, A. Arghami, R. Habib, M. A. Daneshmand, N. Parsons, Z. Elhalabi, C. Krohn, V. Thourani and M. E. Bowdish, Ann. Thorac. Surg., 2023, 115, 566–574.
3. J. Arens, O. Grottke, A. Haverich, L. S. Maier, T. Schmitz-Rode, U. Steinseifer, H. P. Wendel and R. Rossaint, ASAIO J., 2020, 66, 847–854.
4. T. L. Astor and J. T. Borenstein, Artif. Organs, 2022, 46, 1227–1239.
5. The Risks & Complications of ECMO/ECLS, https://www.elso.org/ecmo-resources/ecmo-risks-and-complications.aspx, (accessed June 27, 2023).
6. T. Kniazeva, A. A. Epshteyn, J. C. Hsiao, E. S. Kim, V. B. Kolachalama, J. L. Charest and J. T. Borenstein, Lab Chip, 2012, 12, 1686–1695.
7. R. H. Bartlett, Compr. Physiol., 2020, 10, 879–891.
8. W. J. Federspiel and R. G. Svitek, Encyclopedia of Biomaterials and Biomedical Engineering, 2004, pp. 922–931.
9. W. J. Federspiel and K. A. Henchir, Encyclopedia of Biomaterials and Biomedical Engineering, 2008, pp. 910–921.
10. J. A. Potkay, Lab Chip, 2014, 14, 4122–4138.
11. J. B. White, N. J. Douville, C. Moraes, J. B. Grotberg and S. Takayama, in Microfluidic Cell Culture Systems, ed. C. Bettinger, J. T. Borenstein and S. L. Tao, William Andrew Publishing, Oxford, 2013, pp. 247–278.
12. M. Dabaghi, N. Rochow, N. Saraei, R. K. Mahendran, G. Fusch, A. K. C. Chan, J. L. Brash, C. Fusch and P. R. Selvaganapathy, Adv. Mater. Technol., 2020, 5, 2000136.
13. J. A. Potkay, M. Magnetta, A. Vinson and B. Cmolik, Lab Chip, 2011, 11, 2901–2909.
14. A. J. Thompson, L. H. Marks, M. J. Goudie, A. Rojas-Pena, H. Handa and J. A. Potkay, Biomicrofluidics, 2017, 11, 024113.
15. M. Dabaghi, G. Fusch, N. Saraei, N. Rochow, J. L. Brash, C. Fusch and P. Ravi Selvaganapathy, Biomicrofluidics, 2018, 12, 044101.
16. J. Santos, E. M. Vedula, W. Lai, B. C. Isenberg, D. J. Lewis, D. Lang, D. Sutherland, T. R. Roberts, G. T. Harea, C. Wells, B. Teece, P. Karandikar, J. Urban, T. Risoleo, A. Gimbel, D. Solt, S. Leazer, K. K. Chung, S. Sukavaneshvar, A. I. Batchinsky and J. T. Borenstein, Micromachines, 2021, 12(8) DOI:10.3390/MI12080888.
17. Y. Xia and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 550–575.
18. J. C. McDonald and G. M. Whitesides, Acc. Chem. Res., 2002, 35, 491–499.
19. J. N. Lee, C. Park and G. M. Whitesides, Anal. Chem., 2003, 75, 6544–6554.
20. S. M. Scott and Z. Ali, Micromachines, 2021, 12, 319.
21. H. Matharoo, M. Dabaghi, N. Rochow, G. Fusch, N. Saraei, M. Tauhiduzzaman, S. Veldhuis, J. Brash, C. Fusch and P. R. Selvaganapathy, Biomicrofluidics, 2018, 12, 014107.
22. B. C. Isenberg, E. M. Vedula, J. Santos, D. J. Lewis, T. R. Roberts, G. Harea, D. Sutherland, B. Landis, S. Blumenstiel, J. Urban, D. Lang, B. Teece, W. Lai, R. Keating, D. Chiang, A. I. Batchinsky and J. T. Borenstein, Adv. Sci., 2023, 10(18), 2207455.
23. E. Fleck, A. Sunshine, E. DeNatale, C. Keck, A. McCann and J. Potkay, Micromachines, 2021, 12, 1266.
24. E. Fleck, C. Keck, K. Ryszka, E. DeNatale and J. Potkay, Micromachines, 2023, 14, 773.
25. G. Gonzalez, I. Roppolo, C. F. Pirri and A. Chiappone, Addit. Manuf., 2022, 55, 102867.
26. J. L. Sanchez Noriega, N. A. Chartrand, J. C. Valdoz, C. G. Cribbs, D. A. Jacobs, D. Poulson, M. S. Viglione, A. T. Woolley, P. M. Van Ry, K. A. Christensen and G. P. Nordin, Nat. Commun., 2021, 12, 5509.
27. Boston Micro Fabrication, Introduction to 3D Printing with PuSL, 2020.
28. N. P. Macdonald, J. M. Cabot, P. Smejkal, R. M. Guijt, B. Paull and M. C. Breadmore, Anal. Chem., 2017, 89(7), 3858–3866.
29. N. Bhattacharjee, A. Urrios, S. Kang and A. Folch, Lab Chip, 2016, 16, 1720–1742.
30. N. Bhattacharjee, C. Parra-Cabrera, Y. T. Kim, A. P. Kuo and A. Folch, Adv. Mater., 2018, 30(22), 1800001.
31. T. Femmer, A. J. C. Kuehne and M. Wessling, Lab Chip, 2014, 14, 2610–2613.
32. F. Hesselmann, N. Scherenberg, P. Bongartz, S. Djeljadini, M. Wessling, C. Cornelissen, T. Schmitz-Rode, U. Steinseifer, S. V. Jansen and J. Arens, J. Membr. Sci., 2021, 634, 119371.
33. B. Grigoryan, S. J. Paulsen, D. C. Corbett, D. W. Sazer, C. L. Fortin, A. J. Zaita, P. T. Greenfield, N. J. Calafat, J. P. Gounley, A. H. Ta, F. Johansson, A. Randles, J. E. Rosenkrantz, J. D. Louis-Rosenberg, P. A. Galie, K. R. Stevens and J. S. Miller, Science, 2019, 364, 458–464.
34. N. P. Patel, A. C. Miller and R. J. Spontak, Adv. Funct. Mater., 2004, 14, 699–707.
35. J. A. Potkay, Biomed. Microdevices, 2013, 15, 397–406.
36. A. J. Thompson, L. J. Ma, T. J. Plegue and J. A. Potkay, IEEE Trans. Biomed. Eng., 2019, 66, 1082–1093.
37. J. Lachaux, G. Hwang, N. Arouche, S. Naserian, A. Harouri, V. Lotito, C. Casari, T. Lok, J. Baptiste Menager, J. Issard, J. Guihaire, C. V. Denis, P. J. Lenting, A. I. Barakat, G. Uzan, O. Mercier and A.-M. Haghiri-Gosnet, Lab Chip, 2021, 21, 4791–4804.
38. H. Gong, M. Beauchamp, S. Perry, A. T. Woolley and G. P. Nordin, RSC Adv., 2015, 5, 106621–106632.
39. A. Gokaltun, M. L. Yarmush, A. Asatekin and O. B. Usta, Technology, 2017, 5, 1–12.
40. T. J. Plegue, K. M. Kovach, A. J. Thompson and J. A. Potkay, Langmuir, 2018, 34(1), 492–502.
41. K. M. Kovach, J. R. Capadona, A. S. Gupta and J. A. Potkay, J. Biomed. Mater. Res., Part A, 2014, 102, 4195–4205.
42. H. Zhang and M. Chiao, J. Med. Biol. Eng., 2015, 35, 143–155.
43. G. Gonzalez, A. Chiappone, K. Dietliker, C. F. Pirri and I. Roppolo, Adv. Mater. Technol., 2020, 5, 2000374.
44. M.-C. Sin, S.-H. Chen and Y. Chang, Polym. J., 2014, 46, 436–443.
45. A. Gökaltun, Y. B. Kang, M. L. Yarmush, O. B. Usta and A. Asatekin, Sci. Rep., 2019, 9, 7377.
46. A. S. Münch, S. Adam, T. Fritzsche and P. Uhlmann, Adv. Mater. Interfaces, 2020, 7, 1901422.
47. L. J. Ma, E. A. Akor, A. J. Thompson and J. A. Potkay, Micromachines, 2022, 13, 822.
48. S. S. Shibeshi and W. E. Collins, Appl. Rheol., 2005, 15, 398–405.
49. T. M. Amin and J. A. Sirs, Q. J. Exp. Physiol., 1985, 70, 37–49.
50. A. V. Hill, J. Physiol., 1910, 40, iv–vii.
51. L. Witer, R. Howard, J. Trahanas, B. S. Bryner, F. Alghanem, H. R. Hoffman, M. S. Cornell, R. H. Bartlett and A. Rojas-Peña, ASAIO J., 2016, 62, 110–113.
52. Maquet Cardiopulmonary GmbH, QUADROX-i neonatal & pediatric, https://perfusfind.com/quadrox-i-neonatal-pediatric/, (accessed December 1, 2023).
53. A. A. Gimbel, J. C. Hsiao, E. S. Kim, D. J. Lewis, T. F. Risoleo, J. N. Urban and J. T. Borenstein, Artif. Organs, 2021, 45, E247–E264.
54. LivaNova, EOS ECMO, https://perfusfind.com/eos-ecmo/, (accessed December 1, 2023).
55. T. J. Hewitt, B. G. Hattler and W. J. Federspiel, Ann. Biomed. Eng., 1998, 26, 166–178.
56. Y. Pan, H. He, J. Xu and A. Feinerman, Rapid Prototyp. J., 2017, 23, 353–361.
57. A. Urrios, C. Parra-Cabrera, N. Bhattacharjee, A. M. Gonzalez-Suarez, L. G. Rigat-Brugarolas, U. Nallapatti, J. Samitier, C. A. Deforest, F. Posas, J. L. Garcia-Cordero and A. Folch, Lab Chip, 2016, 16, 2287–2294.
58. Olympus LEXT OLS4000 SOP, https://docs.google.com/document/d/1IpBtLSPSMNwuxRggShyvErHiNBfgXO0x2i8Q0czSLU8/preview?pli=1&rswr=true&usp=embed_facebook, (accessed August 4, 2023).
59. Surface Roughness Measurement—Parameters, https://www.olympus-ims.com/en/metrology/surface-roughness-measurement-portal/parameters/#!cms[focus]=023, (accessed August 3, 2023).
60. Lampire Biological Laboratories, Anticoagulant Ratios & Chemical Compositions, 2020.
61. N. Shaikh, A. Zhang, J. Jenter, B. Nikpreljevic, J. Toomasian, W. Lynch, A. Rojas-Peña, R. H. Bartlett and J. A. Potkay, Bioengineering, 2022, 9, 593.
62. The new IP-PDMS photoresin, https://www.nanoscribe.com/en/products/ip-photoresins/ip-pdms/, (accessed November 26, 2023).
63. A. Sharaf, J. P. Frimat, G. J. Kremers and A. Accardo, Micro Nano Eng., 2023, 19, 100188.
64. V. Harinarayana and Y. C. Shin, Opt. Laser Technol., 2021, 142, 107180.
65. T. Zandrini, S. Florczak, R. Levato and A. Ovsianikov, Trends Biotechnol., 2023, 41, 604–614.
66. L. Lequier, S. B. Horton, D. M. McMullan and R. H. Bartlett, Pediatr. Crit. Care Med., 2013, 14, S7.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc00814b

‡ Rated blood flow is the flow rate at which normal human venous blood is converted to 95% oxygen saturation. This corresponds to a 25% increase in oxygen saturation or a volume percent transfer of oxygen into blood of 4.2%.^8,66

---