DOI:
10.1039/D3LC00722G
(Paper)
Lab Chip, 2024,
24, 966-974
Vibrational manipulation of dry granular materials in lab-on-a-chip devices†
Received
23rd August 2023
, Accepted 30th November 2023
First published on 26th January 2024
Abstract
We present vibrational techniques to pump, mix, and separate dry granular materials using multifrequency vibrations applied to a solid substrate with a standard audio system. The direction and velocity of the granular flow are tuned by modulating the sign and amplitude, respectively, of the vibratory waveform, with typical pumping velocities of centimeters per second. Different granular materials are mixed by combining them at Y-shaped junctions, and mixtures of granules with different friction coefficients are separated along straight channels by judicious choice of the vibratory waveform. We demonstrate that the observed velocities accord with a theory valid for sufficiently large or fast vibrations, and we discuss the implications for using vibrational manipulation in conjunction with established microfluidic technologies to combine liquid and dry solid handling operations at sub-millimeter length scales.
1. Introduction
A variety of different microfluidic techniques1–4 for precise handling of liquids currently exists for various analytic,5–7 synthetic,8–10 and diagnostic11–15 laboratory tasks. Manipulation of dry solid powders, however, remain challenging for sub-millimeter scale devices, where applications in additive manufacturing and pharmaceutical dosing require precise handling.16 For agglomeration-prone powders, a combination of electrostatic, cohesive, and packing properties can severely hamper consistent granular flowrates.17 A pneumatic-assisted approach,18,19 achieved by temporarily fluidizing a bed of powder via pressurized gas flow, induces fluid-like properties to the solid bed to induce granular dispensing. Ultrasound mechanisms20 are also widely employed in various configurations, serving a dual purpose of disrupting adhesive forces and releasing particles confined in a capillary tube by reducing frictional forces along the walls. Pipe vibrations using low frequency, axial vibration can induce net motion by pulsing a high frequency, radial vibration during backflow.21 This method however is highly sensitive to the resonance frequency of the device, a common challenge for ultrasound-modulated methods. Critically, none of these processes provide the level of manipulation necessary for integration to lab-on-a-chip operations; gravity-assisted flow in vertically oriented tubes is not reversible, and continuous pumping around curved or otherwise complex geometries remains untested. Thus, to date no facile technology exists to manipulate dry granular materials with the precision or versatility expected of a lab-on-a-chip device.
In this article, we instead consider the effects of a dual-mode vibratory force, generally of the form
| | x(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) + B sin(ωt) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(γωt + ϕ). sin(γωt + ϕ). | (1) |
Certain types of periodic functions are shift symmetric,
22 also known as antiperiodic,
23 which in simple terms means that the first half of the periodic waveform equals the negative of the second half. All single frequency sinusoidal waveforms have shift symmetry, because sin(
ωt + π) = −sin(
ωt) but dual-frequency waveforms lack shift symmetry if the frequency mode ratio
γ is not the ratio of two odd numbers.
24 For example, if
γ = 2, then no choice of phase shift
t + Δ
t for the waveform in
eqn (1) recovers the negative of the waveform. This type of temporal symmetry breaking has long been recognized in the context of condensed matter physics,
25–27 quantum mechanics,
28,29 and nonlinear optics,
30–32 where it is well established that driving forces that lack shift symmetry can induce a net current in one direction. Temporal symmetry breaking has also been recognized as a potential means of moving objects
via frictional interactions on vibrating surfaces,
33–36 with prior experimental demonstrations involving isolated objects like coins
37–39 or centimeter scale plastic rods. Surprisingly, to date no prior work has investigated temporal symmetry breaking with granular media; the behavior of a granular ensemble experiencing a multimodal vibrational force remains unclear.
Here we report that a dual-mode vibration, induced by a standard subwoofer, drives sustained pumping of dry granular materials along millimeter-scale channels and even around curves or junctions. The direction of pumping is reversible by flipping the sign of the vibration in eqn (1), with typical velocities of centimeters per second. Both the direction and pumping velocity accord with an analytic prediction in the limit of sufficiently large or fast vibrations. We illustrate the versatility of this methodology via controlled mixing using geometries familiar to the lab-on-a-chip community, and we demonstrate that mixtures of different granular materials can be separated based on differences in their frictional coefficients. These findings provide methods to integrate dry material feeds into liquid streams for various lab-on-a-chip applications.
2. Materials and methods
2.1 Speaker apparatus
Fig. 1a depicts the experimental setup. The speaker was a Klipsch R-12SW subwoofer (400 watts, 41 cm × 10 cm × 47 cm), purchased commercially and used as received except that a circular piece of plywood was epoxied to the front diaphragm (12 cm diameter, 0.5 cm thick, depicted in Fig. 1a as light brown). A support platform was 3D-printed using a Raise3D N2 printer, yielding a rectangular slab composed of polylactic acid (PLA) and with dimensions of 20 cm × 12 cm × 0.8 cm. This platform (depicted in yellow in Fig. 1a) was connected to the circular plywood surface using a 4 cm by 1.6 cm L-shaped metallic bracket. A stock 0.8 cm × 1.2 cm × 40 cm linear rail and two MGN12H steel carriages (Iverntech), typically used in 3D printing equipment, were positioned underneath the platform to facilitate unidirectional motion (gray beam under the yellow platform in Fig. 1a). The entire apparatus was mounted on a 2.4 m by 1.2 m Newport optical breadboard table, with stacked 10 cm × 10 cm × 2.2 cm rubber/cork anti-vibration isolation pads (PneumaticPlus) placed underneath the subwoofer to minimize parasitic vibrations.
 |
| | Fig. 1 Vibrationally driven pumping of dry granular material. (a) Schematic of the experimental apparatus. A 3-D printed lab-on-a-chip device is placed on a platform connected to a subwoofer. (b–d) Representative measurements of the vibratory motion of the lab-on-a chip device in response to various applied electrical signals to the subwoofer: (a), 30 Hz, (b) 30 Hz and 60 Hz, and (c) 30 Hz and 60 Hz with negative polarity. Red markers are experimental measurements acquired via high speed video of the horizontal substrate location relative to its original position, and the black curve is the best fit to eqn (1) found via nonlinear regression. (e–g) Photographs of dry, blue-colored glass sand moving in response to the respective waveforms indicated above in (b–d), shown before application of the vibration (t = 0, top row), after 2 s of vibration (middle row), and after 5 s of vibration (bottom row). Rectangular channels have width of 2 mm. See also Video S1 through S3.† | |
2.2 Lab-on-a-chip devices
All devices shown in Fig. 1–4 and Video S1–S8† were fabricated using a Stratasys Polyjet printer (Objet 260 Connex) with Vero+ resin. Each device had overall dimensions of 12 cm × 3.8 cm × 0.8 cm, with two screw holes at either end to rigidly fasten the device to the support platform. Channels within the device were typically 2 mm in width and 5 mm deep. Circular entry or exit reservoirs typically had a raised edge that protruded 2 mm above the nominal top surface of the device to help prevent spillage. For some experiments, it was convenient to use a black device to maximize visual contrast with a white powder. These black devices were printed using a Formlabs Form 2 SLA printer with BioMed Black Formlabs resin, using identical geometry as the white devices.
2.3 Granular materials and test objects
The properties of the granular materials and test objects are summarized in Table S1.† The yeast was active dry baker's yeast (Red Star), purchased from a local grocery, and used as provided. The ibuprofen was generic 200 mg capsules purchased from a local vendor, which were ground into a fine powder using a pestle and mortar; the dark red capsule coating, once pulverized into the powder, provided convenient tracers within the otherwise uniformly white powder to help visualize the motion. The blue-colored silica sand was a recreational sand of the kind typically used decoratively in art projects, purchased from a local art supply store. The sand was filtered using a #140 wire cloth stainless steel mesh sieve to remove larger agglomerates. Boron carbide powder (240 grit) was purchased from Advanced Abrasives and used as provided. Particle sizes were measured via optical microscopy and reported in Table S1.† For the single object experiments (cf.Fig. 2b), 16 mm diameter annular stainless steel disks (Z9181-BEV type, plain steel) were purchased from McMaster Carr, and the lab-on-a-chip device was replaced with a 120 mm × 38 mm × 3.2 mm flat slab of aluminum (5052 aluminum bar).
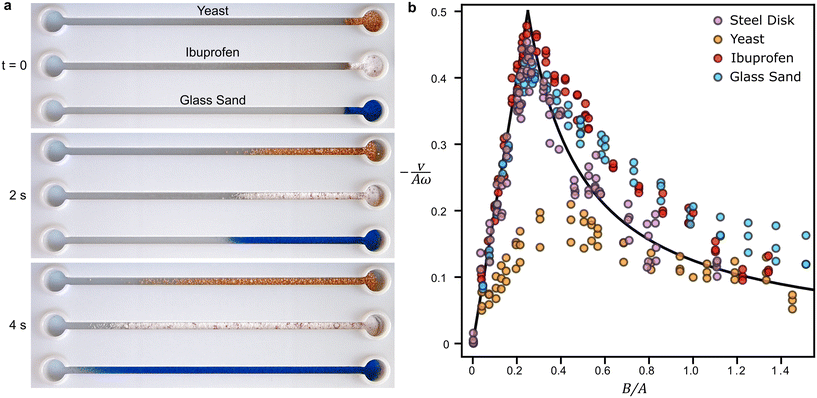 |
| | Fig. 2 Velocity of different materials versus vibration amplitude. (a) Representative images of dry granular materials (yeast agglomerates, crushed ibuprofen powder, and blue-colored silica sand) moving in separate parallel channels in response to a 30 Hz and 60 Hz vibration, shown before application of the vibration (t = 0, top image), after 2 s of vibration (middle image), and after 4 s of vibration (bottom image). Each channel is 2 mm wide; amplitude ratio is B/A = 1. See also Video S4.† (b) The dimensionless velocity versus the amplitude ratio B/A. Markers represent experimental measurements for granular materials (yeast, ibuprofen, and sand are yellow, red, and cyan markers, respectively) moving in channels as shown in (a). Purple markers denote the velocity of individual 16 mm steel disks moving on a flat aluminum substrate. Black curve is the high-friction number theoretical prediction given by eqn (6) with ϕ = 0; see Fig. S1† for velocity measurements versus ϕ. | |
2.4 Determination of friction coefficients
Granular media static friction coefficients were determined using two methods: angle of repose, and onset of sliding. We used a standard angle of repose method40 in which a glass funnel was placed 10 cm over a 3.5 cm diameter metal cylinder. The granular material was poured through the funnel onto the metal surface to form a mound, and images of the side profile were taken using a DSLR camera. The static friction coefficient was calculated as the tangent of the angle of repose. For the sliding method, roughly 15 mg of the granular material was placed in the center of a 3D printed channel. A manual micrometer was used to adjust the tilt of the channel until the powder exhibited downward sliding motion. The DSLR was then used to capture an image of the tilted channel to determine the static coefficient value from the tangent of the tilt angle. To gauge the friction coefficients of the stainless-steel disk on an aluminum substrate, a steel disk was placed on a horizontal aluminum slab and then covered with an extra 360 grams of weights to increase the normal force. A steel wire fastened to the weights was pulled horizontally by a linear actuator at a constant speed of 0.5 cm s−1. A force meter (Vernier) with an accuracy of ±0.1 N recorded the force versus time. Following the standard analysis procedure,41 the static coefficient of friction was extracted from the peak force observed prior to onset of motion, and the kinetic coefficient of friction was extracted from the average pulling force after the disk overcame the static friction and started sliding. The resulting static and kinetic coefficients for the steel disk on aluminum were 0.25 ± 0.03 and 0.17 ± 0.05 respectively, reflecting the mean and standard deviation of 3 replicate measurements.
2.5 Cleaning, leveling, and loading
All lab-on-a-chip devices were cleaned with isopropanol (IPA), rinsed with deionized water, and then air dried prior to each experiment. After attaching the lab-on-a-chip device to the platform, a bubble leveler was used to adjust the horizontal alignment. To further ensure the apparatus was level, prior to each round of experimentation a 16 mm steel disk was placed on top of the lab-on-a-chip device and a unimodal 30 Hz soundwave was applied; if the disk exhibited net drift in one direction, the tilt of the apparatus was corrected until no net drift was observed. To place a granular material into the device, a stopper (or two stoppers) made from transfer pipet tips were placed at the outlet(s) of the desired lab-on-a-chip reservoir to minimize premature spillage. A specified mass of a granular material (typically 50 mg) was then carefully poured into the reservoir, and the stoppers were then gently removed.
2.6 Sound files
A digital sound file controlling the electrical signal driving the motion of the diaphragm within the subwoofer was fed into the speaker to initiate each experiment. This sound file was created using custom python code from the scipy wavfile package, to yield waveforms of the kind described by eqn (1). To minimize transient effects of the speaker upon application of the sound file, the amplitude of the waveform was increased linearly over 0.25 seconds up to the maximum prescribed amplitude; omitting this ramp-up typically caused the diaphragm and lab-on-a-chip device to “jerk” and fling granular materials into the air. Because the platform and lab-on-a-chip device put additional load and corresponding resistance to motion on the dynamic speaker, the sound file waveform typically had a different ratio of amplitudes B/A and phase difference ϕ than was observed in the actual vibratory waveform (cf.Fig. 1b–d). All vibratory waveforms reported here are those observed experimentally by the high-speed camera.
2.7 Image capture
Two Genaray Spectro LED lights were placed over and behind the device, respectively, to provide lighting for two orthogonal cameras (cf.Fig. 1a). A Nikon Z 50 DSLR camera was positioned directly over the lab-on-a-chip device to image the granular motion. The image capture rate was chosen to precisely match the imposed vibrational frequency, so that the lab-on-a-chip device was imaged in the same location during its periodic motion (i.e., the substrate would appear stationary despite its vibratory motion). For the experiments reported here, the image capture rate was typically 30 or 50 frames per second (fps) to accord with the 30 Hz or 50 Hz vibratory waveforms imposed on the device. A Phantom V311 high speed camera acquiring images at 1600 fps was positioned orthogonally to the platform, to track the horizontal motion x(t) of a small vertical post attached to the lab-on-a-chip device to serve as a fiducial (cf. Video S9†). The DSLR camera recorded the granular motion from above over the duration of each experiment. The high-speed camera recorded up to 2 seconds of the fiducial motion, corresponding to 60 or 100 cycles of the oscillatory motion for 30 or 50 Hz respectively. The early ramp-up period (cf. sound file, above) was excluded from the high-speed video measurements.
2.8 Image and data analysis
All image analysis was performed using standard techniques with the OpenCV package in python. A global threshold was applied to each image to convert it to binary and detect the extent of the granular material. The front location p(t) was defined as the leading edge of the largest contiguous detected object within the channel. Accordingly, individual outlier granules moving slightly faster than average but not in apparent contact with the bulk of the granular fluid did not affect p(t). A recurring feature of the data is that the granular materials exhibited a transient acceleration before reaching a steady velocity (see representative trajectory in Fig. S2†). To exclude the transient, the acceleration profile d2p/dt2 was determined by central finite approximation of the position data and then smoothed using a uniform 10-point running average as a smoothing filter. The onset of the steady velocity dp/dt was assessed using linear regression starting at the time point when the granular fluid front acceleration reached zero, i.e., d2p/dt2 = 0. In the case of single object motion, the centroid of the disk was tracked instead; all subsequent data analysis was performed in a similar fashion. The high-speed videos of the fiducial motion were also analyzed using OpenCV to track the fiducial centroid x(t) vs. time (cf. Video S9†). The vertical displacement of the fiducial was less than one pixel, indicating that the maximum vertical component of the vibration conservatively was less than 29 microns. The parameters A, B, ϕ for the horizontal vibratory waveform (cf.eqn (1)) were found via nonlinear regression using minimized least squares. The parameters γ and ω were verified via Fourier analysis to confirm that the peak amplitudes were at the desired ω and γω modes. Experiments were performed in triplicate for each material type and each applied waveform, with all three measured velocities for each condition presented in Fig. 2b.
3. Results and discussion
3.1 Tunable pumping
The controlled motion of granular materials in millimeter-scale channels is readily demonstrated with a consumer-grade audio system (Fig. 1a). A 3D-printed lab-on-a-chip device is fastened to a platform that is directly connected to the front diaphragm of a standard subwoofer, the type of dynamic loudspeaker typically used to create bass soundwaves between 20 to 200 Hz. When activated the subwoofer emits an audible noise, but more importantly the movement of the diaphragm causes the platform and attached lab-on-a-chip device to vibrate back and forth horizontally, with frequency and amplitude defined by the electrical audio signal sent to the subwoofer.
The resulting motion of granular materials placed in the lab-on-a-chip device depends sensitively on the properties of the electrical audio signal (Fig. 1b–g). Application of a single frequency waveform at 30 Hz (Fig. 1b) causes the particles to slowly drift in both directions away from their initial position in a central loading port (Fig. 1e and Video S1†). This slow and symmetric drift is consistent with prior work examining the behavior of granular materials in response to horizontal vibrations;42,43 the particles are fluidized by the vibration and migrate along the direction of the vibration with zero net displacement of the center of mass. Qualitatively different behavior occurs, however, when certain types of dual-frequency waveforms are applied to the device. Here, application of a vibratory waveform with both 30 Hz and 60 Hz frequencies (Fig. 1c) causes the particles to rapidly pump to the left with a velocity of about −2 cm s−1 (Fig. 1f and Video S2†). Almost no rightward drift out of the central port is observed, and the particles readily flow past a T-junction obstacle. The pumping continues until the central port empties and the particulates accumulate in the two separate exit ports. Importantly, the direction of the flow is reversed simply by applying the negative of the electrical dual-frequency audio signal (Fig. 1d). We emphasize that all other conditions here are identical, with the same type of particles placed in the same starting point in the same device. Application of the negative waveform causes the particles to immediately pump to the right, with little evident leftward drift, and with equal but opposite velocity of +2 cm s−1 (Fig. 1g and Video S3†). Repeated trials show that the direction of motion is always the same for a given polarity of the dual-frequency waveform, i.e., the direction is deterministic, not stochastic. Experiments with a variety of other dry granular materials – including brewer's yeast, crushed ibuprofen powder, boron carbide granules, sodium chloride, baking soda, and soluble coffee grounds – all show that the reversible-direction pumping behavior is quite general (cf.Fig. 2a and Video S4†).
3.2 Theoretical asymptotic velocity
Why would a dual-frequency vibration cause the particles to pump in one direction? We interpret the observations in terms of a temporal symmetry breaking in the frictional driving force, and we also derive a concise analytical prediction for the velocity. In brief, by application of Newton's second law, the velocity v(t) of an individual granule of mass m experiencing a frictional force with a substrate vibrating with a waveform specified by eqn (1) must satisfy| |  | (2) |
Here μ is the coefficient of friction, g is the gravitational acceleration, and x′(t) is the velocity of the vibrating substrate (i.e., the time derivative of eqn (1)). The sign function is +1 if the velocity difference is positive, −1 if it is negative, and 0 if they are the same; physically this function describes how the frictional force causes the object to speed up (slow down) if the substrate is moving faster (slower) than the object. Because of the sign function, eqn (2) is nonlinear and difficult to solve in general. To simplify the problem, we ignore the complicated particle–particle interactions in a moving granular fluid and focus instead on the behavior of an isolated particle placed on a substrate vibrating with waveform given by eqn (1). We also assume that the only force acting on the particle is the frictional interaction with the substrate, and we specify the dimensionless quantities ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) = v/(Aω),
= v/(Aω), ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = tω, and
= tω, and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) = x/A. Rearrangement of Newton's second law (cf.eqn (2)) yields24,37
= x/A. Rearrangement of Newton's second law (cf.eqn (2)) yields24,37| |  | (3) |
Here  is the ratio of kinetic and static coefficients of friction, respectively, and the Friction number
is the ratio of kinetic and static coefficients of friction, respectively, and the Friction number  represents the relative magnitudes of the driving and frictional forces acting on the particle. We initially restrict attention to fast and large vibrations such that the acceleration of the substrate always exceeds the static coefficient of friction necessary for slip between the particle and substrate, i.e., |
represents the relative magnitudes of the driving and frictional forces acting on the particle. We initially restrict attention to fast and large vibrations such that the acceleration of the substrate always exceeds the static coefficient of friction necessary for slip between the particle and substrate, i.e., |![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′′(
′′(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )| > Fr−1 for all
)| > Fr−1 for all ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) . If this condition is satisfied, then we avoid situations where the particle becomes “stuck” to the substrate during some part of the vibratory waveform.
. If this condition is satisfied, then we avoid situations where the particle becomes “stuck” to the substrate during some part of the vibratory waveform.
We separate ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) into its steady component and oscillatory component,
into its steady component and oscillatory component, ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (
(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) =
) = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st +
st + ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) osc(
osc(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ), yielding
), yielding
| | 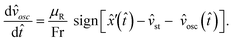 | (4) |
The oscillatory component of the dimensionless velocity therefore varies linearly with time and has slope equal to ±
μRFr
−1, with the sign function determining whether the slope is positive or negative at any particular time. Integration of
eqn (4) with respect to time over the vibratory waveform period
T yields zero on the left-hand-side, and in the limit of asymptotically large friction numbers the oscillatory component
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) osc
osc ∼ Fr
−1 must also vanish, yielding the expression
| | 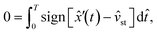 | (5) |
which has the desired steady velocity
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st
st as the only unknown. Notably, in this limit all dependence on Fr and
μR has been removed, meaning that the friction coefficient does not affect the velocity in the limit of sufficiently large and fast vibrations. Solving for
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st
st thus becomes an exercise in finding the roots of
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
′(
t) −
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st
st such that the time integral is satisfied; in simpler terms, over one period the quantity
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
′(
t) −
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st
st must be cumulatively positive over half of the period and cumulatively negative over the other half, such that the signed sum of the durations of each vibratory period spent at positive or negative values is identically zero. Reznik and Canny
37 used analogous arguments to hypothesize a similar result to
eqn (6) for
ϕ = 0. Thus, in the limit Fr ≫ 1 and for the specific case
γ = 2, the predicted steady velocity is
| |  | (6) |
where
A and
B are the amplitudes of the two frequency components, respectively, and
ϕ is the relative phase lag between the two frequency modes (
cf.eqn (1)). A more detailed analysis of
eqn (5) and mathematical proofs of
eqn (6) are provided elsewhere (X. Z., T. H., W. R., & G. M., unpublished work).
A surprising aspect of this prediction is that the velocity is completely independent of the frictional properties of the granule and the substrate, at least in the limit of sufficiently large or fast vibrations, despite the motion being driven entirely by that frictional interaction. Our experimental observations nonetheless strongly accord with this prediction (Fig. 2b). The velocity of individual centimeter-scale steel disks follows the theoretical prediction almost exactly (purple circles) with peak velocities near  . Additional experiments with steel disks further show that the velocity varies as cos
. Additional experiments with steel disks further show that the velocity varies as cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, in accord with the prediction (Fig. S1†). Representative granular media, including sand and crushed ibuprofen powder (blue and red circles in Fig. 2b) likewise follow the theoretical prediction closely. Yeast particles (yellow circles) also generally follow the predicted trend, albeit with maximum values approximately half as large as predicted. This overprediction of the observed velocity for the yeast likely stems from the neglect of vertical motion due to particle collisions; the yeast particles are less dense and tend to bounce off the substrate or other particles and travel momentarily through the air, thus violating the assumption of continuous frictional interaction with the vibrating substrate. Despite this complication, net motion of the predicted magnitude is observed, and the denser granular materials exhibit similar velocities despite differences in their frictional properties (cf. Table S1†).
ϕ, in accord with the prediction (Fig. S1†). Representative granular media, including sand and crushed ibuprofen powder (blue and red circles in Fig. 2b) likewise follow the theoretical prediction closely. Yeast particles (yellow circles) also generally follow the predicted trend, albeit with maximum values approximately half as large as predicted. This overprediction of the observed velocity for the yeast likely stems from the neglect of vertical motion due to particle collisions; the yeast particles are less dense and tend to bounce off the substrate or other particles and travel momentarily through the air, thus violating the assumption of continuous frictional interaction with the vibrating substrate. Despite this complication, net motion of the predicted magnitude is observed, and the denser granular materials exhibit similar velocities despite differences in their frictional properties (cf. Table S1†).
3.3 Mixing and separation granular materials
The ability to pump granular materials in a desired speed and direction enables a variety of “vibrofluidic” operations for lab-on-a-chip devices. For example, different granular materials are readily brought together at Y-junctions for mixing operations (Fig. 3). At higher velocities (Fig. 3a and Video S5†), powders that converge into a straight channel exhibit little cross-stream mixing as they move downstream, remaining mostly segregated as they flow into the exit port; the behavior is qualitatively similar to the behavior of liquids at Y-junctions in microfluidic devices, where cross-stream mixing is governed by a balance between convective and diffusive forces.1 At lower velocities, the powders exhibit more cross-stream mixing (Fig. 3b and Video S6†) and are more mixed at the exit port, reflecting the increased amount of time available for cross-stream diffusion at a lower downstream velocity. To achieve both high speed and high mixing, the device geometry can be modified to include a serpentine geometry following the Y-junction (Fig. 3c and Video S7†). The powders are well-mixed after only a couple S-turns, and appear perfectly mixed when they reach the exit port. Similar serpentine geometries have been heavily explored in the context of microfluidic mixing,44 where it was shown that small but non-zero amounts of transverse momentum within the fluid contribute to chaotic advection and consequent mixing.1 The behavior illustrated in Fig. 3c indicates that analogous effects also occur with granular fluids, and further establishes that powders can be readily mixed on demand at small length scales.
 |
| | Fig. 3 Vibrationally driven mixing of dry granular materials. Representative images of blue- and yellow-colored silica sands, initially placed in separate circular ports at left, after several seconds of vibrational pumping from left to right through a Y-junction. (a) Relatively fast pumping using B/A = 0.23. (b) Relatively slow pumping using B/A = 0.06. (c) Fast pumping using same vibration as in (a) but in a channel with serpentine geometry. Channel width in each is 2 mm; applied frequencies are 30 and 60 Hz in (a) and (c), and 50 and 100 Hz in (b), all negative polarity. See also Video S5–S7.† | |
Another important operation for granular mixtures is separation. The pumping and mixing demonstrated in Fig. 1 through Fig. 3 all pertained in the high Friction number limit, where the vibratory driving force dominates over frictional effects and the velocity is predicted to be independent of the frictional properties of the granules and substrate. Our numerical calculations indicate that the granule velocity is much more sensitive to the frictional properties for vibrations near Fr ≈ 1 (Fig. 4a). At very low friction numbers the average velocity is zero, since the vibration is too weak to cause the granules to displace with respect to the substrate, while at high friction numbers the velocity asymptotically approaches a constant value independent of the Friction number, qualitatively consistent with eqn (6). At intermediate friction numbers, the steady velocity is predicted to be highly sensitive to the ratio of the kinetic and static friction coefficients,  . For vibratory waveforms with
. For vibratory waveforms with 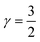 , there are rapid changes in both the amplitude and the direction of the predicted velocity over a very small range in Fr, which means that granules with different frictional properties will move at different velocities in response to the same applied waveform. A key practical consequence of this friction coefficient dependence is that mixtures of granules in theory can be separated using an appropriate vibratory waveform. Indeed, our experimental tests confirm that a vibratory waveform with
, there are rapid changes in both the amplitude and the direction of the predicted velocity over a very small range in Fr, which means that granules with different frictional properties will move at different velocities in response to the same applied waveform. A key practical consequence of this friction coefficient dependence is that mixtures of granules in theory can be separated using an appropriate vibratory waveform. Indeed, our experimental tests confirm that a vibratory waveform with  causes mixtures of granules to separate when they are vibrationally pumped along a straight channel (Fig. 4b and Video S8†). Here, two different granular powders (yellow and black) with similar granular sizes are well mixed and placed in an entry port. Application of the vibratory waveform causes them to move rightward and to clearly separate into yellow-rich powder at the leading edge and black-rich powder at the rear. There are well-established methods for separating granular materials based on their size or density,45 but to our knowledge there are no techniques to separate granules based on their frictional properties, nor any techniques to separate them using devices measured in millimeters. More detailed theoretical analyses that account for particle–particle interactions are needed to predict the frictional separation efficiency, but the results in Fig. 4 provide a clear proof of principle that mixtures of granular materials can be separated at the small lengths scales needed for lab-on-a-chip applications.
causes mixtures of granules to separate when they are vibrationally pumped along a straight channel (Fig. 4b and Video S8†). Here, two different granular powders (yellow and black) with similar granular sizes are well mixed and placed in an entry port. Application of the vibratory waveform causes them to move rightward and to clearly separate into yellow-rich powder at the leading edge and black-rich powder at the rear. There are well-established methods for separating granular materials based on their size or density,45 but to our knowledge there are no techniques to separate granules based on their frictional properties, nor any techniques to separate them using devices measured in millimeters. More detailed theoretical analyses that account for particle–particle interactions are needed to predict the frictional separation efficiency, but the results in Fig. 4 provide a clear proof of principle that mixtures of granular materials can be separated at the small lengths scales needed for lab-on-a-chip applications.
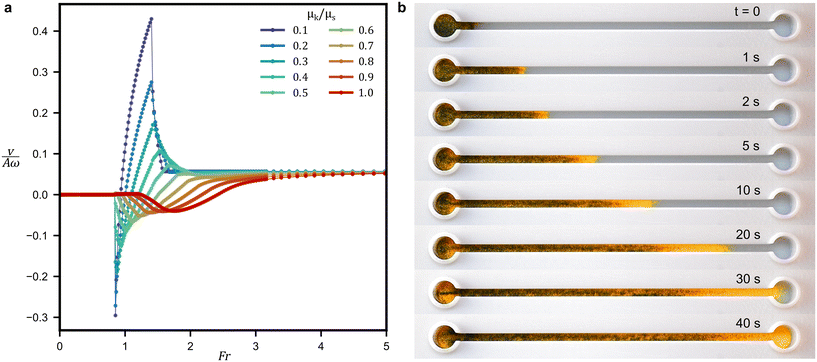 |
| | Fig. 4 Vibrational separation of a dry granular mixture. (a) Numerical simulations of the dimensionless velocity in response to a vibration with γ = 3/2 and B/A = 1 for various ratios of the kinetic and static coefficient of friction, μk/μs. (b) Time-lapse images of a mixture of silica glass sand (yellow) and boron carbide powder (black), moving in response to a vibration with 50 Hz and 75 Hz frequency modes (γ = 3/2) and B/A = 0.13. Channel width is 2 mm. See also Video S8.† | |
4. Conclusions
The above results suggest how liquid and dry handling operations may be combined within one device to achieve the vision of a truly miniaturized laboratory. For example, a ubiquitous laboratory operation involves scooping out a specific mass of a dry powder and placing it into a known mass of liquid to yield a desired solute concentration. To date, such solutions must be prepared by hand prior to insertion into a lab-on-a-chip device, but the vibrational technique established here provides the opportunity to pump desired quantities of a dry granular material into a specific reservoir on a chip, followed by insertion of liquid and dissolution of the granules. Likewise, liquids with mixtures of solutes could potentially be evaporated to leave behind precipitates or crystallized dry materials, which could then be vibrationally pumped out and possibly separated into different material streams. Potential challenges to this vision involve compaction46 and cohesive interactions,47 which are both known to strongly impact the behavior of granular fluids. These complicating effects have not yet been studied in the context of fluidization by horizontal and temporally asymmetric vibrations, so much remains to be investigated regarding how best to control different types of granular motion in lab-on-chip devices.
As a final comment, we note that the underlying physics established here pertain to a large range of length scales and orientations. The predicted velocity of an individual object on the vibrating surface is independent of its mass because both terms in the force balance are proportional to it (cf.eqn (2)). A significant implication is that arbitrarily large collections of objects can be manipulated simply by vibrating the underlying substrate, provided that enough power is available to move both the substrate and the mass resting on it. The pumping, mixing, and separating demonstrated here at small length scales potentially could be applied to larger collections of objects, including agricultural products like fruits or grains,48 mining products like ores or minerals,49 and recyclable materials like scrap metals or plastics.50 Similarly, the underlying physics do not mandate that the bottom surface must vibrate while an object on top moves passively in response; our theory suggests that an active object made to vibrate with two non-antiperiodic frequency modes will translate along a stationary substrate, raising the possibility of autonomous robots and other devices using vibrations as a source of locomotion. The results presented here provide a foundation for considering these more complicated applications.
Author contributions
T. H. and X. Z. performed the experiments with granular fluids. D. A. performed the experiments with the steel disks. X. Z. performed numerical studies, T. H. wrote image analysis code, and X. Z., T. H., and D. A. analyzed data. W. D. R. and G. H. M. conceived the project, performed theoretical derivations, and reviewed data. All authors contributed to experimental design. W. D. R wrote the manuscript, assisted by T. H. with the experimental methods. All authors reviewed and revised the manuscript for accuracy and intellectual content.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
We thank Steven Lucero and the UC Davis TEAM facility for assistance with the 3-D prints. This material is based upon work supported by the National Science Foundation under Grant No. CBET-2125806.
References
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411 CrossRef.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- N. Convery and N. Gadegaard, Micro Nano Eng., 2019, 2, 76–91 CrossRef.
- A. Dalili, E. Samiei and M. Hoorfar, Analyst, 2018, 144, 87–113 RSC.
- P. Cui and S. Wang, J. Pharm. Anal., 2019, 9, 238–247 CrossRef PubMed.
- N. Wongkaew, M. Simsek, C. Griesche and A. J. Baeumner, Chem. Rev., 2019, 119, 120–194 CrossRef CAS PubMed.
- A. Günther and K. F. Jensen, Lab Chip, 2006, 6, 1487–1503 RSC.
- R. L. Hartman and K. F. Jensen, Lab Chip, 2009, 9, 2495–2507 RSC.
- I. Shestopalov, J. D. Tice and R. F. Ismagilov, Lab Chip, 2004, 4, 316–321 RSC.
- P. Yager, T. Edwards, E. Fu, K. Helton, K. Nelson, M. R. Tam and B. H. Weigl, Nature, 2006, 442, 412–418 CrossRef CAS PubMed.
- E. K. Sackmann, A. L. Fulton and D. J. Beebe, Nature, 2014, 507, 181–189 CrossRef CAS PubMed.
- C. D. Chin, V. Linder and S. K. Sia, Lab Chip, 2012, 12, 2118–2134 RSC.
- A. K. Yetisen, M. S. Akram and C. R. Lowe, Lab Chip, 2013, 13, 2210–2251 RSC.
- C. Wang, M. Liu, Z. Wang, S. Li, Y. Deng and N. He, Nano Today, 2021, 37, 101092 CrossRef CAS PubMed.
- S. Yang and J. R. G. Evans, Powder Technol., 2007, 178, 56–72 CrossRef CAS.
- S. Fathollahi, S. Sacher, M. S. Escotet-Espinoza, J. DiNunzio and J. G. Khinast, AAPS PharmSciTech, 2020, 21, 301 CrossRef CAS PubMed.
- T. Vilkner, A. Shivji and A. Manz, Lab Chip, 2005, 5, 140–145 RSC.
- Y. Yuan, K. Yu, H. Zhu and K. F. Ehmann, J. Manuf. Process., 2022, 82, 336–346 CrossRef.
- X. Lu, S. Yang and J. R. G. Evans, Particuology, 2008, 6, 2–8 CrossRef CAS.
- P. Dunst, T. Hemsel and W. Sextro, Sens. Actuators, A, 2017, 263, 733–736 CrossRef CAS.
- S. Denisov, S. Flach and P. Hänggi, Phys. Rep., 2014, 538, 77–120 CrossRef.
- J. G. Freire, C. Cabeza, A. Marti, T. Pöschel and J. A. C. Gallas, Sci. Rep., 2013, 3, 1958 CrossRef PubMed.
- A. Hashemi, M. Tahernia, T. C. Hui, W. D. Ristenpart and G. H. Miller, Physical Review E, 2022, 105, 065001 CrossRef CAS PubMed.
- S. Flach, O. Yevtushenko and Y. Zolotaryuk, Phys. Rev. Lett., 2000, 84, 2358–2361 CrossRef CAS PubMed.
- S. Denisov, S. Flach, A. A. Ovchinnikov, O. Yevtushenko and Y. Zolotaryuk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 041104 CrossRef CAS PubMed.
- A. V. Ustinov, C. Coqui, A. Kemp, Y. Zolotaryuk and M. Salerno, Phys. Rev. Lett., 2004, 93, 087001 CrossRef CAS PubMed.
- S. Denisov, L. Morales-Molina, S. Flach and P. Hänggi, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 063424 CrossRef.
- S. Denisov, L. Morales-Molina and S. Flach, Europhys. Lett., 2007, 79, 10007 CrossRef.
- M. Schiavoni, L. Sanchez-Palencia, F. Renzoni and G. Grynberg, Phys. Rev. Lett., 2003, 90, 094101 CrossRef CAS PubMed.
- R. Gommers, S. Denisov and F. Renzoni, Phys. Rev. Lett., 2006, 96, 240604 CrossRef CAS PubMed.
- A. Eckardt, Rev. Mod. Phys., 2017, 89, 011004 CrossRef.
-
D. Reznik and J. Canny, Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), 1998.
- D. Fleishman, Y. Asscher and M. Urbakh, J. Phys.: Condens. Matter, 2007, 19, 096004 CrossRef.
- C. Viswarupachari, A. DasGupta and S. Pratik Khastgir, J. Vib. Acoust., 2012, 134, 051005 CrossRef.
- J. Nath, S. Das, A. Vishwakarma and A. DasGupta, Phys. D, 2022, 440, 133452 CrossRef.
-
D. Reznik and J. Canny, Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), 1998.
- A. Buguin, F. Brochard and P. G. de Gennes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 19, 31–36 CrossRef CAS PubMed.
- P. Umbanhowar and K. M. Lynch, IEEE Trans. Autom. Sci. Eng., 2008, 5, 537–544 Search PubMed.
- H. M. Beakawi Al-Hashemi and O. S. Baghabra Al-Amoudi, Powder Technol., 2018, 330, 397–417 CrossRef CAS.
-
B. N. J. Persson, Sliding Friction, Springer, Berlin, Heidelberg, 2000 Search PubMed.
- I. Sánchez, F. Raynaud, J. Lanuza, B. Andreotti, E. Clément and I. S. Aranson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 060301 CrossRef PubMed.
- S. M. Khefif, A. Valance and F. Ould-Kaddour, Phys. Rev. E, 2018, 97, 062903 CrossRef CAS PubMed.
- W. Raza, S. Hossain and K.-Y. Kim, Micromachines, 2020, 11, 455 CrossRef PubMed.
- A. Kudrolli, Rep. Prog. Phys., 2004, 67, 209 CrossRef.
- P. Richard, M. Nicodemi, R. Delannay, P. Ribière and D. Bideau, Nat. Mater., 2005, 4, 121–128 CrossRef CAS PubMed.
- A. Castellanos, Adv. Phys., 2005, 54, 263–376 CrossRef CAS.
- T. C. Pearson, Appl. Eng. Agric., 2010, 26, 499–505 Search PubMed.
- X. Luo, K. He, Y. Zhang, P. He and Y. Zhang, Int. J. Miner., Metall. Mater., 2022, 29, 1647–1655 CrossRef.
- G. Wu, J. Li and Z. Xu, Waste Manage., 2013, 33, 585–597 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) + B
sin(ωt) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(γωt + ϕ).
sin(γωt + ϕ).


![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) = v/(Aω),
= v/(Aω), ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = tω, and
= tω, and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) = x/A. Rearrangement of Newton's second law (cf.eqn (2)) yields24,37
= x/A. Rearrangement of Newton's second law (cf.eqn (2)) yields24,37
 is the ratio of kinetic and static coefficients of friction, respectively, and the Friction number
is the ratio of kinetic and static coefficients of friction, respectively, and the Friction number  represents the relative magnitudes of the driving and frictional forces acting on the particle. We initially restrict attention to fast and large vibrations such that the acceleration of the substrate always exceeds the static coefficient of friction necessary for slip between the particle and substrate, i.e., |
represents the relative magnitudes of the driving and frictional forces acting on the particle. We initially restrict attention to fast and large vibrations such that the acceleration of the substrate always exceeds the static coefficient of friction necessary for slip between the particle and substrate, i.e., |![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′′(
′′(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )| > Fr−1 for all
)| > Fr−1 for all ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) . If this condition is satisfied, then we avoid situations where the particle becomes “stuck” to the substrate during some part of the vibratory waveform.
. If this condition is satisfied, then we avoid situations where the particle becomes “stuck” to the substrate during some part of the vibratory waveform.
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) into its steady component and oscillatory component,
into its steady component and oscillatory component, ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (
(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) =
) = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st +
st + ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) osc(
osc(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ), yielding
), yielding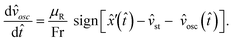
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) osc ∼ Fr−1 must also vanish, yielding the expression
osc ∼ Fr−1 must also vanish, yielding the expression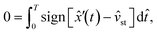
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st as the only unknown. Notably, in this limit all dependence on Fr and μR has been removed, meaning that the friction coefficient does not affect the velocity in the limit of sufficiently large and fast vibrations. Solving for
st as the only unknown. Notably, in this limit all dependence on Fr and μR has been removed, meaning that the friction coefficient does not affect the velocity in the limit of sufficiently large and fast vibrations. Solving for ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st thus becomes an exercise in finding the roots of
st thus becomes an exercise in finding the roots of ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′(t) −
′(t) − ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st such that the time integral is satisfied; in simpler terms, over one period the quantity
st such that the time integral is satisfied; in simpler terms, over one period the quantity ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′(t) −
′(t) − ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) st must be cumulatively positive over half of the period and cumulatively negative over the other half, such that the signed sum of the durations of each vibratory period spent at positive or negative values is identically zero. Reznik and Canny37 used analogous arguments to hypothesize a similar result to eqn (6) for ϕ = 0. Thus, in the limit Fr ≫ 1 and for the specific case γ = 2, the predicted steady velocity is
st must be cumulatively positive over half of the period and cumulatively negative over the other half, such that the signed sum of the durations of each vibratory period spent at positive or negative values is identically zero. Reznik and Canny37 used analogous arguments to hypothesize a similar result to eqn (6) for ϕ = 0. Thus, in the limit Fr ≫ 1 and for the specific case γ = 2, the predicted steady velocity is
 . Additional experiments with steel disks further show that the velocity varies as cos
. Additional experiments with steel disks further show that the velocity varies as cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, in accord with the prediction (Fig. S1†). Representative granular media, including sand and crushed ibuprofen powder (blue and red circles in Fig. 2b) likewise follow the theoretical prediction closely. Yeast particles (yellow circles) also generally follow the predicted trend, albeit with maximum values approximately half as large as predicted. This overprediction of the observed velocity for the yeast likely stems from the neglect of vertical motion due to particle collisions; the yeast particles are less dense and tend to bounce off the substrate or other particles and travel momentarily through the air, thus violating the assumption of continuous frictional interaction with the vibrating substrate. Despite this complication, net motion of the predicted magnitude is observed, and the denser granular materials exhibit similar velocities despite differences in their frictional properties (cf. Table S1†).
ϕ, in accord with the prediction (Fig. S1†). Representative granular media, including sand and crushed ibuprofen powder (blue and red circles in Fig. 2b) likewise follow the theoretical prediction closely. Yeast particles (yellow circles) also generally follow the predicted trend, albeit with maximum values approximately half as large as predicted. This overprediction of the observed velocity for the yeast likely stems from the neglect of vertical motion due to particle collisions; the yeast particles are less dense and tend to bounce off the substrate or other particles and travel momentarily through the air, thus violating the assumption of continuous frictional interaction with the vibrating substrate. Despite this complication, net motion of the predicted magnitude is observed, and the denser granular materials exhibit similar velocities despite differences in their frictional properties (cf. Table S1†).
 . For vibratory waveforms with
. For vibratory waveforms with 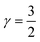 , there are rapid changes in both the amplitude and the direction of the predicted velocity over a very small range in Fr, which means that granules with different frictional properties will move at different velocities in response to the same applied waveform. A key practical consequence of this friction coefficient dependence is that mixtures of granules in theory can be separated using an appropriate vibratory waveform. Indeed, our experimental tests confirm that a vibratory waveform with
, there are rapid changes in both the amplitude and the direction of the predicted velocity over a very small range in Fr, which means that granules with different frictional properties will move at different velocities in response to the same applied waveform. A key practical consequence of this friction coefficient dependence is that mixtures of granules in theory can be separated using an appropriate vibratory waveform. Indeed, our experimental tests confirm that a vibratory waveform with  causes mixtures of granules to separate when they are vibrationally pumped along a straight channel (Fig. 4b and Video S8†). Here, two different granular powders (yellow and black) with similar granular sizes are well mixed and placed in an entry port. Application of the vibratory waveform causes them to move rightward and to clearly separate into yellow-rich powder at the leading edge and black-rich powder at the rear. There are well-established methods for separating granular materials based on their size or density,45 but to our knowledge there are no techniques to separate granules based on their frictional properties, nor any techniques to separate them using devices measured in millimeters. More detailed theoretical analyses that account for particle–particle interactions are needed to predict the frictional separation efficiency, but the results in Fig. 4 provide a clear proof of principle that mixtures of granular materials can be separated at the small lengths scales needed for lab-on-a-chip applications.
causes mixtures of granules to separate when they are vibrationally pumped along a straight channel (Fig. 4b and Video S8†). Here, two different granular powders (yellow and black) with similar granular sizes are well mixed and placed in an entry port. Application of the vibratory waveform causes them to move rightward and to clearly separate into yellow-rich powder at the leading edge and black-rich powder at the rear. There are well-established methods for separating granular materials based on their size or density,45 but to our knowledge there are no techniques to separate granules based on their frictional properties, nor any techniques to separate them using devices measured in millimeters. More detailed theoretical analyses that account for particle–particle interactions are needed to predict the frictional separation efficiency, but the results in Fig. 4 provide a clear proof of principle that mixtures of granular materials can be separated at the small lengths scales needed for lab-on-a-chip applications.
